2. 大连理工大学航空航天学院, 大连116024;
3. 北京宇航系统工程研究所, 北京100076
液体推进火箭是一个复杂的耦合动力学系统,其中的耦合包括姿态控制系统与箭体结构弹性振动的耦合(传统姿控回路),以及箭体结构弹性振动与推进系统的耦合(跷振回路). 随着运载火箭规模的逐渐增大,特别是大型捆绑火箭的出现,箭体的结构动力学特性变得越来越复杂. 一方面,箭体的模态出现密集的低频模态; 另一方面,大量模态的分布呈空间分布,在纵横扭三个方向均存在明显的投影[1, 2]. 结构的某一阶模态可能与推进系统和姿控系统同时出现耦合现象. 例如,土星五、阿里安四和长征二E等火箭,均具有较大的箭体的重量、推力和细长比,推进系统、姿态运动系统和结构振动系统之间的耦合引起了学者的关注. 土星五[3]的一次飞行记录显示,火箭飞行中出现了两个耦合,一个是纵向振动与推进系统耦合产生跷振,振动加速度的幅值为0.72$g$; 另一个为结构纵向振动与横向振动的耦合,在登月舱处产生一个频率为5.3 Hz、幅值为0.65$g$的振动加速度,达到了破坏极限. 肖丽红[4]指出,我国某运载火箭姿控回路的速率陀螺在整个助推段出现高频抖动,而产生抖动的原因是由于助推器的模态、纵向振动与扭转振动之间存在耦合. 因此,对于大型液体火箭,推进系统不仅与结构纵向模态存在耦合,也与结构横向和扭转模态存在耦合. 王建民等[5, 6]提出对于捆绑火箭,必须基于空间模态进行姿控系统稳定性设计和跷振回路设计. 推进系统与结构纵横扭振动的耦合对姿控系统的稳定是一个潜在的威胁. 所以,建立姿控结构推进大回路耦合模型对于研究大型液体捆绑火箭姿控系统稳定性是非常有意义的.
传统的姿控系统设计方法适合用于单根火箭建模[7]. 由于单根火箭的横向振动、扭转振动和纵向振动之间耦合程度很小,因此,这种设计方法可以满足其需要. 随着液体火箭的规模增大,特别是对于箭体结构纵横扭模态存在耦合的大型液体捆绑火箭来说显然不够适用. 文献[5, 6]建立了基于全箭三维模态的有限元分析模型,得到全箭动力学特性,为姿控设计和跷振回路设计提供了理论支持. 文献[1, 2]指出箭体的大型化导致箭体细长比增大以及整箭柔性增加, 在设计姿态控制系统时必须考虑其与结构的弹性振动以及液体晃动的耦合并建立了考虑刚晃 弹以及发动机振动等相互耦合的捆绑火箭姿态动力学模型. 跷振产生的过大的振动加速度会引起火箭上的敏感部件失效, 导致运载效率降低,造成宇航员严重的生理不适. 因此, 该现象受到人们的广泛关注和深入的研究[3, 8, 9, 10, 11, 12, 13, 14]. 在诸多跷振回路建模方法中, 文献[9]提出了一种先进的跷振回路建模方法,利用有限元法将推进系统分为八类基本物理单元, 并推导了每种物理单元的基本方程. 以推进系统节点上的脉动压强、脉动重量位移和结构模态位移为变量, 建立了跷振回路分析模型. 该模型可通过程序自动生成,具有很强的通用性, 已经成功地用于宇宙神二/半人马座[9]和长征二F[11]跷振问题研究中. 但是由于该模型中存在大量代数方程,不但导致计算量增加,而且模型矩阵奇异,不便于时域仿真. 文献[14]在文献[9]的基础之上,基于独立单元的概念,提出了"改进的罗宾模型", 建立了全微分形式的跷振回路分析模型. 与文献[9]中模型相比,维数降低了近一半,大大降低了计算量, 且可直接用于时域仿真.
然而,目前有关姿控回路和跷振回路的耦合建模与分析研究尚不多见. 文献[3]通过时域仿真模拟了土星五出现的横向振动与纵向振动之间的耦合现象. 文献[4] 通过对实验数据的处理分析了运载火箭助推段扭转抖动的原因,提出了进一步研究的方向,但是没有给出具体的解决方案. 文献[15]通过多体动力学建模方法,建立了姿控回路与跷振回路耦合组成的大回路耦合模型,并分析了两者之间的耦合作用. 本文基于文献[1, 2] 和文献[14],深入分析了姿控系统与推进系统之间的耦合机理. 将"改进的罗宾模型"扩展到结构纵横扭振动与推进系统耦合中. 以推进系统对结构纵横扭弹性振动产生的广义力和对姿控回路系数的影响,以及姿控系统对结构弹性振动的影响作为耦合机理,建立了姿控系统和跷振回路的大回路耦合模型. 该模型充分考虑了姿控系统、姿态动力学、结构振动和推进系统的相互耦合作用,可用于大回路机理分析. 且该模型具有非奇异和维数低的优点,可直接用于频域分析和时域仿真. 通过在频域中计算闭环特征值以及在时域中进行变系数仿真,分析了推进系统中重要参数泵增益和蓄压器能量值在合理范围内变化时推进系统对姿控系统的影响.
1 传统的姿控回路模型传统的姿控回路模型包括箭体结构振动系统、姿态动力学系统、控制系统以及观测系统,如图1所示. 控制系统通过伺服机构产生控制输入,作用于箭体的姿态运动以及结构振动,观测系统将姿态运动和结构弹性振动信号作为控制系统的输入,从而产生伺服机构的输入信号.

|
图 1 传统姿控回路结构示意图 Fig. 1 Schematic diagram of traditional attitude control loop model |
根据文献[1, 2],基于混合坐标法,采用质心运动定理和动量矩定理导出火箭的刚体运动方程,采用有限元理论描述捆绑火箭相对于等效刚体的复杂弹性振动进而导出整箭的弹性振动方程. 建模过程中采用的假设包括: 忽略火箭箭体的刚柔耦合效应,刚体运动和弹性振动之间的耦合主要通过结构变形和外力的相互作用实现; 弹性变形为小量,发动机摆角为小量; 偏航角,航迹偏向角,侧滑角滚动角,侧倾角等均为小扰动; 忽略地球自转的影响,得出姿态动力学方程如下:
(1) 俯仰通道姿态运动方程
| $\begin{array}{*{20}{l}} {\Delta \dot \theta = c_1^\varphi \Delta \alpha + c_2^\varphi \Delta \theta + c_4^\varphi \dot \varphi + c_{3x}^\varphi \Delta {\delta _{\varphi {\rm{xj}}}} + c_{3x}^{,,\varphi }\Delta {{\ddot \delta }_{\varphi {\rm{xj}}}} + }\\ {\;\;\;\;\;\;\;\;c_{3z}^\varphi \Delta {\delta _{\varphi {\rm{zt}}}} + c_{3z}^{,,\varphi }\Delta {{\ddot \delta }_{\varphi {\rm{zt}}}} + \sum\limits_{i = 1}^n {\left( {c_{1i}^\varphi {{\dot q}_i} + c_{2i}^\varphi {{\dot q}_i} + c_{3i}^\varphi {{\ddot q}_i}} \right)} + }\\ {\;\;\;\;\;\;\;\;c_1^{,\varphi }\left( {{\alpha _{wp}} + {a_{wq}}} \right) + {{\bar F}_{BY}}} \end{array}$ | (1) |
| $\begin{array}{*{20}{l}} {\Delta \ddot \varphi + b_1^\varphi \Delta \dot \varphi + b_2^\varphi \Delta \alpha + b_{3x}^\varphi \Delta {\delta _{\varphi {\rm{xj}}}} + b_{3z}^{,,\varphi }\Delta {{\ddot \delta }_{\varphi {\rm{xj}}}} + }\\ {\;\;\;\;\;\;\;b_{3z}^\varphi \Delta {\delta _{\varphi {\rm{zt}}}} + b_{3z}^{,,\varphi }\Delta {{\ddot \delta }_{\varphi {\rm{zt}}}} + \sum\limits_{i = 1}^n {\left( {b_{1i}^\varphi {{\dot q}_i} + b_{2i}^\varphi {q_i} + b_{3i}^\varphi {{\ddot q}_i}} \right)} + }\\ {\;\;\;\;\;\;\;b_2^{,\varphi }\left( {{\alpha _{wp}} + {\alpha _{wq}}} \right) = {{\bar M}_{BZ}}} \end{array}$ | (2) |
| $\Delta \varphi = \Delta \alpha + \Delta \theta $ | (3) |
(2) 偏航通道姿态运动方程
| $\begin{array}{*{20}{l}} {\Delta \dot \sigma = c_1^\psi \Delta \beta + c_2^\psi \Delta \sigma + c_4^\psi \dot \psi + c_{3x}^\psi \Delta {\delta _{\psi {\rm{xj}}}} + c_{3x}^{,,\psi }\Delta {{\ddot \delta }_{\psi {\rm{xj}}}} + }\\ {\;\;\;\;\;\;\;\;c_{3z}^\psi \Delta {\delta _{\psi {\rm{zt}}}} + c_{3z}^{,,\psi }\Delta {{\ddot \delta }_{\psi {\rm{zt}}}} + \sum\limits_{i = 1}^n {\left( {c_{1i}^\psi {{\dot q}_i} + c_{2i}^\psi {{\dot q}_i} + c_{3i}^\psi {{\ddot q}_i}} \right)} + }\\ {\;\;\;\;\;\;\;\;c_1^{,\psi }\left( {{\beta _{wp}} + {\beta _{wq}}} \right) + {{\bar F}_{BZ}}} \end{array} $ | (4) |
| $ \begin{array}{*{20}{l}} {\Delta \ddot \psi + b_1^\psi \Delta \dot \psi + b_2^\psi \Delta \beta + b_{3x}^\psi \Delta {\delta _{\psi {\rm{xj}}}} + b_{3x}^{,,\psi }\Delta {{\ddot \delta }_{\psi {\rm{xj}}}} + }\\ {\;\;\;\;\;\;\;\;b_{3z}^\psi \Delta {\delta _{\psi {\rm{zt}}}} + b_{3z}^{,,\psi }\Delta {{\ddot \delta }_{\psi {\rm{zt}}}} + \sum\limits_{i = 1}^n {\left( {b_{1i}^\psi {{\dot q}_i} + b_{2i}^\psi {{\dot q}_i} + b_{3i}^\psi {{\ddot q}_i}} \right)} + }\\ {\;\;\;\;\;\;\;\;b_2^{,\psi }\left( {{\beta _{wp}} + {\beta _{wq}}} \right) = {{\bar M}_{BY}}} \end{array} $ | (5) |
| $ \Delta \psi = \Delta \sigma + \Delta \beta $ | (6) |
(3) 滚转通道姿态运动方程
| $ \begin{array}{l} \Delta \ddot \gamma + {d_1}\Delta \dot \gamma + {d_{3x}}\Delta {\delta _{\gamma {\rm{xj}}}} + {{d"}_{3x}}\Delta {{\ddot \delta }_{\gamma {\rm{xj}}}} + {d_{3z}}\Delta {\delta _{\gamma {\rm{zt}}}} + \\ \;\;\;\;\;\;\;{{d"}_{3z}}\Delta {{\ddot \delta }_{\gamma {\rm{zt}}}} + d_{3x}^\varphi \Delta {\delta _{\varphi {\rm{xj}}}} + \sum\limits_{i = 1}^n {\left( {{d_{1i}}{{\dot q}_i} + {d_{2i}}{q_i} + {d_{3i}}{{\ddot q}_i}} \right)} + \\ \qquad d_{3z}^\varphi \Delta {\delta _{\varphi {\rm{zt}}}} + d_{3x}^\psi \Delta {\delta _{\psi {\rm{xj}}}} + d_{3z}^\psi \Delta {\delta _{\psi {\rm{zt}}}} = {{\bar M}_{BX}} \end{array} $ | (7) |
(4) 弹性振动方程
| $\begin{align} & {{{\ddot{q}}}_{i}}+2{{\xi }_{i}}{{\omega }_{i}}{{{\dot{q}}}_{i}}+\omega _{i}^{2}{{q}_{i}}=D_{1i}^{\varphi }\Delta \dot{\varphi }+D"_{1i}^{\varphi }\Delta \ddot{\varphi }+ \\ & \qquad D_{2i}^{\varphi }\Delta \alpha +D_{2i}^{\varphi }\left( {{\alpha }_{wp}}+{{\alpha }_{wq}} \right)+D_{3xi}^{\varphi }\Delta {{\delta }_{\varphi \text{xj}}}+ \\ & \qquad D"_{3xi}^{\varphi }\Delta {{{\ddot{\delta }}}_{\varphi \text{xj}}}+D_{3zi}^{\varphi }\Delta {{\delta }_{\varphi \text{zt}}}+D_{3zi}^{\varphi }\Delta {{{\ddot{\delta }}}_{\varphi \text{zt}}}+D_{1i}^{\psi }\dot{\psi }+ \\ & \ \ \ \ \ \ \ D"_{1i}^{\psi }\ddot{\psi }+D_{2i}^{\psi }\beta +D_{2i}^{\psi }\left( {{\beta }_{wp}}+{{\beta }_{wq}} \right)+D_{3xi}^{\psi }\Delta {{\delta }_{\psi \text{xj}}}+ \\ & \ \ \ \ \ \ \ D"_{3xi}^{\psi }\Delta {{{\ddot{\delta }}}_{\psi \text{xj}}}+D_{3zi}^{\psi }\Delta {{\delta }_{\psi \text{zt}}}+D_{3zi}^{\psi }\Delta {{{\ddot{\delta }}}_{\psi \text{zt}}}+{{D}_{4i}}\dot{\gamma }+ \\ & \qquad {{{{D}"}}_{4i}}\ddot{\gamma }+{{d}_{3xi}}{{\delta }_{\gamma \text{xj}}}+{{{{d}"}}_{3xi}}{{{\ddot{\delta }}}_{\gamma \text{xj}}}+{{d}_{3zi}}{{\delta }_{\gamma \text{zt}}}+{{{{d}"}}_{3zi}}{{{\ddot{\delta }}}_{\gamma \text{zt}}}+ \\ & \qquad \sum\limits_{j=1}^{n}{\left( {{R}_{ij}}{{q}_{j}}+{{{{R}'}}_{ij}}{{{\dot{q}}}_{j}} \right)}+{{{\bar{Q}}}_{ix}}+{{{\bar{Q}}}_{iy}}+{{{\bar{Q}}}_{iz}}+{{{\bar{Q}}}_{in}} \\ \end{align}$ | (8) |
(5) 测量方程
| $ \left.\begin{array}{l} \Delta \varphi _{gz} = \Delta \varphi - \sum\limits_i {R_{zi} \left( {x_{gz} } \right)q_i } \\ \Delta \dot{\varphi }_{gz} = \Delta \dot{\varphi } - \sum\limits_i {R_{zi} \left( {x_{gz} } \right)\dot{q}_i } \\ \Delta \psi _{gz} = \Delta \psi - \sum\limits_i {R_{yi} \left( {x_{gz} } \right)q_i } \\ \Delta \dot{\psi }_{gz} = \Delta \dot{\psi } - \sum\limits_i {R_{yi} \left( {x_{gz} } \right)\dot{q}_i } \\ \Delta \gamma _{gz} = \Delta \gamma - \sum\limits_i {R_{xi} \left( {x_{gz} } \right)q_i } \\ \Delta \dot{\gamma }_{gz} = \Delta \dot{\gamma } - \sum\limits_i {R_{xi} \left( {x_{gz} } \right)\dot{q}_i } \\ \end{array}\right\} $ | (9) |
其中,$\Delta \varphi$,$\Delta \psi$和$\Delta \gamma$分别为俯仰角、偏航角和滚转角. $\Delta \dot{\varphi }$,$\Delta \dot{\psi }$和$\Delta \dot{\gamma }$分别为俯仰角速度、偏航角速度和滚转角速度,$\Delta \theta$和$\Delta \sigma$分别为速度倾角和航迹偏航角,$\Delta \alpha$和$\Delta \beta$分别为攻角和侧滑角.$q_i$为结构振动广义模态坐标,式(8)中的$q_i$包含了结构的纵横扭振动模态,体现了结构纵横扭振动模态与姿态运动的耦合. 式(1)和式(2)中$\Delta \delta _{\varphi{\rm xj}}$和$\Delta \ddot {\delta }_{\varphi {\rm xj}}$分别俯仰通道芯级发动机摆角和摆角加速度,$\Delta \delta _{\varphi {\rm zt}}$ 和$\Delta \ddot {\delta }_{\varphi {\rm zt}}$分别为助推发动机摆角和摆角加速度,为火箭箭体的控制输入,下标$\varphi$,$\psi$和$\gamma$分别代表俯仰、偏航和滚转通道,xj和zt分别代表芯级和助推,因此可知式(4)$\sim$式(8)对应变量的含义. 方程中$\bar{F}_{BY}$,$\bar{F}_{BZ}$,$\bar{M}_{BY}$,$\bar{M}_{BZ}$和$\bar{M}_{BX}$为干扰力/力矩,$\alpha _{wp}$ 和$\alpha _{wq}$为由于风干扰导致的附加攻角,$\beta _{wp}$和$\beta _{wq}$为由于风干扰导致的附加侧滑角,这些干扰对箭体造成干扰力/力矩. 式(9)中,$R_{zi} \left( {x_{gz} } \right)$和$R_{yi} \left( {x_{gz} } \right)$分别为俯仰通道和偏航通道惯阻平台处第$i$阶弯曲振型斜率,$R_{xi} \left( {x_{gz} } \right)$为滚转通道惯阻平台处第$i$阶扭转振型.$\Delta \varphi _{gz}$ 和$\Delta \dot{\varphi }_{gz}$为测量得到的俯仰角和俯仰角速度,$\Delta \psi _{gz}$和$\Delta \dot{\psi }_{gz}$分别为测量得到的偏航角和偏航角速度,$\Delta \gamma _{gz}$和$\Delta \dot{\gamma }_{gz}$分别为测量得到的滚转角和滚转角速度.
本文的研究是对跷振问题的深入和扩展,重点讨论推进系统与结构系统和姿控系统之间的耦合和影响, 因此本文采用的姿控系统 模型中并没有考虑晃动的影响. 对于小幅晃动的线性化模型[1, 2, 7], 本文的建模方法依然适用. 而贮箱液体大幅度晃动引起的非线性将使火箭的动力学特性变得更加复杂[16], 姿控系统的小扰动线性模型不再适用,已超出了本文的研究范围.
为了方便大回路耦合动力学建模,将姿态动力学方程采用状态空间描述.
引入状态变量
| $ {{ x}}_{\rm a} = [\Delta \varphi ,\Delta \psi ,\Delta \gamma ,{{ q}}^{\rm T},\Delta \theta ,\Delta \sigma ,\Delta \dot{\varphi },\Delta \dot{\psi },\Delta \dot{\gamma }, {{\dot{ q}}}^{\rm T}]^{\rm T}$ |
式(1)$\sim$式(9)描述为
| $ {{ E}}_{\rm a} {{\dot{ x}}}_{\rm a} = {{ A}}_{\rm a} { x}_{\rm a} + {{ B}}_{\rm a} {{ u}}_{\rm a} + {{ w}}_{\rm a}$ | (10) |
| $ {{ y}}_{\rm a} = {{ C}}_{\rm a} {{ x}}_{\rm a} $ | (11) |
其中,${{ E}}_{\rm a}$和${{ A}}_{\rm a}$为系统的状态矩阵,${{ B}}_{\rm a}$为输入矩阵, ${{ C}}_{\rm a}$为观测矩阵,${{ u}}_{\rm a}$为输入向量,${{ w}}_{\rm a}$为干扰向量, ${{ y}}_{\rm a}$为输出向量,分别表示如下
| $\begin{align} & {{E}_{\text{a}}}=\left[\begin{matrix} {{I}_{3}} & 0 & 0 & 0 & 0 \\ 0 & {{I}_{n+2m}} & 0 & 0 & 0 \\ 0 & 0 & {{I}_{2}} & 0 & {{E}_{35}} \\ 0 & 0 & 0 & {{I}_{3}} & {{E}_{45}} \\ 0 & 0 & {{E}_{53}} & {{E}_{54}} & {{E}_{55}} \\ \end{matrix} \right] \\ & {{A}_{\text{a}}}=\left[\begin{matrix} 0 & 0 & 0 & {{I}_{3}} & 0 \\ 0 & 0 & 0 & 0 & {{I}_{n+2m}} \\ {{A}_{31}} & {{A}_{32}} & {{A}_{33}} & {{A}_{34}} & {{A}_{35}} \\ {{A}_{41}} & {{A}_{42}} & {{A}_{43}} & {{A}_{44}} & {{A}_{45}} \\ {{A}_{51}} & {{A}_{52}} & {{A}_{53}} & {{A}_{54}} & {{A}_{55}} \\ \end{matrix} \right] \\ & {{B}_{\text{a}}}=\left[\begin{matrix} 0\ \ \ 0\ \ \ 0 \\ {{B}_{2\varphi }}{{B}_{2\psi }}{{B}_{2\gamma }} \\ 0\ \ \ 0\ \ \ 0 \\ \end{matrix} \right] \\ & {{C}_{\text{a}}}=\left[\begin{matrix} 1\ 0\ 0\ {{C}_{\varphi }}\ 0\ 0\ 0\ 0\ 0\ 0 \\ 0\ 0\ 0\ 0\ 0\ 0\ 1\ 0\ 0\ {{C}_{\varphi }} \\ 0\ 1\ 0\ {{C}_{\psi }}\ 0\ 0\ 0\ 0\ 0\ 0 \\ 0\ 0\ 0\ 0\ 0\ 0\ 0\ 1\ 0\ {{C}_{\psi }} \\ 0\ 0\ 1\ {{C}_{\gamma }}0\ 0\ 0\ 0\ 0\ 0 \\ 0\ 0\ 0\ 0\ 0\ 0\ 0\ 0\ 1\ {{C}_{\gamma }} \\ \end{matrix} \right] \\ \end{align} $ | (12) |
| $\begin{align} & {{u}_{\text{a}}}=[\Delta {{\delta }_{\varphi \text{xj}}},\Delta {{{\ddot{\delta }}}_{\varphi \text{xj}}},\Delta {{\delta }_{\varphi \text{zt}}},\Delta {{{\ddot{\delta }}}_{\varphi \text{zt}}},\Delta {{\delta }_{\psi \text{xj}}},\Delta {{{\ddot{\delta }}}_{\psi \text{xj}}},\\ & \ \ \ \ \ \ \ \Delta {{\delta }_{\psi \text{zt}}},\Delta {{{\ddot{\delta }}}_{\psi \text{zt}}},\Delta {{\delta }_{\gamma \text{xj}}},\Delta {{{\ddot{\delta }}}_{\gamma \text{xj}}},\Delta {{\delta }_{\gamma \text{zt}}},\Delta {{{\ddot{\delta }}}_{\gamma \text{zt}}}{{]}^{\text{T}}} \\ \end{align}$ | (13) |
| $\begin{array}{l} amp;{w_{\rm{a}}} = [0,\;0,\;0,\;{0^{\rm{T}}},\;{0^{\rm{T}}},\;{0^{\rm{T}}},\; - {{\bar F}_{BY}} + c_1^{,\varphi }\left( {{\alpha _{wp}} + {\alpha _{wq}}} \right),\\ amp;\;\;\;\;\;\;\; - {{\bar F}_{BZ}} + c_1^{,\psi }\left( {{\beta _{wp}} + {\beta _{wq}}} \right),\\ amp;\;\;\;\;\;\;\; - {{\bar M}_{BZ}} + b_2^{,\varphi }\left( {{\alpha _{wp}} + {\alpha _{wq}}} \right),\\ amp;\;\;\;\;\;\;\; - {{\bar M}_{BY}} + b_2^{,\psi }\left( {{\beta _{wp}} + {\beta _{wq}}} \right),\\ amp;\;\;\;\;\;\;{{\bar M}_{BX}},\;{{\bar F}_Q},\;{0^{\rm{T}}},{0^{\rm{T}}}{]^{\rm{T}}} \end{array}$ | (14) |
| $ {{ y}}_{\rm a} = \left[{\Delta \varphi _{gz} ,\Delta \dot{\varphi }_{gz} ,\Delta \psi _{gz} ,\Delta \dot{\psi }_{gz} ,\Delta \gamma _{gz} ,\Delta \dot{\gamma }_{gz} } \right]^{\rm T}$ | (15) |
其中,${{ I}}_{n + 2m}$为$n + 2m$维的单位阵,${{ E}}_{ij}$,${{ A}}_{ij}$,${{ B}}_{ij}$和${{ C}}_{ij}$为姿态动力学方程式(1)$\sim$式(9)中对应于${{ x}}_{\rm a}$,${{ u}}_{\rm a}$和${{ y}}_{\rm a}$的系数矩阵,根据${{ x}}_{\rm a}$的排列不难导出. 可以看出,由于状态量排列上的优化,${{ E}}_{\rm a}$具有对角、分块的特性,其求逆的运算可以按照分块矩阵求逆规则来求解.
值得指出的是,式(14)中$\bar{F}_{BY}$,$\bar{F}_{BZ}$,$\bar{M}_{BY}$,$\bar{M}_{BZ}$和$\bar{M}_{BX}$为推力室推力对姿态干扰力/力矩,${{\bar{ F}}}_{Q}$ 为推力室推力对结构振动作用力向量. 推力室产生的推力包括稳态推力和脉动推力,传统上的分析忽略脉动推力的影响. 本文接下来建立的大回路耦合模型将充分考虑脉动推力产生的耦合因素及对稳定性产生的影响.
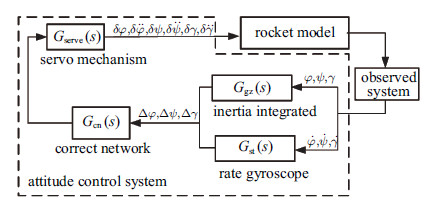
1.2 控制系统模型液体运载火箭的控制系统包括惯阻平台、校正网络和伺服机构[1, 2, 7],如图2中虚线框所示. 测量得到的姿态信号依次经过惯阻平台、校正网络和伺服机构转变为火箭的控制输入,即芯级和助推的发动机摆角及摆角加速度. 惯阻平台、校正网络和伺服机构通常采用传递函数${{G}}\left( s \right)$表示输入输出关系,基本形式为
| $ {{G}}\left( s \right) = \frac{b_n s^n + b_{n - 1} s^{n - 1} + ... + b_1 s + b_0 }{a_n s^n + a_{n - 1} s^{n - 1} + ... + a_1 s + a_0 } $ | (16) |
|
图 2 姿态控制系统示意图 Fig. 2 Schematic diagram of attitude control system |
其中,$s$为拉普拉斯算子,$a_i$和$b_i$多项式的系数.
为了方便大回路耦合系统的建模和分析,本文采用状态空间描述由惯阻平台、校正网络和伺服机构组成 的控制系统(可采用科学计算软件"矩阵实验室(Matlab)"中的函数"dssdata( \ )"实现从传递函数形式到状态空间形式的转换),即
| $ {{ E}}_{\rm c} {{\dot{ x}}}_{\rm c} = {{ A}}_{\rm c} x_{\rm c} + {{ B}}_{\rm c} {{ u}}_{\rm c} $ | (17) |
| $ {{ y}}_{\rm c} = {{ C}}_{\rm c} {{ x}}_{\rm c} $ | (18) |
其中,(${{ E}}_{\rm c}$,${{ A}}_{\rm c}$,${{ B}}_{\rm c}$,${{ C}}_{\rm c}$)为控制系统模型在状态空间的一种描述形式; ${{ x}}_{\rm c}$为控制系统的状态变量; ${{ u}}_{\rm c}$为控制系统的输入,也就是观测系统的输出${{ y}}_{\rm a}$; ${{ y}}_{\rm c}$为控制系统的输出向量,也就是姿态动力系统的输入${{ u}}_{\rm a}$,即
| $ \left. {\begin{array}{l} {{ u}}_{\rm c} = {{ y}}_{\rm a} \\ {{ y}}_{\rm c} = {{ u}}_{\rm a} \\ \end{array}} \right\} $ | (19) |
为了建立大回路耦合模型,需要建立结构纵横扭振动与推进系统耦合的跷振回路模型. 将文献[14] 中的模型扩展到结构的空间模态中,即考虑结构纵横扭振动与推进系统的相互作用. 这种扩展一方面体现在结构纵向和横向振动对推进系统单元中流体压强和重量位移的影响. 另一方面体现在结构系统的振动方程中,即推进系统单元产生的作用力对结构纵横扭模态振动的影响.
2.1 推进系统模型选取推进系统的状态变量为
| $ {{ v}} = [v_1 ,v_2 ,v_3 ,...,v_{N_{\rm p} }]^{\rm T} $ | (20) |
| $ {{ p}}_{{\rm tc}} = [p_{{\rm tco1}} ,p_{{\rm tcf1}} ,...,p_{{\rm tcoN}_{{\rm th}} } ,p_{{\rm tcfN}_{{\rm th}} }]^{\rm T} $ | (21) |
其中,$v_i$为$i$节点上的脉动重量位移. $p_{{\rm tco}j}$和$p_{{\rm tcf}j}$为第$j$ 个推力室中氧路和燃路出口推进剂的脉动压强. 推进系统的方程如式(22)$\sim$式(24) 所示[14].
| $ {{ M}}_{\rm p} {{\ddot{ v}}} + {{ R}}_{\rm p} {{\dot{ v}}} + {{ K}}_{\rm p} {{ v}} + {{ S p}}_{{\rm tc}} = {{ f}}_{{\rm ps}} $ | (22) |
| $ {{\dot{ p}}}_{{\rm tc}} = {{ L p}}_{{\rm tc}} + {{ H\dot{ v}}} $ | (23) |
| $ {{ f}}_{{\rm ps}} = {{ U}}_0 {{ r}}_{\rm p} + {{ U}}_1 {{\dot{ r}}}_{\rm p} + {{ U}}_2 {{\ddot{ r}}}_{\rm p} $ | (24) |
其中,${{ M}}_{\rm p}$,${{ R}}_{\rm p}$,${{ K}}_{\rm p}$,${{ S}}$,${{ L}}$和 ${{ H}}$分别为推进系统的各系数矩阵. ${{ f}}_{{\rm ps}}$为结构纵向和横向振动对推进系统单元的作用力,${{ U}}_0$,${{ U}}_1$和${{ U}}_2$ 分别为各系数矩阵. ${{ r}}_{\rm p}$为推进系统单元管壁上的纵向和横向振动位移向量,体现了结构纵向振动和横向振动对推进系统的影响. ${{ r}}_{\rm p}$与箭体结构的位移${{ r}}$的关系可表示为${{ r}}_{\rm p} = {{ X}}_{{\rm ps}} {{ r}}$,其中${{ X}}_{{\rm ps}}$为转换矩阵. 在空间模态下将结构的振动位移进行模态分解,即${{ r}} ={ \varPhi q}$. 令${{ \varPhi }}_{{\rm ps}} = {{ X}}_{{\rm ps}} {{ \varPhi }}$,因此,结构对推进系统的影响在模态坐标系中可表示为
| $ {{ f}}_{{\rm ps}} = {{ U}}_{\rm 0} {{ \varPhi }}_{{\rm ps}} {{ q}} + {{ U}}_{\rm 1} {{ \varPhi }}_{{\rm ps}} {{\dot{ q}}} + {{ U}}_2 {{ \varPhi }}_{{\rm ps}} {{\ddot{ q}}} $ | (25) |
进一步,将推进系统的变量扩展为
| $ {{ x}}_{\rm p}^{\rm T} = \left[{{{ v}}^{\rm T},p_{{\rm tc}}^{\rm T} ,{{\dot{ v}}}^{\rm T}} \right] $ | (26) |
推进系统的动力学方程式(22),式(23)和式(25)可以描述为如式(27)所示的状态空间形式.
| $ {{ E}}_{\rm p} {{\dot{ x}}}_{\rm p} = {{ A}}_{\rm p} {{ x}}_{\rm p} + {{\tilde{ U}}}_{rq,0} {{ q}} + {{\tilde{ U}}}_{rq,1} {{\dot{ q}}} + {{\tilde{ U}}}_{rq,2} {{\ddot{ q}}} $ | (27) |
其中,
| $ {{ E}}_{\rm p} = \left[{{\begin{array}{*{20}c} {{{ I}}_v } & {{ 0}} & {{ 0}} \\ {{ 0}} & {{{ I}}_{{\rm tc}} } & {{ 0}} \\ {{ 0}} & {{ 0}} & {{{ M}}_{\rm p} } \\ \end{array} }} \right],\ \ A_p = \left[{{\begin{array}{*{20}c} {{ 0}} & {{ 0}} & {{{ I}}_v } \\ {{ 0}} & {{ L}} & {{ H}} \\ { - {{ K}}_{\rm p} } & { - {{ S}}} & { - {{ R}}_{\rm p} } \\ \end{array} }} \right]\\ {{\tilde{ U}}}_{rq,0} = \left[{{\begin{array}{*{20}c} {{ 0}} \\ {{ 0}} \\ {{{ U}}_0 {{ \varPhi }}_{{\rm ps}} } \\ \end{array} }} \right],\ \ {{\tilde{ U}}}_{rq,1} = \left[ {{\begin{array}{*{20}c} {{ 0}} \\ {{ 0}} \\ {{{ U}}_1 {{ \varPhi }}_{{\rm ps}} } \\ \end{array} }} \right],\ \ {{\tilde{ U}}}_{rq,2} = \left[ {{\begin{array}{*{20}c} {{ 0}} \\ {{ 0}} \\ {{{ U}}_2 {{ \varPhi }}_{{\rm ps}} } \\ \end{array} }} \right] $ |
跷振回路模型中,受推进系统作用的全箭纵向、横向和扭转振动方程在空间模态坐标系下的描述为
| $ M_{\rm s} (\ddot{ q} + Z_{\rm s} {{\dot{ q}}} + {{ \varOmega }}_{\rm s} {{ q}}) = {{ \varPhi }}^{\rm T}{{ f}}_{{\rm sp}} $ | (28) |
| $ {{ f}}_{{\rm sp}} = {{ X}}_{{\rm sp}} {{ f}}_{\rm p} = {{ X}}_{{\rm sp}} ( {{ Q}}_0 {{ v}} + {{ Q}}_1 {{\dot{ v}}} + {{ Q}}_2 {{\ddot{ v}}}+\\\qquad {{ Q}}_{\rm p} {{ p}}_{{\rm tc}} + {{ V\ddot { r}}}_{\rm p} ) $ | (29) |
式(29)中${{ f}}_{\rm p}$为推进系统单元对结构系统产生的扰动力向量. 令${{ \varPhi }}_{{\rm sp}} ={{ X}}_{{\rm sp}}^{\rm T} {{ \varPhi }}$,推进系统单元对结构的作用力可表示为
| $ {{ \varPhi }}^{\rm T}{{ f}}_{{\rm sp}} = {{ \varPhi }}^{\rm T}{{ X}}_{{\rm sp}} {{ f}}_{\rm p} = {{ \varPhi }}_{{\rm sp}}^{\rm T}( {{ Q}}_0 {{ v}} + {{ Q}}_1 {{\dot{ v}}} + {{ Q}}_2 {{\ddot{ v}}}+\\\qquad {{ Q}}_{\rm p} {{ p}}_{{\rm tc}} + {{ V \varPhi }}_{{\rm ps}} {{\ddot{ q}}}) $ | (30) |
如1.1节所示,姿态动力学方程中包含了结构的弹性振动方程,因此,式(30)即推进系统对箭体姿态动力学中的结构振动的作用力的表达式.
2.3 跷振回路模型由式(20)$\sim$式(30),选取跷振回路模型的变量
| $ {{\tilde{ v}}} = [{{ v}}^{\rm T},{{ q}}^{\rm T},{{ p}}_{\rm c}^{\rm T} ,{{\dot{ v}}}^{\rm T},{{\dot{ q}}}^{\rm T}]^{\rm T} $ | (31) |
即得到传统的跷振回路的动力学方程
| $ {{ E\dot{\tilde{ v}}}} = {{ A\tilde{ v}}} $ | (32) |
其中,
| $ {{ E}} = \left[{{\begin{array}{*{20}c} {{{ I}}_{\rm w} } & {{ 0}} & {{ 0}} & {{ 0}} & {{ 0}} \\ 0 & {{{ I}}_{\rm q} } & {{ 0}} & {{ 0}} & {{ 0}} \\ 0 & {{ 0}} & {{{ I}}_{{\rm pc}} } & {{ 0}} & {{ 0}} \\ 0 & {{ 0}} & {{ 0}} & {{{ M}}_{\rm p} } & { - {{ U}}_{\rm 2} {{ \varPhi }}_{{\rm ps}} } \\ 0 & {{ 0}} & {{ 0}} & { - {{ \varPhi }}_{{\rm sp}}^{\rm T} {{ Q}}_{\rm 2} } & {{{ M}}_{\rm s} - {{ \varPhi }}_{{\rm sp}}^{\rm T} {{ V \varPhi }}_{{\rm ps}}^{\rm T} } \\ \end{array} }} \right] \\[3mm] {{ A}} = \left[{{\begin{array}{*{20}c} {{ 0}} & {{ 0}} & {{ 0}} & {{{ I}}_{\rm w} } & {{ 0}} \\ {{ 0}} & {{ 0}} & {{ 0}} & {{ 0}} & {{{ I}}_{\rm q} } \\ {{ 0}} & {{ 0}} & {{ L}} & {{ H}} & {{ 0}} \\ { - {{ K}}_{\rm p} } & {{{ U}}_0 {{ \varPhi }}_{{\rm ps}} } & { - {{ S}}} & { - {{ R}}_{\rm p} } & {{{ U}}_1 {{ \varPhi }}_{{\rm ps}} } \\ {{{ \varPhi }}_{{\rm sp}}^{\rm T} {{ Q}}_0 } & { - {{ M}}_{\rm s} {{ \varOmega }}_{\rm s} } & {{{ \varPhi }}_{{\rm sp}}^{\rm T} {{ Q}}_p } & {{{ \varPhi }}_{{\rm sp}}^{\rm T} {{ Q}}_1 } & { - {{ M}}_{\rm s} Z_{\rm s} } \\ \end{array} }} \right] $ |
由式(32)可知,${{ E}}$矩阵在形式上与式(12)中${{ E}}_{\rm a}$矩阵类似,也具有分块对角的特性,因此可根据相同的方法通过分块矩阵的求逆引理简化求逆运算.
可以看出,传统的跷振回路模型主要反映结构系统和推进系统之间的耦合影响,没有考虑推进系统和控制系统之间的耦合影响.
3 姿控与跷振大回路耦合模型姿控与跷振大回路耦合模型由控制系统、姿态动力学系统和推进系统耦合而成,即包含传统的姿控回路和跷振回路两部分,如图3所示. 与传统的姿控回路和跷振回路相比,姿控与跷振大回路耦合模型既考虑了姿态动力学与推进系统的耦合,也考虑了控制系统、姿态动力学与推进系统的耦合.

|
图 3 姿控回路与跷振回路耦合示意图 Fig. 3 Schematic diagram of coupling mechanism of attitude control loop and POGO loop |
姿态动力学与跷振回路的耦合关系可描述如下: (1)姿态动力学中结构的弹性振动对推进系统单元中的流体脉动压强和重量位移产生扰动(如式(27) 所示); (2)推进系统的液路脉动对姿态动力学中结构的弹性振动产生广义脉动力(如式(30)所示),同时,推力室产生的脉动推力对姿态动力学方程中的推力相关系数和干扰力/力矩产生影响,该影响详细陈述如下:
推进系统的脉动推力对姿态运动方程系数的影响导致方程的非线性,由于脉动推力相对于稳态推力幅值很小,因此, 在频域分析中忽略了推力室中的脉动推力对姿态运动方程系数的影响, 只考虑脉动推力对姿态运动方程中干扰力/力矩的影响. 因此,推进系统对姿控回路的影响反映在式(10) 中的干扰力/力矩${{ w}}_{\rm a}$中. 由文献[2]可知,${{ w}}_{\rm a}$中各项表达式与推力的关系是线性的. 因此,可以 将推力分为稳态项和脉动项. 相应的干扰力/力矩${{ w}}_{\rm a}$也可以划分为与稳态推力相关的稳态项${{ w}}_{{\rm a},{\rm s}}$ 和与脉动推力相关的脉动项${{ w}}_{{\rm a},{\rm p}}$,即
| $ {{ w}}_{\rm a} = {{ w}}_{{\rm a},{\rm s}} + {{ w}}_{{\rm a},{\rm p}} $ | (33) |
其中,${{ w}}_{{\rm a},{\rm s}}$为稳态项,与脉动推力无关,可以表述为
| $ {{ w}}_{{\rm a},{\rm s}} = \Big[0,\;0,\;0,\;{{ 0}}^{\rm T},\;{{ 0}}^{\rm T}, \;{{ 0}}^{\rm T},\\ \qquad- \bar{F}_{BY,{\rm s}} + c_1^{'\varphi } \left( {\alpha _{w{\rm p}} + \alpha _{wq} } \right),\\ \qquad- \bar{F}_{BZ,{\rm s}} + c_1^{'\psi } \left( {\beta _{w{\rm p}} + \beta _{wq} } \right),\\ \qquad- \bar{M}_{BZ,{\rm s}} + b_2^{'\varphi } \left( {\alpha _{wp} + \alpha _{wq} } \right),\\ \qquad- \bar{M}_{BY,{\rm s}} + b_2^{'\psi } \left( {\beta _{w{\rm p}} + \beta _{wq} } \right),\\ \qquad\bar{M}_{BX,{\rm s}} ,\;{{\bar{ F}}}_{Q,{\rm s}} ,\;{{ 0}}^{\rm T},{{ 0}}^{\rm T}\Big]^{\rm T} $ | (34) |
对第$i$阶模态振动的作用力$\bar{F}_{Qi,s}$可表示为
| $ \bar{F}_{Qi,s} = D_{2i}^\varphi \left( {\alpha _{w{\rm p}} + \alpha _{wq} } \right) + D_{2i}^\psi \left( {\beta _{w{\rm p}} + \beta _{w{\rm p}} } \right)+\\ \qquad \bar{Q}_{xi,{\rm s}} - \bar{Q}_{yi,{\rm s}} - \bar{Q}_{zi,{\rm s}} - \bar{Q}_{ni,{\rm s}} $ | (35) |
${{ w}}_{{\rm a},{\rm p}}$为脉动项,其表达式为
| $ {{ w}}_{{\rm a},{\rm p}} = \Big[0,\;0,\;0,\;{{ 0}}^{\rm T},\;{{ 0}}^{\rm T},\; {{ 0}}^{\rm T},\; - \bar{F}_{BY,{\rm p}} ,\; - \bar{F}_{BZ,p} ,\\ \qquad - \bar{M}_{BZ,{\rm p}} ,- \bar{M}_{BY,{\rm p}} ,\;\bar{M}_{BX,{\rm p}} ,\;{{\bar{ F}}}_{Q,{\rm p}}^{\rm T} ,\;{{ 0}}^{\rm T},{{ 0}}^{\rm T}\Big]^{\rm T} $ | (36) |
其中,$\bar{F}_{BY,{\rm p}}$,$\bar{F}_{BZ,{\rm p}}$,$\bar{M}_{BY,{\rm p}}$,$\bar{M}_{BZ,{\rm p}}$和$\bar{M}_{BX,{\rm p}}$ 为脉动推力对姿态干扰力/力矩,是发动机脉动推力的线性函数. 其中${{\bar{ F}}}_{Q,{\rm p}}$ 是推进系统液路脉动(包括推进系统中流体的脉动和发动机的脉动推力)对结构振动产生的广义力. 因此, ${{ w}}_{{\rm a},{\rm p}}$可以分为推进系统推力室中的脉动推力和液路脉动产生的干扰力/力矩,即${{ w}}_{{\rm a},{\rm p}} = {{ w}}_{{\rm a},{\rm p}1} + {{ w}}_{{\rm a},{\rm p}2}$. 其中,${{ w}}_{{\rm a},{\rm p}1}$和${{ w}}_{{\rm a},{\rm p}2}$的具体表达式分别为
| $ {{ w}}_{{\rm a},{\rm p}1}^{\rm T} = [0,\;0,\;0,\;{{ 0}}^{\rm T},\;{{ 0}}^{\rm T},\;{{ 0}}^{\rm T},\; - \bar{F}_{BY,p} ,\; - \bar{F}_{BZ,{\rm p}} ,\\ \qquad- \bar{M}_{BZ,{\rm p}} ,- \bar{M}_{BY,{\rm p}} ,\;\bar{M}_{BX,{\rm p}} ,\;{{ 0}}^{\rm T},{{ 0}}^{\rm T},{{ 0}}^{\rm T}]= \tilde{ W}_{F{\rm p}} {{ p}}_{{\rm tc}}\quad \\ {{ w}}_{{\rm a},{\rm p}2}^{\rm T} = [0,0,0,{{ 0}}^{\rm T},{{ 0}}^{\rm T},{{ 0}}^{\rm T},0,0,0,0,0,( {{ M}}_{\rm s}^{ - 1} {{ \varPhi }}_{{\rm sp}}^{\rm T}\cdot$ | (37) |
| $ \qquad\left( {{{ Q}}_0 {{ v}} + {{ Q}}_1 {{\dot{ v}}} + {{ Q}}_2 {{\ddot{ v}}} + {{ Q}}_p {{ p}}_{{\rm tc}} + {{ V \varPhi }}_{{\rm ps}} {{\ddot{ q}}}} \right))^{\rm T},{{ 0}}^{\rm T},{{ 0}}^{\rm T}]=\\ \qquad {{\tilde{ Q}}}_{w,0} {{ v}} + {{\tilde{ Q}}}_{w,1} {{\dot{ v}}} + {{\tilde{ Q}}}_{w,2} {{\ddot{ v}}} + {{\tilde{ Q}}}_{w,p} {{ p}}_{{\rm tc}} + {{\tilde{ V}\ddot { q}}}\quad $ | (38) |
由式(37)和式(38)可知,推进系统产生的干扰力/力矩可表达式为
| $ {{ w}}_{{\rm a},{\rm p}} = {{\tilde{ Q}}}_{w,0} {{ v}} + {{\tilde{ Q}}}_{w,1} {{\dot{ v}}} + {{\tilde{ Q}}}_{w,2} {{\ddot{ v}}}+ \\ \qquad (\tilde { W}_{F{\rm p}} + {{\tilde{ Q}}}_{w,{\rm p}} ){{ p}}_{{\rm tc}} + {{\tilde{ V}\ddot { q}}} $ | (39) |
由式(33)$\sim$式(39)可知,考虑推进系统影响的姿态动力学方程为
| $ {{ E}}_{\rm a} {{\dot{ x}}}_{\rm a} = {{ A}}_{\rm a} x_{\rm a} + {{ B}}_{\rm a} {{ u}} + {{ w}}_{{\rm a},s} + {{\tilde{ Q}}}_{w,0} {{ v}} + {{\tilde{ Q}}}_{w,1} {{\dot{ v}}}+\\ \qquad {{\tilde{ Q}}}_{w,2} {{\ddot{ v}}} + (\tilde { W}_{F{\rm p}} + {{\tilde{ Q}}}_{w,{\rm p}} ){{ p}}_{{\rm tc}} + {{\tilde{ V}\ddot { q}}} $ | (40) |
如式(27)所示,结构的弹性振动直接对推进系统的液路脉动产生影响,而箭体的姿态运动与箭体结构弹性振动的耦合作用对结构弹性振动产生影响,如式(8)所示. 姿控系统通过控制箭体的姿态运动和弹性振动,间接的作用于推进系统的液路脉动.
式(27)和式(40)即姿态动力学与跷振回路耦合模型的方程. 取
| $ {{ x}}^{\rm T} = \left[{{{ x}}_{\rm a}^{\rm T} ,{{ x}}_{\rm p}^{\rm T} } \right] $ | (41) |
其状态空间描述形式为
| $ \left[{{\begin{array}{*{20}c} {{{\tilde{ E}}}_{\rm a} } & {{{ E}}_{{\rm ap}} } \\ {{{ E}}_{{\rm pa}} } & {{{ E}}_{\rm p} } \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {{{\dot{ x}}}_{\rm a} } \\ {{{\dot{ x}}}_{\rm p} } \\ \end{array} }} \right] = \left[{{\begin{array}{*{20}c} {{{ A}}_{\rm a} } & {{{ A}}_{{\rm ap}} } \\ {{{ A}}_{{\rm pa}} } & {{{ A}}_{\rm p} } \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {{{ x}}_{\rm a} } \\ {{{ x}}_{\rm p} } \\ \end{array} }} \right] + \\ \qquad \left[{{\begin{array}{*{20}c} {{{ B}}_{\rm a} } \\ {{ 0}} \\ \end{array} }} \right]{{ u}}_{\rm a}+ \left[{{\begin{array}{*{20}c} {{{ w}}_{{\rm a},s} } \\ {{ 0}} \\ \end{array} }} \right] $ | (42) |
其中
| $ \begin{array}{l} {{\tilde{ E}}}_{\rm a} = {{ E}}_{\rm a} + \left[{{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{\tilde{ V}}},{{ 0}},{{ 0}}} \right] \\ {{ E}}_{{\rm ap}} = \left[{{{ 0}},{{ 0}},- {{\tilde{ Q}}}_{w,2} } \right] \\ {{ E}}_{{\rm pa}} = \left[{{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{\tilde{ U}}}_{rq,2} ,{{ 0}},{{ 0}}} \right] \\ {{ A}}_{{\rm ap}} = \left[{{{\tilde{ Q}}}_{w,0} ,\tilde {W}_{F{\rm p}} + {{\tilde{ Q}}}_{w,{\rm p}} ,{{\tilde{ Q}}}_{w,1} } \right] \\ {{ A}}_{{\rm pa}} = \left[{{{ 0}},{{ 0}},{{ 0}},{{\tilde{ U}}}_{rq,0} ,{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{ 0}},{{\tilde{ U}}}_{rq,1} ,{{ 0}},{{ 0}}} \right] \\ \end{array}$ |
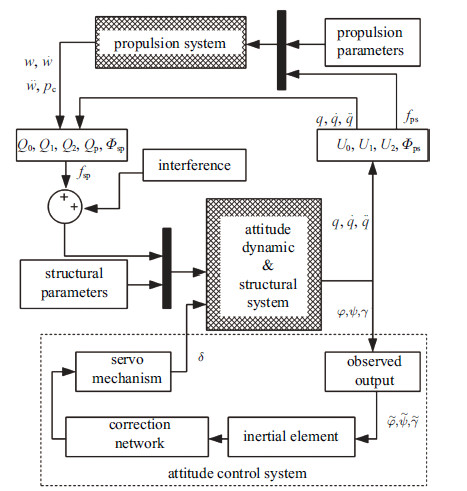
控制系统通过控制力、力矩对箭体的姿态运动产生作用,从而改变其姿态角、抑制其弹性振动,推进系统与结构振动的耦合也会影响控制系统. 在建立姿态动力学与跷振回路耦合模型的基础之上,进一步与式(17)和式(18)所示的姿态控制系统模型耦合可得到如图4所示的姿控结构推进大回路耦合模型. 如1.2节所述,姿控系统和姿态动力学系统构成一个闭环大回路,即姿控系统输入${{ u}}_{\rm c}$ 和输出${{ y}}_{\rm c}$与姿态动力学系统的输入${{ u}}_{\rm a}$和输出${{ y}}_{\rm a}$ 满足式(19).
|
图 4 Simulink 仿真示意图 Fig. 4 Schematic diagram of the simulink |
取大回路耦合模型的状态变量${{\tilde{ x}}}$为
| $ {{\tilde{ x}}} = \left[{{{ x}}_{\rm a}^{\rm T} ,{{ x}}_{\rm p}^{\rm T} ,{{ x}}_{\rm c}^{\rm T} } \right]^{\rm T} $ | (43) |
大回路耦合模型的动力学方程的状态空间描述为
| $ \left[{{\begin{array}{*{20}c} {{{\tilde{ E}}}_{\rm a} } & {{{ E}}_{{\rm ap}} } & {{ 0}} \\ {{{ E}}_{{\rm pa}} } & {{{ E}}_{\rm p} } & {{ 0}} \\ {{ 0}} & {{ 0}} & {{{ E}}_{\rm c} } \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {{{\dot{ x}}}_{\rm a} } \\ {{{\dot{ x}}}_{\rm p} } \\ {{{\dot{ x}}}_{\rm c} } \\ \end{array} }} \right]=\\\qquad \left[{{\begin{array}{*{20}c} {{{ A}}_{\rm a} } & {{{ A}}_{{\rm ap}} } & {{{ B}}_{\rm a} {{ C}}_{\rm c} } \\ {{{ A}}_{{\rm pa}} } & {{{ A}}_{\rm p} } & {{ 0}} \\ {{{ B}}_{\rm c} {{ C}}_{\rm a} } & {{ 0}} & {{{ A}}_{\rm c} } \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {{{ x}}_{\rm a} } \\ {{{ x}}_{\rm p} } \\ {{{ x}}_{\rm c} } \\ \end{array} }} \right] + \left[{{\begin{array}{*{20}c} {{{ w}}_{{\rm a},{\rm s}} } \\ {{ 0}} \\ {{ 0}} \\ \end{array} }} \right] $ | (44) |
| $ {{ y}} = \left[{{\begin{array}{*{20}c} {{{ C}}_{\rm a} } & {{{ C}}_{\rm p} } & {{{ C}}_{\rm c} } \\ \end{array} }} \right]{{\tilde{ x}}} $ | (45) |
式(44)所示的大回路耦合模型中,${{\tilde{ E}}}_{\rm a}$和${{ A}}_{\rm a}$体现了姿态动力学模型与结构弹性振动模型的耦合;${{ E}}_{{\rm ap}}$,${{ E}}_{{\rm pa}}$,${{ A}}_{{\rm ap}}$和${{ A}}_{{\rm pa}}$体现了推进系统模型与姿态动力学模型的耦合;${{ B}}_{\rm a} {{ C}}_{\rm c}$和${{ B}}_{\rm c} {{ C}}_{\rm a}$体现了姿控系统模型与姿态动力学模型的耦合. 大回路模型与跷振回路模型相比,不仅考虑了推进系统对结构振动的影响,还考虑了推进系统与姿态动力学相关系数的影响. 大回路耦合模型的建立不是跷振回路模型、姿态动力学系统模型和控制系统模型的简单组合,而是需要深入分析各模型之间的耦合关系得到.
由式(44)可以看出,由于${{ E}}_{\rm a}$和${{ E}}_{\rm c}$为非奇异阵,因此,大回路耦合模型也是非奇异模型,可直接用于频域分析和时域仿真.
4 算例本节基于第3节建立的大回路耦合模型, 对我国某型号液体捆绑火箭飞行过程中姿态运动、控制系统、结构弹性振动和推进系统的液路脉动之间的耦合进行了频域分析和时域仿真, 以研究大回路的耦合稳定性. 其中控制系统方程和姿态动力学方程的参数为未考虑推进系统影响前的设计参数. 结构系统在分析过程中采用24阶模态,其中箭体俯仰和偏航通道各取横向前8阶模态,纵向取前5阶模态,扭转取前3阶模态. 推进系统中的重要参数泵增益增大为设计值的3倍,蓄压器的能量值比设计值降低50%. 通过求解式(44)的特征值进行频域分析,通过在"矩阵实验室(Matlab)"中建立的"Simulink"(仿真平台)进行时域仿真, 仿真框图如图4所示.
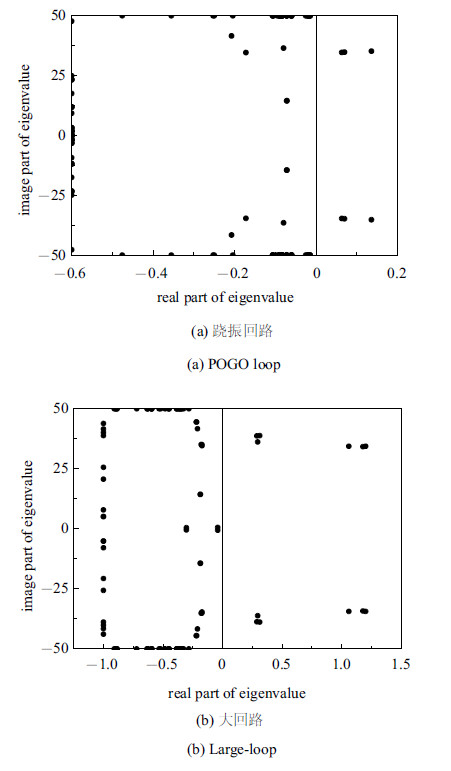
为了研究推进系统对姿控回路的影响,图5给出跷振回路和大回路在第150飞行秒时的特征值分布图. 图5(a)显示推进系统参数变化后,跷振回路出现不稳定的特征值,表明跷振回路失稳. 图5(b)显示,大回路也出现不稳定的特征值,表明泵增益的增大,蓄压器能量值的减小导致大回路失稳.
|
图 5 第150 秒大回路耦合模型特征值分布 Fig. 5 Eigenvalue distribution of the large-loop coupling model at 150th second |
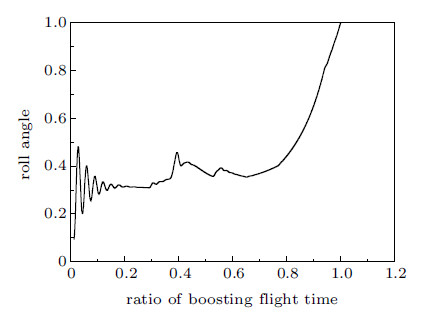
图6给出了未考虑推进系统影响时,姿控回路助推段滚转角的仿真曲线,横纵坐标均除以其最大值进行无量纲化,从仿真曲线可以看出,滚转角在整个助推飞行段是稳定的.
|
图 6 姿控回路模型助推飞行段的滚转角仿真曲线(无量纲) Fig. 6 Simulation curve of roll angle of attitude control model during boosting time (dimensionless) |
在姿控与跷振大回路耦合模型中,推进系统的泵增益增大为设计值的3倍且蓄压器的能量值降低50%时助推 飞行段无量纲化的跷振回路仿真和大回路仿真结果图分别如图7(a)和7(b)所示.

|
图 7 大回路模型助推飞行段滚转角时域仿真曲线(无量纲) Fig. 7 Simulation curve of roll angle of large-loop model during boosting time (dimensionless) |
由图7(a)可以看出,当推进系统中泵增益增大,蓄压器的能量值降低后,跷振回路中助推发动机的振动加速度是发散的,这与图5的特征值分析结果是一致的. 比较图6和图7(b)可以看出,传统姿控回路没有考虑推进系统对姿控回路的影响,因此,无法分析推进系统的参数变化对姿控系统的稳定性的影响. 而基于大回路耦合模型的分析结果显示,推进系统泵增益增大和蓄压器能量值降低后,导致大回路仿真结果中滚转角出现了一个"鼓包",说明推进系统的参数变化,不仅导致了结构的模态失稳,同时也导致了姿态运动不稳定. 该数值算例说明了推进系统与姿控系统之间确实存在耦合,在姿控系统的设计中考虑推进系统的影响是非常有必要的.
5 结 论本文深入研究了姿控回路与跷振回路的耦合机理,以姿态控制系统对箭体姿态动力学和弹性振动的影响以及箭体结构弹性振动与推进系统的耦合作用(跷振)为耦合机理,推导出了姿控与跷振大回路耦合全微分形式的模型. 该模型充分考虑了姿控系统、姿态动力学系统和推进系统的耦合作用,可用于大回路耦合机理研究. 而且该模型为非奇异模型,可直接用于频域分析和时域仿真. 基于该模型,对我国某型号液体捆绑火箭姿控与跷振大回路耦合模型稳定性进行了频域分析和时域仿真,研究了泵增益和蓄压器能量值变化对大回路稳定性的影响,验证了该模型的实用性. 研究得出,泵增益增大为原来的3倍,蓄压器能量值降低50%后,姿控回路和跷振回路之间的耦合作用不但导致结构的模态失稳,而且导致滚转角出现不稳定的"鼓包". 这说明了推进系统确实与姿控系统之间存在不可忽略的耦合. 因此,大型液体捆绑火箭在姿控系统设计时,考虑推进系统对姿控回路的影响是非常有必要的. 液体晃动作为影响火箭姿控系统稳定性的一个重要因素,能否与推进系统产生耦合进而影响火箭大回路的稳定性,将作为我们进一步研究的课题.
| [1] | 杨云飞, 李家文, 陈宇, 等. 大型捆绑火箭姿态动力学模型研究. 中国科学(E辑:技术科学), 2009, 39(3): 490-499 (Yang Yunfei, Li Jiawen, Chen Yu, et al. Study on attitude dynamics modeling for large bundled rockets. Science in China E Series: Technical Science, 2009, 39(3): 490-499 (in Chinese)) |
| [2] | 李家文. 大型捆绑火箭姿态控制系统的建模、设计与分析. [博士论文]. 长沙: 国防科学技术大学, 2011 (Li Jiawen. Modeling, design and analysis of large strap-on launch vehicle's attitude control system.[PhD Thesis].Changsha: National University of Defense Technology, 2011 (in Chinese)) |
| [3] | Rtan RS, Papadopoulos JG, Kiefling LA, et al. A study of saturn As-502 coupling longitidinal structural vibration and lateral bending respnse during boost. Journal of Spacecraft and Rockets, 1970,7(2): 113-118. |
| [4] | 肖利红. 捆绑火箭助推段扭转与纵向振动耦合分析. 航天控制, 2001, 19(2): 14-19 (Xiao Lihong. Coupling analysis of tortional and longitudinal vibration of bundled rocket during boost. Aerospace Control, 2001, 19(2): 14-19 (in Chinese)) |
| [5] | 王建民, 荣克林, 冯颖川 等. 捆绑火箭全箭动力学特性研究. 宇航学报, 2009, 30(3): 821-826 (Wang Jianmin, Rong Kelin, Feng Yingchuan, et al. The research of dynamic characteristics for the strap-on launch vehicle. Journal of Astronautics, 2009, 30(3): 821-826 (in Chinese)) |
| [6] | 王建民, 吴艳红, 张忠 等. 运载火箭全箭动特性三维建模技术. 中国科学:技术科学, 2014, 44(1): 50-61 (Wang Jianmin, Wu Yanhong, Zhang Zhong, et al. Three-dimensional modeling technology for dynamic characteristics of the launch vehicle. Science in China: Technology Science, 2014, 44(1): 50-61 (in Chinese)) |
| [7] | 徐延万. 液体弹道导弹与运载火箭系列---控制系统(上册). 北京: 宇航出版社, 1989 (Xu Yanwan. Liquid Ballistic Missile and Lanuch Vehicle Series-Control System. Beijing: Aerospace Press, 1989 (in Chinese)) |
| [8] | Rubin S. Longitudinal instability of liquid rockets due to propulsion feedback. Journal of Spacecraft and Rockets, 1966, 3(8): 1188-1195. |
| [9] | Oppenheim BW, Rubin S. Advanced POGO stability analysis for liquid rockets. Journal of Spacecraft and Rockets, 1993, 30(3): 360-373. |
| [10] | Zhao ZH, Ren GX, Yu ZW, et al. Parameter study on pogo stability of liquid rockets. Journal of Spacecraft and Rockets, 2011, 48(3): 537-541. |
| [11] | 荣克林, 张建华, 马道远 等. CZ-2F火箭POGO问题研究. 载人航天, 2011, (4): 8-18 (Rong Kelin, Zhang Jianhua, Ma Daoyuan, et al. Research on POGO problem for CZ-2F rocket. Manned Spaceflight, 2011, (4): 8-18 (in Chinese)) |
| [12] | 唐冶, 方勃, 李明明 等. 液体火箭推进系统频率特性的灵敏度分析. 宇航学报, 2014, 35(8): 878-883 (Tang Ye, Fang Bo, LI Mingming, et al. Sensitivity analysis of frequency characteristic for propulsion system in liquid rocket. Journal of Astronautics, 2014, 35(8) :878-883 (in Chinese)) |
| [13] | 徐得元, 郝雨, 杨琼梁 等. 液体火箭纵向耦合振动特性的快速求解方法. 宇航学报, 2014, 35(1): 21-27 (Xu Deyuan, Hao Yu, Yang Qiongliang, et al. Fast matrix algorithm for POGO instability prediction in liquid rocket. Journal of Astronautics, 2014, 35(1): 21-27 (in Chinese)) |
| [14] | Wang QW, Tan SJ, Wu ZG, et al. Improved modelling method of POGO analysis and simulation for liquid rockets. Acta Astronautica, 2015, 107: 262-273. |
| [15] | 胡鹏翔. 液体火箭的多体动力学建模与仿真研究.[博士论文]. 北京: 清华大学, 2012 (Hu Pengxiang. Multibody dynamic modeling and simulation of liquid-propellant launch vehicles.[PhD thesis]. Beijing, Tsinghua University, 2012 (in Chinese)) |
| [16] | Cui DL, Yan SZ, Guo XS, et al. Parametric resonance of liquid sloshing in partially filled spacecraft tanks during the powered-flight phase of rocket. Aerospace Science and Technology, 2014, 35: 93-105. |
2. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China;
3. Beijing Aerospace System Engineering Institute, Beijing 100076, China
 2015, Vol. 47
2015, Vol. 47