将热障涂层(thermal barrier coatings, TBCs)应用到航空发动机涡轮叶片上,能够有效降低基体工作温度,提高发动机效率,延长 使用寿命并减小燃料损耗[1, 2, 3]. 初始热障涂层由三层材料组成:合金基体(superalloy substrate,SUB)、粘结层(bond coat,BC)和陶瓷顶层(ceramic top coat,TC). 在高温环境工作一段时间后,氧透过多孔的陶瓷层在陶瓷层/粘接层界面处发生高温氧化反应,形成一层厚度为几个微米的氧化 层(thermally grown oxide,TGO),从而,热障涂层成为四层结构[4]. 正是由于这一多层结构特性带来的材料参数不匹配以及温度相关等问题,在热载荷作用下,会造成界面区域存在复杂的应力应变 场,并诱发系统出现不稳定,最终导致涂层界面开裂和剥落,影响系统耐久性[5, 6, 7, 8].
结构安定性分析用于研究结构在循环载荷作用下的塑性行为. 与弹性设计相比,极限与安定性分析更能反映结构性态的本质和 安全程度,进一步发挥材料承载能力. 这种分析方法与加载历史无关,可以避免弹塑性增量分析的复杂计算而直接求解. 经典安定分析基础理论是上、下限定理,并采用如下基本假设:(1)材料为理想塑性材料,不考虑强化和软化效应;(2)小变形, 不考虑几何效应;(3)材料服从德鲁克(Drucker)公设,即屈服面是外凸的,而且塑性应变率与屈服面的外法线方向重合; (4)弹性模量是常数,并且温度不影响材料的性质;(5)准静态过程,即加载过程缓慢,没有动力效应;(6)忽略与时间有关 的因素(如速度敏感性、蠕变等). 显然,经典的安定理论难以在实际的工程应用直接使用,必须针对特定的问题进行相应的扩展. 结构在温度载荷作用下,其安定性分析受到如下影响:热应变引起应力场的变化;屈服条件随温度的变化;弹性常数随温度 变化;高温下出现蠕变与松弛等[9, 10]. 因此,对于循环热载荷作用下的热障涂层安定性分析,需要对经典安定定理进行扩展,并考虑温度对材料参数以及屈服强度的影响.
对于相对简单的结构安定问题,有人给出了温度作用下安定定理的一些计算方法和推广形式,求解了桁架和梁结构、圆盘、 环板、多边形板、球形容器等结构在外力和温度作用下的安定问题[11]. 多数研究者从安定定理的本质出发,采用线性规划的方法求解安定极限,有学者基于安定下限定理,考虑了屈服条件对温度 的线性依赖,用线性规划方法对外力和温度荷载联合作用下对称圆柱和球壳结构进行了安定分析[12]. 还有人运用线性匹配方法分析了屈服条件随温度变化的几个算例的安定上限和下限[13]. 对于圆筒结构的安定计算,刘信声等[14]在考虑屈服极限随温度变化的情况下,对内压和温度共同作用的厚壁圆筒进行 了安定分析,给出了几种典型加载模式下的安定范围. 杜森田等[15]在物体承受外载和温度变化的条件下,通过虚设屈服面的建立,导出了一个运动安定定理,温度被隐含在定 理的表达式中. 随后,杜森田等[16]又在此基础上根据经典运动安定定理表达式中各项力学意义借助于载 荷$\!$-$\!$-$\!$温度系数,将温度显含于公 式中并推导了增量破坏准则,避免了复杂的数学规划方法,推导过程中假定材料的屈服强度是与温度呈线性关系的,但事实上, 材料的屈服强度在低温阶段受温度影响很小,仅在高温阶段影响明显,在整个温度载荷作用范围内近似为单一的线性关系可能引 入较大误差. 另一方面,对于热障涂层的安定性,国外部分研究者[17, 18, 19, 20, 21, 22]以氧化层位移变化为重点,提出了``界面位移不稳定'' 的概念,对热障涂层热循环下的位移不稳定进行了试验和仿真分析,指出氧化层生长是诱发位移不稳定性主要因素,并提出了棘 轮效应和粘接层体积减小等可能的不稳定机理. 国内也同样对热障涂层位移不稳定性进行了一些探索,徐颖强等[23]针对多次热循环工作条件下热障涂层的结构不稳定问题, 采用热弹塑性有限元方法,对不规则界面形貌的热障涂层结构进行稳定性分析,分析了不同的粘接层屈服强度对涂层不稳定性的影响. 黄霞等[24]采用``ABAQUS''软件分析了具有表面缺陷的铁铬合金基体界面的位移不稳定性,仿真分析中考虑了氧化生长,并将 计算结果与试验结果进行了对比验证. 热障涂层的安定性不但与界面稳定性相关更与整体结构的安定性密不可分. 朱建国等[1]从残余应力和寿命模型等方面进行了探讨,并指出对于热障涂层寿命的理论研究还有待加强.
本文以热障涂层系统为研究对象,将其外凸和内凹界面微观结构简化为多层圆筒模型,借助机动安定定理,结合特雷斯 卡屈服准则和增量破坏准则,考虑材料参数的温度相关性,建立热障涂层安定极限分析方法,将材料屈服强度随温度变化规律 简化为双线性关系对典型热障涂层安定性进行分析.
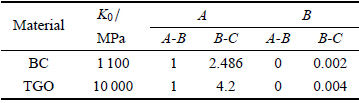
1 圆筒模型安定性分析 1.1 热障涂层界面区圆筒模型在高温环境下服役的热障涂层界面呈现出复杂多变的凹凸形貌特征,如图1(a)所示. 界面形貌的凹凸特征如 图中的区域1(m1)和区域2(m2),可近似为半圆形,将这一形貌特征进行局部抽取即可建立如图1(b)所示圆筒形几何模型. 对于区域1处的内凹模型以及区域2处的外凸模型,由内至外各层代表材料如图1(b)中图例所示,通常,陶瓷层、粘接层和氧 化层的厚度范围分别为130~200μm,30~100μm和5~10μm.
|
图 1 热障涂层界面形貌及几何模型示意图 Fig. 1 Interface geometry of TBCs and schematic of cylinder |
设有理想弹塑性材料构成的单一材料物体,其体积为$V$,在给定面力$ \hat {\pmb p}_i $和位移$ \hat {\pmb u}_i$的表面分别设为$S_P $和$S_u $,而体力为${\pmb Q}_i $,基本方程和边界条件表示为如下形式
| ${\sigma _{ij,j}} + {Q_i} = {\bf{0}}\;\;(V内)$ | (1a) |
| ${\varepsilon _{ij}} = \left( {{u_{i,j}} + {u_{j,i}}} \right)/2\;\;(V内)$ | (1b) |
| ${\sigma _{ij}}{n_j} = {\hat p_i}\;\;({S_P}\;{\rm{上}}{\mkern 1mu} )$ | (1c) |
| ${u_i} = {\widehat u_i}\;\;({S_u}\;{\rm{上}}{\mkern 1mu} )$ | (1d) |
式中,${\pmb \sigma}_{ij}$为应力,${v_{ij}}$为应变,$i,j=1,2,3$.
结合热障涂层多层圆筒模型整体结构,外表面不受面力和位移的约束,不考虑体力,不同材料层构成的界面处存在相应的界面位移 和应变连续条件,因此,设热障涂层多层圆筒模型各层体积为$V_k $,各层内外侧表面$\left( {S_u } \right)_k $,其位移和应变分别为$\left( { \hat{\pmb u }_i } \right)_k $和$\left( { \hat {\pmb \varepsilon }_i } \right)_k $,各层界面间的界面连续条件为应变$\left( { \hat {\pmb \varepsilon }_i } \right)_k $和位移$\left( { \hat {\pmb u }_i } \right)_k $连续,各层内外侧所受压力为$\left( {{\pmb p }_i } \right) _k$. 其中,$k = 1$, 2,3,4表示热障涂层多层圆筒模型中第1,2,3和4层. 从而,涂层多层圆筒的基本方程可化为
| ${\left( {{\sigma _{ij,j}}} \right)_k} = 0\;\;({V_k}\;{\rm{内}})$ | (2a) |
| ${\left( {{\varepsilon _{ij}}} \right)_k} = \left( {{{\left( {{u_{i,j}}} \right)}_k} + {{\left( {{u_{j,i}}} \right)}_k}} \right)/2\;\;({V_k}\;{\rm{内}})$ | (2b) |
| ${\left( {{\varepsilon _{ij}}} \right)_k} = {\left( {{{\hat \varepsilon }_{ij}}} \right)_k}\;\;({\left( {{S_u}} \right)_k}{\kern 1pt} {\kern 1pt} {\rm{上}})$ | (2c) |
| ${\left( {{u_i}} \right)_k} = {\left( {{{\widehat u}_i}} \right)_k}\;\;({\left( {{S_u}} \right)_k}{\rm{上}})$ | (2d) |
下面对热障涂层多层圆筒模型中任意一层圆筒模型进行分析,设
| $\varepsilon _{ij}^{\rm{E}} = {A_{ijkl}}{\sigma _{kl}}{\mkern 1mu} ,\;\varepsilon _{ij}^{\rm{T}} = {a_{ij}}T$ | (3) |
其中,$T$为系统任意位置处实际温度.
在整个变形过程中,忽略黏性效应,总应变$\varepsilon _{ij} $可以表示为
| ${\varepsilon _{ij}} = \varepsilon _{ij}^{\rm{E}} + \varepsilon _{ij}^{\rm{P}} + \varepsilon _{ij}^{\rm{T}}$ | (4) |
式中,$\varepsilon _{ij}^{\rm{E}} = {A_{ijkl}}{\sigma _{kl}}$为弹性应变,${A_{ijkl}}$为对称正定弹性张量,$\varepsilon _{ij}^{\rm{P}}$为塑性应变,$\varepsilon _{ij}^{\rm{T}} = {a_{ij}}T$为热应变,$T$为温度,${a_{ij}}$为热膨胀系数张量.
屈服关系为
| $F = f\left( {{\sigma _{ij}}} \right) - K(T) = 0$ | (5) |
塑性准则为
| \[\dot \varepsilon _{ij}^{\rm{P}} = \dot \lambda \partial F/\partial {\sigma _{ij}}\] | (6) |
当$F = 0,\frac{{\partial f}}{{\partial {\sigma _{ij}}}}{\mathop \sigma \limits^. _{ij}} - \frac{{dK}}{{dT}}\dot T = 0$时,$\dot \lambda \ge 0$
当$F < 0$或$F = 0$但$\frac{{\partial f}}{{\partial {\sigma _{ij}}}}{\mathop \sigma \limits^. _{ij}} - \frac{{dK}}{{dT}}\dot T < 0$时,$\dot \lambda = 0$ 即
| $\dot \lambda \ge 0{\mkern 1mu} ,\;\;\;\dot \lambda F = 0$ | (7) |
塑性比功率为
| \[D = {\sigma _{ij}}\dot \varepsilon _{ij}^{\rm{P}} = D\left( {\dot \varepsilon _{ij}^{\rm{P}},T} \right)\] | (8) |
令
| $K(T) = {K_0}h(T){\mkern 1mu} ,\;\;{K_0} = K\left( 0 \right){\mkern 1mu} ,\;\;h\left( 0 \right) = 1$ | (9) |
根据式(6) $\sim $式(10)可得
| \[D = {D_0}\left( {\dot \varepsilon _{ij}^{\rm{P}}} \right)h\left( T \right)\] | (10) |
此处,$D_0 $是相应于$T =0$时的塑性比功率.
应力可表示为
| ${\sigma _{ij}} = \sigma _{ij}^{\rm{E}} + {\rho _{ij}}$ | (11) |
其中,$\sigma _{ij}^{\rm{E}}$是热弹性应力,将热障涂层视为完全弹性体时外载荷温度所引起的应力. 而${ \pmb\rho }_{ij} $为残余应力,是一个自平衡的应力,它由热障涂层内的瞬时塑性应变场所唯一确定
| ${\rho _{ij}} = {\rm{L}}\left( {\varepsilon _{ij}^{\rm{P}}} \right)$ | (12) |
其中,L 为某一确定的线性积分算子.
为简单起见,仅考虑准静态过程,且假定载荷和温度场是载荷------温度系数$a_s $ ($s =1$,2,$\cdots$,$n_{s}$)的线性化形式,则
| $\sigma _{ij}^{\rm{E}}\left( {r,t} \right) = \sum\limits_{s = 1}^{{n_s}} {{a_s}(t)} \sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)$ | (13) |
式中,$\sigma _{ij}^{{{\rm{E}}_s}}(x)$为${a_s} = 1,{a_i} = 0\left( {j \ne s} \right)$时的热弹性应力场,而$r$为空间坐标,$t$为时间. 于是总应变${\varepsilon _{ij}}$可写为
| ${\varepsilon _{ij}} = {A_{ijkl}}\sigma _{kl}^{\rm{E}} + \varepsilon _{ij}^{\rm{T}} + \varepsilon _{ij}^{\rm{P}} + {A_{ijkl}}{\rho _{kl}}$ | (14) |
其中
| ${A_{ijkl}}\sigma _{kl}^{\rm{E}} + \varepsilon _{ij}^{\rm{T}} = \left( {u_{i,j}^{\rm{E}} + u_{j,i}^{\rm{E}}} \right)/2$ | (15) |
| $\varepsilon _{ij}^{\rm{P}} + {A_{ijkl}}{\rho _{kl}} = \left( {u_{i,j}^{\rm{R}} + u_{ij,i}^{\rm{R}}} \right)/2$ | (16) |
| ${u_i} = u_i^{\rm{E}} + u_i^{\rm{R}}$ | (17) |
式(17)中$u_i^{\rm{E}}$为热弹性位移,$u_i^{\rm{R}}$为残余位移.
$u_i^{\rm{E}}$可表示为
| $u_i^{\rm{E}}\left( {r,t} \right) = \sum\limits_{s = 1}^n {{a_s}\left( t \right)} u_i^{{{\rm{E}}_s}}\left( r \right)$ | (18) |
此处,$u_i^{Es}\left( r \right)$为$a_s = 1$,$a_j = 0\left( {j \ne s} \right)$时的热弹性位移场.
采用上述描述方法,系数$a_s $的变化范围同时规定了机械载荷和温度载荷的变化界限,即
| ${p_i}\left( {r,t} \right) = \sum\limits_{s = 1}^n {{a_s}\left( t \right)} p_i^s\left( r \right){\mkern 1mu} ,\;\;r \in {S_p}$ | (19) |
| ${Q_i}\left( {r,t} \right) = \sum\limits_{s = 1}^n {{a_s}\left( t \right)} Q_i^s\left( r \right){\mkern 1mu} ,\;\;r \in V$ | (20) |
| $T\left( {r,t} \right) = \sum\limits_{s = 1}^n {{a_s}\left( t \right)} {T^s}\left( r \right){\mkern 1mu} ,\;\;r \in V$ | (21) |
设在周期性温度作用下,$\dot \varepsilon _{ij}^{*{\rm{P}}}$为动力允许的塑性应变率循环,即为一个周期内的塑性应变率,而对应的塑性应变增量为
| $\Delta \dot \varepsilon _{ij}^{ * {\rm{P}}} = \int_{{t_0}}^{{t_0} + \tau } {\dot \varepsilon _{ij}^{ * {\rm{P}}}} = \frac{1}{2}\left( {u_{i,j}^ * + u_{j,i}^ * } \right)$ | (22) |
其中$u_i^ * = 0({S_u}上)$.
机动安定定理可描述为:如果在一个循环周期内存在某个载荷------温度路径${a_s}(t) \in G$和塑性应变率循环$\dot \varepsilon _{ij}^{ * {\rm{P}}}$,使得(a) 式(22)成立,(b) 下式成立
| \[\begin{array}{*{20}{l}} {\int_{{t_0}}^{{t_0} + {\tau _s}} {\left[ {\sum\limits_{s = 1}^n {{a_s}\left( t \right)} \left( {\int_V {Q_i^s\dot u_i^*dV} + \int_{{S_P}} {\hat p_i^s\dot u_i^*dS} } \right) + } \right.\left. {\int_V {{a_{ij}}T\dot \rho _{ij}^*dV} } \right]} dt > }\\ {\int_{{t_0}}^{{t_0} + \tau } {\int_V {D\left( {\dot \varepsilon _{ij}^{*{\rm{P}}},T} \right)} dVdt} } \end{array}\] | (23) |
则结构将不安定. 其中,$G$为$n$维空间内所给定的载荷------温度系数$a_s $的变化区域,$\rho _{ij}^ * $表示与塑性应变场$\dot \varepsilon _{ij}^{ * P}$关联的残余应力场.
下面将式(23)进一步简化
| $\begin{array}{l} \sigma _{ij}^E = \sigma _{ij}^{EE} + \rho _{ij}^{\rm{T}} = \\ \sum\limits_{s = 1}^{{n_s}} {{a_s}(t)} \left( {\sigma _{ij}^{{\rm{EEs}}}(x) + \rho _{ij}^{{\rm{Ts}}}(x)} \right) \end{array}$ | (24) |
式中的$\sigma _{ij}^{{\rm{EEs}}}$是由于外载${\hat p_i},{Q_i}$引起的,在${a_s} = 1,{a_j} = 0\left( {j \ne s} \right)$时所确定的弹性应力场$\sigma _{ij}^{{\rm{EE}}}$,而$\rho _{ij}^{{{\rm{T}}_s}}$是由于温度$T$引起的在$a_s = 1$,$a_j = 0\left( {j \ne s} \right)$时所确定的残余应力场.
借助虚功原理,式(23)左端第3项可化为
| \[\int_V {{a_{ij}}T\dot \rho _{ij}^*dV} = \int_V {\varepsilon _{ij}^{\rm{T}}\dot \rho _{ij}^*dV} = - \int_V {\rho _{ij}^{\rm{T}}{A_{ijkl}}\dot \rho _{kl}^*dV} = \int_V {\rho _{ij}^{\rm{T}}\dot \varepsilon _{ij}^{*{\rm{P}}}dV} \] | (25) |
式(23)中,左端前两项通过虚功原理,借助式(8),式(24)和式(25),有
| \[\begin{array}{*{20}{l}} {\int_{{t_0}}^{{t_0} + \tau } {\int_V {\sigma _{ij}^{\rm{E}}\left( {r,t} \right)\dot \varepsilon _{ij}^{*{\rm{P}}}\left( {r,t} \right)dVdt > } } }\\ {\int_{{t_0}}^{{t_0} + \tau } {\int_V {D\left( {\dot \varepsilon _{ij}^{*{\rm{P}}},t} \right)dVdt} } } \end{array}\] | (26) |
利用式(26)可以获得热障涂层四层圆筒各层的安定判断准则,即4个类似于式(26)的不等式,分别对应热障涂层多层圆筒 模型中的陶瓷层、氧化层、粘接层和基体.
为简化起见,考虑$h(T)$为$T$的线性函数,即
| $h(T) = A - BT$ | (27) |
此处$A$和$B$为材料常数. 则有
| \[\begin{array}{*{20}{l}} {D\left( {\dot \varepsilon _{ij}^{*{\rm{P}}},T} \right) = {D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right)h\left( T \right) = }\\ {A{D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right) - BT{D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right)} \end{array}\] | (28) |
从上述安定定理,可得结构安定的必要条件,即,若结构安定,则对任意一个${a_s} \in G,\dot \varepsilon _{ij}^{*{\rm{P}}}$,有
| \[\begin{array}{*{20}{l}} {\eta \int_{{t_0}}^{{t_0} + \tau } {\int_V {\left[ {\sigma _{ij}^{\rm{E}}\left( {r,t} \right)\dot \varepsilon _{ij}^{*{\rm{P}}}\left( {r,t} \right) + BT{D_0}\left( {\dot \varepsilon _{ij}^{*P}} \right)} \right]dVdt \le } } }\\ {\int_{{t_0}}^{{t_0} + \tau } {\int_V {A{D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right)dVdt} } } \end{array}\] | (29) |
式中,$\eta $为安全系数且$\eta \ge 1$.
下面利用增量破坏准则处理对时间的积分.
根据式(22)得
| $\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) = \varepsilon _{ij}^{ * {\rm{P}}}\left( {r,{t_0} + \tau } \right) - \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)$ | (30) |
根据增量破坏的过程,按其概念,如果存在标量函数$\lambda \left( {r,t} \right)$,使
| $\varepsilon _{ij}^{ * {\rm{P}}}\left( {r,t} \right) = \lambda \left( {r,t} \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)$ | (31) |
其中
| $\dot \lambda \left( {r,t} \right) \ge 0{\mkern 1mu} ,\;\lambda \left( {r,{t_0}} \right) = 0{\mkern 1mu} ,\;\lambda \left( {r,{t_0} + \tau } \right) = 1$ | (32) |
则,注意到塑性比功率${D_0}\left( {\dot \varepsilon _{ij}^{ * {\rm{P}}}} \right)$是塑性应变率$\dot \varepsilon _{ij}^{ * {\rm{P}}}$的一次齐次函数,利用式(31)和式(32)得
| \[\begin{array}{*{20}{l}} {\int_{{t_0}}^{{t_0} + \tau } {{D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right)dt} = }\\ {\int_{{t_0}}^{{t_0} + \tau } {{D_0}\left( {\dot \lambda \Delta \varepsilon _{ij}^{*{\rm{P}}}} \right)dt = {D_0}\left( {\Delta \varepsilon _{ij}^{*{\rm{P}}}} \right)} } \end{array}\] | (33) |
根据式(13),式(21)和式(23),取$\eta = 1$,式(29)可写为
| \[\begin{array}{*{20}{l}} {\int_{{t_0}}^{{t_0} + \tau } {\int_V {\sum\limits_{s = 1}^n {{a_s}\left( t \right)} } } \left[ {\sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)\dot \varepsilon _{ij}^{*P}\left( {r,t} \right) + } \right.}\\ {\left. {B{T^s}\left( r \right){D_0}\left( {\dot \varepsilon _{ij}^{*{\rm{P}}}} \right)} \right]dV{\rm{d}}t \le }\\ {\int_V {A{D_0}\left( {\Delta \varepsilon _{ij}^{*{\rm{P}}}} \right)dV} } \end{array}\] | (34) |
考虑到式(31),式(32)与${D_0}\left( {\dot \lambda \Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right) = \dot \lambda {D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)$,则式(34)左端积分改写为
| $\begin{array}{l} \int_{{t_0}}^{{t_0} + \tau } {\int_V {\sum\limits_{s = 1}^n {{a_s}\left( t \right)} } } \left[{\sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)\dot \lambda \left( {r,t} \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) + } \right.\\ \left. {B{T^s}\left( r \right)\dot \lambda \left( {r,t} \right){D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)} \right)} \right]dVdt \end{array}$ | (35) |
另一方面,对于给定的增量破坏机构$\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( x \right)$,如函数$\lambda \left( {r,t} \right)$按以下方式选取,即在${a_s}(t)$的变化区域$G$内,仅当表达式
| $\begin{array}{l} \sum\limits_{s = 1}^n {{a_s}(t)} \left[{\sigma _{ij}^{Es}\left( r \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) + } \right.\\ \left. {B{T^s}\left( r \right)\dot \lambda \left( {r,t} \right){D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)} \right)} \right] \end{array}$ | (36) |
取极大值时,才有$\dot \lambda \left( {x,t} \right) \ne 0$,则式(34)的左端可取其最大值,则令
| $\begin{array}{l} f\left( r \right) = \mathop {\max }\limits_{{a_s} \in G} \{ \sum\limits_{s = 1}^n {{a_s}(t)} \left[{\sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) + } \right.\\ \left. {B{T^s}\left( r \right){D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)} \right)} \right]\} \end{array}$ | (37) |
与${D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)} \right)$相等就得到增量破坏准则,从而增量破坏准则最终可表示为
| $\int_V {f\left( r \right)dV} = \int_V {A{D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)dV} $ | (38) |
将给定的载荷-----温度系数$a_s $的变化区域$G$定义为一组不等式
| $a_s^ - \le {a_s} \le a_s^ + $ | (39) |
从而,式(38)可改写为
| $\int_V {\sum\limits_{s = 1}^n {{\beta _s}\left( r \right){y_s}\left( r \right)dV} } = \int_V {A{D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)dV} $ | (40) |
式中${\beta _s}\left( r \right)$和${y_s}\left( r \right)$分别由下式给出
| $\left. \begin{array}{l} {\beta _s}(r) = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} a_s^ + ,{y_s}(r) > 0\\ a_s^ - ,{y_s}(r) < 0 \end{array} \end{array}} \right.\\ {y_s}(r) = \sigma _{ij}^{{{\rm{E}}_s}}(r)\Delta \varepsilon _{ij}^{ * {\rm{P}}}(r) + B{T^s}(r){D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}(r)} \right)n \end{array} \right\}$ | (41) |
利用式(40)和式(41)即可求得安定极限.
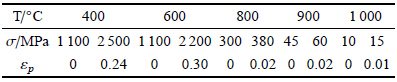
2 热障涂层安定性分析 2.1 材料参数及载荷粘接层不同温度下塑性参数如表1所示[25, 26],图2为氧化层屈服强度随温度变化的曲线图[27],显 然,粘接层和氧化层低温段的屈服强度受温度影响较小,但高温下的屈服强度显著降低,因此,必须考虑材料塑性的影 响且在整个载荷域内将其简化为单一的线性关系并不准确. 陶瓷层和基体按弹性材料计算,具体材料参数详见文献[28]. 考虑热障涂层各层材料参数的温度相关性,将各项物性参数进行参数拟合,使其成为外载荷$T$的函数,以便于利用解析 数学模型进行安定极限的求解.
实际工作中热障涂层陶瓷层外侧受到循环热载荷作用,而基体内侧通以冷却气体以降低系统温度.
为了研究热障涂层的安定问题,热应力计算条件为:在陶瓷层外侧施加1000${^\circ}$C恒温,而基体内侧设定为25${^\circ}$C恒温,考虑稳态传热过程.
从而,对于载荷$\!$-$\!$-$\!$温度系数$a_s $,温度载荷$T$范围为(25${^\circ}$C$\sim$1000${^\circ}$C),其$\Delta T$范围为(0${^\circ}$C$\sim$975${^\circ}$C),此时温度系数$a_s $对应的范围为(0$\sim$1).
设氧化层、粘接层均服从特雷斯卡准则,即
| $\max \left\{ {|{\sigma _r}|,|{\sigma _\phi }|,|{\sigma _\phi } - {\sigma _r}|} \right\} = 2K(T)$ | (42) |
式中
| $K(T) = {K_0}\left( {A - BT} \right){\mkern 1mu} ,\quad 2{K_0} = {\sigma _s}$ | (43) |
式中,$A,B$的含义与式(27)相同.
2.2 屈服强度与温度的双线性模型本文研究对象为小变形模型,物体任意位置处的径向速度为 $\dot u\left( r \right) = \frac{{\dot c}}{r}$.
考虑到增量情况,有
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} \Delta {\varepsilon _r} = \int_{{t_0}}^{{t_0} + \tau } {{{\dot \varepsilon }_r}dt} = \int_{{t_0}}^{{t_0} + \tau } {\frac{{\partial \mathop u\limits^. }}{{\partial r}}dt} = - \frac{{\Delta c}}{{{r^2}}}\\ \Delta {\varepsilon _\varphi } = \int_{{t_0}}^{{t_0} + \tau } {{{\dot \varepsilon }_\varphi }dt} = \int_{{t_0}}^{{t_0} + \tau } {\frac{{\mathop u\limits^. }}{r}dt} = \frac{{\Delta c}}{{{r^2}}} \end{array} \end{array}} \right\}$ | (44) |
式中$\Delta c > 0$. 相应于上述塑性变形状态的${D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)$可以表示为如下形式
| $\begin{array}{l} {D_0} = {\sigma _r}\left( { - \frac{{\Delta c}}{{{r^2}}}} \right) + {\sigma _\varphi }\left( {\frac{{\Delta c}}{{{r^2}}}} \right) = \\ \frac{{\Delta c}}{{{r^2}}}\left( {{\sigma _\varphi } - {\sigma _r}} \right) = 2{K_0}\frac{{\Delta c}}{{{r^2}}} \end{array}$ | (45) |
为计算式(40)左端,需要计算${y_s}\left( r \right)$中$\sigma _{ij}^{{{\rm{E}}_s}}\left( x \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}(x)$,经计算整理得
| $\begin{array}{l} \sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) = \\ \sigma _r^{\rm{E}}\left( r \right)\Delta {\varepsilon _r}\left( r \right) + \sigma _\phi ^{\rm{E}}\left( r \right)\Delta {\varepsilon _\phi }\left( r \right) \end{array}$ | (46) |
式中$\sigma _r^{\rm{E}}\left( r \right)$和$\sigma _\phi ^{\rm{E}}\left( r \right)$为圆筒径向和环向应力分量,可由文献[29]得到.
由于${y_s}\left( r \right) = \sigma _{ij}^{{{\rm{E}}_s}}\left( r \right)\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right) + B{T^s}\left( r \right){D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}\left( r \right)} \right) > 0$始终成立,因此${\beta _s}\left( r \right) = 1$.
由式(40)稍作调整,变换得到
| $\begin{array}{l} {A_{\rm{D}}} = \int_V {} {D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)dV - \int_V {} \sum\limits_{s = 1}^n {} _{}^{}{\beta _s}\left( r \right){y_s}\left( r \right)dV = \\ \int_{{a_i}}^{{a_{i + 1}}} {{D_0}\left( {\Delta \varepsilon _{ij}^{ * {\rm{P}}}} \right)rdr} - \int_{{a_i}}^{{a_{i + 1}}} {\sum\limits_{s = 1}^n {{\beta _s}\left( r \right){y_s}\left( r \right)rdr} } \end{array}$ | (47) |
式(47)中各项分量的表达式均能得到,将其替换为温度载荷$T_{\rm w}$的函数,此时式(47)变为外载$T_{\rm w }$的一元函数. 由于函数$A_{\rm D}$为减函数,且当温度为初始温度25${^\circ}$C时其值大于零,因此,函数$A_{\rm D}$值随着温度$T_{\rm w} $的增大而逐渐减小,当$A_{\rm D}$值等于零时,对应温度$T_{\rm w}$即为所求安定极限.
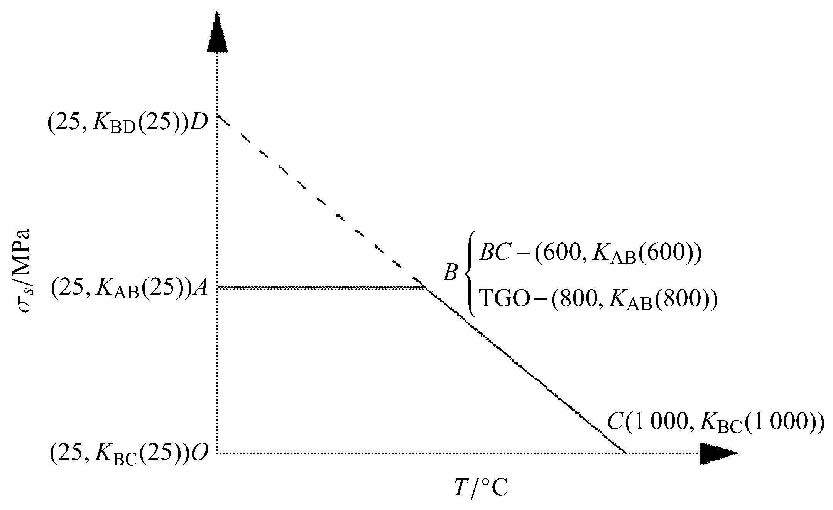
如图3所示,实际材料的屈服强度并非在整个温度范围内呈单一线性关系,而是在低温段影响小,高温段 影响较大,根据实际涂层氧化层和粘接层材料参数,将其屈服强度随温度的变化曲线近似为双线性,即,分为低温和高温段 两部分,第1段为平行于水平坐标轴的平直线低温段($A$-$B$段),第2部分为高温斜直线段($B$-$C$段).
|
图 3 屈服强度与温度双线性简化关系示意图 Fig. 3 Simplified schematic between yield strength and temperature |
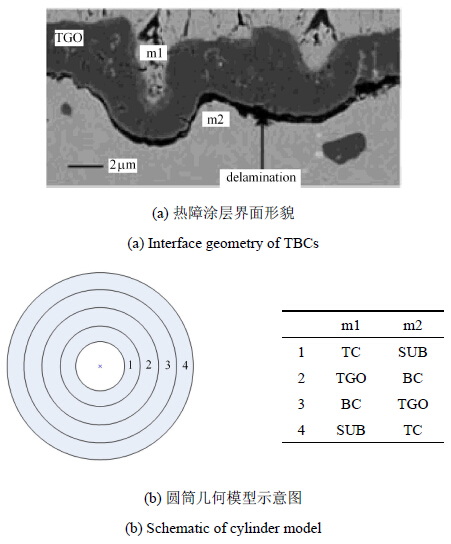
从而,结合屈服准则表达式,式(43)中$K_0 $,$A$和$B$如表2所示.
| 表 2 屈服特性参数转换结果 Table 2 Transform results of yield strength |
热障涂层材料的这一屈服特性增加了式(47)求解复杂程度,下面采用补偿变换法 进行计算:
(1) 如图3所示,图中$B,C$和$D$点位于同一直线,$O,A$和$D$点位于同一直线且直线$AB$平行于横坐标轴$OC$. 设材料屈服特 性随温度的变化关系服从$D$-$B$-$C$直线关系,分别沿$D$-$B$线段和$D$-$B$-$C$线段计算式(47),此时式(44)中$K_0 $, $A$和$B$唯一,计算得到该情况下的式(47)结果,分别记为$A_{\rm D}$1和$A_{\rm D}$2;
(2) 设材料屈服特性随温度的变化关系服从$A$-$B$直线关系,沿$A$-$B$线段计算式(47),此时式(43)中$K_0 $和$B$唯一,计算得到该情况下的式(47)结果记为$A_{\rm D}$3;
(3) 由步骤1和步骤2得到的$A_{\rm D}$1,$A_{\rm D}$2和$A_{\rm D}$3计算式(43)沿$A$-$B$-$D$线段积分结果,为
| ${A_{\rm{D}}} = {A_{\rm{D}}}2 - ({A_{\rm{D}}}1 - {A_{\rm{D}}}3)$ |
(4) 令$A_{\rm D} = 0$,求得$T_{\rm w} $,即为安定极限.
2.3 安定性分析结果结合传统弹性设计方法,基于圆筒模型研究基体曲率半径、不同层厚度等因素下,内凹和外凸模型的安定极限,进行热障涂层 结构安定性分析.
(1) 圆筒模型基体曲率对涂层安定极限的影响
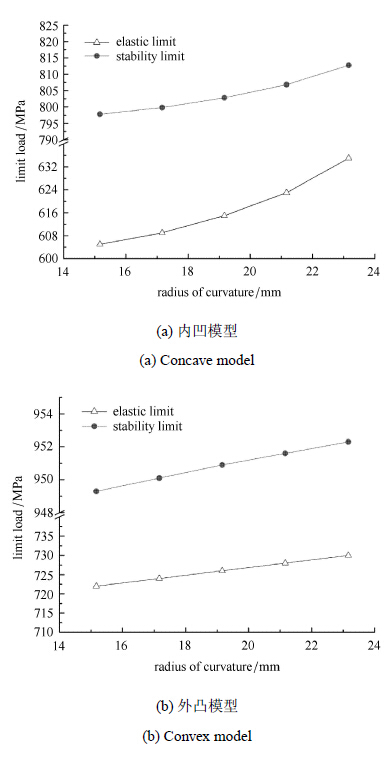
图4(a)和图4(b)分别为圆筒涂层模型基体半径变化对热障涂层内凹和外凸模型弹性极限以及安定极限的影响.图中横轴坐标为基 体上远离圆筒模型轴线的最外侧的曲率半径值,纵轴为相应曲率半径下的系统极限载荷. 由图可以看出,系统的安定极限明显大于其弹性极限. 随着基体半径的增大,系统弹性极限和安定极限不断增大. 此外,外凸模型中不同基体曲率半径下的弹性极限和安定极限均高于内凹模型中不同基体曲率下的弹性极限和安定极限.随着热障涂层研究的深入和制造水平的提升,热障涂层工作环境温度已经达到1000${^\circ}$C以上. 图4中安定极限结果较实际情况偏小(800$\sim $900${^\circ}$C), 这主要是由于实际工况中,高温下应力释放和应力松弛的影响,材料蠕变现象明显,有效释放系统内的应力,而本文 分析模型中,暂未考虑这一材料特性,导致所得热应力较实际情况偏大,安定极限值偏小.
|
图 4 不同基体曲率下热障涂层极限载荷 Fig. 4 Limit load for TBCs with different curvature of SUB |
(2) 材料厚度对热障涂层安定极限的影响
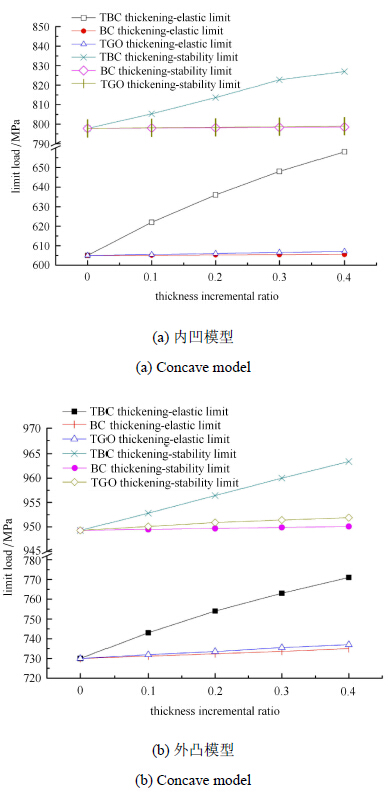
图5(a)和图5(b)分别为热障涂层各层材料厚度变化对应的热障涂层内凹模型和外凸模型弹性极限和安定极限的变化情况. 图中横 轴坐标为各层的厚度增量(增厚值/原厚度),纵轴为相应厚度下系统极限载荷. 首先,该图反映了热障涂层的弹性极限和安定极限与材料厚度间的灵敏度关系. 可以看出,陶瓷层的厚度对热障涂层的弹性极限和安定极限影响远大于粘接层;其次,随着各层厚度的增大,系统弹性极限和 安定极限不断提高,且系统极限载荷变化曲线的斜率越来越小,表明随着涂层厚度的增大,系统极限载荷增量变小,当厚度增 加到一定程度时,系统极限载荷增量会很小,此时再试图利用增加材料厚度以提高系统极限载荷的做法是不科学的.
|
图 5 热障涂层极限载荷与涂层厚度之间的关系 Fig. 5 Relationship between limit load and thickness of TBCs |
图4和图5结果表明,热障涂层外凸模型弹性极限和安定极限均高于内凹模型,即与外凸界面相比,热障涂层内凹界面处的极限承载 能力更差,系统通常首先在该位置发生破坏失效,这与以往的试验研究结果是一致的,如图1(a)所示,长时间工作后的界面内凹处 形成明显的裂纹,出现分层失效.
(3)热障涂层蠕变应力仿真
为分析蠕变因素对热障涂层应力及稳定性的影响,建立考虑蠕变和塑性的热障涂层圆筒模型,材料参数参考文献[25, 26, 27, 28],其中蠕变参数采用诺顿(Norton)蠕变本构[30, 31],即:蠕变应变率$\dot \varepsilon = {C_{{\rm{rp}}}}{\sigma ^n},{C_{{\rm{rp}}}}$为蠕变系数,$n$为蠕变指数,$\sigma $为应力.
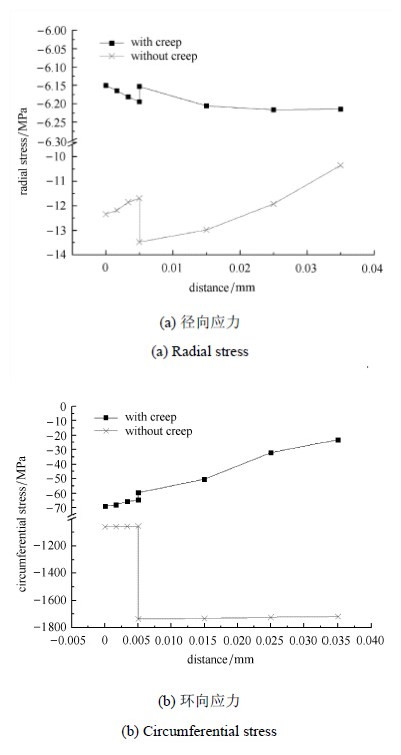
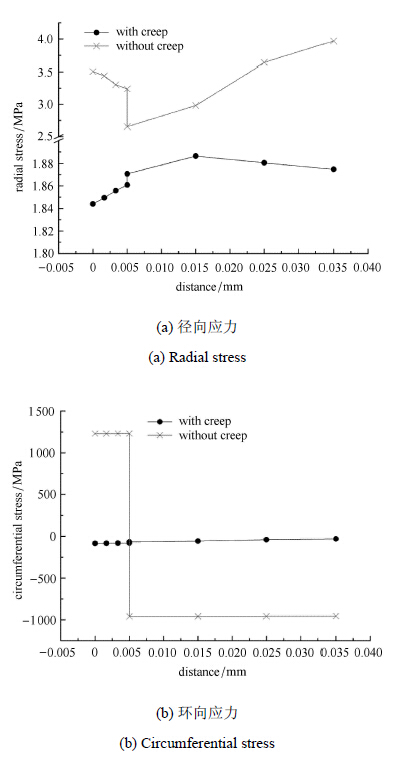
图6和图7分别为内凹模型和外凸模型中材料蠕变特性对粘接层和氧化层中应力场分布的影响. 图中横轴坐标为任意位置至陶 瓷层/氧化层界面的径向距离,纵轴为相应位置处的环向应力或径向应力. 其中,坐标横轴最左端代表陶瓷层/氧化层界面而最右端代表粘接层/基体界面. 从图中可以看出,无论是内凹模型还是外凸模型,材料蠕变特性对应力场影响显著,考虑材料蠕变特性时的应力幅值远小于不考虑材料蠕变特性时的应力幅值. 此外,分别比较图6(a)和图7(a)及图6(b)和图7(b)可以看出,外凸模 型中粘接层和氧化层环向应力场和径向应力场均小于内凹模型,从应力的角度分析,外凸模型热蠕变应力场更有利于系统稳定性.
|
图 6 内凹模型蠕变对应力场的影响 Fig. 6 The influence of creep on stress in concave model |
|
图 7 外凸模型蠕变对应力场的影响 Fig. 7 The influence of creep on stress in concave model |
(1)借助本文给出的安定性分析方法,利用增量破坏准则处理对时间的积分,将材料屈服强度随温度的变化关系简化为双线性模型,能够得到多层结构的安定极限,且方法简单便于实际工程应用;
(2)热障涂层安定极限值明显高于弹性设计值,且界面外凸区域安定极限高于内凹区域极限值,结构优先在内凹处失效,与试验所得结果一致. 同时,圆筒涂层基体曲率半径和涂层厚度越大,安定极限越高;
(3)仿真分析结果表明蠕变引起的应力释放效果明显,本文建立的热障涂层安定分析方法,对进一步研究考虑蠕变因素影响热障涂层安定性具有重要意义.
| [1] | 朱建国, 谢惠民, 刘占伟. 热障涂层力学性能的试验测试方法研究进展. 力学学报,2013,45:45-60 (Zhu Jianguo,Xie Huimin, Liu Zhanwei. Research progress on the experimental measurement methods of mechanical properties of thermal barrier coatings. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45:45-60(in Chinese)) |
| [2] | 周益春, 刘奇星, 杨丽 等. 热障涂层的破坏机理与寿命预测. 固体力学学报, 2010, 31: 504-531 (Zhou Yichun, Liu Qixing, Yang Li, et al. Failure mechanisms and life prediction of thermal barrier coatings. Chinese Journal of Solid Mechanics, 2010, 31: 504-531 (in Chinese)) |
| [3] | 胡浩炬, 张建宇, 杨晓光等.等离子热障涂层失效机理的数值分析研究.航空动力学报, 2010, 25: 1085-1091 (Hu Haoju, Zhang Jianyu, Yang Xiaoguang, et al. Numerical study of failure mechanisms on plasma sprayed thermal barrier coatings. Jourmal of Aerospace Power, 2010, 25: 1085-1091 (in Chinese)) |
| [4] | Padture NP, Gell M, Jordan EH. Thermal barrier coatings for gas-turbine engine applications. Science, 2002, 296: 280-284 |
| [5] | He MY, Hutchinson JW, Evans AG. Simulation of stresses and delamination in a plasma-sprayed thermal barrier system upon thermal cycling. Materials Science and Engineering A, 2003, 345: 172-178 |
| [6] | Karlsson AM, Hutchinson JW, Evans AG. A fundamental model of cyclic instabilities in thermal barrier systems. Journal of the Mechanics and Physics of Solids, 2002, 50: 1565-1589 |
| [7] | Evans HE. Oxidation failure of TBC systems: An assessment of mechanisms. Surface & Coatings Technology, 2011, 206: 1512-1521 |
| [8] | Kyaw S, Jones A, Hyde T. Predicting failure within TBC system: Finite element simulation of stress within TBC system as affected by sintering of APS TBC, geometry of substrate and creep of TGO. Engineering Failure Analysis, 2013, 27: 150-164 |
| [9] | 郑小涛, 程诗, 冯磊等. 循环移动热载荷下压力管道弯头的安定性. 压力容器, 2013, 30: 67-70 (Zheng Xiaotao, Cheng Shi, Feng Lei, et al. Shakedown analysis of the pressure piping bend under cycle moving thermal loadings. Pressure Vessel Technology, 2013, 30: 67-70 (in Chinese)) |
| [10] | 郑小涛, 彭常飞, 喻九阳 等. 热-机械载荷下U形对焊接头的安定性. 焊接学报, 2013, 34: 39-42 (Zheng Xiaotao,Peng Changfei,Yu Jiuyang,et al. Shakedown analysis of U-groove butt welded joints under cyclic thermo-mechanical loadings. Transactions of the China Welding Institution, 2013, 34: 39-42 (in Chinese)) |
| [11] | Gokhfeld DA, Cherniavsky DF. Limit Analysis of Structures at Thermal Cycling. Alphen An der Rijn: Sijthoff & Noordhoff, 1980 |
| [12] | Xue MD, Wang XF, Williams FW, et al. Lower-bound shakedown analysis of axisymmetric structures subjected to variable mechanical and thermal loads. International Journal of Mechanical Sciences, 1997, 39(9): 965-976 |
| [13] | Chen HF. Lower and upper bound shakedown analysis of structures with temperature dependent yield stress. Journal of Pressure Vessel Technology, 2010, 132: 1-8 |
| [14] | 刘信声, 冯西桥. 考虑温度对材料性能影响时厚壁圆筒的安定分析. 工程力学, 1991, 8(3): 36-44 (Liu Xinsheng, Feng Xiqiao. Shakedown analysis of a thick-walled cylindrical tube considering the material property changing with temperature. Engineering Mechanics, 1991, 8(3): 36-44 (in Chinese)) |
| [15] | 杜森田, 徐秉业. 考虑外载荷和温度的运动安定定理. 固体力学学报, 1990, 11(2): 140-147 (Du Sentian, Xu Bingye. A kinematic shakedown theory considering external loading and temperature variation. Acta Mechanica Solida Sinica, 1990, 11(2): 140-147 (in Chinese)) |
| [16] | 杜森田, 刘寒冰, 陈塑寰 等. 弹塑性结构在外载和温度作用下的安定分析. 应用数学和力学, 1995, 16(8): 737-744 (Du Sentian, Liu Hanbing, Chen Suhuan, et al. Shakedown analysis of elasto-plastic structures subjected to external loading and temperature variation. Applied Mathematics and Mechanics, 1995, 16(8): 737-744 (in Chinese)) |
| [17] | Karlsson AM, Hutchinson JW, Evans AG. A fundamental model of cyclic instabilities in thermal barrier systems. Journal of the Mechanics and Physics of Solids, 2002, 50: 1565-1589 |
| [18] | Evans HE. Oxidation failure of TBC systems: An assessment of mechanisms. Surface & Coatings Technology, 2011, 206: 1512-1521 |
| [19] | Mumm DR, Evans AG, Spitsberg IT. Characterization of a cyclic displacement instability for a thermally grown oxide in a thermal barrier system. Acta Materialia, 2001, 49: 2329-2340 |
| [20] | Karlsson AM, Evans AG. A numerical model for the cyclic instability of thermally grown oxides in thermal barrier systems. Acta Materialia, 2001, 49: 1793-1804 |
| [21] | Hille TS, Turteltaub S, Suiker ASJ. Oxide growth and damage evolution in thermal barrier coatings. Engineering Fracture Mechanics, 2011, 78: 2139-2152 |
| [22] | He MY, Evans AG, Hutchinson JW. The ratcheting of compressed thermally grown thin films on ductile substrates. Acta Materialia, 2000, 48: 2593-2601 |
| [23] | 徐颖强, 李世杰, 杨小辉 等. 热循环下热障涂层结构不稳定性的数值模拟. 机械设计与制造, 2009, 5: 115-117 (Xu Yingqiang, Li Shijie, Yang Xiaohui, et al. Numerical simulation of structural instability in thermal barrier system during thermal cycling. Machinery Design & Manufacture, 2009, 5: 115-117 (in Chinese)) |
| [24] | 黄霞, 丁军, 周静 等. 热障涂层界面位移非稳定性的有限元模拟. 表面技术, 2011, 40: 97-100 (Huang Xia, Ding Jun, Zhou Jing, et al. Numerical simulation of interfacial displacement instability in TBC system. Surface Technology, 2011, 40: 97-100 (in Chinese)) |
| [25] | Aktaa J, Sfar K, Munz D. Assessment of TBC systems failure mechanisms using a fracture mechanics approach. Acta Materialia, 2005, 53: 4399-4413 |
| [26] | Rösler J, Bäker M, Aufzug K. A parametric study of the stress state of thermal barrier coatings Part I: creep relaxation. Acta Materialia, 2004, 52: 4809-4817 |
| [27] | Mao WG, Zhou YC, Yang L, et al. Modeling of residual stresses variation with thermal cycling in thermal barrier coatings. Mechanics of Materials, 2006, 38: 1118-1127 |
| [28] | Zhou CG, Wang N, Xu HB. Comparison of thermal cycling behavior of plasma-sprayed nanostructured and traditional thermal barrier coatings. Materials Science and Engineering A, 2007, 452: 569-574 |
| [29] | 陈良玉, 李玉, 姜华. 多层组合圆筒体的轴对称温度和热应力的通用计算方法. 材料与冶金学报, 2007, 6: 297-315 (Chen Liangyu, Li Yu, Jiang Hua. General computation method for axisymmetric temperature and thermal stress of multilayer cylinder. Journal of Materials and Metallurgy, 2007, 6: 297-315 (in Chinese)) |
| [30] | Ranjbar-Far M, Absi J, Mariaux G, et al. Simulation of the effect of material properties and interface roughness on the stress distribution in thermal barrier coatings using finite element method. Materials and Design, 2010, 31: 772-781 |
| [31] | Bialas M. Finite element analysis of stress distribution in thermal barrier coatings. Surface & Coatings Technology, 2008, 202: 6002-6010 |
 2015, Vol. 47
2015, Vol. 47