2. 西安航空学院, 西安710077
结构健康监测系统能够对目标结构的整体或关键部位进行在线实时监测,其通过探测和提取目标结构的力学响应,并进行分析和评价, 从而达到及时发现损伤、预估损伤以及修复损伤的目的,可极大地提高结构的可靠性、维修性和耐久性[1, 2]. 目前,该技术已逐步应用于航空航天领域[3, 4]. 在我国,一种新的结构健康监测技术------智能涂层监测系统已经被研发出来[5, 6, 7]. 智能涂层传感器是该系统最关键的元器件,其主要由驱动层、传感层和保护层组成.
在智能涂层监测系统中,裂纹的监测能力主要依赖于结构基体中的主裂纹能否穿越界面(基体/驱动层/传感层). 当基体中裂纹到 达界面时,裂纹的扩展将会出现两种趋势:(1)如果界面的断裂韧性较高,主裂纹将会直接穿越界面,进入下一层;(2)当界面断裂韧 性较低时,主裂纹可能会沿着界面偏转. 然而,如果基体裂纹沿着界面偏转,将不利于智能涂层监测系统对裂纹的监测[5]. 因此,裂纹扩展路径的准确预测将对智能涂层的优化设计起着关键的作用. 但是到目前为止,在智能涂层监测系统中,关于裂纹的扩展路径及影响因素还缺乏较为深入的理论研究.
应力和能量准则通常被用于判断裂纹的扩展路径. 前者由界面的局部应力渐进场控制. 1964年,有人首次用应力准则给出了当主裂纹 到达界面时裂纹可能的扩展路径[8]. 多年后,又有人扩展了这一概念,认为裂纹的扩展路径由穿越裂纹的最大法向应力与偏转裂纹的最大法向应力之比所决定[9]. 能量准则是建立于可能扩展路径的断裂功的基础之上[10]并且已经进行了很多相关现象的研究[11, 12, 13]. 其中最为熟悉的是文献[10]的工作,他们首次用能量准则研究了裂纹在双材料界面穿越与偏转的竞争行为,并且研究了主裂纹在双材 料界面沿着不同的角度扩展的问题. 测量界面断裂韧性的技术的发展使得能量准则的应用更加简单[14, 15].
在本文中,采取能量准则研究裂纹在智能涂层界面的穿越与偏转行为. 根据能量准则,分别建立了智能涂层的两相与三相模型,并用有限 元法全面分析了假定的裂纹偏转/穿越的长度、弹性错配参数以及界面层的厚度对裂纹偏转/穿越的能量释放率之比的影响,并且将数值 分析结果与实验结果进行了比较.
1 分 析 1.1 问题描述在平面应变条件下,两组弹性错配参数可以被表达为[16]
| \[\left. {\begin{array}{*{20}{l}} \begin{array}{l} {\alpha _i} = \frac{{{E_{i + 1}}(1 - \nu _i^2) - {E_i}(1 - \nu _{i + 1}^2)}}{{{E_{i + 1}}(1 - \nu _i^2) + {E_i}(1 - \nu _{i + 1}^2)}}\\ 2{\beta _i} = \frac{{{E_{i + 1}}(1 + {\nu _i})(1 - 2{\nu _i}) - {E_i}(1 + {\nu _{i + 1}})(1 - 2{\nu _{i + 1}})}}{{{E_{i + 1}}(1 - \nu _i^2) + {E_i}(1 - \nu _{i + 1}^2)}} \end{array} \end{array}} \right\}\] | (1) |
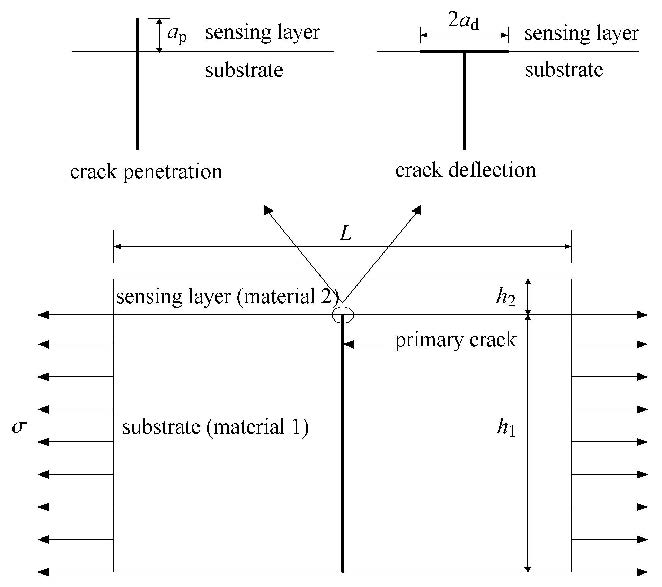
式中,$E$和$v$分别表示材料的弹性模量和泊松比,其下标代表材料的编号. 如图1所示,两相模型包括基体(材料1)与传感 层(材料2). 如图2所示,三相模型包括基体(材料1)、驱动层(材料2)和传感层(材料3).
|
图 1 两相模型中智能涂层基体裂纹的穿越和偏转 Fig. 1 The substrate crack penetration and deflection for the two-phase model of the smart coating |
|
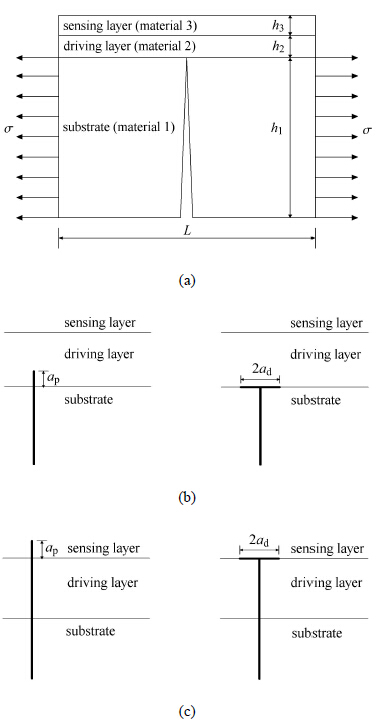
图 2 三相模型中智能涂层基体裂纹的穿越和偏转 Fig. 2 The substrate crack penetration and deflection for the three-phase model of the smart coating |
为了确保智能涂层系统对裂纹的监测能力,当主裂纹到达界面时,应当考虑裂纹的偏转/穿越的相对趋势. 对于两相模型,主裂纹能够穿 越进入下一层而不是沿着界面偏转的必要条件可以表达为[10]
| \[\frac{{{\Gamma _{\rm{d}}}}}{{{\Gamma _{\rm{p}}}}} > K = \frac{{{G_{\rm{d}}}}}{{{G_{\rm{p}}}}} = f(\alpha ,\beta ){(\frac{{{a_{\rm{d}}}}}{{{a_{\rm{p}}}}})^{1 - 2\lambda }}\] | (2) |
式中,$K$代表偏转和穿越裂纹的能量释放率之比;$G_{\rm d}$和$\varGamma_{\rm d}$分别代表沿界面偏转裂纹的能量释放率和表面 能(临界能量释放率);$G_{\rm p}$和$\varGamma_{\rm p}$分别代表穿越裂纹的能量释放率和表面能(临界能量释放率). 如图1所示,$a_{\rm d}$是假定的沿界面偏转的裂纹初始长度,$a_{\rm p}$是假定的穿越到下一界面的裂纹初始长度. 裂纹尖端应力奇异性指数 $\lambda $ 可以表达为[13]
| \[\cos \lambda \pi = \frac{{2(\beta - \alpha )}}{{1 + \beta }}{(1 - \lambda )^2} + \frac{{\alpha + {\beta ^2}}}{{1 - {\beta ^2}}}\] | (3) |
式中,$\lambda $一般从1.0 ($\alpha = - 1.0$)变化到0.3($\alpha= 1.0$)并且决定着裂纹尖端的应力场分布,且服 从$\sigma \sim r^{ - \lambda }$,$r$是到裂纹尖端的长度. 在单一的材料中,$\alpha =0$,$\lambda =0.5$,由此获得常见的$\sigma \sim 1 / {\sqrt r }$关系[13].
对于三相模型如图2(b)的情况,主裂纹穿越至驱动层的条件为
| \[\frac{{{G_{\rm{d}}}}}{{{G_{\rm{p}}}}} < \frac{{{\Gamma _{{\rm{d1}}}}}}{{{\Gamma _{{\rm{p2}}}}}}\] | (4) |
在方程(4)中,\[{\Gamma _{{\rm{d1}}}}\]和\[{\Gamma _{{\rm{p2}}}}\]分别是基体/驱动层界面裂纹和驱动层裂纹的临界能量释放率.
对于三相模型如图2(c)的情况,主裂纹穿越至传感层的条件为
| \[\frac{{{G_{\rm{d}}}}}{{{G_{\rm{p}}}}} < \frac{{_{\Gamma {\rm{d2}}}}}{{{\Gamma _{{\rm{p3}}}}}}\] | (5) |
在方程(5)中,\[{\Gamma _{{\rm{d2}}}}\]和\[{\Gamma _{{\rm{p3}}}}\]分别是驱动层/传感层界面裂纹和传感层裂纹的临界能量释放率.
1.2 数值分析在本文中,所有的数值分析均是在线弹性平面应变条件下进行. 裂纹驱动力$G_{\rm d}$和$G_{\rm p}$用$J$积分进行计算. 文献[10]的结果显示弹性错配参数$\alpha $对裂纹的偏转起着重要的作用,而参数$\beta $对其影响较小. 若忽略$\beta $的影响,方程(1)可以被简化为
| \[\left. {\begin{array}{*{20}{l}} \begin{array}{l} \frac{{{E_{i + 1}}}}{{{E_i}}} = \frac{{(1 - \nu _{i + 1}^2)(1 + {\alpha _i})}}{{(1 - \nu _i^2)(1 - {\alpha _i})}}\\ {\nu _i} = \frac{{2{\alpha _i} - 3{\nu _{i + 1}}{\alpha _i} + {\nu _{i + 1}}}}{{1 + 3{\alpha _i} - 4{\nu _{i + 1}}{\alpha _i}}} \end{array} \end{array}} \right\}\] | (6) |
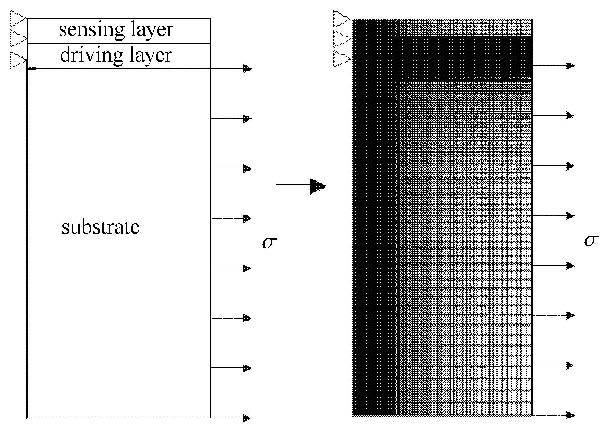
以三相模型为例,在各向同性和线弹性的假设下,三相模型的弹性参数可以由方程(6)计算. 考虑到结构的对称性,取图2(a)中一 半模型进行数值分析. 有限元模型的载荷和约束边界条件如图3所示,对称边施加对称约束,裂纹表面无约束,外部载荷施加在基体的右侧. 运用"Ansys"有限元软件进行数值模拟,采用8节点等参单元,裂纹尖端采用加密等尺寸网格.
|
图 3 三相模型中智能涂层基体裂纹穿越偏转有限元模型 Fig. 3 The finite element model of the substrate crack deflection penetration for three-phase model of the smart coating |
对于两相智能涂层模型,假定的裂纹扩展长度 $a_{\rm d}$和$a_{\rm p}$对能量释放率之比$K=G_{\rm d}/G_{\rm p}$的影响如图4和图5所示. 如图4所示,当$a_{\rm d}=a_{\rm p}=0.02$时,$K$值趋于文献[10]的计算结果. 这表明,与裂纹尖端场解相比,在这种初始长度范围,数值解是收敛的. 当$\alpha >0$时,随着$a_{\rm d}=a_{\rm p}$的增加,$K$值逐渐降低. 然而,当$\alpha < 0$时,$K$值对假定的裂纹扩展长度不是很敏感.

|
图 4 $G_{\rm d}/G_{\rm p}$随不同的$a_{\rm d}=a_{\rm p}$时的变化结果 Fig. 4 Result between the values of $ G_{\rm d}/G_{\rm p}$ for various propagation length $a_{\rm d}=a_{\rm p}$ |

|
图 5 $G_{\rm d}/G_{\rm p}$随不同的$a_{\rm d} \ne a_{\rm p}$时的变化结果 Fig. 5 Result between the values of $G_{\rm d}/G_{\rm p}$ for various propagation length $a_{\rm d} \ne a_{\rm p}$ |
在图5中,如果裂纹穿越的长度比偏转的长度大($a_{\rm d}/a_{\rm p} < 1.0$),且当$\alpha >0$时,对应的$K$值小于 $a_{\rm d}/a_{\rm p}=1.0$时对应的$K$值,表明这种情况更有利于裂纹的穿越. 另一方面,当$\alpha < 0$时,$a_{\rm d}/a_{\rm p} < 1.0$对应的$K$值大于$a_{\rm d}/a_{\rm p}=1.0$对应的$K$值,这表明此种情况更有利于裂纹的偏转. 而对于$a_{\rm d}/a_{\rm p}>1.0$时,情形刚好相反.
从方程(2)中可以看出,对应于不同的$a_{\rm d}/a_{\rm p}$,$K$值随着 $\alpha $ 变化,如图5所示. 从此关系中可以预测到,对于 $\lambda >0.5$ ($\alpha < 0$),随着$a_{\rm d}/a_{\rm p}$的增加,$K$值逐渐降低. 然而,对于 $\lambda < 0.5$ ($\alpha >0$),结果正好相反. 仅当 $\lambda =0.5$ ($\alpha =0$)时,$K$值对$a_{\rm d}/a_{\rm p}$才不太敏感.
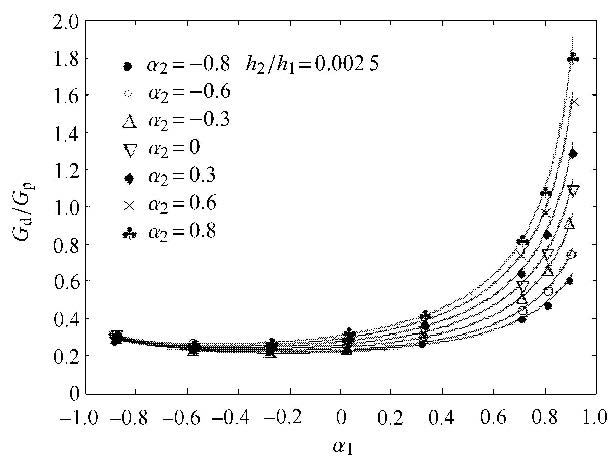
对于三相模型,由于图2(b)的情况与图2(c)情况的相似性,本文中只分析图2(b)的情况. 为了模拟无限小裂纹扩展[10],在智能 涂层的三相模型系统中假设裂纹扩展长度为$a_{\rm d}=a_{\rm p} =0.02$. 对于不同的$h_{2} / h_{1}$,图6 ~图8显示了$K$随 $\alpha_{1}$和 $\alpha_{2}$变化的结果.
|
图 6 $h_{2}/h_{1}= 0.002\,5$时,$G_{\rm d}/G_{\rm p}$随 $\alpha_{1}$和$\alpha_{2}$的变化结果 Fig. 6 Result between the values of $G_{\rm d}/G_{\rm p}$ and $\alpha_{1}$, $\alpha_{2}$ for $h_{2}/h_{1}= 0.002\,5$ |
|
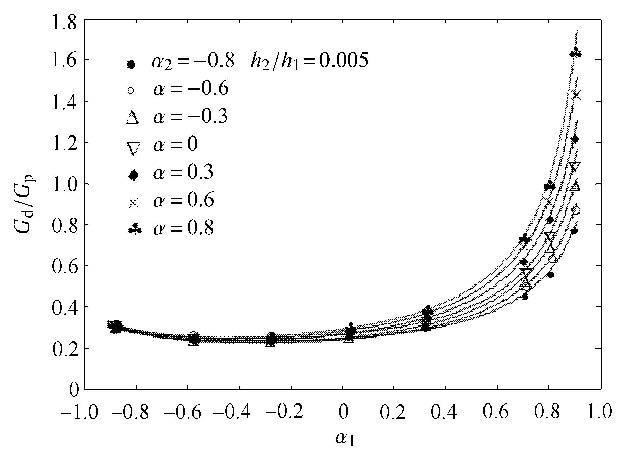
图 7 $h_{2}/h_{1}= 0.005$时,$G_{\rm d}/G_{\rm p}$随$\alpha _{1}$和$\alpha_{2}$的变化结果 Fig. 7 Result between the values of $G_{\rm d}/G_{\rm p}$ and $\alpha_{1}$, $\alpha _{2}$ for $h_{2}/h_{1}= 0.005$ |
|
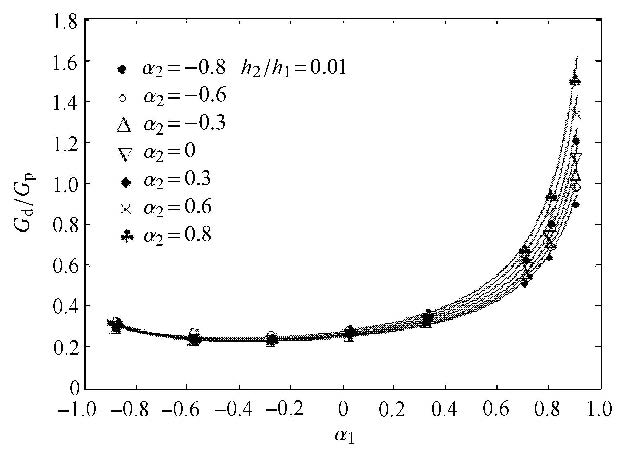
图 8 $h_{2}/h_{1}= 0.01$时,$G_{\rm d}/G_{\rm p}$随$\alpha_{1}$和$\alpha_{2}$的变化结果 Fig. 8 Result between the values of $G_{\rm d}/G_{\rm p}$ and $\alpha_{1}$, $\alpha _{2}$ for $h_{2}/h_{1}= 0.01$ |
如图6 $\sim$图8所示,$K$值不仅依赖于基体(材料1)与驱动层(材料2)之间的弹性错配参数$\alpha_{1}$,而且依赖于驱动层与传感层(材料3)之间的弹性错配$\alpha _{2}$. 一方面,$K$值对于大的正$\alpha_{1}$有较强的依赖性,对大的负$\alpha_{1}$依赖性较小;另一方面,大的$\alpha_{2}$通常产生大的$K$,这种情况会降低裂纹穿越的能力. 因此,应当选择合适的弹性模量以获得优化的穿越界面以实现涂层式裂纹传感器的功能.
另外,对于大的正$\alpha_{1}$,驱动层的厚度也明显影响着$K$值的变化,尽管对于大的负$\alpha_{1}$,其对$K$值的影响较小. 最显著的趋势可以从图6中可以看出,即$h_{2}/h_{1} =0.002\,5$的情形. 对于$h_{2}/h_{1} =0.002\,5$,0.005,0.01,当 $\alpha_{1}$取值范围分别为$\alpha_{1} < -0.4$,$-0.2$,0.0时,$\alpha_{1}$对$K$仅有较小的影响. 从图6 $\sim$图8中可以看出,对于 $\alpha _{2} >0$,较大的$h_{2}/h_{1}$会产生较小的$K$,此种情况有利于裂纹的穿越,而对于 $\alpha_{2} < 0$,较大的$h_{2}/h_{1}$则会产生较大的$K$,此种情况则有利于裂纹的偏转. 此外,随着$h_{2}/h_{1}$的增加,三相材料系统将逐渐收敛于双相材料系统. 这表明随着$h_{2}/h_{1}$的增加,$\alpha_{2}$对能量释放率之比$G_{\rm d}/G_{\rm p}$的影响逐渐降低.
以上讨论可以得出,能量释放率之比不仅依赖于基体与驱动层的弹性错配,而且依赖于驱动层与传感层的弹性错配,并受驱动层和传感层厚度的影响. 因此,选择合理的涂层弹性模量及厚度对获得智能涂层传感器期望的裂纹穿越属性非常重要.
3 实验验证在以上的工作中,对于三相智能涂层模型,数值计算了对于不同的弹性错配参数 $\alpha_{i}$ ($i =1,2$)和不同的驱动层厚 度对应的$G_{\rm d}/G_{\rm p}$值. 这些模拟结果将被下面的实验所验证.
利用纳米技术在7050-T7452铝合金上原位制造了包含驱动层与传感层的智能涂层. 其中驱动层主要由纳米绝缘材料制成,传感层主要由 纳米铜等导电材料构成. 其中,传感层与驱动层的厚度分别约为15μm和2μm,传感层的宽度约为1mm. 如图9所示,对基体进行单轴拉伸测试. 在拉伸测试中,观察试件的断裂演化行为. 另外,作为裂纹穿越的证据,对断裂面也进行了检查,如图10所示.

|
图 9 单轴拉伸测试 Fig. 9 Uniaxial tension tests |
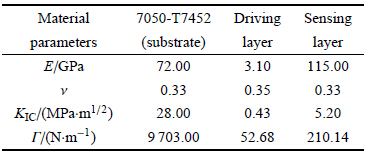
测得材料的力学性能如表1所示[7, 17],在平面应变条件下,临界能量释放率(表面能)可以通过 \[\Gamma = K_{{\rm{IC}}}^2(1 - {\nu ^2})/E\]进行计算. 通过方程(1),利用基体、驱动层及传感层的弹性模量和泊松比计算得出$\alpha_{1}$和$\alpha_{2}$分别为$-0.92$和0.95.
| 表 1 基体、驱动层、传感层的力学性能 Table 1 Mechanical properties of substrate, driving layer and sensing layer |
假设基体与驱动层间的界面断裂韧性为 $\varGamma_{i1}$,驱动层与传感层间的界面断裂韧性为$\varGamma_{i2}$. 当主裂纹尖端到 达基体与驱动层界面时,比值 $\varGamma _{i1}/\varGamma_{i2}$大约为9.24[7, 14]. 由有限元结果知,$K$值大约为0.36. 因此,$K$远远小于 $\varGamma_{i1}/\varGamma_{i2}$. 这表明基体与驱动层之间的脱粘不可能出现并且裂纹将优先穿越进入驱动层,与实验结果一致(图10).

|
图 10 穿越裂纹及断裂面 Fig. 10 The penetrated crack and the fracture surfaces |
另外,对主裂纹穿越进入驱动层并且裂纹尖端到达驱动层与传感层界面时的情形也进行了研究. 此种情况下,比值 \[{\Gamma _{i2}}/{\Gamma _{p3}}\]约为2.68[7, 14]. 由有限元结果知,$K$值大约为1.58. 因此,K < \[{\Gamma _{i2}}/{\Gamma _{p3}}\]. 这表明该种情况下,驱动层与传感层之间的界面脱粘不可能出现,裂纹将直接穿越进入传感层. 这与实验结果吻合得很好(图10). 尽管由于问题的复杂性和材料、几何参数的一些未知性,但依然可以相信,某种程度上,本文建立的模型和数值结果对于揭示智能涂层 中裂纹的演化行为是非常有用的.
4 结 论在智能涂层系统中,基于能量准则,利用建立的两相和三相模型,对裂纹在界面的穿越/偏转行为进行了研究. 通过上述研究,可以得出以下结论:
(1) 对于两相模型,当 $\alpha >0$,随着$a_{\rm d}=a_{\rm p}$的增加,能量释放率之比$K=G_{\rm d}/G_{\rm p}$逐渐降低. 然而,当 $\alpha < 0$时,$K$值对假定的裂纹扩展长度不是很敏感. 对于$a_{\rm d} \ne a_{\rm p}$的情形,数值结果表明,当 $\alpha < 0$时,与$a_{\rm d}=a_{\rm p}$时的$K$值相比,$a_{\rm d}>a_{\rm p}$时产生的$K$值较小,这将有利于裂纹的穿越,而当 $\alpha >0$时,将会产生较大的$K$.
(2) 对于三相模型,数值分析表明$K$值不仅依赖于弹性错配参数 $\alpha_{i}$ ($i =1$, 2),而且依赖于驱动层的相对厚度. 进一步的数值分析表明$K$对大的正 $\alpha_{1}$有较强的依赖性,而对大的负$\alpha_{1}$却不太敏感. 另外,较大的$\alpha_{2}$通常产生较大的$K$值,这将降低裂纹穿越的能力. 数值结果亦表明,对于$\alpha_{2}>0$,驱动层越厚,$K$值越小,这种情况有利于裂纹的穿越. 而对于 $\alpha_{2} < 0$,驱动层越厚,$K$值越大,这种情况不利于裂纹的穿越. 另外,随着驱动层厚度的增加,$\alpha_{2}$对$K$值的影响逐渐降低.
(3) 实验结果表明基体裂纹能够相继穿越进入驱动层和传感层,说明了数值分析的正确性. 合理选择驱动层与传感层的弹性模量及厚度对智能涂层传感器的优化设计具有非常重要的作用.
| [1] | 袁慎芳,梁栋,高宁等. 基于结构健康监测系统的桥梁数据异常诊断研究. 电子科技大学学报,2013 42(1):69-74 (Yuan Shen-fang, Liang Dong, Gao Ning, et al. The bridge data diagnosis research based on structural health monitoring system. Journal of University of Electronic Science and Technology of China, 2013, 42(1): 69-74 (in Chinese)) |
| [2] | 杨建良,郭照华,向清等. 基于神经网络与光纤传感阵列的结构状态监测方法. 力学学报,1998, 30 (2):213-219 (Yang Jianliang, Guo Zhaohua, Xiang Qing, et al. Structural state detec-tion with fiberoptic sensing array and neural network signal processing techniques. Acta Mechanica Sinica, 1998, 30 (2):213-219 (in Chinese)) |
| [3] | Ignatovich SR, Menou A, Karuskevich MV, et al. Fatigue damage and sensor development for aircraft structural health monitoring. Theoretical and Applied Fracture Mechanics, 2013, 65: 23-27 |
| [4] | 孙侠生,肖迎春. 飞机结构健康监测技术的机遇与挑战. 航空学报, 2014,35(12):3199-3212 (Sun Xiasheng, Xiao Yingchen. Opportu-nities and challenges of aircraft SHM. Acta Aeronoutica et Astronautica Sinica, 2014, 35(12): 3199-3212(in Chinese)) |
| [5] | Hu F, Liu MB, Gao H, et al. Flaw-detected coating sensors applied in aircraft R&M. In: Proc. of 55th Annual Reliability & Maintainability Symposium. New York: IEEE, 2009: 95-99 |
| [6] | Liu MB, Sun Y, Wang Z, et al. A validation study for a shm technology under operational environment. In: Proc. of 60th Annual Reliability and Maintainability Symposium (RAMS).New York: IEEE, 2014 |
| [7] | Sun Y, Liu MB. Analysis of the crack penetration/deflection at the inter-faces in the intelligent coating system utilizing virtual crack closure tech-nique. Engineering Fracture Mechanics, 2015, 133: 152-162 |
| [8] | Cook J, Gordon JE, Evans CC, et al. A mechanism for the control of crack propagation in all-brittle systems. Proceedings of the Royal Society of London A, 1964, 282(1391): 508-520 |
| [9] | Gupta V, Suo Z, Argon AS. Crack deflection at an interface between two orthotropic media. Journal of Applied Mechanics, 1992, 59(2): S79-87 |
| [10] | He MY, Evans AG, Hutchinson JW. Crack deflection at an interface between dissimilar elastic material: Role of residual stresses. International Journal of Solids and Structure, 1994, 31(24): 3443-3455 |
| [11] | Liu YF, Tanaka Y, Masuda C. Debonding mechanisms in the presence of an interphase in composites. Acta Materialia, 1998, 46(15): 5237-5247 |
| [12] | Ahn BK, Curtin WA, Parthasarathy TA, et al. Criteria for crack deflec-tion/penetration for fiber-reinforced ceramic matrix composites. Composites Science and Technology, 1998, 58(11): 1775-1784 |
| [13] | Lee W, Yoo YH, Shin H. Reconsideration of crack deflection at planar interfaces in layered systems. Composites Science and Technology, 2004, 64(15): 2415-2423 |
| [14] | Huang B, Zhao MH, Gao CF, et al. Phase angle in indentation-induced delamination with buckling. Scripta Materialia, 2004, 50: 607-611 |
| [15] | Jia HK, Wang SB, Li LA, et al. Application of optical 3D measurement on thin film buckling to estimate interfacial toughness. Optics and Lasers in Engineering, 2014, 54: 263-268 |
| [16] | Dundurs J. Edge-bonded dissimilar orthogonal elastic wedges. Journal of Applied Mechanics, 1969, 36(3): 650-652 |
| [17] | 胡峰. 信息智能涂层及其在飞机结构健康监测技术中的应用研究. [硕士论文]. 西安:西安交通大学,2007 (Hu Feng. Intelligent coating and its application in aircraft structural health monitoring. [Master Thesis]. Xi'an: Xi'an Jiaotong University, 2007 (in Chinese)) |
2. Xi'an Aeronautical University, Xi'an 710077, China
 2015, Vol. 47
2015, Vol. 47