随着新型复合材料的大量使用,在航空、机械和土木工程等领域,叠层构件得到广泛应用. 由于复合材料通常具有各向异性、 不均匀性、厚度大等特点,使得传统的板理论[1]无法满足求解精度. 因此,有人分别建立了考虑剪切变形的中厚板理论[2, 3], 在此基础上提出了高阶剪切理论,得到广泛应用[4, 5]. 但是上述各种理论都是基于某种人为假设,将三维问题简化为二维问题进行求解的,其弹性力学方程不能完全相容,无法获得挠 度和应力分量沿厚度方向变化的精确解.
还有人采用三维弹性力学位移法分析了四边简支叠层矩形板的弯曲、振动与屈服问题[6, 7],也对板的三维弹性力 学精确解做了深入的研究[8, 9, 10]. 范家让[11]应用状态空间法,从弹性力学基本方程出发,采用三角级数形式,建立了正交各向异性叠层板的状态方程,得到了 叠层板的三维弹性力学精确解,该解不受板的厚度限制,但对非四边简支矩形板,依然存在一些求解难度. 为此,范家让和盛宏玉[12]通过引入脉冲函数来假设固支边的边界反力,给出了具有固支边叠层板的精确解. 在此基础上,他们又通过引入边界位移函数得到了收敛性更好的解[13]. 但是这些解在固支边只能通过分层的办法在分层处满足固支边界条件,无法使整个固支边沿厚度方向全部满足固支边界条件. 有人采用数值微分求积方法得到了矩形厚板的精确解[14, 15]; 用状态空间方法与数值微分求积相结合的半逆解法求解了弹性厚\linebreak 板[16]. 将有限条带法与状态空间法结合,给出了叠层板的半解析解[17, 18, 19, 20]. 钟阳及其合作者[21, 22]引入哈密顿体系求解了中厚板问题,田斌等[23]采用有限积分变换和状态空间理论相结 合的方法求得了固支矩形厚板的精确解.
本文在文献[11, 12, 13]的基础上,对固支边的边界位移函数采用新的处理方法,通过把边界位移函数作为状态变量引入状态方程,将非齐 次状态方程的求解变为齐次状态方程的求解,并且省略求解待定常数的过程,使求解过程更加简单. 该解使固支边能严格满足位移边界条件,在同一材料层内不需作分层处理,因而更加精确. 此外,对固支边的应力提出新的计算方法,以使固支边上的计算结果更加精确.
1 单层板的状态方程及其解图1所示为一正交各向异性矩形板,坐标轴沿材料弹性主方向. 正交各向异性体的应力与位移之间的关系为
| $\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\sigma _x}\\ {\sigma _y}\\ {\sigma _z}\\ {\tau _{yz}}\\ {\tau _{zx}}\\ {\tau _{xy}} \end{array} \end{array}} \right\} = \left[{\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0&0\\ {{C_{12}}}&{{C_{22}}}&{{C_{23}}}&0&0&0\\ {{C_{13}}}&{{C_{23}}}&{{C_{33}}}&0&0&0\\ 0&0&0&{{C_{44}}}&0&0\\ 0&0&0&0&{{C_{55}}}&0\\ 0&0&0&0&0&{{C_{66}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \frac{{\partial u}}{{\partial x}}\\ \frac{{\partial v}}{{\partial y}}\\ \frac{{\partial w}}{{\partial z}}\\ \frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}\\ \frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}\\ \frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} \end{array} \end{array}} \right\}$ | (1) |
|
图 1 单层矩形板 Fig. 1 Rectangular single plate |
将式(1)代入平衡微分方程,并消去板的面内应力分量$\sigma_{x}$,$\sigma_{y}$和$\tau_{xy}$后,可得到[11]
| $\frac{{\partial r}}{{\partial z}} = Dr$ | (2) |
式中
| $r = {\left[{u\;\;v\;\;{\sigma _z}\;\;{\tau _{zx}}\;\;{\tau _{yz}}{\rm{ }}w} \right]^{\rm{T}}}$ |
| $D = \left[{\begin{array}{*{20}{c}} 0&0&0&{{C_8}}&0&{ - \alpha }\\ 0&0&0&0&{{C_9}}&{ - \beta }\\ 0&0&0&{ - \alpha }&{ - \beta }&0\\ { - {C_2}{\alpha ^2} - {C_6}{\beta ^2}}&{ - ({C_3} + {C_6})\alpha \beta }&{{C_1}\alpha }&0&0&0\\ { - ({C_3} + {C_6})\alpha \beta }&{ - {C_6}{\alpha ^2} - {C_4}{\beta ^2}}&{{C_5}\beta }&0&0&0\\ {{C_1}\alpha }&{{C_5}\beta }&{{C_7}}&0&0&0 \end{array}} \right]$ |
其中,$C_{1} =-C_{13}/C_{33}$,$C_{2}=C_{11}-C_{13}^{2}/C_{33}$, $C_{3}=C_{12}-C_{23}^{2}/C_{33}$,$C_{4}=C_{22}-C_{23}^{2}/C_{33}$, $C_{5}=-C_{23}/C_{33}$,$C_{6}=C_{66}$,$C_{7}=1/C_{33}$,$C_{8}=1/C_{55}$,$C_{9}=1/C_{44}$,$\alpha =\partial/\partial x$,$\beta =\partial/\partial y$. 应力分量$\sigma_{x}$, $\sigma_{y}$和$\tau_{xy}$则可由下式求得
| $\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\sigma _x}\\ {\sigma _y}\\ {\tau _{xy}} \end{array} \end{array}} \right\} = \left[{\begin{array}{*{20}{c}} {{C_2}\alpha }&{{C_3}\beta }&{ - {C_1}}\\ {{C_3}\alpha }&{{C_4}\beta }&{ - {C_5}}\\ {{C_6}\beta }&{{C_6}\alpha }&0 \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} u\\ v\\ {\sigma _z} \end{array} \end{array}} \right\}$ | (3) |
考虑一对边($x=0$,$a$)固支、另一对边($y=0$,$b$)简支的矩形板,其边界条件为
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} x = 0{\mkern 1mu} ,\;a{\mkern 1mu} ;\;\;u = v = w = 0\\ y = 0{\mkern 1mu} ,\;b{\mkern 1mu} ;\;\;u = w = 0{\mkern 1mu} ,{\sigma _y} = 0 \end{array} \end{array}} \right\}$ | (4) |
为了满足 式(4),根据文献[13],将位移$u$假设成如下形式
| $u = \bar u + {f_1}(x){u^{(0)}} + {f_2}(x){u^{(a)}}$ | (5) |
式中,$u^{(0)}= u^{(0)}(y,z)$和$u^{(a)}= u^{(a)}(y,z)$分别为固支边$x=0$和$x=a$处的待定边界位移函数,由 边界条件确定;$f_{1}(x)$和$f_{2}(x)$是相应的边界位移函数在矩形板域内$x$方向变化的函数,它们的选取不是唯一的, 只需满足在相应固支边处的值为1,而不影响对边边界条件的满足. 文献[13]指出,$f_{1}(x)$和$f_{2}(x)$采用多项式形式时三角级数展开简单且收敛快;而多项式的次数对收敛性和结果精 确度影响很小. 故本文采用如下最简单的一次多项式形式
| ${f_1}(x) = 1 - \frac{x}{a}{\mkern 1mu} ,\;\;{f_2}(x) = \frac{x}{a}{\rm{ }}$ | (6) |
将式(5)代入式(2),可得
| $\frac{{\partial \overline r }}{{\partial z}} = D\overline r + B$ | (7) |
式中,$\overline r = {\left[{\bar u\;\;v\;\;{\sigma _z}\;\;{\tau _{zx}}\;\;{\tau _{yz}}\;\;w} \right]^{\rm{T}}}$,
| $B = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} - \partial /\partial z\\ 0\\ 0\\ - {C_2}{\alpha ^2} - {C_6}{\beta ^2}\\ - ({C_3} + {C_6})\alpha \beta \\ {C_1}\alpha \end{array} \end{array}} \right\}\left[{{f_1}(x){u^{(0)}} + {f_2}(x){u^{(a)}}} \right]$ |
为了求解微分方程(7),采用分离变量法,将位移和应力分量等函数展成如下三角级数
| $\left\{ {\begin{array}{*{20}{c}} {\bar uv{\sigma _z}{\tau _{zx}}{\tau _{yz}}w} \end{array}} \right\} = \sum\limits_m {\sum\limits_n {\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {{\bar U}_{mn}}(z)\cos \zeta x\sin \eta y\\ {V_{mn}}(z)\sin \zeta x\cos \eta y\\ {Z_{mn}}(z)\sin \zeta x\sin \eta y\\ {X_{mn}}(z)\cos \zeta x\sin \eta y\\ {Y_{mn}}(z)\sin \zeta x\cos \eta y\\ {W_{mn}}(z)\sin \zeta x\sin \eta y \end{array} \end{array}} \right\}} } $ | (8) |
| ${u^{(0)}} = \sum\limits_{n = 1}^\infty {U_n^{(0)}} (z)\sin \eta y{\mkern 1mu} ,\;{u^{(a)}} = \sum\limits_{n = 1}^\infty {U_n^{(a)}} (z)\sin \eta y$ | (9) |
| ${f_1}(x) = \frac{1}{2} + \sum\limits_{m = 1}^\infty {\xi \cos \zeta x} ,\;{f_2}(x) = \frac{1}{2} - \sum\limits_{m = 1}^\infty {\xi \cos \zeta x} $ | (10) |
式(8)~式(10)中,$\zeta = m\pi /a,\eta = n\pi /b,\xi = 2(1 - \cos m\pi )/({m^2}{\pi ^2})$. 将式(5),式(6),式(8)和式(9)代入式(3)后,则
| $\begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\tau _{xy}}} \end{array}} \end{array}} \right\} = \sum\limits_n {\sum\limits_m {\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{S_{xmn}}(z)\sin \zeta x\sin \eta y}\\ {{S_{ymn}}(z)\sin \zeta x\sin \eta y}\\ {{S_{xymn}}(z)\cos \zeta x\cos \eta y} \end{array}} \end{array}} \right\}} } + \\ \frac{1}{a}\sum\limits_n {\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} { - {C_2}\left[ {U_n^{(0)}(z) - U_n^{(a)}(z)} \right]\sin \eta y}\\ { - {C_3}\left[ {U_n^{(0)}(z) - U_n^{(a)}(z)} \right]\sin \eta y}\\ {{C_6}\eta \left[ {(a - x)U_n^{(0)}(z) + xU_n^{(a)}(z)} \right]\cos \eta y} \end{array}} \end{array}} \right\}} \end{array}$ | (11) |
式中,$\begin{array}{l} {S_{xmn}}(z) = - {C_2}\zeta {{\bar U}_{mn}}(z) - {C_3}\eta {V_{mn}}(z) - {C_1}{Z_{mn}}(z),{S_{ymn}}(z) = \\ - {C_3}\zeta {{\bar U}_{mn}}(z) - {C_4}\eta {V_{mn}}(z) - {C_5}{Z_{mn}}(z),{S_{xymn}}(z) = {C_6}[\eta {{\bar U}_{mn}}(z) + \zeta {V_{mn}}(z)]. \end{array}$ 将式(8) $\sim$式(10)代入式(7)后,对每对($m, n)$可得下列非齐次状态方程
| $\frac{d}{{dz}}{\overline R _{mn}}(z) = {D_{mn}}{\overline R _{mn}}(z) + {B_{mn}}(z)$ | (12) |
式中,${\overline R _{mn}} = {[{\bar U_{mn}}\;\;{V_{mn}}\;\;{Z_{mn}}\;\;{X_{mn}}\;\;{Y_{mn}}\;\;{W_{mn}}]^{\rm{T}}}$
| $\begin{array}{l} {D_{mn}} = \left[{\begin{array}{*{20}{c}} 0&0&0&{{C_8}}&0&{ - \zeta }\\ 0&0&0&0&{{C_9}}&{ - \eta }\\ 0&0&0&\zeta &\eta &0\\ {{C_2}{\zeta ^2} + {C_6}{\eta ^2}}&{({C_3} + {C_6})\zeta \eta }&{{C_1}\zeta }&0&0&0\\ {({C_3} + {C_6})\zeta \eta }&{{C_6}{\zeta ^2} + {C_4}{\eta ^2}}&{{C_5}\eta }&0&0&0\\ { - {C_1}\zeta }&{ - {C_5}\eta }&{{C_7}}&0&0&0 \end{array}} \right]\\ {B_{mn}}(z) = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} B_{0n}^*\left[{U_n^{(0)}(z) + U_n^{(a)}(z)} \right]\;\;(m = 0)\\ B_{mn}^*\left[{U_n^{(0)}(z) - U_n^{(a)}(z)} \right]\;\;(m \ne 0) \end{array} \end{array}} \right. \end{array}$ |
其中,$B_{0n}^* = {\left[{ - \frac{1}{2}\frac{d}{{dz}}\;\;0\;\;0\;\frac{{{C_6}{\eta ^2}}}{2}\;\;0\;\;0} \right]^{\rm{T}}}$
$B_{mn}^*{\left[{ - \xi \frac{d}{{dz}}\;\;0\;\;0\;\;{C_6}{\eta ^2}\xi \;\;({C_3} + {C_6})\zeta \eta \xi \;\; - {C_1}\zeta \xi } \right]^{\rm{T}}}$
由式(3),式(5),式(6),式(8)和式(9)可知,在简支边($y=0$,$b$)处,$u=w =0$和 $\sigma_{y} =0$的条件已满足;在固支边$(x =0,a)$处,$v=w =0$的条件也已满足,但$u =0$的条件尚未满足,该条件要求
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} \sum\limits_{n = 1}^\infty {\left[{U_n^{(0)}(z) + \sum\limits_{m = 0}^\infty {{{\bar U}_{mn}}(z)} } \right]} \sin \eta y = 0\\ \sum\limits_{n = 1}^\infty {\left[{U_n^{(a)}(z) + \sum\limits_{m = 0}^\infty {{{( - 1)}^m}{{\bar U}_{mn}}(z)} } \right]} \sin \eta y = 0 \end{array} \end{array}} \right\}$ | (13) |
要使上式对任意$y$均成立,必须
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} U_n^{(0)}(z) + \sum\limits_{m = 0}^\infty {{{\bar U}_{mn}}(z) = 0} \\ U_n^{(a)}(z) + \sum\limits_{m = 0}^\infty {{{( - 1)}^m}{{\bar U}_{mn}}(z) = 0} \end{array} \end{array}} \right\}$ | (14) |
文献[13]将单层板分成若干个薄层,并假定位移函数$U_n^{(0)} (z)$和$U_n^{(a)} (z)$在每一个薄层内是线性分布的,把它们在每一个薄层的端点值作为待定常数,先求解含待定常数的非齐次状态方程(12), 解出相同$n$的一组$ \bar {\pmb R}_{mn} (z)$,然后利用式(14)确定出$U_n^{(0)} (z)$和$U_n^{(a)} (z)$在每一个薄层的端点值,之后再得到不含待定常数的$ \bar{\pmb R}_{mn} (z)$. 可见,文献[13]的解只是在分层点处满足固支边界条件,需要通过增加分层数使折线分布的$U_n^{(0)} (z)$ 和$U_n^{(a)} (z)$趋向真实解,才能获得较精确的解,厚宽比越大,所需分层数则越多,求解过程比较繁琐. 本文为了使整个固支边严格满足位移边界条件,把$U_n^{(0)} (z)$和$U_n^{(a)} (z)$也看作是状态变量,将式(12)改写成如下形式
| $\begin{array}{l} \frac{d}{{dz}}{\overline R _{mn}}(z) + B_{mn}^{(0)}\frac{d}{{dz}}U_n^{(0)}(z) + B_{mn}^{(a)}\frac{d}{{dz}}U_n^{(a)}(z) = \\ {D_{mn}}{\overline R _{mn}}(z) + \overline B _{mn}^{(0)}U_n^{(0)}(z) + \overline B _{mn}^{(a)}U_n^{(a)}(z) \end{array}$ | (15) |
式中
| $B_{mn}^{(0)} = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\left[{1/2\;\;0\;\;0\;\;0\;\;0\;\;0} \right]^{\rm{T}}}\;\;(m = 0)\\ {\left[{\xi \;\;0\;\;0\;\;0\;\;0\;\;0} \right]^{\rm{T}}}\;\;(m \ne 0) \end{array} \end{array}} \right.$ |
| $B_{mn}^{(a)} = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\left[{1/2\;\;0\;\;0\;\;0\;\;0\;\;0} \right]^{\rm{T}}}\;\;(m = 0)\\ {\left[{ - \xi \;\;0\;\;0\;\;0\;\;0\;\;0} \right]^{\rm{T}}}\;\;(m \ne 0) \end{array} \end{array}} \right.$ |
| $\overline B _{mn}^{(0)} = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\left[{0\;\;0\;\;0\;\;{C_6}{\eta ^2}/2\;\;0\;\;0} \right]^{\rm{T}}}\;(m = 0)\\ {\left[{0\;\;0\;\;0\;\;{C_6}{\eta ^2}\xi \;\;({C_3} + {C_6})\zeta \eta \xi \;\; - {C_1}\zeta \xi } \right]^{\rm{T}}}\\ (m \ne 0) \end{array} \end{array}} \right.$ |
| $\overline B _{mn}^{(a)} = \left\{ {\begin{array}{*{20}{l}} \begin{array}{l} {\left[{0\;\;0\;\;0\;{C_6}{\eta ^2}/2\;\;0\;\;0} \right]^{\rm{T}}}\;\;(m = 0)\\ {\left[{0\;\;0\;\;0\;\; - {C_6}{\eta ^2}\xi \;\; - ({C_3} + {C_6})\zeta \eta \xi \;\;{C_1}\zeta \xi } \right]^{\rm{T}}}\\ (m \ne 0) \end{array} \end{array}} \right.$ | (09) |
由于式(14)对任意$z$均成立,因此,将 式(14)对$z$求导可得
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} \frac{d}{{dz}}U_n^{(0)}(z) + \sum\limits_{m = 0}^\infty {\frac{d}{{dz}}{{\bar U}_{mn}}(z) = 0} \\ \frac{d}{{dz}}U_n^{(a)}(z) + \sum\limits_{m = 0}^\infty {{{( - 1)}^m}\frac{d}{{dz}}{{\bar U}_{mn}}(z) = 0} \end{array} \end{array}} \right\}$ | (16) |
于是,将相同$n$的 式(15)与 式(16)联立,并写成如下矩阵形式
| ${\theta _n}\frac{d}{{dz}}{\Phi _n}(z) = {\overline \theta _n}{\Phi _n}(z)$ | (17) |
式中
| ${\Phi _n} = {\left[{{{\overline R }_{0n}}\;\;{{\overline R }_{1n}}\;\; \cdots \;\;{{\overline R }_{mn}}\;U_n^{(0)}\;\;U_n^{(a)}} \right]^{\rm{T}}}$ |
| ${\theta _n} = \left[{\begin{array}{*{20}{c}} I&{\bf{0}}& \cdots &{\bf{0}}&{B_{0n}^{(0)}}&{B_{0n}^{(a)}}\\ {\bf{0}}&I& \cdots &{\bf{0}}&{B_{1n}^{(0)}}&{B_{1n}^{(a)}}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\bf{0}}&{\bf{0}}& \cdots &I&{B_{mn}^{(0)}}&{B_{mn}^{(a)}}\\ \theta &\theta & \cdots &\theta &1&{\bf{0}}\\ {{\theta _0}}&{{\theta _1}}& \cdots &{{\theta _m}}&{\bf{0}}&1 \end{array}} \right]$ |
| ${\overline \theta _n} = \left[{\begin{array}{*{20}{c}} {{D_{0n}}}&{\bf{0}}& \cdots &{\bf{0}}&{\overline B _{0n}^{(0)}}&{\overline B _{0n}^{(a)}}\\ {\bf{0}}&{{D_{1n}}}& \cdots &{\bf{0}}&{\overline B _{1n}^{(0)}}&{\overline B _{1n}^{(a)}}\\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ {\bf{0}}&{\bf{0}}& \cdots &{{D_{mn}}}&{\overline B _{mn}^{(0)}}&{\overline B _{mn}^{(a)}}\\ {\bf{0}}&{\bf{0}}& \cdots &{\bf{0}}&{\bf{0}}&{\bf{0}}\\ {\bf{0}}&{\bf{0}}& \cdots &{\bf{0}}&{\bf{0}}&{\bf{0}} \end{array}} \right]$ |
其中,${\pmb I }$为6阶单位阵,$\theta = \left[{1\;\;0\;\;0\;\;0\;\;0\;\;0} \right],{\theta _m} = \left[{{{( - 1)}^m}\;\;0\;\;0\;\;0\;\;0\;\;0} \right]$.
当板受关于$x=a /2$面对称的载荷作用时,由对称性可知
| $U_n^{(0)}(z) = - U_n^{(a)}(z)$ | (18) |
这意味着状态变量$U_n^{(0)} (z)$和$U_n^{(a)} (z)$中只有一个独立. 取$U_n^{(0)} (z)$为独立的状态变量,这样,${\pmb B }_{mn}^{(0)} $与${\pmb B }_{mn}^{(a)} $,$ \bar{\pmb B }_{mn}^{(0)} $与$ \bar {\pmb B }_{mn}^{(a)} $合并为${\pmb B }_{mn} $,$ \bar{\pmb B }_{mn} $,方程(17)可降低一次. 在这种情况下,将载荷按双傅里叶级数展开后,只含奇数项,$ {\pmb B}_{mn} $和$\bar {\pmb B}_{mn} $中也只含奇数项,故$m$只需取奇数项(即$m =1,3,5,\cdots $)即可. 于是 式(17)可简化为
| ${\theta _n}\frac{d}{{dz}}{\Phi _n}(z) = {\overline \theta _n}{\Phi _n}(z)$ | (19) |
式中
| ${\Phi _n} = {\left[{{{\overline R }_{1n}}\;\;{{\overline R }_{3n}}\;\; \cdots \;\;{{\overline R }_{mn}}\;U_n^{(0)}} \right]^{\rm{T}}}$ |
| ${\theta _n} = \left[{\begin{array}{*{20}{c}} I&{\bf{0}}& \cdots &{\bf{0}}&{{B_{1n}}}\\ {\bf{0}}&I& \cdots &{\bf{0}}&{{B_{3n}}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\bf{0}}&{\bf{0}}& \cdots &I&{{B_{mn}}}\\ \theta &\theta & \cdots &\theta &1 \end{array}} \right]$ |
| ${\overline \theta _n} = \left[{\begin{array}{*{20}{c}} {{D_{1n}}}&{\bf{0}}& \cdots &{\bf{0}}&{{{\overline B }_{1n}}}\\ {\bf{0}}&{{D_{3n}}}& \cdots &{\bf{0}}&{{{\overline B }_{3n}}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\bf{0}}&{\bf{0}}& \cdots &{{D_{mn}}}&{{{\overline B }_{mn}}}\\ {\bf{0}}&{\bf{0}}& \cdots &{\bf{0}}&{\bf{0}} \end{array}} \right]$ |
其中
| ${B_{mn}} = {\left[{2\xi \;\;0\;\;0\;\;0\;\;0\;\;0} \right]^{\rm{T}}}$ |
| ${\overline B _{mn}} = {\left[{0\;\;0\;\;0\;\;2{C_6}{\eta ^2}\xi \;\;2({C_3} + {C_6})\zeta \eta \xi \;\; - 2{C_1}\zeta \xi } \right]^{\rm{T}}}$ |
由式(17)或式(19)可以得到如下齐次状态方程
| $\frac{d}{{dz}}{\Phi _n}(z) = {\Pi _n}{\Phi _n}(z)$ | (20) |
式中,${\Pi _n} = \theta _n^{ - 1}{\overline \theta _n}$.
状态方程(20)的解为
| ${\Phi _n}(z) = {{\rm{e}}^{{\Pi _n} \cdot z}}{\Phi _n}(0)$ | (21) |
当$z=h$时,有
| ${\Phi _n}(h) = {{\rm{e}}^{{\Pi _n} \cdot h}}{\Phi _n}(0)$ | (22) |
将上、下表面的已知外力按双傅里叶级数展开后,${\Phi _n}(0)$和${\Phi _n}(h)$中有3$m$个已知量,将式(14)应用于上表面(或下表面)有
| $\left. {\begin{array}{*{20}{l}} \begin{array}{l} U_n^{(0)}(0) + \sum\limits_{m = 0}^\infty {{{\bar U}_{mn}}(0) = 0} \\ U_n^{(a)}(0) + \sum\limits_{m = 0}^\infty {{{( - 1)}^m}{{\bar U}_{mn}}(0) = 0} \end{array} \end{array}} \right\}$ | (23) |
由式(22)和式(23)解出${\pmb \varPhi }_n (0)$和${\pmb \varPhi }_n (h)$中的所有未知量后,再由式(21)可以得到任意位置的${\pmb \varPhi }_n (z)$,即得到$\overline {\pmb R } _{mn} (z)$,$U_n^{(0)} (z)$和$U_n^{(a)} (z)$.
在前面求解过程中,由于将 式(5)中的$f_{1}(x)$和$f_{2}(x)$按照 式(10)展成三角级数形式后,位移$u$在固支边处 对$x$的导数为零,与位移$u$直接由 式(5)对$x$的求导结果不相等,所以在求固支边处的应力分量时应使用 式(5)求位移$u$对$x$的导数. 在固支边($x =0$,$a)$处,因为$\partial v/\partial y=\partial w/\partial z =0$,因此由式(1),式(5),式(6),式(8)和式(9)可得
| ${\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {\sigma _x}\\ {\sigma _y}\\ {\sigma _z} \end{array} \end{array}} \right\}_{x = 0,a}} = - \frac{1}{a}\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {C_{11}}\\ {C_{12}}\\ {C_{13}} \end{array} \end{array}} \right\}\sum\limits_{n = 1}^\infty {\left[{U_n^{(0)}(z) - U_n^{(a)}(z)} \right]} \sin \eta y$ | (24) |
根据求解精度,选择合适的级数项数$m$和$n$,解出每一个$n$对应的$\overline {\pmb R} _{mn} (z)$,$U_n^{(0)} (z)$和$U_n^{(a)} (z)$后,再由式(5),式(6),式(8) $\sim$式(11)和式(24)便可求出任意位置的位移和应力分量.
2 叠层板的状态方程及其解图2(a)所示为一叠层板,共$p$层,每层均为正交各向异性材料,坐标轴沿弹性主方向. 图2(b)是其中第$j$层的放大图. 对于第$j$层,在局部坐标系$O_{j}x_{j}y_{j}z_{j}$中,参照 式(20)可得如下状态方程
| $\frac{d}{{d{z_j}}}\Phi _n^{(j)}({z_j}) = \Pi _n^{(j)}\Phi _n^{(j)}({z_j})$ | (25) |
|
图 2 叠层矩形板 Fig. 2 Rectangular laminated plate |
其解为
| $\Phi _n^{(j)}({z_j}) = {{\rm{e}}^{{\rm{ }}\Pi _n^{(j)} \cdot {z_j}}}\Phi _n^{(j)}(0)$ | (26) |
由此可得第$j$层的上、下面力学量之间的关系为
| $\Phi _n^{(j)}({h_j}) = {{\rm{e}}^{\Pi _n^{(j)} \cdot {h_j}}}\Phi _n^{(j)}(0)$ | (27) |
上式对任一层均成立,由位移和应力的连续性条 件可知,${\pmb \varPhi }_n^{(j)} (0) = {\pmb \varPhi }_n^{(j - 1)} (h_{j - 1} )$,由此从第1层开始,逐层类推,可以得到叠层板的第$j$层的下面与上表面力学量之间的关系为
| $\Phi _n^{(j)}({h_j}) = \Psi _n^{(j)}\Phi _n^{(1)}(0)$ | (28) |
式中,$\Psi _n^{(j)} = {e^{\Pi _n^{(j)} \cdot {h_j}}} \cdots {\rm{ }}{e^{\Pi _n^{(2)} \cdot {h_2}}}{e^{\Pi _n^{(1)} \cdot {h_1}}}$. 当$j=p$时,即得到叠层板的下表面与上表面力学量之间的关系为
| $\Phi _n^{(p)}({h_p}) = \Psi _n^{(p)}\Phi _n^{(1)}(0)$ | (29) |
类似于单层板,将作用在叠层板上、下表面的已知外力展成双傅里叶级数后,由式(23)和式(29)可解出 ${\pmb \varPhi }_n^{(1)} (0)$和${\pmb \varPhi }_n^{(p)} (h_p )$中的未知量,再由式(26)和式(28)便可求得到任意位置的${\pmb \varPhi }_n^{(j)} (h_j )$,最后由式(5),式(6),式(8) $\sim$式(11)和式(24)便可求出任意位置的位移和应力分量.
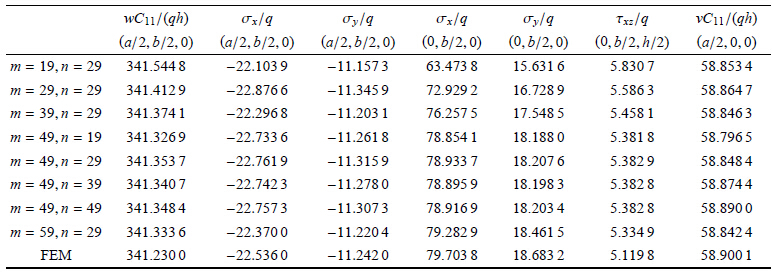
3 算例与分析算例1 单层板的上表面受均布压力$q$作用,几何尺寸为$a=b$,厚宽比$h/a$分别取0.1和0.4,材料参数与文献[13]相同,即 ${C_{12} }/ {C_{11} } = 0.246\,269$,${C_{13} } / {C_{11} } = 0.083\,171\,5$,${C_{22} }/{C_{11} } = 0.543\,103$,${C_{23} } / {C_{11} } = 0.115\,017$,${C_{33} } /{C_{11} } = 0.530\,172$,${C_{44} } /{C_{11} } = 0.266\,810$,${C_{55} } /{C_{11} } = 0.159\,914$,${C_{66} } /{C_{11} } = 0.262\,931$. 先按文献[13]的方法,分层数I分别取不同值进行计算,然后按本文的方法进行计算,两种方法中的级数项数$m$和$n$均分别取到49和29,并与用有限元分析软件ANSYS数值模拟 得到的解进行比较,如表1所列.
| 表 1 单层板位移和应力 Table 1 Displacements and stresses of single plates |
由表1可见,若文献[13]解需要获得较精确的结果,就要对单层板进行分层处理,当厚宽比越大时,需要取更多的分层数. 如果不分 层(即分层数$I= 1$)或分层数$I$较小时,其结果的误差较大. 当分层数$I$取足够多(如算例中两种厚宽比的分层数$I$分别取10和20)时,在板中心和简支边中间处的结果逼近真解, 误差较小,而固支边中间处仍有一定误差. 这是因为该解只是在固支边分层处满足固支边界条件,所以固支边处的误差较大,由圣维南原理可知,在离固支边较远处 (如板中心和简支边中间)影响较小. 本文解不需分层便可在全部区域内获得很精确的结果,这是因为本文解在整个固支边上严格满足固支边界条件,尤其是厚 宽比较大时,其优点更加明显. 此外,表1表明,本文按式(24)求得的固支边处的应力分量 $\sigma_{x}$,$\sigma _{y}$和 $\sigma _{z}$ 与有限元解很接近,而文献[13]没有给出固支边处的 $\sigma _{z}$结果,$\sigma _{x}$和 $\sigma _{y}$ 也没有本文解精确,这给研究固支边的应力带来极大方便.
图3给出了厚宽比$h/a =0.1$单层板的固支边位移$u$本文解和文献[13]解随坐标$z$的变化情况. 从图中可以看出, 文献[13]解中分层数$I$的取值不同,固支边界条件的满足程度也不同,这是导致该解误差的主要原因. 当分层数$I$越大时,固支边界条件的满足程度越好,其解越精确,这在表1中已有体现. 另外,固支边上、下面附近的位移$u$误差较大,这与表1中固支边上、下面处的文献[13]解的误差较大相对应. 本文解则在整个固支边上严格满足位移边界条件$u$=0,这正是本文解更加精确的原因.

|
图 3 固支边位移$u$随$z$的变化情况$(h/a=0.1)$ Fig. 3 Variation of the displacement $u$ with $z$ on clamped boundary of single plate $(h/a=0.1)$ |
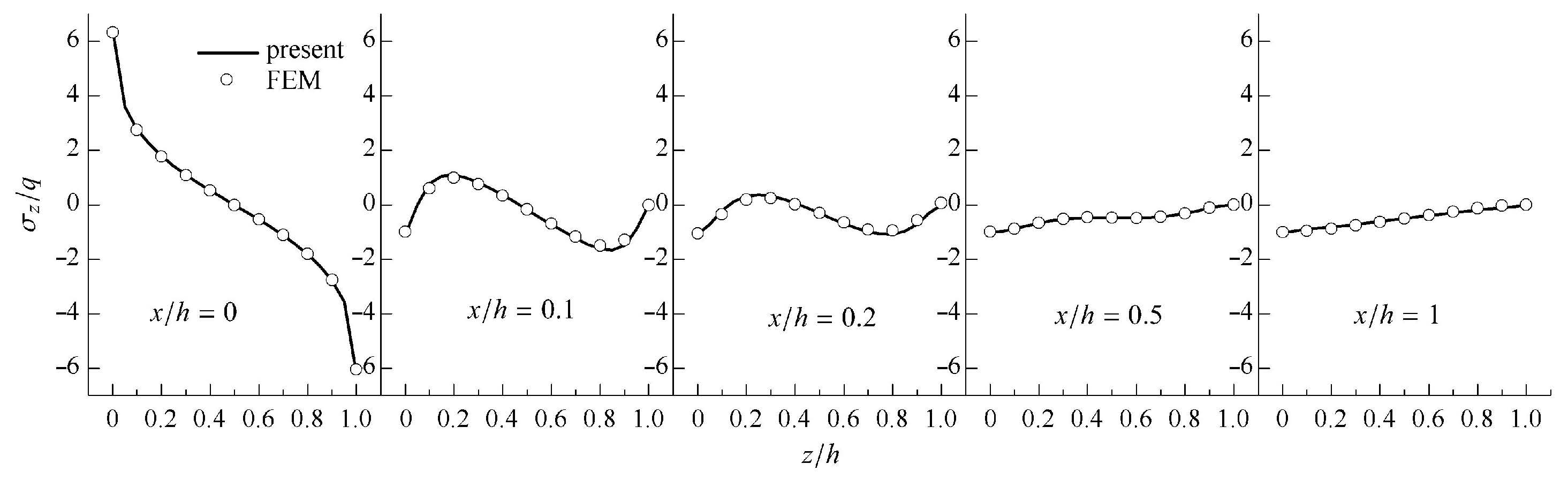
图4和图5分别给出了厚宽比$h/a =0.1$单层板的固支边附近本文解的应力 $\sigma_{z}$和$\tau_{xz}$结果,与有限元解吻合的很好,这是经典板理论无法计算出来的,更加体现了状态空间法的优越性.
|
图 4 固支边附近$\sigma _z $随$x$和$z$的变化情况($h/a =0.1$) Fig. 4 Variation of the stress $\sigma _z $ with $x$ and $z$ near clamped boundary of single plate ($h/a =0.1$) |
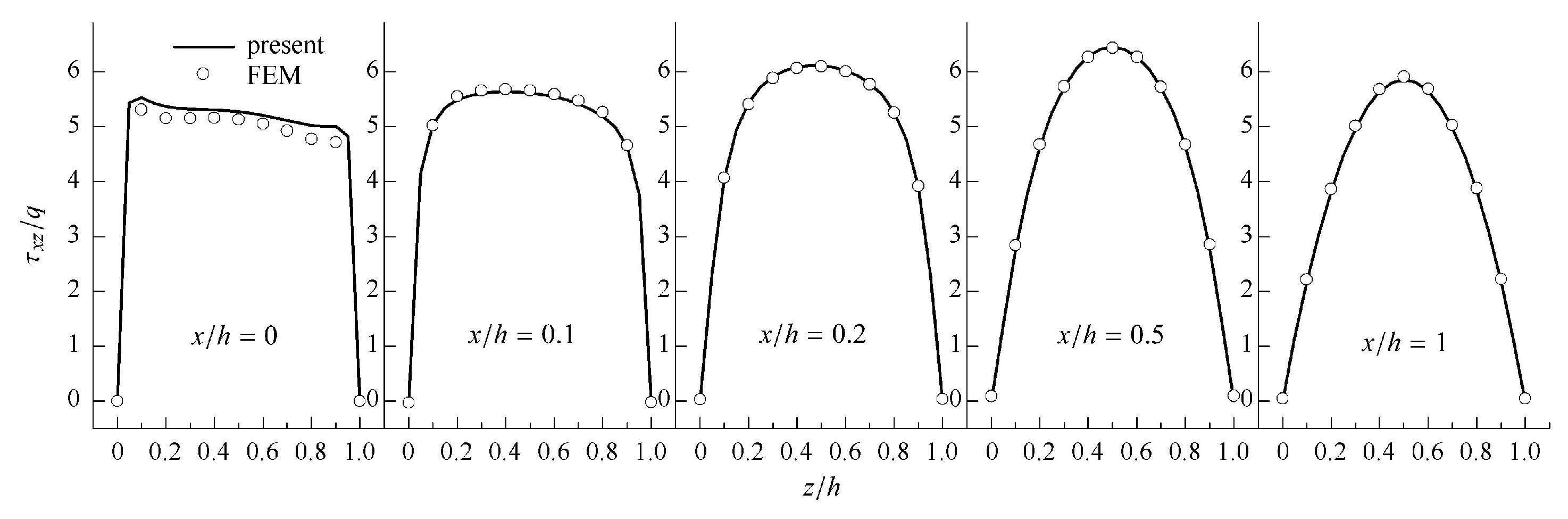
|
图 5 固支边附近$\tau _{xz} $随$x$和$z$的变化情况($h/a=0.1$) Fig. 5 Variation of the shear stress $\tau _{xz} $ with $x$ and $z$ near clamped boundary of single plate ($h/a=0.1$) |
表2给出了厚宽比$h/a =0.1$单层板的本文解中取不同级数项数时的计算结果,当$m$取到49,$n$取到29后,本文解已 基本稳定,本文解的收敛性比文献[13]解好.
| 表 2 取不同的级数项数时单层板内特定点的位移和应力($h/a =0.1$) Table 2 Displacements and stresses under different number of terms for Fourier series ($h/a =0.1$) |
算例2 三层叠合板的上表面受均布压力$q$作用,几何参数为$a=b$,$h_{1}=h_{3}=0.1h$, $h_{2}=0.8h$,厚宽比$h/a$分别取0.4和0.6. 第2层的材料同算例1,第1和第3层的材料相同,材料常数与第2层相应的材料常数的比值均为5,如$ C_{11}^{(1)}/ C_{11}^{(2)} = 5$,其中$C_{11}^{(1)}$和$C_{11}^{(2)}$分别是第1和第2层的$C_{11} $值.
表3给出了文献[13]解、本文解和有限元解的比较. 其中,文献[13]解中对厚宽比$h/a= 0.4$的三层板的各单层分层 数分别为$I_{1}=I_{3} =3$和$I_{2} =10$,对厚宽比$h/a =0.6$的三层板的各单层分层数分别为$I_{1}=I_{3} =4$和$I_{2} =12$,级数项数$m$和$n$分别取到199和29. 本文解中未对各单层进行分层,并且级数项数$m$和$n$只分别取到49和29. 由表3可见,与单层板一样,文献[13]获得较精确的解,需对同一材料层内作分层处理,当厚宽比越大时,需要取更多的分层数. \,\,本文解在不对各单层进行分层且级数项数取得不是很多的情况下,便可得到较好的结果,尤其在固支边处体现得更明显. 计算结果表明,本文解比现有解更精确且收敛速度更快,与有限元解吻合得更好.
| 表 3 三层叠合板的位移和应力 Table 3 Displacements and stresses of laminated plates |
本文在文献[11, 12, 13]的基础上,将固支边的位移函数作为状态变量与同一组$n$的力学量放在一个状态方程中一并求解,从而将非齐次状态方程的求解变成了齐次状态方程的求解,并且省略了求解待定常数的中间过程,使得求解过程更加简单. 本文得到的解在整个固支边上都能严格满足边界条件,同一材料层内不需作分层处理,因而更加精确,尤其对于厚宽比较大的厚板问题体现得更加明显. 此外,对固支边的应力给出了新的计算方法,使计算结果更加精确,并且能够给出固支边的全部应力分布.
本文将同一组$n$的状态方程放在一起求解,使状态方程系数矩阵的阶数增大了很多. 由于本文解中的级数收敛较快,仅需较少的项数就能得到比较精确的结果,求解到结果基本收敛时还是很快的.
本文方法为研究含固支边矩形厚板的精确解提供了一种新的处理方法,只需在固支边添加相应的位移边界函数项,并将其作为状态变量引入状态方程求解,则能得到严格满足三维弹性方程和固支边界条件的精确解,且在固支边上能给出精度更高的边界应力结果.
| [1] | 铁木辛柯, 沃诺斯基著. 板壳理论.《板壳理论》翻译组译. 北京: 科学出版社, 1977 (Timoshenko S, Woinowsky-Krieger S. Theory of Plates and Shells. New York: McGraw-Hill, 1959) |
| [2] | Reissner E. The effect of transverse shear deformation on the bending of elastic plates. Journal of Applied Mechanics, 1945, 12(2): A69-77 |
| [3] | Mindlin RD. Influence of rotatory inertia and shear on flexural motions of isotropic, elastic plates. Journal of Applied Mechanics, 1951, 18(1): 31-38 |
| [4] | Reddy JN. A simple higher-order theory for laminated composite plates. Journal of Applied Mechanics, 1984, 51(4): 745-752 |
| [5] | Reddy JN. A refined nonlinear theory of plates with transverse shear deformation. International Journal of Solids and Structures, 1984, 20(9-10): 881-896 |
| [6] | Srinivas S, Rao AK. Flexure of simply supported thick homogeneous and laminated rectangular plates. Zeitschrift für Angewandte Mathematik und Mechanik, 1969, 49(8): 449-458 |
| [7] | Srinivas S, Rao AK. Bending, vibration and buckling of simply supported thick orthotropic rectangular plates and laminates. International Journal of Solids and Structures, 1970, 6(11): 1463-1481 |
| [8] | Noor AK. Mixed finite-difference scheme for analysis of simply supported thick plates. Computers and Structures, 1973, 3(5): 967-982 |
| [9] | Spencer AJM, Watson P. Buckling of laminated anisotropic plates under cylindrical bending. Journal of the Mechanics and Physics of Solids, 1992, 40(7): 1621-1635 |
| [10] | 钟万勰. 弹性力学求解新体系. 大连: 大连理工大学出版社, 1995 (Zhong Wanxie. A New Systematic Methodology for Theory of Elasticity. Dalian: Dalian University of Technology Press, 1995 (in Chinese)) |
| [11] | 范家让. 强厚度叠层板壳的精确理论. 北京: 科学出版社, 1996 (Fan Jiarang. Exact Theory of Thick Laminated Plates and Shells. Beijing: Science Press, 1996 (in Chinese)) |
| [12] | 范家让, 盛宏玉. 具有固支边的强厚度叠层板的精确解. 力学学报, 1992, 24(5): 574-583 (Fan Jiarang, Sheng Hongyu. Exact solution for thick laminate with clamped edges. Chinese Journal of Theoretical and Applied Mechanics, 1992, 24(5): 574-583 (in Chinese)) |
| [13] | 盛宏玉, 范家让. 具有固支边的强厚度层合板的一种新解法. 计算物理, 1999, 16(6): 682-687 (Sheng Hongyu, Fan Jiarang. A new approach to the thick laminated plates with clamped edges. Chinese Journal of Computational Physics, 1999, 16(6): 682-687 (in Chinese)) |
| [14] | Liew KM, Teo TM. Modeling via differential quadrature method: Three-dimensional solutions for rectangular plates. Computer Methods in Applied Mechanics and Engineering, 1998, 159(3/4): 369-381 |
| [15] | Liew KM, Teo TM, Han J B. Three-dimensional static solutions of rectangular plates by variant differential quadrature method. International Journal of Mechanical Sciences, 2001, 43(7): 1611-1628 |
| [16] | Lu CF, Chen WQ, Shao JW. Semi-analytical three dimensional elasticity solutions for generally laminated composite plates. European Journal of Mechanics A-Solids, 2008, 27(5): 899-971 |
| [17] | Sheng H, Ye J. A semi-analytical finite element for laminated composite plates. Composite Structures, 2002, 57(1-4): 117-123 |
| [18] | Sheng H, Wang H, Ye J. State space solution for thick laminated piezoelectric plates with clamped and electric open-circuited boundary conditions. International Journal of Mechanical Sciences, 2007, 49: 806-818 |
| [19] | Attallah KMZ, Ye J, Sheng H. Three-dimensional finite strip analysis of laminated panels. Computers and Structures, 2007, 85: 1769-1781 |
| [20] | Attallah KMZ, Yu M, Ye J. Three-dimensional state space spline finite strip analysis of angle-plied laminates. Composites(Part B), 2014, 66: 25-35 |
| [21] | 钟阳. 弹性层状体系求解方法. 北京: 科学出版社, 2007 (Zhong Yang. The Solving Method of Elastic Layered System. Beijing: Science Press, 2007 (in Chinese)) |
| [22] | 钟阳, 李锐, 田斌. 矩形中厚板哈密顿体系的一种构造方法及典型算例分析. 应用力学学报, 2009, 26(3): 524-529 (Zhong Yang, Li Rui, Tian Bin. Approach to forming hamiltonian system for rectangular plates with middle thickness. Chinese Journal of Applied Mechanics, 2009, 26(3): 524-529 (in Chinese)) |
| [23] | 田斌, 李锐, 陈凯. 固支三维弹性矩形厚板的精确解. 工程力学, 2012, 29(9): 209-214 (Tian Bin, Li Rui, Chen Kai. Exact solution of clamped three-dimensional elastic rectangular thick plates. Engineering Mechanics, 2012, 29(9): 209-214 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47