多相流体系统广泛存在于自然界和工程领域[1, 2, 3, 4, 5, 6],其基本特点是连续相携带大量的离散相颗粒群一起运动,连续相和离散颗粒相、颗粒相之间存在复杂的相互作用,导致复杂的流动现象和离散相动力学演变过程,如扩散、混合和凝并等. 对于纳米颗粒,当质量浓度不是很高的时候,纳米颗粒的存在对连续相运动几乎没有影响,所以是一个单向耦合的过程,使得问题一定程度的简化. 但此时离散颗粒群的动力学演化过程依然非常复杂. 描述离散相动力学演变过程通常采用颗粒群平衡模拟方法(population balance modeling,PBM)[7]. 均匀流动或静止流体中的颗粒群平衡方程(此时称为零维模型)描述系统中颗粒尺度分布函数的时间演化过程,是一个典型的部分积分微分方程,一般不存在理论分析解,只能求助于数值方法. 目前该方程数值解法主要有矩方法[8]、分区法[9]和蒙特卡洛方法[10]等. 在保证相同精度前提下要得到所需的颗粒群宏观特征量,矩方法的计算效率最高. 如同湍流中的封闭问题,在采用矩方法求解颗粒群平衡方程时,各阶矩方程难以自动封闭. 因解决该封闭问题的方法不同,目前发展的矩方法主要有传统矩方法[8]、积分矩方法[11]、泰勒展开矩方法[12, 13]、直接展开矩方法[14]等等,其中尤以积分矩方法适用范围更广. 借助于理论分析和前述的一些数值模拟方法,零维系统中的颗粒相演化动力学过程研究已经取得了很大的进展.
相对于零维系统,多维系统(此时流场或温度场等是空间非均匀的)中颗粒相的演变过程因其高度复杂性,迄今研究成果报道还很少,少数成果比如采用传统矩方法研究低压化学气相沉积反应器中二氧化硅(SiO2)颗粒的形成和输运问题[15],再如分别采用传统矩方法和泰勒展开矩方法方法研究混合层中纳米颗粒的凝并问题[16, 17],还有采用积分矩方法方法模拟了扩散火焰反应器(diffusion flame reactor)中二氧化钛(TiO2)颗粒的合成过程[18],采用积分矩方法方法研究湍流混合层中气溶胶的成核和生长问题[19]. 因而,对于非均匀多维系统中颗粒的扩散、混合以及动力学演化特性研究还很不充分,需要更多更深入的研究.
本文以纳米颗粒作为离散相,应用泰勒展开矩方法,研究瑞利-贝纳德(Rayleigh--Bènard,RB)热对流系统中颗粒群的扩散、混合以及凝并的行为. 瑞利- 贝纳德对流是从热对流现象中抽象出来的典型的湍流对流模型[20],是指在一个封闭的腔体内,上表面冷却,下表面加热,形成恒定温差,导致腔体内流体流动的现象. 对于该系统中的纳米颗粒,碰撞凝并为导致其数目变化的主要过程,可将其划分为布朗凝并和湍流凝并,而湍流凝并一般对直径大于1μm的颗粒系统有效[21],因此本研究仅考虑布朗凝并的影响. 此外还应考虑流体对颗粒群的输运效应和颗粒群本身的扩散作用. 对于纳米颗粒,其斯托克斯(Stokes)数远小于1,且质量浓度很低,在本论文中不考虑颗粒对流场的影响; 在本文的$Ra$条件下,系统中温度变化较小,忽略其对颗粒扩散及凝并的影响.
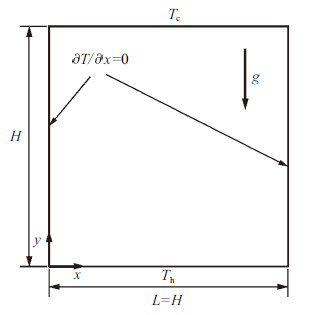
1 数学模型 1.1 控制方程本文所研究问题的物理模型如图1所示,二维矩形区域内充满了不可压缩的气体(本文中气体流动速度较低,因而可以认为其不可压),下底边保持高温而上底边维持低温,左右边壁绝热; 在初始时刻,位于方腔下半区域的纳米颗粒群的尺度分布函数相同.
|
图 1 物理模型示意图 Fig.1 Schematic of nanoparticle in 2-D Rayleigh-Bènard convection |
流动的控制方程为满足布辛涅斯克(Boussinesq)假定的不可压缩纳维- 斯托克斯(Navier--Stokes)方程. 以方腔高度$H$,上下底边温差的绝对值$\Delta T = T_{\rm h} - T_{\rm c}$和类自由落体速度$U = \sqrt{\alpha g\Delta TH}$对方程进行无量纲化,并引入拉普拉斯算子$\nabla^2 = {\partial ^2}/{\partial x^2} + {\partial ^2}/{\partial y^2}$和随体导数${\rm D}/{{\rm D}t} = {\partial }/{\partial t} + u{\partial}/{\partial x} + v{\partial }/{\partial y}$得到气体的无量纲的速度和温度控制方程如下
| $ \left. \begin{array}{l} \frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} = 0\\ \frac{{{\rm{D}}u}}{{{\rm{D}}t}} = - \frac{{\partial P}}{{\partial x}} + \sqrt {\frac{{Pr}}{{Ra}}} {\nabla ^2}u\\ \frac{{{\rm{D}}v}}{{{\rm{D}}t}} = - \frac{{\partial P}}{{\partial x}} + \sqrt {\frac{{Pr}}{{Ra}}} {\nabla ^2}v + T\\ \frac{{{\rm{D}}T}}{{{\rm{D}}t}} = \frac{1}{{\sqrt {PrRa} }}{\nabla ^2}T \end{array} \right\} $ | (1) |
式中瑞利(Rayleigh)数和普朗特(Prandtl)数分别为$Ra = {\alpha gH^3\Delta T}/({\nu \kappa _{\rm g} })$,$Pr = {\nu }/{\kappa _{\rm g} }$; 这里$g$为重力加速度,$\alpha $,$\nu $,$\kappa_{\rm g}$分别为气体的热膨胀系数,动力学黏度系数和热扩散系数.
考虑纳米颗粒的对流、扩散以及布朗凝并的作用,纳米颗粒群的控制方程[1, 21]为
| $ \dfrac{{\rm D}n}{{\rm D}t} = \dfrac{\partial }{\partial x}\left( {D_{\rm fm} \dfrac{\partial n}{\partial x}} \right) + \dfrac{\partial }{\partial y}\left( {D_{\rm fm} \dfrac{\partial n}{\partial y}} \right) + S_{\rm coag}$ | (2) |
其中$n$为颗粒尺度分布函数,为关于位置矢量、时间、颗粒尺度的函数,本文中颗粒尺度为颗粒的体积$\upsilon$; $D_{\rm fm}$为自由分子区颗粒(颗粒的努森(Knudsen)数$Kn$大于10)的扩散系数
| ${D_{{\rm{fm}}}} = \frac{{{{(3/4\pi )}^{1/3}}{k_{\rm{b}}}{T_{\rm{g}}}}}{{{\upsilon ^{2/3}}{\rho _{\rm{g}}}c(1 + \pi {r_{\rm{p}}}/8)}}$ | (3) |
式中,$k_{\rm b} $为玻尔兹曼常数,$\rho_{\rm g}$为气体的密度,$c$为气体分子热运动平均速度,$T_{\rm g}$为气体的温度,由于瑞 利$\!$-$\!$-$\!$贝纳德热对流系统中上下底面温差较小,流体温度取$T_{\rm g}=T_{0}= (T_{\rm h}+T_{\rm c})/2$,$r_{\rm p}$为调节参数,一般由实验测得,这里$r_{\rm p}=0.9$[21]; $S_{\rm coag}$为考虑布朗凝并作用的源项
| ${S_{{\rm{coag}}}} = \frac{1}{2}\int_0^\upsilon {\beta \left( {{\upsilon _1},\upsilon - {\upsilon _1},t} \right)} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n\left( {{\upsilon _1},x,t} \right) \cdot \;n\left( {\upsilon - {\upsilon _1},x,t} \right){\rm{d}}{\upsilon _1} - \int_0^\infty {\beta \left( {{\upsilon _1},\upsilon ,t} \right)} n\left( {{\upsilon _1},x,t} \right) \cdot \qquad \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} n\left( {\upsilon ,x,t} \right){\rm{d}}{\upsilon _1} $ | (4) |
式中$\beta$为碰撞核函数,对于位于自由分子区的纳米颗粒,碰撞核函数为
| ${\beta _{\rm{B}}^{{\rm{fm}}} = {K_{{\rm{fm}}}}{{\left( {{\upsilon ^{1/3}} + \upsilon _1^{1/3}} \right)}^2}{{\left( {\frac{1}{\upsilon } + \frac{1}{{{\upsilon _1}}}} \right)}^{1/2}}}\\ {{K_{{\rm{fm}}}} = {{\left( {\frac{3}{{4\pi }}} \right)}^{1/6}}{{\left( {\frac{{6{k_{\rm{b}}}{T_{\rm{g}}}}}{{{\rho _{\rm{p}}}}}} \right)}^{1/2}}} $ | (5) |
其中,$\rho_{\rm p}$为颗粒的密度,$T_{\rm g}$为气相流体的绝对温度,取为$T_{0}$.
应用泰勒展开矩方法,以初始时刻颗粒尺度分布函数的前三阶矩$M_{00}$,$M_{10}$,$M_{20}$并联合流场的特征尺度对方程进行无量纲化,可以得到
| $ \left. \begin{array}{l} \frac{{{\rm{D}}{M_0}}}{{{\rm{D}}t}} = \sqrt {\frac{{Pr}}{{Ra}}} \frac{1}{{S{c_{\rm{M}}}}}{\nabla ^2}\left( {\frac{{\left( {4 + 5{M_{\rm{C}}}} \right){M_0}{V^{ - 2/3}}}}{9}} \right) + \\ Da\frac{{\left( {65M_{\rm{C}}^2 - 1210{M_{\rm{C}}} - 9223} \right)M_0^2{V^{1/6}}}}{{5184}}\\ \frac{{{\rm{D}}{M_1}}}{{{\rm{D}}t}} = \sqrt {\frac{{Pr}}{{Ra}}} \frac{1}{{S{c_{\rm{M}}}}}{\nabla ^2}\left( {\frac{{\left( {10 - {M_{\rm{C}}}} \right){M_1}{V^{ - 2/3}}}}{9}} \right)\\ \frac{{{\rm{D}}{M_2}}}{{{\rm{D}}t}} = \sqrt {\frac{{Pr}}{{Ra}}} \frac{1}{{S{c_{\rm{M}}}}}{\nabla ^2}\left( {\frac{{\left( {7 + 2{M_{\rm{C}}}} \right){M_2}{V^{ - 2/3}}}}{{9{M_{\rm{C}}}}}} \right) - \\ Da\frac{{\left( {701M_{\rm{C}}^2 - 4210{M_{\rm{C}}} - 6859} \right)M_1^2{V^{1/6}}}}{{2592{M_{{\rm{C0}}}}}} \end{array} \right\}$ | (6) |
式(6)在形式上与文献[17]得出的一致,式中$M_{0}$为颗粒群的数目浓度,$M_{1}$为颗粒群的体积浓度,而二阶矩与颗粒群的瑞利分子散射效率成正比[21]; ${M_{\rm{C}}} = {M_0}{M_2}{M_{{\rm{C0}}}}/M_1^2\$ ,\$ {M_{\rm{C}}}\left( {{M_{\rm{C}}} \ge 1} \right)$的大小表示颗粒群的多分散特性,$M_{\rm C} = 1$ 时,颗粒群为单分散系统; $M_{\rm C} $越大,颗粒群多分散性越强. $V = {M_1}/{M_0 }$,为颗粒群的平均体积. 以下将$M_{0}$,$M_{1}$,$M_{2}$,$M_{\rm C}$和$V$等表征颗粒群宏观统计信息的量统称为颗粒群的特征量.
无量纲参数斯密特(Schmidt)数$Sc_{\rm M}$和达姆科勒(Damköhler)数$Da$分别如下
| $\left. \begin{array}{l} S{c_{\rm{M}}} = \nu V_0^{2/3}/{\kappa _{\rm{p}}},\;\;{\kappa _{\rm{p}}} = {D_{{\rm{fm}}}}{\upsilon ^{2/3}} = \\ Da = \frac{H}{U}\frac{{\sqrt 2 {K_{{\rm{fm}}}}{M_{10}}}}{{V_0^{5/6}}}\\ \frac{1}{{\sqrt {RaPr} }}\frac{{{H^2}}}{{{\kappa _{\rm{g}}}}}\frac{{\sqrt 2 {K_{{\rm{fm}}}}{M_{10}}}}{{V_0^{5/6}}} = \\ \frac{1}{{\sqrt {RaPr} }}\frac{{{H^2}}}{{{\kappa _{\rm{g}}}}}\sqrt 2 {K_{{\rm{fm}}}}{M_{00}}V_0^{1/6} \end{array} \right\}$ | (7) |
式中$Da$的物理意义为对流时间尺度与凝并时间尺度的比值.
方程组(1)和(6)联列后是封闭的,虽然无法求出解析解,但可以进行数值求解. 本文采用``SIMPLE''算法求解流场,分裂法构造 的差分格式求解前三阶矩. 整个算法虽然在对流项的处理上都是一阶精度,但由于本文中涉及到的$Ra$较低,精度完全满足要求. 网格数的选取满足文献[22]提出的速度和温度边界层内网格点数条件,当$1 \times {10^6} \le Ra \le 5 \times {10^6}$,网格数取为120×120,时间步长$\Delta t=0.01$; 当$5 \times {10^6} \le Ra \le 5 \times {10^7}$,网格数取为240×240时间步长$\Delta t=0.005$; 当$6 \times {10^7} \le Ra \le 1 \times {10^8}$,网格数取为320×320,时间步长$\Delta t=0.002$.
1.2 边界条件和初始条件RB系统四周固壁上流动满足无滑移边界条件. 温度在上下底边满足狄利克雷(Dirichlet)边界条件,左右壁面的梯度为0. 颗粒 群的各阶矩在边界上的梯度为0.
在初始时刻,流体温度为$T_{0}$,速度为0,而颗粒尺度分布函数满足对数正态分布,即有
| ${n\left( {\upsilon ,x,y,t} \right) = \frac{N}{{3\sqrt {2\pi } \upsilon \ln {\sigma _0}}}\exp \left( { - \frac{{{{\ln }^2}\left( {\upsilon /{\upsilon _{{\rm{g0}}}}} \right)}}{{18{{\ln }^2}\sigma }}} \right)}\\ {{M_{{\rm{k0}}}} = N\upsilon _{{\rm{g0}}}^{\rm{k}}\exp (9{k^2}{{\ln }^2}{\sigma _0}/2),\;k = 0,1,2}\\ {{\upsilon _{{\rm{g0}}}} = \frac{{M_{10}^2}}{{M_{00}^{3/2}M_{20}^{1/2}}} = \frac{{{V_0}}}{{\sqrt {{M_{{\rm{C0}}}}} }},\;{{\ln }^2}{\sigma _0} = \frac{1}{9}\ln \left( {{M_{{\rm{C0}}}}} \right)}$ | (8) |
其中,$N=M_{00}$为颗粒群的初始数浓度,$\upsilon_{\rm g0}$为几何平均体积,$\sigma _{0}$为颗粒直径分布函数的几何标准差($\sigma _0^3 $为颗粒体积分布函数的几何标准差),这里下角标0表示初始时刻. 取$M_{\rm C0} = {4}/{3}$与文献[17]一致.
2 计算结果及讨论在本文的计算中,分别选取空气和纳米液滴作为气相和颗粒相介质. 当T0=300K,气体的动力学黏度系数$\nu $和热扩散系数$\kappa_{\rm g}$分别为1.59×10-5m2/s,2.25×10-5m2/s, 普朗特数为0.71,气体分子的平均速率c为468m/s; 气体和颗粒的密度$\rho_{\rm g}$和$\rho_{\rm p}$分别为1.16kg/m3和1000kg/m3.
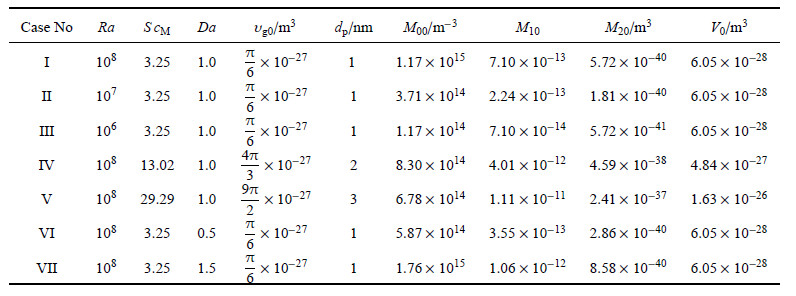
2.1 计算工况本文计算了众多工况(不一一列举了),表1选取了7种主要工况研究无量纲参数$Ra$,$Sc_{\rm M}$和$Da$对颗粒群混合、凝并的影 响. 其中工况I的$Ra$,$Sc_{\rm M}$和$Da$分别为$1\times 10^{8}$,3.25,1.0,而工况II和III相对工况I仅改变$Ra$为10$^{7}$和10$^{6}$,工况IV和V仅改变$Sc_{\rm M}$为13.02和29.29,工况VI和VII仅改变$Da$变为0.5和1.5. 7种工况下的颗粒群几何平均体积及对应的颗粒直径、前三阶矩、平均体积(算术平均)均列于表1.
| 表 1 无量纲参数($Ra$, $Sc_{\rm M}$和$Da$), 初始时刻颗粒群几何平均体积$\upsilon_{\rm g0}$及其对应的颗粒直径,\\前三阶矩$M_{00}$, $M_{10}$, $M_{20}$和平均体积$V_{0}$ Table 1 The non-dimensional parameters ($Ra$, $Sc_{\rm M}$, $Da$) and initial particle geometric mean volume $\upsilon_{\rm g0}$, the corresponding\\diameter $d_{\rm p}$, reference values of moments, $M_{00}$, $M_{10}$, $M_{20}$, and mean particle volume $V_{0}$ |
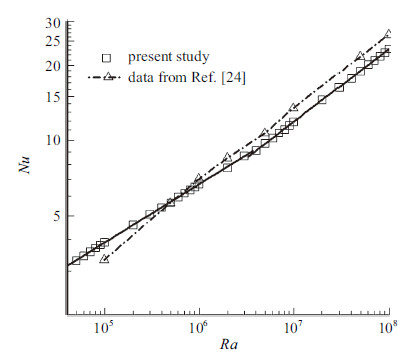
为了验证流场数值模拟结果的准确性,本文计算得到了$Ra$从$5\times 10^{4}$到$1\times 10^{8}$的多种工况下的对流传热参数努塞尔(Nusselt)数$Nu$随$Ra$变化,如图2所示. 结果表明 当5×104≤Ra≤3×106时,$Nu \sim Ra^{0.234}$; 当4×104≤Ra≤1×108时,$Nu \sim Ra^{0.290}$,分别与理论预测[23]的1/4和2/7相近; 而将结果与徐炜等[24]的二维数值结果对比发现两者虽有差别,但后半段的幂数率差距较小,前半段的差距很可能是由后者在该段的计算工况较 少引起的. 这表明了流场的计算结果是合理的. 另外,对颗粒场分布,我们将本文结果与零维情形颗粒分布各阶矩的渐近解进行对比,两者吻合,进一步说明了本文计算的合理性(详见2.4节).
|
图 2 $Nu$与$Ra$关系图 Fig.2 The $Nu$ number vs. $Ra$ number |
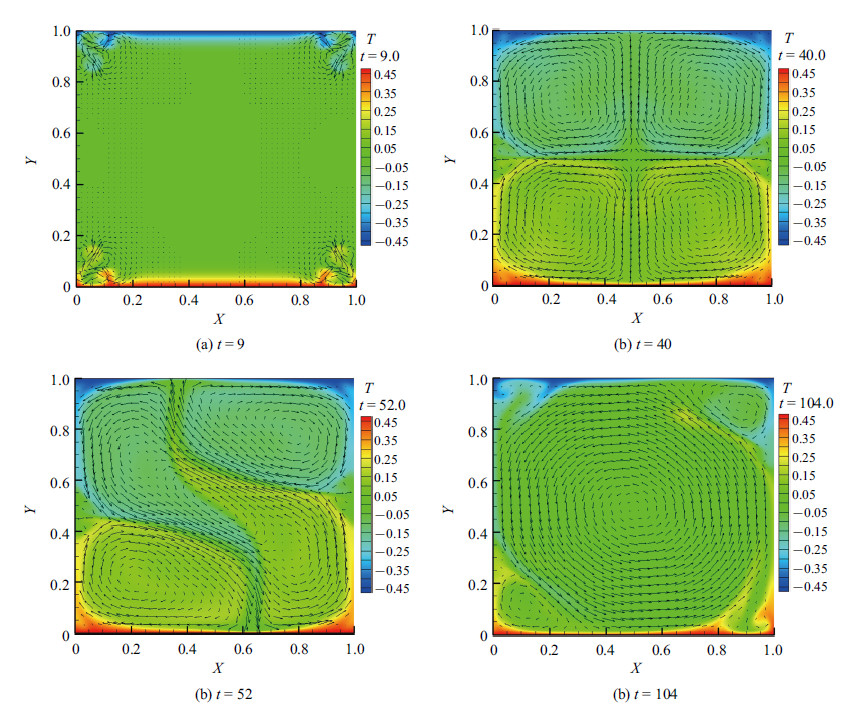
下面,以工况I为例来研究RB对流系统中流场和颗粒场的演化规律. 图3和图4分别给出了几个具有代表性的时刻的温度场、速度场和数目浓度场,根据其演化特征,可以将颗粒群的演化分为三个阶段:
|
图 3 不同时刻下工况I的温度场和速度场(箭头表示速度矢量) Fig.3 The contours of temperature and velocity fields (arrows represent velocity in case I at different times) |
|
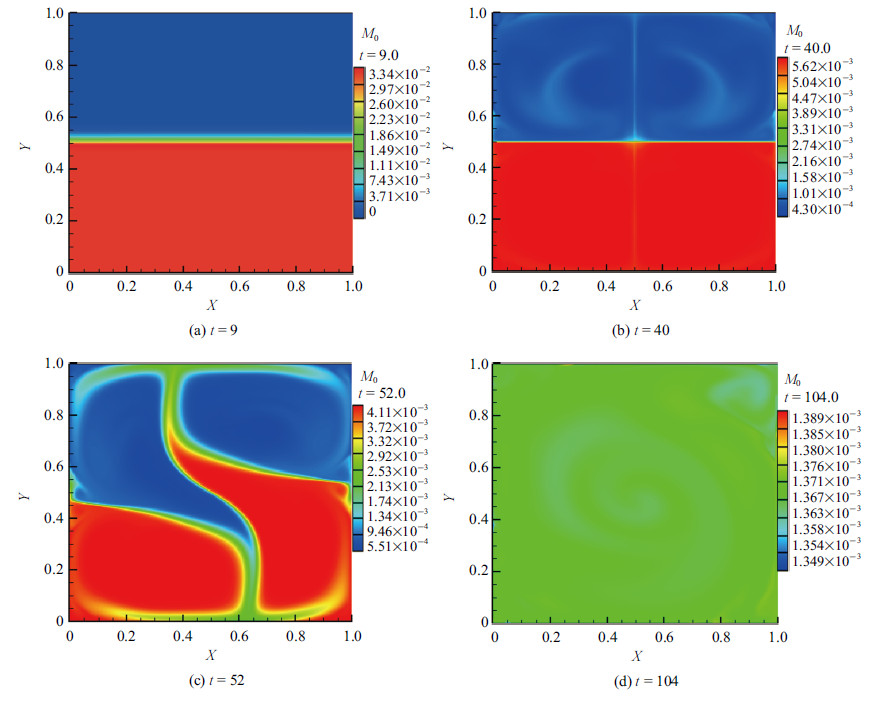
图 4 不同时刻下工况I的颗粒群数浓度云图 Fig.4 The contours of particle number concentration in case I at different times |
(1) 扩散阶段(图3(a),3(b),图4(a),图4(b)). 在流动初始阶段,在方腔四个边角附近产生角涡,温度边界层内的等温面发生凹凸,随着时间的发展,凸起的部分渐渐发展成为蘑菇状的羽流结构,如图3(a)所示; 由于方腔中部流体速度很小,流场对颗粒群空间分布的影响非常小,颗粒群向方腔上半区域缓慢扩散,如图4(a)所示. 随着时间的推进,等温面逐渐往中心区域发展,直至整个温度边界层内都产生往外凸起的局部羽流结构,蘑菇状的羽流在浮力或重力的驱动下向上(热羽流)或向下(冷羽流)运动,方腔中部形成4个中尺度的涡结构,如图3(b)所示; 冷热羽流虽然在方腔中部相遇,但其翻转运动仍分别局限于中尺度涡内,上、下半区域间仍然存在界面,远离界面的颗粒群主要跟随羽流做翻转运动,界面附近的颗粒群一部分通过界面扩散至上半区域,一部分跟随羽流运动,如图4(b)所示.
(2) 混合阶段(图3(c),图4(c)). 上下两股冷热羽流的碰撞引起了流动的不稳定性,冷热羽流在翻转过程中各自分别从某一侧进入到对方区域,如图3(c) 所示; 冷热羽流分别夹带着数浓度较低和较高的颗粒群从某一侧进入下、上半区域,数目浓度较高和较低的颗粒群之间接触界面变大,两者相互混合加快,如图4(c)所示.
(3)充分混合阶段(图3(d),图4(d)). 当冷(热)羽流到达方腔下(上)底板时,将产生更强的流动不稳定性,在上下底板有更多的羽流结构形成,方腔中部 涡结构在冷热羽流碰撞的影响下形成大尺度涡结构,流动逐渐进入大尺度环流状态,如图4(c); 而对于颗粒群数目浓度,随着混合的不断进行,除局部区域外,颗粒群在方腔中空间分布呈现出均匀状态,见图4(d).
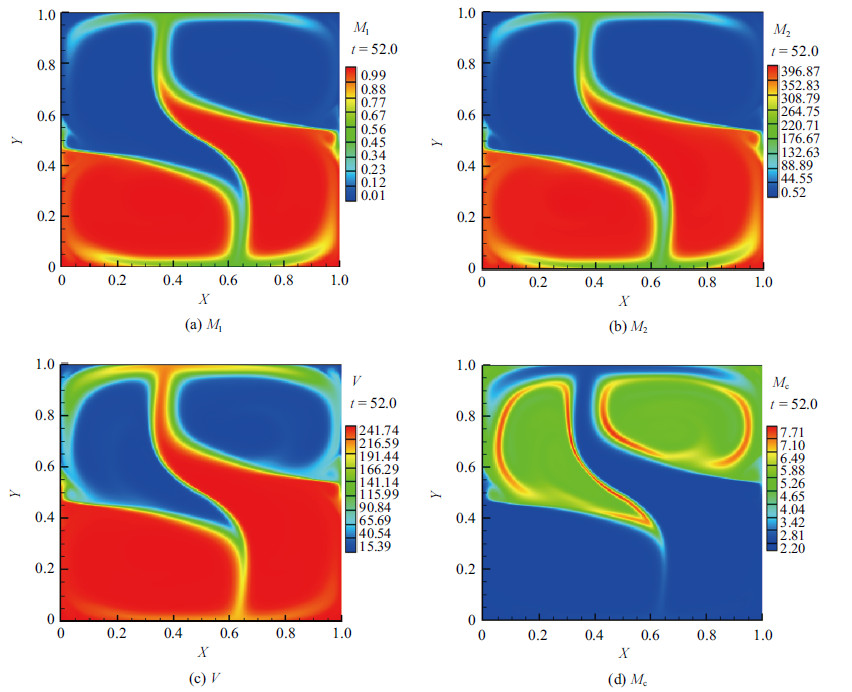
为了分析颗粒群各特征量空间分布的异同,图5给出了t=52时刻的$M_{1}$,$M_{2}$,$M_{\rm C}$和$V$. 对比图4(c)和图5(a)和5(b)前三阶矩的分布,可发现同一时刻颗粒群前三阶矩空间分布极其相似. 而通过对比图5(c)和5(d)可发现一般平均体积大的位置处$M_{\rm C}$相对较小,这是由于在这部分区域凝并为导致其变化的主要原因. 对比图4(c)和图5(d)中可以看到界面附近颗粒群数目较低的一侧的$M_{\rm C}$出现一个峰值,这与与文献[16, 17]在混合层中的结果一致.
|
图 5 $t=52$时颗粒群特征量分布云图(工况I) Fig.5 Contours of moments and mean particle volume at time $t=52$ in case I |
为了进一步研究颗粒场演化3个阶段的典型特征,定义颗粒群特征量与温度之间的相关系数$C_{\rm cor}$,以及各特征 量的空间相对标准偏差$RSD$如下
| ${C_{{\rm{cor}}}^\Phi = \frac{{\int {\int\limits_A {\left( {\Phi - {{\left\langle \Phi \right\rangle }_A}} \right)\left( {T - {{\left\langle T \right\rangle }_A}} \right){\rm{d}}s} } }}{{\sqrt {\int {\int\limits_A {{{\left( {\Phi - {{\left\langle \Phi \right\rangle }_A}} \right)}^2}{\rm{d}}s\int {\int\limits_A {{{\left( {T - {{\left\langle T \right\rangle }_A}} \right)}^2}{\rm{d}}s} } } } } }}}\\ {RSD = \frac{{\sqrt {\int {\int\limits_A {\left( {\Phi - {{\left\langle \Phi \right\rangle }_A}} \right){\rm{d}}s} } } /A}}{{{{\left\langle \Phi \right\rangle }_A}}}}$ | (9) |
式中$C_{{\rm{cor}}}^\Phi $表示$\Phi$与温度$T$的相关系数,$\Phi$为$M_0$,$M_1$,$M_2$,$M_{\rm C}$和 $V$,$\left\langle\cdots \right\rangle _A $表示为某变量对整个区域的平均,$A$为方腔的面积. $ - 1 \le C_{{\rm{cor}}}^\Phi \le 1$,其绝对值越大表明$\Phi $与温度$T$相关性越强; $0 \le RSD \le 1$,其值越接近于0表明颗粒场的空间分布越均匀.
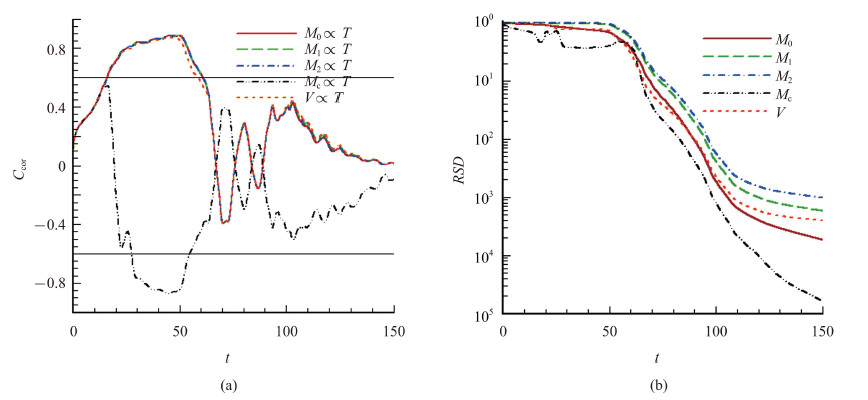
相关系数$C_{{\rm{cor}}}^\Phi $及颗粒群各特征量的相对标准偏差RSD随时间变化见图6. 从图6可以看出相关系数和相对 标准偏差在颗粒场演化的3个阶段具有显著的不同特征. 在扩散阶段相关系数$C_{\rm cor}^\varPhi$绝对值呈增大趋势,颗粒群特征量与温度之间相关特性增强; 颗粒群的混合主要受扩散作用的影响,相对标准偏差下降缓慢. 在混合阶段,由于全区域热对流运动的形成,上部和下部羽流发生相互作用,羽流相关系数$C_{{\rm{cor}}}^\Phi $呈现波动变化,且幅度较大; 相对标准偏差急剧下降,颗粒群混合加快. 在充分混合阶段,由于颗粒群空间分布逐渐趋于均匀状态,相关关系数$C_{{\rm{cor}}}^\Phi $ 绝对值呈减小趋势; 相对标准偏差下降变得缓慢.
|
图 6 (a)相关系数$C_{\rm cor}^\Phi $, (b)相对标准偏差$RSD$随时间演化 Fig.6 (a) The time evolution of correlation coefficient $C_{\rm cor}^\Phi $ and (b) relative standard deviation $RSD$ |
本节将以工况I为例讨论纳米颗粒群在RB系统中长时间演化的渐近行为,并研究无量纲数$Ra$,$Sc_{\rm M}$和$Da$对颗粒 群达到自保持分布时间的影响.
图7实线为工况I条件下颗粒群各特征量的空间平均值随时间变化,从图中可以看出,随着时间的推进,颗粒群数目浓度空间平均值减少,且长时间后以幂函数形式下降; 而$\left\langle {M_2 } \right\rangle _A $以及颗粒群平均体积$\left\langle V \right\rangle _A $增加,长时间演化后以幂函数形式增加; 而$\left\langle {M_{\rm C} } \right\rangle _A$ 先缓慢增大,然后在混合阶段快速增长,而后又急剧变小,最后$\left\langle {M_{\rm C} } \right\rangle _A $趋于不变.

|
图 7 工况I条件下数值解与渐近解比较 Fig.7 The comparison moments between asymptotic solution and numerical solution under case I |
已有研究结果已经证明零维颗粒群在布朗凝并作用下存在自保持分布特性,即当凝并时间足够长时,会出现一种和初始状态无关的颗粒尺度分布形式. 基于此理论,利用泰勒展开矩方法,文献[22]得到颗粒尺度分布函数的矩值渐近解如下
| ${{M_0} = {C_0}K_{{\rm{fm}}}^{ - 6/5}M_1^{ - 1/5}{t^{ - 6/5}}}\\ {{M_2} = {C_2}K_{{\rm{fm}}}^{6/5}M_1^{11/5}{t^{6/5}}}\\ {{M_{\rm{C}}} = 2.20}$ | (10) |
其中$t \to \infty $,$C_0 = 0.31$,$C_2 = 7.02$.
在本文的系统中,当演化至充分混合阶段,颗粒场趋于均匀,即相当于零维颗粒群演化. 将颗粒群特征量的空间平均值应用于式(10),无量纲化后得到
| $\left. {\begin{array}{*{20}{l}} {{{\left\langle {{M_0}} \right\rangle }_A} = {C_0}{2^{3/5}}\left\langle {{M_1}} \right\rangle _A^{ - 1/5}D{a^{ - 6/5}}{t^{ - 6/5}}}\\ {{{\left\langle {{M_2}} \right\rangle }_A} = {C_2}{2^{ - 3/5}}\left\langle {{M_1}} \right\rangle _A^{11/5}D{a^{6/5}}M_{{\rm{C0}}}^{ - 1}{t^{6/5}}}\\ {{{\left\langle V \right\rangle }_A} = C_0^{ - 1}{2^{ - 3/5}}\left\langle {{M_1}} \right\rangle _A^{6/5}D{a^{6/5}}{t^{6/5}}}\\ {{{\left\langle {{M_{\rm{C}}}} \right\rangle }_A} = 2.20,t \to \infty } \end{array}} \right\}$ | (11) |
这里由于质量守恒,$\left\langle {M_1 } \right\rangle _A = 0.5$. 渐近解(11)在图7中以点画线绘出,可以看出在该系统中各阶矩长时间演化结果与渐近解完全吻合,说明流场对纳米颗粒凝并的影响很小.
下面将进一步研究各无量纲参数$Ra$,$Sc_{\rm M}$和$Da$对于颗粒群达到自保持分布的时间影响. 当颗粒群达到自保持分布时,以$\left\langle{M_{\rm C} } \right\rangle _A $ 为例,它应满足如下关系式
| $\left. {\frac{{{{\left\langle {{M_{\rm{C}}}} \right\rangle }_A} - {M_{Ca}}}}{{{M_{Ca}}}} \le 1\% } \right\}$ | (12) |
式中$M_{Ca}$为$M_{\rm C}$的渐近值,为2.20. 基于此判据(与Spicer等[25]给出的类似),得到颗粒群达到自保持分布的时间$t_{a}$与各无量纲参数$Ra$,$Sc_{\rm M}$和$Da$的关系如图8所示.
|
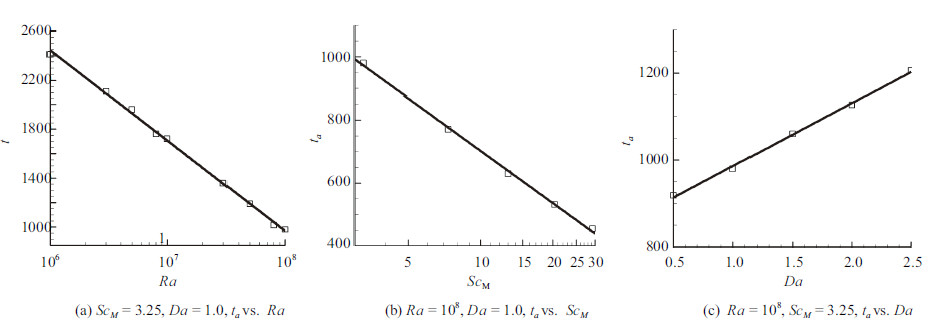
图 8 颗粒群达到自保持分布的时间$t_{a}$与各量纲数$Ra$, $Sc_{\rm M}$和$Da$的关系 Fig.8 The relationship between the time to attain a self-preserving distribution and non-dimensional parameters (i.e., $Ra$, $Sc_{\rm M}$, $Da$) |
图中数据清楚表明,随着$Ra$和$Sc_{\rm M}$的变大,颗粒群达到自保持分布的时间$t_{a}$近似呈对数率减少; 而随着$Da$的变大,$t_{a}$近似线性增加,拟合关系式如下
| $\label{eq13} \left.\begin{array}{l} t_a = 6\,870.87 - 320.39\ln Ra \\ t_a = 1\,255.36 - 240.12\ln Sc_{\rm M} \\ t_a = 8\,641.17 + 114.66Da \\ \end{array}\right\}$ | (13) |
需要指出的是,在RB系统中颗粒分布达到自保持分布的时间依赖于3个无量纲参数, 而式(13)中的简单关系式是固定另外两个参数而计算得到的. 式(13)蕴含的物理含义尚不明确,值得进一步研究.
3 结 论非均匀流动系统中的纳米颗粒扩散、混合和凝并特性的研究迄今还不多,本文结合``SIMPLE''算法和泰勒展开矩方法对低$Ra\left( {1 \times {{10}^6} \le Ra \le 1 \times {{10}^8}} \right)$下RB系统中纳米颗粒群混合和凝并特性进行了详细的数值模拟分析,得到了气相介质的温度和速度场以及纳米颗粒群尺度分布函数各阶矩的演化规律. 主要结果和结论如下:
(1) 纳米颗群的演化过程分为3个不同阶段:扩散阶段,混合阶段,充分混合阶段. 颗粒群各特征量与温度的相关系数以及各特征量空间分布的标准偏差在3个不同阶段特征显著不同. 相关系数在扩散阶段缓慢变大,在混合阶段随流场演化而震荡,而在充分混合阶段单调减小; 对空间分布标准偏差,在扩散阶段下降缓慢,混合阶段快速下降,最后在充分混合阶段趋于稳定.
(2) 纳米颗粒分布函数的各阶矩长时间演化存在渐近行为,且与零维情形的渐近解吻合,说明纳米颗粒群分布最后达到了自保持分布.
(3) 该系统中纳米颗粒群达到自保持分布的时间随着$Ra$和$Sc_{\rm M}$呈对数率减小; 而随着$Da$的变大,近似线性增大.
| [1] | 赵海波, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟. 北京: 科学出版社, 2008, 1-30 (Zhao Haibo, Zheng Chuguang. Population Balance Modeling of Dynamic Evolution in Dispersed System. Beijing: Science Press, 2008, 1-30 (in Chinese)) |
| [2] | Metzger S, Lelieveld J. Reformulating atmospheric aerosol thermodynamics and hygroscopic growth into fog, haze and clouds. Atmospheric Chemistry and Physics, 2007, 7: 3163-3193 |
| [3] | Hanna V, Ilona R. Thermodynamics and kinetics of atmospheric aerosol particle formation and growth. Chemical Society Reviews, 2012, 41: 5160-5173 |
| [4] | Gao Y, Zhang M, Liu Z, et al. Modeling the feedback between aerosol and meteorological variables in the atmospheric boundary layer during a severe fog-haze event over the North China Plain. Atmospheric Chemistry and Physics, 2015, 15: 1093-1130 |
| [5] | 方传波, 夏智勋, 胡建新等. 强迫对流下硼颗粒燃烧特性影响因素研究. 航空学报, 2014, 35: 1-9 (Fang Chuanbo, Xia Zhixun, Hu Jianxin, et al. Influence factors of combustion characteristics of boron particle in forced convective flow. Acta Aeronautica et Astronautica Sinica, 2014, 35: 1-9 (in Chinese)) |
| [6] | Golman B, Julklang W. Simulation of exhaust gas heat recovery from a spray dryer. Applied Thermal Engineering, 2014, 73(1): 899-913 |
| [7] | Shi D, El-Farra NH, Li MH, et al. Predictive control of particle size distribution in particulate processes. Chemical Engineering Science, 2006, 61(1): 261-281 |
| [8] | Lee KW. Change of particle size distribution during Brownian coagulation. Journal of Colloid and Interface Science, 1983, 92(2): 315-325 |
| [9] | Gelbard F, Tambour Y, Seinfeld JH. Simulation of multicomponent aerosol dynamics. Journal of Colloid and Interface Science, 1980, 76(2): 541-556 |
| [10] | Tandon P, Rosner DE. Monte Carlo simulation of particle aggregation and simultaneous restructuring. Journal of Colloid and Interface Science, 1999, 213(2): 273-286 |
| [11] | McGraw R. Description of aerosol dynamic by the quadrature method of moments. Aerosol Science and Technology, 1997, 27(2): 255-265 |
| [12] | 于明州, 江影, 张凯. 湍动剪切微米尺度粒子凝并TEMOM模型研究. 力学学报, 2011, 43(3): 447-452 (Yu Mingzhou, Jiang Ying, Zhang Kai. The study on micro-scale particle coagulation due to turbulent shear mechanism using TEMOM model. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(3): 447-452 (in Chinese)) |
| [13] | Yu MZ, Lin JZ, Chan TL. A new moment method for solving the coagulation equation for particles in Brownian motion. Aerosol Science and Technology, 2008, 42(9): 705-713 |
| [14] | Chen ZL, Lin JZ, Yu MZ. Direct expansion method of moments for nanoparticle Brownian coagulation in the entire size regime. Journal of Aerosol Science, 2014, 67: 28-37 |
| [15] | Suha SM, Zachariaha MR, Girshicka SL. Numerical modeling of silicon oxide particle formation and transport in a one-dimensional low-pressure chemical vapor deposition reactor. Journal of Aerosol Science, 2002, 33(6): 943-959 |
| [16] | Settumba N, Garrick SC. Direct numerical simulation of nanoparticle coagulation in a temporal mixing layer via a moment method. Journal of Aerosol Science, 2003, 34(2): 149-167 |
| [17] | Xie ML, Yu MZ, Wang LP. TEMOM model to simulate nanoparticle growth in the temporal mixing layer due to Brownian coagulation. Journal of Aerosol Science, 2012, 54: 32-48 |
| [18] | Yu MZ, Lin JZ, Chan T. Numerical simulation of nanoparticle synthesis in diffusion flame reactor. Powder Technology, 2008 181(1): 9-20 |
| [19] | Zhou K, Attili A, Alshaarawi A, et al. Simulation of aerosol nucleation and growth in a turbulent mixing layer. Physics of Fluids, 2014, 26: 065106 |
| [20] | 周全, 夏克青. Rayleigh--B′enard 湍流热对流研究的进展、现状 及展望. 力学进展, 2012, 42(3): 231-251 (Zhou Quan, Xia Keqing. Advances and outlook in turbulent Rayleigh--B′enard convection. Advances in Mechanics, 2012, 42(3): 231-251 (in Chinese)) |
| [21] | Friedlander SK. Smoke, Dust and Haze: Fundamentals of Aerosol Dynamics, 2nd ed. New York, Oxford University Press, 2000: 14- 210 |
| [22] | Shishkina O, Stevens RJAM, Grossmann S, et al. Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New Journal of Physics, 2010, 12: 075022 |
| [23] | Ahlers1 G, Grossmann S, Lohse D. Heat transfer & large-scale dynamics in turbulent Rayleigh-B′enard convection. Reviews of Modern Physics, 2009, 81(2): 503-537 |
| [24] | 徐炜, 包芸. 利用FFT 高效求解二维瑞利--贝纳德热对流. 力学学 报, 2013, 45(4): 666-671 (Xu Wei, Bao Yun. An effcient solution for 2-D Rayleigh-B′enard convection using FFT. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(4): 666-671 (in Chinese)) |
| [25] | Xie ML,Wang LP. Asymptotic solution of population balance equation based on TEMOM model. Chemical Engineering Science, 2013, 94: 79-83 |
| [26] | Spicer PT, Pratsinis SE, Trennepohl MD, et al. Coagulation and fragmentation: the variation of shear rate and the time lag for attainment of steady state. Industrial & Engineering Chemistry Research, 1996, 35(9): 3074-3080 |
 2015, Vol. 47
2015, Vol. 47