并列双圆柱流致振动现象广泛地存在于海洋工程和机械工程等诸多领域. 根据圆柱间距比s/D(其中,s为圆柱中心之间的距离,D为圆柱的直径)的不同,两绕流可以分为3种不同的模态[1]. 当间距比较小($s/D<1.1$)时,圆柱间隙内没有旋涡脱落,仅在两圆柱的外侧有交替旋涡脱落,形成单涡街[2, 3]. 当间距比增加到1.2<s/D<2.0时,并列双圆柱后的尾流出现不对称现象,间隙流偏向其中一个圆柱,并在该圆柱后形成较窄的尾流,另一个圆柱后则形成宽尾流[4, 5, 6, 7, 8]. 当圆柱间距进一步增长到$s/D>2.5$时,并列双圆柱后尾流形成两列平行涡街,两圆柱的尾流彼此相似且具有相同脱涡频率,并且根据间距比的不同,旋涡脱落可以是反相的,也可以是同相的,但主要是反相的[4, 5, 7, 8, 9].
Bearman和Wadcock[4]的并列双圆柱绕流实验研究发现,在偏斜间隙流的影响下,并列双圆柱后的尾流呈现为双稳态,间隙流周期性地从一个方向变化到另一个方向. Kim和Durbin[6]将该现象称之为flip-flopping (简称为FF),并进一步研究发现这种间隙流方向偏转来回切换的时间间隔要比旋涡脱落周期大几个量级,且随雷诺数的减小而增加[4, 6, 7, 8, 10]. FF现象中,宽尾流圆柱的脱涡频率和阻力较低,而窄尾流圆柱的脱涡频率和阻力则要大一些,这是因为窄尾流的剪切层卷起时形成的负压区更靠近圆柱的后侧. Williamson[5]对雷诺数200的并列双圆柱绕流实验发现,一定条件下,间隙流始终偏向一个圆柱,而不发生周期性摆动,称为偏斜间隙流 (biased gap flow).
与高雷诺数的FF间隙流偏斜方向切换间隔比旋涡脱落周期大几个量级相比,低雷诺数的FF间隙流方向切换的时间间隔约为几个脱涡周期[11, 12],而且间隙流方向的过渡不再像高雷诺数的那样急剧[11]. Kang[11]对雷诺数40~160的并列双圆柱绕流数值模拟发现,FF现象中的尾流不再具有周期性,呈现为不规律的变化. Carini等[12]研究了雷诺数50~90的并列双圆柱绕流中FF现象的不稳定性来源,认为FF现象的不稳定性来自于两圆柱之间的同相同步旋涡脱落,而不是双稳态中两不对称状态之间的相互作用.
当并列双圆柱自由振动时,由于振动圆柱与周围流体的相互作用,使得圆柱周围的流场更加复杂. Xu等[13]通过数值模拟研究了雷诺数Re=200,间距比s/D在1.2~3.2之间的并列双圆柱受迫振动发现,两圆柱的振动对圆柱尾流模式有非常重要的影响,只有振幅足够大时,振动才会锁定到旋涡脱落频率上. Bao等[14]对雷诺数$Re=100$间距比$s/D$在1.2~4.0之间的并列双圆柱受迫振动研究发现,存在5种不同的流体响应,包括3种非锁定状态和2种锁定状态. Cui等[15]对雷诺数$Re=3\,000$间距比$s/D=3.0$的并列双圆柱流致振动数值模拟研究发现,当圆柱的振动较小时,两圆柱之间的相互作用弱,随着圆柱振幅的增加,两圆柱之间的相互作用增强. Huera-Huarte 和Gharib[16]实验研究了间距比$s/D<5.0$的柔性并列双圆柱流致振动发现,当间距比$s/D>3.5$时,并列双圆柱的振动响应不同步,说明此时两圆柱通过尾流产生的耦合作用非常弱. Chen等[17]对雷诺数$Re=100$间距比$s/D$在2.0~5.0之间的并列双圆柱流致振动进行了详细的数值模拟,研究发现: 当间距比$s/D\geqslant4.0$时,两圆柱之间的相互作用非常弱,此时并列双圆柱响应与单圆柱涡激振动相近. 本文是在前文[17]的基础上展开进一步研究,对并列双圆柱流致振动出现的不对称振动和对称性迟滞现象进行分析.
1 数值方法 1.1 控制方程流固耦合的数值模拟采用浸入边界法[18],控制方程如下
| $\frac{{\partial u}}{{\partial t}} = - \left( {u \cdot \nabla } \right)u - \nabla p + \nu {\nabla ^2}u + f$ | (1) |
| $\nabla \cdot u = 0$ | (2) |
其中,u为速度,t为时间,$p$为压强,$\nu $为运动黏滞系数,$\nabla $为梯度算子,$f$为附加体积力矢量,代表流固耦合边界条件.
对以上控制方程采用二阶精度的Admas-Bashforth时间格式进行离散,可得守恒形式如下
| $\begin{array}{*{20}{l}} {{u^{n + 1}} = {u^n} + \delta t(\frac{3}{2}{h^n} - \frac{1}{2}{h^{n - 1}} - \frac{3}{2}\nabla {p^n} + \frac{1}{2}\nabla {p^{n - 1}}) + }\\ {\;\;\;\;\;\;\;\;\;{f^{n + \frac{1}{2}}}\delta t} \end{array}$ | (3) |
| $\nabla \cdot {u^{n + 1}} = 0$ | (4) |
其中,$h = \nabla \cdot [- uu + \nu (\nabla u + \nabla {u^{\rm{T}}})]$由对流项与扩散项组成,上标T为矩阵转置符号. 附加体积力表示为
| ${f^{n + 1/2}}\delta t = D\{ {V^{n + 1}} - I[{u^n} + \delta t{\mkern 1mu} (\frac{3}{2}{h^n} - \frac{1}{2}{h^{n - 1}} - \qquad \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{3}{2}\nabla {p^n} + \frac{1}{2}\nabla {p^{n - 1}})]\} $ | (5) |
其中,$I$和$D$为插值函数,${V^{n + 1}}$为物面边界的速度,上标$n + 1$,$n + 1/2$,$n$,$n - 1$为时间步.
针对传统浸入边界法施加边界条件精度不高的情况,及春宁等[18]提出了基于嵌入式迭代的浸入边界法,将浸入边界法嵌入到压强泊松方程的迭代求解中,利用压强的中间解比初始值更接近真实值的特点,迭代修正附加体积力,在不显著增加计算耗时的前提下,提高了整个算法的求解精度. 有关浸入边界法的细节,请参考文献[18],此处不再赘述.
对仅做横流向运动的刚性圆柱,其运动方程可以用下述方程来描述
| $m\frac{{{d^2}y}}{{d{t^2}}} + c\frac{{dy}}{{dt}} + ky = {F_y}$ | (6) |
其中,$m$为圆柱质量,$c$为结构阻尼,$k$为弹簧刚度系数,$F_y$为圆柱受到的横流向流体力. 方程采用标准的Newmark-$\beta $法求解.
1.2 问题描述数值模拟的参数为: 雷诺数$Re = 100$,折合流速$U_r = {U_\infty }/{f_n D}$在2.0~10.0之间(其中,$U_\infty$为均匀来流流速,取为1.0; $f_n $为圆柱在真空中的自然频率),圆柱直径$D =1.0$,质量比${m^*} = 4m/({\rho _f}{\rm{ }}\pi {D^2}) = 2.0$,$\rho _f$为流体密度. 两圆柱均为弹性支撑,且仅能在横流向振动. Sen等[19]研究发现,对于单圆柱绕流,当阻流比$B \le 0.01$ ($B = D/H$,$H$为计算域宽度) 时,阻流比对流动特征参数的影响不再显著,因此,本文采用计算域宽 度为200$D$,阻流比$B=0.01$ (按两倍的圆柱直径计算),流向长度为200$D$,加密区域的大小为$4D\times 10D$,如图1所示. 采用正交笛卡尔网格对计算区域划分,$X$ (流向) 和$Y$ (横向) 方向的网格数均为768,加密区域的无量纲网格尺寸$\Delta x / D = \Delta y / D = 1 / 64$.
|
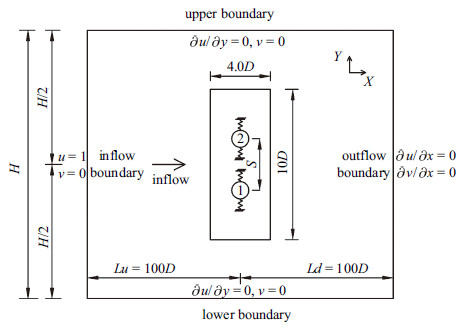
图 1 计算域和边界条件 Fig.1 Computational domain and the boundary conditions |
计算域边界条件设置如下: 入口边界为Dirichlet型边界条件 ($u = 1$,$v =0$); 出口边界为Neumann型边界条件 (${\partial u}/{\partial x}= 0$,${\partial v}/{\partial x} = 0$); 上下边界为滑移边界条件.
为了满足Courant-Friedrichs-Lewy条件,即$CFL = {U_\infty }\Delta t/\Delta x \le 0.5$,时间步长 取为$\Delta t =0.006$.
2 程序验证通过并列双圆柱绕流算例验证本文数值模拟方法的正确性. 算例中,并列双圆柱固定不动,其间距比$s/D $在1.1~2.2之间,$s$为两圆柱中心之间的距离. 来流速度为$U_\infty = 1.0$,圆柱直径$D = 1.0$,雷诺数为$100$. 边界条件、时间步长和网格加密区域与1.2节的相同. 为方便与Kang[11]模拟结果进行对比,验证算例采用的计算域宽度$H=100D$,与Kang[11]相同. 如图2所示,不论阻力系数均方根、升力系数均值和均方根,本文结果与Kang[11]的结果非常接近,验证了本文数值模拟方法的正确性. 需要说明的是,本文采用的数值模型和程序已在文献[17, 18, 20]中针对多种算例 (如单圆柱绕流/涡激振动、串/并列双圆柱绕流/流致振动等) 进行了充分验证,读者可自行查阅.

|
图 2 本文结果与已有文献结果的对比 Fig.2 Comparison of present results with the published data |
并列双圆柱流致振动的最大振动幅值定义为$Y_{\max}=|y_{\max}-y_{\min}|/2$,其中$y_{\max}$和$y_{\min}$分别表示圆柱中心的最大和最小位移.
如图3所示,当间距比为$s/D=2.5$时,并列双圆柱流致振动响应振幅在折合流速${U_r}\le3.0$时很小.当折合流速$U_r>3.0$以后,两圆柱振幅急剧增加,此时两圆柱振幅相同.一直到折合流速$U_r>4.0$时出现了两圆柱振幅不相等情况,随着折合流速的增加,下圆柱(圆柱1)的振幅增加,而上圆柱(圆柱2)的振幅小幅下降.需要指出的是:圆柱振幅或增大或减小由数值模拟的初始条件决定.本文在进行数值模拟时,按照依次增大(或减小)折合流速的顺序进行,即上一个折合流速模拟结束时刻的物理场是下一个折合流速模拟的初始条件.由于本文并没有取一个固定的相位(比如圆柱运动到最大位移处)结束模拟,因此上一折合流速结束的时刻是随机的.这造成了在两圆柱振幅不相等区间内,圆柱振幅增大或减小是随机出现的.例如,本文对$U_r=4.0$增大到$U_r=4.1$的过程进行了多次模拟,出现了两种情况,其一为下圆柱(圆柱1)的振幅增加,而上圆柱(圆柱2)的振幅小幅下降,另一个为上圆柱(圆柱2)的振幅增加,而下圆柱(圆柱1)的振幅小幅下降,分别如图3(a)和图3(b)所示.可见,分叉点存在于$4.0<U_r<4.1$之间,并且一旦圆柱振幅选择了其中的一条路径,随着折合流速的增大,振幅就会沿着该路径变化,不会在两条路径间切换.尽管这种振幅或大或小的随机现象起源于数值模拟的初始条件,但在物理实验中应该是可以观察到的,这是因为双圆柱等幅振动在此工况下是不稳定的,任何小的扰动都会使振动偏向两种不等幅振动情况的一种.为方便讨论,若不加说明,下文所指均为图3(a)的工况.图3的工况与图3(a)的工况相同.在两圆柱振幅不相等区间内,两圆柱振幅相差约0.04$D$,并保持相对稳定.这种圆柱振幅不等的现象一直持续到$U_r=4.8$才消失,此区间($4.0<U_r<4.8$)定义为圆柱振动响应第一不对称区间.

|
图 3 并列双圆柱振幅随折合流速$U_r $的变化 ($s/D=2.5$) Fig.3 The vibration amplitude of two side-by-side circular cylinders versus $U_r$ at $s/D=2.5$ |
进一步地,本文研究了随着折合流速降低两圆柱振幅的变化. 模拟中,折合流速由$U_r= 4.9$逐渐减小至$U_r = 3.9$. 结果发现: 随着折合流速的减小,两圆柱的振幅先是相同,而后在$U_r = 4.4$时两圆柱的振动响应又回到各自增大折合流速时的响应曲线上,一直到$U_r = 4.0$时振幅才重新相等. 可见,在$4.4<U_r<4.8$范围内,增大和减小折合流速时,圆柱振动响应的对称性不同,本文称其为对称性迟滞现象,以与单圆柱的振幅迟滞现象区分. 之所以将其称为对称性迟滞,而不是振幅迟滞,是因为两圆柱的振幅并没有发生明显的跳跃 (约为0.04$D$),只是两圆柱振动的对称性发生了改变,这与单圆柱在振幅迟滞区间内振幅发生较大跳跃 (约为(0.2$\sim $0.4)$D$) 不同. 并列双圆柱流致振动的不对称振动和对称性迟滞现象产生的机理将在3.3节进行详细分析.
在第一不对称区间内,两圆柱均在折合流速$U_r = 4.6$处取得最大值,其中下圆柱的最大振幅为${Y_{\max } }/D = 0.567$,上圆柱的最大振幅为${Y_{\max } }/D = 0.539$. 当折合流速$U_r \geqslant 4.8$之后,两圆柱振幅重新相等,并且随着折合流速的增加,振幅逐渐降低,一直到折合流速$U_r= 7.8$时,两圆柱振幅再次不相等. 此不对称现象在$U_r = 8.2$时消失,本文称此区间 ($7.8 < U_r < 8.2$) 为第二不对称区间. 然而,第二不对称区间范围较窄,并且对应的升阻力系数不相等现象不明显. 更重要地,此时并列双圆柱的振幅不相等来源于两圆柱的不规律振动,限于模拟和统计时长,得到的两个振幅有很小的差别,因此其产生机制并不同于第一不对称区间的. 为此,本文不对其进行过多讨论,而把重点放在第一不对称区间上. 当折合流速$U_r> 8.2$以后,两圆柱振动响应再次重新相等,此时圆柱振幅较小,并随着折合流速的增大缓慢降低. 此工况下,圆柱振动响应的锁定区间为$3.0<U_r< 8.2$.
与间距比$s/D=2.5$的工况相比,间距比$s/D=5.0$工况下,圆柱间距较大,相互作用较弱,并列双圆柱流致振动响应没有出现明显的振幅不对称和对称性迟滞现象. 如图4所示,与单圆柱涡激振动相比,两者的响应振幅较为接近,并列双圆柱的最大振幅均为$Y_{\max}/D=0.56$,与单圆柱涡激振动最大振幅${Y_{\max } }/D = 0.57$基本吻合,而锁定区间为$3.2 < U_r < 8.0$,比单圆柱涡激振动的$3.4 < U_r < 8.4$略微提前. 由此可以认为,当$s/D=5.0$时,并列双圆柱的流致振动可以看做是彼此独立的. Chen等[17]对雷诺数100 的并列双圆柱流致振动研究发现,临界间距比为$s/D=4.0$,当间距比$s/D\geqslant4.0$时,两圆柱之间的相互作用已经非常弱了,这与本文结论相同.

|
图 4 并列双圆柱振幅随折合流速$U_r$的变化 ($s/D=5.0$) Fig.4 The vibration amplitude of two side-by-side circular cylinders versus $U_r$ at $s/D=5.0$ |
如图5所示,当间距比为$s/D=2.5$时,并列双圆柱升力均方根在折合流速$U_r \le 3.0$时较小,而当折合流速$U_r > 3.0$ 以后,升力均方根迅速增加,并在折合流速$U_r = 3.6$处取得最大值1.457. 在第一不对称区间$4.0\le U_r\le4.8$内,两圆柱的升力均方根不相等,出现了与振动响应类似的迟滞现象. 在第一不对称区间内,当下圆柱振幅较大时,下圆柱受到的升力均方根也较大,如图5(a)所示; 相反地,当上圆柱振幅较大,上圆柱受到的升力均方根也较大,如图5(b)所示.

|
图 5 升力均方根随折合流速变化 ($s/D=2.5$) Fig.5 The r.m.s. value of the lift coefficient versus $U_r$ at $s/D=2.5$ |
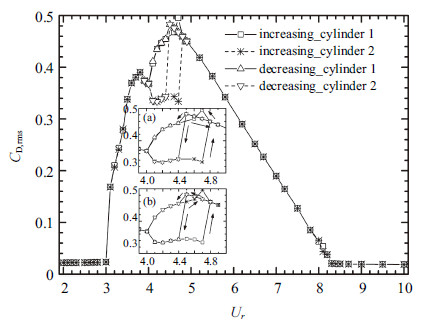
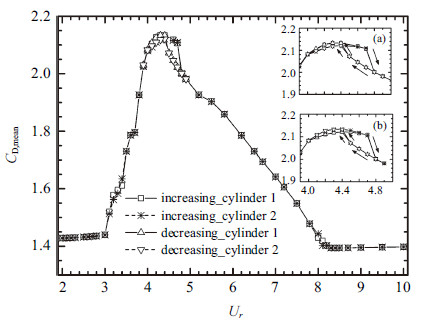
与升力类似,圆柱阻力均方根和均值同样表现出先增大后减小的变化趋势,也出现了不对称和迟滞现象. 在第一不对称区间内,振动幅 值较大的圆柱受到的阻力均方根和均值也较大; 对应地,振动幅值较小的圆柱受到的阻力均方根和均值也较小,如图6和7所示. 与振动响应和升力不同的是,迟滞区间内,减折合流速时的阻力均方根的最大值0.488要稍大于升折合流速时的最大值0.483.
|
图 6 阻力均方根随折合流速变化 ($s/D=2.5$) Fig.6 The r.m.s. value of the drag coefficient versus $U_r$ at $s/D=2.5$ |
|
图 7 阻力均值随折合流速变化 ($s/D=2.5$) Fig.7 The mean drag coefficient versus $U_r$ at $s/D=2.5$ |
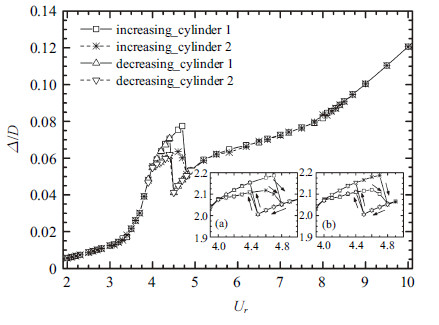
由于圆柱间隙流的作用,两圆柱之间存在排斥力,使得圆柱振动的平衡位置偏离其初始位置. 图8和9分别给出了两圆柱升力均值和振动平 衡位置的偏离量随折合流速变化情况. 此处定义: 下圆柱向下偏离为正,升力也向下为正,上圆柱则相反. 总体来说,随着折合流速的增大,升力均值先增大后减小最终趋于稳定,圆柱振动平衡位置的偏离量则基本表现为单调增大,这与本文通过减小弹簧系数来增大折合流速有关. 升力均值和圆柱振动平衡位置的偏离量在第一不对称区间内存在明显的突变,减流速时对应的折合速度为$U_r=4.4 $,增流速时$U_r=4.8$,恰好对应迟滞区间的开始和结束. 在第一不对称区间内,响应幅值较大的圆柱,升力均值较大,平衡位置偏离量较大,响应振幅较小的圆柱,则升力均值较小,平衡位置偏离量较小. 当折合流速$U_r\ge 8.2$之后,并列双圆柱的平均升力达到了稳定状态,维持在0.15附近.

|
图 8 升力均值随折合流速变化 ($s/D=2.5$) Fig.8 The mean lift coefficient versus $U_r$ at $s/D=2.5$ |
|
图 9 平衡位置无量纲偏移量随折合流速变化 ($s/D=2.5$) Fig.9 The dimensionless shift of the balanced position versus $U_r$ at $s/D=2.5$ |
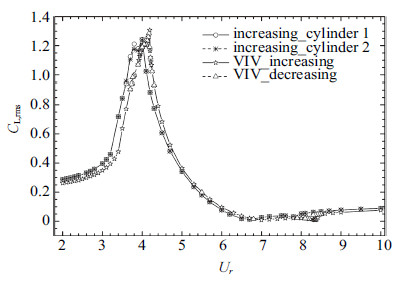
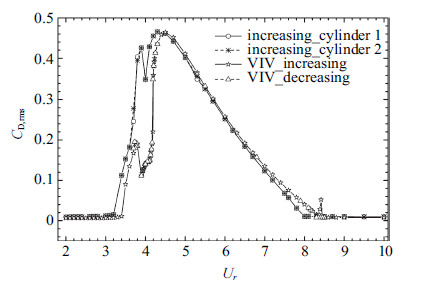
间距比$s/D=5.0$的并列双圆柱流致振动工况中,升力和阻力系数与单圆柱涡激振动的非常接近,没有出现明显的不对称和迟滞现 象,如图10~图12所示. 并列双圆柱的升力均方根的最大值1.243 (在折合流速$U_r=4.0$处取得),与单圆柱涡激振动的升力均方根最大值1.307 (在折合流速$U_r = 4.2$处取得) 接近. 然而,并列双圆柱阻力均值在各折合流速下均要大于单圆柱涡激振动的情况,这是由于临近圆柱的存在一定程度上起到了固壁边界的作用.
|
图 10 升力均方根随折合流速变化 ($s / D = 5.0$) Fig.10 The r.m.s. value of the lift coefficient versus $U_r$ at $s / D = 5.0$ |
|
图 11 阻力均方根随折合流速变化 ($s / D = 5.0$) Fig.11 The r.m.s. value of the drag coefficient versus $U_r$ at $s / D = 5.0$ |

|
图 12 阻力均值随折合流速变化 ($s / D = 5.0$) Fig.12 The mean drag coefficient versus $U_r$ at $s / D = 5.0$ |
如图13所示,圆柱升力均值呈现出先增大后减小的趋势,并在折合流速$U_r = 4.1$处取得最大值0.16. 升力均值在折合流 速$U_r \ge 7.0$以后达到一个稳定值0.05,一直维持到本文模拟的最大折合流速$U_r = 10.0$.

|
图 13 升力均值随折合流速变化 ($s / D = 5.0$) Fig.13 The mean lift coefficient versus $U_r$ at $s / D = 5.0$ |
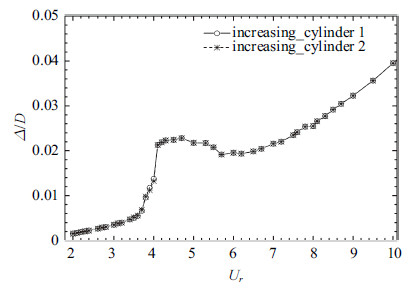
如图14所示,圆柱平衡位置偏离量随着折合流速的增加而增加,一直到折合流速$U_r=4.7$达到局部极大 值$\Delta /D = 0.022{\mkern 1mu} 8$,然后随着折合流速增加而开始下降,在折合流速$U_r=5.7$达到一个局部极小值$\Delta/D = 0.019\,2$,之后随着折合流速的增加又开始增加,与$s / D = 2.5$的情况类似.
|
图 14 平衡位置无量纲偏移量随折合流速变化 ($s / D = 5.0$) Fig.14 The dimensionless shift of the balanced position versus $U_r$ at $s / D = 5.0$ |
由于间距比$s / D = 5.0$的并列双圆柱流致振动没有出现不对称振动和对称性迟滞现象,增大折合流速的响应曲线和减小折合流速的重合,为了表示清楚,图10~图14未给出减小折合流速的情况.
3.3 不对称振动和对称性迟滞现象的产生机制当折合流速$4.0<U_r<4.8$时,并列双圆柱的振动是不对称的,此时一个圆柱的振幅较大,受到的升力和阻力也较大,振动平衡位置偏移初始位置也较远; 与之相反,另一个圆柱的振幅则较小,受到的升力和阻力也较小,振动平衡位置偏移初始位置也较近. 从尾涡模式的角度对圆柱的不对称振动进行 分析. 图15给出了圆柱尾流的瞬时涡量图,箭头表示圆柱运动方向,上下横线分别表示圆柱振动的最大和最小位移位置,中横线表示圆柱振动的平衡位置. 当折合流速$U_r= 4.0$时,圆柱后脱涡为反相同步模式,尾流为两列平行涡街,并关于两圆柱的中心线对称,中间旋涡消散速度较快; 当折合流速$U_r = 4.1$时,圆柱后尾流呈现出明显的不对称,从并列双圆柱的间隙脱落的旋涡偏向下圆柱,并且这种偏斜不随时间变化,这与并列圆柱绕流的偏斜尾流模式有相似之处. 圆柱的后侧形成两列涡街,其中一列涡街的宽度要明显大于另外一列. 与外侧旋涡相比,内侧旋涡的消散要更快,这是由于两个反向旋转的内侧旋涡距离较近,耗散作用明显所致. 进一步研究发现,该尾流模式并不是完全反相的,两列涡街漩涡脱落的相位差维持在150$^\circ$左右. 当下圆柱运动到最大位移(负)并脱落旋涡时,上圆柱尚未达到最大位移(正),可见下圆柱旋涡脱落要早于上圆柱. 由于下圆柱较早脱落的旋涡产生较低的压强,吸引上圆柱脱落旋涡向下偏斜运动,形成偏斜间隙流. 当折合流速$U_r = 4.8$时,圆柱后的旋涡脱落为同相同步模式,尾流关于两圆柱的中心线对称,从圆柱间隙脱落的漩涡受到从外侧脱落的同向旋转漩涡的吸引被逐渐拉长,并最终分裂为两部分,当内侧漩涡很快消散后,形成由外侧漩涡构成的单涡街.

|
图 15 不同折合流速下并列双圆柱流致振动的尾流模式 ($s/D = 2.5$) Fig.15 Wake patterns of flow-induced vibration of two side-by-side circular cylinders with different reduced velocities at the spacing ratio $s/D =2.5$ |
并列双圆柱中出现的振幅不对称现象是由于尾流的不对称引起的. 如图15(b) 所示,对于窄尾流的圆柱,脱涡间距较短,旋涡脱落形成 的负压区距离圆柱更近,圆柱受到的升力和阻力较大,使得振幅较大; 相反,对于宽尾流的圆柱,脱涡间距较长,旋涡脱落形成的负压区距离圆柱较远,圆柱受到的升力和阻力较小,使得振幅较小.
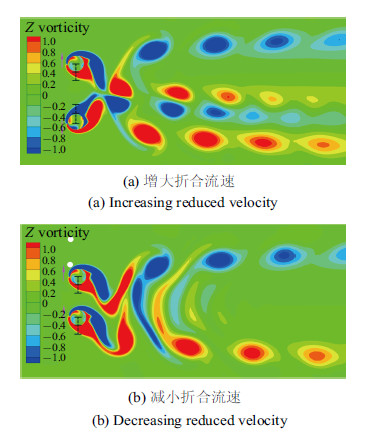
圆柱流致振动的尾流模态具有一定的``惯性'',即随着折合流速的变化,尾流模态倾向于维持原有的状态,当外部因素的改变超出 尾流模态维持原有状态的承受能力后,尾流模态将发生突变. 如图16所示,在同一个折合流速$U_r= 4.6$下,增大和减小折合流速时,圆柱的尾流模态不同,具体为: 增大折合流速时,尾流模式为稳定 的偏斜流模式,与更低折合流速下的尾流模式相同; 当减小折合流速时,尾流为同步同相模式,与更高折合流速下的尾流模式相同. 不同的尾流模式导致圆柱的振动响应和受力对称性不同,对称性迟滞现象出现.
|
图 16 $U_r = 4.6$时增大和减小折合流速并列双圆柱流致振动的尾流模式 ($s/D = 2.5$) Fig.16 Wake patterns of flow-induced vibration of two side-by-side circular cylinders with increasing and decreasing reduced velocities at $U_r = 4.6$ and $s/D = 2.5$ |
通过并列双圆柱绕流验证了本文数值方法的正确性. 对雷诺数100间距比$s/D=2.5$和5.0并列双圆柱流致振动展开了深入研究,主要结论概括如下:
(1) 间距比$s/D=2.5$时,并列双圆柱流致振动中出现了不对称振动和对称性迟滞现象. 其中,不对称振动的折合流 速区间为$ 4.0 <U_r< 4.8$,对称性迟滞对应的折合流速区间为$4.4<U_r <4.8$.
(2) 与振动响应相似,升力和阻力参数也在相同的折合流速区间内出现了不对称和迟滞现象.
(3) 通过对圆柱受力和尾流模式进行分析,解释了并列双圆柱流致振动中的不对称振动和对称性迟滞现象的产生机制. 两圆柱脱涡不完 全反相,其中一个圆柱的脱涡要早于另一个圆柱,造成间隙流稳定地偏斜,形成宽/窄尾流模式; 窄尾流圆柱的脱涡间距短,脱涡位置更靠近圆柱,圆柱受到的升阻力较大,造成圆柱的振幅较大; 相反,宽尾流圆柱的脱涡间距长,脱涡位置距离圆柱更远,圆柱受到的升阻力较小,造成圆柱的振幅较小. 圆柱的尾流模式具有一定的``惯性'',倾向于维持原有的状态,这是形成对称性迟滞现象的原因.
(3) 间距比$s/D=5.0$时,并列双圆柱流致振动响应和受力与单圆柱涡激振动的非常接近,不对称振动和对称性迟滞现象消失.
尽管单圆柱涡激振动的研究成果丰富,并列双圆柱涡激振动由于控制参数众多、机理复杂,其研究成果仍不完备,本文所发现的不对称振 动和对称性迟滞现象对于丰富和完善并列双圆柱涡激振动理论具有一定的价值.
| [1] | Sumner D. Two circular cylinders in cross-flow: A review. Journal of Fluids and Structures, 2010, 26: 849-899 |
| [2] | Sumner D, Wong SST, Price SJ, et al. Fluid behavior of side-by-side circular cylinders in steady cross-flow. Journal of Fluids and Structures, 1999, 13: 309-338 |
| [3] | Alam MM, Zhou Y. Flow around two side-by-side closely spaced circular cylinders. Journal of Fluids and Structures, 2007, 23: 799-805 |
| [4] | Bearman PW, Wadcock AJ. The interaction between a pair of circular cylinders normal to a stream. Journal of Fluid Mechanics, 1973, 61: 499-511 |
| [5] | Williamson CHK. Evolution of a single wake behind a pair of bluff bodies. Journal of Fluid Mechanics, 1985, 159: 1-18 |
| [6] | Kim HJ, Durbin PA. Investigation of the flow between a pair of circular cylinders in the flopping regime. Journal of Fluid Mechanics, 1988, 196: 431-448 |
| [7] | Alam MM, Moriya M, Sakamoto H. Aerodynamic characteristics of two side-by-side circular cylinders and application of wavelet analysis on the switching phenomenon. Journal of Fluids and Structures, 2003, 18: 325-346 |
| [8] | Zhou Y, Zhang HJ, Yiu MW. The turbulent wake of two side-by-side circular cylinders. Journal of Fluid Mechanics, 2002, 458: 303-332 |
| [9] | Meneghini JR, Satara F, Siqueira CLR, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements. Journal of Fluids and Structures, 2001, 15: 327-350 |
| [10] | Chen L, Tu JY, Yeoh GH. Numerical simulation of turbulent wake flows behind two side-by-side cylinders. Journal of Fluids and Structures, 2003, 18: 387-403 |
| [11] | Kang S. Characteristics of flow over two circular cylinders in a side-by-side arrangement at low Reynolds numbers. Physics of Fluids, 2003, 15: 2486-2498 |
| [12] | Carini M, Giannetti F, Auteri F. On the origin of the flip-flop instability of two side-by-side cylinder wakes. Journal of Fluid Mechanics, 2014, 742: 552-576. |
| [13] | Xu YS, Liu Y, Xia Y, et al. Lattice-Boltzmann simulation of two-dimensional flow over two vibrating side-by-side circular cylinders. Physical Review E, 2008, 78: 046314 |
| [14] | Bao Y, Zhou D, Tu JH. Flow characteristics of two in-phase oscillating cylinders in side-by-side arrangement. Computers & Fluids, 2013, 71: 124-145 |
| [15] | Cui ZD, Zhao M, Teng B. Vortex-induced vibration of two elastically coupled cylinders in side-by-side arrangement. Journal of Fluids and Structures, 2014, 44: 270-291 |
| [16] | Huera-Huarte FJ, Gharib M. Flow-induced vibrations of a side-by-side arrangement of two flexible circular cylinders. Journal of Fluids and Structures, 2011, 27: 354-366 |
| [17] | Chen WL, Ji CN, Xu WH, et al. On the responses and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar flow. Journal of Fluids and Structure, 2015, 55: 218-236 |
| [18] | 及春宁, 刘爽, 杨立红等. 基于嵌入式迭代的高精度浸入边界法. 天津大学学报, 2014, 47(5): 377-382 (Ji Chunning, Liu Shuang, Yang Lihong, et al. An accurate immersed boundary method based on built-in iterations. Journal of Tianjin University, 2014, 47(5): 377-382 (in Chinese)) |
| [19] | Sen S, Mittal S, Biswas G. Steady separated flow past a circular cylinder at low Reynolds numbers. Journal of Fluid Mechanics, 2009, 620: 89-119. |
| [20] | 及春宁, 陈威霖, 黄继露等. 串列双圆柱流致振动的数值模拟及其耦合机制. 力学学报, 2014, 46 (6) : 862-870 (Ji Chunning, Chen Weilin, Huang Jilu, et al. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 862-870 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47