2. 重庆大学动力工程学院, 重庆400044
长方体腔内热对流因广泛存在于核动力工程、微电子设备冷却、蓄能技术等诸多领域而日益受到重视,其流动过程具有复杂的非线 性特点[1]. 对于水平温差下的长方体腔内自然对流已有较多研究,且取得了丰硕的成果. 有人对水平温度梯度下长方体腔内自然对流进行了三维数值模拟,得到了不同瑞利数(Rayleigh number) Ra下的流场和温度场分布[2]. 王小华等[3]和孔祥言等[4]研究了长方体腔内自然对流的分岔过程,指出流动分岔的拓扑结构随着Ra的增大呈现出复杂的特性. 与只要存在水平温差就会产生自然对流不同,在竖直温差作用下,液层只有在温差超过某一临界值时才会发生流动,这种热对流称之为 瑞利-贝纳德(Rayleigh-Bènard)对流. 早在19世纪初,有学者确定了无限大水平流体层中瑞 利-贝纳德对流发生的临界$Ra=1\,708$,且流动结构与$Ra$有关[5]. 封闭腔内的瑞利-贝纳德对流因腔体侧壁的作用具有更加丰富的动态行为. 有人采用数值模拟和实验观测研究了长方体腔内空气的瑞利-贝纳德对流,发现了流动和换热的非线性 振荡形式,确定了稳定区域$ \to $单倍周期区域$ \to $多倍周期区域和混沌区域的流动序列[6, 7]. 相同模型下,一些学者还发现了非稳态流动向稳定流动的逆转变,并指出流场在空间上分布的改变是导致该现象的主要 原因[8, 9]. 另一些学者讨论了普朗特数(Prandtl number)Pr对方形腔内瑞利-贝纳德对流的影响,得出了Pr对瑞利-贝纳德对流结构及其稳 定特征的影响规律[10, 11]. 近年来,瑞利-贝纳德对流丰富的流动结构及其转变过程逐渐受到学者们的广泛关注[12, 13, 14]. 有人通过实验观测到了圆柱体腔内瑞利-贝纳德对流所出现的``二涡卷''、``三幅流''和``脉冲轮辐''等多种流动结 构[15]. 还有人进一步对圆柱体腔内瑞利-贝纳德对流进行了数值模拟,获得了Ra < 30000时的各种稳定对流型态,证实了瑞利-贝纳德对流流动结构的多样性[16, 17]. 另外,宁利中等[18]探讨了长方体腔内具有热扩散效应的混合流体的瑞利-贝纳德对流,同样发现了流动的多解现象.
上述研究中,流体的密度通常采用布辛尼斯克(Boussinesq)假设,即针对的是密度随温度线性变化的常规流体. 然而,工业生产中也 存在如纯水、液氦、碲镉汞合金熔体等在某特定温度下有密度极值的特殊工质,例如,纯水的密度在温度低于约4℃时随温度的 增加而增大,在4℃附近时达到最大值,然后随温度的增加而减小,这种密度倒置特性使得热对流流动与传热特性变得更加复杂. 目前,针对具有密度极值流体的热对流研究主要集中在水平温差作用下的矩形腔内[19, 20, 21]. 有人实验研究了长方体腔内冷水在密度最大值附近时的自然对流,结果表明,密度倒置特性对温度场和流型具有重要影 响[22]. 另有人对侧壁为不完全热源及冷源时矩形腔内冷水的自然对流进行了数值模拟,发现了具有密度极值流体特有的双胞流 动结构,并指出热源位于壁面中间时传热效果最好,而冷源位置对传热效果影响较小[23, 24]. 最近,有学者通过对不同几 何结构环形腔内冷水自然对流的研究发现,冷水密度极值的存在削弱了流体流动强度、进而使得壁面传热性能有所减弱,并指出瑞 利-贝纳德对流不稳定性是流动失稳的主要因素[25, 26]. 目前,关于具有密度极值流体的瑞利-贝纳德对 流的研究还十分缺乏. 有人通过对密度极值靠近冷壁时圆柱体腔内冷水瑞利-贝纳德对流数值模拟发现了``四 涡卷''、``脸谱''和``十字镖''等8种流动结构[27],当$Ra$变化时,这些流型也会相互转变. 本文拟通过对长方体腔 内冷水瑞利-贝纳德对流的三维数值模拟,分析密度极值特性、$Ra$、热边界条件以及宽深比对瑞利-贝纳德对流 的影响,揭示长方体腔内具有密度极值流体瑞利-贝纳德对流的复杂特性.
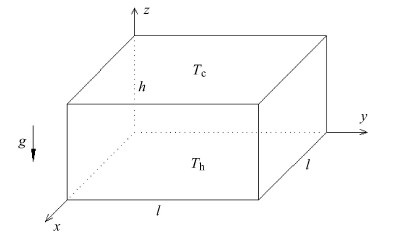
1 物理数学模型物理模型如图1所示,长方体腔体内充满了具有密度极值的冷水,底面为正方形,边长为l,高为h,宽深比$L=l/h$. 腔体上壁为温 度为$T_{\rm c}$的冷壁,下壁为温度为$T_{\rm h}$的热壁,且$T_{\rm c}$和$T_{\rm h}$关于密度最大值所对应的温度$T_{\rm m}$对称,侧壁为完全绝热或完全导热. 为简化起见,采用以下假设:(1)冷水为不可压缩牛顿流体;(2)在所计算参数范围内,流动为三维层流;(3)壁面处流体速度 为零,满足无滑移边界条件;(4)浮力项中的密度随温度呈非线性变化,其余物性参数都为常数.
|
图 1 物理模型 Fig.1 Physical model |
浮力项中冷水的密度采用文献[28]提出的非线性公式
| $\rho = {\rho _{\rm{m}}}{\rm{ }}\left( {1 - \gamma {{\left| {T - {T_{\rm{m}}}} \right|}^q}} \right)$ | (1) |
式中,密度最大值 $\rho _{\rm m}=999.972$kg/m$^{3}$,其对应的温度${T_{\rm{m}}} = 4.03$℃,热膨胀系数 γ=9.297173×10-6(℃)-q,指数$q=1.894\,816$. 另外,其余热物性参数在所研究范围内变化较小,均取Tm-4.03℃作为参考温度时的值.
基于上述假定,无量纲参考长度、速度、时间及压力分别采用$h$,$\nu /h$,$h^{2}/\nu $和 $\nu \mu /h^{2}$,则对应的无量纲控制方程为
| $\nabla \cdot V = 0$ | (2) |
| ${\partial _\tau }V + V \cdot \nabla V = - \nabla P + {\nabla ^2}V + (Ra/Pr){\left| {\Theta - {\rm{ }}{\Theta _{\rm{m}}}} \right|^q}{e_Z}$ | (3) |
| ${\partial _\tau }{\rm{ }}\Theta + V \cdot \nabla {\rm{ }}\Theta = {\nabla ^2}\Theta /Pr$ | (4) |
式中,$V,\tau ,P$和$\Theta $ 分别为无量纲速度矢量、无量纲时间、无量纲压力及无量纲温度,$\Theta = (T-T_{\rm c})/(T_{\rm h}-T_{\rm c})$. 无量纲控制参数$Ra$和$Pr$和密度倒置参数分别定义为$ Ra = g\gamma \left| { {T}_{\rm h} - {T}_{\rm c} } \right|^qh^3 / \left( {\alpha \nu } \right)$,$Pr= \nu/a$,$\Theta_{\rm m}=(T_{\rm m} - T_{\rm c})/(T_{\rm h}-T_{\rm c})$,其中,特别引入 $\Theta_{\rm m}$来描述具有密度极值流体的密度倒置特性,本文中腔体冷、热壁温关于温度$T_{\rm m}$对称,即$\Theta _{\rm m}=0.5$. 另外,$\nu $,$\alpha $ 和${e_Z}$分别为运动黏性系数、热扩散率以及Z方向单位矢量.
如前所述,对应的无因次边界条件为:上、下壁温度分别维持在 $\Theta =0$和 $\Theta =1$,侧壁采用绝热或导热边 界条件,所有固壁满足无滑移条件. 在计算过程中,首先以导热状态为初始状态进行计算,再以导热态一次分岔生成的流型为初始解,计算后续分岔序列出现的流动型态.
底部热壁平均努塞尔数 (Nusselt number) $Nu_{\rm ave}$定义为
| $N{u_{{\rm{ave}}}} = - \frac{1}{{{L^2}{\tau _{\rm{P}}}}}\int {_\tau ^{\tau + {\tau _{\rm{p}}}}} {\rm{ }}\int {_0^L} \int {_0^L} {\left| {\frac{{\partial \Theta }}{{\partial Z}}} \right|_{Z = 0}}{\rm{d}}X{\rm{d}}Yd\tau $ | (5) |
式中,$\tau_{\rm p}$为无因次振荡周期.
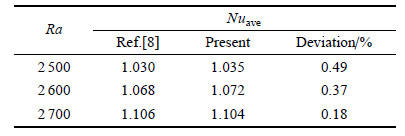
采用有限容积法对控制方程进行求解,扩散项采用中心差分格式,对流项采用``QUICK''格式,压力-速度修 正采用``SIMPLE''算法. 无因次时间步长根据流动转变过程进行调整,介于1×10-4和5×10-3之间,同一时间步长内,收敛标准为温度和速度前后两次迭代的相对误差均需小于10×-5. 经过网格收敛性验证,对于L =1的长方体腔选取网格数为68000,L =2时选取网格数为215000. 为了验证计算结果正确性,在与文献[8]相同条件下对常规流体瑞利-贝纳德对流进行了计算,得到了 不同$Ra$下壁面平均$Nu$,如表1所示,显然两者相差在0.5%以内,因此,计算结果是可靠的.
| 表 1 常规流体瑞利-贝纳德对流壁面平均Nu对比 Table 1 Comparison of the average Nusselt number for R-B convection of common fluid |
首先以导热状态为初始条件,通过改变$Ra$施加扰动,计算$Ra \le 3 \times {10^5}$范围内不同的流动型态. 对于L =1、侧壁为绝热时的长方体腔,当$Ra <26\,400$时,流体层处于静止状态,流体间传 热模式为沿竖直方向的导热模式. 当$Ra \le 26{\mkern 1mu} 400$时,流体开始流动,对流传热为主要的传热模式. 与文献[10]报道的常规流体瑞利-贝纳德对流系统流 动开始的临界$Ra$为$Ra_{\rm cri}=3\,350$相比可知,具有密度极值冷水瑞利-贝纳德对流的临界$Ra$有较大幅 度的增加. 对于具有密度极值的瑞利-贝纳德对流系统而言,密度极值点位于流体层中部,流体层上部密度梯度方向与温度梯度 方向相同,密度随温度增加而增大,对流不易形成,而流体层下部则与常规流体情况相似,即密度梯度方向与温度梯度方向相反,密度随温度增加而减小,流体受热上升,对流容易形成. 正是由于上部稳定流体层的抑制作用,使得具有密度极值流体 瑞利-贝纳德 对流系统更加稳定,流动开始的临界$Ra$较大.
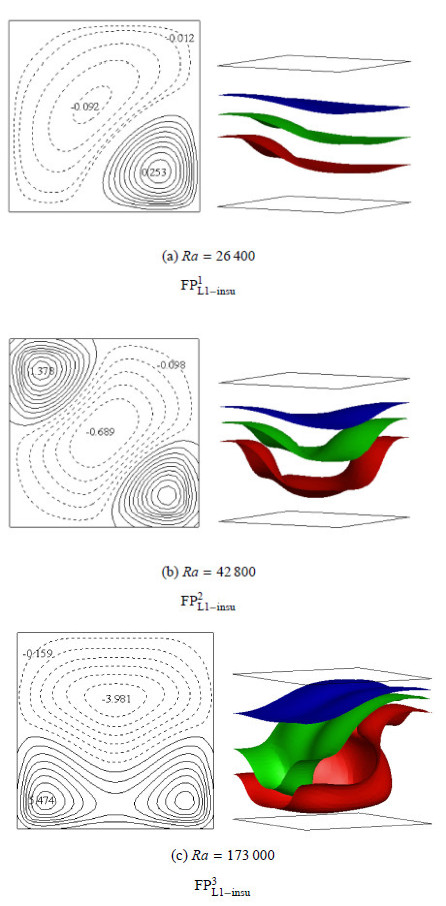
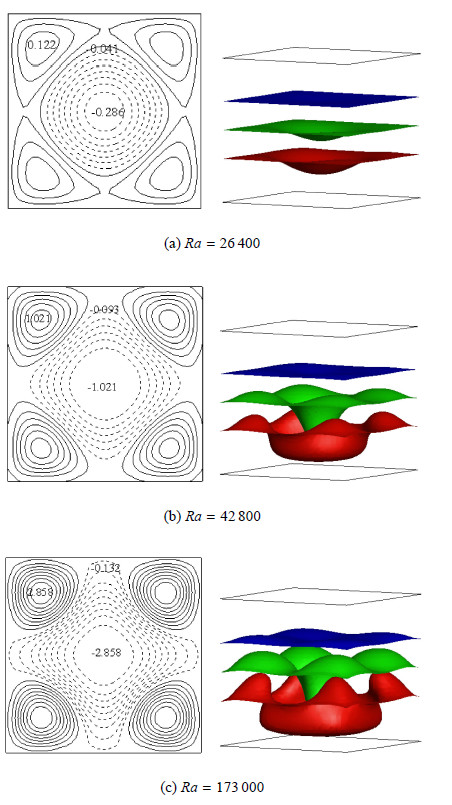
图2给出了不同$Ra$下的稳定流动结构. 当$Ra =26\,400$时,流体刚开始流动,流动强度较低,形成了冷下降流占据腔体大部分区 域、热上升流位于顶角的单涡卷流动结构${\rm{FP}}_{{\rm{L1 - insu}}}^1$,且等温面变形较轻微,如图2(a)所示. $Ra$增大至$Ra =42\,800$时,导热态分岔为如图2(b)所示的二涡卷结构FP$^2_{\rm L1-insu}$,在 ${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型中,两呈扇形分布的热上升流分居两对角处,呈椭圆形分布的冷下降流居于中间位置.此时流动增强,等温面在热上升流与冷下降流相对应的位置分别呈现明显的上凸和下凹变形. 进一步增大$Ra$至$Ra =49\,800$,导热态再次分岔为单涡卷结构${\rm{FP}}_{{\rm{L1 - insu}}}^3$流型,该流型的热上升流及冷下降流呈横胞状,其热上升流胞中具有两个涡流核心,且具有最大流速,但其流 动区域面积较冷下降流区域小,等温面变形更加明显. 与常规流体相比,具有密度极值流体的瑞利-贝纳德对流的流动型态有很大差异.
|
图 2 L=1时绝热侧壁不同Ra下稳态流型. 左:Z=0.5截面等Z向速度线:实线为向上流动,速度为正, 虚线为向下流动,速度为负. 右:温度分别为$\Theta =0.3$(蓝)、0.5(绿)及0.7(红)对应的等温面(下同) Fig.2 Flow patterns for different Ra at L=1 for insulating sidewalls. left: contours of vertical velocity in the Z=0.5 plane. Solid lines denote a positive value and dotted lines denote a negative value. right: isothermal surfaces of $\Theta =0.3$ (blue), 0.5 (green) and 0.7 (red)(similarly hereinafter) |
分别以上述流型为初始条件,在瑞利-贝纳德对流流动拓扑中可以确定各流型的分岔序列及其稳定存在的$Ra$范围. 计算发现,${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型稳定存在于$26{\mkern 1mu} 100 \le Ra \le 43{\mkern 1mu} 600$范围内,直到$Ra <26\,100$时才退化为导热状态. 与导热态在$Ra=26\,400$时才分岔形成${\rm{FP}}_{{\rm{L1 - insu}}}^1 $流型对比可知,此时流动型态的转变存在与常规流体结果相似[11]的滞后现象,这是由于初始条件对流动过程 的影响,不同的初始条件决定了不同的流动路径,当以稳定性更好的流型作为初始条件时,其自身稳定存在$Ra$范围的上下限都 较其他流动状态为初始条件时更宽. 当$43{\mkern 1mu} 600 < Ra \le 55{\mkern 1mu} 000$时,${\rm{FP}}_{{\rm{L1 - insu}}}^1 $流型转变为${\rm{FP}}_{{\rm{L1 - insu}}}^2 $流型;当$Ra>55\,000$时,${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型转变为${\rm{FP}}_{{\rm{L1 - insu}}}^3 $流型. ${\rm{FP}}_{{\rm{L1 - insu}}}^2 $流型稳定存在的$Ra$范围为$39{\mkern 1mu} 400 \le Ra \le 55{\mkern 1mu} 500$. 当$Ra<39\,400$及$Ra>55\,500$时,${\rm{FP}}_{{\rm{L1 - insu}}}^2 $流型分别转变为${\rm{FP}}_{{\rm{L1 - insu}}}^1 $流型和${\rm{FP}}_{{\rm{L1 - insu}}}^3 $流型. ${\rm{FP}}_{{\rm{L1 - insu}}}^3 $流型比上述两种流型更加稳定,其可存在于$39{\mkern 1mu} 500 \le Ra \le 300{\mkern 1mu} 000$这一较宽$Ra$范围内. 与${\rm{FP}}_{{\rm{L1 - insu}}}^1 $和${\rm{FP}}_{{\rm{L1 - insu}}}^2 $流型在分岔序列中都会转变为其他两种流型不同,${\rm{FP}}_{{\rm{L1 - insu}}}^3 $流型的分岔序列更加简单,其在$Ra<39\,500$时仅会转变为${\rm{FP}}_{{\rm{L1 - insu}}}^1 $流型. 当侧壁为导热边界时,导热态失稳开始流动的临界$Ra$增大至$Ra_{\rm cri}=39\,900$. 当$Ra \geqslant 39\,900$时,导热态仅 分岔形成如图3所示的多涡卷结构${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型,该流型下腔体每个角落处都为热上流,中间较大区域为冷下降流. 当$Ra$较小时,冷下降流居于腔体正中间位置,且具有最大$Z$向流动速度,热上升流位于腔体边壁侧. 由于流动强度较低,$\Theta =0.5$和0.7的等温面中间区域仅出现了轻微的下凹变形. 随着$Ra$的增大,冷下降流区域继续向边壁扩张,挤压热上升流使得其区域缩小. 此时,热上升流及冷下降流区域同时具有最大流动速度. 因而等温面不仅在中间区域出现了下凹变形,而且在周围出现了上凸变形. 当$Ra$较大时,冷下降流已触及边壁侧,呈星型分布,且流速进一步加剧,$\Theta =0.3$时的等温面也出现了明显变形.
|
图 3 L=1时导热侧壁不同$Ra$下稳态${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型 Fig.3 Flow patterns of stable ${\rm{FP}}_{{\rm{L1 - insu}}}^1$ state at different $Ra$ for conducting sidewalls at L=1 |
同样,以${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型为初始条件进行计算,可以确定当$Ra$介于39800与300000之间时,${\rm{FP}}_{{\rm{L1 - insu}}}^1$流 型可以稳定存在,当$Ra<39\,800$时,系统退化为导热状态,即在所计算的$Ra$范围内${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型没有生成新的流型. 与侧壁为绝热时的结果相比,侧壁为导热时系统更加稳定,导热态失稳的临界$Ra$更大,且仅有一种流型产生,流动结构也有较 大差异,这是因为相比绝热侧壁,温度扰动在导热侧壁更易耗散,从而使系统对流不易发生.
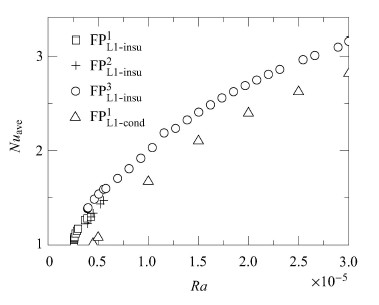
图4给出了L=1时各稳定流型下热壁 $Nu_{\rm ave}$ 随$Ra$的变化. ${\rm{FP}}_{{\rm{L1 - insu}}}^1$和${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型 稳定存在的$Ra$范围很小,${\rm{FP}}_{{\rm{L1 - insu}}}^3$和${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型存在的$Ra$范围较大. 常规流体瑞利-贝纳德对流系统在流动开始后的较宽$Ra$范围内都可观察到流型稳定共存的现象,相比之下,具有密度极值冷 水瑞利-贝纳德对流系统仅在流动开始附近的较窄$Ra$范围内出现流型稳定共存的现象. 显然,随着$Ra$的增加,各流型下热壁 $Nu_{\rm ave}$都增大. 当$Ra$较小时,${\rm{FP}}_{{\rm{L1 - insu}}}^1$与${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型共存,${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型的 $Nu$数略小于${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型,当$Ra$增大到一定程度时,${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型的 $Nu_{\rm ave}$ 略大于${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型. 相同$Ra$下,${\rm{FP}}_{{\rm{L1 - insu}}}^3$流型的 $Nu_{\rm ave}$最大,${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型的 $Nu_{\rm ave}$最小,即绝热侧壁时对流传热能力优于导热侧壁.
|
图 4 L=1时热壁$Nu_{\rm ave}$随$Ra$的变化 Fig.4 The variation of the average Nusselt number at the hot wall at $L=1$ |
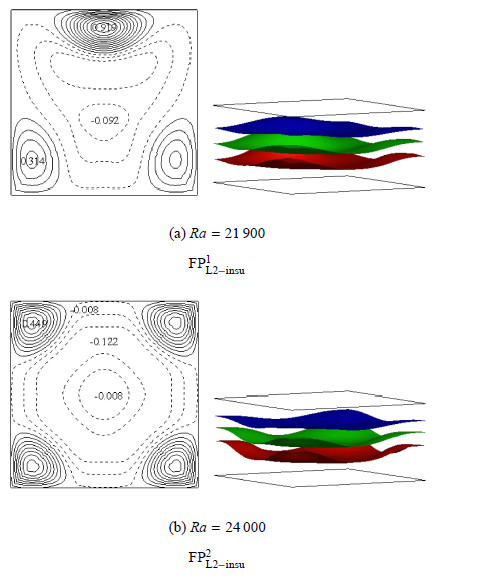
当侧壁为绝热、且L =2时,宽深比较大,侧壁对瑞利-贝纳德对流的影响减弱,系统的稳定性较差,流动更易发生,因而导 热态失稳的临界$Ra$减小至$Ra_{\rm cri} =21\,900$. 当流体开始流动时,导热态第一次分岔形成${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型,如图5(a)所示,该流型下靠近腔体边壁侧有三股点状热上升流,流速较大,中间区域为冷下降流,流速较小,等温面分别在热上升流和冷下降流相应的位置出现了上凸和下凹的变形. 当$Ra >23\,200$时,导热态形成了对角为点状热上升流、其他区域为冷下降流的${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型,等温面变形较为明显,如图5(b)所示. 当$25{\mkern 1mu} 600 \le Ra \le 29{\mkern 1mu} 200$时,导热态再次形成为${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型. 值得注意的是,与L =1时对流结构多为单胞或双胞结构相比,$L =2$时的对流结构为更加复杂的多胞流动结构. 在分别以${\rm{FP}}_{{\rm{L1 - insu}}}^1$和${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型作为初始解的二次分岔计算中,可以确定${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型稳定存在于$21000 \le Ra \le 31700$范围内,当$Ra =20\,900$时,该流型退化为导热状态;${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型稳定存在于$23300 \le Ra \le 25500$范围内,当$21900 \le Ra \le 23300$或$25500 \le Ra \le 31600$时,${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型转变为${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型.
|
图 5 $ L =2$ 时绝热侧壁不同$Ra$下稳态流型 Fig.5 Flow patterns for different $Ra$ at $L =2 $ for conducting sidewalls at $L =2$ |
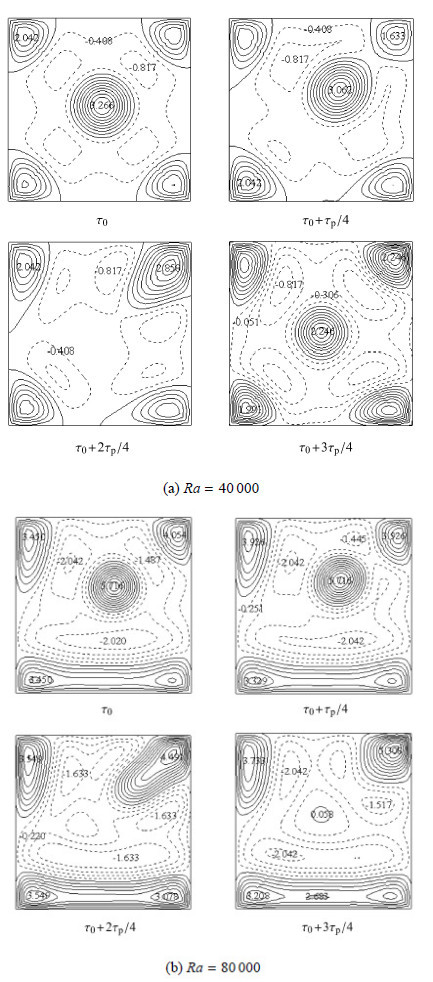
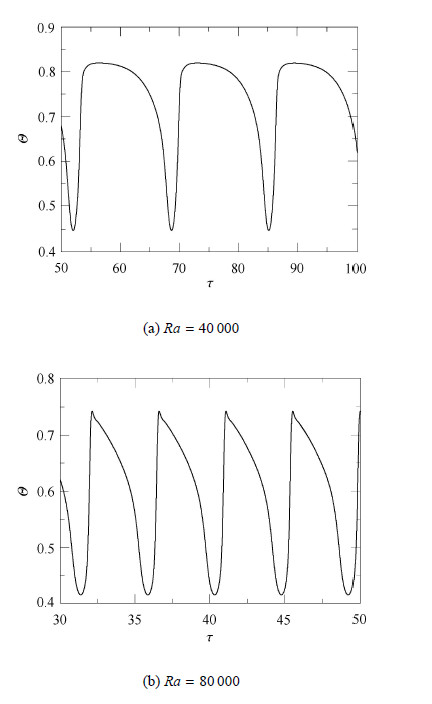
随着$Ra$的进一步增大,腔体内流体流动开始失去其稳定性,由稳态流动转变为非稳态流动. 当$Ra =40\,000$时,腔体对角和 中心位置在 $\tau = \tau_{0}$时分别为扇形及圆形状热上升流,随着时间的推移,中心位置的热上升流逐渐向右上角移动,经半个周期后与右上角 热上升流融合,然后又再次从右上角热上升流中分离,移向中心位置,如图6(a)所示. 此时无因次振荡周期$\tau _{\rm p}=16.77$,且监测点无因次温度振幅较大,如图7(a)所示. 当$Ra$增大至$Ra =80\,000$时,与$Ra =40\,000$时相比,底角两股热上升流融合为一股,各股冷热流的最大流速也有一定程度的增强. 同样地,随着时间的推移,中心位置的热上升流逐渐与右上角热上升流融为一股,如图6(b)所示. 此时系统不稳定性增大,无因次振荡周期减小至 $\tau _{\rm p} =4.26$,无因次温度振幅也相对减小,如图7(b)所示.
|
图 6 $L =2$时一个周期内流型的演变过程 Fig.6 Flow evolution in a period at $L =2$ |
|
图 7 $ L =2$时监测点($X =0.5$,$Y =0.5$,$Z =0.5$)温度随时间演变 Fig.7 Time record of local temperature at a monitoring point ($X =0.5$,$Y =0.5$,$Z =0.5$) at $L =2$ |
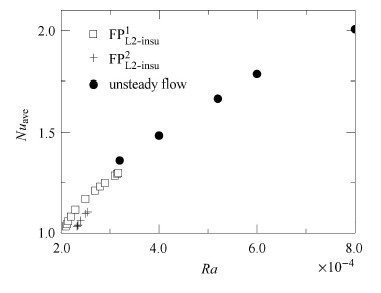
图8给出了$L =2$时热壁 $Nu_{\rm ave}$ 随$Ra$的变化规律,在临界$Ra$附近时,同一$Ra$下,仅有${\rm{FP}}_{{\rm{L1 - insu}}}^1$与 ${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型稳定共存,即此时稳定共存的流型相比常规流体少,且${\rm{FP}}_{{\rm{L1 - insu}}}^1$流型传热能力明显优于${\rm{FP}}_{{\rm{L1 - insu}}}^2$流型. 与$L =1$时的结果相比,热壁 $Nu_{\rm ave}$ 有所增大,即传热能力有所增强. 当流动为非稳态时,流动更加强烈,因而热壁 $Nu_{\rm ave}$随$Ra$增加较稳态流动时更快.
|
图 8 $L =2$时热壁 $Nu_{\rm ave}$随$Ra$的变化 Fig.8 The variation of the average Nusselt number at the hot wall at $L=2$ |
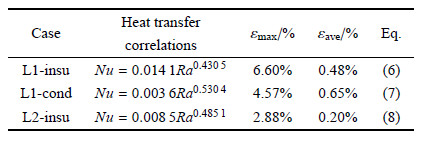
根据计算结果,对数据进行回归整理,可以得到长方体腔内冷水瑞利-贝纳德对流传热关联式,如表2所示,$Nu_{\rm ave}$的计算值 和拟合值的最大误差以及平均误差也在表中给出,传热关联式的应用范围为$2 \times {10^4} < Ra \le 3 \times {10^5}$.
| 表 2 长方体腔热壁$Nu_{\rm ave}$关联式 Table 2 Correlations of the average Nusselt number on the hot wall |
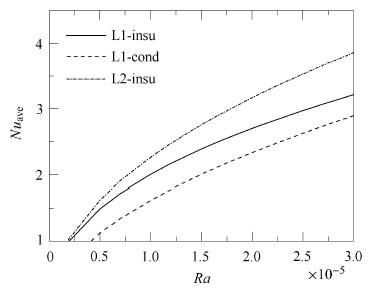
图9给出了3种条件下壁面传热能力的比较. 由图可知,侧壁为绝热时壁面传热能力较侧壁为导热时强,且不同$Ra$下 $Nu_{\rm ave}$的差值几乎是相同的. 当Ra较小时,L =2时壁面$Nu_{\rm ave}$略大于L =1时的结果,随着$Ra$的增加,$Nu_{\rm ave}$的差值是增大的,即$Ra$越大,宽深比增加所强化的传热效果越明显,而绝热侧壁较导热侧壁时强化的传热效果在不 同$Ra$下几乎是恒定的.
|
图 9 不同条件下壁面传热能力比较 Fig.9 Comparison of the heat transfer ability for different conditions |
本文利用有限容积法对长方体腔内具有密度极值冷水的瑞利-贝纳德对流进行了三维数值模拟,得到了不同条件下长方体 腔内流动结 构及各流型的分岔序列,并与常规流体瑞利-贝纳德对流结果进行了对比,分析了密度极值特性、$Ra$、热边界条件以及宽深比对流 动与传热的影响,揭示了长方体腔内具有密度极值流体瑞利-贝纳德对流的复杂特性. 结果表明:(1)与常规流体相比,具有密度极值冷水瑞 利-贝纳德对流系统更加稳定,流动开始的临界$Ra$明显增大,且流动型态及其 分岔序列更加复杂,不同流型下壁面传热能力不同. (2)导热侧壁进一步增大了系统稳定性,流动型态相比绝热侧壁时少,壁面传热能力有所减弱. (3)宽深比的增加削弱了系统的稳定性,易于出现非稳态流动,且无因次振荡周期随$Ra$的增加而减小,壁面传热能力随宽深比的增加 而有所增强. (4)冷水的瑞利-贝纳德对流系统在相同$Ra$下多种流型可以稳定共存,且各流型在相互转变中存在流动滞后现象. (5)基于计算结果,采用线性回归方法,得到了热壁传热关联式,通过比较各传热关联式可知,$Ra$越大,宽深比增加所强化的传 热效果越明显,而绝热侧壁较导热侧壁时强化的传热效果在不同$Ra$下几乎是不变的.
| [1] | Cross MC, Hohenberg PC. Pattern formation outside of equilibrium. Reviews of Modern Physics, 1993, 65: 851-1086 |
| [2] | Padilla ELM, Lourenço MAS, Silveira-Neto A. Natural convection inside cubical cavities: numerical solutions with two boundary conditions. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2013, 35(3): 275-283 |
| [3] | 王小华, 朱文芳. 长方腔自然对流第一次分岔突变现象的数值分析. 力学学报, 2010, 43(3): 389-399 (Wang Xiaohua, Zhu Wenfang. Numerical research on the sudden change characteristic of the first bifurcation for natural convection of air enclosed in 2D rectangular cavity. Chinese Journal of Theoretical and Applied Mechanics, 2010, 43(3): 389-399 (in Chinese)) |
| [4] | 孔祥言, 吴建兵. 多孔介质中的非达西自然对流的分岔研究. 力学学报, 2002, 34 (2): 177-185 (Kong Xiangyan, Wu Jianbing. A bifurcation study of non-Darcy free convection in porous media. Acta Mechanica Sinica, 2002, 34 (2): 177-185 (in Chinese)) |
| [5] | Jeffreys H. Some cases of instability in fluid motion. Proceedings of the Royal Society of London Series A-Containing Papers of A Mathematical and Physical Character, 1928, 118(779): 195-208 |
| [6] | Zhan NY, Xu PW, Sun SM, et al. Studu on the stability and 3-dimensional character for natural convection in a rectangular cavity heated from below. Science China Technological Sciences, 2010, 53(6): 1647-1654 |
| [7] | Zhan NY, Gao Q, Bai L, et al. Experimental research on nonlinear characteristics of natural convection in a 3-D shallow cavity. Science China Technological Sciences, 2011, 54(12): 3304-3310 |
| [8] | Mukutmoni D, Yang KT. Thermal convection in small enclosures: an atypical bifurcation sequence. International Journal of Heat and Mass Transfer, 1995, 38(1): 113-126 |
| [9] | Gollub JP, Benson SV. Many routes to turbulent convection. Journal of Fluid Mechanics, 1980, 100(10): 449-470 |
| [10] | Bousset F, Lyubimov DV, Sedel'Nikov GA. Three-dimensional convection regimes in a cubical cavity. Fluid Dynamics, 2008, 43(1): 1-8 |
| [11] | Puigjaner D, Herrero J, Simó C, et al. Bifurcation analysis of steady Rayleigh-Bénard convection in a cubical cavity with conducting sidewalls. Journal of Fluid Mechanics, 2008, 598: 393-427 |
| [12] | 卞恩杰, 杨茉, 李凌等. 格子Boltzmann方法对Rayleigh-Bénard流的模拟与非线性分析. 工程热物理学报, 2012, 33(4): 685-688 (Bian Enjie, Yang Mo, Li Ling, et al. Simulation and nonlinear analysis for the Rayleigh-Bénard convection with the lattice Boltzmann method. Journal of Engineering Thermophysics, 2012, 33(4): 685-688 (in Chinese)) |
| [13] | Leong SS. Numerical study of Rayleigh-Bénard convection in a cylinder. Numerical Heat Transfer Part A-Applications, 2002, 41: 673-683 |
| [14] | Venturi D, Wan X, Karniadakis GE. Stochastic bifurcation analysis of Rayleigh-Bénard convection. Journal of Fluid Mechanics, 2010, 650(1): 391-413 |
| [15] | Hof B, Lucas P, Mullin T. Flow state multiplicity in convection. Physics of Fluids, 1999, 11(10): 2815-2817 |
| [16] | Borońska K, Tuckerman LS. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. I. Time dependence and oscillations. Physical Review E, 2010, 81: 036320 |
| [17] | Borońska K, Tuckerman LS. Extreme multiplicity in cylindrical Rayleigh-Bénard convection. II. Bifurcation diagram and symmetry classification. Physical Review E, 2010, 81: 036321 |
| [18] | 宁利中, 齐昕, 余荔等. 混合流体Rayleigh-Bénard对流的多重稳定性现象. 应用基础与工程科学学报, 2010, 18(2): 281-290 (Ning Lizhong, Qi Xing, Yu Li, et al. Multistability of Rayleigh-Bénard convection in a binary fluid mixture. Journal of Basic Science and Engineering, 2010, 18(2): 281-290 (in Chinese)) |
| [19] | 苏燕兵, 陆军, 白博峰. 封闭腔内水自然对流换热数值模拟. 化工学报, 2007, 58(11): 2715-2720 (Su Yanbing, Lu Jun, Bai Bofeng. Numerical simulation of natural convection and heat transfer of water in cavities. Journal of Chemical Industry and Engineering (China), 2007, 58(11): 2715-2720 (in Chinese)) |
| [20] | Sivasankaran S, Ho CJ. Effect of temperature dependent properties on natural convection of water near its density maximum in enclosures. Numerical Heat Transfer Part A-Applications, 2008, 53: 507-523 |
| [21] | Kashani S, Ranjbar AA, Mastiani M, et al. Entropy generation and natural convection of nanoparticle-water mixture (nanofluid) near water density inversion in an enclosure with various patterns of vertical wavy walls. Applied Mathematics and Computation, 2014, 226: 180-193 |
| [22] | Braga SL, Viskanta R. Effect of density extremum on the solidification of water on a vertical wall of a rectangular cavity. Experimental Thermal and Fluid Science, 1992, 5(6): 703-713 |
| [23] | Kandaswarmy P, Sivasankaran S, Nithyadevi N. Buoyancy-driven convection of water near its density maximum with partially active vertical walls. International Journal of Heat and Mass Transfer, 2007, 50: 942-948 |
| [24] | Nithyadevi N, Sivasankaran S, Kandaswamry P. Buoyancy-driven convection of water near its density maximum with time periodic partially active vertical walls. Meccanica, 2007, 42: 503-510 |
| [25] | Hu YP, Li YR, Yuan XF, et al. Natural convection of cold water near its density maximum in an elliptical enclosure containing a coaxial cylinder. International Journal of Heat and Mass Transfer, 2013, 60: 170-179 |
| [26] | Hu YP, Li YR, Wu CM. Comparison investigation on natural convection of cold water near its density maximum in annular enclosures with complex configurations. International Journal of Heat and Mass Transfer, 2014, 72: 572-584 |
| [27] | Li YR, Ouyang YQ, Hu YP. Pattern formation of Rayleigh-Bénard convection of cold water near its density maximum in a vertical cylindrical container. Physical Review E, 2012, 86: 046323 |
| [28] | Gebhart B, Mollendorf JC. A new density relation for pure and saline water. Deep-Sea Research, 1977, 24: 831-848 |
2. College of Power Engineering, Chongqing University, Chongqing 400044, China
 2015, Vol. 47
2015, Vol. 47