2. 清华大学工程力学系, 北京100084
透水床面明渠湍流在天然河道中十分常见,但目前许多研究都基于经验模型,类似不透水床面,推导流速分布与流动阻力,无法洞悉其细 部特性. 由于床面透水性及床面地形影响,床面之上与内部会产生显著地交互作用,而且近床区域的时均流动存在很大的空间异构性,现有的研究 方法很难考虑、统计交互作用及空间异构性所造成的影响. 双平均模型通过对时均方程进一步地空间平均,得到了构造应力等描述空间异构性的物理量,为研究透水床面明渠湍流特性提供了新的途径.
粗糙壁面湍流的双平均模型构想,始于大气科学中对于陆生植物冠层的湍流描述与预测. Smith 和 Mclean[1]分析流速曲线时,在距 床面一定距离处采用了空间平均的处理方法,将双平均模型引入到流体力学中. Nikora等[2, 3, 4] 提出了空间平均的定理及步骤,推导了纳维-斯托克斯(N-S)方程、标量物质对流扩散方程的双平均形式,建立了比较 系统的双平均模型理论. 在明渠卵砾石河床实验中,Dey等[5]与Mignot等[6]应用声学多普勒流速仪,得到了双平均流速、双平均构造应力及双平均雷诺应 力的法向分布,对湍流动能分解计算,得到了湍动能生成项、耗散项、扩散项及构造扩散项等各部分的关系,通过象限分析法统计了湍流 猝发事件. Jimènez[7]比较系统地研究了不透水床面的时均流速分布以及高阶湍流特征量,结果与光滑床面有着较大不同. 然而针对透水床面流速的垂向分布、以及透水床面内部的流速情况研究还十分缺乏,在国内流体力学研究中,基于双平均模型的分析也很少.
由于测量仪器的限制,物理模型实验在近床区域测量比较困难,不能够充分反映一些湍流的细部结构. 另外,测量区域有限,大尺度湍流 结构很难被观测到. 而随着计算机运算速度及存储能力的飞速发展,数学模型可以更好地应用在湍流模拟中,得到计算区域内更加精细的湍流瞬时数据. 大涡模拟技术将流动分为大尺度和小尺度,通过对小尺度涡进行过滤模化,而对大尺度涡旋进行模拟,从而能够给出水流的脉动信息,并且对计算能力和计算空间要求相对直接模拟要低. 白静等[5, 8]构建了浸没边界法,用于模拟方腔流动、丁坝扰流等. 可见针对复杂几何边界问题,大涡模拟的作用与优势格外突出.
本文对三层小球组成的理想透水床面进行大涡模拟,在大尺度上对比不同空间位置的双平均统计量,进行双平均特性分析. 本文的研究 目的主要有:(1) 对比前人的物理模型实验,研究透水床面条件下,双平均流速在法向上的分布公式及特点. (2) 研究雷诺剪应力、构造剪应力法向分布. (3) 对比不同空间位置下脉动幅度的法向分布. 通过研究,可以更加深入地认识透水床面的机理,明确床面透水性及地形对流速和各阶统计量的影响.
1 双平均理论粗糙壁面湍流在许多自然环境以及工程中十分常见,这个课题的研究已长达 80多年[9, 10, 11]. 双平均理论为研究粗糙壁面湍流提供了新的途径,它将N-S 方程进行时间尺度和空间尺度的平均[2, 3, 4],产生了构造应力等描述近床空间异构性的物理量.
对于流场中的局部瞬时流动变量θ,可以将其做如下分解
| $\theta = \bar {\theta } + {\theta }'$ | (1) |
| $\bar {\theta } = \left\langle \bar {\theta } \right\rangle + \tilde {\theta }$ | (2) |
式(1)表示局部瞬时变量$\theta $可以分解为局部时间平均变量$\bar {\theta }$和刨除局部时间平均后的脉动量${\theta }'$,这与传统的雷诺平均相同,即时间平均. 式(2)对局部时间平均变量$\bar {\theta }$进一步分解为双平均变量$\left\langle \bar {\theta } \right\rangle $以及刨除双平均后的空间脉动量$\tilde {\theta }$,即空间平均. 试验中采用的空间平均方法为:于高程$z$处,固定$y$值为一个常数,对顺流向一条线上的变量进行双平均统计.
对于粗糙定床,水面平整的恒定流动,双平均的N-S方程针对顺流向的整体双平均流动剪切应力提出了一个新的定义[12, 13, 14, 15]
| $\left\langle {\bar \tau } \right\rangle = - \rho \left\langle {\tilde u\tilde w} \right\rangle - \rho \left\langle {\overline {u'w'} } \right\rangle + \rho v\frac{{{\rm{d}}\left\langle {\bar u} \right\rangle }}{{{\rm{d}}z}}$ | (3) |
其中,$u$与$w$分别指顺流向以及床面法向的瞬时流速;$\rho $为液体密度;$\tau _f = - \rho \left\langle {\tilde {u}\tilde {w}} \right\rangle $表示双平均构造剪应力,含义是时均量的空间异构所产生的动量通量. 粗糙河床的床面附近,时均流场存在较大的空间波动. 在一定区域内,所有空间位置的脉动量$\tilde {u}\tilde {w}$取平均,并假设流场中各处流体密度均为$\rho $,即可得到双平均构造剪应力$\tau _f $;$\left\langle {\tau _{uw} } \right\rangle = - \rho \left\langle {\overline {{u}'{w}'} } \right\rangle $为双平均雷诺剪应力. 在一定时间段内,对所有时刻的脉动量${u}'{w}'$取平均,即可得到时均脉动量$\overline {{u}'{w}'} $,再对一定区域内所有空间位置的时均脉动量$\overline {{u}'{w}'} $取平均,并假设流场中各处流体密度均为$\rho $,即可得到双平均雷诺剪应力$\left\langle {\tau _{uw} } \right\rangle $;$\left\langle {{\tau _{vis}}} \right\rangle = \rho vd\left\langle {\bar u} \right\rangle /dz$为双平均黏性剪应力;$v$为液体的运动黏性系数;$z$为以顶层床面为基准面的高程.
2 数值模拟简介 2.1 控制方程组不可压缩流体的N-S方程组为
| $\dfrac{\partial u_i }{\partial x_i } = 0$ | (4) |
| $\frac{{\partial {u_i}}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {{u_i}{u_j}} \right) = {g_i} - \frac{1}{\rho }\frac{{\partial p}}{{\partial {x_i}}} + \nu \frac{{{\partial ^2}{u_i}}}{{\partial x_j^2}}{\rm{ }}$ | (5) |
其中,$u_i $表示$x_i $ ($i = 1,2,3$)方向上的瞬时流速;$p$表示压强;$\nu $为运动黏性系数;$g_i $为第$i$个方向上的重力加速度分量. 为了简化方程组,将压强分为静水压强与动水压强,即
| $p = p_{\rm s} + p_{\rm d}$ | (6) |
其中,$p_{\rm s}$为静水压强,$p_{\rm d}$为动水压强. 由流体静力学平衡条件知
| ${g_i} = \frac{1}{\rho }\frac{{\partial {p_{\rm{s}}}}}{{\partial {x_i}}}$ | (7) |
因此
| $ g_i - \dfrac{1}{\rho }\dfrac{\partial p}{\partial x_i } = \dfrac{1}{\rho }\dfrac{\partial p_{\rm s} }{\partial x_i } - \dfrac{1}{\rho }\dfrac{\partial \left( {p_{\rm s} + p_{\rm d} } \right)}{\partial x_i } = - \dfrac{1}{\rho }\dfrac{\partial p_{\rm d} }{\partial x_i }$ | (8) |
为表达方便,将用$p$来代替$p_{\rm d} $. 将方程用水深$H$、断面平均流速$U$、压强$\rho U^2$无量纲化,并做过滤运算,最终得到大涡模拟的控制方程为
| $\dfrac{\partial \bar {u}_i }{\partial x_i } = 0$ | (9) |
| $ \dfrac{\partial \bar {u}_i }{\partial t} + \dfrac{\partial }{\partial x_j }\left( {\overline {u_i u_j } } \right) = \dfrac{1}{Re}\dfrac{\partial ^2\bar {u}_i }{\partial x_j^2 } - \dfrac{\partial \bar {p}}{\partial x_i } $ | (10) |
式中,顶标``$-$''表示过滤后的变量,其中,$\overline {u_i u_j } = \overline {\left( {\bar {u}_i + {u}'_i } \right)\left( {\bar {u}_j + {u}'_j } \right)} = \bar {u}_i \bar {u}_j + \overline {{u}'_i {u}'_j } $,$\overline {{u}'_i {u}'_j } $表示亚格子尺度运动对可解尺度运动的影响,用亚格子应力的涡黏模式进行计算.
| $- \overline {{u}'_i {u}'_j } = 2\nu _t \bar {S}_{ij} - \dfrac{1}{3}\delta _{ij} \overline {{u}'_k {u}'_k }$ | (11) |
其中,$\bar {S}_{ij} = \dfrac{1}{2}\left( {\dfrac{\partial \bar {u}_i }{\partial x_j } + \dfrac{\partial \bar {u}_j }{\partial x_i }} \right)$为过滤后的应变率张量,$\nu _t $为亚格子黏性系数,由Germano等[16]提出的动力Smagorinsky模式求得.
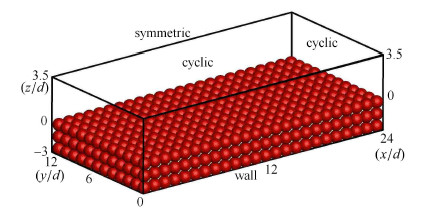
2.2 数值模拟参数设置大涡模拟通过过滤的方法将流动分为大尺度与小尺度,直接求解对紊流起主要作用的大尺度流动,对于小尺度流动,则采用亚格子 应力模型. 图1为模拟计算示意,小球在$x,y,z$方向按照$24\times 12\times 3$紧密排列,构成模拟透水床面. 顶层床面到自由水面的水深$h$是球直径$d$的3.5倍,床面之上表层流动的计算区域大小为$6.8h\times 3.4h\times h$,比$2\pi h \times {\rm{ }}\pi h \times h$稍大,可以认为包含了所有的湍流相干结构[17]. 数值模拟实验的雷诺数为15000,入口断面平均流速设置为1,模拟开始后将在区域内自动形成速度分布.
|
图 1 模拟河床示意 Fig.1 Variation of roughness geometry |
如图中所示,此次数值模拟采用压力梯度驱动,在纵向及横向上采用循环边界条件,也称为周期性边界条件,它将计算区域出口处水 流的特征量包括流速、压强等重新赋值给进口边界. 采用周期性边界条件可以减少计算网格量,缩短统计结果收敛的时间. 流场的水面处采用刚盖假定,采用滑移边界条件来模拟水面,这在低弗劳德数的情况下,是一种十分有效的模拟方法. 在球体表面以及底部,采用的是无滑移条件,壁面处法向和切向速度为0. 网格数据为$4\,800\times 2\,400\times 130$,由于小球顶部与水流交界面附近紊动比较强烈,网格采用了加密处理(见图2).

|
图 2 数值网格示意 Fig.2 The numerical grid |
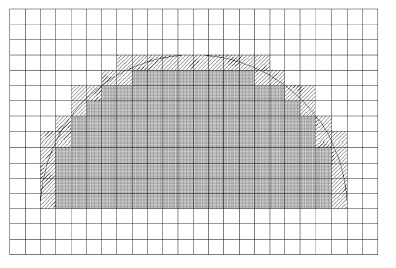
处理小球边界时,采用了浸没边界法中的直接强迫力法. 如图3所示,根据小球边界和网格的相对位置,将网格分为固体网格、边界 网格与流体网格. 固体网格中,流速设置为0;流体网格中,流速采用离散化的N-S方程进行计算;边界网格中,在动量方程中增加源项,从而使得网 格中心计算所得流速与实际值相等.
|
图 3 浸没边界法不同类型网格示意图(灰色为固体网格,阴影为边界网格,白色为流体网格) Fig.3 Schematic of different types of grids in IBM (solid grids:girds filled with grey,boundary grids: grids filled with slashes,flow grids:grids filled with white) |
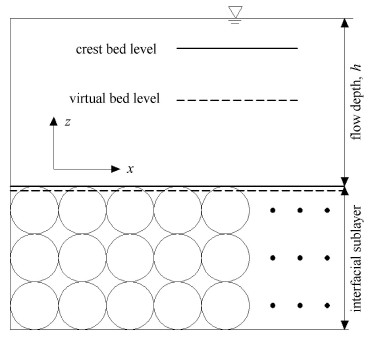
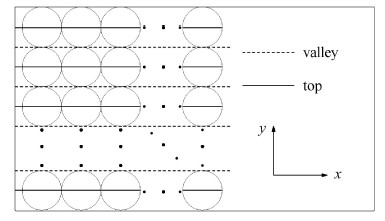
图4显示的是$x$-$z$平面,该平面穿过球心. 根据Dey等[5]的研究,定义透水床面两个参考水平面:第一,顶 层床面(crest bed level),为表层小球顶部所在的平面;第二,平均床面(virtual bed level),顶层床面与平均床面相距$z_0 $. 若仅考虑透水床面地形,采用空间平均,得到的Z0=0.2d,$d$为小球直径;若对时均流速进行对数拟合,拟合最优时得到的z0 = 0.21d,二者相差较小,本文中取Z0=0.2d. 另外,为了从细节上分析透水床面不同部位的特性,试验中还定义了两种统计位置,如图5所示. 图5展示了$x$-$y$平面,两种统计取样位置,球的沟谷处及顶部.
|
图 4 流层示意 Fig.4 Illustration of the flow sublayers |
|
图 5 取样位置示意 Fig.5 Illustration of the sample position |
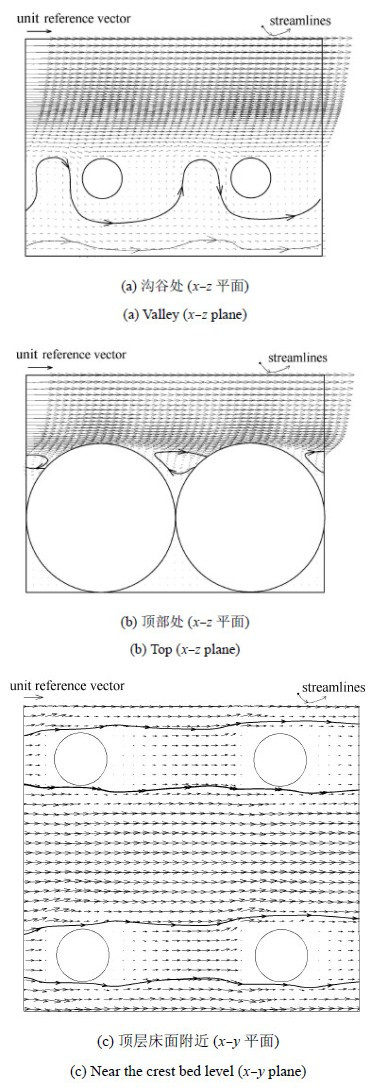
图6展示了时均流速的矢量图以及流线图,其中,图6(a)与图6(b)显示了$x$-$z$平面内,两个小球之间沟谷与 顶部处的流场. 图6(c)显示了$x$-$y$平面内,顶层床面附件的流场. 图中空白圆表示靠近小球,流速接近于零的区域. 可以看出,在近壁区域,时均流速存在着明显的空间异构性. 以往常用的雷诺平均方程没有考虑空间异构性,使得在描述壁面流动时十分困难,无法反映空间异构性对湍流特性造成的 影响,这也是双平均模型所要解决的问题.
|
图 6 沟谷与顶部的时均流速矢量和流线图 Fig.6 Time-averaged velocity vectors and streamlines |
粗糙透水床面明渠流动中,对于顶层床面之上,即$z_1 ^ + > 80$范围内,为对数分布区,流速分布遵循对数公式[18]
| $u^ + = \dfrac{1}{\kappa }\ln \dfrac{z_1 ^ + + z_0 ^ + }{k_{\rm s}^ + } + B $ | (12) |
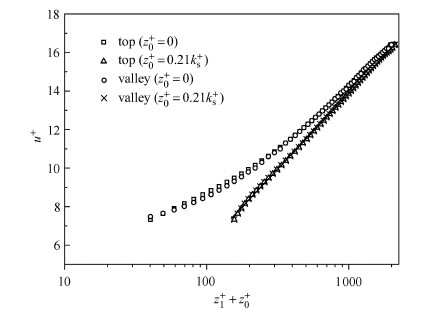
式中,$u$为距顶层床面$z$处的流速,$u_\ast $为剪切流速,$z_1 ^ + $表示无量纲化的高程,即$z_1^ + = {zu_\ast }/\nu $. $u^ + $表示无量纲化的顺流流速,即$u^ + = {\left\langle \bar {u} \right\rangle } /{u^\ast }$. $\kappa $为卡门常数,$z_0 $为平均床面距顶层床面的高度,无量纲后为 $z_0 ^ + = z_0 \cdot u_\ast /\nu $,$k_s $为粗糙高度(文中取值球体直径$d$),无量纲后位$k_{\rm s}^ + = k_{\rm s} \cdot u_\ast /\nu $,$B$为积分常数. 图7表示平均床面高程修正前后,顶部及沟谷处的流速分布 情况. 图中横坐标$z_1 ^ + + z_0 ^ + $表示以平均床面为零基准面的高程,纵坐标为无量纲化的顺流流速. 根据公式$u_\ast = \left. {( - \left\langle {{u}'{w}'} \right\rangle )^{0.5}} \right|_{z = 0} $,得$u_\ast =0.133$.
|
图 7 平均床面修正前后的流速分布 Fig.7 Velocity distribution with and without the modification of theoretic |
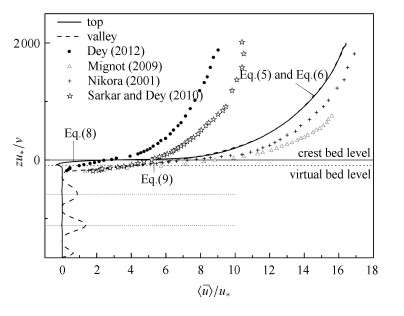
顶部与沟谷统计结果表明,当$z_0 = 0.21k_{\rm s} $时,流速分布遵循对数律,如图8所示. 两处统计位置均用 式(12)进行拟合,可以得到顶部的拟合公式为
| $u^ + = \dfrac{1}{0.292}\ln \dfrac{z_1 ^ + + 0.21k_{\rm s}^ + }{k_{\rm s} ^ + } - 9.76 $ | (13) |
|
图 8 双平均顺流流速垂向分布 Fig.8 DA streamwise velocity profiles obtained from LES and data points of previous experimental studies |
相关系数为0.999 7.
沟谷的拟合公式为
| $u^ + = \dfrac{1}{0.286}\ln \dfrac{z_1 ^ + + 0.21k_{\rm s}^ + }{k_{\rm s}^ + } - 10.232$ | (14) |
相关系数为0.9999. 值得注意的是,此处的卡门常数$\kappa $与一般认为的0.4相差较远,这是由于透水床面的可渗性,导致了水流阻力问题的复杂. 陈兴伟等[19]的水槽实验发现相同水流条件下,透水床面的摩阻流速大于不透水床面. Nezu等[20]的实验发现,卡门常数$\kappa $随着渗透能力的增强而减小. Ashim Das Gupta和Paudyal的实验[18]研究得到了类似的结论,实验得出的透水床面流速分布为
| $u^ + = \dfrac{1}{0.28}\ln \dfrac{z + 0.32}{D_{50} } + 8.21$ | (15) |
式中,$D_{50} $为中值粒径. 比较可知,一方面透水床面流速原点发生位移,位于$z = - 0.21k_{\rm s}^ + $处,另一方面,卡门常数也发生了较大的变化.
对比图7和图8可知,顶层床面之上,即$z_1 ^ + > 80$的范围内,顶部与沟谷处的双平均流速垂向分布类似,说明湍流紊动造成的空间异构性对于上层流速分布并没有太大影响.
当$ - 98 < z_1 ^ + < 80$时,由于湍流紊动增强,可以发现流速分布并不符合对数分布,而且顶部与沟谷处的流速分布产生了差异. Dey[5]在顶层床面与平均床面间发现了多项式型的流速分布,而Nikora与Mignot等[6, 14, 20],发现了线性的流速分布. 本次数值模拟实验发现,当$ - 98 < z_1 ^+ < 80$时,流速符合多项式分布,拟合公式为
| $z_1 ^ + = 5.823\,3u^ {+ 3} - 31.939u^{ + 2} + 64.839u^ + - 57.312$ | (16) |
相关系数$r^2=0.926\,5$. 而沟谷流速符合线性分布,其拟合公式为
| $z_1 ^ + = 36.545u^ + - 244.05 $ | (17) |
相关系数$r^2=9\,986$. 在透水床面内部,球层间流速存在突增. 值得注意的是,靠近底层的球孔流速大约为上层 对应流速的1.55倍. 这与Manes等[21]的水槽试验相吻合,其原因可能是在靠近底层时,透水率急剧减小,考虑到流体的连续性,流体被挤压,使得双平均流速增大.
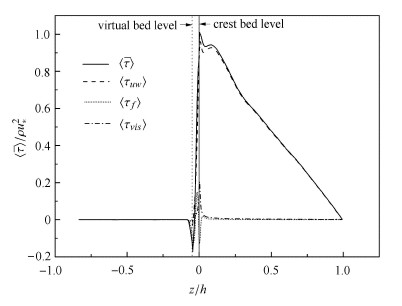
3.2 时空双平均总剪应力式(3)已经对双平均总剪应力进行了分解. 通过分解可以得到:双平均总剪应力由双平均构造剪应力$\left\langle {\tau _f } \right\rangle = - \rho \left\langle {\tilde {u}\tilde {w}} \right\rangle $,双平均雷诺剪应力$\left\langle {\tau _{uw} } \right\rangle = - \rho \left\langle {\overline {{u}'{w}'} } \right\rangle $,以及黏性剪应力$\left\langle {{\tau _{vis}}} \right\rangle = \rho v{\rm{d}}\left\langle {\bar u} \right\rangle /{\rm{d}}z$构成. 由受力平衡分析可知,双平均总剪应力与重力相平衡. 由图中可知,在界面顶层之上,即$ z/h > 0.01$时,总剪应力与雷诺剪应力基本重合,呈线性分布,说明流场上部雷诺剪应力占有主体地位,约占总剪应力的95%. 在顶层界面附近,即$ -0.1 < z/h < 0.01$时,由于湍流紊动较大,构造剪应力不能忽略,其值大约占总剪应力的15%.
|
图 9 双平均剪应力垂向分布 Fig.9 DA fluid shear stress |
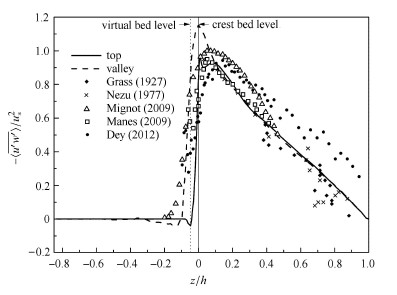
将雷诺剪应力和水深无量纲化,如图10所示. 通过对比顶部及沟谷处的双平均雷诺剪应力法向分布,可以看出,在顶层床面之上,$z/h > 0.1$的范围内,双平均雷诺剪应力近似呈线性增大,这是因为总剪应力与重力相平衡,而双平均雷诺剪应力在整个流深中都占有主体地位,所以会出现近似线性增大的结果. $z/h = 0$时,顶部及沟谷处的双平均雷诺剪应力均达到了峰值,说明此处的湍流脉动比较强烈. 而沟谷处的双平均雷诺剪应力要大于顶部处的剪应力,这是由于在靠近顶部时,小球的存在限制了脉动流速,导致湍流脉动的双平均值比较小. 当$z/h > 0.25$时,二者基本重合,说明随着高程的增加,透水床面地形的影响逐渐减小,空间异构性作用也随之减弱.
|
图 10 顶部及沟谷双平均雷诺剪应力 Fig.10 DA Reynolds shear stress |
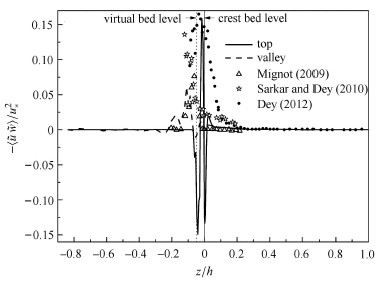
图11显示了双平均构造剪应力的垂向分布,构造剪应力表示由时均量的空间异构所产生的动量通量. Dey等[5]及Manes等[22]实 验中的峰值都在顶层床面附近,这与数值模拟结果相吻合. 在构造剪应力峰值的部分,由于构造应力的影响,流速分布并不符合对数分布,这与之前关于流速沿高程分布的结果相吻合. 另外,当$ - 0.2 < z/h < 0.1$时,模拟数据的统计结果出现了比较大的波动,甚至出现了负的构造剪应力. 这是由于时均流场在顶层小球之间出现了明显了涡旋结构. 这种涡旋结构在时间序列上比较稳定,导致了时均量的空间脉动格外剧烈. 而以往物理模型中由于测量精度、以及近壁距离的限制,较难得到贴近壁面的旋涡结构,流速均同主流向速度一致,所以得到 的剪应力均为正,与数值模拟结果有一定区别.
|
图 11 顶部及沟谷双平均构造剪应力 Fig.11 DA Form-induced shear stress |
图12表示顺流向及床面法向的双平均脉动幅度的垂向分布. 双平均脉动幅度通过以下公式求得
| ${\sqrt {\overline {{u}'{u}'} } } / {u^\ast }$ | (18) |

|
图 12 双平均脉动幅度的垂向分布 Fig.12 DA Reynolds turbulence intensities |
通过观察公式可以看出,双平均脉动幅度经过平方后即为雷诺正应力$RNS= {{u}'{u}'} / {u^{\ast 2}}$,其反映了某个方向的湍流脉动强度.
从图中可以看出,在整个流场中,顺流向及法向的脉动幅度与实验数据符合较好. 二者存在类似的特性:在构造层内部增长得很快,并于$z/h \approx 0.1$处达到了极值. 随着$ z/h $的增加,又逐渐减小,但一直保持着顺流向的脉动幅度大于垂向脉动幅度的大小关系. Nezu等[23]提到,产生这种大小关系的原因可能是流场中的各向异性造成的. 以沟谷处为例,可以得到具体的峰值为:${\sqrt {\overline {{u}'{u}'} } } /{u^\ast } \approx 2.252$; $ {\sqrt {\overline {{w}'{w}'} } } / {u^\ast } \approx 1.183$.
另外,观察$u$的脉动幅度峰值,小球沟谷处要比顶部小,原因是突出的小球顶部在顺流方向引起了更大的湍流紊动,而且小球顶部脉动 幅度峰值所在高程要比沟谷处大,大约高出$0.05z/h$. 另外,顶部统计值在$z/h = 0$处出现峰值,沟谷处统计值在$ - 0.05 < z/h < 0$的范围内出现峰值,这说明构造层内湍流脉动加强了混合过程,使得此处的脉动幅度会比较大. 不同实验中脉动幅度峰值出现的位置有所不同,这与床面形态有关,一般来说,粗糙高度越小、透水率越大的床面,脉动幅度达到峰值的位置越低.
观察透水床面内部,可以看出,小球空隙处(透水率最大处)脉动幅度有明显的突增. 而在透水床面上部,顶部与沟谷处湍流脉动的影响逐渐消失,两条曲线趋于一致. 说明上层流场脉动幅度受透水床面地形的影响逐渐消失.
对比顺流向及垂直水平面方向的脉动幅度,在接近自由水面时,顺流方向的双平均脉动幅度仍然存在,大约为0.8,而垂向的双平均脉动幅度在流场上部先呈线性减小,接近自由水面时,剧烈降低至0. 在接近自由水面时,顺流向仍然存在一定程度的湍流紊动,而垂向上紊动趋于零,这与湍流的大尺度结构,以及数值模拟中上表面设置的刚盖滑移边界条件有关.
4 结 论本文通过大涡模拟方法,利用双平均理论,分析了理想透水床面明渠湍流的时空平均特性. 统计结果对比前人实验,说明大涡模拟计算结果能够合理地反映流场规律. 通过精细模拟近壁及床面以下的透水区域流场,得到了一些新的结论,这是以往水槽实验和数值模拟实验很难反映的. 具体如下:
(1)理想粗糙透水床面明渠湍流,顶层床面上部流场中,即$z_1 ^ + > 80$范围内,双平均流速分布符合对数分布,且基本不受空间异构性影响. 但由于透水率较大,卡门常数变小,为0.29左右;
(2)靠近顶层床面,即$ - 98 < z_1 ^ + < 80$范围内,由于空间异构性增强,不同位置的双平均流速分布出现了差异. 其中,顶部双平均流速分布符合多项式分布,沟谷双平均流速分布符合线性分布;
(3)透水床面内部,靠近底面球孔双平均流速约为靠近上部球孔双平均流速的1.55倍.
(4)在顶层床面之上,即$z/h> 0.01$时,雷诺剪应力占有主体地位,大约为总应力的95%. 靠近顶层床面,即$ - 0.1 < z/h < 0.01$时,由于紊动增强,空间异构性增大,构造剪应力不能忽略,约占总应力的15%.
(5)由于空间异构性,在靠近顶层床面时,不同空间位置的剪应力及湍流脉动幅度峰值大小及峰值出现的位置有所不同.
根据计算得到的透水床面三维流动特性,可以模拟污染物质的输移规律,计算其在透水床面停留时间. 进而分析沉积物颗粒不同粒径分布、河道不同平面形态对污染物质输移、降解的影响,为正确评价透水床面中受污染水体的自净能力影响、底泥污染影响打下基础.
| [1] | Smith JD, Mclean SR. Spatially averaged flow over a wavy surface. Journal of Geophysical Research-Oceans and Atmospheres, 1977, 82(12): 1735-1746 |
| [2] | Nikora V, Koll K, Mcewan I, et al. Velocity distribution in the roughness layer of rough-bed flows. Journal of Hydraulic Engineering-ASCE, 2004, 130(10): 1036-1042 |
| [3] | Coleman SE, Nikora VI, Mclean SR, et al. Subelement form-drag parameterization in rough-bed flows. Journal of Hydraulic Engineering-ASCE, 2007, 133(2): 121-129 |
| [4] | Aberle J. Measurements of armour layer roughness geometry function and porosity. Acta Geophysica, 2007, 55(1): 23-32 |
| [5] | Dey S, Das R. Gravel-Bed hydrodynamics: Double-averaging approach. Journal of Hydraulic Engineering-ASCE, 2012, 138(8): 707-725 |
| [6] | Mignot E, Hurther D, Barthelemy E. On the structure of shear stress and turbulent kinetic energy flux across the roughness layer of a gravel-bed channel flow. Journal of Fluid Mechanics, 2009, 638: 423-452 |
| [7] | Jimenez J. Turbulent flows over rough walls. Annual Review of Fluid Mechanics, 2004, 36: 173-196 |
| [8] | 白静,方红卫,何国建. 非淹没丁坝绕流的三维大涡模拟研究. 力学学报, 2013, 45(2): 151-157 (Bai Jing, Fang Hongwei, He Guojian. Study of non-submerged groin turbulence flowin a shallowopen channel by LES. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 151-157 (in Chinese)) |
| [9] | Nikora VI, Smart GM. Turbulence characteristics of New Zealand gravel-bed rivers. Journal of Hydraulic Engineering-ASCE, 1997, 123(9): 764-773 |
| [10] | Kironoto BA, Graf WH. Turbulence characteristics in rough uniform open-channel flow. Proceedings of the Institution of Civil Engineers-Water Maritime and Energy, 1994, 106(4): 333-344 |
| [11] | Nikora VI, Rowinski PM. Rough-bed flows in geophysical, environmental, and engineering systems: Double-averaging approach and its applications - preface. Acta Geophysica, 2008, 56(3): 529-533 |
| [12] | Gimenez-Curto LA, Corniero MA. Flow characteristics in the interfacial shear layer between a fluid and a granular bed. Journal of Geophysical Research-Oceans, 2002, 107(C5): 12-1-12-9 |
| [13] | Nikora V, Mcewan I, Mclean S, et al. Double-Averaging concept for rough-bed open-channel and overland flows: Theoretical background. Journal of Hydraulic Engineering-ASCE, 2007, 133(8): 873-883 |
| [14] | Manes C, Pokrajac D, Mcewan I. Double-averaged open-channel flows with small relative submergence. Journal of Hydraulic Engineering-ASCE, 2007, 133(8): 896-904 |
| [15] | Nikora V, Goring D, Mcewan I, et al. Spatially averaged open-channel flow over rough bed. Journal of Hydraulic Engineering-ASCE, 2001, 127(2): 123-133 |
| [16] | Germano M, Piomelli U, Moin P, et al. A dynamic subgrid-scale eddy viscosity model. Physics of Fluids A-Fluid Dynamics, 1991, 3(7): 1760-1765 |
| [17] | Bomminayuni S, Stoesser T. Turbulence statistics in an open-channel flow over a rough bed. Journal of Hydraulic Engineering-ASCE, 2011, 137(11): 1347-1358 |
| [18] | Dasgupta A, Paudyal GN. Characteristics of free-surface flow over gravel bed. Journal of Irrigation and Drainage Engineering-ASCE, 1985, 111(4): 299-318 |
| [19] | 陈兴伟,林木生,程年生等. 粗糙透水床面明渠水流的垂线流速分布. 水科学进展, 2013, 24(6): 849-854 (Chen Xingwei, Lin Musheng1, Cheng Niansheng, et al. Velocity profile of turbulent open-channel flows over rough and permeable beds. Advances in Water Science, 2013, 24(6): 849-854 (in Chinese)) |
| [20] | Nezu I, Kadota A, Nakagawa H. Turbulent structure in unsteady depth-varying open-channel flows. Journal of Hydraulic Engineering-ASCE, 1997, 123(9): 752-763 |
| [21] | Manes C, Pokrajac D, Nikora VI, et al. Turbulent friction in flows over permeable walls. Geophysical Research Letters, 2011, 38: L03402 |
| [22] | Manes C, Pokrajac D, Mcewan I, et al. Turbulence structure of open channel flows over permeable and impermeable beds: A comparative study. Physics of Fluids, 2009, 21: 12510912 |
| [23] | Nezu I, Nakagawa H. Turbulence in Open-Channel Flows. Balkema, Rotterdam, Netherlands. 1993 |
2. School of Aerospace, Tsinghua University, Beijing 100084, China
 2015, Vol. 47
2015, Vol. 47