不同时间尺度耦合系统具有广泛的工程背景,涉及到科学和工程技术的各个领域,如飞行器中存在着快速的旋转运动与相对较慢 的平动之间的耦合[1],催化反应中存在着不同的量级反应速率[2]. 特别地,迄今为止几乎所有的神经元模型都包含快慢两时间尺度,如霍奇金$\!$-$\!$-$\!$赫克斯利(Hodgkin-$\!$-Huxley)模 型[3],莫里斯$\!$-$\!$-$\!$莱卡尔(Morris-$\!$-Lecar)模型[4]等. 不同时间尺度耦合系统通常表现为大幅振荡和微幅振荡,也即激发态(spiking states,SP)和沉寂 态[5] (quiescent states,QS)组合的簇发振荡.
自诺贝尔奖获得者霍奇金(Hodgkin)和赫克斯利(Huxley)通过建立两时间尺度模型成功地模拟了神经元的簇发放电行为以来, 不同尺度耦合系统的复杂性及其机理研究一直是国内外学者广泛关注的热点和前沿课题之一[6],大量相关成果见诸报 道[7, 8, 9]. 从最初的准静态的引入到利用摄动法的逼近等[10],虽然能够得到其相应的近似解,但无法解决其中的动力学特性,直到快 慢分析法的引入[11],能够很好地解释激发态和沉寂态之间的分岔连接,从而揭示了簇发振荡的产生机制[12]. 基于该方法,得到了各种不同的簇发振荡模式,诸如折分岔(fold/fold)簇发,折/霍普夫分岔(fold/Hopf)簇 发等等[13, 14],尽管有基于3个不同时间尺度的四维双慢变系统的相关研究成果[15]. 但是,目前的成果大都基于含低维(2$\sim$3维)快子系统和单维慢子系统的两尺度系统的基础上得到的,然而,在其相应的快子 系统中,平衡态数量较少且形式简单[16],从而导致所产生的簇发振荡一般仅包含单一形式的沉寂态和激发态.
为进一步研究不同时间尺度效应的复杂性,必须深入考察高维耦合系统,尤其当快子系统存在多平衡态时的簇发振荡. 本文通 过修正哈特利(Hartley)模型[17],改变其中的非线性阻尼特性,并适当选择参数,构建了含多平衡态快子系统的四维多时 间尺度模型,进而探讨两种典型参数条件下的不同簇发振荡,揭示其相应的产生机制.
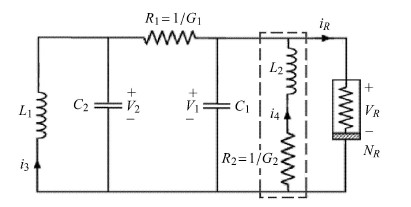
1 数学模型经典的三维哈特利电路模型能够很好地展示从平衡点到周期振荡进而到混沌振荡的过程. 我们在哈特利模型的基础上,并联一由 电感和电阻组成的子电路模块(虚线框内部分),如图1所示,其相应的数学模型可以表示为
| $\left. \begin{array}{*{35}{l}} \begin{align} & \frac{\text{d}{{V}_{1}}}{\text{d}t}=\frac{1}{{{C}_{1}}}[{{G}_{1}}({{V}_{2}}-{{V}_{1}})-g({{V}_{1}})+{{i}_{4}}] \\ & \frac{\text{d}{{V}_{2}}}{\text{d}t}=\frac{1}{{{C}_{2}}}[{{G}_{1}}({{V}_{1}}-{{V}_{2}})+{{i}_{3}}] \\ & \frac{\text{d}{{i}_{3}}}{dt}=-\frac{1}{{{L}_{1}}}{{V}_{2}} \\ & \frac{\text{d}{{i}_{4}}}{dt}=-\frac{1}{{{L}_{2}}}{{V}_{1}}-\frac{{{R}_{2}}}{{{L}_{2}}{{i}_{4}}} \\ \end{align} \\ \end{array} \right\} $ | (1) |
|
图 1 电路模型 Fig. 1 Circuit model |
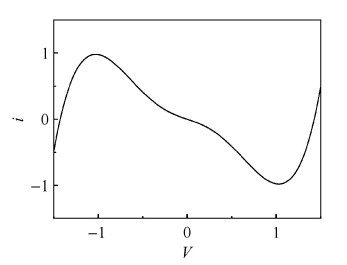
其中,$G_1 = 1 / R_1 $,$g(V_1 )$表示非线性电阻的伏安特性. 为考察多平衡态的影响,在此引入更高次非线性项, 取$g(V_1 ) = [- \alpha V_1 - \beta V_1^5 - \gamma \tanh (\delta V_1 )] / R_1 $ (见图2).
|
图 2 非线性电阻$V$-$\!$-$i$特性曲线 Fig. 2 The $V$-$\!$-$i$ character of the nonlinear resistor |
引入变换$x = V_1 $,$y = V_2 $,$z = i_3 R_1 $,$w = i_4 R_1 C_2 / C_1 $,$\tau = t / (R_1 C_2 )$,式(1)可以表示为如下无量纲形式
| $ \left.\begin{array}{l} \dfrac{\text{d} x}{\text{d}\tau } = p\left[{y - x - f\left( x \right)} \right] + w \\ \dfrac{\text{d} y}{\text{d}\tau } = x - y + z \\ \dfrac{\text{d} z}{\text{d}\tau } = - qy \\ \dfrac{\text{d} w}{\text{d}\tau } = - e(x + \kappa w) \end{array}\!\! \right\} $ | (2) |
其中,$p = C_2 / C_1 $,$q = R_1^2 C_2 / L_1 $,$e = R_1^2 C_2^2 / (L_2 C_1 )$,$\kappa = R_2 C_1 / (R_1 C_2 )$,$f(x) = - a_1 x - a_2 x^5 - b\tanh (\text{d} x)$,参数 $a_1 = \alpha$,$a_2 = \beta$,$b = \gamma$,$d = \delta$. 当取 $e \ll 1$,而其他参数为常规量时,则式(2)可以看作由前3个变量$x$,$y$,$z$组成的快子系统(前3式)和最后一个变 量$w$组成的慢子系统(第4式)的四维快慢耦合非线性系统,其相互作用会导致系统产生簇发振荡. 这种簇发振荡不仅导致电路中各物理量诸如电压等相关状态量会在不同物理参数(状态形式)下的突变,也会使得电压等值出 现复杂的振荡形式. 可以利用此结果对避免产生这种簇发振荡的电路设计提供理论基础,还可以为生物耦合模型簇发研究提供相关的辅助模型.
2 快子系统多平衡态下的分岔分析由于快子系统的平衡态及其分岔会影响簇发振荡的行为,首先考虑快子系统的动力特性. 取定参数
| $ \ \left. \begin{align} & e=0.03,\kappa =1.667,{{a}_{1}}=2.46,{{a}_{2}}=-0.4 \\ & b=-1.1547,d=1.732,q=10 \\ \end{align} \right\} $ | (3) |
考察快子系统随参数$p$及慢变量$w$变换时的各种平衡点及其分岔模式. 显然快子系统的平衡点可以表示为 $E_0 (x,y,z) = E_0 (x_0 ,0,- x_0 )$,其中$x_0 $满足方程
| $ p[1.46x_0 - 0.4x_0^5 - 1.1547\tanh (1.732x_0 )] + w = 0 $ | (4) |
其相应的雅可比矩阵所对应的特征方程可以表示为
| $ \lambda ^3 + (1 - mp)\lambda ^2 + (10 - mp - p)\lambda - 10mp = 0 $ | (5) |
其中$m = - 0.54 - 2x_0^4 + 2.0\tanh ^2(1.732x_0 )$. 由于参数$p > 0$,因此当$m < 0$,且$(1 - mp)(10 - mp - p) + 10mp > 0$时,$E_0 $为稳定的平衡点,其存在着两种余维一退化形式, 分别对应于式(5)中的特征值具有单零特征值及一对纯虚根情形,产生两种余维一分岔情形.
2.1 分岔集由特征方程(5)可知,当参数满足$m = 0$,$p < 10$时可能会产生折(fold)分岔,也即存在着如下4条折分岔集(直线).
| $FB_{1}$: $0.116\,367\,179\,5p + w = 0$ |
| $FB_{2}$: $0.024\,462\,835p + w = 0$ |
| $FB_{3}$: $ - 0.024\,462\,835p + w = 0$ |
| $FB_{4}$: $ - 0.116\,367\,179\,5p + w = 0$ |
折分岔会导致系统在不同平衡点之间的跳跃. 同样由特征方程(5)可知,当参数满足
| $\begin{array}{l} \;\;\;HB:\\ \left. {\begin{array}{*{20}{l}} \begin{array}{l} (1 - mp)(10 - mp - p) + 10mp = 0\\ p[1.46{x_0} - 0.4x_0^5 - 1.1547\tanh (1.732{x_0})] + w = 0 \end{array} \end{array}} \right\} \end{array}$ | (6) |
可能会产生霍普夫(Hopf)分岔,导致周期振荡. 当然系统还可能存在着其他余维二分岔模式,但由于参数条件非常特殊,在此不 作进一步的展开.
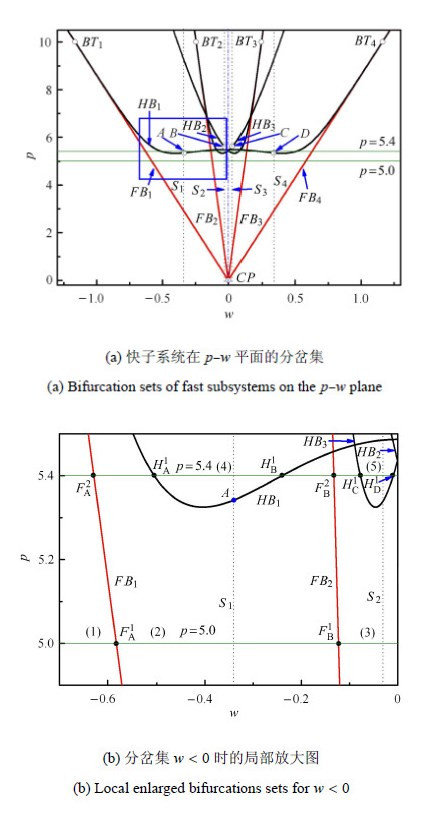
2.3 分岔行为根据上述分岔分析可知,随着参数$w$的变化,快子系统产生多种不同的平衡态,并产生了折和霍普夫两种分岔行为,图3(a)给出 了快子系统在$p$-$\!$-$w$平面上的折和霍普夫分岔集. 这些分岔集将参数平面划分为不同的区域,分别对应不同的动力学特性. 如图3所示,$FB_i$ ($i = 1,2,3,4$) 和$HB_i$ ($i = 1,2,3$) 分别对应折和霍普夫分岔集. $BT_i$ ($i = 1,2,3,4$) 对应余维2 的零-$\!$-零(Bugbanov-$\!$-Takens)[18]分岔点,$CP$对应余维2 的尖(cusp)[18]分岔点. 进一步分析可以发现,对于霍普夫分岔集$HB_i $ ($i = 1,2,3$),分隔直线$S_{1}$ ($w = - 0.336\,6$) 和$S_{4}$ ($w = 0.336\,6$) 将$HB_{1}$划分为3段,其中间段对应于亚临界,其余2段对应于超临界,$HB_{2}$由$S_{2}$ ($w = - 0.005\,2$) 划分为2段,其左边为亚临界,其右边则对应于超临界,$HB_{3}$由$S_{3}$ ($w = 0.005\,2$) 划分为2段,其左边为超临界,而右边为亚临界.
|
图 3 Fig. 3 |
由于分岔集关于直线$w = 0$对称,在此,对$w < 0$时矩形框内快子系统具有更为复杂平衡态演化过程的参数部分进行分析,对 于具有较为简单行为的其它参数部分已有大量研究成果,在此不再赘述. 选取其中具有代表性的$p = 5.0$和$p = 5.4$两种情况下的动力学行为进行研究(图3(b)).
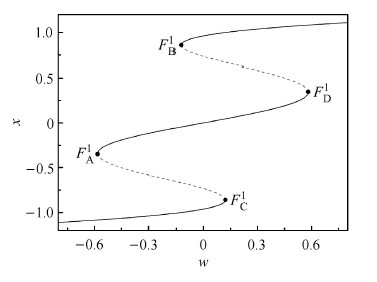
2.3.1 $p = 5.0$时的分岔行为图4给出了快子系统$p = 5.0$时的平衡点曲线. 其中虚线所画为不稳定的平衡点,实线所画为稳定的平衡点. 在$w < 0$区域内,随着$w$由小到大的变化,系统经过了图3(b)中的(1),(2),(3)三个区域. 当$w \in ( - 0.122\,3,0)$即 (3) 区域时,快子系统存在5个平衡点(图4),其中3个为稳定的平衡点,2个为不稳定的平衡点. 这是一个具有5个平衡 点的多平衡态区域. 随着参数$w$的减小,经过折分岔集$FB_{2}$后,当$w \in ( - 0.581\,8,- 0.122\,3)$即(2)区域时,系统会因为一个稳定的平衡点和一个不稳定的平衡点相碰而消失,快子系统变为3个平衡点共存,其中2个为 稳定的平衡点,一个为不稳定的平衡点. 这是一个具有3个平衡点的多平衡态区域(图4). 随着参数$w$继续减小,经过折分岔集$FB_{1}$后,即(1)区域, 同样会由于一个稳定的平衡点和一个不稳定的平衡相碰而消失,此时系统只有一个稳定的平衡点. 另外系统会由于发生折分岔,使系统稳定的平衡点和不稳定的平衡点相碰消失,这也是导致快慢耦合系统轨线跳跃的原因. 另外,由于图3(a)对$w = 0$的对称性,在$w > 0$区域内可做同样的分析得到相同的结论.
|
图 4 $p = 5.0$ 快子系统平衡点曲线 Fig. 4 Equilibrium branch of fast subsystems for $p = 5.0$ |
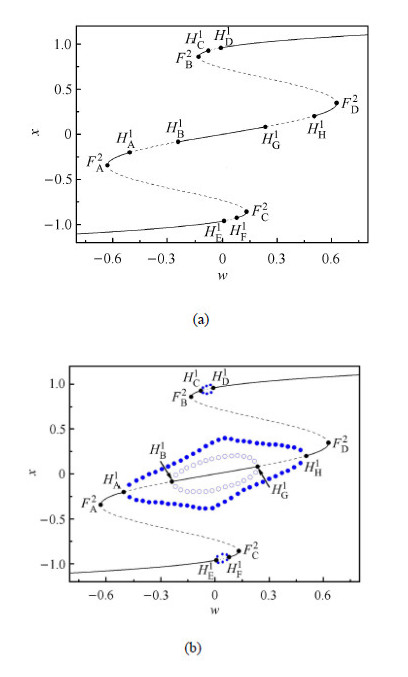
图5(a)给出了快子系统$p = 5.4$时的平衡点曲线. 实线为稳定平衡点,虚线为不稳定平衡点. 在图3(b)中$w < 0$区域内, 当$w < - 0.628\,4$时快子系统在(1)区域,系统只有一个稳定的平衡点. 与图5(b)对照(下同),当$w \in ( - 0.628\,4,- 0.132\,1)$时,即两个折分岔集$FB_{1}$、$FB_{2}$之间,快子系统经过(2)(4)两个区域,出现了较为复杂的3平衡态现象,既有稳定与不稳定的平衡点,同时又有极限环的存在. 当$w \in ( - 0.132\,1,0)$时,即两个折分岔集$FB_{2}$, $FB_{3}$之间,快子系统经过(3)(5)两个区域,出现了5平衡态共存现象. 这两个区间为既有稳定与不稳定平衡点,又有极限环存在的区域. $w \in ( - 0.628\,4,- 0.505\,2)$为一个不稳定的平衡点和两个稳定的平衡点共存,$w \in ( - 0.505\,2,- 0.239\,0)$ 3个平衡点中一个稳定的平衡点变为不稳定的平衡点且出现了稳定的极限环,$w \in ( - 0.239\,0,- 0.132\,1)$ 3个平衡点中一个不稳定的平衡点变为稳定的平衡点,且同时存在稳定的极限环和不稳定的极限环,$w \in ( - 0.132\,1,- 0.077\,1)$为3个不稳定的平衡点和2个稳定的平衡点共存,稳定的极限环和不稳定的极限环同时存在,$w \in ( - 0.077\,1,- 0.008\,7)$ 5个平衡点中一个稳定的平衡点变为不稳定的平衡点,且伴随有稳定的极限环的产生,此时有两个稳定的极限环和一个不稳定的极限环共存,$w \in ( - 0.008\,7,0)$ 5个平衡点中一个不稳定的平衡点变为稳定的平衡点,并伴随一个稳定的极限环的消失,此时只有一个稳定的极限环和一个不稳定的极限环存在.
|
图 5 $p = 5.4$ (a)快子系统平衡点曲线; (b)快子系统极限环 Fig. 5 $p = 5.4$ (a) Equilibrium branch of fast subsystems; (b) Limit cycle of fast subsystems |
由于高次非线性项的引入,会导致系统呈现更多的平衡态及其分岔行为,从而导致更为复杂的多时间尺度效应.
3 快慢效应由于$p = 5.0$和$p = 5.4$时快子系统具有更为复杂的动力学分岔行为和多个不同性质平衡态之间的转变,下面 考虑$p = 5.0$和$p = 5.4$两种快子系统存在典型分岔行为时的快慢耦合系统的多时间尺度效应及其产生机理.
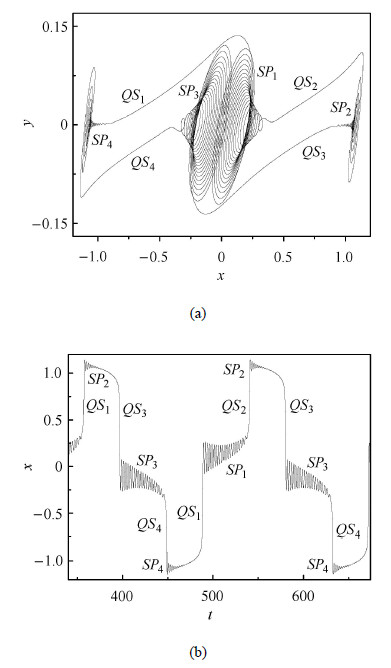
3.1 ${\pmb p}\,{\bf = 5.0}$时的簇发振荡图6分别给出了$p = 5.0$时系统$x $-$\!$-$ y$平面相图和相应$x$的时间历程,系统存在4个激发态和4个沉寂态,分别用$SP_{i}$和$QS_{i}$ ($i = 1,2,3,4$)表示. 根据图6(b)可以看出,系统轨迹表现为大幅的周期振荡, 在局部区域,则为微幅振荡.
|
图 6 $p = 5.0$ 系统的簇发 (a) $x $-$\!$-$ y$平面相图;(b) 时间历程 Fig. 6 Bursting phenomena for $p = 5.0$ (a) phase portrait on the $x $-$\!$-$ y$ (b) time history |
为揭示图6中的簇发振荡的机理,图7给出了快子系统随$w$变化的平衡点及其分岔,并与簇发振荡在$(w,x)$平面上的转换相图叠加.
|
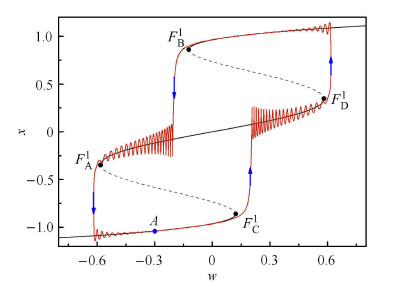
图 7 $p = 5.0$快子系统的平衡点及其分岔分析图与快慢耦合系统相图在$(w,x)$平面上的叠加 Fig. 7 Overlap between Equilibrium branch of fast subsystems and the phase portrait of slow-fast coupled system on the $(w,x)$ plane for $p = 5.0$ |
在图7中,平衡点的实线部分对应的特征值为一个负实数和一对具有负实部的共轭复数,称为稳定焦点[19]),而虚线部分对应的特征值是一个正实数和一对具有负实部的共轭复数(称为鞍焦型奇 点[19]),故此两部分平衡点既有结点性质,又有焦点性质. 在$F_{\rm A}^1 $,$F_{\rm B}^1 $,$F_{\rm C}^1 $,$F_{\rm D}^1 $点处,实根的正负号发生了变化,实数的特征根变成了零,而这对共轭复根的实部保持原有的正负号性质. 这种由实数特征值正负号发生了变化引起的分岔为鞍结分岔,而共轭复根实部符号没有变化,也就没有霍普夫分岔发生,只存在鞍结分岔即这里称为折分岔. 必须指出,随着慢变量$w$的变化,系统轨线在折分岔点处产生跳跃,到达上(下)侧稳定的平衡点时,由于平衡点的焦点性质,使轨线绕着平衡点旋转且有一定的幅值. 由于平衡点的稳定性质,该轨线随参数$w$的变化而旋转并逐渐收缩到稳定的平衡点上,此时投影到$w $-$\!$-$x$平面内就看到轨线的波动并逐渐收缩到平衡线上. 但如果这个平衡点只是稳定的结点那么就直接进入平衡点,不出现旋转,在$w $-$\!$-$ x$平面内就没有轨线的波动,类似的现象可以在文献[20]中的图3(b)和图6中找到.
下面分析图7中簇发振荡的形成机制,设轨迹从$A$点出发. 随着$w$的增加,几乎严格沿着快子系统稳定的平衡点运动,构成沉寂态$Q S_{1}$,一直到$F_{\rm C}^1$ $(w = 0.122\,3)$点,由于快子系统产生折分岔,导致跳跃现象,围绕快子系统平衡线中间分支产生激发态$SP_{1}$. 由于此时快子系统平衡点为稳定的焦点,随着$w$值的增加,轨迹会由于稳定焦点的吸引作用,激发态$SP_{1}$的振荡幅值越来越小,进入沉寂态$QS_{2}$. 当$w$增加到$F_{\rm D}^1$ $(w = 0.581\,8)$点时,快子系统再次产生折分岔,使得轨迹跳跃到快子系统平衡线的上支,由于初值原因,导致轨迹围绕该平衡点振荡,产生激发态$SP_{2}$. 随着$w$的减少,由于稳定焦点的吸引,其振荡幅值不断减少,形成沉寂态$QS_{3}$. 当$w$减少到$F_{\rm B}^1$ $(w = - 0.122\,3)$点,快子系统的折分岔使得轨迹跳跃到中间分支,并围绕平衡点不断振荡. 随着$w$值不断减小,轨线由于受到稳定焦点的吸引振荡幅值不断减小,形成沉寂态$QS_{4}$. 在$F_{\rm A}^1$ $(w = - 0.581\,8)$点再次由于折分岔跳跃到下分支,不断振荡形成激发态$SP_{4}$,直到轨迹回到起始点$A$,完成一个周期的簇发振荡.
由于在$p = 5.0$时,快子系统存在着多个平衡态,且此时这些平衡态只会产生折分岔,在系统相应的簇发振荡中,存在着多个沉寂态和激发态,并由折分岔导致相互之间的转换.
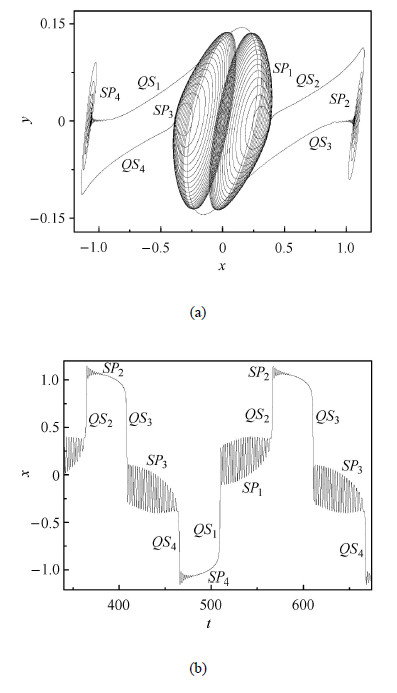
3.2 ${\pmb p}\,{\bf = 5.4}$时的簇发振荡由图3可知,随着系统$p$值增加,快子系统会产生复杂的分岔现象和多种平衡态,此时的簇发现象更为复杂. 图8(a)和图8(b) 分别给出了$p = 5.4$时快慢系统在$x$-$\!$-$y$ 平面的相图和相应$x$的时间历程,显然此时的周期簇发振荡的结构相对较为复杂.
|
图 8 $p = 5.4$ 系统的簇发 (a) $x $-$\!$-$ y$平面相图;(b) 时间历程 Fig. 8 Bursting phenomena for $p = 5.4$ (a) phase portrait on the $x $-$\!$-$ y$; (b) time history |
图5(a)给出了快子系统随$w$变化的平衡点及其分岔图,图中平衡点曲线中实线为稳定的焦点,虚线为不稳定的焦点. 由该图 可知,平衡线共有8个霍普夫分岔点,4个LP点. 根据图3中超临界霍普夫分岔和亚临界霍普夫分岔分隔线$S_{1}$和$S_{2}$可知$H_A^1 (w = - 0.505\,2)$,$H_{\rm C}^1 (w = - 0.077\,1)$,$H_{\rm D}^1 (w = - 0.087)$,$H_{\rm E}^1 (w = 0.008\,7)$,$H_{\rm F}^1 (w = 0.077\,1)$, $H_{\rm H}^1 (w = 0.505\,2)$为超临界霍普夫分岔点,$H_{\rm B}^1 (w = - 0.239\,0)$,$H_{\rm G}^1 (w = 0.239\,0)$,为亚临界霍普夫分岔点. $F_{\rm A}^2 (w = - 0.628\,4)$,$F_{\rm B}^2 (w = - 0.132\,1)$,$F_{\rm C}^2 (w = 0.132\,1)$,$F_{\rm D}^2 (w = 0.628\,4)$为折分岔点.
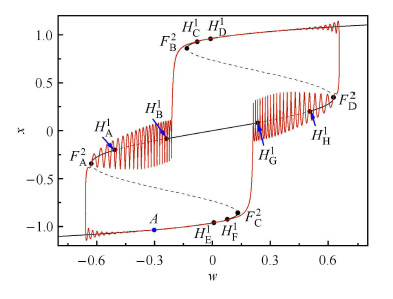
为揭示图8(a) 中的簇发振荡机理,在此将图5(a)中的平衡曲线与簇发振荡轨迹在$w $-$\!$-$x$平面的相图叠加(见图9).
|
图 9 $p = 5.4$快子系统的平衡点及其分岔分析图与快慢耦合系统相图在$(w,x)$平面上的叠加 Fig. 9 Overlap between Equilibrium branch of fast subsystems and the phase portrait of slow-fast coupled system on the $(w,x)$ plane for $p = 5.4$ |
可以看到图9中轨迹在下分支$A$点处,系统处 于沉寂态. 随着$w$的增加,轨迹会依次经过$H_{\rm E}^1 (w = 0.008\,7)$和$H_F^1 (w = 0.077\,1)$两个霍普夫分岔点,由于这两个霍普夫分岔点同为$HB_{2}$分岔集上超临界霍普夫分岔点,该区域内没有微幅振荡,没有改变系统原有的沉寂态. 在轨线经过$H_{\rm F}^1 (w = 0.077\,1)$点之后,轨线随着$w$增加到$F_{\rm C}^2 (w = 0.132\,1)$点时由于折分岔跳跃到中间的平衡点曲线上,此时轨线在稳定极限环附近振荡,因此会由于同时受到稳定焦点的吸引,振荡幅值逐渐减小. 但随着$w$继续增加,由于亚临界霍普夫分岔点$H_{\rm G}^1 (w = 0.239\,0)$的存在,快子系统不稳定的焦点和稳定极限环出现,使轨线微幅振荡的运动幅值随极限环幅值变化,直到$H_{\rm H}^1 (w = 0.505\,2)$点由于超临界霍普夫分岔和稳定的焦点的共同作用,使轨线幅值减小. 随后当$w$增加到$F_{\rm D}^2 (w = 0.628\,4)$点时,由于折分岔,轨线又跳跃到上分支平衡曲线上,轨线被稳定的焦点所吸引,因此随着$w$的折回,幅值不断减小,逐渐趋于平衡点曲线. 随着$w$继续减少,轨线依次经过$H_{\rm E}^1 (w = 0.008\,7)$和$H_{\rm F}^1 (w = 0.077\,1)$点,这两个霍普夫分岔点同为超临界霍普夫分岔点. 轨线在$H_{\rm D}^1 (w = - 0.087)$至$H_{\rm C}^1 (w = - 0.077\,1)$区间,没有进入激发态,仍为沉寂态,仍重合于平衡点曲线. 当轨线到达$F_{\rm B}^2 (w = - 0.132\,1)$点时由于折分岔跳跃到中间轨线分支,由于受到稳定焦点的吸引以及不稳定极限环的影响,运动幅值不断减小. 随着$w$继续减少,到达亚临界霍普夫分岔点$H_{\rm B}^1 (w = - 0.239\,0)$ 附近时,快子系统出现稳定的极限环,且平衡点由稳定的焦点变为不稳定的焦点,使快慢系统轨线幅值缓慢增加,进入激发态. 直到$H_{\rm A}^1 (w = - 0.505\,2)$ 点由于超临界霍普夫分岔,使轨线进入沉寂态. 随后当$w$减少到$F_{\rm A}^2 (w = - 0.628\,4)$ 点时,由于折分岔,轨线跳跃到下分支,并随着$w$的折回幅值不断减小. 直到轨迹回到$A$点,完成一个周期的运动,形成新的4-状态具有霍普夫分岔点的更为复杂的簇发现象. 可以看到由于折分岔的存在,系统可以产生簇发现象,而且由于超临界亚临界霍普夫分岔点交替出现,系 统也会产生簇发现象,但两个超临界霍普夫分岔点之间不产生簇发现象.
4 结 论对于具有多平衡态的高维快慢耦合自治系统,当快子系统和慢子系统之间的运动存在量级差距时,会形成不同的时间尺度,产生多时间尺度效应,表现为沉寂态和激发态之间相互转化的系统簇发振荡. 对于具有多平衡态快子系统的非线性系统,由于快子系统在不同区域中平衡点数量及分岔类型的不同,导致多个沉寂态和激发态,也会产生多种沉寂态和激发态的分岔连接,进而产生不同的簇发振荡. 系统会由于折分岔的存在产生折分岔簇发,并且由于超临界和亚临界霍普夫分岔点的交替出现产生折/霍普夫分岔簇发现象,同时由于快子系统的多平衡态,不仅会导致簇发振荡中存在多个沉寂态和激发态,同时多个平衡态的不同分岔行为也会影响沉寂态和激发态之间的转换模式,因此,多平衡态下快子系统所诱发的簇发振荡会呈现出更为复杂的结构特征.
| [1] | Theodosiou C, Sikelis K, Natsiavas S. Periodic steady state response of large scale mechanical models with local nonlinearities. Int J Solids Struct, 2009, 46(20): 3565-3576. |
| [2] | Bi QS. The mechanism of bursting phenomena in Belousov-Zhabotinsky(BZ) chemical reaction with multiple time scale. Sci China-Technol Sci, 2010, 53(3): 748-760. |
| [3] | Yang ZQ, Lu QS, Li L. The genesis of period-adding bursting without bursting-chaos in the Chay model. Chaos Solitons Fractals, 2006, 27(3): 689-697. |
| [4] | Wang HX, Lu QS, Wang QY. Bursting and synchronization transition in the coupled modified ML neurons. Commun Nonlinear Sci, 2008, 13(8): 1668-1675. |
| [5] | 陈章耀, 张晓芳, 毕勤胜. 周期激励下Hartley模型的簇发及其分岔机制. 力学学报, 2010, 42(4): 765-773 (Chen Zhangyao, Zhang Xiaofang, Bi Qinsheng. Bursting phenomena as well as the bifurcation mechanism in periodically excited Hartley model. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 765-773 (in Chinese)) |
| [6] | Abobda LT, Woafo P. Subharmonic and bursting oscillations of a ferromagnetic mass fixed on a spring and subjected to an AC electromagnet. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(7): 3082-3091. |
| [7] | 张正娣, 毕勤胜. 自激作用下洛伦兹振子的簇发现象及其分岔机制. 中国科学: 物理学力学天文学, 2013, 43(4): 511-517 ( Zhang Zhendi, Bi Qinsheng. Bursting phenomenon as well as the bifurcation mechanism of self-excited Lorenz system. Sci Sin-Phys Mech Astron, 2013, 43(4): 511-517 (in Chinese)) |
| [8] | Wang HX, Wang QY, Lu QS. Bursting oscillations, bifurcation and synchronization in neuronal systems. Chaos Solitons Fractals, 2011, 44(8): 667-675. |
| [9] | 陈章耀, 毕勤胜. 非线性电路的簇发现象及其分岔机制. 控制理论与应用, 2011, 28(10): 1413-1420 (Chen Zhangyao, Bi Qinsheng. Bursting phenomena as well as bifurcation mechanism in nonlinear circuit. Control Theory & Applications, 2011, 28(10): 1413-1420 (in Chinese)) |
| [10] | Shen JH, Zhou ZY. Fast-slow dynamics in logistic models with slowly varying parameters. Commun Nonlinear Sci Numer Simul, 2013, 18(8): 2213-2221. |
| [11] | Perc M, Marhl M. Different types of bursting calcium oscillations in non-excitable cells. Chaos Solitons and Fractals, 2003, 18(4): 759-773. |
| [12] | Simo H, Woafo P. Bursting oscillations in electromechanical systems. Mechanics Research Communications. 2011, 38(8): 537-547 |
| [13] | Han XJ, Jiang B, Bi QS. Symmetric bursting of focus-focus type in the controlled Lorenz system with two time scales. Physics Letters A, 2009, 373(40): 3643-3649. |
| [14] | Bi QS, Zhang ZD. Bursting phenomena as well as the bifurcation mechanism in controlled Lorenz oscillation with two scales. Physics Letters A, 2011, 375(8): 1183-1190. |
| [15] | 杨卓琴, 张璇. 3个不同时间尺度的电耦合模型的组合簇放电. 物理学报, 2013, 62 (17): 1705081-1705088 (Yan Zhuoqin, Zhang Xuan. Compound bursting in an electrical coupling model with three different time scales. Acta Phys Sin, 2013, 62(17): 1705081-1705088 (in Chinese)) |
| [16] | Kingni ST, Keuninckx L, Woafo P, et al. Dissipative chaos, Shilnikov chaos and bursting oscillations in a three-dimensional autonomous system: theory and electronic implementation. Nonlinear Dynamics, 2013, 73(1-2): 1111-1123. |
| [17] | Hartley TT, Monssayebi F. Matrix integrators for real-time simulation of singular systems. In: Proc of Amer Control Conf, Ptiisburgh, USA, 1989. 419-423 |
| [18] | Kuzenetsov YA. Elements of Applied Bifurcation Theory. 2nd ed, New York: Springer-Verlag, 1998. 265-277 |
| [19] | 陈予恕. 非线性振动系统的分岔和混沌理论. 北京: 高等教育出版社, 1993 |
| [20] | Han XJ, Bi QS. Bursting oscillations in Duffing's equation with slowly changing external forcing. Commun Nonlinear Sci Numer Simul, 2011, 16(8): 4146-4152 |
 2015, Vol. 47
2015, Vol. 47