激光水下爆炸推进是利用激光维持的水下爆轰及产物气泡的后续振荡来实现航行体的水下运动. 激光水下爆炸推进是一项充满挑 战的新概念推进技术,近几年来才引起大家关注[1, 2, 3]. 与传统的化学燃料推进方法相比,激光水下爆炸推进安全性高、推力输出易于控制、可以实现柔性和微型推进, 展示着良好的发展前景.
激光水下爆炸推进过程中航行体尾部工质在激光辐照下经过熔化、气化、电离等形成的高压等离子体作为驱动源, 在航行体表面形成瞬时的高压力,并在水介质中形成冲击波[4, 5, 6]. 尔后,激光诱导的气泡发生膨胀- 收缩的脉动,并伴随着不稳定性的射流、破裂、飞溅等过程[7, 8]. 气泡的脉动过程提供了航行体在运动阶段的关键推进力. 同时, 气泡的运动还与后续激光能量的吸收、航行体的运动相互作用[9]. 与激光推进的其他分支相比[10, 11],激光水下爆炸推进的研究工作还十分少见, 且主要停留在演示性实验阶段,几乎没有形成推进过程整体的定量化认识. 相对而言, 关于激光冲量耦合系数已经获得了更丰富的实验结果. Yabe 等[12]利用激光诱导等离子体膨胀时溅射出的水滴推进目标靶运动,其冲量耦合系数$C_{\rm m}$达到$350\times10^{ - 5}$ N$\cdot$s/J,但是能量转化率小于1%. 中国科学技术大学激光推进实验室通过试验得到了不同靶材和水层厚度的冲量耦合系数. 其中水层厚度为3 mm 时铝靶结构的冲量耦合系数最高可达$399\times 10^{ - 5}$ N$\cdot$s/J, 比激光直接烧蚀铝靶提高了两个数量级[13, 14, 15]. Pakhomov等[16, 17, 18, 19]研究了不同液态工质下的激光爆炸推进冲量耦合系数, 发现己烷对于提高冲量耦合系数的效果最明显. 如果只考虑气化过程中的质量消耗,比冲约为$I_{\rm sp}= 6$\;s; 但是如果考虑整个过程中的质量消耗,比冲降为$I_{\rm sp}= 0.4$\;s,能量转化效率约为7%. 中国科学院物理研究所研究了水、墨水等液体工质的冲量耦合系数,发现墨水的冲量耦合系数达到$178\times10^{ - 5}$ N$\cdot$s/J[2, 3, 20, 21, 22].
目前看来,激光水下爆炸推进虽然获得了比空气和真空介质中靶板激光烧蚀更高的冲量耦合系数,但仍然存在比冲小,能量利用率低的问题. 激光水下爆炸推进作为一项新的推进技术,还存在一些相对空白的区域: 在推力方面,初步考虑了激光辐照瞬间的冲量耦合,但没有考虑烧蚀产物气泡对航行体运动提供的长时程作用力,这是航行体运动中的关键推力之一; 在航行体阻力方面,还几乎没有针对性的研究. 特别是冲量耦合加载和气泡脉动加载阶段,航行体的阻力来源和特征是不同的,阻力的转换特别是阻力的总体评估还没有定量化的方法. 要定量化描述激光水下推进,就需要对这一复杂过程的演化机理和参数影响规律进行深入研究,特别是水下爆炸的短期冲击波效应向长期气泡脉动过渡的能量分配机制、冲击波/气泡/结构运动的相互作用,以及多次加载机理[23]和航行体非定常阻力特性等关键问题,为激光水下爆炸推进方式的改进及效率的提高提供依据.
本文围绕强激光水下爆炸推进效应中的关键物理过程,采用实验测量和数值模拟相结合的方法,系统研究了激光水下爆炸推进的物理机制和参数的影响规律. 实验获得了不同参数下激光水下爆炸推进航行体的运动特性,包括不同环境介质(空气,水)中激光推进的效率、航行体水深以及用于约束气泡的附加壁面的影响. 在此基础上,建立了激光水下爆炸推进的物理模型,获得激光能量沉积---工质动态响应---爆轰波压力特征的短时作用机理,以及爆炸产物气泡脉动---航行体运动的长时作用机理. 基于物理模型,分析了激光水下推进过程中航行体的运动特征. 计算得到的气泡脉动特征以及航行体运动速度与实验测量结果吻合,验证了计算的模型和方法,为激光水下聚焦爆炸推进机理的研究提供了一种有效的方法.
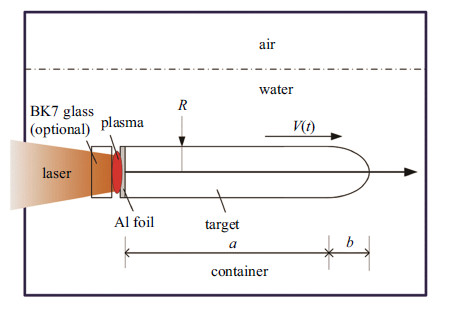
1 实验研究 1.1 实验方法实验在中国科学院力学研究所强激光爆炸与推进实验平台开展,实验装置的示意图如图1所示. 短脉冲强激光经过聚焦后辐照航行体背表面的铝膜,诱导生成等离子体. 等离子体继续与激光相互作用,内能迅速升高,并急剧向外膨胀. 高温等离子体由于受到环境介质的限制膨胀作用而产生短脉冲、高幅值的等离子体压力,并对航行体做功; 后续爆炸产物气泡脉动,对航行体提供长时推力,使航行体在环境介质内运动.
|
图 1 激光聚焦爆炸推进实验示意图 Fig. 1 Schematic of laser propulsion experiment |
实验中Nd: YAG激光器(Spectrum 350)重频工作模式下的单次脉冲能量最高为2.5 J,波长为1 064 nm或532 nm可选; 激光时间分布为高斯分布,有长脉冲与短脉冲两种模式,对应半峰宽时间分别为10 ns和200 ns; 激光空间分布为高斯分布. 通过调整辐照区光斑直径获得不同的激光功率密度. 实验中由于在短波长激光辐照下水介质更易击穿[24],因此采用的激光波长为1 064 nm; 实验中激光器为单次工作模式,测得的激光能量约为2.0 J,激光辐照区域的光斑直径为3 mm,实验的峰值功率密度为2.83 GW/cm$^{2}$. 为了增加航行体对激光能量的吸收率,在航行体尾部贴一层铝膜,厚度为60 μm. 航行体尾部铝膜表面附近可固定附加挡板. 附加挡板选用直径25.4 mm、厚度4 mm 的BK7光学玻璃,来研究附加挡板条件下航行体的运动特征. 附加挡板的作用为: (1)激光与航行体相互作用阶段,由于附加挡板材料的惯性约束作用强于环境介质,限制等离子体的快速膨胀,因此能显著提高等离子体的压力,从而提高对航行体的短时推力; (2)在产物气泡脉动阶段,附加挡板材料约束气泡脉动,增加气泡脉动压力,从而提高对航行体的长时推力. 航行体长为15 mm,直径3 mm,头部为半圆形,沿轴线设置一直径为0.3 mm的通孔与滑轨配合,材料为2024铝合金,质量0.3 g. 实验中在水箱内部水平固定一根直径0.3 mm长为100 mm表面抛光钢圆柱作为航行体运动的滑轨. 航行体可在滑轨上自由运行. 航行体的环境介质可为空气或水(去离子水). 实验过程采用高速摄像机(Photron Fastcam SA-1.1)进行图像捕捉,采样频率为20 000 帧每秒. 实验研究以下条件下航行体的运动特性:
(1) 不同环境介质(空气、水)中,航行体的运动特性
为了研究环境介质的影响,分别开展环境介质分别为空气和水条件下的激光爆炸推进实验. 航行体尾部不设置附加挡板. 环境介质为水的条件下,航行体的轴线距离水面约20 mm.
(2) 航行体尾部约束壁面的影响
环境介质分别为空气和水的条件下,在航行体尾部设置一固定的附加挡板(BK7光学玻璃,直径25.4 mm,厚度4 mm),研究附加挡板对航行体运动特性的影响规律; 另外,在环境介质为水的条件下,在距离航行体尾部3 mm处固定附加挡板,研究该条件下航行体的运动特性. 实验环境介质为水的条件下,航行体的轴线距离水面约20 mm.
(3) 不同水深条件下航行体的运动特性
实验环境介质为水,航行体轴线距离水自由表面约2.5 mm,研究不同水深下航行体的运动特性.
1.2 实验结果 1.2.1 不同环境介质(空气、水)中,航行体的运动特性 1.2.1.1 空气中航行体的运动特性该实验条件下的结果如图2所示. 短脉冲强激光经过聚焦后与航行体尾部端面的铝膜相互作用,使铝膜熔化、气化、电离,形成等离子体. 等离子体团在空气快速向外喷溅并迅速冷却,逐渐湮灭. 之后高温气团继续膨胀,持续大约500 μs后气体冷却. 该过程中等离子体由于在空气中快速膨胀,峰值压力很小[25],推力小于航行体的最大静摩擦阻力,导致航行体的速度为零.

|
图 2 空气中航行体的运动特性(无附加挡板) Fig. 2 Movement of propelled object in air induced by laser propulsion. Note that no constrained plate is used in the experiment |
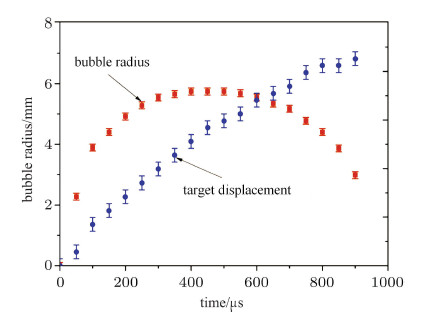
将航行体置于水中,可沿滑轨自由航行,航行体尾部不设置附加挡板. 该实验条件下的激光水下推进结果如图3所示. 在激 光作用的初始阶段,激光诱导的等离子体在水介质的惯性约束下膨胀,之后等离子体快速冷却湮灭. 等离子体的持续时间小于50 μs. 等离子体湮灭后,在激光爆炸位置产生高压气核,并逐步形成爆炸产物气泡, 同时航行体受到等离子体的压力作用开始运动. 气泡在脉动过程中对航行体提供一定的推力,同时自身向后运动. 气泡收缩过程中破裂,形成反向射流,进一步对航行体作用. 该实验过程中航行体的位移和速度历程如图4所示. 气泡脉动过程中在450 μs达到最大半径5.74 mm. 航行体的位移在前50 μs快速增加, 航行体的速度达到3.4 m/s,冲量耦合系数$C_{\rm m}=52.7\times 10^{ -5}$ N$\cdot$s/J, 激光的能量转化效率约为0.1%. 之后航行体位移线性增加,在800 μs时刻的增长速度有所降低. 在第一个气泡脉动周期内,航行体的位移超过1.7 mm.

|
图 3 水中航行体的运动特性(无附加挡板) Fig. 3 Movement of propelled object in water induced by laser propulsion and laser induced bubble pulsation. Note that no constrained plate is used in the experiment |
|
图 4 水中航行体运动的位移历程和气泡脉动规律(无附加挡板) Fig. 4 Displacement of propelled object and bubble radius during laser propulsion underwater. No constrained plate is used in the experiment |
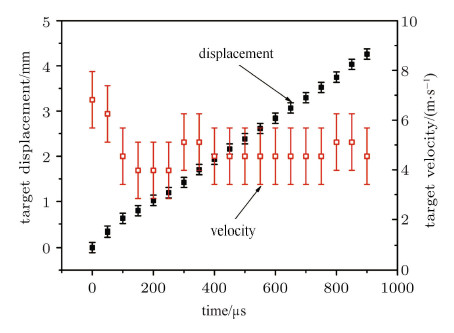
将航行体置于空气中,可沿着滑轨自由航行. 在航行体尾部紧贴铝膜固定一厚度4 mm厚直径25.4 mm BK7光学玻璃. 该实验条件下的实验结果如图5所示. 该过程中激光诱导的等离子体受到BK7光学玻璃的约束作用. 由于BK7玻璃的波阻抗高于空气介质的波阻抗,等离子体的压力比没有附加挡板条件下的压力要大,使航行体获得较高的运动速度. 文献所述实验中发现乙烷和墨水冲量耦合系数高,也是由于其波阻抗比纯水高导致的[2, 3, 20, 21, 22]. 该实验条件下航行体的位移和速度历程如图6所示. 航行体位移几乎呈线性增加,在900 μs达到4.26 mm. 从图6中可以看出,在激光与航行体相互作用阶段,航行体的速度先快速升高到6.8 m/s,冲量耦合系数$C_{\rm m}=105.4\times10^{ - 5}$ N$\cdot$s/J,激光的能量转化效率约为0.36%; 之后在150 μs后近似定常运动,速度为3.98 m/s.

|
图 5 空气介质中附加挡板对航行体运动特性的影响 Fig. 5 Movement of propelled object in air induced by laser propulsion. |
|
图 6 空气介质中附加挡板条件下航行体的位移和速度历程 Fig. 6 Displacement and velocity of propelled object during moving in air induced by laser propulsion. |
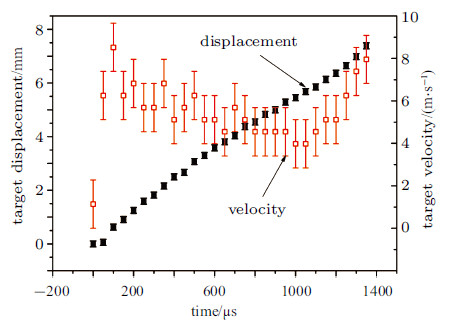
将航行体置于水中,可沿滑轨自由航行. 在其尾部紧贴铝膜位置固定厚度4 mm厚直径25.4 mm BK7光学玻璃. 该实验条件下的结果如图7所示. 在水下用BK7玻璃紧贴航行体时,由于BK7玻璃的阻抗比水的阻抗高一 个数量级, 使得等离子体的压力更高,对航行体的推力更大,使航行体获得较高的初速度. 另外,由于BK7壁面的影响, 形成半圆形气泡,泡收缩导致泡内压力升高,溃灭后形成的反向射流冲击壁面,也会进一步提高壁面压力, 在皮面压力的辐射作用下加速航行体的运动. 图8为该实验条件下航行体的位移和速度历程. 航行体的位移初始缓慢增加, 在50 μs迅速增加,然后近似呈线性增加,在1 050 μs位移为5.68 mm,之后位移增长速度降低, 在1 350 μs 达到7.39 mm. 对应的航行体速度在开始阶段快速升高到8.52 m/s,冲量耦合系数$C_{\rm m}= 132.1\times 10^{ - 5}$ N$\cdot$s/J,激光的能量转化效率约为0.56%; 然后缓慢降低,在1 050 μs速度降到3.98 m/s, 之后速度快速升高,在在1 350 μs达到7.95 m/s.

|
图 7 水介质中附加挡板对航行体运动特性的影响 Fig. 7 Movement of projectile in water induced by laser propulsion. |
|
图 8 水介质中附加挡板条件下航行体的位移和速度历程 Fig. 8 Displacement and velocity of target during moving in water induced by laser propulsion. |
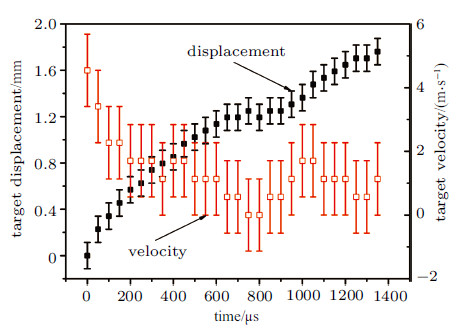
将航行体置于水中,可沿滑轨自由航行. 在其尾部距离铝膜3 mm位置固定一块厚度4 mm厚直径25.4 mm BK7光学玻璃. 该实验条件下的结果如图9所示. 在等离子体的演化阶段以及气泡脉动的初始阶段,附加挡板对于航行体的运动没有影响. 爆炸产物气泡在脉动后期与BK7玻璃壁面接触,产生附壁效应,在BK7壁面快速的溃灭,并产生溃灭压力. 经过与BK7玻璃壁面几次作用后,气液混合物快速消失. 相比于水中附加挡板紧贴铝膜的情形,由于水的阻抗低于玻璃阻抗,使得靶体的初速度要小. 另外,由于气泡收缩过程中向附加挡板移动,使水向附加挡板流动,进一步降低了靶体的运动速度. 图10给出了该实验条件下航行体的位移和速度历程. 航行体的位移在650 μs时为1.19 mm,之后一段时间内位移增加缓慢,在900 μs后位移继快速增加,在1 350 μs后位移达到 1.76 mm. 在650~900 μs时间段内航行体的位移增加缓慢,可能是由于气泡收缩过程中向更宽的BK7玻璃壁面偏移,导致收缩压力未能作用在航行体尾部,另一方面收缩溃灭过程中会产生较高的指向气泡和BK7玻璃方向的诱导速度,相当于给航行体附加了一个额外的阻力. 在900 μs之后航行体位移快速增加,可能是气泡溃灭对航行体作用所导致. 航行体在初始时刻的最高速度达到4.5 m/s,冲量耦合系数$C_{\rm m}= 69.8\times 10^{ - 5}$ N$\cdot$s/J,激光的能量转化效率约为0.16%,略高于水中自由条件下的激光能量转化率.

|
图 9 水介质中距离航行体3 mm处附加挡板距的影响 Fig. 9 Movement of propelled object in water induced by laser propulsion |
|
图 10 水介质中距离航行体3 mm处附加挡板距条件下航行体的位移和速度历程 Fig. 10 Displacement and velocity of propelled object during moving in water induced by laser propulsion |
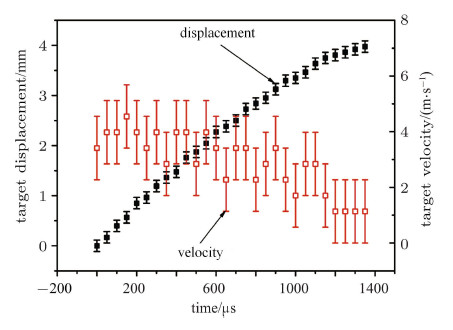
最后,为了考察航行水深对航行体运动特性的影响,将航行体置于水面附近(航行体轴线距离水面2.5 mm),可沿滑轨自由 航行,开展激光水下爆炸推进实验. 该实验条件下的结果如图11所示. 与深水(航行体轴线距离水面20 mm)的情形类似, 激光初始诱导等离子体演化,并快速湮灭形成爆炸产物气泡. 当气泡膨胀到水的自由表面时,首先在自由表面溃灭, 沿着航行体轴线水平面位置分成两部分. 上部分由于气泡溃灭形成射流,使得水膜向上喷溅,形成"喷泉"现象, 喷泉高度可达5 cm. 下部分气泡受到气泡溃灭部分的反向作用,向左下方快速运动,并使得航行体上下振动. 该实验条件下航行体向前的位移和速度历程如图12所示. 航行体的位移开始近似线性增加,在850 μs时达到3.13 mm,高于深水时的航行位移(在850 μs时为1.64 mm). 之后位移增加速度缓慢减小, 在350 μs时位移为3.97 mm. 对应的航行体速度在850 μs之前几乎不变,为3.97 m/s, 高于深水条件下的航行速度(在850 μs为1.13 m/s),冲量耦合系数$C_{\rm m}= 61.5\times10^{ - 5}$ N$\cdot$s/J,激光的能量转化效率约为0.12%. 之后速度缓慢下降,在1\,350 μs时的速度为1.14 m/s.

|
图 11 浅水条件下航行体的运动特性(无附加挡板) Fig. 11 Movement of propelled object in water near the free surface induced by laser propulsion. No constrained plate is used in the experiment |
|
图 12 浅水条件下航行体的运动特性(无附加挡板) Fig. 12 Movement of propelled object in water near the free surface induced by laser propulsion. No constrained plate is used in the experiment |
激光爆炸推进可以分为两个物理过程. 第一个物理过程为强激光与铝膜相互作用,使铝膜熔化、气化、电离,形成等离子体. 等离子体继续与激光作用,吸收激光能量,内能快速升高. 在该过程中等离子体膨胀与约束介质(包括航行体铝膜、环境介质,在附加挡板紧贴铝膜的条件下,还包括附加挡板)变形耦合,产生短脉冲、高幅值的等离子体压力,并对航行体作用,使航行体运动[4, 6]. 第二个物理过程为具有一定体积的等离子体湮灭后形成的气泡,由于内外压力差,使得气泡产生脉动,并对航行体继续产生推力,使得航行体运动. 该过程的作用时间比较长,对航行体的推力可以认为是气泡内的压力[7].
第一个物理过程可以分为两个作用阶段. 在第一阶段,一定波长的激光束辐照到铝膜,在很短时间内将激光的部分能量沉积于铝膜的一个薄层内,使得材料的熔化、气化、电离,并迅速变成高温的等离子体; 后续的激光将辐照到薄层等离子体,主要以逆韧致吸收机制吸收激光能量,进一步提高等离子体的能量以及压力和温度[26]. 假定材料的熔化和气化吸收的能量相比沉积的激光能量只占很小的比例,能量主要被等离子体吸收,转变为等离子体的内能和对约束介质做功. 该阶段激光输入的能流密度为$J$,激光半峰宽时间为$\tau $,诱导的等离子体厚度为$L$; 环境介质材料的波速为$D_{\rm c}$,密度为$\rho _{\rm c}$,与等离子体的接触界面运动速度为$u_{\rm c}$; 铝膜的波速为$D_{\rm t}$,密度为$\rho_{\rm t}$,与等离子体的接触界面的运动速度为$u_{\rm t}$. 因变量为随时间变化的等离子体压力$p$.
单位时间内等离子体吸收的激光能量转化为对约束介质做功以及等离子体内能的增加[25]
| $ AJ\left( t \right) t = W + e $ | (1) |
其中
| $W = p\left( t \right) L$ | (2) |
计算的初始条件为
| $ L\left( 0 \right) = 0\,,\ \ \ p\left( 0 \right) = 0 $ | (3) |
边界条件为
| $ L\left( t \right) / t = u_{\rm c} + u_{\rm t} $ | (4) |
该阶段,环境介质和航行体材料满足
| $ u_{\rm c} = Y/{\left( {\rho _{\rm c} c^2} \right)}\,,\ \ u_{\rm t} = Y/{\left( {\rho _{\rm t} c^2}\right)} $ | (5) |
因此,对第一个作用阶段,控制方程和定解条件为
| $\left. {\begin{array}{*{20}{l}} {AJ\left( t \right) = p\frac{{L\left( t \right)}}{t} + \frac{3}{{2\alpha }}\frac{{\left( {p\left( t \right) \cdot L\left( t \right)} \right)}}{t}}\\ {{{\left. L \right|}_{t = 0}} = 0;{{\left. p \right|}_{t = 0}} = 0}\\ {L\left( t \right)/t = {u_{\rm{c}}} + {u_{\rm{t}}}}\\ {{u_{\rm{c}}} = Y/\left( {{\rho _{\rm{c}}}{c^2}} \right),{u_{\rm{t}}} = Y/\left( {{\rho _{\rm{t}}}{c^2}} \right)} \end{array}} \right\} $ | (6) |
采用自编程的显式差分有限元程序对该方程进行计算,得到激光能量沉积阶段结束后等离子体的厚度$L(\tau )$、压力特征$p(\tau )$. 计算的特征时间步长为$\Delta t = \tau /{100}$.
在第二个作用阶段,具有一定压力$p(\tau )$和厚度$L(\tau )$的等离子体受到环境介质和航行体材料的惯性约束,加强了对航行体的作用. 该阶段认为等离子体绝热膨胀,其压力和厚度的变化满足如下关系
| $ \label{eq5} p\left( t \right) = p\left( \tau \right)\left( {\frac{L\left( \tau \right)}{L\left( t \right)}} \right)^\gamma $ | (7) |
其中,$\gamma$为等离子体的绝热指数,取2.0.
计算的初始条件为
| $ \label{eq6} \left. L \right|_{t = \tau } = L\left( \tau \right)\,,\ \ \left. p \right|_{t = \tau } = p\left( \tau \right) $ | (8) |
边界条件为
| $ \label{eq9} { L}/{ t} = u_{\rm c} + u_{\rm t} $ | (9) |
$u_{\rm c}$,$u_{\rm t}$由材料的本构方程和受力状态唯一确定
| $ \label{eq8} u_{\rm c} = f\left( {p,\dot {p}} \right)\,,\ \ \ u_{\rm t} = g\left( {p,\dot {p}} \right) $ | (10) |
为了获得第二个作用阶段的压力特征$p(t)$,需要建立等离子体膨胀过程中环境介质以及航行体材料变形的三维数值模型,结合自编程的显式差分程序和LS-DYNA以及LS-PREPOSTD程序来进行迭代求解,计算的特征时间步长为$\Delta t = \tau / 50$.
对于第二个物理过程,采用描述气泡脉动的瑞利- 普莱赛特(Rayleigh--Plesset)方程,来得到该阶段的气泡脉动规律[27, 28, 29, 30]
| $\rho \left( \frac{3}{2}{{{\dot{R}}}^{2}}+R\ddot{R} \right)=-{{P}_{\infty }}+{{P}_{\text{g0}}}{{\left( \frac{{{R}_{0}}}{R} \right)}^{3\gamma }} $ | (11) |
其中,$\rho $为流体的密度,$R$为气泡半径,$-P_{\infty}$为流体远场压力,取1个标准气压,$P_{\rm g0}$为气泡内的压力,$\gamma$为空气绝热指数.
气泡对航行体的推力为
| $ \label{eq10} p(t) = P_{\rm g0} \left( {\frac{R_0 }{R}} \right)^{3\gamma } $ | (12) |
通过对第二个物理过程的数值求解,得到该过程中铝膜表面的压力历程,从而得到两个物理过程中的完整压力历程$p(t)$.
航行体在航行过程中其头部会受到介质的阻力$f(t)$. 阻力$f(t)$与航行体的动压有如下关系
| $ \label{eq11} f\left( t \right) = C_{\rm d} \cdot \frac{1}{2}\rho v^2\left( t \right) $ | (13) |
其中$C_{\rm d}$为阻力系数$\rho $为介质的密度,$v(t)$为航行体的运动速度.
航行体在运动过程中垂直方向的运动速度相对于水平方向的运动速度可以忽略,假设航行体为刚体,其运动方程为
| $ \label{eq12} p\left( t \right) S - C_{\rm d} \frac{1}{2}\rho v^2\left( t \right) = m \frac{ v\left( t \right)}{ t} $ | (14) |
其中$S$为激光作用光斑面积,$m$为航行体的质量.
对方程(14)进行离散,得到一阶精度的显示差分计算方程
| $ \label{eq13} p^i S - C_{\rm d} \frac{1}{2}\rho \left( {v^i} \right)^2 = m \frac{v^{i + 1} - v^i}{\Delta t} $ | (15) |
通过求解,得到航行体的运动速度历程$v(t)$.
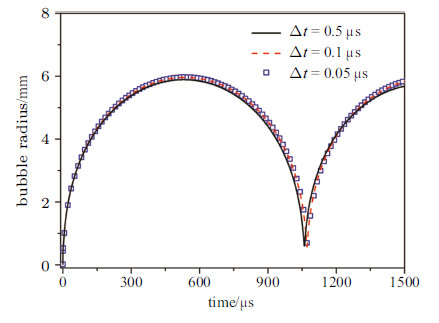
2.2 数值模拟结果与讨论 2.2.1 数值模拟验证采用上述物理模型,对水中无附加挡板条件下激光水下爆炸推进航行体的运动特征进行了模拟,并与实验结果对比,验证计算模型与计算参数的可靠性. 图13为气泡脉动阶段不同时间步长计算得到的气泡脉动规律. 从中可以看出,时间步长为0.05 μs时计算收敛.
|
图 13 不同时间步长计算得到的气泡脉动规律 Fig. 13 Pulsation of bubble for various time increments |
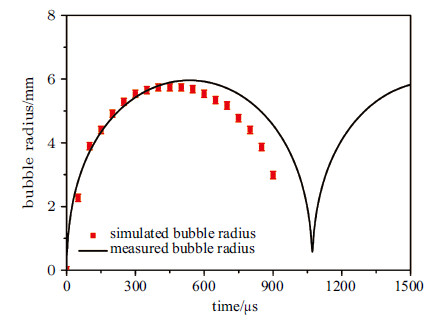
图14和图15分别为水介质推进过程中气泡的脉动规律以及航行体的位移历程. 计算中依据航行体的头型取$C_{\rm d}=0.4$. 从图14中可以看出数值计算结果得到的气泡脉动最大半径与实验测量结果一致,而计算得到的气泡脉动周期大于实验的测量结果. 这可能是由于实验测量中气泡脉动过程中收到航行体尾部结构壁面的影响导致的. 类似地,从图15中可以看出,计算得到的航行体位移历程在700 μs以前与实验的测量结果比较一致,但是在后期由于气泡的非对称脉动,导致理论计算结果与实验测量结果有一定的误差,但是整体差别不大,验证了计算方法的可靠性.
|
图 14 水介质激光爆炸推进中气泡脉动规律(无附加挡板) Fig. 14 Characteristics of bubble pulsation in water induce by laser propulsion. No constrained plate is used in experiment |

|
图 15 水介质激光爆炸推进航行体运动的位移历程(无附加挡板) Fig. 15 Displacement of propelled object in water induced by laser propulsion. No constrained plate is used in the experiment |
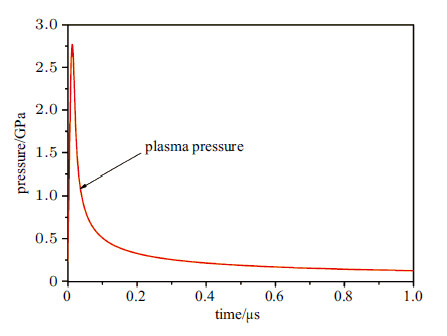
通过上述计算模型和计算方法,得到在水中没有附加挡板条件下,在1\;s内等离子的压力特征如图16所示. 在激光初始作用时间内,等离子体压力在12.3 ns内快速到达压力峰值2.77 GPa; 之后激光功率密度降低,等离子体压力快速下降; 激光停止辐照后,等离子体快速冷却,其压力以指数快速衰减,在1.0 μs时刻的压力为0.12 GPa.
|
图 16 激光推进过程中等离子体压力特征 Fig. 16 Simulated plasma pressure induced by laser propulsion |
在1.0 μs之后,等离子体的厚度为$L_{0}$,假设此时气泡为球形,半径为$R_{0}$,圆柱形等离子体积与球形气泡体积相等
| $ \label{eq14} L_0 S = \frac{4}{3}\pi R_0^3 $ | (16) |
其中$S$为光斑的作用面积. 由此来确定气泡的初始半径.
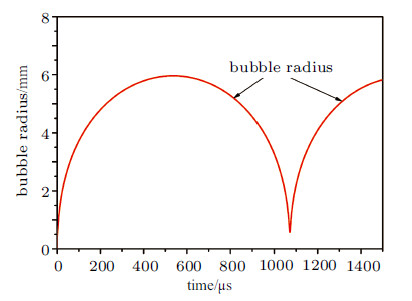
2.2.2.2 爆炸产物气泡脉动压力采用瑞利--普莱赛特方程计算气泡的脉动规律和气泡对航行体的推力. 通过计算,得到$1.50\times 10^{3}\;μ$s内气泡半径的变化规律,如图17所示. 气泡的第一次膨胀周期为$1.07\times 10^{3}\;μ$s,在第一个周期内,最大半径为5.96 mm. 根据前人研究结果[27, 28, 29, 30],产物气泡达的脉动半周期与最大半径有如下关系
| $ \label{eq15} T_{\rm c} = 0.915R_{\max } \sqrt {\dfrac{\rho }{p_\infty - p_v }} $ | (17) |
|
图 17 气泡脉动规律 Fig. 17 Simulated bubble pulsation |
通过计算,当最大半径为5.96 mm时,对应的脉动半周期为554\;μs,与理论结果吻合较好.
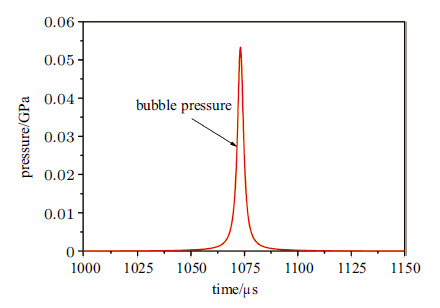
气泡脉动阶段气泡内压力如图18所示. 气泡在第一个脉动周期内,气泡内的压力较小,且变化缓慢. 在$1.07\times10^{3}\;μ$s时刻气泡被压缩到最小半径时,气泡内形成短脉冲的较高压力,脉宽约为50 μs,压力峰值约为53 MPa.
|
图 18 气泡脉动压力 Fig. 18 Simulated pressure induced by bubble pulsation during laser propulsion underwater |
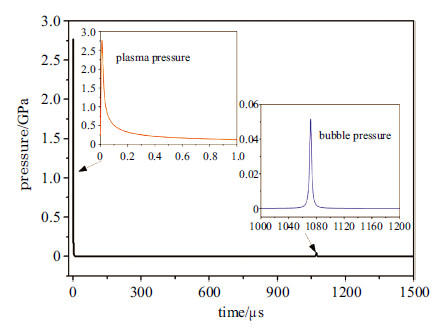
结合图16和图18,可以得到激光水下爆炸推进过程中,航行体所受的推力,如图19所示.
|
图 19 激光水下爆炸推进过程中航行体的推力 Fig. 19 Simulated pressure applied on the target during laser propulsion underwater |
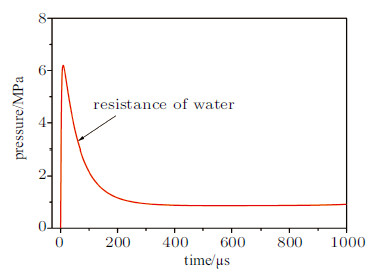
在水介质无挡板约束条件下,激光水下爆炸推进航行体过程中,航行体头部受到的阻力历程如图20所示. 航行体头部阻力在航行体运动初期快速上升,在7.92 μs到达第一个峰值6.18 MPa;随后缓慢下降,在300 μs时刻航行体的阻力到达定值约0.87 MPa.
|
图 20 航行体头部受到的阻力历程 Fig. 20 Simulated resistance of water during laser propulsion underwater |
计算中依据半圆头型回转体定常航行过程的阻力特性,给定阻力系数为常数$C_{\rm d}= 0.4$,存在一定误差. 一方面航行体在激光冲击与射流冲击的过程中,存在较大的加速度,加速度造成的附加阻力以及附连水阻力并没有考虑; 另一方面,航行体的阻力系数在小雷诺数条件下往往不是一个定值,而是在一定范围内随雷诺数发生变化. 对激光水下爆炸推进中航行体的阻力特性及其相关的影响参数,将在后期采用流固耦合数值模拟方法进行深入分析.
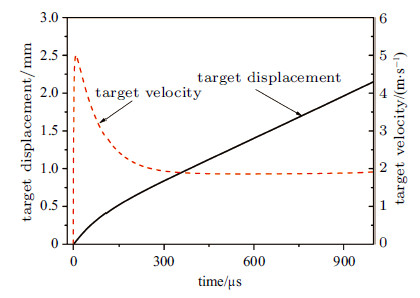
2.2.4 航行体的运动特性图21为水介质无附加挡板调价下,激光水下爆炸推进过程中航行体在水平方向的运动位移和速度历程. 在激光- 航行体相互作用阶段以及第一个气泡脉动周期内,航行体的水平运动位移近似成二次曲线增长,对应的航行体速度在8.7 μs时刻快速增加到4.98 m/s; 之后航行体的位移近似呈线性缓慢增加到2.3 mm,对应的航行体速度变化比较缓慢,近似为定常运动,速度为1.88 m/s; 在$1.07\times 10^{3}\; μ$s时刻位移曲线出现间断点,快速线性增加,对应的航行体速度在20 μs内快速增加到7.59 m/s,冲量耦合系数$C_{\rm m}=117.6\times10^{ - 5}$ N$\cdot$s/J,激光的能量转化效率约为0.45%. 计算得到的航行体最高速度及冲量耦合系数要高于实验测量结果,主要是由于实验中的图像采集速度不够高,没有捕获到最快的航行体速度时刻. 航行体在$1.07\times10^{3}\;μ$s时刻的速度突然增加是由于在气泡进入到第二次脉动周期时,气泡内产生的短瞬时压力脉冲对航行体做功,使得航行体加速所导致.
|
图 21 航行体运动的位移历程 Fig. 21 Simulated displacement of target motion during laser propulsion underwater |
上述计算中仅考虑了等离子体与气泡脉动两种大面积驱动源. 应当注意在没有附加挡板的条件下,气泡在航行体尾部溃 灭过程中能够形成朝向壁面的高速射流,如图7所示. 射流作用面积较小但仍有一定的总冲量. 另外, 计算中仅考虑了气泡自由膨胀过程的推进效应,实验过程中发现尾部附加固定挡板之后, 约束条件下气泡的膨胀能够形成更高的推进压力,获得更快的航行速度,提高推进效率. 但由于应用中挡板不能与航行体相连,因此这一般法只能应用于启动条件而不能用于连续推进条件. 后续会探讨一些新的方法,例如采用喷管约束的方法,来提高推进的效率. 最后,在约束气泡的条件下, 激光能量的有效转化率有所提高,但是整体而言激光聚焦爆炸推进的能量转化率比较低. 其原因一方面是因为激光诱导等离子体生成、演化的过程中,在激光烧蚀、等离子体演化过程中消耗了部分量能; 另一方面是航行体受到水介质较大阻力. 后期将探索采用激光聚焦辐照含能材料爆炸推进的方法来提高推进的效率. 上述3个方面的问题,需要引入多相流动与航行体运动的耦合算法,在本文中未涉及. 考虑到其对于深化激光水下爆炸推进机理研究的重要意义,将在未来加以考虑.
3 结 论本文对激光水下聚焦爆炸推进方法的作用机理和物理过程开展了研究工作,通过实验测量和数值模拟, 获得了不同条件下激光推 进过程中航行体的运动特征. 主要结论如下:
(1) 环境介质的波阻抗对于激光爆炸推进效率有重要影响. 在水介质中可以实现激光对水下航行体的推进,而在空气中难以获得有效推力.
(2) 附加挡板(BK7)能显著提高激光推进的效率. 一方面是由于具有较高的波阻抗,增强对等离子体的惯性约束作用, 提高等离子体 压力; 另一方面是由于约束爆炸产物气泡脉动,显著提高了气泡的脉动压力.
(3) 建立了激光水下聚焦爆炸推进的物理模型,并发展了相应的数值计算方法. 模型中考虑了不同时间尺度的推力物理机制、航行体 的阻力机制. 通过计算得到了激光水下爆炸推进过程中不同时间尺度的推力特征、阻力特征以及航行体的运动规律.
(4) 激光水下聚焦爆炸推进实验方法提供了一种理想的水下点爆炸实验手段,为水下爆炸中冲击\linebreak 波---结构动态响应、产物气 泡脉动、破裂、射流---结构运动等问题的研究提供了一种新的手段.
| [1] | Han B, Shen ZH, Lu J, et al. Numerical study of water-confinement geometries for laser propulsion. Optics and Lasers in Engineering, 2010, 48(10): 950-957. |
| [2] | Zheng Z, Zhang J, Zhang Y, et al. Enhancement of coupling coefficient of laser plasma propulsion by water confinement. Applied Physics A, 2006, 85(4): 441-443. |
| [3] | Zhang ZY, Zhang Y, Zhou WG, et al. High coupling efficiency generation in water confined laser plasma propulsion. Chinese Physics Letters, 2007, 24(2): 501. |
| [4] | Wu X, Duan Z, Song H, et al. Shock pressure induced by glass-confined laser shock peening: Experiments, modeling and simulation. Journal of Applied Physics, 2011, 110(5): 053112. |
| [5] | Wu X, Huang C, Wang X, et al. A new effective method to estimate the effect of laser shock peening. International Journal of Impact Engineering, 2011, 38(5): 322-329. |
| [6] | 吴先前, 段祝平, 黄晨光等. 激光冲击强化过程中蒸气等离子体压力计算的耦合模型. 爆炸与冲击, 2012, 32(1): 1-7 (Wu Xianqian, Duan Zhuping, Huang Chenguang, et al. A new coupling analytical method for plasma pressure induced by laser shock peening. Explosion and Shock Waves, 2012, 32(1): 1-7 (in Chinese)) |
| [7] | 库尔. 水下爆炸. 北京: 国防工业出版社, 1960 (Cole RH. Underwater Explosion. Beijing: National Defence Industry Press, 1960 (in Chinese)) |
| [8] | 姚熊亮, 张阿漫. 简单 Green 函数法模拟三维水下爆炸气泡运动. 力学学报, 2006, 38(6): 749-759 (Yao Xiongliang, Zhang Aman. Simulation of the motion of three-dimensional underwater explosion bubble using simple Green function method. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(6): 749-759 (in Chinese)) |
| [9] | Cui C, Hong Y, Ye J, et al. Effects of laser energy density on impulse coupling coefficient of laser ablation of water for propulsion. Applied Physics A, 2011, 103(1): 239-243. |
| [10] | Phipps C, Birkan M, Bohn W, et al. Review: laser-ablation propulsion. Journal of Propulsion and Power, 2010, 26(4): 609-637. |
| [11] | 李修乾, 洪延姬, 何国强等. 激光推进器概念设计研究现状及发展趋势, 强激光与粒子束, 2005, 17(3): 363-368 (Li Xiuqian, Hong Yanji, He Guoqiang, et al. Status and development trend of concept studies on laser propulsion thruster. High Power Laser and Particle Beams, 2005, 17(3): 363-368 (in Chinese)) |
| [12] | Yabe T, Ohzono H, Ohkubo T, et al. Proposal of liquid cannon target driven by fiber laser for micro-thruster in satellite. In: Beamed Energy Propulsion: Second International Symposium on Beamed Energy Propulsion, AIP Publishing, 2004, 503-512 |
| [13] | 蔡建, 王彬, 胡晓军等. 激光水推进技术的实验研究. 实验力学, 2007, 22(1): 43-48 (Cai Jian, Wang Bin, Hu Xiaojun, et al. Experimental study of laser propulsion underwater. Journal of Experimental Mechanics, 2007, 22(1): 43-48 (in Chinese)) |
| [14] | 唐志平. 烧蚀模式激光推进的机理和应用探索. 中国科学技术大学学报, 2008, 37(10): 1300-1305 (Tang Zhiping. Exploration of mechanism and applications for ablation laser propulsion. Journal of University of Science and Technology of China, 2008, 37(10): 1300-1305 (in Chinese)) |
| [15] | 王彬, 唐志平, 蔡建等. 激光水推进的机理研究及参数优化, 推进技术, 2007, 28(5): 586-589 (Wang Bin, Tang Zhiping, Cai Jian, et al. Mechanism for water-powered laser propulsion. Journal of Propulsion Technology, 2007, 28(5): 586-589 (in Chinese)) |
| [16] | Sinko J, Kodgis L, Porter S, et al. An analysis of force generation in TEA CO2 laser ablation of liquids. In: High-Power Laser Ablation 2006, International Society for Optics and Photonics, 2006, 62611W-62611W-62612 |
| [17] | Sinko JE, Dhote NB, Pakhomov AV. Laser propulsion with liquid propellants Part II: thin films. In: Beamed Energy Propulsion: Fifth International Symposium on Beamed Energy Propulsion, AIP Publishing, 2008, 209-221 |
| [18] | Sinko JE, Pakhomov AV. Laser propulsion with liquid propellants Part I: an overview. In: Beamed Energy Propulsion: Fifth International Symposium on Beamed Energy Propulsion, AIP Publishing, 2008, 195-208 |
| [19] | Sterling E, Pakhomov AV, Larson CW, et al. Absorption-enhanced liquid ablatants for propulsion with TEA CO2 laser. In: Beamed Energy Propulsion: Third International Symposium on Beamed Energy Propulsion, AIP Publishing, 2005, 474-481 |
| [20] | Zheng ZY, Zhang J, Hao ZQ, et al. Paper airplane propelled by laser plasma channels generated by femtosecond laser pulses in air. Optics Express, 2005, 13(26): 10616-10621. |
| [21] | Zheng ZY, Zhang J, Hao ZQ, et al. The characteristics of confined ablation in laser propulsion. Chinese Physics, 2006, 15(3): 580. |
| [22] | 张翼, 鲁欣, 郑志远等. 透射式水工质的高耦合效率激光推进模式, 推进技术, 2007, 28(5): 534-537 (Zhang Yi, Lu Xin, Zheng Zhiyuan, et al. High coupling coefficient laser propulsion mode. Journal of Propulsion Technology, 2007, 28(5): 534-537 (in Chinese)) |
| [23] | 郑哲敏, 杨振声. 爆炸加工. 北京: 国防工业出版社, 1981 (Zheng Zhemin, Yang Zhensheng. Explosive Working. Beijing: National Defence Industry Press, 1981 (in Chinese)) |
| [24] | Peyre P, Berthe L, Fabbro R, et al. Experimental determination by PVDF and EMV techniques of shock amplitudes induced by 0.6-3 ns laser pulses in a confined regime with water. Journal of Physics D: Applied Physics, 2000, 33: 498-503 |
| [25] | Fabbro R, Fournier J, Ballard P, et al. Physical study of laser-produced plasma in confined geometry. Journal of Applied Physics, 1990, 68: 775-784. |
| [26] | Wu X, Tan Q, Huang C. Geometrical scaling law for laser shock processing. Journal of Applied Physics, 2013, 114(4): 043105. |
| [27] | Hilgenfeldt S, Brenner MP, Grossmann S, et al. Analysis of Rayleigh-Plesset dynamics for sonoluminescing bubbles. Journal of Fluid Mechanics, 1998, 365: 171-204. |
| [28] | Brennen CE. Cavitation and Bubble Dynamics, Oxford University Press, USA, 1995 |
| [29] | Lauterborn W, Kurz T. Physics of bubble oscillations, Reports on Progress in Physics, 2010, 73: 106501 |
| [30] | Plesset MS, Prosperetti A. Bubble dynamics and cavitation. Annual Review of Fluid Mechanics, 1977, 9(1): 145-185. |
 2015, Vol. 47
2015, Vol. 47