18世纪后期,克拉尼在一个水平放置的上面撒有稀薄沙粒的薄金属平板的边缘用小提琴弓进行上下拉锯以产生小振动, 发现细沙会聚集到驻波波节线上形成对称性的图形,现称为克拉尼图形[1]. 此后,对克拉尼图形的研究在理论上和实验上都有重要的进展和应用[2, 3, 4, 5, 6]. 若所用的细沙研制得象粉末一样很细很轻,则细沙还会聚集在波腹上而不是在波节上,形成所谓的逆向克拉尼图形, 又称法拉第堆[7](或克拉尼堆[8]). 根据瑞利的记载[9], 泊松理论上计算了圆形薄板的低频端克拉尼图形的前几个圆形波节线的半径, 萨伐尔在实验上进行了一系列的观测,证实了理论跟实验非常吻合.到目前为止, 对克拉尼图形的研究多限于方形薄板[10]、圆形薄板[9,11]、小提琴形薄板[12]或体育场形状薄板[6, 12]等模型, 且除了我们的工作[10, 11]外其他仅限于中低频.上世纪末,文献[13, 14, 15]对弹性地基下环形薄板的振动 问题的求解作了一些探讨,但其工作是纯理论性的,且其所做的数值计算也是非常初步的, 只求出了相当于最前面的几个简正模式解对应的本征值. 对圆形薄板的振动还有其他研究[16], 但对环形薄板的高低频段的克拉尼图形的研究无论理论上和实验上都未见报道. 在通常的弹性力学和理论声学教科书或参考书[17, 18, 19]中, 对薄板的小振动通常只求解部分边界卡住(固定边条件)、部分边界弹性支承和弹性固定或部分边界简单支承(或铰链支承)的情形,很 少求解全部边界悬空(即自由边条件)的情形,即使有也仅限于中低频段[9, 12],即$f < 6$ kHz. 全部边界悬空的情形下求解比较困难,需进行数值计算.
本文针对环形薄板的小振动偏微分方程,拟参照圆形薄板的情形[9],采用极坐标系将方程分离变量,并可将方程的阶数从四阶降 为二阶,分别求解在内边界悬空和内边界简支两种边条件下的解析解,并将数值计算的结果和实验进行比较.
1 理论模型及方程的解考虑一块水平放置的内外半径分别为$a$和$b$的环形黄铜薄板,其质量均匀分布,厚度为$2 h (h \ll a)$.薄板上有一振动源,可以某一恒定圆频率$\omega_0=2\pi f$ 垂直板面作竖向简谐振动. 若将振动源看成是点源,则可严格求解薄板振动方程的简正模式及薄板发生共振时驻波波节线的位置和半径.
假定薄板的体密度为$\rho$,弹性模量(杨氏模量)为$Y$. 设其传播竖向的简谐小振动的相速度的径向分量为$u$, 则$u$通常与板上的位置有关. 取环的中心为坐标原点,($x,y$)点处$t$时刻的竖向振动位移(挠度)为$\eta (x,y,t)$ (取静止时的位移为0),则$\eta$满足以下方\linebreak 程[17, 20]
| $ \nabla ^4\eta + \dfrac{1}{c^2}\dfrac{\partial ^2\eta }{\partial t^2} = 0 $ | (1) |
其中,$\nabla ^4 = \nabla ^2\nabla ^2,\;\nabla ^2$为拉普拉斯算符,$c$为常数,满足$1 / c^2 = 3\rho (1 - \mu ^2) / (Yh^2)$,$\mu $是泊松比.对大多数材料,$\mu $约为0.25 $\sim$ 0.33. 类似参考文献[17], 为了研究板的简谐振动,取极坐标系$(r,\;\theta )$,令$\eta = Z(r,\;\theta ){\rm e}^{ -{\rm i}\omega t}$, 则$Z$满足的微分方程可写为
| $ (\nabla ^2 - k^2)(\nabla ^2 + k^2)Z = 0 $ | (2) |
其中
| $ k^4 = \dfrac{\omega ^2}{c^2} $ | (3) |
方程(2)的解的简正模式为
| $ \begin{array}{l} Z = H(r)\Phi (\theta ) = \\ \;\;\;\;\;[A{{\rm{J}}_m}(kr) + B{{\rm{Y}}_m}(kr) + C{{\rm{I}}_m}(kr) + D{{\rm{K}}_m}(kr)] \cdot \\ \;\;\;\;\;[R\cos (m\theta ) + T\sin (m\theta )] \end{array} $ | (4) |
其中
| $H(r) = A{\rm J}_m (kr) + B{\rm Y}_m (kr) + C{\rm I}_m (kr) + D{\rm K}_m (kr) $ | (5) |
| $\Phi (\theta ) = R\cos (m\theta ) + T\sin (m\theta )$ | (6) |
${\rm J}_m (kr)$,${\rm Y}_m (kr)$,${\rm I}_m (kr)$和${\rm K}_m (kr)$ 分别为$m$阶贝塞耳函数、$m$阶诺埃曼函数、第1类$m$阶变形贝塞耳函数和第2类$m$阶变形贝塞耳函数. ${\rm I}_m(kr)$和${\rm K}_m(kr)$分别满足 ${\rm I}_m (x) ={\rm i}^{ - m}{\rm J}_m ({\rm i}x)$,${\rm K}_m (x) = (\pi / 2) \cdot {\rm i}^{m + 1}[{\rm J}_m ({\rm i}x) +{\rm iY}_m ({\rm i}x)]$,这 里$m=0,1,2,\cdots$. 式(5)和式(6)中的系数$A,B,C,D,R,T$待定. 对于确定的频率$f$,若边条件确定,则式(4)中的$ B / A,C / A,D / A $ 及$k$可完全确定.
2 环内外边界均悬空设环形薄板的固定支撑点与环心距离为$d$,有$a < d < b,$ 环的内外边界悬空. 则$Z$在边界$r=a$,$b$处的弯曲力矩$M_r $、 扭转力矩$M_{r{\rm t}}$ 及竖向剪力$Q_r $均为0,而连续分布的扭矩$M_{r{\rm t}}$ 静力上等效于剪力$\dfrac{\partial M_{r{\rm t}} }{r\partial \theta }$,则环形薄板振动方程满足边条件[18]
| $M_r |_{r = a,b} = 0 $ | (7) |
| $\Big(Q_r + \dfrac{\partial M_{r{\rm t}} }{r\partial \theta } \Big)\Big |_{r = a,b} = 0 $ | (8) |
其中
| $M_r = - E\left[{\dfrac{\partial ^2Z}{\partial r^2} + \mu \left( {\dfrac{1}{r}\dfrac{\partial Z}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial ^2Z}{\partial \theta ^2}} \right)} \right] $ | (9) |
| $M_{r{\rm t}} = - E(1 - \mu )\left( {\dfrac{1}{r}\dfrac{\partial ^2Z}{\partial r\partial \theta } - \dfrac{1}{r^2}\dfrac{\partial Z}{\partial \theta }} \right) $ | (10) |
| $Q_r = - E\left( {\nabla ^2Z} \right) = - E\dfrac{\partial }{\partial r}\left( {\dfrac{1}{r}\dfrac{\partial }{\partial r}r\dfrac{\partial Z}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial ^2Z}{\partial \theta ^2}} \right) $ | (11) |
$E$是薄板的抗挠刚度,$E = 2h\rho c^2$; 对于黄铜,泊松比$ \mu = 0.324$.由 式(7)和式(9)可得
| $ \left[{\dfrac{\partial ^2Z}{\partial r^2} + \mu \left( {\dfrac{1}{r}\dfrac{\partial Z}{\partial r} + \dfrac{1}{r^2}\dfrac{\partial ^2Z}{\partial \theta ^2}} \right)} \right]\Bigg |_{r = a,b} = 0 $ | (12) |
由式(8)、式(10) 和式(11) 可得
| $ \left[{\dfrac{\partial }{\partial r}\left( {\dfrac{1}{r}\dfrac{\partial }{\partial r}r\dfrac{\partial Z}{\partial r}} \right) + \dfrac{\partial }{\partial r}\left( {\dfrac{1}{r^2}\dfrac{\partial ^2Z}{\partial \theta ^2}} \right) + }\right. \\ \qquad \left.{(1 - \mu )\left( {\dfrac{1}{r^2}\dfrac{\partial ^3Z}{\partial r\partial \theta ^2} - \dfrac{1}{r^3}\dfrac{\partial ^2Z}{\partial \theta ^2}} \right)} \right]\Bigg|_{r = a,b} = 0 $ | (13) |
把方程(2)的解式(4)代入式(12),得
| $\alpha _1 (a) + \beta _1 (a) \cdot \dfrac{B}{A} + \gamma _1 (a) \cdot \dfrac{C}{A} + \delta _1 (a) \cdot \dfrac{D}{A} = 0 $ | (14) |
| $\alpha _1 (b) + \beta _1 (b) \cdot \dfrac{B}{A} + \gamma _1 (b) \cdot \dfrac{C}{A} + \delta _1 (b) \cdot \dfrac{D}{A} = 0 $ | (15) |
其中
| $\alpha _1 (x_i ) = k^2{\rm J}''_m (kx_i ) + \dfrac{\mu k}{x_i }{\rm J}'_m (kx_i ) - \mu \cdot \dfrac{m^2}{x_i^2 }{\rm J}_m (kx_i ) $ | (16) |
| $\beta _1 (x_i ) = k^2{\rm Y}''_m (kx_i ) + \dfrac{\mu k}{x_i }{\rm Y}'_m (kx_i ) - \mu \cdot \dfrac{m^2}{x_i^2 }{\rm Y}_m (kx_i ) $ | (17) |
| $\gamma _1 (x_i ) = k^2{\rm I}''_m (kx_i ) + \dfrac{\mu k}{x_i }{\rm I}'_m (kx_i ) - \mu \cdot \dfrac{m^2}{x_i^2 }{\rm I}_m (kx_i ) $ | (18) |
| $\delta _1 (x_i ) = k^2{\rm K}''_m (kx_i ) + \dfrac{\mu k}{x_i }{\rm K}'_m (kx_i ) - \mu \cdot \dfrac{m^2}{x_i^2 }{\rm K}_m (kx_i ) $ | (19) |
这里$i=$1,2,对应$x_1 = a,\;x_2 = b$,以下相同.
同样,把式(4)代入式(13),得
| $\alpha _2 (a) + \beta _2 (a) \cdot \dfrac{B}{A} + \gamma _2 (a) \cdot \dfrac{C}{A} + \delta _2 (a) \cdot \dfrac{D}{A} = 0 $ | (20) |
其中
| $\begin{array}{l} {\alpha _2}({x_i}) = {k^3}{{\rm{J}}^{\prime \prime \prime }}_m(k{x_i}) + \frac{{{k^2}}}{{{x_i}}}{{\rm{J}}^{\prime \prime }}_m(k{x_i}) - \frac{k}{{x_i^2}}\left[ {1 + (2 - \mu ){m^2}} \right]{{\rm{J}}^\prime }_m(k{x_i}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3 - \mu ) \cdot \frac{{{m^3}}}{{x_i^3}}{{\rm{J}}_m}(k{x_i}) \end{array} $ | (22) |
| $\begin{array}{l} {\beta _2}({x_i}) = {k^3}{{\rm{Y}}^{\prime \prime \prime }}_m(k{x_i}) + \frac{{{k^2}}}{{{x_i}}}{{\rm{Y}}^{\prime \prime }}_m(k{x_i}) - \frac{k}{{x_i^2}}\left[ {1 + (2 - \mu ){m^2}} \right]{{\rm{Y}}^\prime }_m(k{x_i}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3 - \mu ) \cdot \frac{{{m^3}}}{{x_i^3}}{Y_m}(k{x_i}) \end{array} $ | (23) |
| $\gamma _2 (x_i ) = k^3{\rm I}'''_m (kx_i ) + \dfrac{k^2}{x_i }{\rm I}''_m (kx_i ) - \dfrac{k}{x_i^2 }\left[{1 + (2 - \mu )m^2} \right]{\rm I}'_m (kx_i ) + (3 - \mu ) \cdot \dfrac{m^3}{x_i^3 }{\rm I}_m (kx_i ) $ | (24) |
| $\begin{array}{l} {\delta _2}({x_i}) = {k^3}{{\rm{K}}^{\prime \prime \prime }}_m(k{x_i}) + \frac{{{k^2}}}{{{x_i}}}{{\rm{K}}^{\prime \prime }}_m(k{x_i}) - \frac{k}{{x_i^2}}\left[ {1 + (2 - \mu ){m^2}} \right]{{\rm{K}}^\prime }_m(k{x_i}) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3 - \mu ) \cdot \frac{{{m^3}}}{{x_i^3}}{{\rm{K}}_m}(k{x_i}) \end{array} $ | (25) |
由式(14)、式(15)、式(20)和式(21)可知,只要知道$k$,即可解出 $(B/A)$,$(C/A)$和 $(D/A)$分别为
| $\begin{array}{*{20}{l}} \begin{array}{l} \frac{D}{A} = \left[ {\frac{{{\alpha _2}(a){\beta _2}(b) - {\alpha _2}(b){\beta _2}(a)}}{{{\gamma _2}(a){\beta _2}(b) - {\gamma _2}(b){\beta _2}(a)}} - \frac{{{\alpha _1}(a){\beta _1}(b) - {\alpha _1}(b){\beta _1}(a)}}{{{\gamma _1}(a){\beta _1}(b) - {\gamma _1}(b){\beta _1}(a)}}} \right]\\ \;\;\;\;\;/\left[ {\frac{{{\delta _1}(a){\beta _1}(b) - {\delta _1}(b){\beta _1}(a)}}{{{\gamma _1}(a){\beta _1}(b) - {\gamma _1}(b){\beta _1}(a)}} - \frac{{{\delta _2}(a){\beta _2}(b) - {\delta _2}(b){\beta _2}(a)}}{{{\gamma _2}(a){\beta _2}(b) - {\gamma _2}(b){\beta _2}(a)}}} \right] = \end{array}\\ \begin{array}{l} \qquad \left[ {\frac{{{\alpha _2}(a){\beta _1}(b) - {\alpha _1}(b){\beta _2}(a)}}{{{\gamma _1}(b){\beta _2}(a) - {\gamma _2}(a){\beta _1}(b)}} - \frac{{{\alpha _1}(a){\beta _1}(b) - {\alpha _1}(b){\beta _1}(a)}}{{{\gamma _1}(b){\beta _1}(a) - {\gamma _1}(a){\beta _1}(b)}}} \right]\\ \;\;\;\;\;/\left[ {\frac{{{\delta _1}(b){\beta _2}(a) - {\delta _2}(a){\beta _1}(b)}}{{{\gamma _1}(b){\beta _2}(a) - {\gamma _2}(a){\beta _1}(b)}} - \frac{{{\delta _1}(b){\beta _1}(a) - {\delta _1}(a){\beta _1}(b)}}{{{\gamma _1}(b){\beta _1}(a) - {\gamma _1}(a){\beta _1}(b)}}} \right] \end{array} \end{array}$ | (26) |
| $ \dfrac{C}{A} = \dfrac{\alpha _1 (a)\beta _1 (b) - \alpha _1 (b)\beta _1 (a)}{\gamma _1 (b)\beta _1 (a) - \gamma _1 (a)\beta _1 (b)} - \dfrac{\delta _1 (b)\beta _1 (a) - \delta _1 (a)\beta _1 (b)}{\gamma _1 (b)\beta _1 (a) - \gamma _1 (a)\beta _1 (b)} \cdot \dfrac{D}{A} $ | (27) |
| $\dfrac{B}{A} = - \dfrac{\alpha _1 (b)}{\beta _1 (b)} - \dfrac{\gamma _1 (b)}{\beta _1 (b)} \cdot \dfrac{C}{A} - \dfrac{\delta _1 (b)}{\beta _1 (b)} \cdot \dfrac{D}{A} $ | (28) |
实验时取$a =4.0$ cm,$b =12$ cm,$d =5.0$ cm. 由式(26),通过数值计算,可求出$k$对应于$m$的第$n$个正根 $ k_{mn}$,$(n = 0,1,2,\cdots )$,即可解出所有可能的$ k_{mn}$. 为了方便,对所有的 $ k_{mn} $从小到大排列,即取 $k_{m0} < k_{m1} < k_{m2} < \cdots $,等. 例如对于$m= 16$,可解出$k_{16,0} = 1.106\,01$, $k_{16,1} = 1.449\,26$,$k_{16,2} = 1.889\,58$,$k_{16,3} = 2.226\,21$,$k_{16,4} = 2.537\,19$,$k_{16,5} = 2.835\,11$,$k_{16,6} = 3.124\,06$,$k_{16,7} = 3.403\,08$,$k_{16,8} = 3.667\,55$,$k_{16,9} = 3.924\,66$, $k_{16,10} = 4.199\,61$,$\cdots $,注意$k_{mn} $ 的单位为 cm$^{-1}$(以下同). 可见,对$m=16$,若令 $r_0 = 10$ cm,则有 $ k_{mn} r_0 = \pi \beta _{mn}$,$\beta _{mn} \approx n + m / 2 - 5$ (当$n$比较大时), 注意这规律仅近似对$m= 16$成立,对不同的$m$有不同的$r_0 $ 取值和$\beta _{mn} $表达式,即对环形薄板, 并没有与圆形薄板相应的克拉尼定律[9, 21].
对于给定的$m$,解出所有可能的$k_{mn} $ 后,就可根据式(3)确定容许的简谐振动的频率,即简正频率 $ \omega _{mn}$ 或$ f_{mn}$. 把解出的 $ k_{mn}$ 数值依次代回式(26)$\sim$式(28),即可求出 $D/A$,$C/A$和 $B/A$. 再根据式(4),即可得方程(2)的简谐振动解的特征函数为
| $ Z_{mn} (r,\;\theta ) = \left( {R_{mn} \cos m\theta + T_{mn} \sin m\theta } \right) \cdot \\ \qquad \left[{ {\rm J}_{m } (k_{mn} r) + \dfrac{B_{mn} }{A_{mn} }{\rm Y}_{m } (k_{mn} r) + }\right. \\ \qquad \left.{\dfrac{C_{mn} }{A_{mn} }{\rm I}_{m } (k_{mn} r) + \dfrac{D_{mn} }{{ A}_{mn} }{\rm K}_{m } (k_{mn} r)} \right] $ | (29) |
这里$A,B,C,D,R$和$T$已加上与$k_{mn}$ 相应的下标$m$\linebreak 和$n$.
令$Z_{mn} (r,\;\theta ) = 0$,解出的$r$ (记为 $r_{mnl}$)和 $\theta$ 即分别为此频率下的圆形波节线的半径和径向波节线的角度,下标$l$表征了$r$的大小. 注意此时除了有若干条以原点为圆心的圆形波节线外,还可有沿$r$方向的$2m$条均匀对称的辐射状波节线. 这两种波节线可以分别独立存在或同时存在.
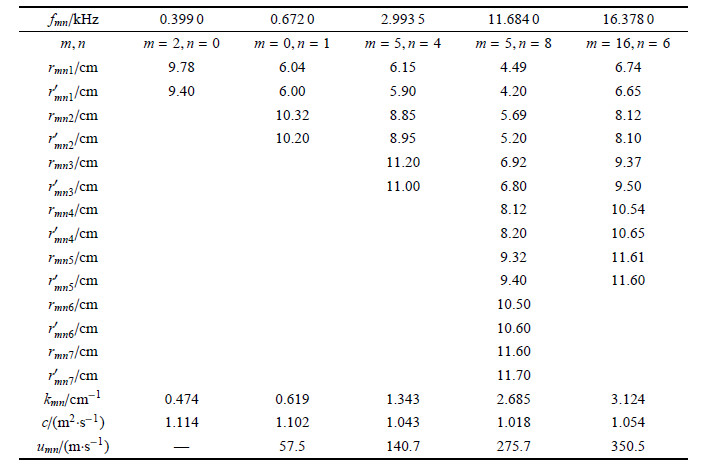
表1给出各种频率$f_{mn} $ 下 当$\omega _0 = \omega _{mn} = 2\pi f_{mn} $时的圆形波节线半径的理论值 $ r_{mnl} $和实验观察值$ {r}'_{mnl}$,其 中 $c = {\omega _{mn} } \big/ {k_{mn}^2 }$,$c$为式(1)中的系数,$ k_{mn}$ 即式(3)中的 $k$对应于$m$,$n$的取值. 可见理论值与实验值符合得很好.
| 表 1 不同频率$f_{mn}$ 下圆形波节线半径$r$的理论计算值$r_{mnl}$与实验 观测值$r'_{mnl}$ ($l=0,1,2,\cdots$) Table 1 Comparison of radii of circular nodal lines in different frequencies $f_{mn}$ between theoretical values $r_{mnl}$ and experiment values $r'_{mnl}$ ($l=0,1,2,\cdots$) |
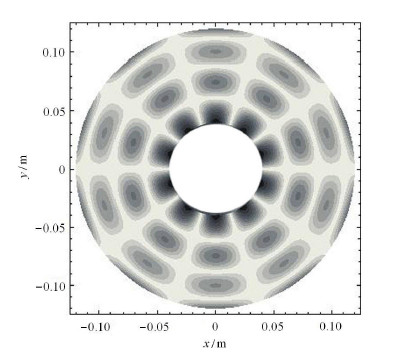
图1为 $f_{mn} = 2.993\,5$\,kHz时的环形薄板克拉尼图形实测图,图2为$m=5$,$n=4$时根据式(29)作出的数值模拟图, 其中白色代表波节(振幅为0),颜色越深振幅越大. 可见两者符合得很好.

|
图 1 频率为2.993 5 kHz时的实测图($m=5$, $n=4$) Fig. 1 Experiment result while frequency is 2.993 5 kHz($m=5$, $n=4$) |
|
图 2 $m=5$, $n=4$时的数值模拟图 Fig. 2 Simulation result while $m=5$, $n=4$ |
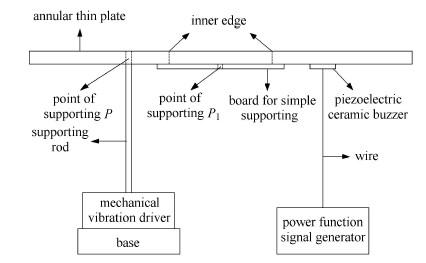
实验装置如图3所示,内外边界均悬空时需撤去简支板,支撑杆固定在支撑点$P (d,0)$处,其中$d =5$ cm. 当$f < 800$ Hz时,振源采用PASCO公司的SF-9324型机械振动驱动器,此时支撑点$P$即为振源,蜂鸣片先撤去. 当$f>800$ Hz时, 撤去机械振动驱动器,支撑杆不变,装上压电陶瓷蜂鸣片作为振源,由DDC功率函数信号发生器驱动,此时振源位置和支撑点$P$的连线落在径线上,并分布在环形板圆心两边. 由表1可求出$c$的平均值 $ \bar {c} = 1.066$\,m$^2$/s,测出板的质量密度$\rho = 8.59 \times 10^3$\,kg/m$^3$, 厚度$2h=9.70\times 10^{ - 4}$\,m,由 $ Y = [3\rho (1 - \mu ^2)\bar {c}^2] / h^2$可求出黄铜板的弹性模量 $Y=1.11\times 10^{11}$\,kg/(m$\cdot$s$^2$), 进一步求出 $\left| {c_{\max } - c_{\min } } \right| / \bar {c} = 0.090$,可见,$c$比较稳定,跟理论较为符合. 另外,还可根据$ u = \lambda f$,对于频率 $f_{mn}$,可估算出简谐波的径向传播速度(相速)的近似值 $u_{mn} = \lambda _{mn} f_{mn}$,结果示于表1的最后一行.显然,频率不同波速也不同,即薄板是一种频散媒质, 且泛音不成谐波关系. 径向波速估算方法如下,如$f=11.684$\,kHz时,由表1可算出两相邻圆波节线之间的径向距离 $\delta \approx 1.18$ cm,故径向波长$ \lambda = 2\delta \approx 2.36$ cm,径向波速$u= \lambda f \approx 275.7$\,m/s,且理论计算和实验数据表明(见表1),对于内外边界悬空,当频率不太低时, 相邻圆波节线之间的径向距离$\delta$ 的最大值和最小值相差甚小或基本一致,即$\delta$ 近似与 $r_{mnl}$中的$l$无关,只与$ f_{mn}$ 有关,且 $ 2\pi / \lambda _{mn}$ 近似等于 $k_{mn}$. 与圆形薄板的情形[9]不同,对应于$n$,环形薄板并不恰好有$l=n$个圆形波节线. 图4为简谐波的径向波速$u_{mn} $ 与频率$ f_{mn}$ 的近似关系,其中实线为根据 $u = \sqrt {2\pi cf}$作出的拟合曲线(取$c= \bar {c}$),三角形点为根据表1数据得到的实验点,可见两者基本符合.
|
图 3 克拉尼图形实验装置图 Fig. 3 Experiment setup for Chladni figure |

|
图 4 简谐波的径向波速 $ u_{mn} $与频率$f_{mn} $的依赖关系 Fig. 4 The relationship between radial harmonic wave velocity and frequency |
内边界简单支承时,内边界条件为[18]
| $ Z |_{r = a} = 0 $ | (30) |
| $ M_r \vert _{r = a} = 0 $ | (31) |
其中$M_r$ 由式(9)给出,式(31)等同于式(12)中$r=a$的情形.
外边界悬空,等同于式(12)和式(13)中 $r=b$的情形. 于是,有
| ${\rm J}_m (ka) + \dfrac{B}{A}{\rm Y}_m (ka) + \dfrac{C}{A}{\rm I}_m (ka) + \dfrac{D}{A}{\rm K}_m (ka) = 0 $ | (32) |
| $ \alpha _1 (a) + \beta _1 (a) \cdot \dfrac{B}{A} + \gamma _1 (a) \cdot \dfrac{C}{A} + \delta _1 (a) \cdot \dfrac{D}{A} = 0 $ | (33) |
| $ \alpha _1 (b) + \beta _1 (b) \cdot \dfrac{B}{A} + \gamma _1 (b) \cdot \dfrac{C}{A} + \delta _1 (b) \cdot \dfrac{D}{A} = 0 $ | (34) |
| $\alpha _2 (b) + \beta _2 (b) \cdot \dfrac{B}{A} + \gamma _2 (b) \cdot \dfrac{C}{A} + \delta _2 (b) \cdot \dfrac{D}{A} = 0 $ | (35) |
由式(32) $\sim $式(35)联立,可解出
| $\begin{array}{l} \frac{D}{A} = \left[{\frac{{{\alpha _2}(b){{\rm{Y}}_m}(ka) - {\beta _2}(b){{\rm{J}}_m}(ka)}}{{{\gamma _2}(b){{\rm{Y}}_m}(ka) - {\beta _2}(b){{\rm{I}}_m}(ka)}} - \frac{{{\alpha _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{J}}_m}(ka)}}{{{\gamma _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{I}}_m}(ka)}}} \right]/\\ \;\;\;\;\left[{\frac{{{\delta _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{K}}_m}(ka)}}{{{\gamma _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{I}}_m}(ka)}} - \frac{{{\delta _2}(b){{\rm{Y}}_m}(ka) - {\beta _2}(b){{\rm{K}}_m}(ka)}}{{{\gamma _2}(b){{\rm{Y}}_m}(ka) - {\beta _2}(b){{\rm{I}}_m}(ka)}}} \right] = \\ \;\;\;\;\;\;\left[{\frac{{{\alpha _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{J}}_m}(ka)}}{{{\gamma _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{I}}_m}(ka)}} - \frac{{{\alpha _1}(b){{\rm{Y}}_m}(ka) - {\beta _1}(b){{\rm{J}}_m}(ka)}}{{{\gamma _1}(b){{\rm{Y}}_m}(ka) - {\beta _1}(b){{\rm{I}}_m}(ka)}}} \right]/\\ \;\;\;\;\left[{\frac{{{\delta _1}(b){{\rm{Y}}_m}(ka) - {\beta _1}(b){{\rm{K}}_m}(ka)}}{{{\gamma _1}(b){{\rm{Y}}_m}(ka) - {\beta _1}(b){{\rm{I}}_m}(ka)}} - \frac{{{\delta _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{K}}_m}(ka)}}{{{\gamma _1}(a){{\rm{Y}}_m}(ka) - {\beta _1}(a){{\rm{I}}_m}(ka)}}} \right] \end{array}$ | (36) |
| $ \dfrac{C}{A} = - \dfrac{\alpha _1 (a){\rm Y}_m (ka) - \beta _1 (a){\rm J}_m (ka)}{\gamma _1 (a){\rm Y}_m (ka) - \beta _1 (a){\rm I}_m (ka)} - \dfrac{D}{A} \cdot \dfrac{\delta _1 (a){\rm Y}_m (ka) - \beta _1 (a){\rm K}_m (ka)}{\gamma _1 (a){\rm Y}_m (ka) - \beta _1 (a){\rm I}_m (ka)} $ | (37) |
| $ \dfrac{B}{A} = - \dfrac{{\rm J}_m (ka)}{{\rm Y}_m (ka)} - \dfrac{C}{A} \cdot \dfrac{{\rm I}_m (ka)}{{\rm Y}_m (ka)} - \dfrac{D}{A} \cdot \dfrac{{\rm K}_m (ka)}{{\rm Y}_m (ka)} $ | (38) |
由式(36),同样可求出$k$对应于$m$的第$n$个根$k_{mn} $,$(n = 0,\;1,\;2,\; \cdots \;)$, 即可解出所有可能的$k_{mn} $. 类似内外边界均悬空的情形,为了方便,对所有的 $ k_{mn}$ 从小到大排列,即取 $k_{m0} < k_{m1} < k_{m2} < \cdots $,等.例如对于$m= 8$,可解出$k_{8,0} = 0.750\,058$,$k_{8,1} = 1.122\,47$, $k_{8,2} = 1.426\,12$,$k_{8,3} = 1.726\,11$,$k_{8,4} =2.040\,26$,$k_{8,5} = 2.372\,74$,$k_{8,6} = 2.720\,23$,$k_{8,7} = 3.078\,49$,$k_{8,8} = 3.444\,33$,$k_{8,9} = 3.815\,58$,$k_{8,10} = 4.191\,15$,$ \cdots $. 此可见,对$m=8$,若令$r_0 = 8$ cm,则有$ k_{mn} r_0 = \pi \beta _{mn}$,$\beta _{mn} \approx n + (m / 2) - 3$ (当$n$比较大时),这规律仅近似对$m= 8$成立,对不同的$m$有不同的 $ r_0$ 取值和 $\beta _{mn}$ 表达式,即此时的环形薄板同样没有与圆形薄板相应的克拉尼定律[9, 21]. 把解出的 $ k_{mn}$ 依次代入式(36)、式(37) 和式(38),即可求出 $D/A$,$C/A$和 $B/A$. 再根据式(4),即得方程(2)的简谐振动解的特征函数为
| $ Z_{mn} (r,\;\theta ) = \left( {R_{mn} \cos m\theta + T_{mn} \sin m\theta } \right) \cdot \\ \qquad \left[{ {\rm J}_{m } (k_{mn} r) + \dfrac{B_{mn} }{A_{mn} }{\rm Y}_{m } (k_{mn} r) + }\right. \\ \qquad \left.{ \dfrac{C_{mn} }{A_{mn} }{\rm I}_{m } (k_{mn} r) + \dfrac{D_{mn} }{A_{mn} }{\rm K}_{m } (k_{mn} r)} \right] $ | (39) |
这里标记的处理同式(29),即$A,B,C,D,R$和$T$已加上与 $k_{mn} $相应的下标$m$和$n$.
令 $Z_{mn} (r,\;\theta ) = 0$,解出的$r$ (记为 $ r_{mnl} $)和 $\theta $即分别为此 $k_{mn}$ 下的圆形波节线的半径和径向波节线的角度,注意此时除了有若干条以原点为圆心的圆形波节线外,还有沿$r$方向的$2 m$条均匀对称的辐射状波节线.
实验装置如图3所示,支撑杆由固定在$P$点改为固定在简支板的支撑点$P_{1}$处,环形薄板内边界由圆形简支板简单支承,撤 去机械振动驱动器,装上压电陶瓷蜂鸣片作为振源. 表2给出几种 $ f_{mn}$ 下 当$\omega _0 = \omega _{mn} = 2\pi f_{mn} $时的圆形波节线半径的理论计算值 $ r_{mnl} $和实验观察值$ {r}'_{mnl}$,以及相应的$ k_{mn}$ 的值. 由表2可见,理论值与实验值也符合得很好. 求出$c$的平均值 $ \bar {c} = 1.048$\,m$^2$/s,进一步求出 $\left| {c_{\max } - c_{\min } } \right| / \bar {c} = 0.015$,可见$c$也比较稳定,且表2中的$c$值与表1中的$c$值相符合, 这是因为实验采用的是同一块环形黄铜薄板,其弹性模量和密度等参数相同,只是边条件不同. 由表2知对不同的半径, 径向波矢(或波长)的变化比较大,故与内、外边界均悬空时不同,内边界简支、外边界悬空时的径向波长 $\lambda _{mn}$ 和径向波速 $ u_{mn}$ 与半径 $ r_{mnl}$ 中的$l$有关. 同样地,对应于$n$并不恰好有$l=n$个圆形波节线.
| 表 2 不同频率$f_{mn}$ 下圆形波节线半径$r$的理论计算值$r_{mnl}$与实验 观测值$r'_{mnl}$ ($l=0,1,2,\cdots$) Table 2 Comparison of radii of circular nodal lines in different frequencies $f_{mn}$ between theoretical values $r_{mnl}$ and experiment values $r'_{mnl}$ ($l=0,1,2,\cdots$) |
图5为 $f_{mn} = 3.915\,3$\,kHz时的实验结果,图6为$m=9$和$n=2$时根据式(39)作出的数值模拟图, 其中白色代表波节(振幅为0),颜色越深振幅越大. 可见图5跟图6符合得很好. 由前面的分析知,同样泛音不成谐波关系.

|
图 5 频率为3.915 3 kHz时的实测图($m=9$, $n=2$) Fig. 5 Experiment result while frequency is 3.915 3 kHz ($m=9$, $n=2$) |

|
图 6 $m=9$, $n=2$时的数值模拟图 Fig. 6 Simulation result while $m=9$, $n=2$ |
下面讨论支撑点与振源的影响. 假定振源是集中在点 $ \left( {{r}'_0 ,\;\theta _0 } \right)$以角频率 $\omega$ 作简谐振动的点源,则稳态运动由格林函数$G$给出[17],$G$是方程
| $ \nabla ^4G - k^4G = \dfrac{1}{r}\delta \left( {r - {r}'_0 } \right)\delta \left( {\theta - \theta _0 } \right) $ | (40) |
的解,内、外边界均悬空且$f> 800$ Hz时支撑点要求
| $ G |_{r = d,\theta = 0} = 0 $ | (41) |
显然方程(40)的解$G$自动满足式(41). 由文献[17]中的公式知,若把$G$按式(29)或式(39)的特性函数 $Z_{mn}$ 作广义傅里叶展开,则$G$可表示为
| $ {G_\omega }\left( {r\theta |{{r'}_0}{\theta _0}} \right) = \frac{1}{{\pi \left( {{b^2} - {a^2}} \right)}}\sum {_{m,n}\frac{{{Z_{mn}}(r,\theta ){Z_{mn}}({{r'}_0},{\theta _0})}}{{{\Lambda _{mn}}(k_{mn}^4 - {k^4})}}} $ | (42) |
其中$k$由式(3)给出,注意此时的$k$一般情况下并不等于波矢的径向分量,$\pi \left( {b^2 - a^2} \right)\varLambda _{mn}$为类似于文献[17]中公式的归一因子. 显然由式(42)知,当$k =k_{mn} $ (即 $\omega = \omega _0 = \omega _{mn}$)时,可发生共振,相应的驻波波节线由 $Z_{mn} (r,\;\theta ) = 0$给出,此即前面的分析.
5 结 论本文讨论了两种边条件下环形薄铜板的二维振动解及其驻波模型. 当内外边界悬空时,此时若振源与支撑点重合, (1)振源频率很小(只有几十赫兹)时,只有径向波节线或其他对称形状(例如`` $\varPsi $''形状)波节线而没有圆形波节线; (2)当振源频率到达某一适当频率时,可以有$m =0$从而只有圆形波节线而无辐射状波节线,当然也可以 $ m \ne 0$.当振源与支撑点不重合时,一般情况下,$m \ne 0$,克拉尼图形中圆形波节线和辐射状波节线通常都同时存在. 在以上3种情况下,只要振源和支撑点位置确定,适当调节振源到某一频率,则波节线的位置及数目可完全确定,且实验值跟理论值符合得很好.而当内边界简支外边界悬空时,只要频率恰当,也可出现$m =0$或 $m \ne 0$这两种情况,此时无论频率如何,圆形波节线不少于一条(即内圆边界),并且理论与实验相符合. 由于薄板所受的重力和内摩擦力及不均匀性以及细沙的质量没有考虑等原因, 部分圆形波节线半径的理论值跟实验值有少量偏差.
从应用的角度来看,用本文的方法确定式(3)中的常数$c$ (或弹性模量$Y$),以及式(29)或式(39)中的$k_{mn} $, 即可由式(3)求出容许的自然频率$\omega _{mn} $ (或$f_{mn} $),其中最低自然频率 $f_{00}$ 最为重要.因为共振现象是振动系统(如汽车的板件、飞机的机翼、大楼的楼盖等)中最危险的现象, 它可以造成系统结构的破坏或断裂. 故在设计时若避开这些共振频率,可在一定程度下避免这些破坏的发生, 同时这也给出了测量正在发生共振的薄板的振动频率的一种简单方法,即只要数出$m$和$n$,量出波节线的位置(如 $r_{mnl}$)既可,而对于某些不能承受剧烈振动的零部件或配件可将其安装在波节线的位置上.
总的来说,以上对高频段的讨论都以压电陶瓷蜂鸣片作为振源. 若遇其他振源,对受迫振动的研究还有其他方法[22]. 最近,对压电晶体片或压电金属板的振动也有了一些探究[23, 24], 相信采用高频振源来进行振动的研究将越来越普遍.
| [1] | Chladni EFF. Entdeckungenüber die Theory des Klanges, Breitkopf und Härtel, Leipzig, 1787. |
| [2] | Hawkes JJ, Radel S. Acoustofluidics 22: Multi-wavelength resonators, applications and considerations. Lab on a Chip, 2013, 13: 610-627. |
| [3] | Ochs JB, Snowdon JC. Transmissibility across simply supported thin plates. II. Rectangular plates with loading masses and straight ribs. The Journal of the Acoustical Society of America, 1976, 59: 350-354. |
| [4] | Hodges CH, Woodhouse J. Theories of noise and vibration transmission in complex structures. Reports on Progress in Physics , 1986, 49: 107-170. |
| [5] | Dorrestijn M, Bietsch A, Acikalin T, et al. Chladnifigures revisited based on Nanomechanics. Physical Review Letters , 2007, 98: 026102. |
| [6] | Stein J, Stöckmann H-J. Experimental determination of billiard wave functions. Physical Review Letters , 1992, 68: 2867-2870. |
| [7] | Proefschrift. Newton vs Stokes: Competing Forces in Granular Matter. Henk Jan van Gerner, Enschede, The Netherlands, 2009 |
| [8] | Thomas B, Squires AM. Support for faraday's view of circulation in a fine-powder chladniheap. Physical Review Letters , 1998, 81: 574-577. |
| [9] | Rayleigh L. The Theory of Sound (Vol. I) (2st Ed. revised and enlarged), New York: Dover Publication, 1945: 358-363 |
| [10] | 方奕忠, 王钢, 沈韩等. 方形薄板二维驻波的研究. 物理实验, 2014, 34(1): 33-36 (FangYizhong, Wang Gang, Shen Han, et al. Research of 2-dimensional standing waves in square plate. Physics Experimentation, 2014, 34(1): 33-36 (in Chinese)) |
| [11] | 方奕忠, 王钢, 沈韩等. 圆形薄板二维驻波的研究. 大学物理, 2015, 34(3): 19-24 (Fang Yizhong, Wang Gang, Shen Han, et al. Research for two-dimensional standing waves on circular plate. College Physics, 2015, 34(3): 19-24 (in Chinese)) |
| [12] | Chladni patterns in vibrated plates, http://www.physics.utoronto.ca/ enonlinear/chladni.html. 2013-12-1 |
| [13] | 宋力, 张平. 关于弹性地基上圆环形薄板振动问题的解答(续一). 沈阳工业学院学报, 1996, 15(1): 85-94 (Song Li, Zhang Pin. Solutions to the vibration of ring-shaped thin plate on the elastic base (continuation 1). Journal of Shenyang Institute of Technology, 1996, 15(1): 85-94 (in Chinese)) |
| [14] | 宋力, 张景异. 关于弹性地基上圆环形薄板振动问题的解答. 金属成型工艺, 1997, 15(4): 34-38 (Song Li, Zhang Jinyi. Solutions to the vibration of ring-shaped thin plate on the elastic base. Metal Forming Technology, 1997, 15(4): 34-38 (in Chinese)) |
| [15] | 吴伟, 宋力. 弹性地基上圆环形薄板振动问题的研究. 沈阳工业学院学报, 1997, 16(3): 46-50 (Wu Wei, Song Li. Solutions to the vibration of ring-shaped thin plate on the elastic base. Journal of Shenyang Institute of Technology, 1997, 16(3): 46-50 (in Chinese)) |
| [16] | 肖世富, 陈学前. 挠性边界圆薄板的半解析模态分析. 应用力学学报, 2014, 31(5): 667-670 (Xiao Shifu, Chen Xueqian. Semi-analytic modal analysis of the circular thin plate with a flexible boundary. Chinese Journal of Applied Mechanics, 2014, 31(5): 667-670 (in Chinese)) |
| [17] | 莫尔斯 PM, 英格特KU. 理论声学(上册). 吕如榆, 杨训仁译. 北京:科学出版社, 1984: 210-211, 252-257 (Morse PM, Ingard KU. Theoretical Acoustics. Lü RY, Yang XR, transl. Beijing: Science Press, 1984: 210-211, 252-257 (in Chinese)) |
| [18] | 钱伟长, 叶开沅. 弹性力学. 北京:科学出版社, 1956. 285-286 (Qian Weizhang, Ye Kaiyuan. Elastic Mechanics. Beijing: Science Press, 1956. 285-286(in Chinese)) |
| [19] | 王龙甫. 弹性理论. 北京:科学出版社, 1978. 357-360 (Wang Longfu. Theory of Elasticity. Beijing: Science Press, 1978. 357-360 (in Chinese)) |
| [20] | 朗道 LD, 栗弗席兹 EM. 弹性理论(第五版). 武际可, 刘寄星译. 北京: 高等教育出版社, 2011. 115-116 (Landau LD, Lifschitz EM. Theory of Elasticity. Wu JK, Liu JX, transl. Beijing: Higher Education Press, 2011. 115-116 (in Chinese)) |
| [21] | Rossing TD. Chladni's law for vibrating plates. American Journal of Physics , 1982, 50: 271-274. |
| [22] | 黄迪山, 邵何锡. 多自由度参数振动受迫响应的三角级数逼近. 应用力学学报, 2014, 31(5): 703-709 (Huang Dishan, Shao Hexi. Vector trigonometric series approach to forced response of a multiple freedom parametric vibration. Chinese Journal of Applied Mechanics, 2014, 31(5): 703-709 (in Chinese)) |
| [23] | Fan YP, Ji XJ, Liu XP, et al. The nonlinear analysis of elastic wave of piezoelectric crystal plate with perturbation method. Wave Motion, 2014, 51(5): 798-803. |
| [24] | Zhang CL, Chen WQ, Yang JS, et al. Equations for high-frequency vibrations of piezoelectric plates derived from a semi-mixed variational principle and applications in resonators. International Journal of Applied Electromagnetics and Mechanics, 2013, 41(4): 361-373 |
 2015, Vol. 47
2015, Vol. 47