2. 西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安710049;
3. 西安交通大学多功能材料与结构教育部重点实验室,西安710049
闭孔泡沫铝受压时具有低应力水平、高效吸能、低回弹等特性,是用作轻质防护结构的绝佳材料,如军用汽车的防爆底板(防地雷)、坦克的防爆装甲、处置疑似爆炸物的防爆罐、宇宙飞船的起落架、空间探测器着陆系统、汽车保险杠、重要建筑物的防撞结构等.但是,闭孔泡沫铝的抗拉力学性能很差,在单轴拉应变达到0.5%左右时即发生断裂破坏,故一般将其用作超轻夹芯构件(如梁板壳或其他异形构件)的芯体材料.闭孔泡沫铝夹芯构件的形状通常较复杂,用解析的方法难以求解,工程设计时多采用数值方法(如有限元法、无网格法)研究其承载变形和破坏模式.在外载荷尺度远大于闭孔泡沫铝细观结构尺度情况下,通常可忽略胞孔结构的影响,将其等效为宏观连续体,而建立合理的唯象本构模型并确定合适的本构参数,是针对填充闭孔泡沫铝的夹芯结构开展吸能防护设计的基础,也是近二十年来该领域的热点问题[1, 2].
闭孔泡沫铝材料在宏观上具有非线性大变形、体积可压缩、拉压不对称和应变率效应等复杂特性,相对于密实材料,其最重要的力学特征是体积可压缩性.目前常见的弹塑性唯象可压缩本构模型有:有限元软件"LS-DYNA"内置的75#模型[3]和154#模型[3, 4, 5, 6, 7],有限元软件"ABAQUS"[8]内置的体积强化可压缩模型(crushable foam model with volumetric hardening)和各向同性强化可压缩模型(crushable foam model with isotropic hardening),文献[9]提出的自相似模型(self-similar model)和微分强化模型(differential hardening model),米勒(Miller)模型[10],陈卢(Chen-Lu)模型[11],张(Zhang)模型[12, 13],弗雷斯特(Forest)模型[14]以及康巴兹(Combaz)模型[15, 16]等.在平均应力和有效应力平面上,这些唯象可压缩本构模型的屈服面函数均为二次函数;根据可调整参数的数量,强化法则可分为单参数形式、二参数形式、三参数形式以及四参数形式;流动法则分为关联流动和非关联流动两种形式.
为了验证这些唯象可压缩本构模型对闭孔泡沫铝材料的适用性,除了单轴实验(压缩和拉伸),更需要开展多轴应力状态下力学性能的研究.一些学者对几种常见的商用闭孔泡沫铝进行了单轴、双轴和三轴试验,如"Alporas"[9, 17, 18, 19]、"Cymat"[20]、"Hydro"[7, 19, 21]、"Alulight"[22, 23]、"IFAM"[24, 25]、"SEU"[26, 27]、"CSIC"[28, 29]和"HongBo"[30]等品牌的闭孔泡沫铝,但实验结果离散性很大.也有学者讨论了闭孔泡沫铝的屈服面.对以大变形为主要特征的闭孔泡沫铝而言,后继屈服面显然更重要,但这方面的研究极少,主要原因是闭孔泡沫铝的多轴压缩实验难度很大,其可靠性也缺少验证[31].大部分本构模型中需要输入的重要参数在实验中也很难确定,如在有限元软件"ABAQUS"内置的各向同性强化可压缩泡沫本构模型[8]中,需要输入单轴压缩和静水压缩的屈服应力比值、塑性泊松比和单轴压缩的柯西应力对数塑性应变曲线,但由于闭孔泡沫铝试件在单轴大变形压缩过程中的侧面位移变化很不均匀,无法准确获得塑性泊松比和柯西应力.因此,如何获得闭孔泡沫铝有效可信的多轴加载数据,进而对各类本构模型的精度和适用性进行验证是非常重要且紧迫的工作.目前,一些唯象本构模型的本构参数只能通过数值模拟的方法确定[32, 33, 34].
闭孔泡沫铝的微细观组织结构通常具有亚毫米或毫米量级尺寸,较易识别,故可采用细观有限元模型表征其复杂的几何构型并研究其宏观力学性能.例如,基于代表性体积单元(representative volume element)尺度的细观有限元模型.本文关注的三维有限元模型可分为3类[35]:几何模型、结构模型和离散模型.几何模型一般采用规则分布的圆球代表胞孔结构,包括简单立方(primitive cubic)、体心立方(body centred cubic)或面心立方(face centred cubic)分布,或通过施加不同程度的随机扰动生成的随机球形胞孔结构有限元模型[36].该类模型与高相对密度(低孔隙率)的球形孔泡沫金属有一定的相似度.结构模型采用壳或梁单元构造胞孔孔壁,如椭球随机模型[37]和泰森多边形(Voronoi)模型[38, 39, 40, 41, 42, 43].由于壳单元假定其厚度尺寸远小于其他相关尺寸,故结构模型仅适用于近似表征孔壁很薄的低相对密度(高孔隙率)泡沫金属.离散模型的构建基于真实多孔材料的显微计算机断层扫描影像信息,可在不损坏试样的前提下快速重构真实泡沫金属内部胞孔的形状和分布的三维影像,因此可定量表征泡沫金属的几何构型,即对泡沫金属进行显微计算机断层扫描后得到影像信息,然后据此直接生成".STL"格式的点云模型文件.一般而言,建立有限元模型的方法有二:(1)使用通用有限元前处理软件(如"ANSYS/Icem"和"HyperMesh")直接生成立方体单元(voxel)模型[44, 45, 46];由于这种模型的胞孔表面单元呈阶梯状,在大变形计算时不会形成接触面,故无法模拟泡沫金属的孔壁接触、滑移直至密实化过程,仅适合进行接触之前的小变形分析.(2)采用逆向工程方法[47, 48],先建立泡沫金属的几何模型,再生成光滑表面单元的有限元模型;但是,由于该方法的建模过程复杂,且计算量庞大,目前仅有少数研究者能够掌握并使用这项技术.基于对闭孔泡沫铝的逆向建模方法的长时间摸索,作者目前已掌握建立光滑表面的三维细观离散模型的方法[49].
采用离散模型定量研究闭孔泡沫铝的力学性能,必须输入其孔壁材料的本构参数[50].除了基体成分(即铝)、在制备过程中引入的合金成分、增粘剂等,孔壁材料还包含各类制备缺陷.目前,针对表征几何构型的建模方法研究较多,但针对闭孔泡沫铝孔壁材料力学性能的研究很少.文献[51]采用闭孔泡沫铝的外表皮试件进行单轴压缩试验,包括7075,6061和AlSi7三种基体材料;由于无法采用闭孔泡沫铝的孔壁材料制备标准试件,仅直观上发现7075铝合金孔壁较脆,6061和AlSi7铝合金孔壁的延性较好.因此,欲确定闭孔泡沫铝孔壁材料的本构参数,目前只能采用逆向反演方法.例如,针对不同基体的闭孔泡沫铝,文献[52, 53, 54, 55]基于纳米压痕(nanoindentation)实验结果,文献[47, 48]基于单轴压缩的位移-荷载曲线,逆向反推了其孔壁材料的弹性模量、屈服强度和指数强化模型的本构参数.但是,这些孔壁材料本构参数仅能吻合特定闭孔泡沫铝的小变形实验结果.对具有不同基体成分、不同相对密度、不同生产工艺的闭孔泡沫铝而言,其孔壁材料的本构参数仍需进一步研究.
针对目前多孔金属多轴加载实验难以实施和唯象本构参数难以确定的现状,本文以填充闭孔泡沫铝的超轻夹芯结构的吸能防护设计为导向,以闭孔泡沫铝单轴实验结果为基础,采用三维细观离散有限元模型,定量研究闭孔泡沫铝在多轴压缩载荷作用下的大变形力学行为;三维细观有限元建模时,通过逆向思路解决复杂无序的几何构型和难以测量的孔壁材料本构参数两大难题,计算获得了闭孔泡沫铝可信的多轴加载数据,确定了闭孔泡沫铝的唯象本构参数,进而验证了常见多孔金属唯象可压缩本构模型的精度和适用性.
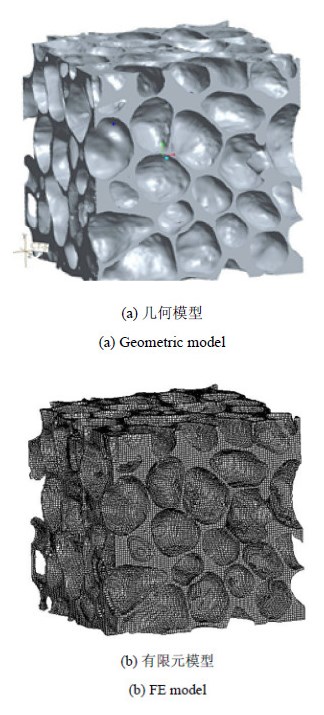
1 闭孔泡沫铝的逆向建模 1.1 显微计算机断层扫描及影像重构本文研究的闭孔泡沫铝采用粉末冶金发泡法制备[26, 27],其孔壁材料的成分为A1 7% Si (质量分数).试件为边长18 mm的立方体,称重法测量其相对密度为0.19.根据文献[56]的实验结果,相对密度近似,如果没有结构上的缺陷如耦合胞孔、缺失胞孔和坍塌胞孔等,较小的闭孔泡沫铝试件在单轴压缩时可以表现出和大块泡沫试件完全相同的应力应变曲线.利用显微电子计算机断层摄影设备(μCT80,SCANCO,Switzerland,四川大学华西口腔疾病国家重点实验室),获得236张断面照片,层间距0.072 mm,照片尺寸236×236像素.采用三维图像处理和编辑软件"Mimics",建立闭孔泡沫铝的点云格式三维模型,然后采用逆向工程软件"Rapidform"重新构建闭孔泡沫铝几何实体模型,结果如图1(a)所示;最后利用"ANSYS/Icem"软件,对闭孔泡沫铝几何模型划分六面体单元,试件的单元剖分结果如图(b)1所示:单元尺寸约为泡沫铝试件尺寸的百分之一,单元数量总计259 306个.
|
图 1 闭孔泡沫铝的逆向建模 Fig.1 Reverse modeling of closed-cell aluminum foam |
闭孔泡沫铝采用粉末冶金发泡法制备,其基体成分除了铝外,还有适量的硅、钛等元素,尤其是材料的孔壁存在多种几何缺陷,这些缺陷导致孔壁材料的力学性能与密实的铝合金材料相差甚远[57].此外,对具有不同基体成分、不同相对密度、不同生产工艺的闭孔泡沫铝而言,其孔壁材料的力学性能也会存在差异.本文在建立几何模型的过程中,忽略直径太小的胞孔,并通过调整孔壁材料的本构参数以减少几何模型的误差.
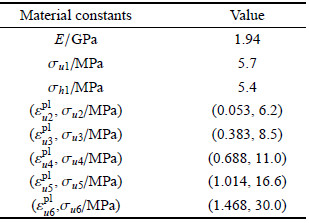
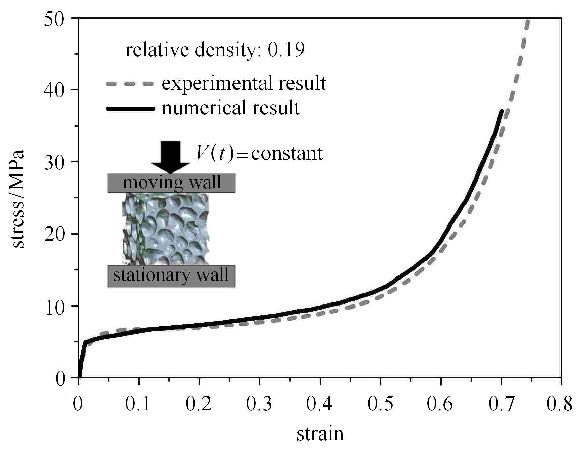
假定闭孔泡沫铝的孔壁材料的密度为2 700 kg/m3,本构模型选为软件内置的弹塑性模型[3](*MAT_PLASTIC_KINEMATIC),该本构模型采用米塞斯屈服准则、关联流动和各向同性强化假定.采用细观三维有限元模型,开展系统的准静态单轴压缩模拟计算,调整孔壁材料的本构参数,促使有限元模型的计算结果与闭孔泡沫铝试件单轴压缩实验的应力应变曲线相吻合,如图2所示,相应的孔壁材料本构参数见表1.简便起见,本文忽略准静态单轴压缩的实验细节.图2结果表明,相较于实验曲线,数值计算结果在初始段有明显的误差.分析认为,一方面,由于实验中的压头不平导致实验曲线的弹性变形部分存在较大误差;另一方面,计算时选用的简单弹塑性本构关系或许不能反映孔壁材料的初始变形特性.但是,总体而言,数值计算结果与实验结果吻合良好,尤其是在本文重点关注的闭孔泡沫铝大变形方面,所采用的有限元模型和孔壁材料的弹塑性本构具有足够精度.
|
图 2 闭孔泡沫铝单轴压缩名义应力应变曲线:有限元计算与实验结果比较 Fig.2 Comparison of numerically predicted uniaxial compressive stress versus strain curve with that experimentally measured for closed-cell aluminum foam |
| 表 1 泡沫铝孔壁材料的弹塑性本构参数 Table 1 Elasto-plastic constitutive parameters for cell-wall material |
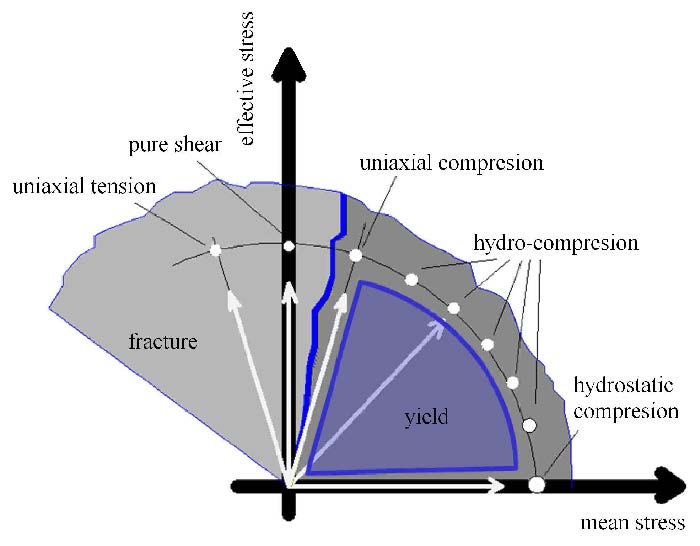
如图3所示,在平均应力和有效应力组成的应力平面上,闭孔泡沫铝的屈服面一般为二次曲线,初始屈服面和后继屈服面需结合拉伸、剪切、压缩等应力状态下的实验结果共同确定.在受压为主导的应力状态下(图3中深灰色部分),闭孔泡沫铝表现为大变形的塑性屈服;在受拉或受剪为主导的应力状态下(图3中浅灰色部分),则表现为脆性断裂.
|
图 3 闭孔泡沫铝的应力状态 Fig.3 Stress state of closed-cell aluminum foam |
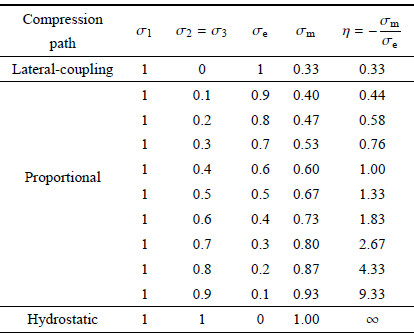
针对图3所示扇形区域部分的应力状态,改变三维细观有限元模型的加载边界,本文实现了闭孔泡沫铝力学行为的数值模拟,具体加载路径如表2所示. 其中,定义加载路径的比例系数$\eta$ 为
| $\eta =-\frac{{{\sigma }_{m}}}{{{\sigma }_{e}}}$ | (1) |
| 表 2 数值计算应力加载路径 Table 2 Stress loading path for numerical simulation |
3种边界分别为侧面耦合单轴压缩、静水压缩和等比压缩. 下文介绍每一种边界的具体实现方法.
2.1 侧面耦合单轴压缩对闭孔泡沫铝试件的三维细观有限元模型进行单轴压缩计算,发现其在变形过程中有明显的侧向变形,但由于侧面的位移变化很不均匀,无法得到柯西应力、弹塑性泊松比等重要本构参数.有鉴于此,本文尝试分别耦合有限元模型的每个侧面节点位移,计算了轴向压缩时的柯西应力对数应变曲线,并监测泊松比的变化过程.
模拟准静态单轴压缩过程时,将试件包夹在两个刚性平面之间,下刚性面静止,上刚性面以恒定速率向下对试件进行缓慢压缩加载.
将侧面节点进行耦合的效果是对试件侧面的节点位移平均化,这种边界可使试件在平面内无限拓展,相当于对无限大板进行单轴压缩,从而消除试件的边界效应.需要指出,采用连续型模型模拟闭孔泡沫铝的力学性能时忽略了其局部化变性特征;单轴压缩时,如果不考虑上下压头的摩擦力,得到的侧面位移一致,与作者采用的侧面耦合边界具有相同效果.
2.2 静水压缩由于闭孔泡沫铝在宏观上可近似为均匀材料,采用位移控制加载即可实现准静态静水压缩:分别建立3个静止刚性面以限制试件沿X,Y,Z 3个方向的法向位移,另建立3个运动刚性面以相同的恒定速度分别对试件沿3个方向进行缓慢压缩.
通过输出试件角点的位移和3个静止刚性面的反力,可分别求得闭孔泡沫铝试件沿3个方向的柯西应力对数应变曲线.计算发现,试件3个方向的应力应变曲线基本重合:换言之,在压缩过程中,有效应力保持在零附近,加载的比例系数趋近于无穷大.
2.3 等比压缩控制位移(速度)边界可实现闭孔泡沫铝的单轴压缩和静水压缩,但无法实现等比压缩.由于在大变形时试件各加载面的面积变化很大,也不能通过控制加载面上合力的比例来实现.本文通过摸索尝试,成功使用如下边界来近似实现闭孔泡沫铝在大变形时的等比压缩过程.
如图4(a)所示,以试件的一个角点为原点O,分别建立3个刚性面用来限制闭孔泡沫铝试件3个方向的位移,试件的另外3个面外分别被一层很薄(厚0.1 mm)的实体单元包裹(简称包裹单元),相当于静水压缩实验中使用的橡胶皮套[9, 27],为了简化起见,将该层单元的材料属性设成理想弹塑性,密度0.027 g/cm3,弹性模量1 GPa,泊松比0.3,屈服强度0.1 MPa,由于密度、弹性模量和屈服强度取值相对孔壁材料都很小,忽略了其对闭孔泡沫铝性能的影响.为防止包裹单元产生过大面外变形,分别耦合包裹单元的面外自由度,并且限定包裹单元边界的位移,防止包裹单元应力传递到刚性面上.试件的切面如图4(b)所示.在包裹单元所在的3个面上沿坐标轴负方向施加随时间变化的压强曲线,该曲线可根据单轴压缩轴向的应力应变曲线来确定.设定Y轴方向的曲线缩放系数(scale factor)为1.0,同时改变另外两个方向的缩放系数可以实现对闭孔泡沫铝的不同比例下的等比压缩过程.输出试件的角点D沿X,Y和Z方向的位移和3个静止刚性面的反力,可以求出不同方向的真实应力对数应变曲线.

|
图 4 三轴等比压缩示意图 Fig.4 Three axial compression diagram for proportional compression loading |
通过侧面耦合单轴压缩、静水压缩和等比压缩3种边界条件实现闭孔泡沫铝试件11个加载路径的大变形压缩过程,得到的比例系数范围为$\eta\geqslant$ 0.33.两个试件的加载比例系数变化过程如图5所示,可以看到,等比压缩边界得到的比例系数并非恒值,存在一定的波动,并不是严格意义上的等比加载.但是我们认为比例系数已经拉开,加载路径覆盖了足够的应力空间,可以为研究闭孔泡沫铝受压本构关系提供数据支持.

|
图 5 加载比例系数变化图 Fig.5 Stress states variation diagram |
将侧面耦合以后求得两个闭孔泡沫铝试件的轴向柯西应力对数应变曲线,如图6所示.可以看到,和图2所示的名义应力应变曲线差异较大,主要原因是由于闭孔泡沫铝在单轴压缩过程中侧向会发生明显的变形,对于大变形是不能忽略的.试件可以看做弹塑性强化材料,取吸能效率极值点的应变[58]为密实对数应变$\varepsilon$D,求得$\varepsilon$ D=0.78.弹性模量Ef=1.94 GPa,将曲线转折点处的应力值定为初始平台应力$\sigma$ u1,则$\sigma$ u1=5.7 MPa.

|
图 6 闭孔泡沫铝单轴压缩的应力应变曲线 Fig.6 Simulated uniaxial compressive stress versus strain curves for closed-cell aluminum foams |
泊松比定义为单向受压时横向对数应变与轴向对数应变的绝对值的比值,弹性变形阶段称为弹性泊松比,塑性变形阶段称为塑性泊松比.一般密实材料在塑性流动中体积恒定,塑性泊松比为0.5,而泡沫金属作为可压缩材料,其塑性泊松比必然小于0.5.通过侧面耦合单轴压缩得到了闭孔泡沫铝有限元试件的泊松比随轴向对数应变的变化曲线,如图7所示.
|
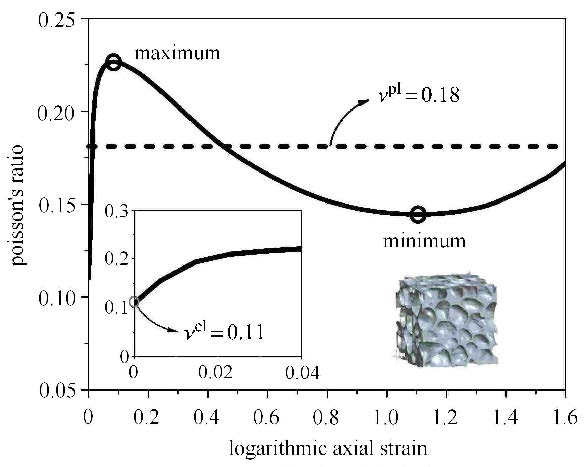
图 7 闭孔泡沫铝的弹塑性泊松比 Fig.7 Elastic-plastic Poisson's ratio for closed-cell aluminum foams |
从图7可以看到,随着轴向应变的增大,泊松比经历了增高---降低---再增高的"S"型变化过程,存在一个极大值点和一个极小值点将曲线分为3部分,但是,对比图6,并没有发现泊松比随轴向对数应变的变化和应力随轴向对数应变变化之间的对应关系,由于三维细观有限元模型复杂,也难以建立细观结构变形特征和泊松比变化的关系,下面仅研究表征唯象本构关系的本构参数的确定.
在初始变形阶段,泊松比单调增加,弹性泊松比可以取弹性变形阶段的平均值,但由于闭孔泡沫铝的弹性变形很小(对数应变0~0.002,见图6),简化起见,直接取轴向对数应变接近零时的泊松比为弹性泊松比$v^{el}$,则$v^{el}$=0.11.试件的塑性泊松比在对数应变0.08时达到极大值0.227,在对数应变1.11时到极小值0.144.在常见的唯象本构模型中,一般将塑性泊松比视为常量,同样为了简化起见,忽略弹性变形阶段,直接求得泊松比在整个对数应变区间(对数应变0~1.6,见图6)的均值为特征塑性泊松比$v^{pl}$=0.18.
3.2 静水压计算结果图8为计算得到的闭孔泡沫铝静水压缩应力应变曲线,横轴为对数体积应变,纵轴为压强,也就是3个方向的柯西应力.可以看到,试件在静水压作用下的初始平台应力$\sigma$ h1=5.4 MPa,和相应的单轴压缩初始平台应力$\sigma$ u1比较接近.同时,也可以看到,静水压作用下的强化模量比单轴压缩时大很多.

|
图 8 闭孔泡沫铝静水压缩的应力应变曲线 Fig.8 Simulated hydrostatic compressive stress versus strain curves for closed-cell aluminum foams |
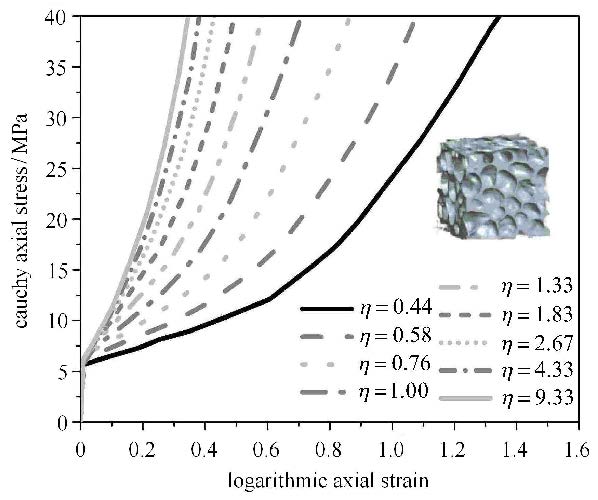
通过改变加载的比例系数$\eta$,得到一系列加载路径下的应力应变曲线,图9给出了Y轴方向的柯西应力对数应变曲线.可以看到,等比加载下的闭孔泡沫铝试件的初始平台应力都基本重合,并且和单轴压缩和静水压缩的初始平台应力相近.随着比例系数的增大,曲线的强化模量增大很快.
|
图 9 闭孔泡沫铝等比压缩的应力应变曲线 Fig.9 Simulated proportional compressive stress versus strain curves for closed-cell aluminum foams |
根据闭孔泡沫铝有限元模型不同加载路径下的数值计算结果,可以确定几个常见可用于泡沫金属材料的本构模型参数,也可以对这些本构模型在描述多轴压缩应力状态下的精度进行验证.
4.1 可压缩泡沫本构模型屈服面根据有限元软件"ABAQUS"内置的各向同性强化可压缩泡沫模型(crushable foam model with isotropic hardening)[8],定义屈服面为
| $f = \sqrt {\sigma _e^2 + \alpha ^2\sigma _m^2 } - B = 0$ | (2) |
| $\alpha = \dfrac{k}{\sqrt {1 - \dfrac{1}{9}k^2} }\,, k = \dfrac{\sigma _u^0 }{\sigma _h^0 }$ | (3) |
| $B = \dfrac{1}{3}\sqrt {9 + \alpha ^2} \left| {\sigma (\bar {\varepsilon }^{pl} )} \right|$ | (4) |
| $\bar {\varepsilon }^{\,\rm pl} = \sqrt {\left[{1 + \left( {\dfrac{\beta }{3}} \right)^2} \right]\left( {\varepsilon_e^2 + \dfrac{1}{\beta ^2}\varepsilon _v^2 } \right)}$ | (5) |
参数$\beta$ 定义为
| $\beta = \sqrt {\dfrac{9\left( {1 - 2\nu ^{pl}} \right)}{2\left( {1 + \nu ^{pl}} \right)}}$ | (6) |
| $- v^{pl}\varepsilon _11^{pl} = \varepsilon _22^{pl} = \varepsilon _33^{pl}$ | (7) |
由式(6)得到
| $v^{pl} = \dfrac{9 - 2\beta ^2}{18 + 2\beta ^2}$ | (8) |
得到塑性有效应变和体积应变为
| $\varepsilon _e = \dfrac{9}{9 + \beta ^2}\varepsilon _11^{pl}\,,\ \ \varepsilon _v = \dfrac{3\beta ^2}{9 + \beta ^2}\varepsilon _11^{pl}$ | (9) |
代入式(5)得到
| $\bar {\varepsilon }^{\,\rm pl} = \varepsilon _11^{pl} = \varepsilon _u^{pl}$ | (10) |
则式(4)可以表示为
| $B = \dfrac{1}{3}\sqrt {9 + \alpha ^2} \left| {\sigma _u (\varepsilon _u^{pl} )} \right|$ | (11) |
各向同性强化可压缩泡沫材料模型通过单轴压缩和静水压缩的初始平台应力值确定初始屈服面,而后继屈服面只需要通过单轴压缩的结果确定.根据三维细观有限元模型的计算结果,可以确定闭孔泡沫铝的可压缩泡沫材料模型屈服面参数如表3所示.
| 表 3 团孔泡沫铝的本构参数1 Table 3 Constitutive parameters for closed-cell aluminum foams (1) |
其中,$(\varepsilon _ui^{pl},\sigma _ui )$,i=2,3,4,5,6为根据单轴压缩应力应变曲线求得的轴向对数塑性应变和对应的柯西应力值,在本构模型中用以确定后继屈服面.
轴向对数塑性应变根据下式计算
| $\varepsilon _u^{pl} = \varepsilon _u - \varepsilon _u^{el} = \varepsilon _u - \dfrac{\sigma _u1 }{E}$ | (12) |
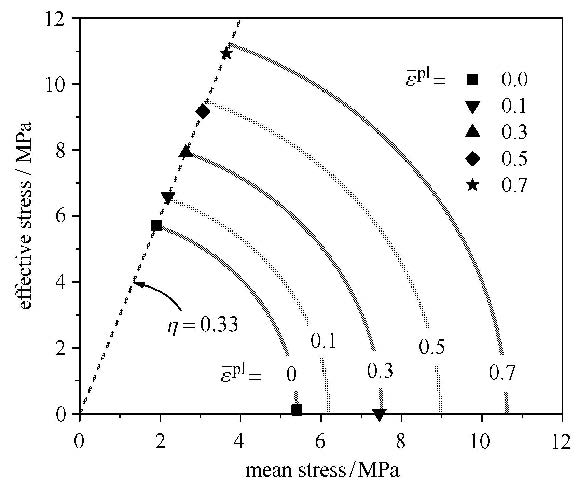
闭孔泡沫铝试件初始屈服面及其演化关系如图10所示,可以看到初始屈服面在平均应力与有效应力空间是一个以原点为中心的椭圆(只给出了比例系数$\eta \ge $ 0.33的区间范围).由于闭孔泡沫铝在单轴压缩和静水压缩时的初始平台应力相当,计算得到的椭圆长、短轴长度也近似相等.随着等效应变的增大,屈服面的长、短轴也按比例增大,形成一组相似的椭圆.根据各个特征应变下的屈服面,预测单轴压缩时的屈服点在图10中为屈服面与比例系数$\eta$=0.33所示虚线的交点,预测的静水压缩时的屈服点为屈服面与横坐标轴的交点.相同特征塑性应变下根据前面三维细观有限元模型计算得到的屈服点为在图中表示的散点.可以看到,单轴压缩的结果吻合良好,而静水压缩时只有初始屈服点吻合良好,在特征塑性应变$\bar{\varepsilon}^{pl}$=0.1时,预测的静水压缩屈服应力和数值计算结果相比就会产生超过20%的偏差,而且随着特征塑性应变的增大而增大.可压缩泡沫本构模型屈服面在大变形时会严重低估闭孔泡沫铝静水压缩的屈服应力.
|
图 10 可压缩泡沫模型屈服面验证 Fig.10 Yield surface validation for the crushable foam model |
陈-卢本构[11]中,分别定义了特征应力$\bar {\sigma }$和能量共轭的特征应变$\bar {\varepsilon }$
| $\bar {\sigma }^2 = \sigma _e^2 + \beta ^2\sigma _m^2$ | (13) |
| $\bar {\varepsilon }^2 = \varepsilon _e^2 + \dfrac{\varepsilon _v^2 }{\beta^2}$ | (14) |
| $\beta = \sqrt {\dfrac{9\left( {1 - 2\nu ^{el}} \right)}{2\left( {1 + \nu ^{el}} \right)}}$ | (15) |
陈-卢本构并没有区分弹性和塑性,不存在弹塑性本构框架内的屈服面,定义类似"屈服面"的应力势函数为
| $\begin{align} & f={{{\bar{\sigma }}}^{2}}+A\left( \bar{\varepsilon } \right)\sigma _{m}^{2}-B\left( \bar{\varepsilon } \right)= \\ & \sigma _{e}^{2}+\left( A\left( \bar{\varepsilon } \right)+{{\beta }^{2}} \right)\sigma _{m}^{2}-B\left( \bar{\varepsilon } \right)=0 \\ \end{align}$ | (16) |
| $A\left( \bar {\varepsilon } \,\right) = \dfrac{\bar {\sigma }_h^2 \left( \bar {\varepsilon }\, \right) - \bar {\sigma }_u^2 \left( \bar {\varepsilon } \,\right)}{\dfrac{\bar {\sigma }_u^2 \left( \bar {\varepsilon } \,\right)}{\left( {9 + \beta ^2} \right)} - \dfrac{\bar {\sigma }_h^2 \left( \bar {\varepsilon } \,\right)}{\beta ^2}}$ | (17) |
| $B\left( \bar {\varepsilon }\,\right) = \bar {\sigma }_h^2 \left( \bar {\varepsilon } \,\right)\bar {\sigma }_u^2 \left( \bar {\varepsilon } \,\right)\dfrac{\dfrac{1}{\left( {9 + \beta ^2} \right)} - \dfrac{1}{\beta ^2}}{\dfrac{\bar {\sigma }_u^2 \left( \bar {\varepsilon }\,\right)}{\left( {9 + \beta ^2} \right)} - \dfrac{\bar {\sigma }_h^2 \left( \bar {\varepsilon } \,\right)}{\beta ^2}}$ | (18) |
单轴压缩时
| $\bar {\sigma }_u = \dfrac{1}{3}\sqrt {9 + \beta ^2} \left| {\sigma _u } \right| \,, \bar {\varepsilon } = \dfrac{3}{\sqrt {9 + \beta ^2} }\left| {\varepsilon _u } \right|$ | (19) |
静水压缩时
| $\bar {\sigma }_h = \beta \left| {\sigma _h } \right| \,,\ \ \bar {\varepsilon } = \dfrac{\left| {\varepsilon _h } \right|}{\beta }$ | (20) |
陈-卢本构模型需要通过单轴压缩和静水压缩的特征应变特征应力曲线确定应力势函数及其演化,还需要知道弹性泊松比$v^{el}$. 对于泡沫金属,发生大变形时忽略弹性变形,近似取$\varepsilon_ij \cong \varepsilon_ij^{pl} $,对数塑性体积应变
| $\varepsilon _h^{pl} = \varepsilon _h - \varepsilon _h^{el} = \varepsilon _h - \dfrac{3\sigma _h1 }{E}$ | (21) |
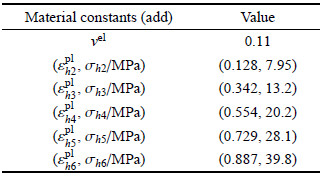
除了表3中列出的参数外,增加的屈服面参数根据三维细观有限元模型的计算结果得到,如表4所示. 表中,$(\varepsilon_hi^{pl},\sigma _hi )$,i = 2,3,4,5,6 为根据静水压缩应力应变曲线求得的对数塑性体积应变和对应的压强值.
| 表 4 闭孔泡沫铝的本构参数2 Table 4 Constitutive parameters for closed-cell aluminum foams (2) |
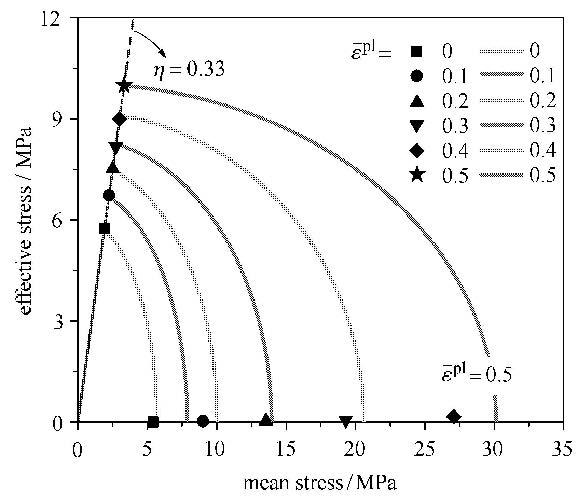
两个试件的应力势函数及其演化关系如图11所示,可以看到屈服面在平均应力-有效应力空间是以原点为中心的一系列椭圆,初始屈服面长、短轴长度近似相等,随着等效应变的增大,屈服面在横轴方向的扩张明显大于沿纵轴方向,这反映了闭孔泡沫铝试件在静水压缩时强化模量比单轴压时大的情况.可以看到,单轴压缩的结果吻合良好,而静水压缩时初始屈服点吻合良好,试件在特征塑性应变$\bar{\varepsilon}^{pl}$=0.4时,预测的静水压缩屈服应力和数值计算结果相比偏差超过20%,而且偏差都随着特征塑性应变的增大而增大.
|
图 11 陈-卢本构模型"屈服面"验证 Fig.11 "Yield surface" validation for the Chen Lu constitutive model |
需要说明的是,陈-卢本构模型需要根据式(19)和式(20)分别计算单轴压缩和静水压缩特征应变特征应力曲线.根据三维细观有限元模型计算得到的试件单轴压缩的最大特征应变$\bar{\varepsilon}_u,\max$ 和静水压缩的最大特征应变$\bar{\varepsilon}_h,\max$ ,可以发现两种加载边界下的最大特征应变相差很大,$\bar{\varepsilon}_h,\max /{\bar{\varepsilon}_u,\max }$=0.39,这导致单轴压缩的结果不能在本构模型中得到充分利用.虽然可以增加静水压缩的压缩量来提高$\bar{\varepsilon}_h,\max$ ,但如果要使得$\bar{\varepsilon}_u,\max =\bar{\varepsilon}_h,\max$ ,则得到$\varepsilon _h,\max ^{pl}=\dfrac{3\beta}{\sqrt{9+\beta^2}}\varepsilon _u,\max ^{pl}$.如果取$\varepsilon _u,\max ^{pl}=\varepsilon _u6^{pl}$,则试件在静水压缩时的最大塑性体积应变为2.25,闭孔泡沫铝在静水压缩实验中不可能达到如此大的体积应变.
4.5 体积强化本构模型屈服面| $\bar {\varepsilon }^{\,\rm pl} = \left| {\varepsilon _v>^{\,\rm pl} } \right|$ | (22) |
则特征塑性应变在单轴压缩为
| $\bar {\varepsilon }^{\,\rm pl} = \left( {1 - 2v^{pl}} \right)\left| {\varepsilon _u^{pl} } \right|$ | (23) |
在静水压缩时
| $\bar {\varepsilon }^{\,\rm pl} = \left| {\varepsilon _h^{pl} } \right|$ | (24) |
| $f = \sqrt {\sigma _e^2 + A\left( {\bar {\varepsilon }^{\,\rm pl}} \right)\sigma _m^2 } - B\left( {\bar {\varepsilon }^{\,\rm pl}} \right) = 0$ | (25) |
屈服面参数$A\left( {\bar {\varepsilon }^{\,\rm pl}} \right)$和$B\left( {\bar {\varepsilon }^{\,\rm pl}}\right)$分别为
| $A\left( {{{\bar \varepsilon }^{{\kern 1pt} {\text{pl}}}}} \right) = {\text{ }}\frac{{\sigma _h^2\left( {{{\bar \varepsilon }^{{\kern 1pt} {\text{pl}}}}} \right)}}{{\sigma _u^2\left( {{{\bar \varepsilon }^{{\kern 1pt} {\text{pl}}}}} \right) - \frac{1}{9}\sigma _u^2\left( {{{\bar \varepsilon }^{{\kern 1pt} {\text{pl}}}}} \right)}}$ | (26) |
| $B\left( {\bar {\varepsilon }^{\,\rm pl}} \right) = \sigma _h \left( {\bar {\varepsilon }^{\,\rm pl}} \right)\sqrt {\dfrac{\sigma _u^2 \left( {\bar {\varepsilon }^{\,\rm pl}} \right)}{\sigma _h^2 \left( {\bar {\varepsilon }^{\,\rm pl}} \right) - \dfrac{1}{9}\sigma _u^2 \left( {\bar {\varepsilon }^{\,\rm pl}} \right)}}$ | (27) |
其中,$\sigma _u \left( {\bar {\varepsilon }^{\,\rm pl}}\right)$为单轴压特征塑性应变轴向真实应力曲线;$\sigma _h \left( {\bar {\varepsilon }^{\,\rm pl}}\right)$为静水压缩特征塑性应变压强曲线.
4.6 体积强化本构模型屈服面的验证体积强化本构模型需要通过单轴压特征塑性应变轴向真实应力曲线和静水压缩塑性特征应变压强曲线确定初始屈服面和后继屈服面,在计算单轴压缩的特征塑性应变时还需要知道塑性泊松比$v^{pl}$. 在表3和表4给出的参数基础上,增加的参数如下:
| 表 5 闭孔泡沫铝的本构参数3 Table 5 Constitutive parameters for closed-cell aluminum foams (3) |
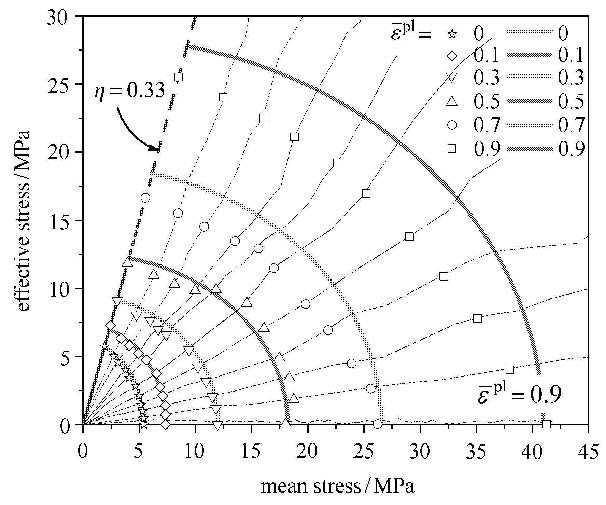
闭孔泡沫铝试件初始屈服面及其演化关系如图12所示,可以看到屈服面在平均应力-有效应力空间是以原点为中心的一系列椭圆,初始屈服面长、短轴长度近似相等,随着等效应变的增大,屈服面在横轴方向的扩张明显大于沿纵轴方向,这反映了闭孔泡沫铝试件在静水压缩时强化模量比单轴压时大很多的情况.图12中给出了根据三维细观有限元模型计算得到的不同特征塑性应变下不同加载路径时的屈服点,可以看到,静水压缩的结果吻合很好,单轴压缩和等比加载的屈服点在应变较小时吻合良好,在大应变时也都在屈服面附近,虽然有一些偏差,但注意到$\bar{\varepsilon }^{\,\rm pl}$ = 0.9时,对应的单轴压缩时的轴向对数应变为1.4,应变值已经很大了.同时也可以发现,单轴压缩的结果在体积强化本构模型中可以得到充分利用.
|
图 12 体积强化本构模型屈服面验证 Fig.12 Yield surface validation for the volumetric hardening model |
为了更清楚地展示3个屈服面对闭孔泡沫铝受压行为的描述能力,图13给出根据屈服面反求单轴压缩和静水压缩的应力应变曲线,横轴为塑性对数应变或体积应变.可以看到,对于单轴压缩,3个屈服面都有着很好的精度,对于静水压缩,有限元软件"ABAQUS"的可压缩泡沫本构模型屈服面会发生非常严重的偏离,陈-卢本构模型"屈服面"会略微低估静水压缩的屈服应力,而体积强化本构模型的屈服面有很好的精度.

|
图 13 反求的单轴压缩和静水压缩应力应变曲线 Fig.13 Uniaxial and hydrostatic compressive stress versus strain curves for closed-cell aluminum foams by reverse calculation |
本文通过逆向重建闭孔泡沫铝三维细观有限元模型定量研究闭孔泡沫铝在多轴压缩载荷作用下的大变形力学行为,通过侧面耦合单轴压缩、静水压缩和等比压缩3种边界条件实现闭孔泡沫铝试件11个加载路径的大变形压缩过程.得到了闭孔泡沫铝试件在不同加载路径下的轴向柯西应力对数应变曲线和压强对数体积应变曲线,给出了弹塑性泊松比随轴向对数应变的变化曲线.讨论了泡沫金属唯象弹塑性本构参数的确定方法,根据计算结果确定了3个有代表性的泡沫材料本构模型的本构参数,并验证了这些本构模型在描述多轴压缩应力状态下的精度.
各应力状态下闭孔泡沫铝试件的初始平台应力都基本重合,随着轴向应变的增大,泊松比经历了增高---降低---再增高的"S"型变化过程.随着加载比例系数的增大,轴向柯西应力对数应变曲线的强化模量增大很快.
对于单轴压缩,选择的3个屈服面都有着很好的精度;对于静水压缩,有限元软件"ABAQUS"的可压缩泡沫本构模型屈服面会发生非常严重的偏离,陈-卢本构模型"屈服面"会略微低估静水压缩的屈服应力,而体积强化本构模型的屈服面有着很好的精度.后续工作是编制材料用户子程序对体积强化本构模型进行进一步的验证.
| [1] | Daxner T. Plasticity of Cellular Metals (Foams)/Plasticity of Pressure-Sensitive Materials, Berlin Heidelberg: Springer, 2014: 153-204 |
| [2] | Shahbeyk S. Yield/Failure Criteria, Constitutive Models, and Crashworthiness Applications of Metal Foams, Metal Foams: Fundamentals and Applications. DEStech Publications, Inc; 1 edition.2012: 131-217 |
| [3] | Hallquist JO. LSTC. LS-DYNA user's manual. Livermore Software Technology Corporation, Livermore, CA, US. 2007 |
| [4] | Reyes A, Hopperstad OS, Berstad T. Constitutive modeling of aluminum foam including fracture and statistical variation of density. European Journal of Mechanics-A/Solids, 2003, 22: 815-835. |
| [5] | Reyes A, Hopperstad OS, Berstad T, et al. Implementation of a constitutive model for aluminum foam including fracture and statistical variation of density. In: Proc. of 8th International LS-DYNA Users Conference. 2004;Material Technology:11-24 |
| [6] | Reyes A, Hopperstad OS, Hanssen AG, et al. Modeling of material failure in foam-based components. International Journal of Impact Engineering, 2004, 30: 805-834. |
| [7] | Hanssen AG, Hopperstad OS, Langseth M, et al. Validation of constitutive models applicable to aluminium foams. International Journal of Mechanical Sciences, 2002, 44: 359-406. |
| [8] | ABAQUS User's Manual. Hibbitt, Karlsson & Sorensen, Inc 2005 |
| [9] | Deshpande VS, Fleck NA. Isotropic constitutive models for metallic foams. Journal of the Mechanics and Physics of Solids, 2000, 48: 1253-1283. |
| [10] | Miller RE. A continuum plasticity model for the constitutive and indentation behaviour of foamed metals. International Journal of Mechanical Sciences, 2000, 42: 729-754. |
| [11] | Chen C, Lu TJ. A phenomenological framework of constitutive modelling for incompressible and compressible elasto-plastic solids. International Journal of Solids and Structures, 2000, 37: 7769-7786. |
| [12] | Zhang J, Kikuchi N, Li V, et al. Constitutive modeling of polymeric foam material subjected to dynamic crash loading. International Journal of Impact Engineering, 1998, 21: 369-386. |
| [13] | Zhang J, Lin Z, Wong A, et al. Constitutive modeling and material characterization of polymeric foams. Journal of Engineering Materials and Technology-Transactions of the Asme, 1997, 119: 284-291. |
| [14] | Forest S, Blazy JS, Chastel Y, et al. Continuum modeling of strain localization phenomena in metallic foams. Journal of Materials Science, 2005, 40: 5903-5910. |
| [15] | Combaz E, Bacciarini C, Charvet R, et al. Yield surface of polyurethane and aluminium replicated foam. Acta Materialia, 2010, 58: 5168-5183. |
| [16] | Combaz E, Bacciarini C, Charvet R, et al. Multiaxial yield behaviour of Al replicated foam. Journal of the Mechanics and Physics of Solids, 2011, 59: 1777-1793. |
| [17] | Andrews E, Sanders W, Gibson LJ. Compressive and tensile behaviour of aluminum foams. Materials Science and Engineering A, 1999, 270: 113-124. |
| [18] | Gioux G, McCormack TM, Gibson LJ. Failure of aluminum foams under multiaxial loads. International Journal of Mechanical Sciences, 2000, 42: 1097-1117. |
| [19] | Doyoyo M, Wierzbicki T. Experimental studies on the yield behavior of ductile and brittle aluminum foams. International Journal of Plasticity, 2003, 19: 1195-1214. |
| [20] | Ruan D, Lu G, Ong LS, et al. Triaxial compression of aluminium foams. Composites Science and Technology, 2007, 67: 1218-1234. |
| [21] | Blazy JS, Marie-Louise A, Forest S, et al. Deformation and fracture of aluminium foams under proportional and non proportional multi-axial loading: statistical analysis and size effect. International Journal of Mechanical Sciences, 2004, 46: 217-244. |
| [22] | McCullough KYG, Fleck NA, Ashby MF. Uniaxial stress-strain behaviour of aluminium alloy foams. Acta Materialia, 1999, 47: 2323-2330. |
| [23] | Sridhar I, Fleck NA. The multiaxial yield behaviour of an aluminium alloy foam. Journal of Materials Science, 2005, 40: 4005-4008. |
| [24] | Peroni L, Avalle M, Peroni M. The mechanical behaviour of aluminium foam structures in different loading conditions. International Journal of Impact Engineering, 2008, 35: 644-658. |
| [25] | Avalle M, Lehmhus D, Peroni L, et al. AlSi7 metallic foams - aspects of material modelling for crash analysis. International Journal of Crashworthiness, 2009, 14: 269-285. |
| [26] | Lu TJ, Ong JM. Characterization of close-celled cellular aluminum alloys. Journal of Materials Science, 2001, 36: 2773-2786. |
| [27] | 冯勃. 多孔材料静水压多轴加载实验系统及其在泡沫铝多轴力学行为研究中的应用.[博士论文]. 西安: 西安交通大学, 2010 (Feng Bo. Hydrostatic multiaxial loading experiment system for porous materials and study on multiaxial mechanical behavior aluminum for aluminum foams.[PhD Thesis]. Xi'an: Xi'an Jiaotong University, 2010 (in Chinese)) |
| [28] | Zhou ZW, Wang ZH, Zhao LM, et al. Uniaxial and biaxial failure behaviors of aluminium alloy foams. Composites Part B: Engineering, 2014, 61: 340-349. |
| [29] | Zhou ZW, Wang ZH, Zhao LM. Loading rate effect on yield surface of aluminum alloy foams. Materials Science and Engineering A, 2012, 543: 193-199. |
| [30] | 王二恒, 虞吉林, 王飞等. 泡沫铝材料准静态本构关系的理论和实验研究. 力学学报, 2004, 36(6): 673-679 (Wang Erheng, Yu Jilin, Wang Fei, et al. A theoretical and experimental study on the quasi-static constitutive model of aluminum foams. Acta Mechanica Sinica, 2004, 36(6): 673-679 (in Chinese)) |
| [31] | Lachambre J, Maire E, Adrien J, et al. In situ observation of syntactic foams under hydrostatic pressure using X-ray tomography. Acta Materialia, 2013, 61: 4035-4043. |
| [32] | Jin MZ, Chen CQ, Lu TJ. The mechanical behavior of porous metal fiber sintered sheets. Journal of the Mechanics and Physics of Solids, 2013, 61: 161-174. |
| [33] | Alkhader M, Vural M. A plasticity model for pressure-dependent anisotropic cellular solids. International Journal of Plasticity, 2010, 26: 1591-1605. |
| [34] | Alkhader M, Vural M. An energy-based anisotropic yield criterion for cellular solids and validation by biaxial FE simulations. Journal of the Mechanics and Physics of Solids, 2009, 57: 871-890. |
| [35] | Alvarez P, Mendizabal A, Petite MM, et al. Finite element modelling of compressive mechanical behaviour of high and low density polymeric foams. Materialwissenschaft und Werkstofftechnik, 2009, 40: 126-132. |
| [36] | Yang CH, An Y, Tort M, et al. Fabrication, modelling and evaluation of microstructured materials in a digital framework. Computational Materials Science, 2014, 81: 89-97. |
| [37] | De Giorgi M, Carofalo A, Dattoma V, et al. Aluminium foams structural modelling Finite element analysis of closed-cell aluminium foam under quasi-static loading. Computers and Structures, 2010, 88: 5-35 |
| [38] | Roberts AP, Garboczi EJ. Elastic moduli of model random three-dimensional closed-cell cellular solids. Acta Materialia, 2001, 49: 189-197. |
| [39] | Song YZ, Wang ZH, Zhao LM, et al. Dynamic crushing behavior of 3D closed-cell foams based on Voronoi random model. Materials and Design, 2010, 31: 4281-4289. |
| [40] | Zheng ZJ, Liu YD, Yu JL, et al. Dynamic crushing of cellular materials: Continuum-based wave models for the transitional and shock modes. International Journal of Impact Engineering, 2012, 42: 66-79. |
| [41] | Liao SF, Zheng ZJ, Yu JL. Dynamic crushing of 2D cellular structures: Local strain field and shock wave velocity. International Journal of Impact Engineering, 2013, 57: 7-16. |
| [42] | Yang B, Tang LQ, Liu YP, et al. Localized deformation in aluminium foam during middle speed Hopkinson bar impact tests. Materials Science and Engineering A, 2013, 560: 734-743. |
| [43] | Zheng ZJ, Yu JL, Wang CF, et al. Dynamic crushing of cellular materials: A unified framework of plastic shock wave models. International Journal of Impact Engineering, 2013, 53: 29-43. |
| [44] | Wicklein M, Thoma K. Numerical investigations of the elastic and plastic behaviour of an open-cell aluminium foam. Materials Science and Engineering A, 2005, 397: 391-399. |
| [45] | Zhu XL, Ai SG, Lu XF, et al. Collapse models of aluminum foam sandwiches under static three-point bending based on 3D geometrical reconstruction. Computational Materials Science, 2014, 35: 38-45 |
| [46] | Huang M, Li YM. X-ray tomography image-based reconstruction of microstructural finite element mesh models for heterogeneous materials. Computational Materials Science, 2013, 67: 63-72. |
| [47] | Jeon I, Katou K, Sonoda T, et al. Cell wall mechanical properties of closed-cell Al foam. Mechanics of Materials, 2009, 41: 60-73. |
| [48] | Jeon I, Asahina T, Kang K-J, et al. Finite element simulation of the plastic collapse of closed-cell aluminum foams with X-ray computed tomography. Mechanics of Materials, 2010, 42: 227-236. |
| [49] | 张健. 泡沫金属的本构关系及吸能特性.[博士论文]. 西安:西安交通大学, 2013 (Zhang Jian, Constitutive modeland energy absorption capacity of metallic cellular materials.[PhD Thesis]. Xi'an: Xi'an Jiaotong University, 2013 (in Chinese)) |
| [50] | Zhang J, Zhao GP, Lu TJ, et al. Strain rate behavior of closed-cell Al-Si-Ti foams: experiment and numerical modeling. Mechanics of Advanced Materials and Structures, 2015, 22(7): 556-563. |
| [51] | Campana F, Pilone D. Effect of wall microstructure and morphometric parameters on the crush behaviour of Al alloy foams. Materials Science and Engineering A, 2008, 479: 58-64. |
| [52] | Hasan MA, Kim A, Lee HJ. Measuring the cell wall mechanical properties of Al-alloy foams using the nanoindentation method. Composite Structures, 2008, 83: 180-188. |
| [53] | Kim A, Tunvir K, Jeong GD, et al. A multi-cell FE-model for compressive behaviour analysis of heterogeneous Al-alloy foam. Modelling and Simulation in Materials Science and Engineering, 2006, 14: 933-945. |
| [54] | Kim A, Tunvir K. Study of Al-alloy foam compressive behavior based on instrumented sharp indentation technology. Journal of Mechanical Science and Technology, 2006, 20: 819-827. |
| [55] | Něček J, Kralik V, Vondrejc J. A two-scale micromechanical model for aluminium foam based on results from nanoindentation. Computers & Structures, 2013, 128: 136-145. |
| [56] | Jeon I, Asahina T. The effect of structural defects on the compressive behavior of closed-cell Al foam. Acta Materialia, 2005, 53: 3415-3423. |
| [57] | Hall IW, Guden M, Yu CJ, Crushing of aluminum closed cell foams: Density and strain rate effects. Scripta Materialia, 2000, 43: 515-521 |
| [58] | Li QM, Magkiriadies I, Harrigan JJ. Compressive strain at the onset of densification of cellular solids. Journal of Cellular Plastics, 2006, 42: 371-392. |
2. State key Laboratory for Strength and Vibration of Mechanical Structure,School of Aerospace,Xi'an Jiaotong University,Xi'an 710049,China;
3. MOE key Laboratory for Multifunctional Materials and Structures,Xi'an Jiaotong University,Xi'an 710049,China
 2015, Vol. 47
2015, Vol. 47