引言
自然条件下的岩体结构经过漫长的地质演化过程而处于天然的平衡状态,即预先存在平衡[1].剧烈的工程扰动,例如开挖、蓄水等,破坏了这种平衡使得扰动岩体出现与时间有关的应力和变形重分布过程,该过程可称为非平衡演化过程,将直接影响岩体工程结构正常运行、长期稳定和安全[2].例如,锦屏一级左岸高边坡长期蠕变,地下岩盐容腔收敛变形[3],金川矿区水平巷道变形破坏[2]以及南非某金矿交通隧洞洞壁大变形[4]等,均是工程实践中与时间有关的变形破坏现象.洞室开挖的新奥法施工原理(NATM)是岩体结构非平衡演化的最好例证[5],陈宗基就曾指出:"新奥法原理是一般流变结构演化规律甚至地球动力学演化规律在隧道工程背景下的缩影"[2].
稳定是岩石力学与工程研究的核心内容.目前工程结构的稳定性研究广泛采用极限分析有限元\linebreak法[6, 7],也有学者采用力学稳定分析方法,如能量法[8]、扰动能量法[9]等.杨强等提出的变形加固理论也在我国高拱坝、高边坡和地下能源储库等大型岩土工程结构中得到应用[5].但是这些分析方法均没有考虑岩体结构变形的时间效应,因此很难采用这类方法对结构时效力学响应和长期稳定性进行准确的分析和评价.
随着计算机技术和数值仿真计算的发展,越来越多的学者开始基于流变学和数值计算对岩体结构的时效变形和长期稳定性进行分析.根据计算采用的流变本构方程和数值分析方法的不同大致可分为5大类:黏弹性问题有限元法[10]、黏弹-塑性问题有限差分法[11]、黏塑性问题有限元法[12]、黏塑性问题有限差分法[4, 13]和黏塑性问题离散元法[14].长期稳定性评价方面,目前岩石工程普遍采用特征点的收敛性或者突变性、应力场分布、塑性区[15]、蠕变损伤区[16]、开挖损伤区[14]范围等指标进行评价,这些评价指标基本上是非定量的,相应地也缺乏严格、明确的稳定性判据.其主要原因在于大多数的数值计算采用的流变本构方程无法表征结构非平衡演化过程中的能量变化,也无法在此基础上进一步采用严格、成熟的稳定分析方法进行材料和结构的稳定性分析.
基于不可逆热力学理论建立的流变本构方程具有热力学的一致性,能将材料的内部状态和外部响应联系起来,能表征材料内部的不可逆能量耗散过程,具有深刻的热力学背景和严格的理论基础,因此越来越多的学者基于不可逆热力学构建流变本构方程[17, 18, 19, 20].
本文首先对考虑时效的变形加固理论及其核心的最小塑性余能原理进行了概述.在赖斯(Rice)不可逆内变量热力学理论框架下研究岩体结构非平衡演化问题,提出了岩体结构非平衡演化的有效应力原理,指出有效应力是总应力中驱动岩体结构非平衡演化的有效部分,并推导出了有效应力形式的非弹性应变本构方程和能量耗散率方程,提出非弹性余能的概念.同时构建考虑损伤的内变量黏塑性应变率方程,通过模型相似材料单轴加卸载蠕变试验结果验证方程的合理性,并采用内变量率形式和有效应力形式的方程分别计算黏塑性应变率,并对能量耗散率与非弹性余能进行了对比探讨.本文最后以深埋双洞为工程算例,采用能量耗散率域内积分及其时间导数分析和评价结构长期稳定性.
1 考虑时效的变形加固理论
传统的变形加固理论在数值上采用超出屈服面的残余不平衡节点力表征结构的非平衡状态[21, 22],这种基于弹塑性理论的静态失稳分析忽略了岩体结构变形的时间效应.为了克服上述缺点,杨强等基于迪沃-莱恩斯(Duvaut-Lions)黏塑性模型建立了考虑时效的变形加固理论[23].
1.1 迪沃-莱恩斯黏塑性模型
迪沃-莱恩斯模型采用率形式本构关系
|
$\dot \varepsilon = {\dot \varepsilon ^e} + {\dot \varepsilon ^{vp}},{\dot \varepsilon ^e} = C:\mathop \sigma \limits^. $
|
(1)
|
|
${\dot \varepsilon ^{vp}} = \frac{1}{\mu }C:(\sigma - \overline \sigma ){\mkern 1mu} ,\overline \sigma = \overline \sigma (\sigma )$
|
(2)
|
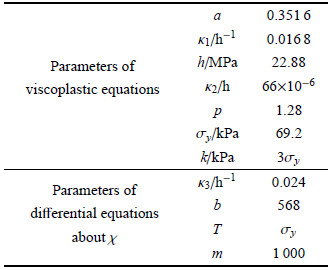
其中,${\dot \varepsilon ^e}$为弹性应变率,${\dot \varepsilon ^{vp}}$为黏塑性应变率,C为弹性柔度张量,$\mu$ 为黏滞系数,$\mu$ >0. $\overline \sigma $为$\sigma$在屈服面上的最近点投影,$\sigma - \overline \sigma $ 称为过应力,如
图1所示.
由方程(2)可知,过应力$\sigma - \overline \sigma $ 决定了黏塑性应变率的大小和方向,是黏塑性应变的驱动力,也是总应力中实际驱动材料发生时效变形的应力部分,类似于材料科学研究领域提的主动应力[24],但过应力的概念更具有广泛性.
1.2 最小塑性余能原理
考虑时效的变形加固理论定义了结构的塑性余能为
|
$E(\sigma ) = \frac{1}{2}\int {_V(\sigma - \bar \sigma ):C:(\sigma - \bar \sigma ){\text{ d}}V}$
|
(3)
|
其中
V为连续体所占体积.
研究结构演化规律必须固定外部边界,恒定的外部作用条件包括
|
$\dot g = 0{\mkern 1mu} ,in\;V{\mkern 1mu} ;\;\;\dot t = 0{\mkern 1mu} ,\;on\;{S_\sigma }{\mkern 1mu} ;\;\dot u = 0{\mkern 1mu} ,\;on\;{S_u}$
|
(4)
|
其中,
g表示体力,
t表示面力,
u表示位移,S$\sigma$为面力边界,S
u为位移边界. 根据式(3)和加卸载定理,可以得到下式
[5, 23]
|
${\smallint _V}\dot \sigma :{\dot \varepsilon ^{VP}}{\text{ d}}V{\text{ \& }}lt;0,{\smallint _V}\mathop {\bar \sigma }\limits^ \cdot :{\dot \varepsilon ^{VP}}{\text{d}}V \geqslant 0$
|
(5)
|
结合式(2)可得到塑性余能的时间导数
|
$E(\dot{\sigma })=\text{ }\int{_{{}}}(\dot{\sigma }-\dot{\bar{\sigma }}):{{\dot{\varepsilon }}^{VP}}\text{d}V<\text{0}$
|
(6)
|
式(6)表明:在恒定外部条件下,理想黏塑性结构始终朝向塑性余能减小的方向变形,直到塑性余能达到其最小值,此后塑性余能保持恒定,即最小塑性余能原理.
2 非平衡演化有效应力原理
2.1 岩体结构的非平衡演化规律
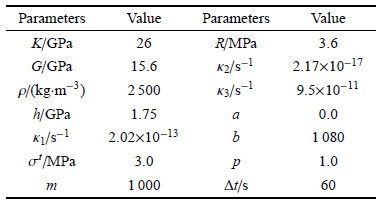
受外部载荷和环境长期作用的岩体,材料性质将不可避免的发生劣化.图2所示的新奥法施工原理表明,成洞后期损伤发展到一定程度时,围岩的完整性被破坏,自承能力降低,所需的支护力急剧增加.
新奥法施工原理虽然只是唯象的、定性的实用原理,却揭示了岩体结构非平衡演化的基本规律.岩体结构的非平衡演化其实是两种演化趋势的组合效应.一是材料硬化以及结构的自我调整能抵抗扰动使结构朝向平衡态演化,称之为自平衡演化趋势,该趋势可以通过最小余能原理表征.另外一种趋势是扰动和变形造成材料损伤发展,使结构背离平衡态演化,称为损伤演化趋势.虽然非平衡演化可以分解为两种演化趋势,但两者必定是相互耦合的.
由上述分析可知,时效变形和损伤发展是结构非平衡演化的核心,也是岩体工程结构长期稳定性研究无法回避的问题.
2.2 非平衡演化的有效应力
赖斯采用一组标量内变量表征材料内部的结构重排列,其演化率假设仅与同自身共轭的热力学力有关,且可以由一个广义流动势函数导出,即正则结构[25].在该理论框架下,表征材料硬化、损伤效应的岩体细观变量能以内变量的方式引入,以准确、全面地描述岩体在非平衡演化过程中的非弹性变形行为.
赖斯正则结构将非弹性应变率表示为[25]
|
${\varepsilon ^i} = \frac{{\partial {f_\alpha }(\sigma ,\theta ,\zeta )}}{{\partial \sigma }}{\dot \zeta _\alpha }$
|
(7)
|
其中,$\sigma $为应力张量;$\theta$ 为温度;$\zeta = ({\zeta _1},{\zeta _2} \cdots ,{\zeta _ > }n)$为内变量; ${f}=(f_1,f_2,\cdots ,f_n)$为与内变量$\zeta $共轭的热力学力,$\alpha$=1,2,$\cdots$,n.如果本文没有特别注明(如下式(12))或采用求和公式(如式(13)),方程中的重复下标将遵循爱因斯坦求和约定.由式(7)可知,非弹性应变率与内变量变化率直接相关,因此本文将式(7)称为内变量率形式的非弹性应变率方程.
内变量热力学理论中,如果内变量演化方程仅与同自身共轭的热力学有关,那么材料系统处于平衡状态的必要充分条件是[26]
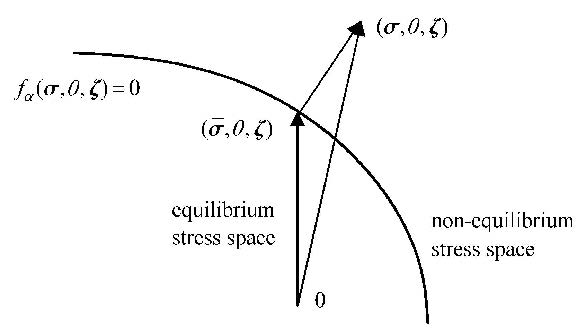
某一时刻某个共轭热力学力函数${f_\alpha }(\sigma ,\theta ,\zeta ) = 0$在应力空间(约束了内变量和温度的热力学状态子空间)中是一个空间曲面(本文称之为零值曲面),该曲面将应力空间划分为两个区域,$f_\alpha=0$曲面以内的可称为平衡应力空间,以外可称为非平衡应力空间,如图3所示.如果材料热力学状态($\sigma ,\theta ,\zeta $)处于平衡应力空间中,内变量不产生不可逆变化,材料始终处于平衡状态,表现出如弹性变形一类的力学行为;当($\sigma ,\theta ,\zeta $)落入非平衡应力空间中,热力学力f$\alpha$ 大于0,材料系统处于非平衡状态,并将发生不可逆的非弹性变形.
图3中的($\overline {(\sigma } ,\theta ,\zeta )$)是($\sigma ,\theta ,\zeta $)在零值曲面上的最 近点投影,可以将当前时刻的热力学力f$\alpha $在该投影点处展开
|
${f_\alpha }(\sigma ,\theta ,\zeta ) = {f_\alpha }(\bar \sigma ,\theta ,\zeta ) + {\left. {\frac{{\partial {f_\alpha }}}{{\partial \sigma }}} \right|_{\hat \sigma }}:(\sigma - \bar \sigma )$
|
(9)
|
其中${f_\alpha }(\bar \sigma ,\theta ,\zeta ) = 0{\text{;}}\hat \sigma $是$\bar {\sigma }$到${\sigma }$应力路径上的某一点. 如果$\hat {\sigma } ={\sigma }$,式(9)可简化为
|
$f_\alpha ({\sigma},\theta ,{\zeta }) ={Y}^\alpha :({\sigma} - \bar {\sigma })$
|
(10)
|
其中
|
${Y^\alpha }(\sigma ,\theta ,\zeta ) = \partial {f_\alpha }/\partial \sigma {|_\sigma }$
|
(11)
|
是表征方向的张量函数;热力学f
$\alpha$ 的大小由$\sigma {\text{ - }}\bar \sigma $ 控制.内变量热力学理论认为热力学力
f驱动内变量$\zeta $发生演化,使得材料内部表现出硬化、损伤特征,外部表现出与时间有关的非弹性变形,结构出现非平衡演化过程. 可见,控制热力学力大小的$\sigma {\text{ - }}\bar \sigma $是总应力$\sigma $中能够有效驱动材料和结构发生非平衡演化的部分,本文称之为有效应力.
有效应力是针对某一个共轭热力学力f$\alpha$ 而言,不同的热力学力对应不同的有效应力.
2.3 有效应力形式本构方程及非弹性余能
赖斯正则结构中,某内变量的演化率仅与同自身共轭的热力学力有关,内变量的运动方程可写为如下形式[27]
|
${\zeta _\alpha } = {\kappa ^\alpha }{L^\alpha }(\theta ,\zeta ){f_\alpha }(\alpha 不求和)$
|
(12)
|
其中,$\kappa ^\alpha$ 控制着内变量演化的快慢;L$\alpha$控制内变量在构型空间(约束了应力和温度的热力学状态子空间)中的演化路径. 结合式(7)、式(10)和式(12)得
|
$\begin{gathered}
{{\dot \varepsilon }_i}{j^i} = \sum\limits_{\alpha = 1}^n {{Y_i}{j^a}{\kappa ^\alpha }{L^\alpha }{Y_k}{l^a}({\sigma _k}l - {{\bar \sigma }_k}{l^a}) = } \hfill \\
\sum\limits_{\alpha = 1}^n {{\kappa ^\alpha }{L^\alpha }{R_i}jk{l^a}({\sigma _k}l - {{\bar \sigma }_k}{l^a}) = } \hfill \\
\sum\limits_{\alpha = 1}^n {{\kappa ^\alpha }{{\bar R}_i}jk{l^a}({\sigma _k}l - {{\bar \sigma }_k}{l^a})} \hfill \\
\end{gathered} $
|
(13)
|
其中,$\partial {f_\alpha }/\partial {\sigma _i}j = {Y_i}{j^\alpha }{\text{ ;}}{R_i}jk{l^a} = {Y_i}{j^a}{Y_k}{l^a}{\text{,}}{\bar R_i}jk{l^\alpha } = {L^\alpha }{R_i}jk{l^\alpha }{\text{ ,}}{\bar \sigma _k}{l^a}$为$\sigma _kl $在$ f_\alpha =0$上的最近点投影. 式(13)便是有效应力形式的非弹性应变率方程.与式(7)相比,有效应力形式的本构方程物理意义更加直观和明确.
忽略温度梯度条件下,材料系统的能量耗散率\varPhi 为
|
$\Phi = \theta \dot \eta = {f_\alpha }{\dot \zeta _\alpha }$
|
(14)
|
其中,$\eta$ 为熵增. 同样地,能量耗散率也可以表示为有效应力形式
|
$\Phi = {\text{ }}\sum\limits_{\alpha = 1}^n {{\kappa ^\alpha }({\sigma _i}j - {{\bar \sigma }_i}{j^a}){{\bar R}_i}jk{l^\alpha }({\sigma _k}l - {{\bar \sigma }_k}{l^a})} $
|
(15)
|
如果式(15)右面各项不考虑$\kappa^{\alpha }$值,稍加改造并在材料体积V内积分,得到
|
$\Omega = \frac{1}{2}\int {_V} \sum\limits_{\alpha = 1}^n {{\text{ }}(\sigma - {{\bar \sigma }^a}):{{\bar R}^\alpha }:(\sigma - {{\bar \sigma }^a})dV{\text{ }}} $
|
(16)
|
参考式(3)的塑性余能,$\Omega $可称为非弹性余能.非弹性余能是在内变量热力学理论框架下推导得到的,同时考虑硬化、损伤效应,比塑性余能更具 有一般性.
如果当n=1时,且共轭力f仅是应力${\sigma }$ 的函数,且如果有
|
$\kappa = \frac{1}{\mu }{\mkern 1mu} ,\;\;\;{\bar R_i}jkl = {C_i}jkl$
|
(17)
|
那么式(13)和式(16)将分别退化为迪沃-莱恩斯模型的黏塑性本构方程和塑性余能.
2.4 岩体结构非平衡演化及稳定性
赖斯正则结构中,内变量的演化率仅与同自身共轭的热力学力有关,且可以由一个广义流动势函数导出[25]
|
${\dot \zeta _a} = \frac{{\partial Q}}{{\partial {f_\alpha }}}/td>
|
(18)
|
其中
Q为流动势函数.
方程(12)遵从内变量演化的齐次运动率定律
|
${f_\beta }\frac{{\partial {{\dot \zeta }_\alpha }}}{{\partial {f_\beta }}} = q{\dot \zeta _\alpha }$
|
(19)
|
其中
q为方程阶数.
根据 式(14)、式(18)和式(19) 可得
|
$\Phi = \left( {1 + q} \right)Q$
|
(20)
|
因此能量耗散率的全域积分为
|
$L = {\text{ }}\int {_V} {\text{ }}\Phi {\text{d}}V = \left( {1 + q} \right)\int {_V} Q{\text{ d}}V = \left( {1 + q} \right){L_1}$
|
(21)
|
其中L
1为广义流动势函数的全域积分,冷旷代曾在赖斯内变量热力学理论框架下采用L
1作为李雅普诺夫函数,并据此深入分析了岩体结构的非平衡演化规律和长期稳定性
[5]. 式(21)表明L和L
1具有相同的数学性质,因此基于L
1对岩体结构的非平衡演化和长期稳定性分析方法和结论对L都是适用和成立的. 因此,能量耗散率及其时间导数的全域积分可以表征结构非平衡演化状态,分析结构长期稳定性问题.
3 本构方程
本节将在恒定应力和温度条件下讨论考虑硬化和损伤效应的蠕变问题. 蠕变过程中,与内变量演化有关的变形都可以称为非弹性变形,如黏性、黏弹性、黏塑性变形等,其中黏塑性变形直接影响岩体结构长期稳定,是岩体工程特别关心的时效变形,因此本节只讨论蠕变过程中黏塑性变形情况,若无特殊说明,本节的非弹性变形就是指黏塑性变形.
3.1 基本热力学方程
由方程(7)可知,要确定任意时刻的非弹性应变率,需要确定共轭热力学力和内变量演化率. 为此需要构建余能密度函数. 参考文献[28]中的吉布斯自由能密度函数,可以得到类似的余能密度函数表达式
|
$\psi = {\psi _e} + A\xi - \frac{1}{2}B{\xi ^2} + {P_\alpha }{\lambda _\alpha }\;(\alpha = 1,2)$
|
(22)
|
其中$\xi ,\lambda ({\lambda _1},{\lambda _2})$和\chi 为宏观内变量,$\xi$ 和$\lambda $分别用于描述在黏弹性和黏塑性变形过程中材料的内部结构调整,$\chi $用于描述引起损伤效应的结构变化;$\psi_e$,A,B和P (P
1,P
2)均可以是$\sigma ,\theta $和$\chi$ 的函数.假设在初始状态下,材料处于热力学平衡态,即在t=0时刻,$\sigma = 0,\zeta (\xi ,{\lambda _1},{\lambda _2},\chi ) = 0,\theta = {\theta _T}.$
|
$\varepsilon \left( {\sigma ,\theta ,\zeta } \right) = \frac{{\partial \psi }}{{\partial \sigma }} = \frac{{\partial {\psi _e}}}{{\partial \sigma }} + \frac{{\partial A}}{{\partial \sigma }}\xi + \frac{{\partial {P_\alpha }}}{{\partial \sigma }}{\lambda _\alpha }$
|
(23)
|
式(23)后面第一项表示弹性变形,它只与应力和温度有关;第二项可以视为黏弹性变形,其对蠕变本构方程的影响可参考文献
[29],本节仅考虑蠕变过程中的黏塑性变形项
|
${\varepsilon }^i\left( {{\sigma} ,\theta ,\zeta } \right) = \dfrac{\partial P_\alpha }{\partial {\sigma} }\lambda _\alpha$
|
(24)
|
与内变量$\lambda $和$\chi$ 共轭的热力学力为
|
$f_\alpha ^p = \frac{{\partial \psi }}{{\partial {\lambda _\alpha }}} = {P_\alpha }$
|
(25a)
|
|
${f_s} = \frac{{\partial \psi }}{{\partial \chi }} = \frac{{\partial {P_\alpha }}}{{\partial \chi }}{\lambda _\alpha }$
|
(25b)
|
非弹性应变率为
|
$\dot {\varepsilon }^{i} = \dfrac{\partial f^p_\alpha }{\partial {\sigma} }\dot
{\lambda }_\alpha + \dfrac{\partial f_s }{\partial {\sigma }}\dot {\chi } =
\dfrac{\partial P_\alpha }{\partial {\sigma} }\dot {\lambda }_\alpha +
\dfrac{\partial }{\partial {\sigma }} \Big (\dfrac{\partial P_\alpha }{\partial \chi }\lambda _\alpha \Big)\dot {\chi }$
|
(26)
|
参考文献
[20, 28],假设各内变量演化率为
|
$\dot {\lambda }_1 = \kappa _1 a_1 f^{p}_1$
|
(27a)
|
|
$\dot {\lambda }_1 = \kappa _1 a_1 f^{p}_1$
|
(27b)
|
|
$\dot {\chi } = \kappa _3 \lambda _2 \exp(m\chi )\left( {\dfrac{f_s }{T}} \right)^n$
|
(27c)
|
其中 $\kappa$
1,$\kappa$
2,$\kappa$
3,m和n均为材料参数;T是类似阻应力的参数;为了保证与式(12)一致,特别地n=1;a
1和a
2可视为平衡等式左右两边的量纲的参数,本文均设其为1.0Pa
-1.
3.2 非弹性应变率方程
假设共轭力P1和P2的具体形式如下
|
$f_1^p = {P_1} = a{I_1} + \sqrt {{J_2}} - h{\lambda _1}$
|
(28a)
|
|
$f_2^p = {P_2} = k\left( {1 + b\chi } \right){\left( {\frac{{\sqrt {{J_2}} - R}}{R}} \right)^p}$
|
(28b)
|
根据式(25b)可以得到
|
$f_s = kb\lambda _2 \left( {\dfrac{\sqrt {J_2 } - R}{R}} \right)^p$
|
(28c)
|
其中
|
$I_1 = \sigma _kk ,\ \ J_2 = \dfrac{1}{2}s_ij s_ij ,\ \ s_ij =
\sigma _ij - \dfrac{1}{3}\sigma _kk \delta _ij$
|
(28d)
|
a,h,b,k,p和
R均为材料常数;根据式(26) \sim式(28)便得到非弹性应变率本构方程
|
$dot \varepsilon _i^ij = (a{\delta _i}j + \frac{{{s_i}j}}{{2\sqrt {{J_2}} }}){\dot \lambda _1} + \frac{{pk\left( {1 + b\chi } \right)}}{R}{\left( {\frac{{\sqrt {{J_2}} - R}}{R}} \right)^{p - 1}} \cdot {\text{ }}\frac{{{s_i}j}}{{2\sqrt {{J_2}} }}{\dot \lambda _2} + \frac{{pkb{\lambda _2}}}{R}{\left( {\frac{{\sqrt {{J_2}} - R}}{R}} \right)^{p - 1}}\frac{{{s_i}j}}{{2\sqrt {{J_2}} }}\dot \chi {\text{ }}$
|
(29a)
|
|
${\dot \lambda _1} = {\kappa _1}{a_1}\left( {a{I_1} + \sqrt {{J_2}} - h{\lambda _1}} \right)$
|
(29b)
|
|
$\dot {\lambda }_2 = \kappa _2 a_2 \left[{k\left( {1 + b\chi } \right)\left(
{\dfrac{\sqrt {J_2 } - R}{R}} \right)^p} \right]$
|
(29c)
|
|
$\dot \chi = \frac{{{\kappa _3}{\lambda _2}\exp (m\chi )}}{T}\left[{kb{\lambda _2}{{\left( {\frac{{\sqrt {{J_2}} - R}}{R}} \right)}^p}} \right]$
|
(29d)
|
式(29)便是恒定温度和应力条件下的,基于内变量热力学理论的蠕变本构方程,如果已知材料参数和当前的应力状态,根据(29)式变可以求得非弹性应变率.
规定单轴受压为负,在单轴受压条件下轴力方向非弹性应变率为
|
$\begin{gathered}
\dot \varepsilon _1^i1 = (a - \frac{1}{{\sqrt 3 }}){{\dot \lambda }_1} - \frac{{pk\left( {1 + b\chi } \right)}}{{\sqrt 3 {\sigma _y}}}{\left( {\frac{{\left| \sigma \right|/\sqrt 3 - {\sigma _y}}}{{{\sigma _y}}}} \right)^{p - 1}} \cdot \hfill \\
{{\dot \lambda }_2} - \frac{{pkb{\lambda _2}}}{{\sqrt 3 {\sigma _y}}}{\left( {\frac{{\left| \sigma \right|/\sqrt 3 - {\sigma _y}}}{{{\sigma _y}}}} \right)^{p - 1}}\dot \chi \hfill \\
\end{gathered}$
|
(30a)
|
|
$\dot {\lambda }_1 = \kappa _1 a_1 \left( {a\sigma + \left| \sigma \right| / \sqrt 3 - h\lambda
_1 } \right)$
|
(30b)
|
|
$\dot {\lambda }_2 = \kappa _2 a_2 \left[{k\left( {1 + b\chi } \right)\left( {\dfrac{\left|
\sigma \right| / \sqrt 3 - \sigma _y }{\sigma _y }} \right)^p} \right]$
|
(30c)
|
|
$\dot {\chi } = \dfrac{\kappa _3 \lambda _2 \exp(m\chi )}{\sigma _y }\left[{kb\lambda _2
\left( {\dfrac{\left| \sigma \right| / \sqrt 3 - \sigma _y }{\sigma _y }} \right)^p} \right]$
|
(30d)
|
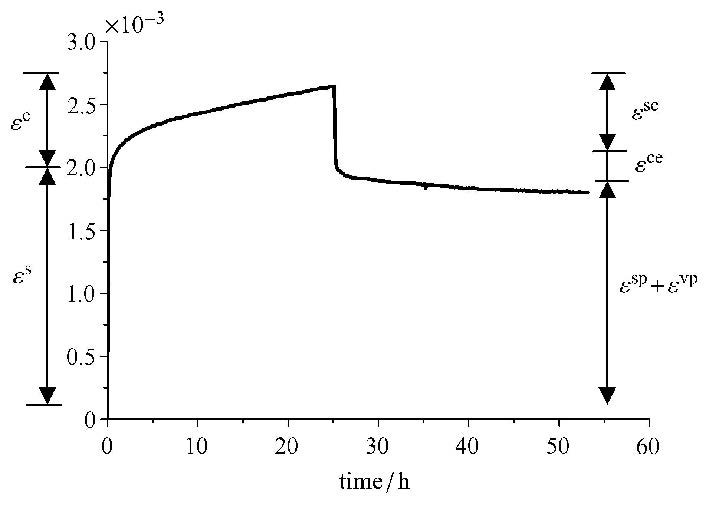
式(30)便是一维形式轴向非弹性应变本构方程,式中假定了T=R.本文对由重晶石粉、膨润土和胶水组成的模型 试验相似材料[30]制成的试件开展单轴蠕变加卸载试验.加载后载荷保持恒定一段时间后再卸载,并测量卸载后的试件随时间变化的变形.图4为一条典型的单轴加卸载蠕变试验全曲线,通过该曲线可以将加载过程中总应变$\varepsilon$分解为瞬时应变$\varepsilon ^{s}$和蠕变应变$\varepsilon^{c}$[31],瞬时应变可分为瞬时弹性应变$\varepsilon ^{se}$和瞬时塑性应变$\varepsilon ^{sp}$,蠕变应变又可分解为黏弹性应变 $\varepsilon^{ce}$和黏塑性应变$\varepsilon^{cp}$.本文主要采用试验得到的黏塑性应变对数据对式(30)中参数进行辨识,辨识的方法和步骤可参考文献[29],参数辨识结果如表1所示.
表 1(Table 1)

表 1 本构方程基本参数Table 1 The fundamental parameters
|
表 1 本构方程基本参数
Table 1 The fundamental parameters |
因为单轴试验数据有限,上述拟合过程中根据各参数的作用和特点做了相应假设,例如k=3$\sigma$y,m=1 000,T=$\sigma$y.
图5为采用表1中的材料参数计算的单轴360 kPa压应力水平的蠕变理论曲线和试验曲线比较图. 理论曲线和试验曲线吻合较好,说明内变量蠕变本构方程能很好地模拟材料蠕变全过程.为了得到蠕变全曲线,无法进行卸载试验将黏弹性应变从蠕变应变中分离[31],因此图5中试验曲线为蠕变全曲线,必然包含黏弹性变形,计算理论曲线时也考虑了黏弹性变形,计算黏弹性变形的黏弹性内变量本构方程和相关试验数据可参考文献[29].
式(30)也可改写成有效应力形式的一维非弹性应变本构方程
|
$\begin{gathered}
\dot \varepsilon _1^i1 = {\kappa _1}{a_1}(a - \frac{1}{{\sqrt 3 }})(a{\delta _k}l + \frac{{{s_k}l}}{{2\sqrt {{J_2}} }})({\sigma _k}l - {{\bar \sigma }_k}{l^1}) \hfill \\
- {\kappa _2}M\left[{\frac{{{s_i}j}}{{2\sqrt {{J_2}} }}({\sigma _i}j - {{\bar \sigma }_i}{j^2})} \right] - \hfill \\
{\kappa _3}N\left[{\frac{{{s_m}n}}{{2\sqrt {{J_2}} }}({\sigma _m}n - {{\bar \sigma }_m}{n^3})} \right] \hfill \\
\end{gathered} $
|
(31a)
|
其中
|
$M = \sqrt 3 a_2 \left[{\dfrac{pk\left( {1 + b\chi } \right)}{\sqrt 3 \sigma
_y }\left( {\dfrac{\left| \sigma \right| / \sqrt 3 - \sigma _y }{\sigma _y }}
\right)^{p - 1}} \right]^2$
|
(31b)
|
|
$N = \sqrt 3 \frac{{{\lambda _2}\exp (m\chi )}}{{{\sigma _y}}}{\left[{\frac{{pkb{\lambda _2}}}{{\sqrt 3 {\sigma _y}}}{{\left( {\frac{{\sigma /\sqrt 3 - {\sigma _y}}}{{{\sigma _y}}}} \right)}^{p - 1}}} \right]^2}$
|
(31c)
|
${\bar \sigma _k}{l^1},{\bar \sigma _i}{j^2}$和$\bar {\sigma }_mn^3$分别是当前应力状态在$f_1^{p}=0,f_2^{p}=0$和$f_s=0$零值曲面上的投影.
图6为根据拟合的材料参数通过式(30)和式(31)计算得到在单轴压应力320 kPa条件下的非弹性应变速率曲线比较图.可见在蠕变第一和第二阶段两种本构方程的计算得到蠕变率相差不大,在进入加速蠕变阶段过后差值逐渐扩大.
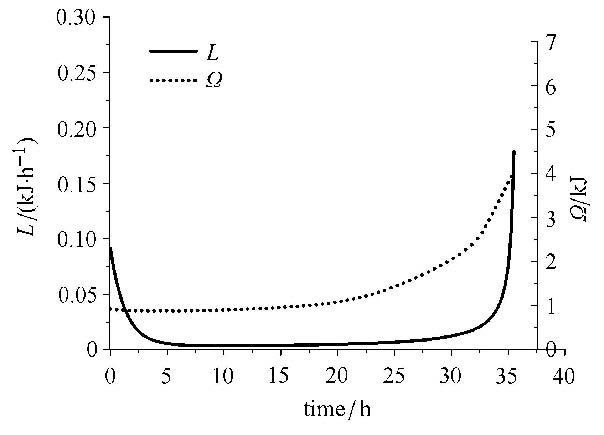
图7为单位体积内的能量耗散率积分L与非弹性余能Ω随时间关系变化图.
3.3 讨论
与率形式的本构方程相比,有效应力形式更加直观,物理意义也更加明晰,但是需要在求解内变量演化率方程的基础上求解当前应力状态在零值曲面上的最近点投影. 对于一些简单热力学力方程,最近点投影具有解析解[22],因此不会额外增加大量计算量;而对于复杂形式的共轭力曲线,只有通过数值求解得到投影点,计算量将剧烈增加.
同时为了简化计算,式(12)中$\hat {\sigma }$一般取为当前应力状态$\sigma$ ,这种处理将产生理论误差. 由图6可知,在蠕变初期,两种本构方程得到的蠕变率几乎相同,而在蠕变后期相差逐渐变大,这是因为不断增加的内变量值将理论误差放大的结果.
能量耗散率全域积分L可以表征结构当前非平衡状态离平衡状态的距离,可以刻画蠕变中结构非平衡演化全过程. 因此恒定大于0的标量值L可用于判定结构长期稳定性的评价指标. 作为塑性余能概念的推广,非弹性余能同样可用于结构长期稳定性分析和评价. 从图7可知,在蠕变过程中能量耗散率全域积分L与非弹性余能$\Omega $具有随时间相同的变化的趋势,不过L的变化更加剧烈且更加明显. $\Omega $实际是热力学力的乘积,表征了驱动结构非平衡演化的内在潜力;而L考虑了表征内变量演化快慢的物理量$\kappa^{\alpha }$,实际表征结构非平衡演化效果. 因为各个$\kappa^{\alpha }$的量值相差极大,所以使得即使是两个相同大小驱动力,但可表现出不同的演化效果.
此外,采用能量耗散率全域积分作为长期稳定性评价指标,还能采用李雅普诺夫稳定性理论进行分析,得到明确的稳定性判据[5]. 因此,能量耗散率全域积分值更适合用于评价结构的长期稳定性.
能量耗散率越大的部位越不稳定,越容易发生局部破坏,因此需要进行加固控制. 根据有效应力得到类似变形加固理论中不平衡力[12],从而获得精确到节点的最优加固力,指导加固设计. 这便是有效应力研究的工程意义,相关研究还需要继续开展.
4 算例分析
本小节将对深埋双隧洞进行计算并对其长期稳定性进行分析. 首先将提出的流变本构方程程序实现,通过FLAC3D软件 二次开发程序接口编译用户自定义计算模型,结构计算时主程序将调用该自定义模型进行计算.
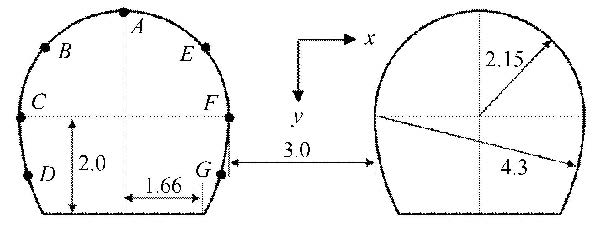
深埋双隧洞由两条平行隧洞组成,隧洞最近距离为3.0 m,顶部以上埋深700 m,隧洞截面呈马蹄形,平面几何尺寸如图8所示. 计算时在网格顶部施加16.53 MPa的均匀应力以模拟覆盖岩体自重,网格其余表面均施加法向约束.计算参数见表2.
表 2(Table 2)

表 2 计算参数Table 2 Calculated parameters of model
|
表 2 计算参数
Table 2 Calculated parameters of model |
表2中K和G为弹性体积模量和弹性剪切模型;$\rho$ 为岩石密度,$\sigma^{t}$为岩石抗拉强度,$\Delta $为时间步长,且令式(28b)中k=R.
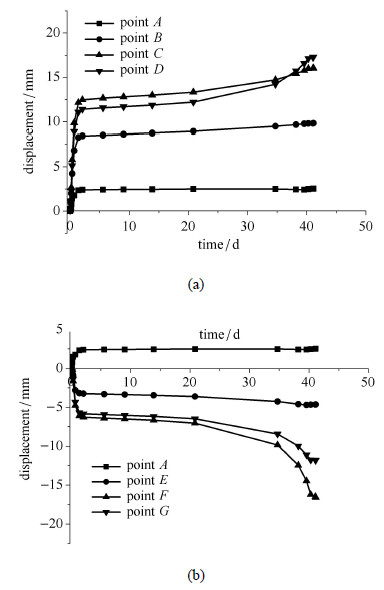
图9是隧洞特征点(如图8所示)在x方向位移随时间的变化曲线.
由图9可知,各位移-时间曲线的变化趋势不尽相同,因此很难通过不同测点的时效变形判定结构是局部破坏还是将整体失稳,这实际暗示了采用位移(场)对结构长期稳定性评价的不足.
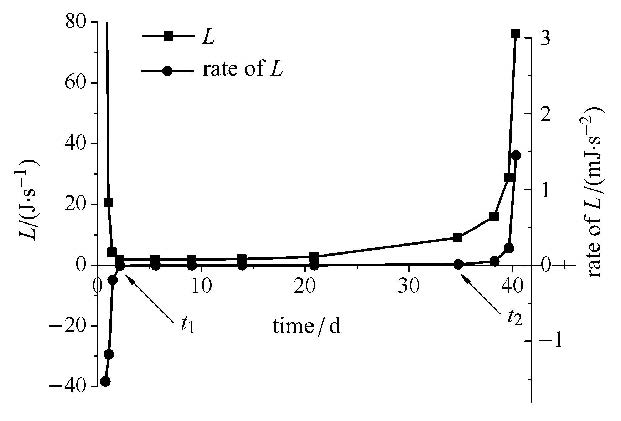
图10为能量耗散率域积分及其时间导数随时间的变化曲线,隧洞整体的非平衡演化过程和状态可以通过L-t 和 $\dot L - t$ 曲线进行评估. 长期稳定性判定准则很简单,如果L > 0 且 $\dot {L}$ < 0,结构趋于平衡状态;当L >0且$\dot {L}$ = 0表明结构处于稳定演化状态; 当L > 0且$\dot {L}$ >0表明结构状态背离平衡态演化,结构趋于失稳.
由图可知,初始的L值和$\dot {L}$较大,并随时间迅速趋近于0;从2.08 d (图10中所示t1时刻)起,$\dot {L}$的数量级为10-6,数量级极小,量值为负,可近似等于0.可以认为开挖后2.08 d以内,结构趋于平衡态,是渐进稳定的. t1至t2(约为34.7 d)时间段内,L几乎保持不变(在4.21~9.03 J/s范围内变化),$\dot {L}$的值有负有正,量级小于10-6;该时段内结构处于恒定演化阶段,保持动态稳定.从t2时刻开始,L和$\dot {L}$明显增加,即开挖34.7 d以后深埋双隧洞开始背离平衡态演化,结构趋于整体失稳.
5 结论
本文提出了结构非平衡演化的有效应力原理,指出有效应力是总应力中能够有效驱动结构非平衡演化的部分,而非弹性应变率和能量耗散率均可以表示为有效应力的形式.提出的非弹性余能可视为变形加固理论中塑性余能的推广,与能量耗散率的全域积分一样可以表征结构的非平衡状态.非平衡演化有效应力研究的工程意义在于可以得到类似变形加固理论中不平衡力,并用于指导加固设计.
通过给定具体的余能密度函数和内变量演化方程,得到了考虑损伤的蠕变本构方程. 蠕变本构方程可以写为内变量率形式和有效应力的形式,因为理论误差两者计算的非弹性应变率在蠕变后期相差较大. 非弹性余能和能量耗散率全域积分别从驱动结构非平衡演化的内在潜力的角度和实际演化效果的角度表征结构的非平衡状态,后者更适合作为长期稳定性评价指标.
参考文献
| [1] |
Fakhimi AA. Fairhurst C. A model for the time-dependent behavior of rock. Int. J. Rock Mech. Min. Sci. & Geomech. Abstr., 1994, 31: 117-126
|
| [2] |
陈宗基. 根据流变学与地球动力学观点研究新奥法. 岩石力学与工程学报, 1988, 7(2):97-106 (Tan Tjong Kie. The NATM studied from the viewpoint of rheology and geodynamics. Chinese Journal of Rock Mechanics and Engineering, 1988, 7(2):97-106 (in Chinese))
|
| [3] |
周宏伟, 王春萍, 丁靖洋等. 盐岩流变特性及盐腔长期稳定性研究进展. 力学与实践, 2011, 33(5):1-7 (Zhou Hongwei, Wang Chunping, Ding Jingyang, et al. Developments in researches on time-dependent behavior of salt rock and long-term stability. Mechanics in Engineering, 2011, 33(5):1-7(in Chinese))
|
| [4] |
Malan DF. Simulating the time-dependent behavior of excavation in hard rock. Rock Mechanics and Rock Engineering, 2002, 35: 225-254.
|
| [5] |
冷旷代. 岩体结构非平衡演化稳定与控制理论基础研究.[博士论文]. 北京: 清华大学, 2013 (Leng Kuangdai. Research on the fundamental of stability and control of non-equilibirum evolution of rock mass structures.[PhD Thesis]. Beijing: Tsinghua University, 2013 (in Chinese))
|
| [6] |
郑颖人, 赵尚毅. 岩土工程极限分析有限元法及其应用. 土木工程学报, 2005, 38(1):91-98 (Zheng Yingren, Zhao Shangyi. Limit state finite element method for geotechnical engineering and its application. China Civil Engineering Journal, 2005, 38(1):91-98 (in Chinese))
|
| [7] |
郑宏, 李春光, 李焯芬等. 求解安全系数的有限元法. 岩土工程学报, 2002, 24(5): 626-628 (Zheng Hong, Li Chunguang, Li Zhuofen, et al. Finite element method for solving the factor of safety. Chinese Journal of Geotechnical Engineering, 2002, 24(5):626-628 (in Chinese))
|
| [8] |
蔡美峰, 孔广亚, 贾立宏. 岩体工程系统失稳的能量突变判断准则及其应用. 北京科技大学学报, 1997, 19(4):325-328 (Cai Meifeng, Kong Guangya, Jia Lihong. Criterion of energy catastrophe for rock project system failure in underground engineering. Journal of University of Science and Technology Beijing, 1997, 19(4):325-328 (in Chinese))
|
| [9] |
邵国建, 卓家寿, 章青. 岩体稳定性分析与评判准则研究. 岩石力学与工程学报, 2003, 22(5):691-696 (Shao Guojian, Zhuo Jiashou, Zhang Qing. Research on analysis method and criterion of rockmass stability. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(5):691-696 (in Chinese))
|
| [10] |
陈卫忠, 朱维申, 李术才. 节理岩体断裂损伤耦合的流变模型及应用. 水利学报, 1999, 12:33-37 (Chen Weizhong, Zhu Weishen, Li Shucai. Rheology and fracture damage coupled model for rock mass and its application. Journal of Hydraulic Engineering, 1999, 12:33-37 (in Chinese))
|
| [11] |
熊良宵, 杨林徳, 张尧. 硬岩的复合粘弹塑性流变模型. 中南大学学报(自然科学版), 2010, 41(4):1540-1548 (Xiong Liangxiao, Yang Linde, Zhang Yao. Composite viscoelasto-plastic rheological model for hard rock. Journal of Central South University (Science and Technologym ), 2010, 41(4):1540-1548 (in Chinese))
|
| [12] |
Deng JQ, Yang Q, Liu YR. Time-dependent behavior and stability evaluation of gas storage caverns in salt rock based on deformation reinforcement theory. Tunnelling and Underground Space Technology, 2014, 42: 277-292.
|
| [13] |
刘建华, 朱维申, 李术才等. 小浪底水利枢纽地下厂房岩体流变与稳定性FLACm 3D数值分析. 岩石力学与工程学报, 2005, 24(14):2484-2489 (Liu Jianhua, Zhu Weishen, Li Shucai, et al. Analysis of rheological characteristics and stability of surrounding rock mass of Xiaolangdi hydrojunction underground caverns by using FLACm 3D. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14):2484-2489 (in Chinese))
|
| [14] |
Masoud G, Mostafa S. Long term stability assessment of Siah Bisheh powerhouse cavern based on displacement back analysis method. Tunnelling and Underground Space Technology, 2009, 24: 574-583.
|
| [15] |
张梅花, 高谦, 翟淑花. 高地应力围岩流变特性及竖井长期稳定性分析. 力学学报, 2010, 42(3):474-481 (Zhang Meihua, Gao Qian, Zhai Shuhua. Study on creep properties of rock and long-time stability of shaft in high ground stress zone. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(3):474-481 (in Chinese))
|
| [16] |
陈卫忠, 伍国军, 戴永浩等. 废弃盐穴地下储气库稳定性研究. 岩石力学与工程学报, 2006, 25(4):848-854 (Chen Weizhong, Wu Guojun, Dai Yonghao, et al. Stability analysis of abandoned salt caverns used for underground gas storage. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(4):848-854 (in Chinese))
|
| [17] |
Park SW, Richard Kim Y, Schapery RA. viscoelastic continuum damage model and its application to uniaxial behavior of asphalt concrete. Mechanics of Materials, 1996, 24: 241-255.
|
| [18] |
Chaboche JL. Thermodynamic formulation of application to the viscoplasticity and viscoelasticity of metal and polymers. International Journal of Solids and Structure, 1997, 34: 2239-2254.
|
| [19] |
Voyiadis GZ, Shojaei A, Li GQ. A thermodynamic consistent damage and healing model for self healing materials. International Journal of Plasticity, 2011, 27: 1025-1044.
|
| [20] |
Zhu HR, Sun L. A viscoelastic-viscoplastic damage constitutive model for asphalt mixtures based on thermodynamics. International Journal of Plasticity, 2013, 40: 81-100.
|
| [21] |
Yang Q, Liu YR, Chen YR, et al. Deformation reinforcement theory and its application to high arch dam. Science in China Series E: Technological and Sciences, 2008, 51(Supp I): 32-47
|
| [22] |
杨强, 刘耀儒, 陈英儒等. 变形加固理论及高拱坝整体稳定与加固分析. 岩石力学与工程学报, 2008, 27(6):1121-1136 (Yang Qiang, Liu Yaoru, Chen Yingru, et al. Deformation reinforcement theory and global stability and reinforcement of high arch dams. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(6):1121-1136 (in Chinese))
|
| [23] |
Yang Q, Leng KD. Chang Q, et al. Failure Mechanism and Control of Geotechnical Structures. In: Proceedings of the 2nd International Symposium on Constitutive Modeling of Geomaterials - Advances and New Applications, Beijing, China, 2012, 63-87
|
| [24] |
Evans WJ, Harrison GF. The development of universal equation for secondary creep rates in pure metals and engineering alloys. Metal Science, 1976, 10(9): 307-313.
|
| [25] |
Rice JR. Inelastic constitutive relation for solids: an internal- variable theory and its application to metal plasticity. Journal of Mechanics and Physics of Solids, 1971, 19: 433-455.
|
| [26] |
Yang Q, Liu YR, Feng XQ, et al. Time-independent plasticity related to critical point of free energy function and functional. Journal of Engineering Materials and Technology, 2014, 136: 0210011-2010019
|
| [27] |
Fischer FD, Svoboda J, Petryk H. Thermodynamic extremal principle for irreversible processes in material science. Acta Material, 2014, 67: 1-20.
|
| [28] |
Schapery RA. Nonlinear viscoelastic and viscoplastic constitutive equations with growing damage. International Journal of Fracture, 1999, 97: 33-66.
|
| [29] |
张泷, 刘耀儒, 杨强等. 考虑损伤的内变量黏弹-黏塑性本构方程. 力学学报, 2014, 46(4): 572-581 (Zhang Long, Liu Yaoru, Yang Qiang, et al. An internal state variable viscoelastic-viscoplastic constitutive equation with damage. Chinese Journal of Theoretical and applied mechanics, 2014, 46(4): 572-581 (in Chinese))
|
| [30] |
Zhang L, Liu YR, Yang Q. Evaluation of reinforcement and analysis of stability of high arch dam based on gaomechanical model testing. Rock Mechanics and Rock Engineering, 2015, 48(2): 803-818.
|
| [31] |
Li YS, Xia CC. Time-dependent tests on intact rocks in uniaxial compression. International Journal of Rock Mechanics and Mining Science, 2000, 37: 467-475.
|
EFFECTIVE STRESS PRINCIPLE OF NON-EQUILIBRIUM EVOLUTION AND LONG TERM STABILITY ANALYSIS OF ROCK MASS STRUCTURE
Zhang Long , Liu Yaoru, Yang Qiang
, Liu Yaoru, Yang Qiang
State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 100084, China
Fund: The project was supported by the National Natural Science Foundation of China (11172150,51279086),State Key Laboratory of Hydroscience and Engineering (2013-KY-2),and program for New Century Excellent Talents in University (NCET-13-0323).
Abstract: After excavation, the disturbed natural rock mass tends to be in non-equilibrium evolution state and affects the safety and stability of engineering structure. The time-dependent deformation and damage evolution are the cores of the non-equilibrium evolution process of rock mass structure. In this paper, the effective stress principle of non-equilibrium evolution is proposed within thermodynamics with internal state variables. The effective stress, which can really derive non-equilibrium evolution process, is only a portion of total stress. The rate of inelastic strain and energy dissipation rate can be expressed in form of effective stress, and concept of inelastic complementary energy is proposed. A creep constitutive equation with damage is derived through giving specific complementary energy density function and evolution function of internal state variables. Parameters identification of degraded one-dimension equation is conducted under one dimensional scene through uniaxial creep test of analogue material by load and unload method. Viscoplastic strain rate, rate of energy dissipation and inelastic complementary energy can be calculated, and the comparative discussion is illustrated. The results indicate that the difference between rates of inelastic strain is minor in primary and secondary creep stages but is major in tertiary stage because of theoretical error. The integral value of rate of energy dissipation in domain and inelastic complementary energy can characterize the non-equilibrium process of structure in actual effect and driving potential perspective respectively, and the latter is a more applicable one to assess the long-term stability of structure. At last, a case about deep buried tunnels is shown and its long-term stability is studied.
Key words:
effective stress thermodynamics with internal state Variable inelastic complementary energy energy dissipation rate long-term stability



 2015, Vol. 47
2015, Vol. 47