引言

沙纹广泛存在于河流、海洋和沙漠环境中，对泥沙输运、流动阻力、分选沉积、物质搬运、乃至地形地貌演变都有着重要的影响，因此研究沙纹演变的机理和规律具有重要的科学价值.

早期的有关沙纹形成的理论研究多是基于微小扰动平整床面的不稳定性概念.文献^[1]首先研究了势流作用下床面的不稳定性.在此基础上，更多的研究者在黏性层流^{[2, 3, 4, 5]}和湍流^{[6, 7]}条件下的对此问题进行了研究.在实验研究方面，主要的成果见文献[8, 9, 10]，对沙纹的形成和演变已有不少规律性认识，然而这些实验的结果往往离散度较大，而且由于受到量测手段的限制，有些重要的物理过程(如床面层中泥沙颗粒的运动和流动三维特性等)很难甚至无法测量，导致理论方法和模型无法得到有效的验证和调校.在数值模拟方面，近年来研究者们开展了离散泥沙输运的研究，通过求解大量泥沙颗粒的运动，并考虑泥沙颗粒与湍流之间的相互作用，泥沙颗粒之间、泥沙与床面之间的碰撞，泥沙颗粒之间的遮蔽和咬合作用等，运用统计手段来获取泥沙运动的整体特性，如输沙率、泥沙浓度分布、泥沙颗粒跳跃长度和高度、泥沙颗粒运动速度，甚至沙纹、沙浪和沙垄的形成和演变过程、泥沙颗粒分选等.在此方面，文献[11]对来流采用对数速度剖面，颗粒与床面碰撞的入射角和反射角按照正态分布，应用元胞自动机法对沙纹进行了模拟，得到了非对称的沙纹形状.文献[12]应用离散模拟方法，考虑沙粒的跃移和蠕移过程，对二维风成沙纹的演变进行了模拟.文献[13]采用相似的方法，考虑沙粒的跃移、蠕移和稳定模型，对风成沙纹的形成过程进行了二维数值模拟研究.基于单颗沙粒动力学的离散颗粒模型，孙其诚等^[14]模拟了4 000个沙粒在风力作用下由静止不动到充分发展的全过程，得到了沙床形态以及沙粒运动轨迹.采用一维统计耦合模型来计算稳态风沙流，郑晓静等^[15]考虑颗粒运动对流场的影响，模拟了沙纹的演变过程，得到了真实情况相近的结果.

借助于高性能计算技术的发展,离散泥沙颗粒在三维湍流场中输运的数值模拟逐渐引起研究者们的关注,其优势为可以考虑湍流拟序结构对泥沙输运的影响,得到的结果也更为真实.此方面的研究分为两类,一类是网格长度远小于泥沙粒径(一般为1/10的泥沙粒径),对湍流采用直接数值模拟或大涡模拟,对颗粒接触力采用颗粒离散元方法计算,对泥沙颗粒受到的流体力和周围流体受到泥沙颗粒的反作用力直接数值模拟(浸入边界法),不引入任何经验模型,模拟精度高,被认为是"数值实验".然而,由于"刻画"泥沙颗粒和"解析"湍流结构所需的网格数量巨大,此类研究无法研究大量泥沙颗粒的运动,仅能模拟少量(数千个)泥沙颗粒在较小计算区域内的运动.在此方面的研究包括:有人研究了单层固定颗粒受到的脉动流体压力在球面上的分布^[16];低固体体积比(泥沙颗粒的总体积与计算域体积之比)的小粒径泥沙颗粒的起动和悬移过程^{[17, 18]},较小粒径的泥沙颗粒在明渠湍流中的运动^[19];文献[20, 21, 22, 23]研究了较高固体体积比的大粒径泥沙颗粒在明渠湍流中的运动,得到了泥沙颗粒的平均速度剖面,速度紊动强度沿高度的分布,流体力随高度的变化及其概率密度函数(PDF),以及湍流场的一阶和二阶的统计量等.值得一提的是,文献[24]开展了超大规模的数值模拟(网格结点数约为9.1×10⁸,颗粒数为263 412),首次对沙纹的形成和演变的全过程进行了直接数值模拟研究.另一类研究中,泥沙粒径小于或等于网格长度,泥沙颗粒被当作"点球"处理,泥沙颗粒所受的流体力通过经验模型来模拟,泥沙颗粒运动对周围流场的影响通过在流体控制方程中增加附加体积力(浸入边界法)实现,湍流多通过大涡模拟求解,泥沙颗粒之间的接触力通过颗粒离散元计算.此类方法可模拟百万甚至千万量级的泥沙颗粒的运动,而需要的计算资源较少,适合研究较大空间尺度的泥沙演变过程.文献[25, 26, 27]等利用大涡模拟和颗粒离散元方法数值模拟了明渠湍流中沙纹、沙垄和沙浪的发展和演变,以及桩柱周围的局部冲刷和淤积问题,然而其仅对现象进行了简单的描述,未给出统计特征结果.文献[28]应用类似的方法,模拟了沙纹的演变,所不同的是其采用沙粒团的概念(即将多个沙粒当作一个整体来处理),以降低颗粒运动和碰撞的计算量,并且采用沙粒起跳模型来模拟其起动(实际上是省略了沙粒起动的模拟,转而用经验模型代替).本文显式数值模拟大量泥沙颗粒的起动、输运和沉积全过程,考虑泥沙颗粒运动与明渠湍流之间的相互作用,考虑颗粒之间和颗粒与床面之间的碰撞,以及颗粒之间的遮蔽作用,研究明渠湍流中沙纹的演变过程,并对其统计特征进行分析.

1 数值模拟方法

泥沙颗粒在明渠湍流中运动的数值模拟问题可以分解为3个子问题:明渠湍流的数值模拟,泥沙颗粒的运动和碰撞,湍流与泥沙颗粒之间的相互作用.本文采用基于有限体积法的高效能湍流并行计算程序－CgLES^[29]对湍流进行大涡模拟;采用基于"事件驱动"模型和"弹簧-阻尼"模型的颗粒离散元方法模拟颗粒的碰撞和运动;采用"点球"浸入边界法来模拟湍流和泥沙颗粒之间的相互作用.

"点球"浸入边界法基于浸入边界法^{[30, 31, 32]}发展而来，其基本思想是，采用固定的笛卡尔网格对计算域进行空间离散，将颗粒模化成为位于颗粒中心、随颗粒一起运动的浸入边界点，颗粒受到的流体力根据颗粒和流场的相对运动应用经验模型计算，而流体受到颗粒的反作用力施加到浸入边界点上，并通过插值函数映射到笛卡尔网格点上，最终附加到流体动量方程中，从而达到颗粒与流体的双向耦合.

基于"点球"浸入边界法的流体控制方程为格子滤波后的纳维－斯托克斯方程，采用具有二阶时间精度的亚当斯－巴什福斯(Adams-Bashforth)格式进行时间离散，其守恒形式为

${u^{n + 1}} = {u^n} + \delta t(\frac{3}{2}{h^n} - \frac{1}{2}{h^{n - 1}} - \frac{3}{2}\nabla {p^n} + \frac{1}{2}\nabla {p^{n - 1}}) + {f^{n + \tfrac{1}{2}}}\delta t$

(1)

$\nabla \cdot {u^{n + 1}} = 0$

(2)

其中，u为速度矢量，ρ为压强，${h} = \nabla \cdot ( - {uu} + (\nu + \nu_t )(\nabla {u} + \nabla {u}^{T}))$为对流项和扩散项的组合，$\nu$ 为分子运动黏滞系数，$\nu _t$为涡黏系数，$\delta t$ 为时间步长，$\nabla$ 为梯度算子，上标T为矩阵转置，上标n-1,n,n +1/2和n+1为时间步. f为附加体积力矢量，表示为

${f^{n + \tfrac{1}{2}}} = {D_h}( - {F_D} - {F_L})$

(3)

式中，${D_h}{\text{ }}(\Phi ,x)$为分布函数，将物理量从浸入边界点${{\text{X}}_{{\text{i }}}}$向笛卡尔网格点x映射，表示为

$\varphi (x) = {D_h}(\Phi ,x) = \sum\limits_{i = 1}^{{N_I}_{BP}} \Phi ({X_i}){\delta _h}(x - {X_i})\Delta {V_i}$

(4)

式中，${\varphi }({x})$ 为定义在笛卡尔网格点上的物理量，如${u}$,p和f等,$\Phi ({X_i}{\text{ )}}$ 为定义在浸入边界点上的物理量，如物面边界上的速度V和力F. N_IBP 为所有浸入边界点的个数，$\Delta V_i$ 为物面边界点的体积，$\delta _h ({x})$ 为狄拉克函数，表示为

$\delta ({x}) = d_h (x)d_h (y)d_h (z)$

(5)

式中，${{\text{d}}_{\text{h}}}{\text{ (r)}}$为线性插值函数，表示为

${d_h}(r) = \left\{ \begin{gathered} 0(1 - \left| r \right|/h),\left| r \right| \leqslant h \hfill \\ 0{\mkern 1mu} ,\left| r \right| > h \hfill \\ \end{gathered} \right.$

(6)

式中，r为任意点到浸入边界点的距离，h为网格边长. F_D 和F_L分别为颗粒受到的流体拖曳力和升力，通过经验公式(式(10)和式(13))确定. 大涡模型采用斯马林斯基(Smagrinsky)亚格子模型，压力泊松方程采用多重网格法求解，并行计算采用区域分解法，将整个计算域分为若干个子块，并平均分配给计算节点，子块之间共享一层网格结点，并通过MPI消息传递函数实现计算节点之间的通讯.

颗粒运动模型基于牛顿第二定律，将颗粒假设为均匀刚性球体，利用拉格朗日追踪法研究单个颗粒在自身重力、流体力以及颗粒与颗粒之间、颗粒与壁面之间相互作用力下的运动特性. 颗粒的轨迹方程和动量方程如下

$\frac{{{\text{d}}X}}{{{\text{d}}t}} = V$

(7)

$m\frac{{{\text{d}}V}}{{{\text{d}}t}} = F$

(8)

式中，X和V分别为颗粒的位移矢量和速度矢量，F为作用在颗粒上的合力矢量，m为颗粒的质量. 作用在颗粒上的力包括颗粒自身的有效重力，水流拖曳力和升力，颗粒之间、颗粒与壁面之间的法向接触力和切向摩擦力. 由于泥沙粒径较小，模型不考虑颗粒转动. F的表达式如下

$F{\text{ = }}{F_{\text{G}}}{\text{ + }}{F_{\text{D}}}{\text{ + }}{F_{\text{L}}}{\text{ + }}{F_{\text{n}}}{\text{ + }}{F_{\text{s}}}$

(9)

式中，${F_G} = \frac{\pi }{6}{D^3}\left( {{\rho _p} - {\rho _f}} \right)g$为颗粒所受有效重力，D为颗粒粒径，$\rho $_p 和$\rho $ _f 分别为颗粒和流体密度，g为重力加速度向量. F_D为水流拖曳力，与颗粒和水流相对速度的平方成正比，表示为

${F_D} = {C_D}\frac{\pi }{8}{D^2}{\rho _f}\left( {U - V} \right)\left| {U - V} \right|$

(10)

式中，$U = I_h ({u})$为颗粒中心位置的水流速度矢量，$I_h ({\varphi },{X}_i )$为插值函数，与${D_h}{\text{ }}(\Phi ,x)$相反，其将物理量从笛卡尔网格向浸入边界点映射，表示为

$({X_i}) = {I_h}(\varphi ,{X_i}) = {\text{ }}\sum\limits_{x \in {g_h}} {\varphi (x){\delta _h}(x - {X_i})} $

(11)

式中，$g_h$ 为所有笛卡尔网格点的集合. C_D 为拖曳力系数，是颗粒雷诺数Re_p = $\left| {{U} - {V}} \right|D / (\nu + \nu _t)$的函数. 文献[33]通过实验研究近似给出C_D 与Re_p之间的关系，表达式如下

${C_D} = {a_0} + \frac{{{a_1}}}{{R{e_p}}} + \frac{{{a_2}}}{{R{e_p}}}$

(12)

式中，a₀ ,a₁ ,a₂ 的取值取决于Re_p ，具体参考文献^[33].

F_L 为颗粒受到的水流升力，表示为

${F_L} = \left[{{C_L}\frac{\pi }{4}{D^3}{\rho _f}\left( {{u_f} - {u_p}} \right)\frac{{{\text{d}}{u_f}}}{{{\text{d}}y}}} \right]j$

(13)

式中，u_f 为颗粒中心位置的水流顺流向速度，u_p 为颗粒的顺流向速度，C_L为升力系数，根据文献^[34]的建议取值为0.2，j = (0,1,0)为竖向单位向量.

颗粒之间、颗粒与壁面之间的接触力计算采用"事件驱动"模型^[35](硬球模型)和"弹簧－阻尼"模型^[36](软球模型)的联合模型,即:在颗粒碰撞时刻,采用"事件驱动"模型,而在颗粒持续接触时,采用"弹簧－阻尼"模型.文献[37]指出,当两个球体高速碰撞时,若采用"弹簧－阻尼"模型来计算碰撞接触力,受稳定性条件限制,所需的时间步长极小,对于泥沙颗粒的碰撞而言,在10^-4~10^-5s左右,约为湍流模拟时间步长的1/100~1/1 000.显然,对于两者的耦合数值模拟而言,如此小的固体时间步长是不能接受的.另一方面,由于本文关注的不是几个泥沙颗粒之间的碰撞问题,而是数以百万计的泥沙颗粒的输运问题,因此无须解析出颗粒碰撞如此极小时间内的接触力的变化,而仅需要得到碰撞结束后颗粒的速度.事件驱动"模型基于碰撞恢复系数(即碰撞后的颗粒速度与碰撞前速度的比值,可通过实验测得)计算一个时间步内的平均接触力,对时间步长的限制很小,因此在本文模拟中得到应用.然而,"事件驱动"模型无法模拟球体的持续接触(如颗粒堆积问题),为此本文采用"弹簧－阻尼"模型来计算颗粒持续接触时的接触力,由于此时颗粒的相对速度很小,因此其对时间步长的限制较宽.

颗粒与颗粒(壁面)接触判断条件为

$r = {\left\{ {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2} + {{\left( {{z_i} - {z_j}} \right)}^2}} \right\}^{\tfrac{1}{2}}} \leqslant D$

(14)

式中，r为颗粒与颗粒(壁面)之间间距，$\left( {x_i ,y_i ,z_i } \right)$和$\left( {x_j ,y_j ,z_j } \right)$分别为第i个颗粒和第j个颗粒(或壁面)的坐标. 定义法向向量n和切向向量s分别为平行和垂直于颗粒中心连线的单位向量. "事件驱动"模型的法向接触力和切向摩擦力通过下式计算

${F_n} = \left[{\left( {1 + {e_n}} \right){m_e}\left( {{V_i}j \cdot n} \right)/\delta t} \right] \cdot n$

(15)

${F }_s = \dfrac{2}{7}\left[{\left( {1 + e_s } \right)m_e \left( {{V }_ij \cdot {s }} \right) / \delta t} \right] \cdot {s}$

(16)

"弹簧－阻尼"模型的法向接触力和切向摩擦力通过下式计算

${F}_n = \left\{ {k_n \left[{(D_i + D_j ) / 2 - r} \right]^{\tfrac{3}{2}} - \gamma _n m_e \left( {{V}_ij \cdot {n}} \right) / \delta t} \right\} \cdot {n}$

(17)

${F}_s = \left[{ - {sign}\left( {\delta _s } \right)\min \left( {k_s \delta _s - \gamma _s m_e \left( {{V }_ij \cdot {n}} \right) / \delta t,\;\mu \left| {{F}_n } \right|} \right)} \right] \cdot {s}$

(18)

式中，V_ij = V_i - V_j为颗粒与颗粒(壁面)相对速度(颗粒与壁面相互作用时，${V_j} = 0){\text{,}}{m_e} = {m_i}{m_j}/\left( {{m_i} + {m_j}} \right)$为等效质量(颗粒与壁面相互作用时，m_e = m_i )，e_n 和e_s分别为法向和切向碰撞恢复系数，k_n 和k_s分别为法向和切向弹簧系数，$\gamma$ _n和$\gamma$ _s分别为法向和切向阻尼系数，D_i 和D_j 分别为颗粒i和颗粒j的直径，$\gamma$ _s为颗粒之间相对滑动的距离(相对于初始接触位置)，\mu 为动摩擦系数.在本文数值模拟中，泥沙颗粒的沉降斯托克斯数为$St = \frac{{{\rho _s}}}{{9{\rho _f}}}\frac{{{w_s}D}}{\nu } \approx 15$，其中w_s为颗粒在静水中的最终沉降速度. 根据文献[38]归纳的试验结果(见图3)，St $\approx$15时，颗粒的法向碰撞恢复系数为e_n =0.3，考虑到明渠湍流中泥沙颗粒与床面碰撞时的接近速度要大于其在静水中的沉速，因此本文取e_n = 0.5.切向碰撞恢复系数e_s = - 1.0，即忽略颗粒的切向碰撞. k_n = 10k_s = 100mg /D，以保证颗粒相互侵入的距离较小. 其他参数的取值为： $\gamma$ _n = $\gamma$ _s = 0.1，$\mu$ = 0.2.文献[24]应用相近的参数组合(e_n = 0.3，e_s = - 1.0，$\mu$ = 0.4)对沙纹进行了直接数值模拟.参数敏感性分析结果显示，$\mu$对自然休止角的影响较显著，e_n 对自然休止角的影响较小，而$\gamma$ _n 和 $\gamma$ _s 的影响可以忽略. 尽管本文的颗粒动摩擦系数 $\mu$要小于文献[24]的取值，然而文献[24]并未对沙堆的水下休止角进行验证，而应用本文的参数组合可以较好地重现沙堆在水下的自然休止角，证明了本文参数取值的合理性(结果未附).

联合求解时，将颗粒视为浸入边界点，以其位置和速度以及当前流场作为已知条件计算颗粒的流体力(式(7)~(9))和接触力(式(11)~(14))，并求解颗粒运动控制方程(式(4)~(6))得到颗粒下一时刻的位置和速度；随后，将流体力反向施加到流体网格上(式(3))，求解流场(式(1)~(2))，得到下一时刻的流场.

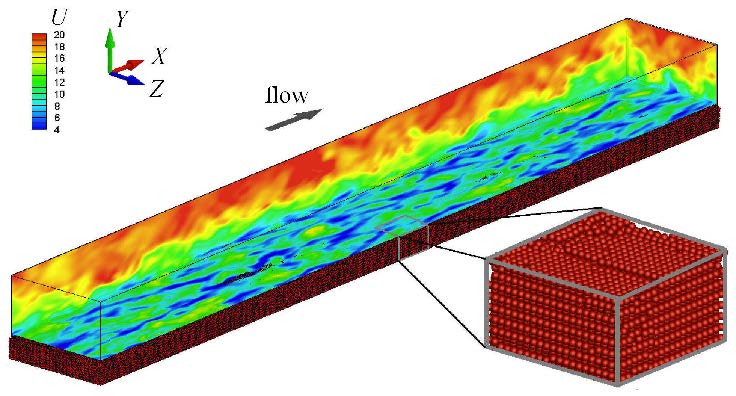
2 明渠沙纹演变及其统计特征

本文考察充分发展明渠湍流中沙纹的演变及其统计特征.数值模拟的边界条件为:明渠在流向(x轴)和展向(z轴)对流动和泥沙运动均采用周期边界(从下游边界移出的泥沙颗粒将从上游边界的对应位置进入计算域),在底面采用不可滑移边界,顶面采用可滑移边界.水流通过重力加速度的水平流向分量g_x=0.01m/s²驱动,令其自由充分发展.网格采用均匀网格,3个方向上的网格数量为256× 48×48,网格边长为$0.5\Delta x^+=\Delta y^+=0.75\Delta z^+\approx 9.45$,其中,上标"+"表示网格边长以黏性长度计.泥沙颗粒为圆球,直径为D=0.5 mm,与网格的高度$\Delta $y相等,个数为N_p=524 288.初始时,颗粒按照正方体规则排列,即在3个方向上(x,y,z)的个数为512× 16× 64,而后在重力和小随机扰动速度作用下自由堆积,形成自然密实的平整沙床,其厚度约为12.4倍的颗粒直径,即初始床面高度为y_b0≈0.259d (根据文献^[24]的建议,等效床面的高度可根据泥沙浓度等于0.1确定),孔隙率约为33.8%,略大于球按照四面体堆积(最紧密堆积)的孔隙率25.9%,如图1所示.整个数值模拟分为两阶段.阶段一,自然沉积定床上的明渠湍流模拟,模拟的无量纲时长为40T (T=h₀/u_τ0为大涡回转时间,h₀=d-y_b0和u_τ0分别初始状态下的等效水深和摩阻流速).图1给出了湍流充分发展后的3个剖面(端面、侧面和平面y=0.292d)上的瞬时顺流向速度云图.可以看出,在平面y=0.292d上(略高于初始等效床面,即(y-y_b0)⁺+≈15.1)高流速区和低流速区形成的条带结构非常明显,与光滑平面上的条带结构无明显区别.对等效床面上的流速进行平均得到体积流速为U_b0≈11.73u_τ0,对应的基于体积流速的雷诺数为Re_b0⁺=U_b0 h₀≈3 971;阶段二,待湍流充分发展后,释放泥沙颗粒(固定最下一层颗粒,以防止沙床出现整体平动),在湍流的作用下,泥沙颗粒发生起动和输移,并逐渐形成沙纹.沙纹稳定后,平均等效床面比初始状态略有升高,约为13倍的颗粒直径,即y_b≈0.271d.此时,由于沙纹形状阻力的作用,体积流速降低为U_b≈9.94u_τ,对应的基于体积流速的雷诺数为Re_b⁺=U_b h/v≈3 287.

其他无量纲参数如下

明渠尺寸：${L_x} \times {L_y} \times {L_z} = 10.67d \times d \times 1.33d = 512D \times 48D \times 64D$

等效水深：定床，h₀ $\approx$ 0.741d，动床，h $\approx$ 0.729d

雷诺数：定床，$Re_{_{\tau 0}}^{^ + } = {u_\tau }0{h_0}/\nu \approx 339$动床$Re_\tau ^ + = {u_\tau }h/\nu \approx 331$

网格结点数 256×48×48

网格边长$ 0.5\Delta x^ + = \Delta y^ + = 0.75\Delta z^ + \approx 9.45$

密度比 $ s_s = \rho _s / \rho _f = 2.65$

颗粒直径 $D = d / 48 = \Delta y$

颗粒雷诺数 $Re_D^ + = u_\tau D / \nu \approx 9.45$

谢尔兹数 $\varTheta = \tau _w / [gD(\rho _s - \rho _f )] \approx 0.286$

输沙强度$ T^\ast = \varTheta / \varTheta _c \approx 6.1$ 其中，d 为明渠高度，$u_\tau$ 为摩阻流速，$\nu$ 流体的分子运动黏性系数,$\rho $_f和$\rho $_s 为流体和颗粒的密度，$\tau$ _w是无量纲的床面剪切应力，g为重力加速度大小，$\Theta $ _c为泥沙起动的谢尔兹参数临界值，根据颗粒雷诺数Re_D⁺$\approx $9.45，取为0.047，上标⁺ 表示无量纲变量.

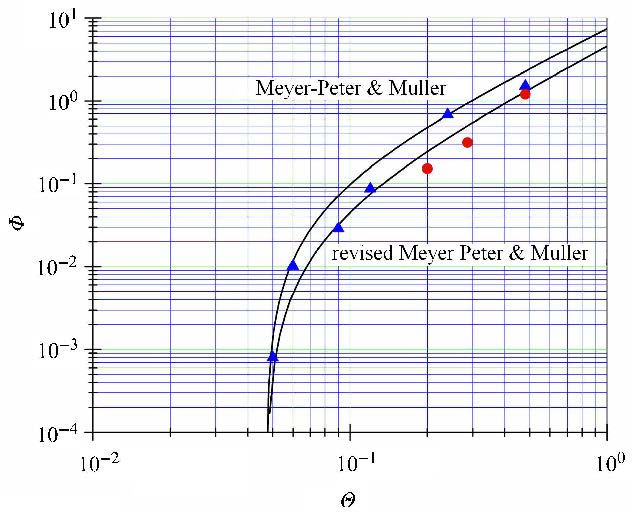
2.1 输沙率验证

为了验证程序的正确性,本文计算了不同谢尔兹数下无沙纹床面明渠湍流的输沙率.为了减小计算量和抑制沙纹的产生,本文采用较少的泥沙颗粒和较小的计算域,相应的计算条件如表1所示.需要说明:本文通过改变颗粒的重力加速度来调节谢尔兹参数,而水流条件不变,这样可以保证每个工况的泥沙颗粒雷诺数相同,得到的结果更具可比性.图2给出了无沙纹床面的无量纲输沙率随谢尔兹数的变化,如图中的三角形散点所示.与经典的迈耶－彼得(Meyer-Peter)和穆勒(Muller)公式$\Phi$ =8($\Theta $-0.047)^1.5及其修正的公式$\Phi$ =4.93($\Phi$ -0.047)^1.6相比,数值结果与经验值吻合良好.此外,图2还给出了沙纹床面的无量纲输沙率随谢尔兹数的变化,如图中的3个圆形散点所示.可以看出,由于沙纹的作用,无量纲输沙率有所降低.为了分析沙纹的形成和发展过程,下文针对中间的沙纹床面算例($\Theta $≈ 0.286)进行了深入研究.

2.2 明渠沙纹的演变及其统计特征

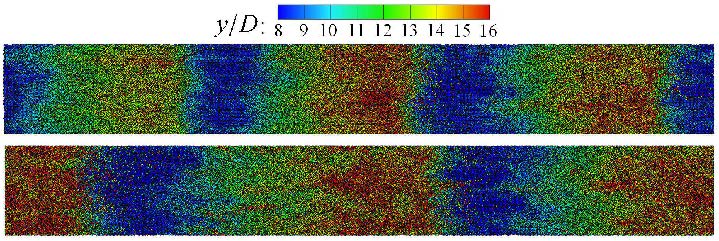
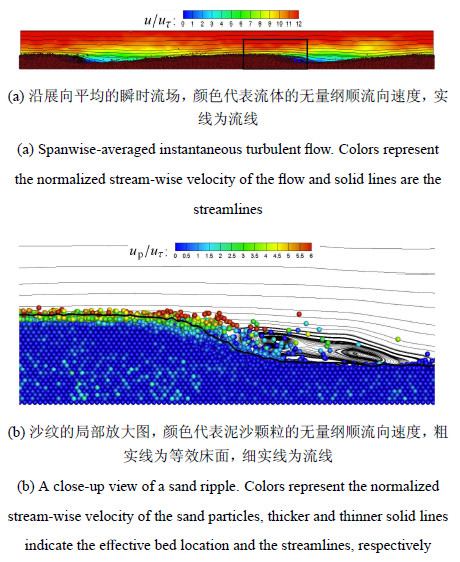
图3为两个不同时刻(tU_b/h≈ 1 200和3 000)的表层泥沙颗粒的无量纲高度.在上图中(tU_b/h≈ 1 200),整个计算域中有3个沙纹,沙纹的平均无量纲长度和高度分别为$\lambda$/h≈ 4.858和A/h≈ 0.229;而在下图中(tU_b/h≈ 3 000),由于沙纹合并,仅剩下两个沙纹,沙纹的平均无量纲长度和高度分别为$\lambda$/h≈ 7.316和A/h≈ 0.314.这与文献^[10]的实验结果(当tU_b/h=1 200时,$\lambda$/h≈ 5.1±1.8,A/h≈ 0.21±0.07;当tU_b/h=3 000时,$\lambda$/h≈ 9.0±1.0,A/h≈ 0.36±0.04,见其图3(a))较为吻合.对比两种情况可以看出:当沙纹合并时,沙纹的长度和高度显著增大,但其形状基本保持不变,沙纹指标$\lambda$/A分别为21.25(3个沙纹)和23.28(2个沙纹),比实际观测值^[15]15~20略大.由于计算域的宽度的限制,沙纹基本上是二维的,并且在迎流侧和背流侧不对称,这一点可以从图4中得到更明显的体现.此外,在等效床面附近存在一个床面层,其高度约为2~3个颗粒直径,在床面层内,泥沙颗粒的运动速度较大(图4下图中的颗粒的颜色代表颗粒的顺流向速度),并且,迎流侧的颗粒顺流向速度明显大于背流侧的,这主要是由于在背流侧存在一个回流区.

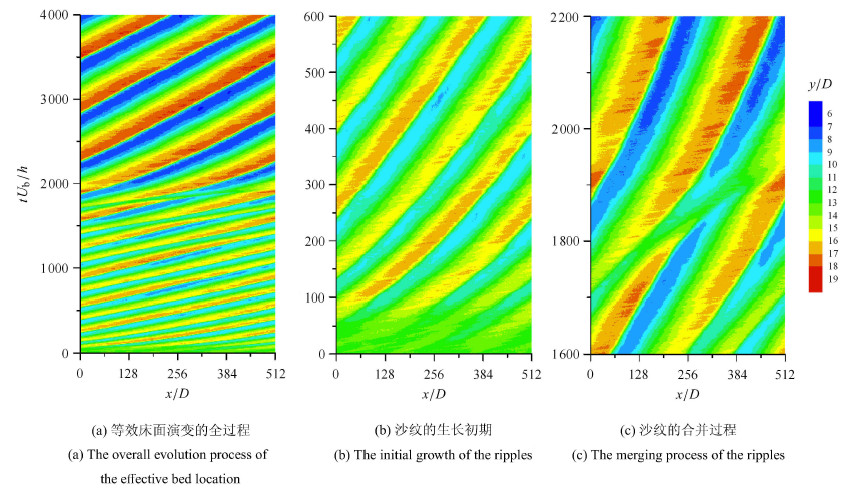
图5给出了沙纹演变的全过程.可以看出,沙纹在初期生长地很快,到tU_b/h≈100时,即可观察到明显的沙纹.在形成初期,沙纹的"行走"速度较快,但随着沙纹高度的增加,沙纹的"行走"速度逐渐降低并趋于稳定.这点可以从沙脊对时间的斜率的变化得到佐证,如中图所示.右图给出了沙纹合并的过程.可以看出,当tU_b/h≈1 600时,可以观察到3条沙纹(尽管最右侧的沙纹不太明显,但生长的速度非常快),然而当tU_b/h≈1 800时,由于受到上游沙纹的快速生长,中间的沙纹被迅速抹平,到tU_b/h≈2 000时,仅剩下2条沙纹.观察沙纹的演变,可以看出:沙纹的生长对于沙纹的"行走"速度有明显影响.3条沙纹时,沙纹的"行走"速度约为0.029U_b,而2条沙纹时,则降低到0.012U_b.其主要原因为:沙纹的生长,沙纹对水流的形状阻力增大,降低了流速和输沙率,而输沙的多少正是决定沙纹"行走"速度的主要因素.本文得到的沙纹"行走"速度随时间的变化与文献[10]的实验结果(当tU_b/h=900时,为0.021±0.008 U_b;当tU_b/h=2 000时,为0.005±0.004 U_b;见其图3(b))吻合较好.

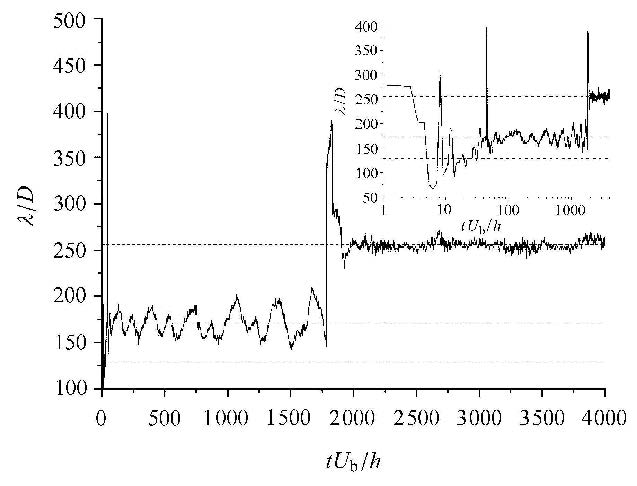
图6给出了无量纲沙纹长度随时间的变化.沙纹的无量纲长度根据文献^[24]建议的方法计算,即:计算每个时刻等效床面高度脉动量$y'_b(x,t)=y_b(x,t)-\left\langle{y_b}\right\rangle_x (t)$的自相关系数$R (r_x,t)=\left\langle{y'_b(x,t)y'_b(x+r_x,t)}\right\rangle_x$,沙纹长度确定为两倍的最小(负最大)自相关系数对应的$r_x$,其中,x为顺流向的坐标,t为时间,$r_x$为顺流向的间隔长度,$\left\langle\right\rangle_x$表示沿顺流向空间平均.从图中可以看出,沙纹的长度大部分时间为$L_x/3$和$L_x/2$,并且沙纹较长时,其长度的脉动值较小,即沙纹更加稳定.在沙纹合并时,沙纹长度出现一个不连续的跳跃,这对应沙纹被抹平的时刻.如果将时间用对数坐标轴表示,很容易看到,在沙纹形成初期的很短的时间段内(20 < $tU_b$/h < 30),沙纹的长度为$L_x$/4.从以上结果可以看出,较为稳定的沙纹长度是整数分之一的计算域长度,这与数值模拟采用周期边界有关.文献[24]的直接数值模拟也得到了类似的结果.如果以颗粒的直径作为比尺,则沙纹的长度$\lambda$/D为170~256,比文献[24]的100~150较大,这与其在顺流向采用较少的颗粒数量($L_x$/D=307.2)有关.若以等效水深为比尺,则沙纹的长度$\lambda$/h为4.9~7.3,这与文献[10]的实验结果(当t$U_b$/h=900时,$\lambda$/h≈5.0±1.5;当t$U_b$/h=2 000时,$\lambda$/h≈9.0±0.5;见其图3(c))吻合良好.

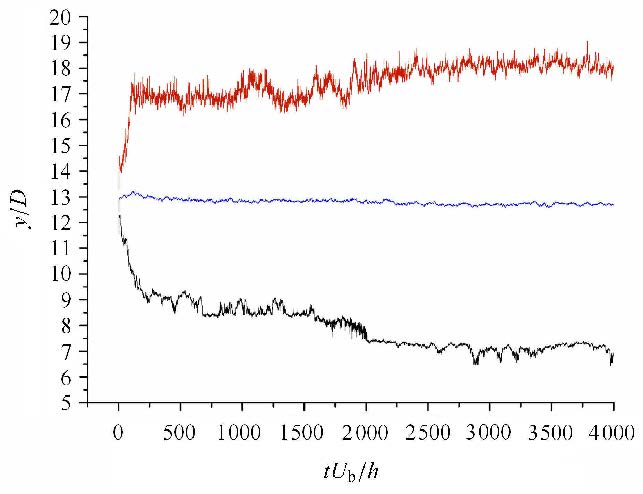
图7给出了瞬时等效床面无量纲高度的最大值、平均值和最小值(从上至下)随时间的变化.在沙纹发展的初期，等效床面的最大值和最小值发展非常迅速(最大值收得更快一些)，而后趋于稳定，仅当沙纹合并时，等效床面的最大值和最小值有进一步的小幅发展.与之相反，除了在模拟的开始，等效床面的平均值出现一个小幅的跳跃外(约为0.6D)，其长时间内一直保持稳定，即便在沙纹合并时，也没有明显变化.

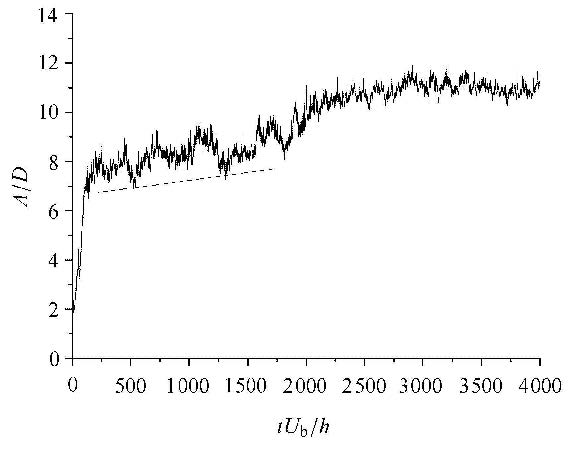
图8给出了无量纲沙纹高度随时间的变化.沙纹高度通过等效床面的最大值和最小值的差值确定.可以看出,在沙纹形成的初期,高度增长很快,而后趋于平缓,仅在沙纹合并时,沙纹高度有较快速度增长.沙纹的高度有两个较为稳定的值为A/D≈ 8和A/D≈11(分别对应3个沙纹和2个沙纹的情况).需要指出的是:即便在沙纹数量不变的情况下,沙纹的高度也在缓慢增长,这与文献[39, 40]在水槽中观察到的实验现象一致.沙纹高度增长的斜率约为5.6×10^-4,如图8中斜线所示(斜率计算基于图中的坐标单位),与文献[24]的结果6.0×10^-4吻合良好.沙纹高度在模拟的后期逐渐趋于平稳,这是由于计算域周期边界的使用限制了沙纹长度的进一步增加.

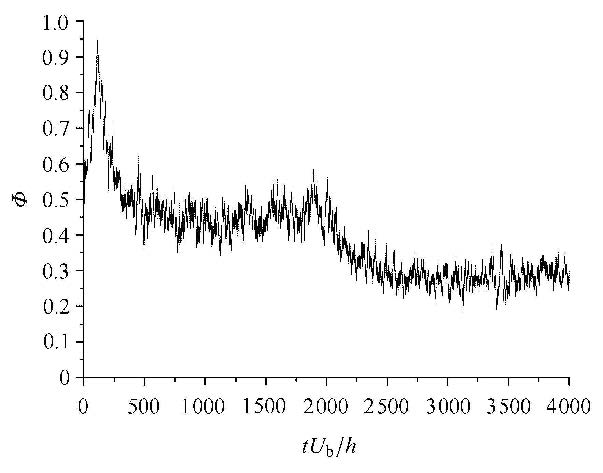
图9给出了无量纲输沙率随时间的变化.在沙纹形成之前,输沙率快速增长,并在tU_b/h≈100时刻,达到峰值;而后,随着沙纹生长,输沙率逐渐降低并趋于稳定.当沙纹合并时tU_b/h≈2 000,由于沙纹形状阻力的增大,输沙率进一步降低,并逐渐稳定在$\Phi $≈0.314.

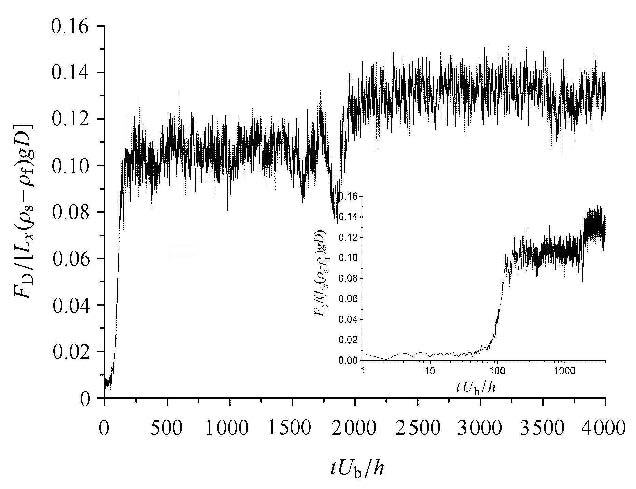
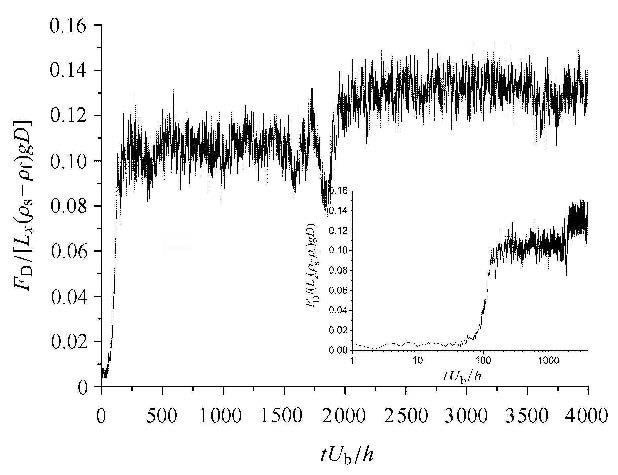
图10给出了沙纹的无量纲形状阻力$F_D / [L_x (\rho _s - \rho _f )gD]$ 随时间的变化.单位宽度形状阻力通过沿床面对瞬时压强进行积分得到，即${F_D} = {\text{ }}\int_0^{{L_x}} {pS{\text{d}}x{\text{ }}} $，式中，p为压强，S 为沙纹的坡度，迎流面为正，背流面为负.可以看出，在沙纹形成的初期，沙纹无量纲形状阻力迅速增大，而后趋于平缓，在沙纹合并时，无量纲形状阻力进一步增大.与沙纹高度的两个稳定值相对应，无量纲形状阻力也存在两个稳定值，即$F_D / [L_x (\rho_s - \rho_f)gD] \approx 0.108 $(3个沙纹、沙纹高度A / D $\approx$ 8 (A / h $\approx$ 0.23))和0.135 (2个沙纹、沙纹高度A/ D $\approx$ 11 (A / h $\approx$ 0.31))，分别占无量纲总阻力(即谢尔兹数)$\tau _w / [(\rho _s -\rho _f )gD] \approx 0.286$的37.7%和47.2%. 床面上的无量纲摩擦阻力为${\tau }'_w / [(\rho_s - \rho _f)gD] \approx 0.178和0.151，其中，{\tau }'_w = \tau_w - F_D /L_x $为床面摩擦阻力. 若以此摩擦阻力用迈耶－彼得和穆勒公式计算输沙率，可得$\Phi \approx 0.38$和0.27，与本文数值模拟的输沙率$\Phi \approx 0.42$和 0.27相近. 进一步，根据$C_D $= 2$F_D /(n\rho _f U_b^2 A)$ 计算形状阻力系数，其中n为沙纹的个数，可得形状阻力系数的稳定值为C_D$\approx$ 0.19 (3个沙纹)和 0.24 (2个沙纹)，比根据经验公式

${C_D} = \left\{ \begin{gathered} \hfill \\ \begin{array}{*{20}{l}} {\frac{4}{9}{{(A/h)}^{0.375}}{\mkern 1mu} ,}&{A/h \leqslant 0.34}&{} \end{array} \hfill \\ \frac{3}{2}{(A/h)^{1.5}}{\mkern 1mu} ,A/h > 0.34 \hfill \\ \end{gathered} \right.$

计算得到的值(C_D $\approx$ 0.26 和0.29)略小，其中A / h为沙纹高度和水深的比值.

图11给出了无量纲体积流速随时间的变化. 可见，在沙纹形成的初期，随着沙纹高度的增大，无量纲体积流速快速减小，并 逐渐趋于稳定U_b / $u_\tau \approx$ 11.04 ，当沙纹合并后，无量纲体积流速进一步减小为U_b / $u_\tau \approx$ 9.94.

综合对比三沙纹和两沙纹的情况，无量纲沙纹高度增大了37.5%，无量纲沙纹形状阻力增大了25%，无量纲床面摩擦阻力减小了15%，无量纲输沙率减小了35.7%，无量纲体积流速减小了10%.

3 结论

本文应用大涡模拟、"点球"浸入边界法和基于"事件驱动"模型和"弹簧－阻尼"模型的颗粒离散元法数值模拟了明渠湍流中沙纹的演变,并对其统计特征进行了分析.论文首先计算了小尺度无沙纹明渠中不同谢尔兹数下的输沙率,并于经验公式进行了对比,吻合良好;而后对大尺度明渠中的沙纹的演变及其统计特征进行了模拟和分析.研究发现:在明渠湍流的作用下,初始平整的床面很快(tU_b/h$\approx$ 100)发展出沙纹,在tU_b/h为1 600~2 000时,沙纹发生合并;沙纹的形状不对称,迎流侧缓,而背流侧陡;随着沙纹的发展,沙纹的高度逐渐增加,近似符合线性关系(斜率约为5.6×10^-4),而在沙纹合并时,沙纹高度增长速度加快;沙纹长度在同等沙纹数量情况下其平均值保持不变,而较长的沙纹的长度更为稳定,稳定的沙纹长度为整数分之一的计算域长度,这与数值模拟采用周期边界有关;输沙率和体积流速在沙纹形成前较高,随着沙纹高度的增加,输沙率和体积流速减小并趋于稳定,仅在沙纹合并时,有较大幅度的减小;沙纹形状阻力与沙纹的高度相关,当沙纹合并时,有较大幅度增大;在同等的水流强度条件下,有沙纹床面的输沙率小于平整床面的输沙率.