飞行器设计和使用过程中存在飞机本身参数和使用环境等诸多不确定因素,导致出现飞机性能波动的现象,这将严重影响飞机的性 能稳定性和飞行安全性. 因此,在飞行器设计阶段,关注不确定因素对飞行器性能的影响显得尤为重要. 近几年,基于不确定性的稳健性优化设计和可靠性优化设计得到了广泛研究[1, 2]. 在空气动力学设计中,传统的确定性优化设计仅考虑提高气动性能[3, 4, 5],并没有考虑不确定性因素的影响,实际上 在跨声速区域,由于流场高度非线性,这些不确定性因素可能对气动性能产生较大的影响. 与传统的确定性优化问题相比,稳健性优化基本思想是减小不确定性因素对产品质量的影响,所以基于不确定性的稳健性优化设计 得到了一定研究[6, 7, 8, 9]. 不确定性分析是稳健性优化设计的前提条件,Padulo等[9]比较几种不确定分析方法并发展了一种新的高效高精度的不确定性分析方法用 于翼型的稳健性优化设计. 目前,大多数关注气动特性不确定性的分析仅考虑不确定参数对气动力系数的影响,并没有反映不确定性因素对整个流场分布的影 响,这不利于分析不确定性因素造成气动特性波动的主要原因.
不确定性分析只能得到不确定因素对输出的影响,在实际工程问题中,人们更关注哪些不确定因素的影响更大,这就需要进行灵敏度 分析. 全局灵敏度分析即重要性测度,可以求出每个不确定因素的贡献程度. 近年来,基于方差的重要性测度得到了广泛的研究可应用,该方法研究输入随机变量对输出的贡献程度,不仅可以计算每个输入的贡 献程度还可以求出个变量交叉影响[10, 11].
从试验角度进行气动特性的不确定性分析存在统计数据量巨大、过程复杂等问题,而非嵌入式不确定性分析方法耦合计算流体力学 工具(CFD)十分适用于气动特性的不确定性分析. 文献[12, 13]对计算流体力学中的不确定来源做了详细的描述. 文献[14]把计算流体力学中不确定性分析方法做了总结,具体包括矩方法、区间方法、随机方法等. 近年来,混沌多项式方法(PCE)在流体力学不确定性分析中广泛应用,文献[15, 16]综述了混沌多项式方法在流体力学中的不确定性 分析及应用. 该方法由开始的嵌入式方法逐渐发展成非嵌入式方法. Mathelin等[17]采用嵌入式混沌多项式展开的方法研究了准一维管道流动不确定性传输问题,需要对计算流体力学求解程序进行更改,如果求解纳维-斯托克斯方程,修改程序将相当困难. 后来研究人员发展了一种非嵌入的混沌多项式方法,该方法直接调用程序,不需要对计算流体力学程序进行更改,这一突破使得 非嵌入的混沌多项式方法在随机空气动力学研究中得到广泛应用. 文献[18, 19]采用非嵌入式的混沌多项式方法进行了翼型表面的气动载荷分布的不确定性分析,发现飞行状态不确定性对激波和激波后 的边界层分离有很大影响. 随机流场的全局灵敏度分析鲜有涉及,Chassaing等[18]仅进行了翼型表面气动载荷分布的方差降维分析. 国内,王晓东等[20]采用嵌入式的混沌多项式法求解随机伯格斯方程. 赵轲等[21]考虑单个变量马赫数的不确定性,进行了基于混沌多项式方法的翼型不确定性分析及稳健性优化设计. 本文采用非嵌入式混沌多项式方法进行绕翼型跨声速气动特性的不确定性及全局灵敏度分析,通过研究马赫数和仰角的随机不确定 性对绕NACA0012翼型流场的影响,分析气动特性波动的原因,并通过全局灵敏度分析找出流场性能波动的主要因素.
1 多项式混沌理论多项式混沌的基本思想是用含有独立随机变量的正交多项式混沌之和来表示随机过程. 将随机函数分解成确定和随机两部分,得到下式[22]
| $ {\alpha ^*}(x,\xi ) = \sum\limits_{j = 0}^\infty {{\alpha _j}} (x){\psi _j}(\xi ) \approx \sum\limits_{j = 0}^P {{\alpha _j}} (x){\psi _j}(\xi ) $ | (1) |
式中,$\alpha _j ({\pmb x} )$和$\varPsi _j ({\pmb \xi})$分别表示第$j$阶模态的确定和随机部分,$P$是所截取的有限阶 模态阶数. 认为$\alpha^* $是确定独立变量$x$和$n$维随机变量${\pmb \xi} = (\xi _1 ,\xi _2 ,\cdots ,\xi _n )$的函数,${\pmb \xi}$服从特定的概率分布. 方程(1)包括无限阶模态,现实中只能取有限阶模态,模态阶数可有下式确定
| $ N_t = P + 1 = \dfrac{(n + p)!}{n!p!} $ | (2) |
式中,$n$是随机变量的维数,$p$是多项式混沌的阶数. 当随机变量服从高斯分布,基函数$\varPsi_j ({\pmb \xi })$可以表 示为埃尔米特多项式.
多项式混沌方法的目的是求出多项式系数$\alpha _k $,对方程(1)做如下变换
| $ \left\langle {{\alpha ^*}(x,\xi ),{\psi _k}(\xi )} \right\rangle = \left\langle {{\rm{ }}\sum\limits_{j = 0}^P {{\alpha _j}} (x){\psi _j}(\xi ),{\psi _k}(\xi )} \right\rangle $ | (3) |
$\left\langle \cdot \right\rangle $表示内积,函数$f({\pmb \xi })$和 $g({\pmb \xi })$在区域$\Re$ 上的内积可表示为下式
| $ \left\langle {f(\xi )g(\xi )} \right\rangle = \int_R f (\xi )g(\xi )w(\xi )d\xi $ | (4) |
对于服从高斯分布的随机变量,基函数是埃尔米特正交多项式.
| $ \left\langle {{\alpha ^*}(x,\xi ),{\psi _k}(\xi )} \right\rangle = {\alpha _k}(x)\psi _k^2(\xi ) $ | (5) |
进而可以推导出
| $\begin{array}{*{20}{l}} {{\alpha _k}(\backslash {\rm{pmb}}x) = \frac{{\left\langle {{\alpha ^*}(x,\xi ),{\psi _k}(\xi )} \right\rangle }}{{\psi _k^2(\xi )}} = }\\ {\frac{1}{{\psi _k^2(\xi )}}\int_R {{\alpha ^*}} (x,\xi ){\psi _k}(\xi )w(\xi )d\xi } \end{array}$ | (6) |
多维的埃尔米特多项式
| $ H({\xi _{i1}},\cdots ,{\xi _{in}}) = {e^{\frac{1}{2}{\xi ^{\rm{T}}}\xi }}{( - 1)^n}\frac{{{\partial ^n}}}{{\partial {\xi _1},\cdots ,\partial {\xi _n}}}{e^{ - \frac{1}{2}{\xi ^{\rm{T}}}\xi }} $ | (7) |
权重系数$w({\pmb \xi })$
| $ w(\xi ) = \frac{1}{{\sqrt {{{(2\pi )}^n}} }}{{\rm{e}}^{ - \frac{1}{2}{\xi ^{\rm{T}}}\xi }} $ | (8) |
有两种方法去求解方程(1)的系数$\alpha _j ({\pmb x})$即嵌入式方法和非嵌入式方法. 嵌入式方法将响应量投影 到基函数$\varPsi ({\pmb \xi })$上,这一方法在早期计算流体力学不确定分析中广泛使用,但是需要对计算流体力 学程序进行更改,对于复杂的纳维-斯托克斯方程,极为不方便. 非嵌入式方法将确定性系统当做黑箱处理,通过回归分析求解系数$\alpha _j ({\pmb x })$,从而得到近似的数学模型,这将大幅度减小不确定性分析的工作量[9].
2 全局灵敏度分析通过不确定性分析,可以得到不确定性因素对输出的影响,但是要确认每一个不确定性变量对这一影响的贡献程度,还需要进 行灵敏度分析. 灵敏度分析分为全局灵敏度分析和局部灵敏度分析. 局部灵敏度分析通过求某一点处导数${\partial Y_j }{\partial X_i }$只能计算出给定点处的导数信息,而且该结果依赖于参数空间名义值的选取,当输入参数不确定性或者模 型具有非线性时,局部灵敏度分析存在较大缺陷. 全局灵敏度分析在整个参数空间中考虑输入参数的不确定性对输出响应不 确定性的影响,且能够反映参数之间的相互作用. 目前,基于方差的全局灵敏度分析应用比较广泛,该方法研究输入参数对 输出参数波动的重要性影响,同时考察参数的交叉耦合作用. 由方差降维分析[10],总方差可以由下式表示
| $ V(Y) = \sum\limits_i {{V_i}} + {\rm{ }}\sum\limits_i {\sum\limits_{j > i} {{V_{ij}}} } + \cdots + {V_{12 \cdots k}} $ | (9) |
其中$V_i = V[E(Y\left| {X_i } \right.)]$,$V_{ij} = V[E(Y\left| {X_i } \right.,X_j )],\cdots $,式(9)两边除以$V(Y)$,得到下式
| $ \sum\limits_i {{S_i}} + {\rm{ }}\sum\limits_i {\sum\limits_j {{S_{ij}}} } + \sum\limits_i {\sum\limits_{j > i} {\sum\limits_{l > j} {{S_{ijl}}} } } + \cdots + {S_{123 \cdots k}} = 1 $ | (10) |
其中,$S_i $是主灵敏度指标,$S_{ij} ,S_{ijl} ,\cdots ,S_{123\cdots k} $体现交叉影响. 主要灵敏度指标可以表示为单个输入变量条件下输出响应条件期望的方差与总方差之比
| $ {S_i} = \frac{{V[E(Y\left| {{X_i}} \right.)]}}{{V(Y)}} $ | (11) |
对于二维问题
| $ S_1 + S_2 + S_{12} = 1 $ |
本文计算全局灵敏度采用文献[11]发展的基于蒙特卡洛模拟的计算方法. 下面用一个简单的数值算例验证本文混沌多项式方法 进行不确定性及全局灵敏度分析的准确性及效率.
| $ Y = X_1 \times X_2 $ |
其中参数服从正态分布,$\mu _1 = 1$,$\mu _2 = 2$,$\sigma _1 = 3$,$\sigma _2 = 2$. 分别采用混沌多项式方法和蒙特卡洛方法进行不确定性及全局灵敏度分析,并与解析解进行对比. 计算采用4阶的混沌多 项式方法,建模时抽取30个样本点. 蒙特卡洛进行不确定性分析抽取5\,000样本点,进行全局灵敏度需要抽取20\,000个样本点. 计算结果对比情况如表1,表1对比结果可以看出混沌多项式方法的准确性.
| 表 1 混沌多项式和蒙特卡洛方法不确定性及全局灵敏度分析的结果比较 Table 1 The result of uncertainty analysis and global sensitivity analysis by PCE, MCS and analytic solution |
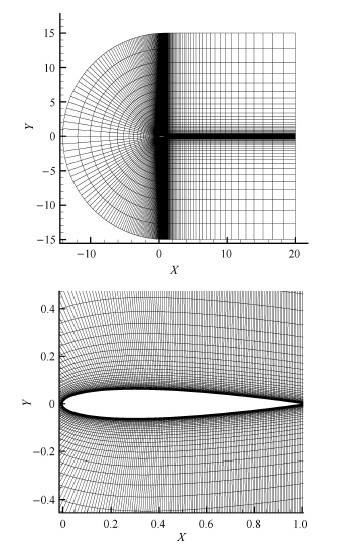
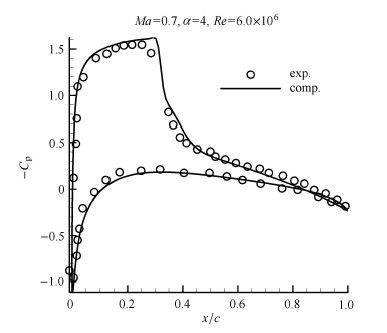
采用有限体积法求解基于单方程湍流模型的可压缩雷诺平均纳维-斯托克斯控制方程. 本文采用NACA0012翼型的C型网格,见图1. 网格分为两区域:第1区域为前面半圆形区域,共有300$\times $150个网格;第2区域为翼型后面矩形区域,共有200$\times $150个网格. 翼型表面均匀布300个点,网格较密是为了更好地捕捉流场的变化. 图2验证了计算流体力学模拟的可靠性.
|
图 1 NACA0012翼型计算网格 Fig.1 C mesh of NACA0012 |
|
图 2 $C_p$分布比较 Fig.2 Pressure distribution |
本节研究飞行状态参数(马赫数、仰角)的随机扰动对绕NACA0012翼型的气动特性的影响. 计算状态为 $Re = 3.0\times 10^6$,假 设马赫数服从$N(0.65,(0.005)^2)$正态分布,仰角服从$N(5,(0.2)^2) $的正态分布. 分别采用混沌多项式方法和蒙特卡洛方法进行不确定性分析. 蒙特卡洛模拟是一种传统的解决随机偏微分方程的方法,使用非常方便且与随机变量维数无关,但其收敛效率低,需要抽取大 量样本,因此本文进行2\,000次蒙特卡洛模拟分析,验证混沌多项式方法的精度和效率. 混沌多项式方法通过多项式混沌理论构建代理模型,然后调用该代理模型进行不确定性分析和全局灵敏度分析.
4.1 载荷及流场分布的不确定性分析采用5 阶的混沌多项式对翼型表面的气动载荷分布(压力系数及摩擦力系数分布)以及整个流场进行不确定性分析,并用蒙特卡洛方法对分 析结果进行验证. 由图3和图4可以看出混沌多项式方法和蒙特卡洛方法吻合很好,两者相比,混沌多项式方法的分析效率较蒙特卡洛方法有很大提高.
|
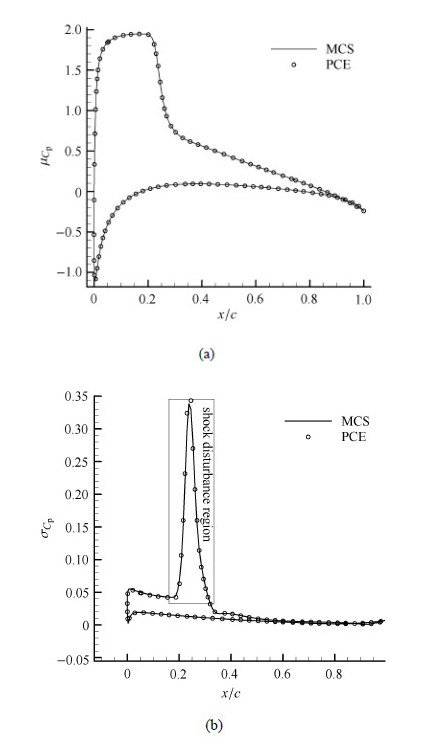
图 3 翼型表面压力系数的(a)均值和(b)标准差分布 Fig.3 Mean value distribution (a) and Standard deviation distribution of the pressure coefficient along the chord |
|
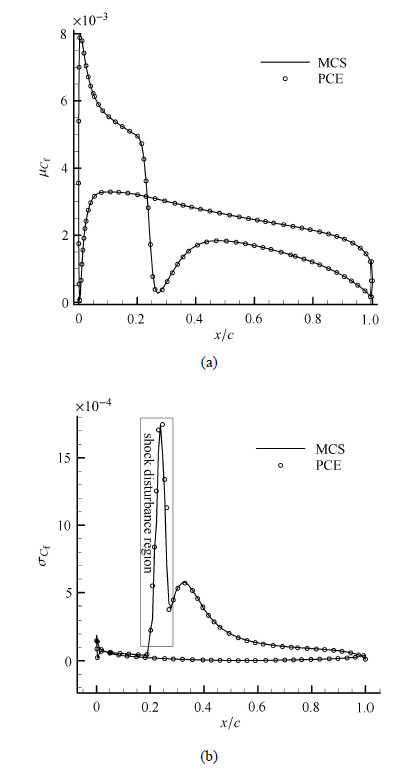
图 4 翼型表面摩擦力系数的(a)均值和(b)标准差分布 Fig.4 Mean value distribution (a) and Standard deviation distribution of the skin-friction coefficient along the chord |
图3和图4分别给出了翼型表面压力系数和摩擦力系数的均值分布和标准差分布. 可以看出马赫数和仰角的随机扰动只对翼型上表 面的气动载荷分布影响明显,对下表面的气动载荷分布几乎没有影响. 图3和图4中标准差陡然变大的那一部分区域(图中矩形框标出)我们称为激波散布区域. 我们认为两个原因造成这一区域的标准差之很大:激波强度变化剧烈;激波位置来回晃动,导致这一区域的物理量一会在激波前,一会在激波后,物理量变化比较剧烈.
由图3看出,在翼型上表面,激波散布区域之前,压力系数标准差保持在0.05左右;在激波散布区域,压力系数标准差陡然上升,最大值达到了0.35;激波散布区域之后,压力系数标准差迅速减小到零. 由图4 看出,在激波散布区域及激波散布区域之前的区域,摩擦力系数的标准差分布变化规律与图3中压力系数的变化规律基本一样,但是,在激波散布区域之后,摩擦力系数标准差没有迅速减到零,而是在激波后某一区域保持较大值,过了这一区域才迅速减为零. 究其原因是激波后出现边界层分离,分离泡的强度和位置随着不确定性参数的扰动而产生波动. 这说明:对与压力系数分布,飞行状态的不确定性对激波特性的影响大;而对于摩擦力系数分布,飞行状态的不确定性对激波以及 激波后的边界层分离影响大. 这也正是气动特性波动的原因.
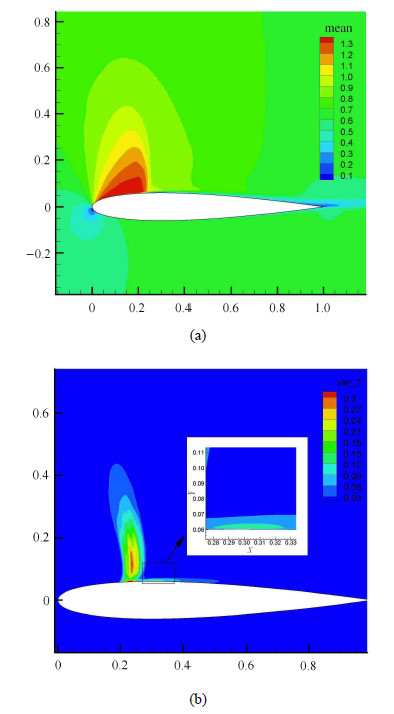
图5给出了整个流场马赫数的均值和标准差分布,可以看出不确定性对流场的影响主要分布在激波和激波后分离泡处,其中最大影 响在激波位置上方,还可以看出激波位置处的标准差大概是分离泡处标准差的2.5倍,这说明激波处的流场参数较分离泡处的流场 参数对飞行状态的不确定性更加敏感一些.
|
图 5 流场马赫数云图的(a)均值分布及(b)标准差分布 Fig.5 Mean value distribution (a) and Standard deviation distribution (b) of the $Ma$ distribution of flow field |
本文对翼型表面的气动载荷分布和流场进行了全局灵敏度分析. 图6给出了翼型表面的压力系数以及阻力系数分布的全局灵敏度 分析结果. 其中,压力系数分布具体表现为:激波散布区域以前,仰角和马赫数重要性程度相当;在激波散布区域,马赫数重要性占主要程度,而且马赫数和仰角还有一定的耦合作用.

|
图 6 翼型表面(a) 压力标准方差分布和(b)表面摩擦力分布(马赫数服从$N(0.65,(0.005)^2)$,仰角服从$N(5,(0.2)^2)$正态分布 Fig.6 Standard deviations of the pressure (a) and skin-friction (b) coefficient from global sensitivity analysis($Ma \sim N (0.65,(0.005)^2)$,$\alpha \sim N (5,(0.2)^2)$ |
摩擦力系数分布具体表现:在激波散布区域,马赫数占主导,也有一定的耦合作用而且耦合作用对摩擦力系数分布的贡献和仰角的贡 献基本相当;在激波散布区域之后,马赫数和仰角对摩擦力系数贡献相当且逐渐减小,耦合作用很弱.
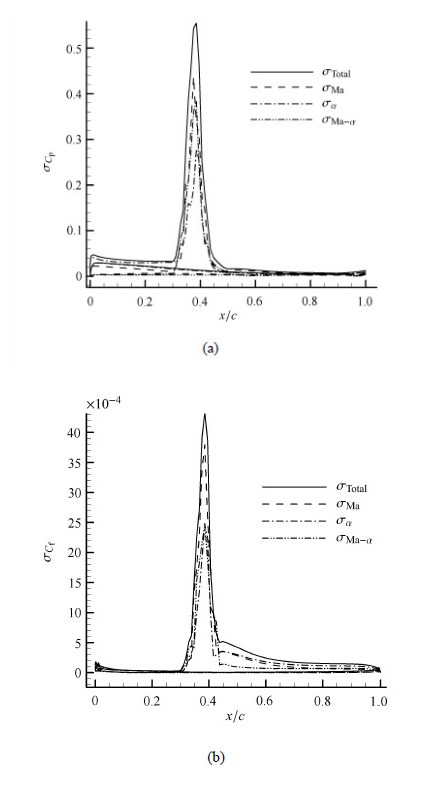
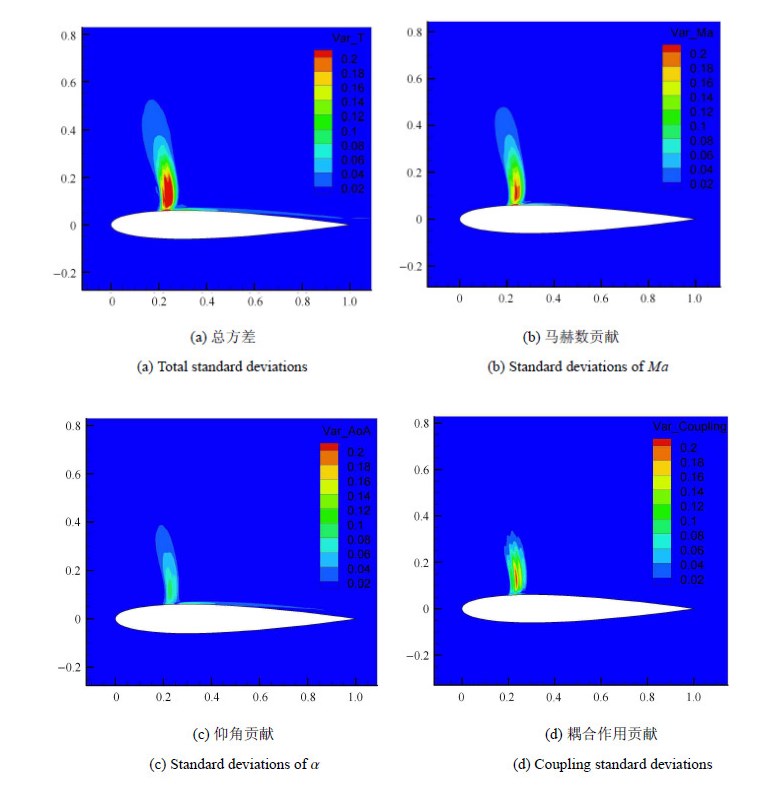
本文还进行了马赫数服从$N(0.73,(0.005)^2)$,仰角服从$N(2.5,(0.2)^2)$正态分布时的不确定性及灵敏度分析,分析结果 如图7. 从图6和图7对比可以看出:本文进行不确定性分析和灵敏度分析的结果和所选取的马赫数和仰角的均值和方差的大小有关. 对于不确定性分析,马赫数和仰角的均值和方差不同,计算出来的气动载荷分布的标准差($\sigma_{\rm Total} $)数值上会有一些不同,但总会表现出激波处以及激波后分离泡处的波动较大,这是由激波及边界层分离的非线性导致的,这正好 解释了气动特性波动的原因,这个结论适合整个跨声速. 此外,灵敏度分析的结果反映出:在跨声速区域,马赫数对气动特性更加敏感一些,马赫数是衡量空气压缩性的最重要参数,所以,对于跨声速流动,空气压缩性是主导因素. 从图8流场全局灵敏度分析结果可以看出马赫数对激波波动贡献最大,激波处交叉耦合作用甚至要强于仰角贡献.
|
图 7 翼型表面(a) 压力标准方差分布和(b)表面摩擦力分布(马赫数服从$N(0.73,(0.005)^2)$,仰角服从$N(2.5,(0.2)^2)$正态分布 Fig.7 Standard deviations of the pressure (a) and skin-friction (b) coefficient from global sensitivity analysis($Ma \sim N(0.73,(0.005)^2)$, $\alpha \sim N(2.5,(0.2)^2))$ |
|
图 8 马赫数云图的全局灵敏度结果 Fig.8 Standard deviations of the $Ma$ distribution of flow field from global sensitivity analysis |
基于后续稳健性优化设计的需要,本小节考虑飞行状态的不确定性对气动力系数的影响,进行全灵敏度分析,找出对气动 力系数影响较大的重要因素.
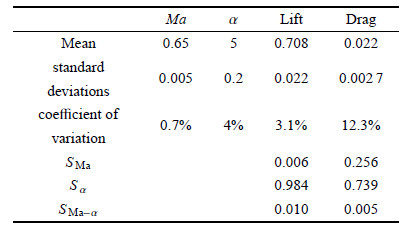
表2给出了气动力系数的不确定及全局灵敏度分析结果,从表中看出,升力系数的变异系数为3.1%,阻力系数变异系数 达到12.3%,可见,在跨声速区域,飞行状态的不确定性可引起阻力系数的剧烈的波动,升力系数波动较小. 全局灵敏度分析结果显示:(1)升力系数的仰角一阶灵敏度指标高达0.983,仰角的变化占主要贡献;(2)马赫数0.7%的波 动的阻力系数变化的贡献为0.256,仰角4%的阻力系数变化的贡献为0.739,这说明跨声速马赫数波动占相当重要作用. (3)马赫数和仰角的耦合交互作用的贡献很小,对升力系数、阻力系数以及升阻比的贡献仅为0.010,0.005,说明马赫数和攻 角的耦合交互作用对气动力系数波动的贡献很小.
| 表 2 气动力系数的不确定性分析及灵敏度结果 Table 2 The results of uncertainty quantification and global sensitivity analysis for aerodynamic coefficients |
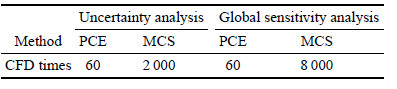
现对混沌多项式方法和蒙特卡洛方法的计算效率进行对比分析,本文采用5阶的混沌多项式方法,混沌多项式方法是一种代理模型方法,根据 式(2),2维5阶的混沌多项式一共有21项,本文抽取60个样本(抽取样本点数一般为项数的1.5$\sim $3倍)用于建模,然后采用蒙特卡洛方法调用所建立的代理模型进行不确定性分析及全局灵敏度分析,调用代理模型进行不确定性及全 局灵敏度分析的时间相对于建模时间是可以忽略的,计算时间主要花费在建立模型上,所以混沌多项式方法进行不确定性及全局灵敏度 分析只需调用60次计算流体力学工具. 蒙特卡洛方法抽取样本数为2\,000个,即要调用2\,000次进行计算流体力学不确定性分析. 蒙特卡洛方法进行全局灵敏度分析,所取的总样本数为$N(k +2)$,其中$N$为所取样本数,$k$为自变量个数[11]. 若$N$取2\,000,由此可以确定若采用蒙特卡洛方法进行全局灵敏度分析 的计算样本量为8\,000次. 表3给出了两种方法进行不确定性分析及全局灵敏度分析调用计算流体力学次数的对比情况,可以看出混沌多项式方法效率较蒙特卡洛 方法有很大的提高.
| 表 3 混沌多项式和蒙特卡洛方法的计算效率的比较 Table 3 CFD times of PCE and MCS for uncertainty analysis and global sensitivity analysis |
本文采用混沌多项式方法对绕NACA0012翼型跨声速流场进行不确定性分析和全局灵敏度分析,得到结论如下:
(1)计算效率方面,在精度满足的条件下混沌多项式方法的计算效率较蒙特卡洛方法有较大提高.
(2)通过对气动载荷及流场不确定性分析,发现飞行状态(马赫数和仰角)不确定性对激波位置、强度变化以及激波后边界层分离影响较 大,这是由激波以及激波后的边界层分离非线性引起的. 通过气动力系数的不确定性分析发现飞行状态对阻力特性的影响较大. 流场的不确定分析可以解释为什么不确定性因素对阻力特性影响大.
(3)从流场灵敏度分析结果看出,跨声速区域,马赫数对激波以及激波后分离泡的影响占主导,在激波处马赫数和仰角交叉耦合作用 不能忽略. 对于气动力系数灵敏度,仰角对升力系数占绝对主导,跨声速马赫数波动占相当重要作用,而且马赫数和仰角耦合作用对力系数的 影响很小,几乎可以忽略.
| [1] | Zang TA, Hemsch MJ, Hilburger MW, et al. Needs and opportunities for uncertainty-based multidisciplinary design methods for aerospace vehicle. NASA/TM-2002-211462, 2002 |
| [2] | Yao W, Chen XQ, Luo WC, et al. Review of uncertainty-based multidisciplinary design optimization methods for aerospace vehicles. Progress in Aerospace Sciences, 2011, 47: 450-479 |
| [3] | Jaekwon A, Kim HJ, Dong HL, et al. Response surface method for airfoil design in transonic flow. Journal of Aircraft, 2001, 38 (2): 231-238 |
| [4] | Armando V, Ning Q. Iterative response surface based optimization scheme for transonic airfoil design. Journal of Aircraft, 2007, 44 (2): 365-376 |
| [5] | Leifur L, Slawomir K. Multi-fidelity design optimization of transonic airfoils using physics-based surrogate modeling and shape-preserving response prediction. Journal of Computational Science, 2010, 1: 98-106 |
| [6] | Li W, Huyse L, Padula S. Robust airfoil optimization to achieve consistent drag reduction over a mach range. NASA/CR-2001-211042, 2001 |
| [7] | Padulo M, Maginot J, Guenov M. Airfoil design under uncertainty with Robust geometric parameterization. AIAA Paper 2009-2270, 2009 |
| [8] | Croicu AM, Hussaini MY, Jameson A, et al. Robust airfoil optimization using maximum expected value and expected maximum value approaches. AIAA Journal, 2012, 50 (9): 1905-1919 |
| [9] | Padulo M, Campobasso MS, Guenov MD. Novel uncertainty propagation method for robust aerodynamic design. AIAA Journal, 2011, 49 (3): 530-543 |
| [10] | Sobol IM. Global sensitivity indices for nonlinear mathematical models and their monte carlo estimates. Mathematics and Computers in Simulation, 2001, 55: 271-280 |
| [11] | Saltelli A, Ratto M, Andres T, et al. Global Sensitivity Analysis. The Primer. England: John Wiley & Sons, Ltd, 2008 |
| [12] | Pelletier D, Turgeon E, Lacasse D. Adaptivity, sensitivity, and uncertainty: toward standards of good practice in computational fluid dynamics. AIAA Journal, 2003, 41 (10): 1925-1932 |
| [13] | Luckring JM, Hemsch MJ, Morrison JH. Uncertainty in computational aerodynamics. AIAA Paper 2003-409, 2003 |
| [14] | Walters RW, Huyse L. Uncertainty analysis for fluid mechanics with applications. NACA/CR-2002-211449, 2002 |
| [15] | Knio OM, Maitre OPL. Uncertainty propagation in CFD using polynomial chaos decomposition. Fluid Dynamics Research, 2006, 38: 616-640 |
| [16] | Najm HN. Uncertainty quantification and polynomial chaos techniques in Computational fluid dynamics. Annual Review of Fluid Mechanics, 2009, 41: 35-52 |
| [17] | Mathelin L, Hussaini MY, Zang TZ. Stochastic approaches to uncertainty quantification in CFD simulations. Numerical Algorithms, 2005, 38(1): 209-236 |
| [18] | Simon F, Guillen P, Sagaut P, et al. A GPC-based approach to uncertain transonic aerodynamics. Computer Methods in Applied Mechanics and Engineering, 2010, 199: 1091-1099 |
| [19] | Chassaing JC, Lucor D. Stochastic investigation of flows about airfoils at transonic speeds. AIAA Journal, 2010, 48(5): 918-949 |
| [20] | 王晓东, 康顺. 多项式混沌法求解随机Burgers 方程.工程热物理学报, 2010, 31(3): 393-398 (Wang Xiaodong, Kang Shun. Solving stochastic burgers equation using polynomial chaos decomposition. Journal of Engineering Thermophysics, 2010, 31(3): 393-398 (in Chinese)) |
| [21] | 赵轲, 高正红, 黄江涛等. 基于PCE方法的翼型不确定分析及稳健设计.力学学报, 2014, 46 (1): 10-19 (Zhao Ke, Gao Zhenghong, Huang Jiangtao, et al. Uncertainty quantification and robust design of airfoil based on polynomial chaos technique. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46 (1): 10-19 (in Chinese)) |
| [22] | Xiu D, Karniadakis GE. Modeling uncertainty in flow simulations via generalized polynomial chaos. Journals of Computational Physis, 2003, 187: 137-146 |
 2015, Vol. 47
2015, Vol. 47