半浮区液桥是指被表面张力限制在两根同轴圆柱间的一段液体,当两端存在温差时,液桥内部会产生对流,当温差超过临界值或对应 临界马兰哥尼数时,内部流动就会由定常流动转变为振荡流动[1, 2]. 在常重力地面实验中,液桥的流动为浮力对流和热毛细对流耦合的对流模式,即浮力-热毛细对流;而在微重力的空 间实验中,热毛细力是引起失稳的机制. 其中无量纲参数马兰哥尼数($Ma$)表征热毛细力作用强弱,动态邦德(Bond)数($Bd$)用于表征热毛细力与浮力作用的强弱关系. 其定义如下
| $ \begin{array}{l} Ma = \frac{{\left| {\Delta \sigma } \right|\Delta TH}}{{\mu \kappa }}\\ Bd = \frac{{\rho g\beta {H^2}}}{{|{{\sigma '}_T}|}} \end{array} $ |
浮区法地面单晶生长尺寸受到重力限制,空间微重力环境为大尺寸的单晶生长提供了可能,但此时其生长仍然受到表面张力的 影响. 在地面常重力环境下开展的实验研究中,为减小重力影响突出表面张力作用,通常选取桥柱直径范围为3$\sim$5mm小尺寸液 桥作为实验研究模型. 由于大尺寸液桥在地面环境中难于建立,特别是大高径比的大尺寸液桥在地面重力环境中根本无法建立. 因此,只能寻求空间实验机会开展大尺寸液桥热毛细对流问题研究. 鉴于空间实验机会少且费用极高,首先在地面开展大尺寸液桥小高径比情况下的科学研究,为空间试验提供参考显得尤为重要.
以晶体生长为背景,国内外学者对半浮区晶体生长进行了大量的理论和实验研究. 在液桥热毛细对流转捩过程的研究中大部分研究把 注意力集中在液桥内部温度振荡上. 根据温度振荡提出了流动存在转捩,临界值受几何参数的影响[3, 4],并且由温度分布情况研究了流动模式[5]. 其实,随着马兰哥尼数增加,液桥流场从定常流动转化到振荡流,都必然会伴随着速度场变化. 目前地面实验局限于小尺寸液桥的研究[6, 7],有关大尺寸液桥的研究仅日本在国际空间站[8, 9, 10, 11, 12]开展 了空间实验,但并未考虑体积比对临界参数的影响.
本文为配合正在开展的天宫2号载人航天项目,在地面常重力条件下开展桥柱直径为20mm的大尺寸液桥匹配实验研究. 不仅仔细测量和分析了大尺寸液桥流场结构,还给出了转捩的临界条件和临界状态附近的流动规律. 实验观测了液桥自由面温度分布情况,得到各种波形出现的条件及特征,并且首次在地面实验中验证了大尺寸液桥体积比效应.
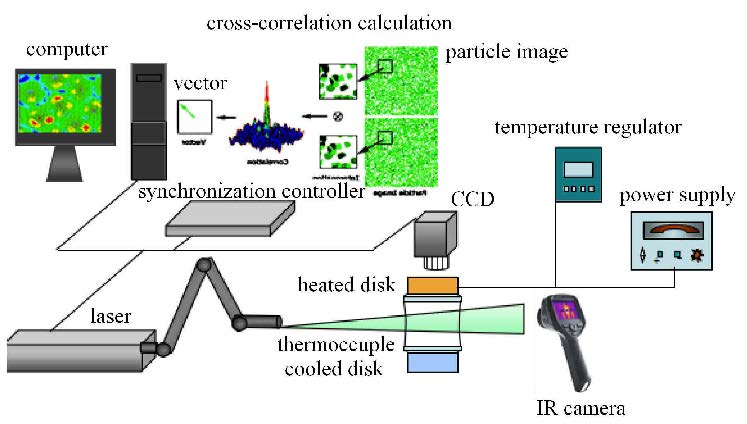
1 实验系统与方法实验装置如图1所示,在两个同轴的桥端面间注入2号硅油形成液桥. 上、下桥柱直径均为20mm,上桥采用导热耐热性好、透明 度高的蓝宝石,下桥为铜柱(见图2(b));上桥采用电热膜加热,加热的额定功率为38W,下桥用制冷片散热. 由于蓝宝石的导热率比硅油大2个量级,上桥端面沿径向的温度分布接近于常数,本文中的半浮区液桥模型可近似于通常的两 端皆为铜柱的半浮区模型. 实验的温控部分采用欧陆(ERUOTHERM)3504型温度调节器采用比例积分微分(PID)算法进行控制,温度的稳定性为0.01${^\circ}$C. 并可以根据设定程序线性升温或者控制在某一温度. 实验中可通过移动上桥控制桥 高,获得不同的高径比. 上下两桥柱为防止液体爬升,均在桥柱侧面做了微小的倒角,并涂上防爬液FC-4430,防止液体静压导致体积比的减小. 在实验过程中,注液产生的误差为2.22%,模型加工引起的误差为1.24%,整个实验误差为3.46%.
|
图 1 测量系统 Fig.1 Measurement system |

|
图 2 液桥示意图 Fig.2 Liquid bridge schematic diagram |
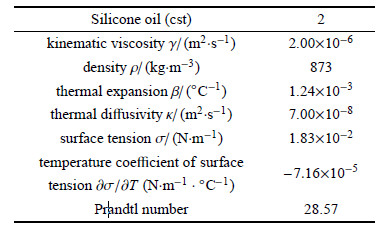
实验流体介质选取日本Shin-Etsu Chemical公司的2号硅油. 物性参数如表1所示.
| 表 1 2号硅油的物性参数 Table 1 Physical properties of KF96-2 |
根据理论和日本空间实验结果,温度振荡发生在马兰哥尼数为20000时. 选取2号硅油是因为在可以实现的温差下能够获得较大的 马兰哥尼数,这使得能够在一次实验中观察到对流由定常到振荡的整个过程. 实验中控制高径比($As=H/D$)为0.15$\sim $0.2,体积比($Vr=V/V_{0}$,$V$是两桥柱间液体体积,$V_{0}$是两桥柱间的体积)为0.7$\sim $1.0.
粒子图像采集系统是由计算机、摄像机(CCD)、激光器、粒子图像测速处理软件等组成. 摄像机的分辨率为640$\times $480像素,最高 采样频率达到200帧每秒,由于实验中粒子速度较小,采用的采样频率为140帧每秒. 用10μm的镀银空心玻璃小球作为示踪粒子. 由于液桥本身相当于一个放大率在中心和边缘不同的透镜,会使结果产生相当大的误差. 因此,在实验中激光通过柱透镜形成水平片光,照亮流场的水平截面,通过摄像机在上桥柱正上方俯拍粒子图像. 图像经自相关运算[13]得到流场的速度矢量图,进而研究液桥浮力-热毛细对流的流动特性和涡胞结构.
温度采集系统由计算机、HP34970A型6位半数字万用表以及T型热电偶组成. 其中热电偶共有7路,2路控温,其余5路从下桥柱 的同一圆周(直径15mm) 上5 个孔中(孔径1mm),向上伸出桥柱2mm,并用导热硅胶填满小孔防止漏液(如图2(a)). 加热空载时5路热电偶间最大温差为0.15${^\circ}$C,选取中值作为测量结果. 测量灵敏度可达$\pm $0.01${^\circ}$C,采样率为6.67Hz,满足实验测量要求.
为了得到温度场的全貌,本文用美国FLIR公司分辨率为320$\times $240像素、热灵敏度小于$ 0.05{^\circ}$C的红外热像仪对液 桥自由面进行温度采集. 实验在封闭的暗室中进行,保持室温恒定,设置正确的发射率和工作距离.
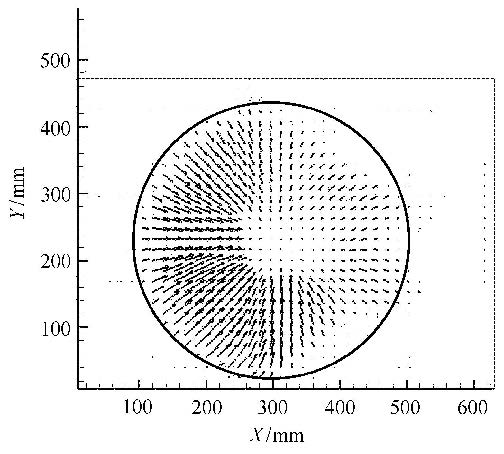
2 实验结果及分析 2.1 测速结果维持冷端温度为室温,热端以0.3${^\circ}$C/min的升温速率升高至温差为30${^\circ}$C,通过粒子图像采集系统,得到不同马 兰哥尼数下的流场结构,有助于认识液桥热毛细对流结构及其转捩过程. 图3所示的是高径比为0.18,体积比为0.9的速度矢量图.
|
图 3 粒子图像测速定常流动 Fig.3 Stationary flow observed by PIV |
在未达到临界值时,从水平截面可观测到流体在表面张力和浮力的共同作用下由边缘向中部区域均匀流动,流场呈现定常流动.
逐渐增大液桥两端温差,当刚达到临界马兰哥尼数时,流场出现如图4所示涡胞结构,与地面小尺寸液桥涡胞充满整个流场 不同[14],大尺寸液桥涡胞仅限于周边区域,这说明大尺寸模型与实际工业晶体生长更为相符. 涡胞的周向运动导致了行波运动,由于液桥是轴对称模型,行波旋转的方向和上下桥柱的水平性、同轴度、加热的均匀性均有关,具有不确定性.

|
图 4 流动模式随高径比变化 Fig.4 Change of flow patterns with ratio of height to diameter |
不仅临界参数受高径比的影响,流动模式同样会随高径比发生变化. 由于重力的限制,本文仅对小高径比情况下的液桥流动模式进行研究. 维持体积比为0.9,随着高径比的增大,液桥流动模式逐级减少. 当液桥高径比为0.15时,流场形成6对小涡胞结构,流动模式($m$)为6. 当时高径比为0.18,流场具有5对小涡胞结构,流动模式是5. 当高径比增大到0.2时,流场减为4对涡胞,流动模式为4. 这和李凯等[15]计算所得温度场的结果相一致(图4). 体积比相同时,高径比越大,液桥两端的温度梯度分布不均匀性也越大,液桥内出现冷点和热点的概率增大,导致稳定流动模式的临界值降低. 但此时流体质点在液桥表面附近运动一个周期所经过的路程变长,这与流动模式减小有关. 同理,高径比相同时,体积比越大,在重力的作用下,液桥自由面的变形越小,浮力对流的作用更加明显导致出现振荡的临界参数降低.
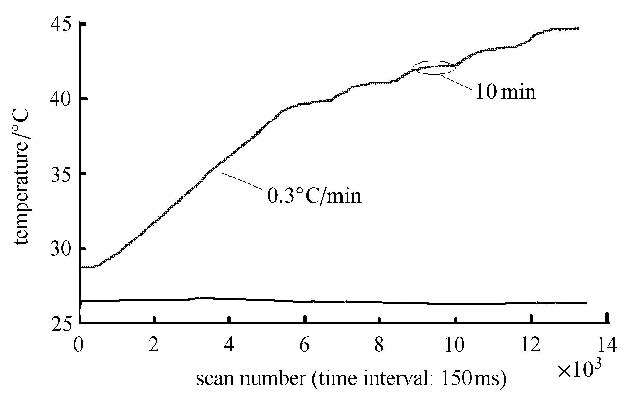
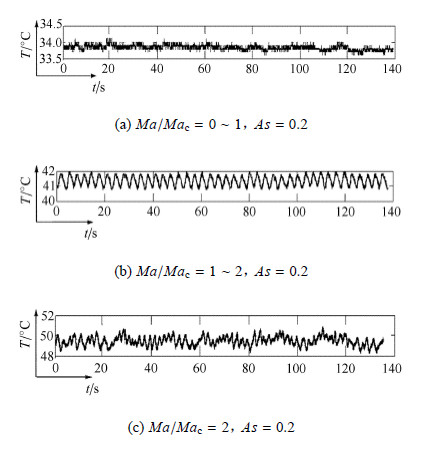
2.2 测温结果热毛细对流是温度不均匀引起的,另一方面对流又会影响温度分布. 本文通过红外测温系统观测液桥自由面的温度分布情况. 实验 中采用如图5在振荡之前线性升温,出现振荡后台阶式升温的升温方式. 当温度未超过临界值时,图6伪彩色处理的红外图像(a)中自由面温度场未出现波动,自由面上的温度自上桥端面至下桥端面呈现 条带状逐渐降低的分布. 对比热电偶同时测定的单点温度图7(a),此时温度没有明显的变化规律,显示为幅值很小的扰动. 当超过临界值,自由面会出现图6(b)中沿周向传播的波,这和粒子图像测速中观测到的旋转涡胞相一致. 当两端温差进一步加大,由于温度梯度分布不均匀性增大,使得自由面的温度分布会变得更极为不规则,见图6(c).
|
图 5 液桥升温曲线 Fig.5 Liquid bridge heating curve |

|
图 6 液桥红外图像 Fig.6 Liquid bridge infrared image |
|
图 7 热电偶单点温度振荡曲线 Fig.7 Single point temperature oscillation curve |
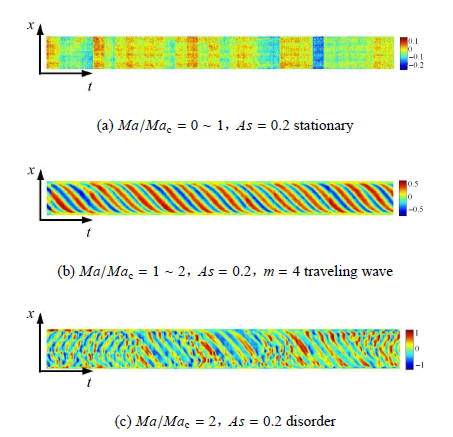
为了更加清晰地得到液桥自由面上各个阶段温度演化,对各个温度振荡过程进行时间演化. 选取实验所得结果中液桥弯液面最窄处的 直线(图6中水平黑线),如图8所示,横轴代表时间,纵轴代表位置,颜色代表温度幅值. 通过时间演化可以清楚地看到,随马兰哥尼数增大,温度振荡由规则向着无规则的方向发展. 当高径比是0.20,体积比为0.9,马兰哥尼数与临界马兰哥尼数之比($Ma/Ma_{\rm c})$在1$\sim $2,液桥自由面上出现沿单一方向传播的行波,这说明此时热电偶测得的单点温度开始出现较为规则的周期性振荡是由行波引起的. 当比值超过2时,液桥自由面上出现的多条波相互间作用强烈,以致出现无规则的运动状态,热电偶单点温度出现周期性不明显的较大的波动. 在此过程中,温度振荡的幅值随温差的增大也在增大. 与上述相同条件下的粒子图像测速实验结果对比,如图8(b)在180$^\circ$的视角范围内可见有两条行波,由此推之,整个液桥 流场模式为4,和图4(c)两者在相同条件下拥有相同的流场模式.
|
图 8 红外温度波动时间演化 Fig.8 Time evolution of temperature fluctuation |
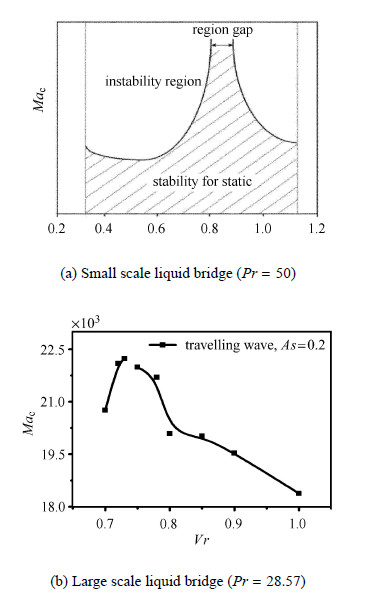
结合热电偶和红外结果,得到图9(b)所示大尺寸液桥行波临界参数与体积比的关系. 对比图9(a)胡院士[16]对小尺寸液桥理论 结果,两者具有相同的变化趋势,表现出非线性特征. 发生振荡的临界值随体积比的变化曲线分为两支-瘦桥分支和胖桥分支,典型的半浮区液桥热毛细对流存在稳定区域. 这是大尺寸液桥地面实验体积比效应的首次验证. 基于工业应用,体积比效应的研究有助于在晶体尺寸和高径比固定情况下选择合适的体积比,延迟或者避免液桥内部振荡的产生.
|
图 9 热毛细对流起振的临界马兰哥尼数与液桥体积比的关系曲线 Fig.9 Typical Marginal curves depending on liquid bridge volume for onset of oscillatory thermocapillary convection |
本实验在地面常重力环境中研究了大尺寸液桥小高径比条件下液桥内部的浮力-热毛细对流流场结构和流动模式. 得到了流场结构和流动模式随临界值和几何参数的变化关系.
通过粒子图像测速测速技术测得了定常和非定常情况下液桥内部的流场运动情况,同时测定了不同高度条件下流动模式的变化情况. 液桥流动模式随着液桥高径比增加而呈现减小的趋势. 为了获得液桥自由面的温度分布情况,利用高精度红外热像仪采集温度,随着温差的增大,浮力-热毛细流动更加强烈,自由面的温度会产生定常到行波再到不规则的运动规律. 在体积比相同的情况下,液桥高度越高,桥两端温度分布不均匀性增大,温度分布在液桥两端处达到最值,中段温度梯度较小,这种差异导致液桥更容易失稳发生温度振荡,此时所需要的临界温度差要小.
本文主要研究了大普朗特数大尺寸液桥浮力-热毛细对流流动结构、模式转换、高径比、体积比问题,实验为天宫2号空间实验研究提供了地面科学匹配实验结果,为空间实验成功提供基本保障,也希望本文的结果能够为今后半浮区液桥的研究提供一定的实验参考.
| [1] | 胡文瑞.微重力科学概论. 北京:科学出版社, 2010: 55-56 (Hu Wenrui. Overview of Microgravity Science. Beijing: Science Press, 2010: 55-56 (in Chinese)) |
| [2] | Levenstam M, Amberg G. Hydrodynamic instabilities of thermocapillary flow in half zone. Fluid Mechanics, 1995, 297: 357-372 |
| [3] | 吴勇强, 段俐, 李永强等.大普朗特数大液桥浮力-热毛细对流地面实验.力学学报, 2012, 44(6):981-989 (Wu Yongqiang, Duan Li, Li Yongqiang, et al. Ground experiments of bouyant-thermocapillary convection of large scale liquid bridge with large prandtl number. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(6):981-989 (in Chinese)) |
| [4] | Chen QS, Hu WR. Influence of liquid bridge volume on instability of floating half-zone convection. Heat Mass Transfer, 1998, 41: 825-837 |
| [5] | Zeng Z, Mizuseki H, Higashino K. Direct numerical simulation of oscillatory Marangoni convection in cylindrical liquid bridges. Journal of Crystal Growth, 1999, 204: 395-404 |
| [6] | 解京昌, 唐泽眉, 胡文瑞. 半浮区液桥热毛细对流速度场特征. 力学学报,1993, 25(1):111-115 (Xie Jingchang, Tang Zemei, Hu Wenrui. Velocity field of thermocapillary convection in liquid bridge of half floating zone. Acta Mechanica Sinica , 1993, 25(1):111-115 (in Chinese)) |
| [7] | Ueno I, Tanaka S, Kawamura H. Oscillatory and chaotic thermocapillary convection in a half-zone liquid bridge. Physics of Fluid, 2003, 15 (2): 408-416 |
| [8] | Kawamura H, Nishino K, Mastumoto S. Report on microgravity experiments of Maragoni convection aboard international space station. Transactions of ASME. Journal of Heat Transfer, 2012, 134: 031005-031018 |
| [9] | Yano T, Nishino K, Kawamura H, et al. Space experiment on the instability of Marangoni convection in large liquid bridge-MEIS-4: Effect of Prandtl number. Journal of Physics, 2011, 327: 012029-012036 |
| [10] | Yano T, Nishino K, Kawamura H, et al. 3-D PTV measurement of Marangoni convection in liquid bridge in space experiment. Exp Fluids , 2012, 53: 9-20 |
| [11] | Sato F, Ueno I, Kawamura H, et al. Hydrothermal wave instability in a high-aspect-ratio liquid bridge of Pr > 200. Microgravity Sci Technol , 2013, 25: 43-58 |
| [12] | Yano T, Nishino K, Kawamura H, et al. Effect of liquid bridge shape on the instability of marangoni convection in space experiment. In: Proc. of 15th International Symposium on Flow Visualization, Belarus, 2012, 6: 25-28 |
| [13] | 段俐, 康琦,申功忻.粒子图像测速技术的粒子图像处理方法.北京航空航天大学学报, 2000, 26(1): 79-82 (Duan Li, Kang Qi, Shen Gongxin. The particle image processing method of PIV technology. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(1): 79-82 (in Chinese)) |
| [14] | Sakuraia M, Ohishib N, Hirata A. Oscillatory thermocapillary convection in a liquid bridge: Part 1-1g Experiments. Journal of Crystal Growth , 2007, 308: 352-359 |
| [15] | 寻波.液桥热毛细对流及其稳定性的研究. [博士论文]. 北京:中国科学院力学研究所, 2011(Xun Bo. Study of the thermocapillary flow in liquid bridge and its stability. [PhD Thesis]. Beijing: Institute of Mechanics, Chinese Academy of Sciences, 2011 (in Chinese)) |
| [16] | Hu WR, Tang ZM. Floating Zone Convection in Crystal Growth Modeling. Beijing, New York: Science Press, 2003: 90-92 |
 2015, Vol. 47
2015, Vol. 47