壁面湍流的流动控制技术因其广泛的应用范围被大量研究[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]. 绝大多数壁面湍流的流动控制技术都是基于近壁区拟 序结构控制的. 近年的研究已经表明拟序结构可以在$20<y^{+}<60$的近壁区形成一种自维持的循环机制,在这一循环中,流向涡通过对周围流体的 剪切输运过程来产生交错的流向条带,而条带反过来会通过失稳而形成流向涡. 流向涡、条带或流向流动强弱的改变会造成整个循环机制相应的变化. 由于流向涡是诱导湍流猝发的重要因素,而湍流猝发是雷诺应力的来源,因此流向涡$\!$-$\!$-$\!$条带的循环过程是近壁区湍流形成 和维持的主要机理,也是壁面产生摩擦阻力的重要原因. 如果能够中断或抑制上述循环过程,如抑制流向涡的形成,就可能减弱湍流猝发,从而减小雷诺应力,最终达到减少壁面摩擦阻力的目的.
目前许多减小摩擦阻力的方式是通过减弱湍流猝发,减小或抑制壁面结构再生过程而实现. 常用的控制手段有定常吹吸气控制,周期吹吸气控制及合成射流控制.
定常吹吸气控制由于可以向湍流边界层注入或带走质量与动量,被认为可以有效地对壁面结构再生过程进行控制而被大量研究. Antonia等[1, 2, 3]通过对二维均匀狭缝吸气研究,发现更长的流向保持性及更弱的展向波动会加强低速条带的稳定性. 壁面区域中加强的流动结构则意味着更大的非各项同性. Chung等[4] 通过直接数值模拟的方式证明了吹气控制会增加横向和展向速度脉动并减弱近壁湍流的各项异性性质;与此相反,吸气控制则会加强近壁湍流的各项异性性质. Park等[5]通过DNS方法验证了狭缝均匀吹气会减小壁面摩擦,增大脉动变动量;而狭缝均匀吸气则会起到相反的效果. Yoshida等[6]通过DNS方法发现吸气可以刺激流向涡结构的出现,吹气则会抑制流向涡结构的出现,因此可以实现对壁面湍流的抑制.
相对于定常吹气,周期性吹吸气由于其更灵活参数控制方式和更有效的与近壁区流动结构相耦合而被认为是一种控制壁面湍流的十分有效方式,不少研究人员对其进行了深入的研究. Kim和Sung[7, 8]通过一个展向狭缝的定常及周期性吹气的研究,发现周期性吹气可以使靠近狭缝的区域摩擦应力减小,得到了与定常吹气相同的控制效果. 此外,Kim和Sung总结出周期性吹气和定常吹气减阻机理的不同之处主要在于:周期性吹气与定常吹气在狭缝下游摩擦应力减小区域的范围稍有不同;相较连续吹气抬升流向涡的减阻机理,周期性吹气在狭缝的下游产生负涡量的运动展向涡结构,且频率越高,展向涡尺度越小. 由于负展向涡结构会引起近壁的反向流动,从而也减小摩阻. 此外,周期性吹气相对于定常吹气减弱了流向涡的脉动,加强了壁面法向和展向的脉动. 国内的姜楠等[9, 10, 11, 12] 利用扬声器也展开了周期性吹吸实验研究. 结果表明周期性吹吸随着扰动频率的增大,黏性底层有增厚的现象,这是典型的壁面减阻的特征;此外,扰动引起的负展向涡会产生``流体滚动轴承''的作用而使得壁面摩阻减小.
总之,大量的研究结果表明定常吸气控制通常会增加壁面摩擦,减小湍流度,加强近壁湍流的各项异性性质;定常吹气控制通常会减小壁面摩擦,增大湍流度,减小近壁湍流的各项异性性质. 定常吹气的减阻效果是通过减小或抑制壁面结构再生过程而实现的,即湍流的猝发被抑制了. 其中,湍流的猝发事件可由Variable Interval Time Average(VITA)技术检测. VITA技术最初由Blackwelder[13]提出. 该技术的原理是:认为一次上抛和一次下扫组成一次猝发事件,当局部方差大于所设定的条件时便认为出现了一次下扫事件,即出现了一次猝发事件. 这样,通过探测壁面附近高速事件(下扫),就可以统计出猝发事件的次数,再对发生猝发的时刻做条件平均,便可得出该时刻猝发事件的强度. 这样,近壁区的猝发事件的次数和强度便都可获得.
相较而言,周期吹气控制将不仅仅产生吹气的效果,其引入的运动展向涡结构将会引起更复杂的流动现象[14, 15, 16, 17, 18]. 频率不同的周期扰动将产生相应尺度大小的展向涡结构,频率越高,负展向涡尺度越小. 显然,更高频的扰动,将产生与猝发引起的结构变化尺度相当的负展向涡结构. 这些结构的存在将直接影响近壁区拟序结构产生与发展的统计特性. 因此,这种更高频的非定常流动控制引起的复杂流动现象值得进一步的研究.
为了引入高频周期性扰动,合成射流是一种理想的激励器. 合成射流控制由于具有不需要流场中注入质量,且其振幅与频率均可调整而能针对特定的流动实现最佳的控制效果等优点而有着可观的应用潜力[19, 20]. 本文为研究高频周期扰动对于壁面湍流结构统计特性的影响,将激励器的无量纲频率设为猝发事件的持续时间对应的频率,以考察该频率的周期扰动产生的与猝发引起的拟序结构变化尺度相当的运动展向涡结构对湍流边界层的统计特性影响;同时,将射流强度设计为较大的值以实现吹气狭缝下游区域流动的显著变化.
1 实验设备和装置本实验是在北京航空航天大学流体所D3二元低速风洞中完成的. 风洞为水平直流闭口式结构,实验段尺寸为:高2.8m,宽0.2m,长2m,实验段最大风速可达25m/s,气流湍流度为0.3%. 实验测量仪器为Dantec公司所产StreamLine CTA (Constant Temperature Anemometer)恒温热线风速仪系统,数据采集采用1维边界层探头55P15,采样频率为32kHz,样本数为3840000.
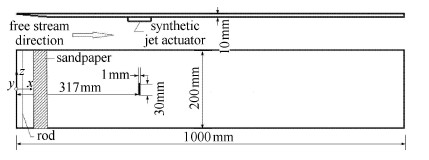
平板实验模型选用长1000mm,宽200mm,厚10mm,前缘为5$^\circ$ 斜角的铝板. 人工转捩措施由1根直径1mm的圆棒和沿流向50mm的40号砂纸组成. 合成射流激励器位于平板来流317mm位置处,射流狭缝出口流向长度1mm,展向宽度30mm. 平板水平固定在风洞实验段内,楔形前缘正对来流方向,平板模型如图1所示. 本文坐标系设置为右手直角坐标系,坐标原点位于前缘线与对称面的焦点,$x$轴沿流向,$y$轴沿法向,$z$轴沿展向.
|
图 1 实验模型图 Fig.1 Experimental model |
周期性扰动主要由两个参数来定义其强度. 一个参数是吹吸率$C_{\rm q}$,$C_{\rm q}=V_{\rm slot}/U_{\rm free}$,其中$V_{\rm slot}$为吹吸速度,$U_{\rm free}$为自由来流速度. Ugrina\,[20]根据吹吸率$C_{\rm q}$将合成射流与来流速度的相互作用分为两类:当$C_{\rm q}>1$时射流将穿透边界层,这通常用于分离控制;当$C_{\rm q}<1$时,射流将被束缚在边界层内,这通常用于减阻控制. 另一个参数为$\sigma $,$\sigma =V_{\rm slot}b/(U_{\rm free} \theta_{\rm slot})$,其中$\theta_{\rm slot}$为无扰动时狭缝处的动量厚度. Kim 等[18]提出了另一种评估方式$\sigma^+$,$\sigma^+ =V_{\rm slot}^{ + }b^{ + }= \sigma Re_{\theta ,\rm slot}$. 由于$\sigma^{+}$是雷诺数相关的,因此被认为是更加合理的描述参数. 对于扰动的频率$f_{\rm a}$,通常选用激励器的无量纲频率$f_{\rm a}^{ + }$来描述,其中$f_{\rm a}^{ + }=f_{\rm a} \nu/u_{\tau }^{2}$. 对于已有的大部分实验,均将$f_{\rm a}^{ + }$选为猝发事件的间隔时间对应的频率来实现射流与拟序结构更充分的相互作用.
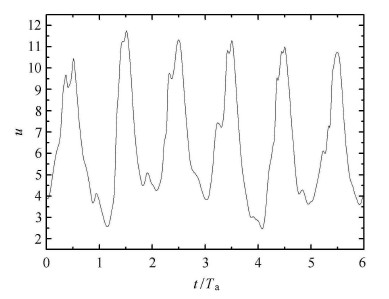
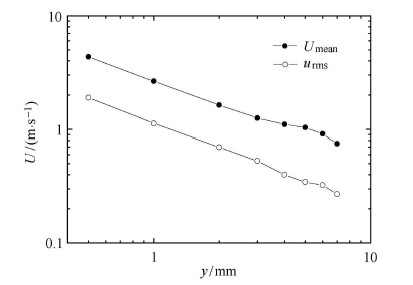
实验中采用的合成射流激励器为压电陶瓷控制式合成射流. 压电式合成射流激励器的振动膜片采用黄铜和压电陶瓷片黏结而成,采用螺栓进行固定,通过橡胶圈来保持腔体的密封. 压电陶瓷片的尺寸为:陶瓷片$D =30$mm,铜片$D=50$mm,腔体直径选择为$D=40$mm,选取腔体深度为4mm. 激励器激励频率设定为$f_{\rm a}=1\,600$\,Hz,对应的无量纲频率$f_{\rm a}^{ + }=0.1$,接近于猝发事件的持续时间(其中摩擦速度为狭缝位置无控时的摩擦速度). 在激励器狭缝口上方0.5mm测得的 速度信号如图2所示,可见合成射流形成高频周期吹气扰动效果. 该周期扰动的时均速度及脉动速度的衰减如图3所示. 激励器的吹吸率$C_{\rm q} =0.6$,无量纲吹气强度$\sigma^+=431$.
|
图 2 6个周期的吹气扰动速度时间序列信号 Fig.2 Oscillating velocities during six cycles of the synthetic jet actuator |
|
图 3 扰动时均速度及脉动速度在法向的衰减 Fig.3 The decay of injection |
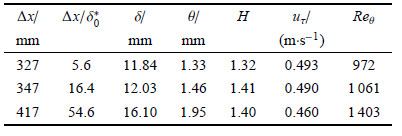
实验中的自由来流速度为10.9m/s. 使用边界层探头55P15对狭缝口及距狭缝口下游距离$\Delta x$ (10mm,30mm和100mm)的位置沿法向测量. 无扰动时狭缝口的动量厚度雷诺数约为966,边界层厚度为$\delta _{0} =11.24$mm,位移厚度为$\delta _{0}^{*}=1.832$mm. 狭缝下游各测量位置的边界层主要参数如表1所示.
| 表 1 各测量站位无扰动时的边界层参数 Table 1 Boundary parameters for each testing location |
本文中,空心圆圈表示无扰动实验结果,实心圆圈表示有扰动实验结果. 扰动前后的时均速度型如图4所示. 横轴为$y^{ + }=yu_{\tau }/\nu $,其中$u_{\tau }$是摩擦速度,$\nu $是运动黏性系数;纵轴为$U^{ + }=U/u_{\tau}$. 摩擦速度$u_{\tau }$通过Clauser图表法确定,各个站位的$u_{\tau }$已列于表1中. 图中曲线是White\,[21]给出的壁面积分律
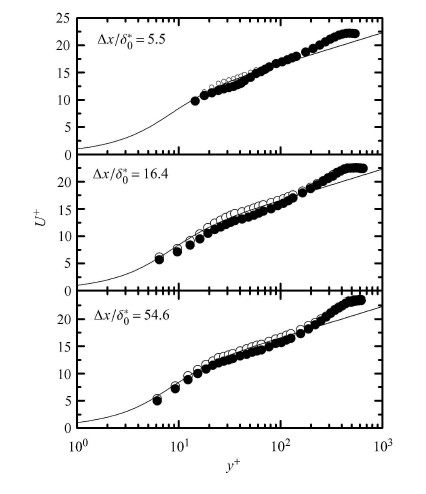
|
图 4 各流向位置的时均速度型 Fig.4 Streamwise mean velocity profiles |
| $ {U^ + } = {\rm{ }}\int_0^{{y^ + }} {\frac{2}{{1 + {{\{ 1 + 4{\kappa ^2}{y^{ + 2}}{{[1 - \exp ( - {y^ + }/A)]}^2}\} }^{1/2}}}}} d{y^ + } $ | (1) |
式中,$\kappa = 0.41$,$A = 25.0$.
从图4可知扰动后狭缝下游的3个流向位置均出现了速度亏损. 速度亏损表明了减阻效果:这是因为各个站位都是由其所对应的无控壁面 变量$u_{\tau }$进行无量纲的;速度亏损意味着同一高度时均速度变小,因此加控后的壁面摩擦速度$u_{\tau }$减小,相应的壁面摩阻减小. 从图4还可以看出,速度亏损区的范围随着远离狭缝而变大. 由于扰动作用前后尾迹区的数据重合,因此在本文观测范围内扰动的作用范围始终处于边界层内部.
各流向位置扰动前后的脉动速度对比如图5所示. 脉动速度由无扰动时的壁面变量无量纲化. 扰动后的脉动速度型在近壁区(黏性底层,过渡区及对数区的内侧)减小,而在对数区外侧的区域增加,出现``双峰''的效果. 这种结果与大量的减阻实验有着相似效果,如Park 等[14]的DNS结果. 近壁区脉动速度的减小,实际是近壁区拟序结构被吹气抬升而造成的. 大量吹气研究认为拟序结构被抬升导致了拟序结构与壁面的作用变弱,因而是壁面摩擦阻力 减小的一个因素,并且这个因素也是导致``双峰''效果出现的原因.
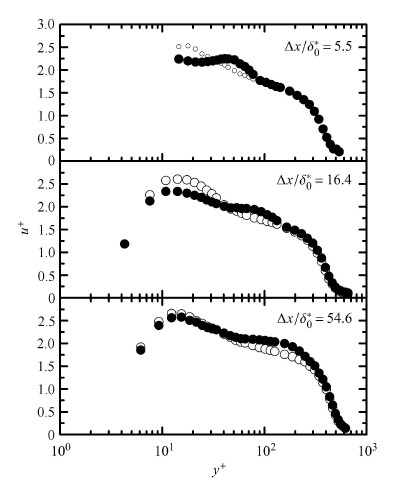
|
图 5 各流向位置脉动速度型 Fig.5 Streamwise velocity fluctuation profiles |
从高频周期扰动对于壁湍流时均流场的影响可 知,周期吹气扰动产生了与连续吹气相似的减阻效果. 显然,该扰动将在湍流边界层内引入一个高频周期扰动. 各流向位置扰动前后不同法向位置无量纲能谱曲线如图6 所示. 图中虚线与实线分别为吹气前后无量纲能谱曲线. 无量纲量选择所在位置无扰动时的脉动均方差. 受扰动作用的曲线有一个尖峰,对应的频率为1\,600\,Hz,即为引入扰动的频率$f_{\rm a}$. 该尖峰在距离激励器狭缝最近位置$\Delta x/ \delta _{0}^{*} =5.5$处十分显著,随着与狭缝距离增加而减弱,到了$\Delta x /\delta_{0}^{*}=56.4$处明显变弱. 这个现象表明合成射流将一个频率为1\,600\,Hz的高频周期扰动引入了流场,且该扰动随着远离狭缝而减弱. 此外在狭缝附近($\Delta x/\delta_{0}^{*}=5.5$和$\Delta x/\delta _{0}^{*}=16.4$),靠近壁面位置($y^{+} <80$),扰动在激励器激发频率附近激起更多的能量,且由于扰动为高频,故扰动后的小尺度漩涡的强度得到加强. 这些小尺度漩涡将因与猝发的尺度相当,将对猝发的统计特性产生显著影响. 在远离激励器处($\Delta x /\delta _{0}^{*}=54.6$),扰动不断衰减,在边界层内显示很微弱,各法向位置扰动前后的能谱曲线除了1\,600\,Hz外基本重合. \,\,能谱 曲线反应了合成射流引入的周期扰动在湍流边界层的发展演化,即该扰动在靠近狭缝的位置非常显著的激发高频小尺度漩涡尺度 能量,而随着与狭缝距离的增加这种激发不断衰减,在远离狭缝的位置表现出很弱的效果.
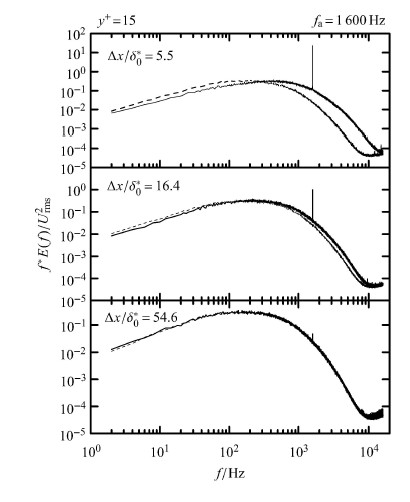
|
图 6 各流向站位在$y^{ + }=15$处的能谱曲线:扰动前(虚线),扰动后(实线) Fig.6 Spectra of the streamwise velocity fluctuations:unperturbed (dash) and perturbed (solid) |
为进一步研究高频周期扰动对下游边界层湍流结构统计特性的影响,需考察周期扰动在边界层湍流中的相对强度大小.
相速度分解方法是研究含有周期性脉动湍流的一个有效手段. Hussain与Reynolds,[22]将瞬时速度场$U$分解为3部分
| $ U = U_{\rm p} + U_{\rm b} = \overline U + \tilde {U} + U_{\rm b} $ | (2) |
式中,$U_{\rm p}$为相平均速度,$U_{\rm b}$为去除相平均速度后的背景脉动速度;相平均速度$U_{\rm p}$进一步可分解为时均速度$\overline U $与相平均脉动速度$\tilde {U}$. 时均速度$\overline U $为
| $ \bar U = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_0^T {Udt} $ | (3) |
相平均速度$U_{\rm p}$分解为
| $ {U_{\rm{p}}} = \bar U + \tilde U = \mathop {\lim }\limits_{N \to \infty } \frac{1}{N}\sum\limits_{n = 0}^N {U(t + nT)} $ | (4) |
式中$T$为相平均速度的周期. 由式(2),可得各速度的均方根关系
| $ \sigma ^2 = \sigma _{\rm p}^2 + \sigma _{\rm b}^2 $ | (5) |
其中,$\sigma $,$\sigma_{\rm p}$,$\sigma_{\rm b}$分别为瞬时速度、相平均速度、背景速度的均方根. 显然,可用$\sigma_{\rm p}$与$\sigma $的比值来衡量周期扰动引起的相平均脉动速度在湍流场中的相对强度大小.
图7给出了周期扰动后$\Delta x/\delta_{0}^{*} =5.5$与$\Delta x/\delta_{0}^{*}=16.4$处 $\sigma_{\rm p}$与 $\sigma $ 的比值. 从图中可以看出,在$\Delta x / \delta _{0}^{*}=5.5$处周期扰动在整个边界层内的强度明显强于$\Delta x/\delta_{0}^{*}=16.4$处的结果. 因此,利用相速度分解得到的 $\sigma_{\rm p}$与$\sigma $ 的比值可以衡量周期扰动的相对大小. 值得注意的是,在边界层外侧 $\sigma _{\rm p}$与 $\sigma $ 的比值迅速增加,这个现象主要是由于在边界层外侧的湍流脉动强度大大减弱. 虽然 $\sigma_{\rm p}$在边界层的边缘很小,但是在这个法向位置湍流的脉动强度的减弱幅度更大(如图6所示),因此 $\sigma _{\rm p}$与 $\sigma $ 的比值迅速增加.
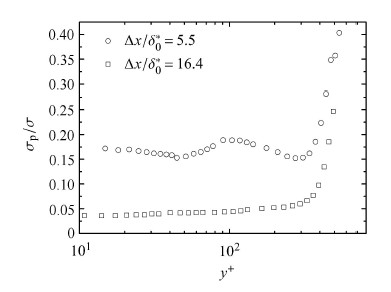
|
图 7 周期扰动相对强度沿法向分布 Fig.7 The distribution of periodic perturbation along vertical direction |
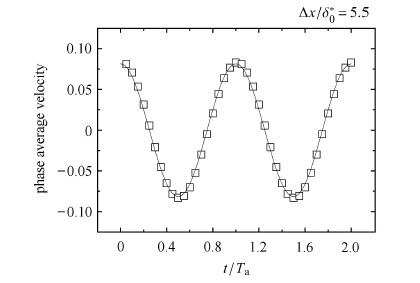
对$\Delta x/\delta_{0}^{*}=5.5$处$y^{ + } =410$位置的速度信号作相速度分解,得出该位置的相速度如图8所示. 可知,合成射流形成的周期扰动在平板湍流边界层内形 成频率为$T_{\rm a} =1\,600$ Hz的余弦分布相速度,即${U_{\rm{p}}}(t) = \bar U + \sqrt 2 {\sigma _{\rm{p}}}\cos (2\pi t/{T_{\rm{a}}})$. 此时,周期扰动的相对强度也可由自相关分析得出.
|
图 8 $\Delta x / \delta _{0}^{*}=5.5$, $y^{ + }= 410$处相平均速度 Fig.8 The phase average velocity at $\Delta x/\delta _{0}^{*}=5.5$, $y^{+}= 410$ |
由速度的自相关系数定义,则可将瞬时速度的自相关系数$C(\tau )$两部分
| $ \begin{array}{l} C(\tau ) = \frac{{\overline {U(t)U(t + \tau )} - {{\overline {U(t)} }^2}}}{{{\sigma ^2}}} = \\ \frac{{\overline {{U_{\rm{b}}}(t){U_{\rm{b}}}(t + \tau )} + \overline {{U_{\rm{p}}}(t){U_{\rm{p}}}(t + \tau )} - {{\overline {{U_{\rm{p}}}(t)} }^2}}}{{{\sigma ^2}}} = \\ \left( {1 - \frac{{\sigma _{\rm{p}}^2}}{{{\sigma ^2}}}} \right){C_{\rm{b}}}(\tau ) + \frac{{\sigma _{\rm{p}}^2}}{{{\sigma ^2}}}{C_{\rm{p}}}(\tau ) \end{array} $ | (6) |
其中,背景速度及相平均速度的自相关系数分别为
| $C_{\rm b} (\tau ) = \dfrac{\overline {U_{\rm b} (t)U_{\rm b} (t + \tau )} }{\sigma _{\rm b}^2 }$ | (7) |
| $C_{\rm p} (\tau ) = \dfrac{\overline {U_{\rm p} (t)U_{\rm p} (t + \tau )} - \overline {U_{\rm p} (t)}^2}{\sigma _{\rm p}^2 } $ | (8) |
显然,因相速度$U_{\rm p}$为周期$T$的函数,$C_{\rm p} (\tau )$也为周期$T$的函数. 如图9所示,若相速度为周期$T_{\rm a}$的余弦分布${U_{\rm{p}}}(t) = \bar U + \sqrt 2 {\sigma _{\rm{p}}}\cos (2\pi t/{T_{\rm{a}}})$,则

|
图 9 不同流向站位的自相关系数 Fig.9 Autocorrelation functions of velocity fluctuations |
| $ {C_{\rm{p}}}(\tau ) = \cos (2\pi \tau /{T_{\rm{a}}}) $ | (9) |
这说明$C_{\rm p}(\tau)$为周期为$T_{\rm a}$的余弦函数,在$\tau \to \infty $的时候,$C_{\rm p} (\tau ) \ne 0$,表现出远程相关的周期波动性质. 背景湍流信号应为稳态,远程则无相关,即$\tau \to \infty ,C_{\rm b} (\tau ) \to 0$. 由式(6),可得
| $ C(\tau \mapsto \infty ) = \frac{{\sigma _{\rm{p}}^2}}{{{\sigma ^2}}}{C_{\rm{p}}}(\tau ) = \frac{{\sigma _{\rm{p}}^2}}{{{\sigma ^2}}}\cos (2\pi \tau /{T_{\rm{a}}}) $ | (10) |
因此,也可由自相关系数是否远程相关来判定湍流场中周期扰动的相对强度大小.
扰动前后的自相关系数如图9所示. 从图中可以看出,在靠近狭缝处($\Delta x/\delta^*_0=5.5$和$\Delta x / \delta ^*_0=16.4$),扰动后的自相关系数曲线表现出了明显的远程相关的周期波动现象,尤其是前者. 而在远离狭缝($\Delta x / \delta ^*_0=56.4$)处,扰动后的相关系数曲线并没有表现出远程周期相关的现象. 这个结果反应出周期扰动的相对强对大小在边界层的发展演化. 在靠近狭缝处,扰动很强烈,因此在这个区域中自相关系数出现了远程周期相关的波动现象.
另一方面,在靠近壁面区域($y^{ + } <80$),扰动后的自相关系数表明流动结构在靠近狭缝的流向位置变小,而在远离狭缝的位置稍稍变大. 自相关系数变小(变大)意味着积分时间尺度的变小(变大),而这个积分尺度是流动结构尺度的一个直接的指标. 已有的吹气减阻实验的流动结构(条带结构)在狭缝下游是稍稍增大的,高频扰动后流动结构变小这个结果则与已有的吹气减阻实验结果矛盾. 这种现象是由于合成射流引入了一个很强的高频周期扰动,该扰动在激励器下游产生的负的运动展向涡结构尺度较小,从而影 响了靠近狭缝的原有流动结构(条带结构),导致了这个区域的流动结构减小;随着与狭缝距离的增加,该扰动强度不断衰减,流动结构趋向定常吹气效果,导致了在远离狭缝的位置流动结构变大.
因此,在靠近狭缝的下游,湍流场中受高频射流影响,产生了较小尺度的负的运动展向涡结构,使得速度的自相关系数出现 了远程周期相关的波动现象;而随着流向距离的增加,该扰动不断减弱,最终体现出与现有定常吹气减阻实验相似的影响结果. 这也说明了高频周期扰动产生的一定强度的负展向涡结构将影响近壁区的循环机制,从而影响其统计特性,如湍流猝发.
2.3 高频周期扰动对湍流猝发的统计影响在周期扰动的强度分析中,靠近狭缝的流场结构由于受到较强的高频周期扰动的影响而表现出了异于常规吹气(连续或低 频吹气)的减小,这表明高频周期扰动产生的小尺度负的运动展向涡结构在减少摩阻的同时将可能影响近壁区湍流的统计特性. 由于VITA可通过检测猝发事件的变化来揭示减阻机理,本文进一步结合VITA技术,考察近壁区湍流在周期性扰动作用下的影响.
VITA方法的两个参数分别是$k$和$T$. 其中,参数$k$一般取为1或比1大的数(也有一些文献根据自己的需要取为小于1的值);参数$T^{ + } = Tu_{\tau }^{2}/\nu $ 一般取为10,要求该参数至少包含所研究问题的最小时间尺度. 本文选择$k =1$,$ T^{ + }=10$.
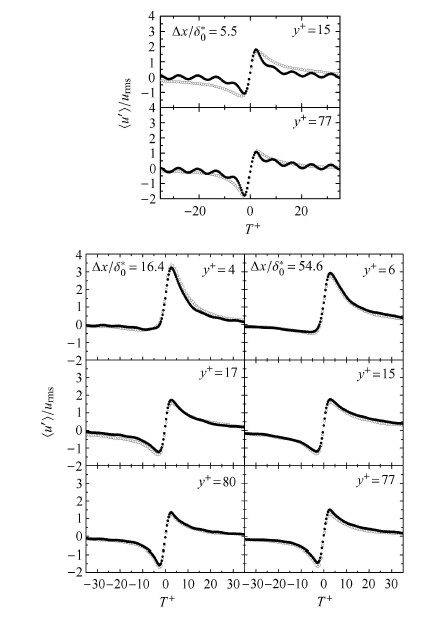
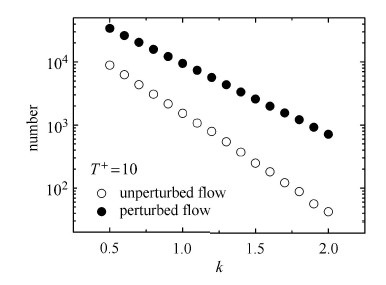
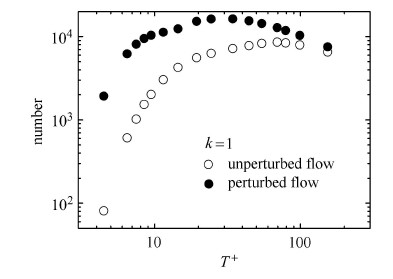
高频周期扰动前后猝发事件的次数及速度条件平均结果分别如表2和图10所示,其中条件平均是通过对应位置的无扰动数据 进行无量纲化的,空心圆圈对应无控时的结果,实心圆圈对应加控后的结果. 现有减阻研究表明,扰动后猝发事件的次数减少,强度降低,即猝发事件变弱. 由于猝发事件是导致壁面雷诺应力的主要原因,因此猝发事件变弱对应着壁面摩阻的减弱. 但从表2可以看出,在靠近狭缝口区域($\Delta x/\delta^*_0=5.5$和$\Delta x/\delta^*_0=16.4$),高频扰动后猝发的次数反而大大增加,这与现有的减阻研究结果并不相符. 如图11与图12所示,在$\Delta x/\delta^*_0= 5.5$,选择不同的参数,吹气扰动后的猝发次数仍然远远大于未扰动的猝发次数. 这是由于高频周期扰动产生的小尺度的负的运动展向涡结构的存在,在检测函数判据猝发时带来了巨大的影响,以至 于检测函数把一部分的展向涡脉动信号当成了下扫,从而增加猝发次数. 由图10可知,本文的高频扰动频率与猝发的持续频率相当. 因而,展向涡的尺度与猝发引起的下扫条带结构变化尺度相当,从而影响了猝发的判据. 此时,经典的VITA方法不再适用. 这种现象在低频周期扰动时候,将不会发生. 因为低频扰动产生的展向涡结构偏大,对猝发判据的影响较弱.
| 表 2 加控前后猝发次数统计 Table 2 Numbers of bursting events |
|
图 10 各流向位置加控前后速度条件平均结果 Fig.10 Conditional averages of the velocity fluctuation |
|
图 11 $\Delta x/\delta^*_0= 5.5 $位置扰动前后猝发次数随$k$的变化 Fig.11 Burst number vs. $k$ at $\Delta x/\delta^*_0= 5.5 $ |
|
图 12 $\Delta x/\delta^*_0= 5.5 $位置扰动前后猝发次数随$T^{+}$的变化 Fig.12 Burst number vs. $T^+$ at $\Delta x/\delta^*_0= 5.5 $ |
值得注意的是,$\Delta x/\delta^*_0= 5.5 $和$\Delta x/\delta^*_0=16.4$的条件平均结果表明猝发的强度稍有降低,这与已有的吹气减阻研究一致,引起这个主要原因可 能是作条件平均时用到了积分运算,而积分运算具有``取平均''的效果,这个效果正好在很大程度上消除了高频的强扰动脉动信号的影响. 由于$\Delta x/\delta^*_0= 5.5 $和$\Delta x/\delta^*_0=16.4$猝发事件的时刻探测受到影响,因此即使这里的条件平均结果与已有的微控减阻研究结果相一致,也 不会影响经典的VITA方法不再适用的结论. 在扰动下游$\Delta x/\delta^*_0=54.6$处,猝发事件的次数减少、强度降低,表明猝发事件变弱,这与已有的减阻实验研究结果是一致的. 结合之前的分析,可认为这是由于高频扰动在该位置的强度很弱而没有对VITA方法的检测函数的检测造成影响.
总之,VITA方法在靠近高频扰动处失效而在远离扰动处有效,表明引入的高频扰动产生的运动展向涡结构因其与猝发引 起的湍流结构尺度相当,导致VITA检测猝发失效.
3 结 论本文通过对合成射流产生的高频周期扰动在充分发展的平板湍流边界层中的速度信号进行测量,分析探讨了高频周期扰动对近壁 区湍流统计特性的影响,得出了以下结论:
(1) 高频周期性吹气扰动的引入,将导致湍流边界层内时均速度与脉动速度的分布产生改变,增厚了黏性底层,抬升了拟序结构,减小了壁面摩阻.
(2) 相速度分解、能谱与自相关系数均反应了高频周期扰动沿流向及法向的演化,表明狭缝下游附近扰动的相对强度较强,而在远 离狭缝的下游由于扰动强度的大幅衰减而对流场产生较弱影响.
(3) 高频吹气扰动引起壁面摩阻的减小,这意味着壁面结构再生过程应受到抑制. 但这种现象在扰动相对强度较大区域,因高 频吹气产生的运动展向涡结构与猝发引起的结构变化尺度相当,从而影响了VITA方法对猝发的判据,无法利用VITA检测出猝发 事件变弱. 高频吹气扰动使得VITA方法表现出与低频或定常吹气减阻机理相异的现象.
| [1] | Antonia RA, Fulachier L. Topology of a turbulent boundary layer with and without wall suction. Journal of Fluid Mechanics, 1989, 198: 429-451 |
| [2] | Antonia RA, Fulachier L, Krishnamoorthy L, et al. Influence of wall suction on the organized motion in a turbulent boundary layer. Journal of Fluid Mechanics, 1988, 190: 217-240 |
| [3] | Antonia RA, Spalart PR, Mariani P. Effect of suction on the near-wall anisotropy of a turbulent boundary layer. Physics of Fluids, 1994, 6: 430-432 |
| [4] | Chung YM, Sung HJ, Krogstad PA. Modulation of near-wall turbulence structure with wallblowing and suction. AIAA Journal, 2002, 40(8): 1529-1535 |
| [5] | Park J, Choi H. Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer. Physics of Fluids, 1999, 11(10): 3095-3105 |
| [6] | Yoshida H, Kobayashi HP, Tada S, et al. Responses of low and high speed streaks to injection or suction in a minimal flow unit. In: Banerjee S, Eaton JK, Eds. Proceedings of 1st International Symposium on Turbulence and Shear Flow, 1999, Santa Barbara, CA, USA, Begell House, 1333-1338 |
| [7] | Kim K, Sung HJ. Effects of periodic blowing from spanwise slot on a turbulent boundary layer. AIAA Journal, 2003, 41(10): 1916-1924 |
| [8] | Kim K, Sung HJ. Effects of unsteady blowing through a spanwise slot on a turbulent boundary layer. J Fluid Mech, 2006, 557: 423-450 |
| [9] | 夏振炎,姜楠,王振东等. 湍流边界层多尺度相干结构的子波自相关辨识. 天津大学学报, 2005, 38(11): 970-974 (Xia Zhenyan, Jiang Nan, Wang Zhendong, et al. Wavelet auto-correlated identification of multi-scale coherent structures in turbulent boundary layer. Journal of Tianjin University, 2005, 38(11): 970-974 (in Chinese)) |
| [10] | 王玉春,姜楠,田砚. 吹吸扰动对湍流边界层多尺度相干结构的影响. 天津大学学报, 2007, 40(1): 51-57 (Wang Yuchun, Jiang Nan, Tian Yan. Effect of blow-suction disturbance on multi-scale coherent structures in turbulent boundary layer. Journal of Tianjin University, 2007, 40(1): 51-57 (in Chinese)) |
| [11] | 姜楠. 湍流边界层相干结构研究五十年. 见: 第八届全国实验流体力学学术会议论文集, 2010 (Jiang Nan. Five decades research of coherent structures in turbulent boundary layer. Proceedings of Eighth National Experimental Fluid Mechanics Conference, 2010 (in Chinese)) |
| [12] | 田砚,姜楠. 温度边界层对壁湍流多尺度相干结构的影响. 航空动力学报, 2007, 22(6): 981-986 (Tian Yan, Jiang Nan. Experimental investigation of effects of temperature boundary layer on multi-scale coherent structures in wall turbulence. Journal of Aerospace Power, 2007, 22(6): 981-986 (in Chinese)) |
| [13] | Blackwelder RF, Kaplan RE. On the wall structure of the turbulent boundary layer. J Fluid Mech, 1976, 76(1): 89-112 |
| [14] | Park SH, Lee I, Sung HJ. Effect of local forcing on a turbulent boundary layer. Exp Fluids, 2001, 31(4): 384-393 |
| [15] | Park J, Choi H. Effects of uniform blowing or suction from a spanwise slot on a turbulent boundary layer flow. Phys Fluids, 1999, 11: 3095-3105 |
| [16] | Park YS, Park SH, Sung HJ. Measurement of local forcing on a turbulent boundary layer using PIV. Exps Fluids, 2003, 34: 697-707 |
| [17] | Iuso G, Di Cicca GM. Interaction of synthetic jets with a fully developed turbulent channel flow. Journal of Turbulence, 2007, 8(11): 1-33 |
| [18] | Cannata M, Iuso G. Spanwise directed synthetic jets for wall turbulence control. In: Proc. of 4th Flow Control Conference. AIAA, 2008-4205 |
| [19] | Lasagna D, Orazi M, Iuso G. Streamwise vortices originating from synthetic jet-turbulent boundary layer interaction. Fluid Dyn Res, 2014, 46: 015501 |
| [20] | Ugrina S. Experimental analysis and analytical modeling of synthetic jet cross flow interations. [PhD Thesis]. Maryland: University of Maryland, 2007 |
| [21] | White FM. Viscous Fluid Flow, 2nd edn. New York: McGraw-Hill, 1991 |
| [22] | Hussain AKMF, Reynolds WC. The mechanics of an organized wave in turbulent shear flow. J Fluid Mech,1970, 41: 241-258 |
 2015, Vol. 47
2015, Vol. 47