近几十年来,飞机的噪声问题受到了各国越来越多的关注,飞机的噪声载荷主要分两类: 一类是飞机发动机喷流的气动噪声; 另一类是飞机整体的结构振动噪声. 近几年来随着科技的进步,追求更高的速度使得气动噪声相较于结构振动噪声显著增大,为此国内外研究人员对圆管湍流射流做了大量的研究工作,文献[1]总结了很多成果. 文献[2]表明冷态射流的噪声产生机理的关键因素是湍流中大尺度的拟序结构. Hileman等^[3]在用于湍流研究的消声室内对不同马赫数下射流噪声的声源及其传播特性进行了研究分析. 文献[4]直接模拟了轴对称射流的流场和远场声场,计算得到的轴对称射流涡合并过程产生的声波与莱特希尔声比拟理论得到的结果符合得很好; 文献[5]对湍流射流及其声场进行了直接数值模拟,发现射流噪声的主要来源是超声速流动的马赫波辐射产生的; 文献[6]也对湍流射流及其声场进行了研究,阐释了非线性效应在噪声的产生机制的重要性. 文献[7]采用大涡模拟方法研究了超声速射流噪声的问题,结果发现激波通过剪切层与涡的相互作用造成了压力梯度的迅速变化,从而导致声波的产生,一定程度上从物理层面解释了超声速射流噪声模型,同时也验证了文献[8]中的激波泄漏机制. 此外,国内不少学者对自由剪切层失稳和其内部的声涡机理进行了深入细致的研究. 沈清等^[9]直接数值模拟了二维超声速平面自由剪切层流动中小扰动波在时间和空间上的发展,得到了流动由线性到非线性的失稳过程的部分特征; 孙晓峰等^[10]基于锐缘处声涡转化机理建立了一种关于穿孔板切向流效应的小扰动势流模型,初步研究了声波透过剪切层传播的物理现象. 热声现象也是气动声学中较为关注的课题,王晓宇等^[11]采用等价分布源方法研究了流管声传播与膜结构相互作用的机理.

大量的研究工作表明,采用主动流动控制技术可以有效增强射流掺混和减小射流噪声. 例如,文献[12]测量了高速圆管射流 在声学激励器以最佳激励频率作用下得到的声场,结果表明射流原有的宽频噪声受到了抑制,而在激励谐频上的噪声成为射流噪声主要成分. 文献[13]发现在声学激励器激励下的圆管射流的声场与多个静止声源产生的声场相一致,并将这些声源与涡配对的不稳定波幅值的非线性饱和度联系起来. 近几年来,采用等离子激励器实现超声速流动的流动控制取得了采用声学激励器难以实现的成果. 文献[14]数值模拟了直流放电等离子激励器对高速、高雷诺数流动的影响,结果发现较小功率的输入就足以改变局部流场,达到控制的效果; Yan等^{[15, 16, 17, 18, 19]}数值模拟了局部电弧等离子丝激励器(LAFPA)产生的热扰动对超声速边界层的影响. 此外,严红等^{[20, 21, 22]}采用大涡模拟方法研究了等离子体热激励器用于超声速剪切流和圆管射流流动控制的控制机理. 航空发动机在不同工况下的射流情况不同,研究用这种主动控制技术来满足不同应用需求有着重要的理论和工程意义.

本文采用大涡模拟方法研究了马赫数1.3的超声速圆管射流在热激励器以不同激励模态作用下的流场特性,对比分析了不同激励 模态对射流涡结构的影响.

本文采用大涡模拟方法来捕捉瞬态的射流流场. 大涡模拟方法的思路是直接数值模拟大尺度湍流运动,而利用湍流湍流这样的 处理使得在相对较粗的网格下也能较准确地捕捉湍流中的涡结构以及涡在流场中的运动规律.

质量、动量和能量的控制方程如下

式中,$\tau_{ij}$是剪切应力张量,表达式为

$\mu $为黏性系数. 大涡模拟采用空间平均方法将动量方程中变量$u$分解为大尺度可求解变量$\overline u $ 和亚网格变量(模化变量)${u^\prime }$,即$u = \overline u + {u^\prime }$,文献[23]提出的算式表示为

其中,$G(x - {x}')$被称为滤波函数,显然$G(x)$满足$\int_{ - \infty }^{ + \infty } G (x)x = 1$. 滤波函数$G$用来区分可求解的大尺度涡和待模化的小尺度涡. 常用的过滤函数有帽型函数、高斯函数等. 帽型函数形式简单而被广泛使用,表达式为

$\varDelta$为网格平均尺度,三维情况下,$\varDelta = (\varDelta _1 \varDelta _2 \varDelta _3 )^{1 / 3}$,　$\varDelta _1 ,\varDelta _2 ,\varDelta _3$分别为$x_1$,$x_2$,$x_3$方向的网格尺度. 将滤波函数作用于纳维\dk 斯托克斯方程各项,得到过滤后的湍流控制方程组

由于无法同时求解出变量$\overline{u_i } $和$\overline {u_i u_j } $,所以将$\overline {u_i u_j } $分解为$\overline {u_i u_j } = \overline {u_i } \cdot \overline {u_j } +s_{ij} $,$s_{ij} $称为亚网格剪应力张量. 故动量和能量方程可写成

式中,$s_{ij} $代表了小涡对大涡的影响,$\mu _{\rm SGS} $和$Pr _{\rm SGS} $分别是亚网格黏性和亚网格普兰特数,均需要采用模型进行模化.

本文采用有限体积法,选用斯马格林斯基\dk 莉莉(Smagorinsky--Lilly)亚网格模型进行数值模拟,空间离散采用三阶保守型单调迎风/中心差分隐式格式(monotonic upstream/centered scheme for conservation laws,MUSCL),时间用二阶隐式格式,模拟非定常可压缩流动.

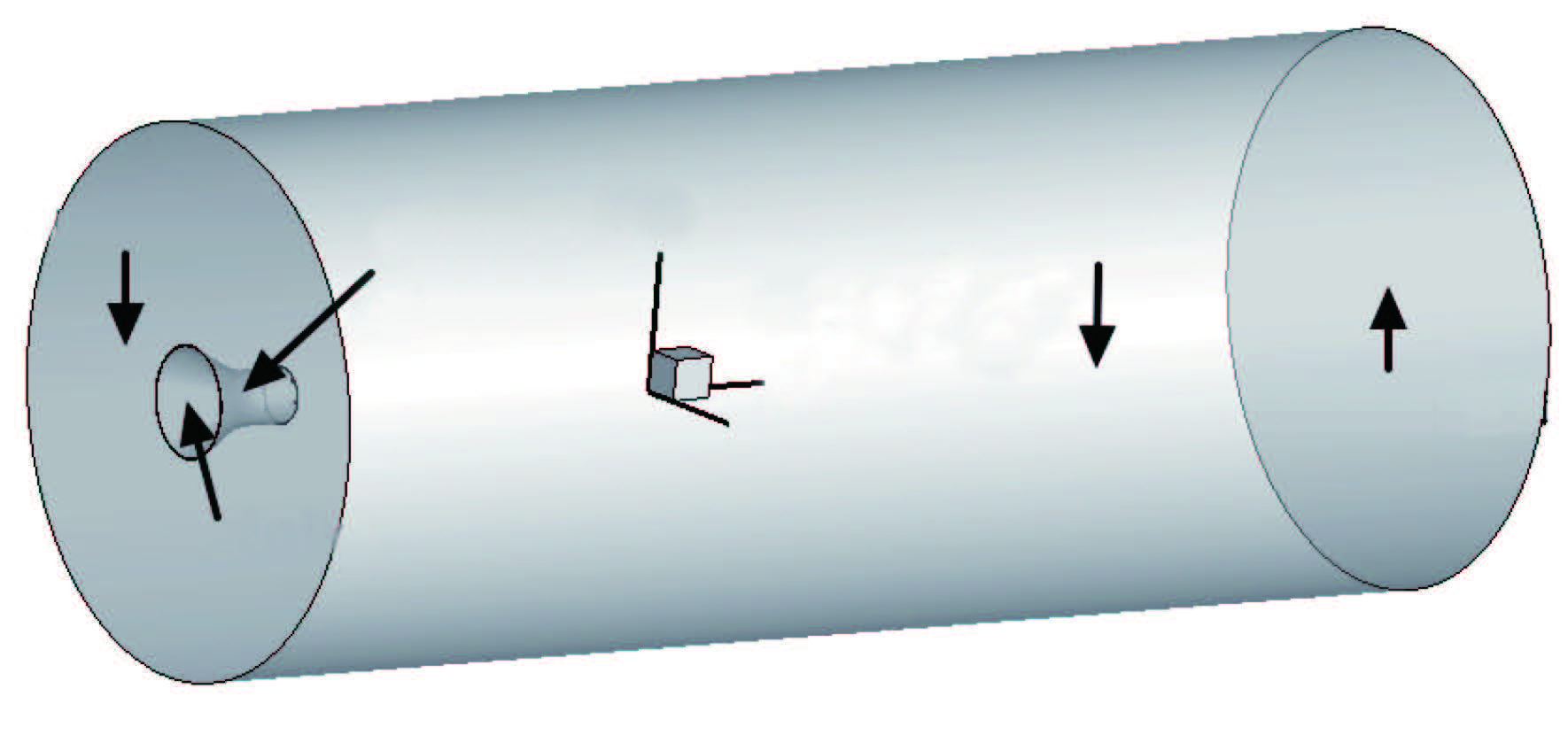
马赫数1.3的完全膨胀圆管射流进入静止的大气环境会产生强烈的卷吸作用,从而使射流形成速度变化小的高速核心区和有较大速度梯度的低速掺混区,并且随着射流剪切层的发展会有大涡拟序结构的生成和发展,同时伴随着噪声的产生. 文献[24, 25]的研究表明脉冲放电式等离子体激励器影响射流发展的主要因素是等离子体的热效应,可以忽略等离子体的电磁效应. 本文采用在凹槽区域加入净热源的方法来模拟激励器的热效应,故称之为热激励器. 热激励器的工作原理是利用一对高压电极针在凹槽内产生高温电弧,加热凹槽内空气,产生高温高压的等离子体. 凹槽可形成低速区,用以保护热激励器产生的等离子体气团不会立即被超声速气流``吹灭'',从而有效地形成局部高温、高压区域,对下游流动产生显著影响. 采用三维模型进行热激励器对超声速圆管射流控制机理的研究(流动设置如图1所示). 在距离喷管出口上游1mm处沿周向等距开了8个长3mm(沿周向)、宽1mm(沿流向)、深0.5mm的方形凹槽,每组热激励器占据其所在的整个凹槽空间.

图 1(Fig.1)

图 1 流动设置 Fig.1 Flow configuration

喷管出口直径$D$为50mm,壁厚为1mm,以喷管出口截面圆心为原点建立笛卡尔坐标系,$x$轴正向为流向. 整个圆柱形计 算域的$x$轴范围为$-2D$至24$D$,$y$和$z$轴范围均为$-5D$至$5D$. 整个流场以静止大气环境参数进行初始化,其中$p_{\infty }=101\,325$\;Pa,$T_{\infty}=300$\;K,$U_{\infty }=0$\;m/s. 流场边界条件设置如图2所示,3出口边界即图2中的``out-left'',``out-round''和``out-right'',均给定静压101\,325\;Pa,总温300\;K,速度为0; 喷管进口``inlet''的边界条件为给定总温300\;K和总压280\,746\;Pa. 喷管壁面条件选择绝热壁面,由于热源产生的热功率主要用于加热流体,而且相对于整个超声速流动的能流密度是很小的一个量级,故可以忽略壁面的热通量. 通过控制周向8个凹槽内热激励器的开启顺序来实现不同的激励方式.

图 2(Fig.2)

图 2 边界条件 Fig.2 Boundary conditions

根据萨瑟兰定律(Sutherland Law),取完全膨胀射流出口理论静温值$T_{j}$ (224.2\;K),得到喷管出口黏性系数 为$1.463\times 10^{ - 5}$\;kg/(m$\cdot$s),以喷管出口直径$D$为特征长度,得到射流出口的雷诺数$Re_{j}=\rho_{j}u_{j}D/\mu_{j}=2.106\times 10^6$.

流体流经整个计算域的时间$t_{0}=L/u_{j} \approx 3$ms ($L$为计算域流向总长度),时间步长$\Delta t$选为 0.5μs以保证$CFL < 1$. 在结果分析中,以喷管出口直径$D$,出口速度$u_{j}$,环境静压$p_{\infty}$和环境温度$T_{\infty}$分别代表长度,速度,压力和温度的特征量对各物理量进行了无量纲化.

射流剪切层处各气动参数的梯度很大,也是研究射流人们最关心的流域,故此处需要高密度的网格来捕捉流动的微小变化,三维网 格分布如图3所示.

图 3(Fig.3)

图 3 网格分布 Fig.3 Grid configuration

本文研究了疏密两套网格下的稳态流场,来确定最合适的网格. 这两套网格沿流向,周向和径向3个方向的节点数分别为$163\times 121\times 87$和$203\times 121\times 102$. 射流中轴线的稳态静压分布如图4所示,其中$x^{0}$表示无量纲化的轴向距离,$y$轴的$p$表示本地静压与环境静压$p_{\infty}$之差.

图 4(Fig.4)

图 4 轴线静压分布 Fig.4 Static pressure distribution along center\\ axis in coarse and fine grid

两套网格得到的射流核心区长度完全一致,且由凹槽造成的射流核心区内的斜激波位置和强度也基本一致,综合考虑后,选择$163\times 121\times 87$网格进行数值模拟.

该套网格凹槽内、剪切层和喷管壁面处的网格较密,在凹槽内沿流向、径向和周向分别分布有$3\times 3\times 6$个网格点. 在$r=R$ $(r$表示径向距离,$R$为喷管出口半径)处沿径向的最小网格尺寸为0.2mm,在$r>R$区域,由剪切层和壁面处向外作1.02倍的等比拉伸; 在$r<R$区域内,采用O型网格结构,保证壁面边界层和射流剪切层处的高质量网格,沿径向向内作1.05倍的等比拉伸. 喷管出口处沿流向的最小网格为0.5mm,沿流向正方向作1.04倍的等比拉伸; 喷管出口上游的网格要求不高,沿流向负方向上做了1.1倍的等比拉伸.

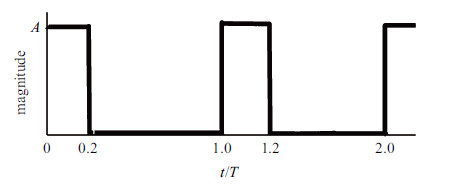
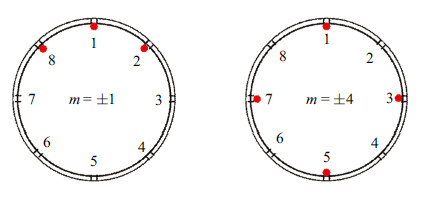
强三维性的激励作用可以有效改变射流结构,影响射流剪切层内拟序结构的发展,位于喷管出口上游沿周向均匀分布的8个热激励器能够实现多种激励模态,本文着重分析了激励模态$m=\pm1$和$m=\pm4$对射流涡结构的影响. 文中还数值模拟了无激励工况(baseline),作为分析比较的基准态. 激励工况的激励幅值、激励频率和占空比分别为10\;GW/m$^{3}$,2.5kHz和20%. 激励工况的热功率输入采用方波形式,如图5所示,其中$T$表示激励循环周期,$A$表示激励幅值. 激励频率取2.5kHz时,斯特劳哈尔数$St_{D}=fD/u_{j}=0.32$接近于圆管喷管最佳射流柱模态对应的$St_{D}= 0.3$^[20]. 图6展示了8个热激励器在不同激励模态下的激励组合方式. 在$m=\pm1$模态下,8,1,2号和4,5,6号热激励器分别组成两组,两者间的激励相位差为180$^\circ$,3号和7号在此激励模态下一直保持关闭状态; $m=\pm4$模态下的8个热激励器按奇偶数分为两组,两者相位差也为180$^\circ$. 在任何激励模态下,同一时间内只有一组热激励器处于打开状态,且激励持续时间为激励周期$T$的20%.

图 5(Fig.5)

图 5 占空比为20%的激励信号 Fig.5 Input pulse of thermal actuator at 20% duty cycle

图 6(Fig.6)

图 6 $m=\pm1$和$m=\pm4$的激励模态 Fig.6 Actuation modes $m=\pm1$ and $m=\pm4$

对于无激励工况,首先计算了约4ms (略大于流经时间$t_{0}$)使得初始流场从出口边界离开计算域,再计算约2ms使无激励作用下的流场达到准稳态,之后又计算了8000个时间步长(约为1倍流经时间)来得到流场的时均值,并分析了瞬态流场. 下述二维切面流场云图均采用无量纲量.

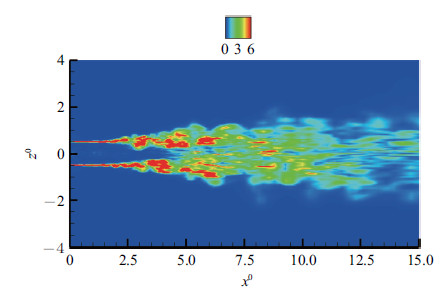
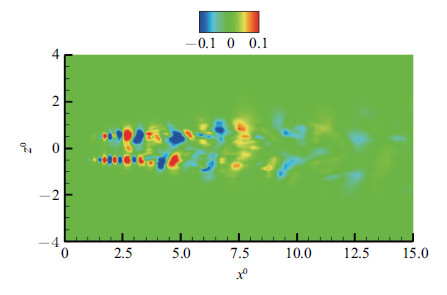
在无激励工况下,射流初始区域($x^{0}<1.5$)由于高速射流与静止大气环境间的强剪切作用成为高涡量区域,此处剪切层薄,涡量强度大而集中,剪切层厚度增长慢,且压力脉动甚微,图7和图8描述了$y^{0}=0$面总涡量和压力脉动的分布,其中$x^{0}$和$z^{0}$分别是无量纲化的$x$和$z$坐标值. 图中可以看到越往下游,流场的总涡量和压力脉动峰值均有所减弱.

图 7(Fig.7)

图 7 无激励工况下的瞬时总涡量云图 Fig.7 Instantaneous vorticity magnitude contours in the baseline

图 8(Fig.8)

图 8 无激励工况下的压力脉动云图 Fig.8 Pressure fluctuation contours in the baseline

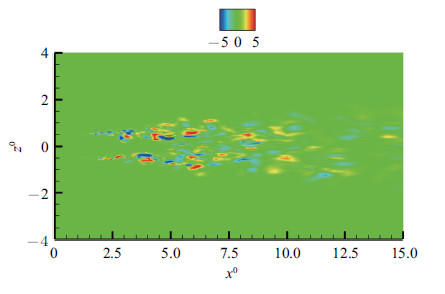
图9显示了$x$方向涡量在$y^{0}=0$面的分布. $x$方向涡量作为流向涡的主要涡量分量可以在一定程度上反映出流向 涡的强弱. 从图中同样可以看到$x$方向涡量值在射流初始区域很小. $x$方向涡量的增长与初始区域后出现的涡的脱落现象有着密切联系,结合涡量分布图和压力分布图可知,流向涡的产生促进了动量在空间的输运,使得剪切层厚度显著增长,气流掺混增强,压力脉动更加剧烈.

图 9(Fig.9)

图 9 无激励工况的瞬时$x$方向涡量云图 Fig.9 Instantaneous $x$-vorticity contours in the baseline

图10的均方根压力云图表明射流初始区域($x^{0}<1.5$)的压力脉动很弱,即剪切层开始发展时的初始脉动小,之后的迅速发展形 成了一个压力强脉动区域,是主要的噪声源之一. 压力脉动越强,对噪声的贡献就越大.

图 10(Fig.10)

图 10 无激励工况的均方根压力分布图 Fig.10 Rms-pressure contours in the baseline

在基准态的基础上加入热激励作用进行数值模拟,得到激励模态$m=\pm1$工况下的准稳态后,再数值模拟了10个激励循环周期(用$T$表示)以获取可供分析的准稳态流场和瞬态流场信息,并与无激励工况进行了比较.

激励作用的加入改变了喷管出口截面的流场特征,这必然导致与无激励工况不同的剪切层发展. 研究表明^[15]非定常的激励作用能产生强而有效的扰动,从而改变剪切层的流动特性,定常的激励作用效果甚微. 在不同激励模态下,流场受到的扰动规律不同,形成的流动反馈也会不同,这也是导致不同激励模态下大尺度拟序结构的表现形态不同的关键因素.

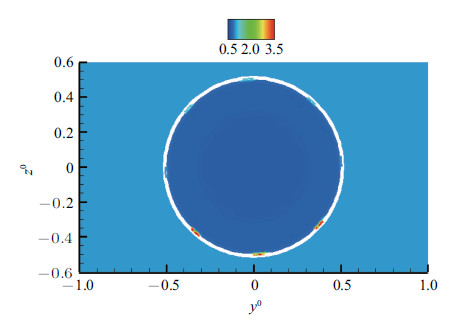
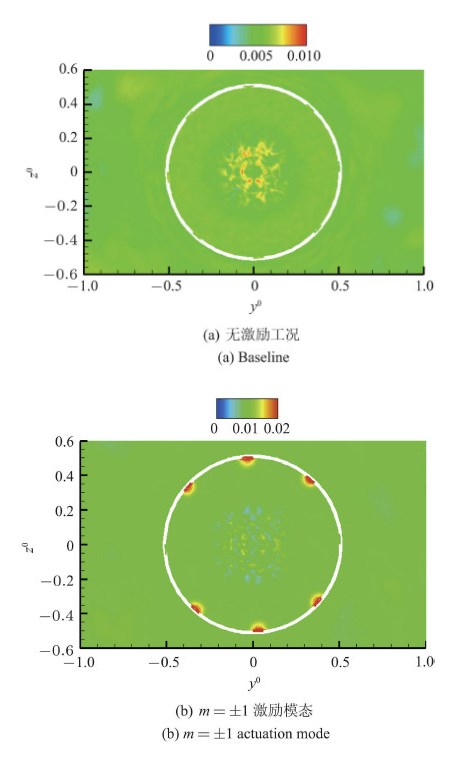
图11显示了$m=\pm1$模态下在$t=9.2\;T$时刻热激励器所在截面的温度分布. 热激励器区域的高温流体对流动产生的阻碍效果类似``物理突起'',可加强近壁面流层的速度扰动,增强下游的涡量发展,并且对流向涡的产生起着关键性的作用,由此产生的扰动流经剪切层后被加强,使得大尺度涡结构在更上游的位置出现. 图12是$m=\pm1$和无激励工况在$t=9.2\;T$时刻热激励器所在横截面上的均方根压力云图. 从图中可以看到激励作用的加入增强了凹槽内和凹槽出口附近的压力脉动,对主流施以脉动式的冲击力,在一定程度上加强了射流的初始压力波动和湍流强度.

图 11(Fig.11)

图 11 $t/T =9.2$时刻的瞬时温度云图 Fig.11 Instantaneous temperature contours at $t/T=9.2$

图 12(Fig.12)

图 12 $t/T =9.2$时刻均方根压力云图 Fig.12 Rms-pressure contours at $t/T=9.2$

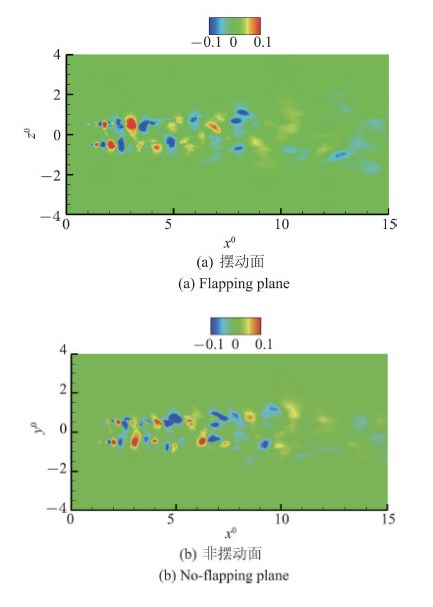
在$m=\pm1$激励模态下,3号和7号激励器一直处于关闭状态,两组激励器以相差180$^\circ$的相位交替开启 和关闭,使得射流不再是轴对称的. 3号和7号所在的$z=0$平面被称为非摆动面,1号和5号所在平面被称为摆动面,如图13所示. 摆动面能充分体现热激励器加入的扰动对剪切层的发展、径向速度和涡量的分布的影响.

图 13(Fig.13)

图 13 摆动面和非摆动面的位置示意图 Fig.13 Sketch of the flapping and no-flapping planes

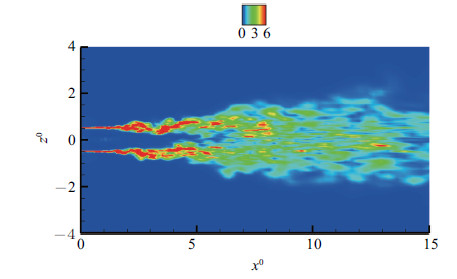
在$m=\pm1$模态下,$t=9.2\;T$时刻摆动面的总涡量分布如图14所示. 相较于无激励作用的无激励工况,该平面表现出更快的涡 量增长速度,剪切层的发展也相对较快. 摆动面和非摆动面的$x$方向涡量分布如图15所示. 在受到激励作用的工况中,产生了更大的径向和周向的速度脉动,这有利于流向涡的形成,正如图15中$x$方向涡量相较于无激励工况出现在了更上游的位置. 激励作用产生类似``物理突起''的效果,这与文献[21]研究的``tabs''对射流的影响类似,同时激励作用下的流向涡分布相比无激励工况更加有序. $m=\pm1$模态的非轴对称性导致了摆动面与非摆动面压力脉动衰减程度的不同,从图16的压力脉动分布图中可以看到摆动面的压力脉动在$x^{0}=7.5$之后就很小了,而非摆动面压力脉动值的减小发生在$x^{0}=10$之后. 压力脉动的非轴对称性必然会导致噪声场的非轴对称性.

图 14(Fig.14)

图 14 $t/T =9.2$时刻摆动面的瞬时总涡量云图 Fig.14 Instantaneous vorticity magnitude contours of the flapping plane at $t/T=9.2$

图 15(Fig.15)

图 15 $t/T =9.2$时刻瞬时$x$方向涡量云图 Fig.15 Instantaneous $x$-voticity contours at $t/T=9.2$

图 16(Fig.16)

图 16 $t/T=9.2$时刻压力脉动云图 Fig.16 Pressure fluctuation contours at $t/T=9.2$

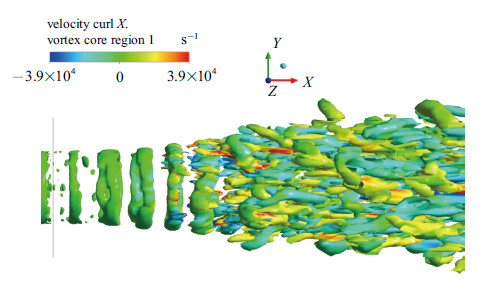
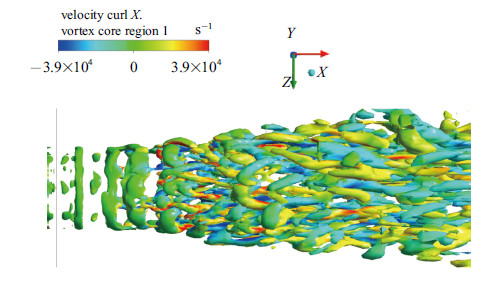
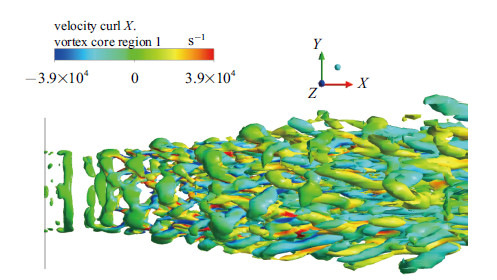
运用$Q$法则捕捉射流涡结构,选取$Q=0.1$等势面,根据$x$方向涡量值给等势面上色,无激励工况和$m=\pm1$模态下的流 场涡结构分别如图17和图18所示. 在无激励工况中,喷管出口出现3个或4个环状涡结构,而后脉动增强,导致环状涡结构的``失稳'',并发展产生发卡涡. 从图中可以清楚的看到发卡涡由展向涡量为主的头部和$x$方向涡量为主的腿部组成,发卡涡的头部远离射流中心,而两条腿部则靠近射流中心. 在$m=\pm1$模态的激励作用影响下,射流中的环状涡结构更早地``失稳'',产生错落排布的小型发卡涡结构. 激励作用下的射流涡结构中包含更多的发卡涡,这些都有助于剪切层的发展,能增强射流的卷吸和掺混效果.

图 17(Fig.17)

图 17 $t/T=9.2$时刻基准态中$Q$等势面的瞬时$x$方向涡量云图 Fig.17 $x$-vorticity contours on the iso-surface of $Q=0.1$ in the baseline at $t/T=9.2$

图 18(Fig.18)

图 18 $t/T=9.2$时刻$m=\pm1$中$Q$等势面的瞬时$x$方向涡量云图 Fig.18 Instantaneous $x$-vorticity contours on the iso-surface of $Q=0.1$ in $m=\pm1$ at $t/T=9.2$

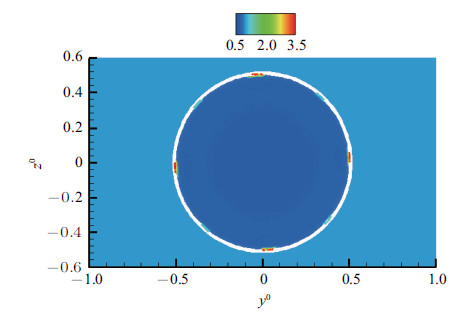
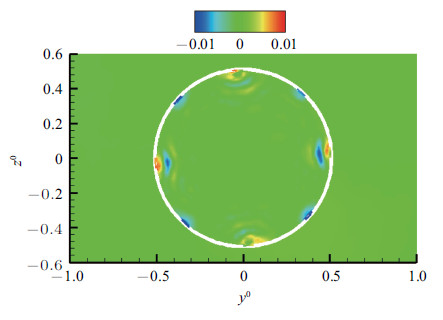
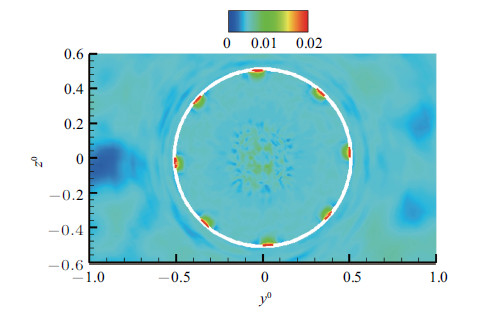
$m=\pm4$模态与$m=\pm1$模态的激励参数相同,该激励模态是具有轴对称性的激励模态,奇数组和偶数组的热激励器交替 工作,每组热激励器沿周向的分布都是轴对称的. 图19给出了$t/T=9.2$时刻热激励器所在截面的温度分布图,沿周向每隔90$^\circ$有一个高温区域. 此时高温凹槽内形成了高压脉动源影响主流流动,而另一组处于关闭状态的热激励器将形成低压区域,如图20所示. 激励作用使得凹槽成为了压力扰动的发生源,这也是激励作用的机理之一. 从该平面的均方根压力云图(见图21),可以发现$m=\pm4$模态下的初始压力脉动明显低于$m=\pm1$模态,说明$m=\pm1$模态能产生更显著的压力扰动,激励强度更大.

图 19(Fig.19)

图 19 $t/T=9.2$时刻的瞬时温度云图 Fig.19 Instantaneous temperature contours at $t/T=9.2$

图 20(Fig.20)

图 20 $t/T=9.2$时刻的压力脉动云图 Fig.20 Instantaneous pressure fluctuation contours at $t/T=9.2$

图 21(Fig.21)

图 21 $t/T=9.2$时刻的均方根压力云图 Fig.21 Instantaneous rms-pressure contours at $t/T=9.2$

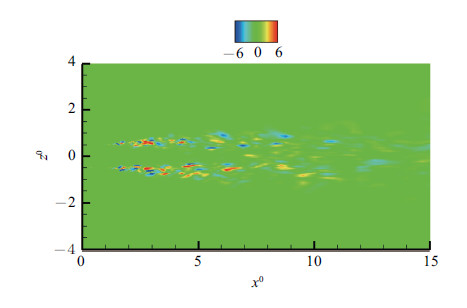
不同的温度分布影响了喷管出口截面的速度分布,从而形成了不同的涡量场. $m=\pm4$属于轴对称激励模态,取$t=9.2\;T$时 刻$y^{0}=0$平面的流场进行比较分析,图22和图23显示了$y^{0}=0$平面上瞬时总涡量和$x$方向涡量的分布. 与无激励工况和$m=\pm1$模态的涡量分布类似,射流初始区域的剪切层薄且增长缓慢,$x$方向涡量很小,这一分布特点与射流中环状涡结构的存在有很大关联. $m=\pm4$模态下的激励作用使得环状涡结构 ``失稳'',导致剪切层的发展速度明显快于无激励工况中剪切层的发展速度,同样该激励模态下流向涡的产生和发展也明显强于无激励工况.

图 22(Fig.22)

图 22 $t/T=9.2$时刻平面$y^{0}=0$的瞬时总涡量云图 Fig.22 Instantaneous vorticity magnitude contours at the plane $y^{0}=0$ at $t/T=9.2$

图 23(Fig.23)

图 23 $t/T=9.2$时刻平面$y^{0}=0$的瞬时$x$方向涡量云图 Fig.23 Instantaneous $x$-vorticity contours on the plane $y^{0}=0$ at $t/T=9.2$

该激励模态下的压力脉动分布也有轴对称的特点,如图24所示. 相比于无激励工况和$m=\pm1$模态,该激励模态下的压力脉动 相对较弱,且分布更为均匀,每个正压脉动和负压脉动区域都较小. $m=\pm4$模态下$Q$法则等势面捕捉的射流涡结构流场如图25所示,等势面颜色表示$x$方向涡量的大小.

图 24(Fig.24)

图 24 $t/T=9.2$时刻压力脉动云图 Fig.24 Pressure fluctuation contours at $t/T=9.2$

图 25(Fig.25)

图 25 $t/T=9.2$时刻$Q$等势面的瞬时$x$方向涡量云图 Fig.25 nstantaneous $x$-vorticity contours on the iso-surface of $Q=0.1$ at $t/T=9.2$

在射流初始区域,不同于无激励工况的环状结构和$m=\pm1$模态下不对称的长条流向涡结构,在 $m=\pm4$模态下,流场沿周向周期性地出现了轴对称的树枝状涡结构,其中连接上下游涡结构的是类似发卡涡的拟流向涡结构. 这是$m=\pm4$激励模态的特点之一,这种激励方式产生了周向分布较为均匀的发卡涡.

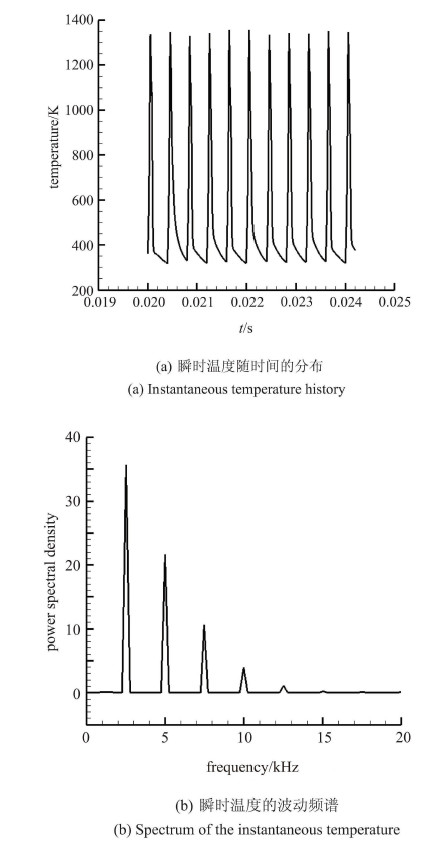
此外,还采用脉动频谱方法分析了热激励器的激励作用. 在$m=\pm1$模态下,监测凹槽内部温度的变化趋势,运用傅里叶变换得 到其频谱分布,如图26所示. 因为激励频率为2.5kHz,故其对应的频谱中只有2.5kHz及其倍频上出现了尖峰,同时随着频率的升高,能量迅速减小. $m=\pm4$模态下也得到同样的温度分布及其波动频谱.

图 26(Fig.26)

图 26 $m=\pm1$模态下$t/T=9.2$时刻凹槽内温度趋势及其频谱图 Fig.26 The history and spectrum of the temperature inside\\ the groove in $m=\pm1$ at $t/T=9.2$

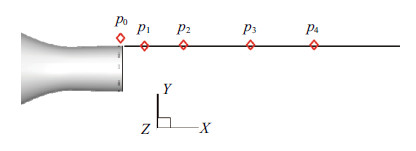
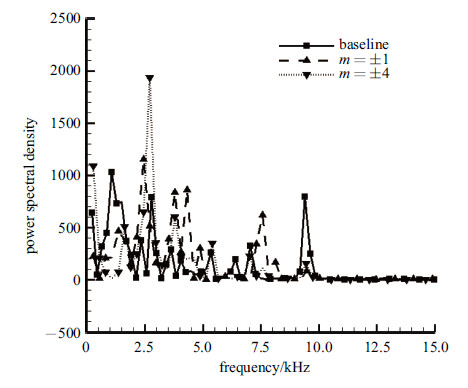
在剪切层内和喷管出口附近设置监测点,记录10个激励周期内压力或速度的变化,并对此作频谱分析,监测点位置的示意图 见图27. 其中$p_0$点(0,0,0.026)监测静压,$p_1$,$p_2$,$p_3$和$p_4$点分别监测在$z=0$平面上$y^{0}=0.5$,$x^{0}=1$,2,4和6四处的速度波动. 位于喷管出口上方的监测点$p_0$没有直接受到流场扰动的影响,故其频谱分布没有出现激励频率及其谐频所对应的尖峰,$p_0$点在各工况下得到的压力波动频谱如图28所示.

图 27(Fig.27)

图 27 监测点分布示意图 Fig.27 Sketch of the monitors location

图 28(Fig.28)

图 28 各工况下$p_0$点的压力波动频谱 Fig.28 Spectrum of the pressure at $p_0$

图28中无激励工况显示了射流剪切层的脉动频带,其中包括低频的两个尖峰和接近10kHz的高频尖峰,这之间还有两个峰值较小的 尖峰. 而激励模态下的尖峰多在小于10kHz的低频段,特别在激励频率2.5kHz附近,10kHz处的峰值明显受到了激励作用的抑制.

距离喷管出口1倍直径处的$p_1$点监测到的速度波动受激励作用很明显,如图29所示. 在$m=\pm1$模态和$m=\pm4$模态下,$p_1$点 的频谱在激励频率及其谐频上均有尖峰. 相比$m=\pm4$模态,$m=\pm1$模态下$p_1$点速度脉动更为剧烈,激励频率及其2倍和3倍谐频也有更高的幅值.

图 29(Fig.29)

图 29 各工况下$p_1$点的速度波动频谱 Fig.29 Spectrum of the velocity at $p_1$ in the baseline,\\$m=\pm1$ and $m=\pm4$

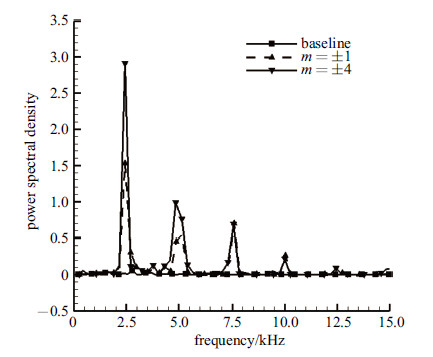
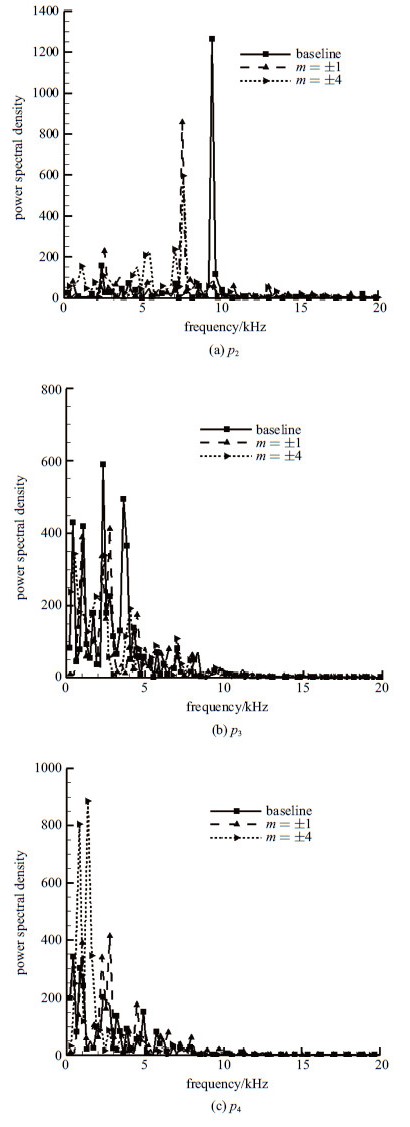
图30是$p_2$,$p_3$和$p_3$点速度波动的频谱. $p_2$点的频谱有着最高幅值的尖峰,无激励工况的该尖峰出现在大约10kHz处,即为射流剪切层本身的脉动频率. 而在$m=\pm1$和$m=\pm4$激励工况下,该尖峰位于激励频率的3倍谐频上,且均低于无激励工况最高尖峰的峰值,说明激励作用抑制了$p_2$点原有的速度脉动频率,并减弱了脉动幅值. 位于相对上游位置的$p_2$点,其速度脉动频率明显高于下游的$p_3$点和$p_4$点. 激励作用的加入减弱了无激励工况流场中$p_2$点和$p_3$点速度脉动的幅值,使得各监测点的频谱分布向激励频率及其倍频靠近,却加强了下游$p_4$点的低频速度脉动.

图 30(Fig.30)

图 30 各工况下$p_2$, $p_3$和$p_4$点的速度波动频谱 Fig.30 spectrum of the velocity at $p_2$, $p_3$ and $p_4$

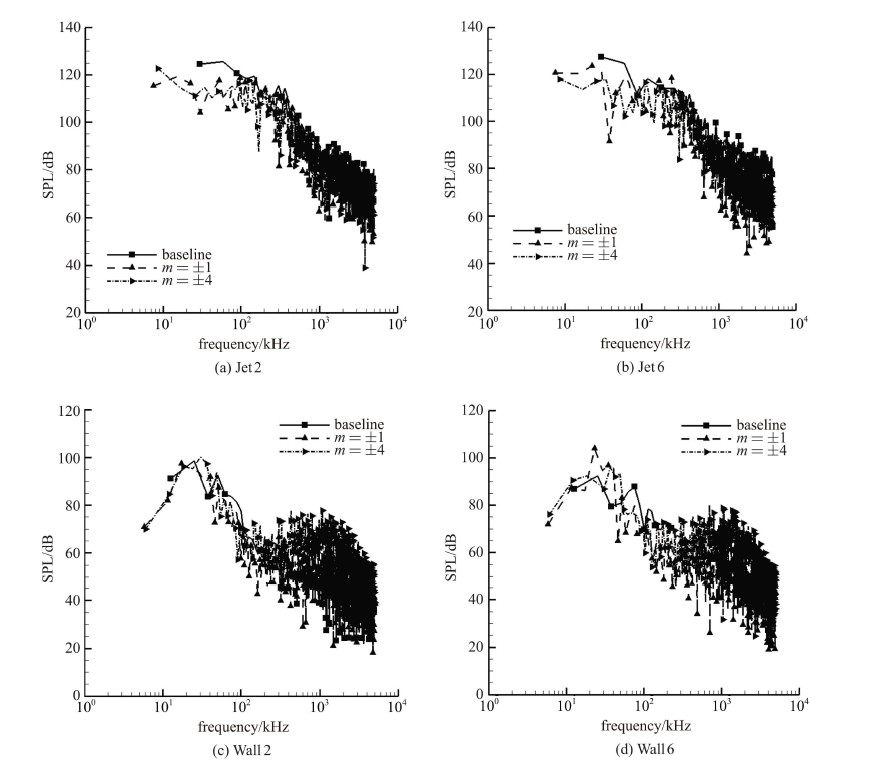
利用FW-H方法计算了位于$x=0.5$\;m横截面上距轴线半径为0.5\;m的圆周上均匀布置的8个监测位置的声压,如图31所示,图中仅显示了$z=0$平面上的两个监测点位置(图31中的``monitor-2''和``monitor-6''). 本文分别计算了由气流在喷管壁面处产生的固壁噪声和由射流包络面内气体产生的气动噪声,下面分析比较无激励工况,$m=\pm1$模态和$m=\pm4$模态下得到的噪声频谱分布. 无激励工况该两点得到的噪声频谱如图32所示,其中``jet2''表示``monitor-2''监测到的由射流包络面产生的噪声,以此类推``jet6''等. 从无激励工况的噪声频谱分布中可以得知由射流包络面产生的气动噪声远大于由壁面产生的固壁噪声,且低频段的噪声分贝值高于高频段,气动噪声分布的频带很宽,在高频段仍有较高的分贝值. 比较由壁面和由射流包络面产生的噪声在无激励工况和激励工况下的频谱特性,``monitor-2''和``monitor-6''监测到的噪声频谱见图33. 从图33(a)和图33(b)可知,激励 作用对抑制气动噪声有一定作用,在``monitor-6''位置处抑制作用体现的更明显. 此外,对于气动噪声,激励作用对高频段的抑制作用明显强于对低频段的影响. 图33(b)显示在高于100kHz的频带范围内,$m=\pm1$和$m=\pm4$工况下的噪声相比无激励工况有所降低. 图33(c)和图33(d)显示了固壁噪声的频谱特性,可以发现$m=\pm1$工况的噪声强度和无激励工况相当,而$m=\pm4$工况的噪声高于无激励工况,所以激励作用在一定程度上加强了固壁噪声.

图 31(Fig.31)

图 31 噪声监测示意图 Fig.31 Sketch of the sound monitors

图 32(Fig.32)

图 32 无激励工况的噪声频谱图 Fig.32 Sound spectrum of monitor-2 and monitor-6 in the baseline

图 33(Fig.33)

图 33 不同工况下两处监测点的噪声频谱 Fig.33 Sound spectrum of monitor-2 and monitor-6

采用大涡模拟方法研究了热激励器在不同激励模态对超声速圆管射流近场的影响,在喷管出口附近用凹槽``保护''热激励器以维持局部高温区域,形成对下游流场的扰动作用. 数值模拟中采用加入净热功率区域的方法来模拟热激励器的热效应,分析比较了$m=\pm1$模态和$m=\pm4$模态的激励作用对射流的影响,并从射流大涡拟序结构和频谱分布的角度研究了这种热激励器的控制机理.

通过比较分析,得到的结论如下: (1)热激励器形成的高温流体区域对下游流动产生了类似``物理突起''的效果,在高温流体区域附近形成的高涡量区加强了射流剪切层的发展,增强了射流掺混; (2)在激励工况中,激励作用产生了更大的径向速度和周向速度脉动,促进了发卡涡的形成,而不同激励模态下射流涡结构的发展不同,形成不同的射流掺混效果和不同频率的气动噪声; (3)气动噪声的频带很宽,激励作用在一定程度上改变了射流脉动频谱特性,能有效地抑制气动噪声的高频段; (4)对于固壁噪声,$m=\pm4$工况的噪声明显高于无激励工况,说明激励作用会加强固壁噪声.

Yan Hong, Lin Ke