引 言
弹性介质中夹杂周边的动应力集中问题在基础研究和工程实践中有重要的理论意义和应用价值.
经典的均匀介质中圆夹杂的散射问 题已有系统的论 述[1, 2, 3, 4].
在不同类型的空间模型中对圆夹杂散射问题的研究衍生出诸多方法,如:复变函数法,边界积分法,积分方程法,波函数展开法等.
由于介质非均匀性引起波动方程发生变化,以致采用上述方法已无法求得波动问题的解析解,因此研究非均匀介质中波的传播问题相对较困难.
科学技术的飞速发展和工程建设的迫切需求为构造自然界不存在的新材料提供了可能性和必然性,这些人工材料为力学分析和工程应用提出了新挑战.
因此,对非均匀介质中缺陷的力学问题研究显得日益重要.
基于介质径向非均匀的特殊性,到目前为止,极少数的文献涉及到径向非均匀圆形孔洞的静力
学[5, 6, 7]和动力学[8]问题.
近几年,关于均匀介质中含有径向非均匀球体的声波散射问题已有较为详尽的研究成果[9, 10, 11, 12].
然而,针对均匀圆夹杂,关于指数功能梯度材料的弹性波散射问题也有过尝试[13],但对于径向非均匀介质中的弹性动力学问题还没有人研究.
本文从较为简单的含有均匀圆夹杂的径向非均匀介质模型出发,通过坐标变化转换将非均匀亥姆霍兹方程标准化之后,利用复变函数法[14]对夹杂周边的动应力集中分布情况做了分析.
通过算例分析给出了基体和夹杂性质,基体的非均匀参数和入射波参考波数对动应力集中系数的影响.
1 模型建立和控制方程
本文主要研究弹性剪切波在径向非均匀介质中沿任意角$\alpha $入射时均匀圆夹杂的散射问题(见图1). 介质I
(基体)为非均匀介质,介质密度是沿$r$方向变化的幂函数形式,而弹性模量是常数,其中$\mu _1 $和$\rho _1
$分别代表介质I的剪切弹性模量和参考密度. 介质Ⅱ(夹杂)是均匀介质,其中$\mu_2 $和$\rho _2
$分别代表介质Ⅱ的剪切弹性模量和密度. 同时,圆形夹杂的半径为$R$,其圆心位于笛卡尔坐标系$\left( {x,y}
\right)$原点. 介质I中密度的变化形式可以表示如下
|
\[\rho \left( r \right)={{\rho }_{1}}{{\beta }^{2}}{{r}^{2\left( \beta -1 \right)}}\]
|
(1) |
其中,$\beta $表示介质I中密度参数的非均匀参数.
在柱坐标系$\left( {r,\theta ,z} \right)$下,考虑时间简谐波,略去时间因子的变系数波动方程为
|
\[{{r}^{2}}\frac{{{\partial }^{2}}W}{\partial {{r}^{2}}}+r\frac{\partial W}{\partial r}+\frac{{{\partial }^{2}}W}{\partial {{\theta }^{2}}}+{{r}^{2}}{{k}^{2}}\left( r,\theta \right)W=0\]
|
(2) |
其中,$k\left( {r,\theta } \right) = \omega /{c\left( {r,\theta } \right)}$是波数,$\omega
$是对应$W$的圆频率. $c\left( {r,\theta } \right) = \sqrt {\mu / {\rho \left( {r,\theta } \right)}}
$是剪切波波速,$\rho $和$\mu $分别代表密度和剪切弹性模量.
利用$k$与$\rho $的相互关系,方程(2)可以写为
|
\[\frac{{{\partial }^{2}}W}{\partial {{r}^{2}}}+\frac{1}{r}\frac{\partial W}{\partial r}+\frac{1}{{{r}^{2}}}\frac{{{\partial }^{2}}W}{\partial {{\theta }^{2}}}+k_{0}^{2}{{\beta }^{2}}{{r}^{2(\beta -1)}}W=0\]
|
(3) |
其中,$k_0 $为参考波数.
应力分量可以表示为
|
\[{{\tau }_{rz}}=\mu \frac{\partial W}{\partial r}, {{\tau }_{\theta z}}=\mu \frac{1}{r}\frac{\partial W}{\partial \theta }\]
|
(4) |
基于复变函数理论,引入一组复变量$z = x + {\rm i}y$和$\bar {z} = x -
{\rm i}y$,方程(3)可写为
|
\[\frac{{{\partial }^{2}}W}{\partial z\partial \bar{z}}+\frac{1}{4}{{\beta }^{2}}{{\left( z\bar{z} \right)}^{\beta -1}}k_{0}^{2}W=0\]
|
(5) |
引入新的变量
|
\[\zeta ={{z}^{\beta }},\bar{\zeta }={{\bar{z}}^{\beta }}\]
|
(6) |
将式(6)代入方程(5),可得到标准亥姆霍兹方程
|
\[\frac{{{\partial }^{2}}W}{\partial \zeta \partial \bar{\zeta }}+\frac{1}{4}k_{0}^{2}W=0\]
|
(7) |
对应的应力分量可以表示为
|
\[{{\tau }_{rz}}=\mu \beta \left( \frac{\partial W}{\partial \zeta }{{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}+\frac{\partial W}{\partial \bar{\zeta }}{{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right)\]
|
(8) |
|
\[{{\tau }_{\theta z}}=\text{i}\mu \beta \left( \frac{\partial W}{\partial \zeta }{{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}-\frac{\partial W}{\partial \bar{\zeta }}{{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right)\]
|
(9) |
2 位移和应力场
基于模型和介质性质的对称性,弹性剪切波在
介质I中沿水平方向入射,可以写为
|
\[W_{\text{I}}^{(i)}={{W}_{0}}\exp \left[ \text{i}{{k}_{1}}(\zeta +\bar{\zeta })/2 \right]\]
|
(10) |
其中,$W_0 $为入射波的振幅,$k_1 $为介质I的参考波数.
将式(10)代入式(8)和式(9),可以得到对应入射波的应力分量
|
\[\begin{align}
& \tau _{rz,\text{I}}^{(i)}=\frac{\text{i}}{2}\beta {{\mu }_{1}}{{k}_{1}}{{W}_{0}}\left( {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}+{{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right)\cdot \\
& \exp \left[ \text{i}{{k}_{1}}\left( \zeta +\bar{\zeta } \right)/2 \right] \\
\end{align}\]
|
(11) |
|
\[\begin{align}
& \tau _{\theta z,\text{I}}^{(i)}=-\frac{1}{2}\beta {{\mu }_{1}}{{k}_{1}}{{W}_{0}}\left( {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}-{{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right)\cdot \\
& \exp \left[ \text{i}{{k}_{1}}\left( \zeta +\bar{\zeta } \right)/2 \right] \\
\end{align}\]
|
(12) |
由夹杂引起的散射波满足方程(7),具体形式可表示为
|
\[W_{\text{I}}^{(s)}\left( \zeta ,\bar{\zeta } \right)=\sum\limits_{n=-\infty }^{\infty }{{{A}_{n}}H_{n}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right)}{{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n}}\]
|
(13) |
其中,$A_n $为待定系数.
将式(13)代入式(8)和式(9),得到散射波的应力分量
|
\[\begin{align}
& \tau _{rz,\text{I}}^{(s)}=\frac{\beta {{\mu }_{1}}{{k}_{1}}}{2}\sum\limits_{n=-\infty }^{\infty }{{{A}_{n}}}\left[ H_{n-1}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot \right. \\
& \left. {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}-H_{n+1}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
\end{align}\]
|
(14) |
|
\[\begin{align}
& \tau _{\theta z,\text{I}}^{(s)}=\frac{\text{i}\beta {{\mu }_{1}}{{k}_{1}}}{2}\sum\limits_{n=-\infty }^{\infty }{{{A}_{n}}\left[ H_{n-1}^{\left( 1 \right)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot \right.} \\
& \left. {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}+H_{n+1}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
\end{align}\]
|
(15) |
在圆弹性夹杂内激发的驻波可以写成如下形式
|
\[W_{\text{II}}^{(t)}=\sum\limits_{n=-\infty }^{\infty }{{{B}_{n}}{{J}_{n}}\left( {{k}_{2}}\left| \zeta \right| \right)}{{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n}}\]
|
(16) |
其中,$B_n $为待定系数,$k_2 $为介质Ⅱ的波数.
将式(16)代入式(8)和式(9),得到驻波的应力分量
|
\[\begin{align}
& \tau _{rz,\text{II}}^{(t)}=\frac{\beta {{\mu }_{2}}{{k}_{2}}}{2}\sum\limits_{n=-\infty }^{\infty }{{{B}_{n}}\left[ {{J}_{n-1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot \right.} \\
& \left. {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}-{{J}_{n+1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left[ \frac{\zeta }{\left| \zeta \right|} \right]}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
\end{align}\]
|
(17) |
|
\[\begin{align}
& \tau _{\theta z,\text{II}}^{(t)}=\frac{\text{i}\beta {{\mu }_{2}}{{k}_{2}}}{2}\sum\limits_{n=-\infty }^{\infty }{{{B}_{n}}\left[ {{J}_{n-1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot \right.} \\
& \left. {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}+{{J}_{n+1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
\end{align}\]
|
(18) |
3 边界条件和动应力集中系数
基于基体和夹杂的界面条件,边界条件应为位移和应力在$r = R$处连续
|
\[\left. \begin{array}{*{35}{l}}
W_{\text{I}}^{(i)}+W_{\text{I}}^{(s)}=W_{\text{II}}^{(t)} \\
\tau _{rz,\text{I}}^{(i)}+\tau _{rz,\text{I}}^{(s)}=\tau _{rz,\text{II}}^{(t)} \\
\end{array} \right\}\]
|
(19) |
将式(10)、(11)、(13)、(14)、(16)和(17)代入上述方程组(19),整理得
|
\[\left. \begin{array}{*{35}{l}}
\sum\limits_{n=-\infty }^{\infty }{\left( {{A}_{n}}\xi _{n}^{\left( 11 \right)}+{{B}_{n}}\xi _{n}^{\left( 12 \right)} \right)={{\xi }^{\left( 1 \right)}}} \\
\sum\limits_{n=-\infty }^{\infty }{\left( {{A}_{n}}\xi _{n}^{\left( 21 \right)}+{{B}_{n}}\xi _{n}^{(22)} \right)={{\xi }^{\left( 2 \right)}}} \\
\end{array} \right\}\]
|
(20) |
其中
|
\[\begin{align}
& \xi _{n}^{(11)}=-H_{n}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n}} \\
& \xi _{n}^{\left( 12 \right)}={{J}_{n}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n}} \\
& {{\xi }^{(1)}}={{W}_{0}}\exp \left[ \text{i}{{k}_{1}}\left( \zeta +\bar{\zeta } \right)/2 \right] \\
& \xi _{n}^{(21)}=-\frac{\beta {{\mu }_{1}}{{k}_{1}}}{2}\left[ H_{n-1}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot {{z}^{\beta -1}}{{e}^{\text{i}\theta }}- \right. \\
& \left. H_{n+1}^{(1)}\left( {{k}_{1}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
& \xi _{n}^{(22)}=\frac{\beta {{\mu }_{2}}{{k}_{2}}}{2}\left[ {{J}_{n-1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n-1}}\cdot {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}- \right. \\
& \left. {{J}_{n+1}}\left( {{k}_{2}}\left| \zeta \right| \right){{\left( \frac{\zeta }{\left| \zeta \right|} \right)}^{n+1}}\cdot {{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right] \\
& {{\xi }^{(2)}}=\frac{\text{i}}{2}\beta {{\mu }_{1}}{{k}_{1}}{{W}_{0}}\left( {{z}^{\beta -1}}{{\text{e}}^{\text{i}\theta }}+{{{\bar{z}}}^{\beta -1}}{{\text{e}}^{-\text{i}\theta }} \right)\cdot \\
& \exp \left[ \text{i}{{k}_{1}}\left( \zeta +\bar{\zeta } \right)/2 \right] \\
\end{align}\]
|
方程组(20)两端乘以${\rm e}^{ - {\rm i}m\theta }$后在$\left( { - \pi ,\pi }
\right)$上积分,得到可以确定$A_n $和$B_n $的无限代数方程组
|
\[\sum\limits_{n=-\infty }^{\infty }{\left[ \begin{array}{*{35}{l}}
\xi _{mn}^{(11)} & \xi _{mn}^{(12)} \\
\xi _{mn}^{(21)} & \xi _{mn}^{(22)} \\
\end{array} \right]}\left[ \begin{array}{*{35}{l}}
{{A}_{n}} \\
{{B}_{n}} \\
\end{array} \right]=\left[ \begin{array}{*{35}{l}}
\xi _{m}^{(1)} \\
\xi _{m}^{(2)} \\
\end{array} \right]\]
|
(21) |
其中,$ m = 0,\pm 1,\pm 2,\cdots $
|
\[\begin{align}
& \xi _{mn}^{(11)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{\xi _{n}^{(11)}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
& \xi _{mn}^{(12)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{\xi _{n}^{(11)}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
& \xi _{m}^{(1)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{{{\xi }^{(1)}}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
& \xi _{mn}^{(21)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{\xi _{n}^{(21)}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
& \xi _{mn}^{(22)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{\xi _{n}^{(22)}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
& \xi _{m}^{\left( 2 \right)}=\frac{1}{2\pi }\int_{-\pi }^{\pi }{{{\xi }^{(2)}}{{\text{e}}^{-\text{i}m\theta }}}\text{d}\theta \\
\end{align}\]
|
本文主要研究圆夹杂周边的动应力集中系数,由$\tau _{\theta z}^{\left( \cdot
\right)} $与$\tau _0 $的比值表示
|
\[\tau _{\theta z}^{*}=\left| \tau _{\theta z}^{\left( \cdot \right)}/{{\tau }_{0}} \right|\]
|
(22) |
其中,$\tau _{\theta z}^{\left( \cdot \right)} = \tau _{\theta z,{\rm I}}^{\left( i \right)} + \tau _{\theta
z,{\rm I}}^{(s)} $,$\tau _0 = {\mu k_1 W_0 } /2$.
将式(12)和(15)代入式(22),可以得到动应力集中系数DSCF的最终表达式.
4 数值结果和讨论
基于以上理论推导,下面给出在非均匀无限介质中圆夹杂周边的动应力集中系数的数值结果分析. 文中采用以下无量纲定义:参考波数$k_1 R$,非均匀参数$\beta R$,夹杂和参考基体的波数比$k^ * = {k_2 } /{k_1 }$和剪切模量比$\mu ^ * = {\mu _1 } /{\mu _2
}$. 分别取3种情况作为算例对比讨论:(1) $k^ * = 0.5$,$\mu ^ * = 0.25$;(2) $k^ * = 2.0$,$\mu ^ * = 4.0$;(3) $k^ * = 4.0$,$\mu ^ * = 16.0$,分别代表夹杂与参考基体相对较硬、较软和更软.
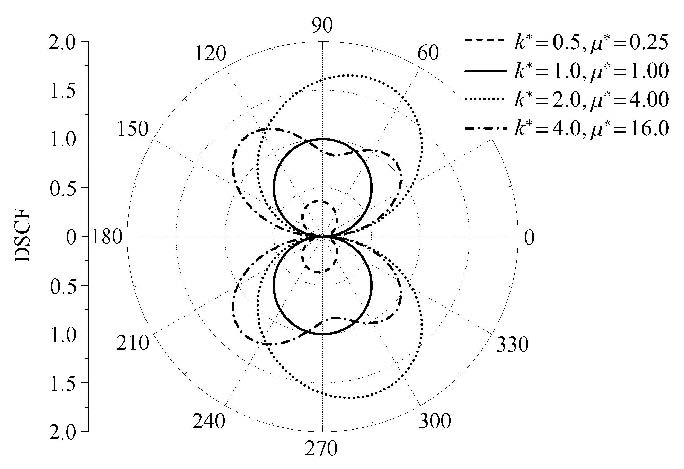
图2是基体退化为均匀介质的情况($\beta R = 1.0)$. 当$k^ * = 1.0$,$\mu ^ * =
1.0$时,基体和夹杂是相同参数下的同种介质,夹杂周边的DSCF最大值为1,此结果与实际情况完全一致. 当夹杂与基体相对较硬时,DSCF明显减小;相反,当夹杂与基体相对较软时,DSCF明显增大.
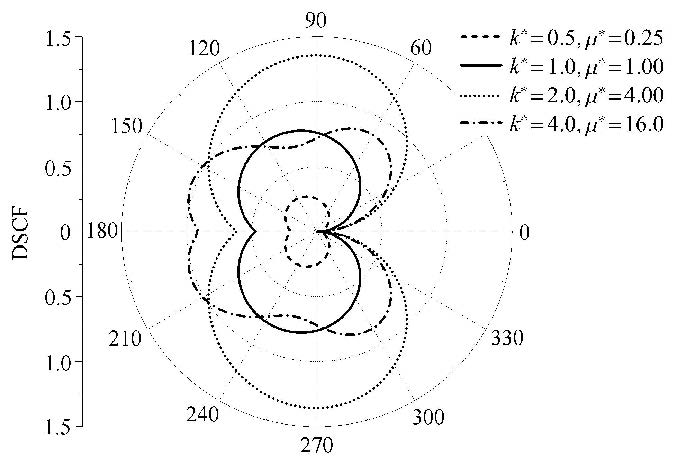
图3 给出了径向非均匀介质中圆夹杂周边的动应力集中系数随不同$k^ * $和$\mu ^ * $的分布情况.
从图中可以看出,DSCF关于$x$轴对称,这是在入射波水平入射情形下由模型和介质的对称性造成的. 当$\beta R = 0.8$
时,基体密度随着$r$的增大而减小的情况. 由于介质非均匀性的影响,DSCF的分布相对图2有较大的变化.
尤其在迎波面$\theta = \pi $处的DSCF明显增大.
图4给出了径向非均匀介质中圆夹杂周边的动应力集中系数随不同基体非均匀参数$\beta R$的分布情况.
从图中可看出,在密度密度按幂函数变化情形下,非均匀参数的微小变化对DSCF造成的影响较大. 随着$\beta
R$的增大,DSCF的最大值也在逐渐增大,同时由$\theta = \pi $向$\theta = \pi /2$和$\theta = - \pi / 2$逼近.
图5给出了不同$k^ * $和$\mu ^ * $情形下径向非均匀介质中圆夹杂周边的动应力集中系数随$\beta R$的变化情况.
当$0.3 ≤ \beta R ≤ 1.4$时,夹杂相对基体较硬和较软时,DSCF的变化趋势与$k^ * = 1.0$,$\mu ^ * =
1.0$的情形基本一致. 当夹杂相对基体更软时,DSCF的变化趋势出现波动现象.
5 结 论
本文采用复变函数法对径向非均匀介质中圆夹杂的散射问题进行研究. 通过对均匀介质的情况和不同介质参数做比较,分析了圆夹杂周边的动应力响应,进而得到以下结论:
(1)
基体密度的非均匀变化对圆夹杂周边的动应力集中系数影响较大. 尤其当基体参考波数较大,或夹杂与参考基体相对更软时动应力集中系数均会出现波动现象;
(2)
基体密度的径向非均匀变化引起了入射波、散射波和驻波的变化,进而导致圆夹杂周边的动应力集中系数在迎波面变化较明显;
(3)
基于复变函数理论对保角映射的优越性,该方法可以拓展到对任意形夹杂周边的散射问题进行研究.
参考文献
| [1] |
Pao YH, Mow CC. Diffraction of Elastic Waves and Dynamic Stress Concentrations. Crane and Russak, New York, 1973 |
| [2] |
黎在良, 刘殿魁. 固体中的波. 科学出版社, 1995 (Li Zailiang, Liu Diankui. Wave in Solid. Beijing: Science Press, 1995 (in Chinese)) |
| [3] |
Mow CC, Mente LJ. Dynamic stresses and displacements around cylindrical discontinuities due to plane harmonic shear waves. ASME Journal of Applied Mechanics, 1963, 30(4): 598-604 |
| [4] |
杨在林, 闫培雷, 刘殿魁. SH波对浅埋弹性圆柱及裂纹的散射与地震动.力学学报, 2009, 41(2): 229-235 (Yang Zailin, Yan Peilei, Liu Diankui. Scattering of SH-waves and ground motion by an elastic cylindrical inclusion and a crack in half space. Acta Mechanica Sinica, 2009, 41(2): 229-235 (in Chinese)) |
| [5] |
Kubair DV, Bhanu-Chandar B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension. International Journal of Mechanical Sciences, 2008, 50(4): 732-742 |
| [6] |
Yang Q, Gao CF, Chen W. Stress analysis of a functional graded material plate with a circular hole. Archive of Applied Mechanics, 2010, 80(8): 895-907 |
| [7] |
Mohammadi M, Dryden JR, Jiang L. Stress concentration around a hole in a radially inhomogeneous plate. International Journal of Solids and Structures, 2011, 48(3): 483-491 |
| [8] |
Yang Q, Gao CF. Dynamic stress analysis of a functionally graded material plate with a circular hole. Meccanica, 2013, 48(1): 91-101 |
| [9] |
Kokkorakis GC, Fikioris JG, Fikioris G. Field induced in inhomogeneous spheres by external sources. I. The scalar case. Journal of the Acoustical Society of America, 2002, 112(4): 1297-1306 |
| [10] |
Martin PA. Acoustic scattering by inhomogeneous spheres. Journal of the Acoustical Society of America, 2002, 111(5): 2013-2018 |
| [11] |
Bilgin E, Yapar A. An acoustic inverse scattering problem for spheres with radially inhomogeneous compressibility. Journal of the Acoustical Society of America, 2002, 133(4): 2097-2104 |
| [12] |
Zouros GP, Kokkorakis GC. Green's function of radial inhomogeneous spheres excited by internal sources. Journal of the Acoustical Society of America, 2011, 129(1): 24-31 |
| [13] |
Fang XQ, Liu JX, Zhang LL, et al. Dynamic stress from a subsurface cylindrical inclusion in a functionally graded material layer under anti-plane shear waves. Materials and Structures, 2010, 44(1): 67-75 |
| [14] |
Liu DK, Gai BZ, Tao GY. Applications of the method of complex functions to dynamic stress concentrations. Wave Motion, 1982, 4(3): 293-304 |
DYNAMIC ANALYSIS ON A CIRCULAR INCLUSION IN A RADIALLY INHOMOGENEOUS MEDIUM
Yang Zailin

, Hei Baoping, Yang Qinyou
College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China
Fund: The project was supported by the Natural Science Foundation of Heilongjiang Province, China (A201310), the Scientific Research Starting Foundation for Post Doctorate of Heilongjiang Province, China (LBH-Q13040) and the National Natural Science Foundation of China (10972064).
Abstract: Based on the complex function theory, scattering by elastic waves around a homogeneous circular inclusion buried in a radially inhomogeneous elastic medium is investigated in the paper. The inhomogeneity of the medium is assumed that the density depends on the radial distance as a power-law function and the shear modulus is constant. Inhomogeneous wave equation with variable coefficient is converted to the standard Helmholtz equation by using the coordinate transformation. The expressions of displacement and stress fields in complex coordinate are presented due to the existing of both the inhomogeneous base and homogeneous inclusion. The dynamic stress concentration factor (DSCF) around the inclusion is illustrated numerically by examples. Results show that wave number and shear modulus ratios between the base and inclusion, wave number of the base, inhomogeneous parameter have great influence on the dynamic stress concentration.
Key words:
radially inhomogeneous medium wave equation with variable coefficient homogeneous circular inclusion dynamic stress concentration factor



 2015, Vol. 47
2015, Vol. 47