航空航天领域的研究中涉及到很多几何变形或者相对运动问题,如气动弹性分析、气动优化设计、控制面的运动、飞机投弹问题、弹射问题等. 在针对这些问题的数值分析中,需要根据几何变形或物体的运动更新流场网格,高效稳定的网格变形方法是获得高质量变形网格的关键.
在20世纪90年代,Gaitonde等[1]提出了适用于结构网格变形的无限代数插值方法(TFI),该方法计算量小,可以高效生成变形网格,但是对复杂几何外形的变形问题,生成的网格质量很难保证. 与TFI方法利用物面位置重新生成网格的方法不同,基于不同物理模型的网格变形方法被广泛应用,如温度体模型法[2]、弹性体方法[3]等. 这一类方法使用最广泛的是Batin提出的弹簧网络法[4, 5]:将网格变形等效为弹簧网络系统的受力平衡问题,此后局部重构及扭转弹簧模型被引入弹簧网络方法中,提高三维网格在大变形下的处理能力[6, 7]. 弹簧网络方法稳定性较好,但在变形时需要确定弹簧网络的拓扑关系,需要存储的信息较多,计算效率较低.
Delaunay图方法是一种生成非结构网格的算法,刘学强等[8]将Delaunay图映射方法引入动网格的处理中提出了Delaunay背景网格插值法. Delaunay方法对于复杂几何外形尤其是凹物面的处理仍存在缺陷. 针对这一问题,郑冠男等[9, 10]结合弹簧网络方法与代数背景网格插值方法各自优点,提出多套重叠背景网格插值方法:利用弹簧网络方法求解背景网格的变形,在保证网格质量的同时提高变形效率.
近几年,对离散数据具有较强处理能力的径向基函数(RBF)插值方法得到了广泛关注[11, 12, 13]. 张伟伟和叶正寅[14, 15]指出基于RBF的动网格方法相对弹簧网络法具有计算效率高、变形能力强的特点,并能够得到高质量的变形网格. Rendall等[16]提出了一种精简控制点的贪婪算法,大幅提高了网格变形的效率,但也带来变形后物面误差过大的问题. 针对这一问题,Rendall等[17]提出一种临近误差修正方法,但经该方法处理后的边界层网格容易发生交错.
本文在贪婪算法的基础上,提出了一种适用于带有边界层的黏性网格变形方法. 该方法利用少量控制点粗略给出变形后网格位置和误差分布,根据误差分布选择第二组控制点. 利用第二组控制点将误差函数重新插值,便可得到较准确的变形网格. 相对临近误差修正方法,该方法避免遍历所有物面点,保证了较高的计算效率;该方法也适合并行处理,保证对大规模网格变形的高效处理能力. 为验证本文的方法,选取带襟翼的NLR 7301二维构型和带短舱的DLR F6三维构型的网格变形问题作为验证算例. 计算结果表明:本文方法可以大幅降低网格变形后的物面误差,有效避免边界层网格发生交错,也具有处理大规模网格复杂变形问题的能力.
1 基于RBF的动网格方法 1.1 RBF插值方法
基于径向基函数,利用给定的控制点$ { X} = \left\{ { r}_1 ,\cdots ,{ r}_{ N_s } \right\}$可以将目标函数${ f}$插值到空间中任意位置${ r}$处
\[g(r)=\sum\limits_{i=1}^{{{N}_{c}}}{{{\alpha }_{i}}}\phi (\left\| r-{{r}_{i}} \right\|)\]
(1)
\[g({{r}_{i}})=f({{r}_{i}}),i=1,2,\cdots ,{{N}_{c}}\]
(2)
基于RBF的动网格方法的计算量与网格点和控制点数量有关. 在待插值点数量一定的情况下,减少控制点数量可以提高网格变形的效率. Rendall和Allen[16]提出精简控制点数量的贪婪算法,以降低插值结果与目标函数之间误差的前提下,尽可能减少控制点数量以达到提高网格变形效率的目的.
该方法首先在物面上随机选择$N$个控制点,利用这些控制点计算插值后的物面位移与插值误差,并将误差最大的点添加到控制点中,得到新的控制点集合. 重复上述过程,直到插值后的物面与目标函数的误差达到误差限,这样便得到一组数量远小于物面点数量的控制点集合.
1.3 黏性网格变形方法针对基于RBF的贪婪算法插值结果存在较大误差和临近误差修正方法在处理带有边界层的网格易发生网格交错的问题,本文提出了一种基于RBF的黏性网格变形方法.
使用贪婪算法的动网格方法,所选择控制点${ X}_c $是所有物面点的一个子集,用这有限的控制点近似表达物面上的函数分布. RBF插值在控制点上可以得到精确的插值结果,在 除控制点外其他点上的插值结果是不准确的. 基于RBF插值的这一特点,在网格变形前利用贪婪算法选择一组控制点${ X}_{\rm pre} $,计算插值后的物面上的误差分布${ E}_x ,{ E}_y ,{ E}_z $. 给定物面误差限${ E}_{\rm lim } $,搜索插值误差超过误差限${ E}_{\rm lim } $的网格点,构成另一组控制点${ X}_{\rm cor} $. 由RBF插值的性质可知,${ X}_{\rm pre} $和${ X}_{\rm cor} $一定是物面点的互斥子集.
在随后的网格变形过程中,首先在控制点${ X}_{\rm pre}
$的基础上对网格变形进行预处理,得到一个带有较大物面误差的变形网格
\[\left. \begin{align}
& \Delta {{x}_{\text{pre}}}={{\Phi }_{cv}}\Phi _{cc}^{-1}\Delta {{x}_{c}} \\
& \Delta {{y}_{\text{pre}}}={{\Phi }_{cv}}\Phi _{cc}^{-1}\Delta {{y}_{c}} \\
& \Delta {{z}_{\text{pre}}}={{\Phi }_{cv}}\Phi _{cc}^{-1}\Delta \\
\end{align} \right\}\]
(3)
物面误差${ E}_x ,{ E}_y ,{ E}_z
$反映变形后的物面与真实物面之间的差异. 将误差分布看做变形后的网格运动到真实位置的位移,再次插值有
\[\left. \begin{align}
& \Delta {{x}_{\text{cor}}}={{\Phi }_{rv}}\Phi _{rr}^{-1}{{E}_{x}} \\
& \Delta {{y}_{\text{cor}}}={{\Phi }_{rv}}\Phi _{rr}^{-1}{{E}_{y}} \\
& \Delta {{z}_{\text{cor}}}={{\Phi }_{rv}}\Phi _{rr}^{-1}{{E}_{z}} \\
\end{align} \right\}\]
(4)
其中,${ \Phi }_{rv} $和${ \Phi }_{rr} $是对应于控制点$ { X}_{cor} $的插值系数矩阵.
经过两步变形后空间网格点上的变形量为
\[\left. \begin{align}
& \Delta {{x}_{RBF}}=\Delta {{x}_{\text{pre}}}+\Delta {{x}_{\text{cor}}} \\
& \Delta {{y}_{RBF}}=\Delta {{y}_{\text{pre}}}+\Delta {{y}_{\text{cor}}} \\
& \Delta {{z}_{RBF}}=\Delta {{z}_{\text{pre}}}+\Delta {{z}_{\text{cor}}} \\
\end{align} \right\}\]
(5)
该方法可以大幅度降低物面插值误差,并有效解决边界层网格的交错问题,也避免了遍历所有物面点,保证了较高的计算效率. 同时该方法也适合并行处理,保证对大规模网格变形的高效处理能力.
2 算 例本节以带襟翼的NLR-7301襟翼绕前缘点下偏20° 和带发动机短舱的DLR-F6翼身组合体上仰40°为例. 分别采用贪婪算法和本文发展的变形方法计算变形后网格,对比研究两种方法物面变形精度,并验证其对大规模网格变形问题的处理能力.
2.1 带襟翼的NLR-7301两段翼对于襟翼的NLR-7301两端翼,假定襟翼绕其前缘点向下偏转20°. 变形前网格选用多块对接结构化网格,网格数量为15万,物面点数量为661,边界层首层网格高度为$1.0\times 10^{-6}$.
网格变形的径向基函数选用Wendland's C2,误差限取$1.0\times 10^{ - 5}$. 图1给出了所选取的两组控制点在物面上的分布:其中红色的为预处理时贪婪算法选取的控制点共68个,蓝色的为另外一组控制点共287个,可以看出在主翼前缘插值误差较小,误差较大的点大多集中在主翼和襟翼搭接的位置附近.

|
图1 两组控制点在物面上的分布 Fig.1 Control points distribution on surface |
图2给出了贪婪算法计算得到的物面附近的变形网格,此时变形后的物面与真实位置间存在较大误差,最大变形误差为0.003 8. 从图 中可以看出,在主翼和襟翼搭接的位置上,两段翼型的插值结果出现较大的误差,本不该发生变形的主翼后缘也因受襟翼运动影响,插值后物面产生了扭曲变形.
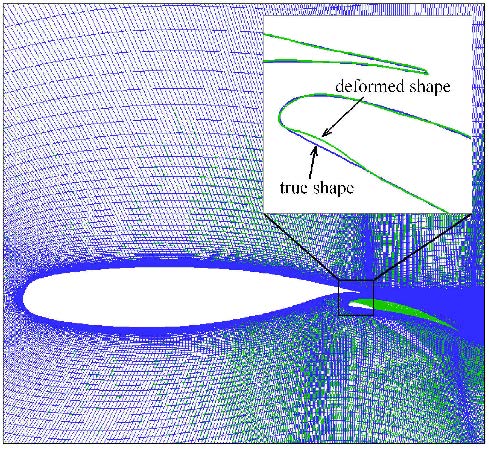
|
图2 贪婪算法的插值误差在物面上的分布 Fig.2 Interpolation error of greedy method on surface |
由于前一组控制点上变形后物面位置是准确的,在采用本文发展的保形方法时应控制物面误差的传播范围,避免将误差再次传递到这些点上;另一方面,为了避免边界层网格发生交错,保形修正的物面误差的传播距离应该适当远.
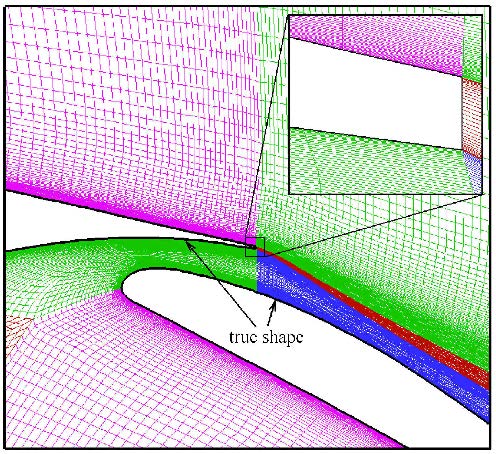
|
图3 变形后边界层网格分布 Fig.3 Deformed boundary layer meshes |
以带发动机短舱的DLR F6翼身组合体上仰40°的网格变形问题为例,研究本文发展的方法对大规模网格变形问题的处理能力. 变形的初始网格为多块对接的结构网格,网格规模为6.41×10$^6$,边界层首层网格高度大约为$1.0\times 10^{-4}$.
图4为以单位函数为目标函数,使用贪婪算法搜索控制点过程中最大误差随控制点数量增加的变化,在43 931个物面网格点中,一共选出了314个控制点.
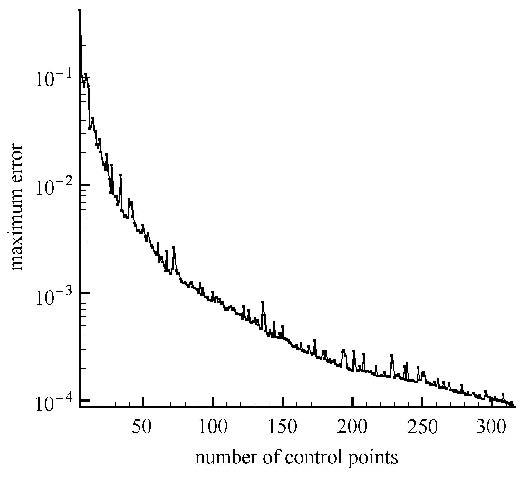
|
图4 物面最大误差随控制点变化历程 Fig.4 Convergence of maximum error on surface |
图5给出了两组控制点在物面上的分布情况,第2组控制点的误差限选为边界层首层网格高度,即$1.0\times 10^{ - 4}$,共选出2 560个点. 第二组控制点大多集中在机翼尖端的上下表面、后机身及发动机短舱上,曲率变化较小的机身分布较少.
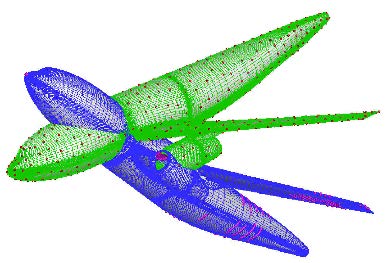
|
图5 控制点在物面上的分布 Fig.5 Control points distribution on surface |
图6给出了2种方法变形后物面上误差的分布情况. 对于贪婪算法,最大变形误差为$3.8\times 10^{-4}$,误差较大的位置在机翼尖端的上下表面、后机身及发动机短舱上. 本文的网格变形方法得到的变形网格最大插值误差为$9.9\times 10^{-5}$,平均误差为$2.6\times 10^{-5}$,物面网格变形精度得到有效的改善.

|
图6 插值误差在物面上的分布 Fig.6 Interpolation error distribution on surface |
采用缩减控制点的贪婪算法,可以大幅度提高网格变形效率,并可以并行处理大规模网格变形问题. 气动分析中物体表面压力分布对外形变化十分敏感,该方法变形后网格与真实位置存在较大误差,临近误差修正方法在处理带有边界层的网格时,存在边界层网格容易发生交错,且变形效率较低. 针对这一问题本文在上述方法的基础上,提出了一种基于RBF的物面保形的黏性动网格方法,数值试验结果表明:
(1) 本文发展的动网格方法变形后网格与真实位移基本一致,相对于贪婪算法物面误差可以降低两个量级以上,大幅减小网格变形的物面变形误差. 对于带有边界层的黏性网格,本文的方法可以有效避免边界层网格交错问题.
(2) 对利用第一组控制点预估的变形网格进行误差修正时,控制半径对计算结果影响显著,控制半径的选取应综合考虑物面网格尺度与边界层网格的高度,选用合适的控制半径将明显减小网格的变形误差.
(3) 降低误差限可以显著减小变形后网格的物面误差,但也会引起控制点数量增多降低计算效率的问题. 对于大规模网格变形问题,适当选取误差限和采用并行处理可以提高网格变形效率.
| [1] | Gaitonde AL, Fiddes SP. A moving mesh system for the calculation of unsteady flows. AIAA Paper, 1993: 93-461 |
| [2] | 陈炎,曹树良,梁开洪 等. 射流放水阀动态关闭过程研究. 流体机械, 2009, 37(12): 9-13 (Chen Yan, Cao Shuliang, Liang Kaihong, et al. Research on dynamic closing process of hollow-jet valve. Fluid Machinery, 2009, 37(12): 9-13 (in Chinese)) |
| [3] | Tezduyar TE. Stabilized finite element formulations for incompressible flow computations. Advances in Applied Mechanics, 1991, 28: 1-44 |
| [4] | Batina JT. Unsteady Euler algorithm with unstructured dynamic mesh for complex-aircraft aerodynamic analysis. AIAA Journal. 1991, 29(3): 327-333. |
| [5] | Batina JT. Unsteady Euler airfoil solutions using unstructured dynamic meshes. AIAA Journal , 1990, 28(8): 1381-1388 |
| [6] | Farhat C, Degand C, Koobus B, et al. Torsional springs for two-dimensional dynamic unstructured fluid meshes. Computer Methods in Applied Mechanics and Engineering, 1998, 163(1): 231-245 |
| [7] | Burg CO. A robust unstructured grid movement strategy using three-dimensional torsional springs. 34th AIAA Fluid Dynamics Conference and Exhibit, Portland, June-July 2004. AIAA Paper 2004-2529 |
| [8] | Liu X, Qin N, Xia H. Fast dynamic grid deformation based on Delaunay graph mapping. Journal of Computational Physics, 2006, 211(2): 405-423 |
| [9] | Zheng G, Yang G, Qian W. Flutter analyses of complete aircraft based on hybrid grids and parallel computing. Science China Technological Sciences, 2013, 56(2): 398-404 |
| [10] | 郑冠男,杨国伟. 基于背景网格的混合网格变形方法. 振动工程学报, 2011, 24(5): 473-481 (Zheng Guannan, Yang Guowei. Hybrid grid deformation method based on background grid. Journal of Vibration Engineering, 2011, 24(5): 473-481 (in Chinese)) |
| [11] | 姚拴宝,郭迪龙,杨国伟. 基于径向基函数网格变形的高速列车头型优化. 力学学报, 2013, 45(6): 982-986 (Yao Shuanbao,Guo Dilong,Yang Guowei. Aerodynamic optimization of high-speed train based on rbf mesh deformation. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 982-986 (in Chinese)) |
| [12] | Tanbay T, Ozgener B. A comparison of the meshless RBF collocation method with finite element and boundary element methods in neutron diffusion calculations. Engineering Analysis With Boundary Elements, 2014, 46: 30-40 |
| [13] | Biancolini ME, Viola IM, Riotte M. Sails trim optimisation using CFD and RBF mesh morphing. Computers & Fluids, 2014, 93: 46-60 |
| [14] | 张伟伟,高传强,叶正寅. 气动弹性计算中网格变形方法研究进展. 航空学报, 2014, 35(2): 303-319 (Zhang Weiwei, Gao Chuanqiang, Ye Zhengyin. Research progress on mesh deformation method in computational aeroelasticity. Acta Aeronautica et Astronautica Sinica, 2014, 35(2): 303-319 (in Chinses)) |
| [15] | 高传强,张伟伟,蒋跃文等. 两种典型非结构网格变形方法特性对比研究. 航空工程进展, 2014, 5(2): 212-219 (Gao Chuanqiang, Zhang Weiwei, Jiang Yuewen, et al. A comparative study on two typical unstructured grid deformation methods. Advances in Aeronautical Science and Engineering, 2014, 5(2): 212-219 (in Chinses)) |
| [16] | Rendall TCS, Allen CB. Efficient mesh motion using radial basis functions with data reduction algorithms. Journal of Computational Physics, 2009, 228(17): 6231-6249 |
| [17] | Rendall TCS, Allen CB. Parallel efficient mesh motion using radial basis functions with application to multi-bladed rotors. International Journal for Numerical Methods in Engineering, 2010, 81(1): 89-105 |
 2015, Vol. 47
2015, Vol. 47