2. 天津大学机械工程学院力学系, 天津300072;
3. 天津市现代工程力学重点实验室, 天津300072
沟槽(riblets),是指横截面为固定形状的、沿展向周期排列的一系列流向的微小肋条结构. 大量研究发现:与光滑壁面湍流边界层相比,它们在一定物理尺寸范围内具有减阻效应;并在其黏性内尺度无量纲参数$L_{g}^{+ }$ (展向横截面积的平方根)约为11个黏性长度单位(对应沟槽的脊-脊内尺度无量纲展向间距$s^{ + } \approx 17$)时达到最优减阻效果;但随着雷诺数的增加,沟槽减阻效应会随之减弱,甚至反而使得壁面摩擦阻力增加,表现出大扰动粗糙元效应[1, 2]. 沟槽壁面湍流边界层减阻的原因,特别是减阻率线性相关于$s^{ + }$的"黏性区"的减阻机理可归纳为沟槽对湍流边界层近壁区(准)流向涡或发卡涡(涡包)结构的有效抑制和重组[3, 4, 5, 6]; 而对应地,沟槽减阻在达到最优之后表现出大扰动粗糙元效应的原因,已有文献也给出了两种可能解释:(1)沟槽谷内准流向涡与沟槽的相互作用[7];(2)沟槽脊处二次流向涡的脱 落[8]. 可见沟槽减阻失效, 之前文献大都归因于沟槽壁面湍流边界层内的流向涡或准流向涡的行为随沟槽展向尺度的变化. 但文献 [9] 在2011年首次基于其沟槽壁面湍流边界层直接数值模拟数据库的分析,指出限制沟槽减阻效应甚至使阻力增加的原因是一种"类开尔文-亥姆霍兹"不稳定性;这种不稳定性现象在沟槽刚刚达到最优尺寸($s^{+}\approx 17$)时出现;伴随其产生了一种之前未曾被实验观察到的展向"类开尔文-亥姆霍兹"涡结构. 本文使用烟雾流动显示技术,首次在风洞实验中清晰地观察到这种展向"类开尔文-亥姆霍兹"涡结构,并在前期讨论"开尔文-亥姆霍兹"不稳定性现象及其原理[10]的基础上,进一步详细描绘这种"类开尔文-亥姆霍兹"展向涡.
1 实验设备与流场参数实验在英国诺丁汉大学低速回流式风洞中完成. 风洞采用变频调速;其实验段长3 m,截面为508 mm$\times $508 mm八角形;风洞最大稳定风速为10 m/s,自由来流背景湍流度约为0.24%. 实验室温控为22 $\pm $ 0.5°C; 环境压强约为0.101 2 MPa;因此,空气密度$\rho $ 和运动黏度$\nu $分别为1.2 kg/m$^{3}$,1.53 × 10$^{-5}$ m$^{2}$/s.
边界层流场在风洞实验段内水平放置的一块长约3 m的平板上发展. 平板前缘以椭圆半轴长75 mm修缘,并在前缘下游100 mm处布置高$h= 10$ mm,直径为3 mm的微小圆柱阵列触发流场提前转捩为湍流. 距离板前缘下游约1.5 m处嵌入烟雾/粒子播撒器,其高约115 mm. 而沟槽相邻脊-脊物理间距 $s$,脊-谷高度都为7.2 mm;沟槽板截面为三角形,被相邻地嵌入到烟雾/粒子播撒器下游的平板内,即沟槽起点距离平 板前缘的流向距离$x = 1.7$ m. 通过调节平板的尾翼,经过尾翼前缘近壁区的热线信号及其谱分析确认,得到沟槽壁面处零压力梯度且流动未分离的湍流边界层. 使用丹尼尔科技(DANTEC)有限公司54T29型速度测量仪(标定误差为0.02 m/s)测量边界层多个自由来流速度$U_{\infty }$,控制其在0.38 m/s,0.68$\sim$1.62 m/s之间. 实验装置及平板布置参数图1给出. 对应的边界层流场参数,即摩擦速度$u_{\tau } \approx U_{\infty } /22$ (经验公式[11]),边界层厚度 $\delta \approx 0.37 x /Re_{x}^{1 / 5 }$ (普朗特近似公式[12])及雷诺数$Re_{\tau = } u_{\tau} \delta /\nu $ 见表1.
|
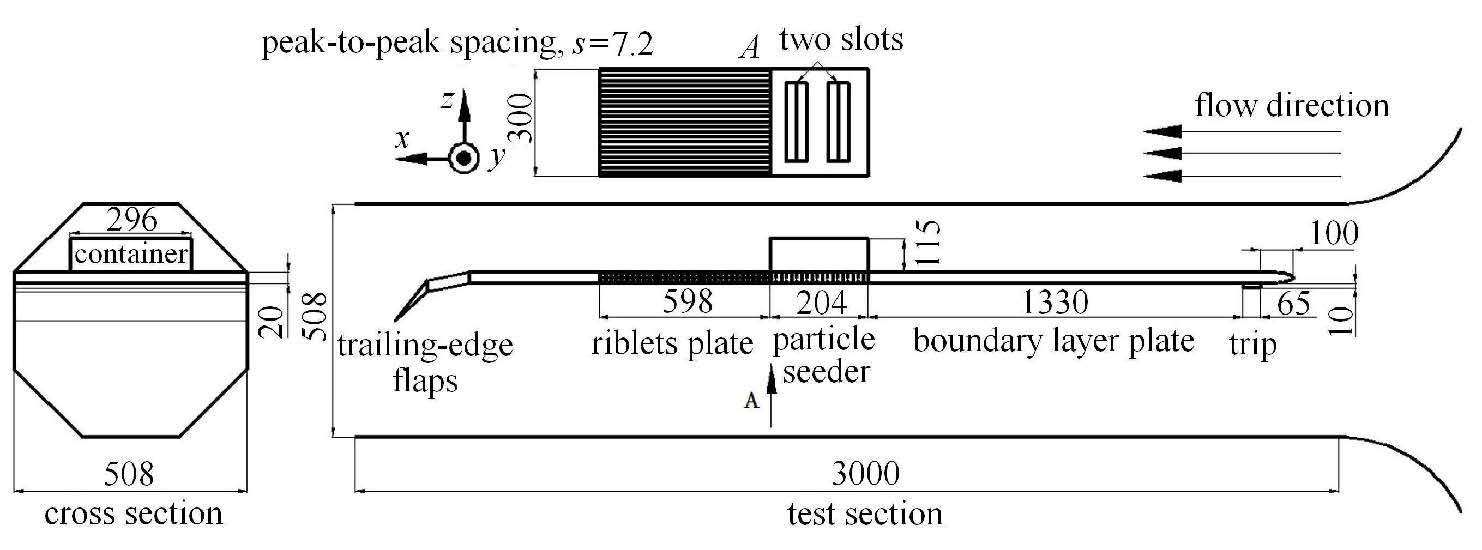
图1 风洞及实验平板布置参数 Fig.1 Schematic of the test section of the closed-loop wind tunnel and test plates |
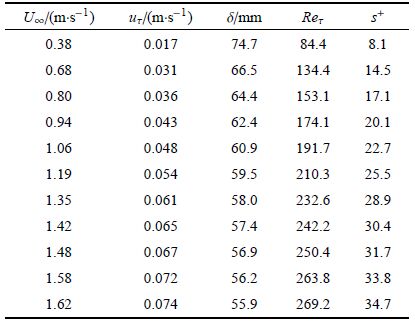
| 表1 沟槽壁面湍流边界层流场基本参数 Table 1 Experimental parameters of the TBLs over riblets |
本文采用烟雾流动显示技术研究上述条件下的沟槽壁面湍流边界层内"类开尔文-亥姆霍兹"不稳定性现象, 即"类开尔文-亥姆霍兹"展向涡结构[9]. 实验使用 TSI 9307-6型烟雾发生器产生平均直径为1 μm的烟雾颗粒作为示踪粒子;使用幻灵(Phantom) 牌SpeedSense 9060型高速互补金属氧化物半导体(CMOS)相机(1024×800 pixels)仰视拍摄上述湍流边界层流场的近壁区域;流场被丽创(Litron)牌 LDY302型Nd: YLF双腔激光器照亮,激光器最大输出功率为100 W,激光波长为527 nm,调节片光厚度约为1 mm (研究"类开尔文-亥姆霍兹"涡在不同法向位置$y$的流动情况时,片光厚约2 mm). 使用丹尼尔科技有限公司同步器同步激光和相机;相机触发频率设置为500 Hz (或800 Hz),曝光时间500 μs (或1 000 μs),且经标定后,相机最大视场约为425 mm×260 mm (流向$\times $展向;注:下文中边界层流场流向、法向、展向分别用$x$,$y$,$z$表示).
2 实验结果及分析烟雾流动显示实验共分两部分进行. 首先,观察平面(或激光平面)平行于沟槽壁面,相机拍摄$x$-$z$面视场. 片光恰好相切于沟槽脊峰,即片光中心距离脊峰平面法向位置$y$约为0.5 mm. 流向突出高度$h_{\rm pl}$取0.18$s$[13],即片光平面中心位于沟槽流向速度剖面虚拟原点以上1.796 mm处. 实验记录11个不同雷诺数下的沟槽壁面边界层流场,流场参数及其在减阻曲线上的对应位置分别在前文表1及图2中给出. 边界层流场流动显示结果如图3和图4所示,流动方向从左至右.

|
图2
顶角为60°三角形沟槽的一般减阻曲线[2] (图中红色$\bigcirc $为本文测点) Fig.2 Effect of the peak-to-peak spacings,$s^{+}$,on the drag of a triangular riblet with 60° peak sharpness[2] (the red circle the measuring point of this paper) |
图3给出了$y^{ + }=2$,$s^{ + } =8.1$时$x$-$z$面内沟槽壁面边界层流场结构. 有效视场大小$x^{ + }$-$z^{ + }$: 478.1×180.0 (黏性内尺度无量纲). 此时沟槽减阻,$s^{ + }$ 处于减阻曲线的黏性区,沟槽减阻率线性相关于$s^{ + }$,边界层内流场流向涡占主导[9]. 图示视场上游(黄色矩形区)处呈现有较多流向或准流向涡结构,相互间间距小于$s^{ + }$;中游部分(橙色矩形区) 3个发卡涡涡包结构清晰可见,其展向平均间距约为7.5$s^{ + }$ (约60个黏性内尺度无量纲单位),而3个发卡涡涡包相邻涡流向平均距离约为9$s^{ + }$;涡包中各发卡涡在向下游发展演化过程中"长大"并逐渐远离壁面. 这一过程可以看作:沟槽作用下,边界层内流场结构由流向涡/准流向涡逐渐发展演化为发卡涡,形成发卡涡包并向外区抬升的湍流边界层发展过程. 这也是实验中少有地在沟槽壁面边界层底层内观察到完整清晰的发卡涡/涡包结构[3].

|
图3 $s^{ + } =8.1$时沟槽壁面边界层$x-z$面内流场结构(有效视场为$x\times z$: 425 mm×160 mm) Fig.3 Flow structures in the $x-z$ plane of the TBL over riblets when $s^{ + } =8.1$ ($x\times z$: 425 mm×160 mm) |
图4显示的是不同雷诺数($s^{ + }$)下沟槽壁面边界层$x-z$ 面内流场结构. 有效视场$x\times z$:200 mm× 160 mm. 具体地,$s^{ + } =14.5$时沟槽处于减阻曲线的最优减阻区之前,即线性黏性区,未见较明显的"类开尔文-亥姆霍兹"涡结构; 当$17.1\leq s^{+} \leq 34.7$时,从减阻曲线可以看出,沟槽尺寸位于最优减阻区和$k$粗糙元效应区,沟槽减阻效应即将趋弱直至阻力增加,表现出大粗糙元效应[11]. 图示视场中可以较清晰的观察到"类开尔文-亥姆霍兹"涡结构. 该"类开尔文-亥姆霍兹"展向涡结构在流场条件($s^{ + }$)刚刚超出最优减阻区时出现,可能是沟槽减阻达到最优后减阻效应趋弱直到增阻的主要原因. 此时,在片光平面内,烟雾粒子跟随该"类开尔文-亥姆霍兹"展向涡运动,形成黑白相间的展向可视涡:黑色较暗处粒子法向速度垂直于片光平面向里亦或向外;白色较亮处的粒子因涡心(核)旋转聚集,整体表现为"类开尔文-亥姆霍兹"展向涡棍结构. 它们与文献[9]图4(b)中直接数值模拟展向涡棍结构相同.

|
图4 不同雷诺数($s^{ + }$)下沟槽壁面边界层$x-z$面内"类开尔文-亥姆霍兹"涡结构(有效视场为$x\times z$: 200 mm×160 mm) Fig.4 Kelvin-Helmholtz-like rollers in the $x-z$ plane of the TBL over riblets at different $s^{ + }$ ($x\times z$: 200 mm×160 mm) |
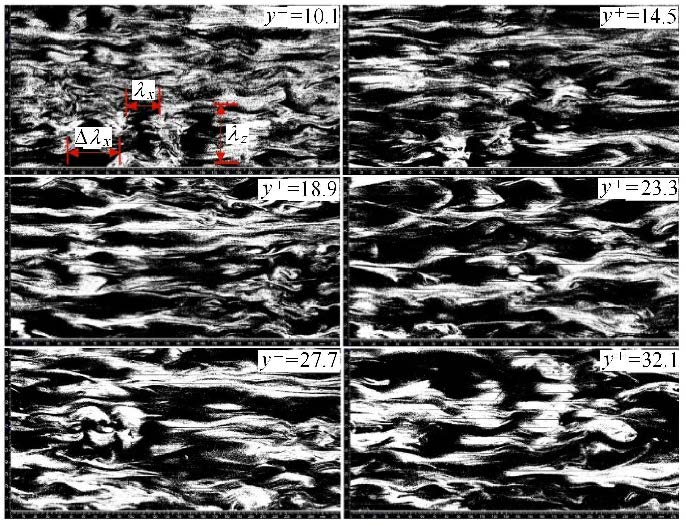
为了研究"类开尔文-亥姆霍兹"涡结构在不同法向位置$y$处的流动情况,第2部分选取$s^{ + }=31.7$重复沟槽 壁面湍流边界层流场烟雾流动显示实验. 但相机拍摄频率设置为800 Hz,曝光时间为1 000μs,内尺度无量纲化后的有效视场大小$x^{ + }\times z^{ + }$: 1 191.7×585.0. 流动显示结果如图5所示. 在最近壁区,$y^{ + }=10.1$及14.5处,"类开尔文-亥姆霍兹"展向涡结构二维性更好,其平均流向波长$40 \leq \lambda_{x}^{ + } \leq 90$,相邻典型展向涡之间的流向距离$150 \leq \Delta \lambda _{x}^{ + } \leq 200$; 平均展向波长$\lambda _{z}^{ + } ≥ 100$,这些参数与文献[9]的直接数值模拟结果基本一致. 另外,有趣地, 该"类开尔文-亥姆霍兹"展向涡结构表现出准三维性:随着观察(激光)平面逐渐远离壁面,视场内该展向涡 沿流向被拉伸,相邻展向涡之间出现连接两者的类似混合层中相邻展向涡之间的流向涡或准流向涡结 构[13],且此时 该"类开尔文-亥姆霍兹"展向涡数量趋少,尺度趋大,二维性趋弱,准三维性明显变强;但$y^{ + }$继续增加后少有"类开尔文-亥姆霍兹"展向涡出现.
|
图5 $s^{ + }=31.7$时沟槽壁面湍流边界层$x-z$面内不同法向位置 $y^{ + }$处的"类开尔文-亥姆霍兹"涡结构(有效视场为$x\times z$: 275 mm×135 mm) Fig.5 Kelvin-Helmholtz-like rollers in the $x-z$ plane of the TBL over riblets at different $y^{ + }$ when $s^{ + } =31.7$ ($x\times z$: 275 mm×135 mm) |
文献[9]的直接数值模拟数据表明边界层流场中,沟槽湍流减阻效应趋弱直至阻力增加的原因可能是"开尔文-亥姆霍兹"不稳定性现象的出现.
本文使用烟雾流动显示技术,首次通过风洞实验显示了由于"开尔文-亥姆霍兹"不稳定性的出现,使得沟槽边界层时-空平均流向速度剖面出现拐点而形成的展向"类开尔文-亥姆霍兹"涡结构,并给出沟槽壁面湍流边界层内"类开尔文-亥姆霍兹"涡结构模型示意图(图6)及以下结论:
(1) 当沟槽脊-脊间距$s^{ + }$位于减阻曲线的线性黏性区时,边界层亚层内的流向涡及准流向涡随时间发展形成发卡涡及发卡涡涡包结构;
(2) 在$s^{ + }$刚刚超出最优减阻区时,流动因"开尔文-亥姆霍兹"不稳定性失稳,形成"类开尔文-亥姆霍兹"展向涡结构;
(3) 典型的"类开尔文-亥姆霍兹"展向涡其流向波长$40 \leq \Delta \lambda _{x}^{ + } \leq 90$,展向波长$\lambda _{z}^{ + } ≥ 100$;流向相邻展向涡之间的距离$150 \leq \Delta \lambda _{x}^{ + } \leq 200$,这些参数与文献[8]的直接数值模拟结果基本一致;
(4) "类开尔文-亥姆霍兹"展向涡主要出现在沟槽壁面边界层$y^{ + } \approx 26$以内.

|
图6 沟槽壁面湍流边界层内"类开尔文-亥姆霍兹"涡结构模型 Fig.6 Conceptual model of the Kelvin-Helmholtz-like roller structures |
致谢 感谢英国诺丁汉大学传热及流体力学实验室减阻与流动控制组(Thermo and Fluid Mechanics---Drag Reduction and Flow Control Group)费尔$\cdot$巴里(Faycal Bahri)对本文的指导和帮助;感谢刘建华,吴云,宋龙飞,巴索$\cdot$阿莱西奥(Basso Alessio), 基奥瓦克$\cdot$诺拉(Rkiouak Noura),菲利普$\cdot$科恩(Phillip Cohen)在实验过程中给予的建议和协助.
| [1] | Brian D, Bharat B.湍流流动中鲨鱼皮表面流体减阻研究进展. 力学进展, 2012, 42(6): 821-836 (Brian Dean, Bharat Bhushan. Shark skin surfaces for fluid-drag reduction in turbulent flow: A review. Advances in Mechanics, 2012, 42(6): 821-836 (in Chinese)) |
| [2] | Bechert DW, Bruse M, Hage W, et al. Experiments on drag-reducing surfaces and their optimization with an adjustable geometry. Journal of Fluid Mechanics, 1997, 338: 59-87 |
| [3] | Choi KS. Near-wall structure of a turbulent boundary layer with riblets. Journal of Fluid Mechanics, 1989, 208(1): 417-458 |
| [4] | 王晋军,兰世隆,陈光. 沟槽面湍流边界层结构实验研究. 力学学报, 2000, 32(5): 621-626 (Wang Jinjun, Lan Shilong, Chen Guang. Experimental study on the turbulent boundary layer flow over riblets surface. Acta Mechanica Sinica, 2000, 32(5): 621-626 (in Chinese)) |
| [5] | 李山,杨绍琼,姜楠. 沟槽面湍流边界层减阻的TRPIV测量. 力学学报, 2013, 45(2): 183-192 (Li Shan, Yang Shaoqiong, Jiang Nan. TRPIV measurement of drag-reduction in the turbulent boundary layer over riblets plate. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 183-192 (in Chinese)) |
| [6] | Yang Shaoqiong, Li Shan, Tian Haiping et al. Coherent spanwise structures in turbulent boundary layer over drag-reducing riblets[J]. Transactions of Tianjin University, DOI 10.1007/s12209-015-2526-5 |
| [7] | Choi H, Moin P, Kim J. Direct numerical simulation of turbulent flow over riblets. Journal of Fluid Mechanics, 1993, 255: 503-539 |
| [8] | Goldstein DB, Tuan TC. Secondary flow induced by riblets. Journal of Fluid Mechanics, 1998, 363: 115-151 |
| [9] | García-Mayoral R, Jiménez J. Hydrodynamic stability and breakdown of the viscous regime over riblets. Journal of Fluid Mechanics, 2011, 678: 317-347 |
| [10] | 杨绍琼,姜楠. 奇妙的"波浪云"-浅谈开尔文-亥姆霍兹不稳定性现象. 力学与实践, 2014(06): 802-805 (Yang Shaoqiong, Jiang Nan. On Kelvin-Helmholtz instability in wave clouds. Mechanics in Engineering, 2014(06): 802-805 (in Chinese)) |
| [11] | Jiménez J. Turbulent flows over rough walls. Annual Review of Fluid Mechanics, 2004, 36(1): 173-196 |
| [12] | White FM. Fluid mechanics. Seventh Edition. New York: McGraw-Hill Companies, Inc, 2011:513 |
| [13] | Bechert DW, Bartenwerfer M. The viscous flow on surfaces with longitudinal ribs. Journal of Fluid Mechanics, 1989, 206: 105-129 |
| [14] | 张洪泉. 混合层中的流向涡与Rayleigh离心不稳定. 力学学报, 1997, 29(2): 129-135 (Zhang Hongquan. Streamwise vortices in a plane mixing layer and Rayleigh's centrifugal instability. Acta Mechanica Sinica, 1997, 29(2): 129-135 (in Chinese)) |
2. Department of Mechanics, School of Mechanical Engineering, Tianjin University, Tianjin 300072, China;
3. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300072, China
 2015, Vol. 47
2015, Vol. 47