引 言

连接结构广泛存在于各类工程结构中，在外力作用下引发连接接触部位复杂的微、宏观滑移现象，并对连接结构的整体力学行为产生显著的影响. 这种复杂的滑移行为会造成结构系统刚度非线性，引起结构阻尼，并产生能量耗散^{[1, 2, 3]}. 已有研究表明，由连接接触滑移所引起的能量耗散是结构阻尼的重要来源，占到整体的90%^[4]. 在复杂的组合工程结构系统动力学分析中，采用直接数值模拟(DNS,direct numericalsimulation)方法往往会受到计算规模和时间步长的限制而不可行. 例如，航空发动机整体具有米级尺度，而有效描述连接力学行为的单元为10$^{-5}$米级尺度；另一方面，达到稳态响应需要数秒的计算时长，显式时间步长将在纳秒量级. 综合这两方面的因素可知，问题的规模和总时步将异常庞大而使计算无法进行下去^[5]. 因此，开展连接接触非线性特性研究，并建立描述其非线性力学行为的理论模型，有效降低这类问题的求解规模和总计算时步，具有重要的意义^[6].

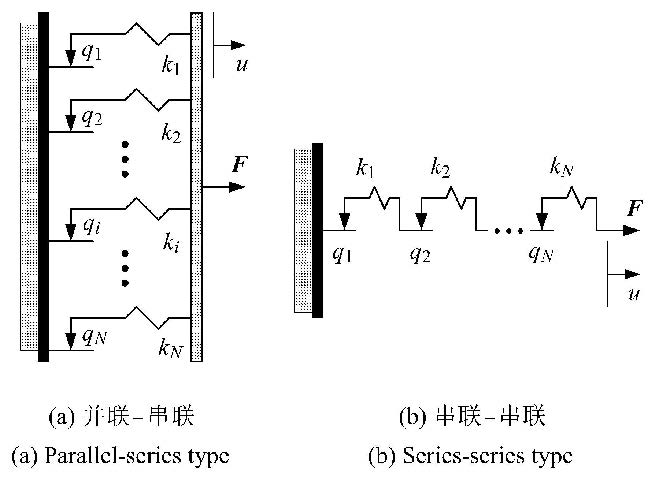
文献^{[7, 8, 9]}介绍了几种具有代表性的连接接触理论模型，如法兰尼斯模型(Valanis model)、布斯温模型(Bouc-Wenmodel)和伊万模型. 其中伊万模型得到了广泛的应用^[10]. 伊万模型由若干詹金斯 单元(Jenkinselement)组成，每一个詹金斯单元由一个线性弹簧和滑块串联而成^[11].根据詹金斯单元的不同组合方式，伊万模型有"并联-串联"和"串联-串联"等形式，如图1所示.

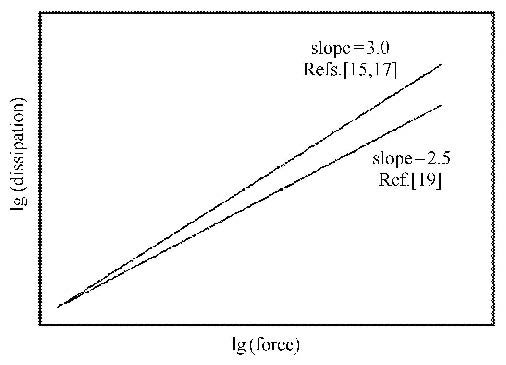
伊万模型最早被用于描述金属材料的弹塑性行为^[12].文献^[13]首先将"并联-串联"形式的伊万模型应用于接触界面力学行为的研究，并讨论了伊万模型密度函数与能量耗散的关系.文献^[14]中的实验研究表明，宏观滑移情况下连接接触界面存在残余刚度.为了描述这一实验现象，文献^[15]提出了基于均匀密度函数的改进伊万模型.文献^[16]在文献^[15]的工作基础上提出了交替参数估计法用于改进伊万模型的参数识别.文献^[17]基于均匀密度函数，推导了伊万模型力-位移关系和能量耗散-位移关系的解析表达式，得到能量耗散幂次关系的理论值为3.0，与文献^[18]中的连接结构能量耗散理论解一致.如图2所示，该理论值虽然能够定性地反映连接结构能量耗散现象，但仍不能够准确描述文献^[19]的实验结果.

为了准确描述文献^[19]中的实验现象，文献^[20]提出了含截断幂律分布和单脉冲的四参数非均匀密度函数，并建立了基于该密度函数的四参数伊万模型.文献^{[21, 22]}研究了非恒定法向约束力下连接结构的响应，根据连接结构能量耗散的实验，构造出伊万模型的密度函数.

现有的研究工作中，仅有文献^{[23, 24, 25]}开展了基于"串联-串联"形式的伊万模型研究.文献^[26]指出，任意满足马辛(Masing)准则的本构模型都可表述为"并联-串联"形式的伊万模型；文献^[27]认为"并联-串联"形式的伊万模型具有更好的适用性.

根据现有的连接结构实验研究^{[5, 14, 19]}可归纳出以下两个现象：一是宏观滑移阶段，接触界面存在残余刚度；二是微观滑移阶段，能量耗散幂次关系介于2.5$\sim$3.0之间.文献^{[15, 17]}基于均匀密度函数的伊万模型仅可以描述现象一；文献^[20]基于含截断幂律分布和单脉冲函数的四参数伊万模型仅可以描述现象二.

本文建立了可同时描述这两个现象的六参数伊万模型. 首先提出了含截断幂律分布和双脉冲的六参数非均匀密度函数.基于该密 度函数，推导得到六参数伊万模型在微观滑移阶段和宏观滑移阶段的力-位移关系以及能量耗散-位移关 系的解析表达式.

1 伊万模型

詹金斯单元的受力情况可表述为

\[{{f}_{i}}={{f}_{i}}\left( x \right)=\left\{ \begin{array}{*{35}{l}} {{k}_{i}}x, & 0<x\le {{x}_{i}} \\ {{k}_{i}}{{x}_{i}}, & x>{{x}_{i}} \\ \end{array} \right.\]

(1)

其中，$k_{i}$表示詹金斯单元中线性弹簧的刚度，$x$为位移载荷，$x_{i}$为詹金斯单元的屈服位移，$k_{i}x_{i}$为詹金斯单元的屈服力.

假设$N$个詹金斯单元组成一个并联系统. 在单调位移$x$作用下，有$n$个詹金斯单元发生了屈服.那么该系统的力-位移关系可写为

\[F\left( x \right)=\sum\limits_{i=1}^{n}{{{k}_{i}}{{x}_{i}}}+\sum\limits_{j=n+1}^{N}{{{k}_{j}}x}\]

(2)

当该系统中詹金斯单元的个数$N \to \infty$时，使用密度函数$r(f)$来表示詹金斯单元屈服力$f$的分布. 假设每一个詹金斯单元的刚度均为$k$，式(2)可以改写为

\[F\left( x \right)=\int_{0}^{kx}{f\cdot r\left( f \right)}\text{d}f+\int_{kx}^{\infty }{kx\cdot r\left( f \right)}\text{d}f\]

(3)

式(3)即为伊万模型的数学表达式. 其中含有两个参数：密度函数$r(f)$和詹金斯单元刚度$k$.式(3)对位移$x$求二阶导数，整 理后得到密度函数$r(f)$与$F(x)$和$k$关系为

\[r\left( f \right)={{\left. -\frac{1}{{{k}^{2}}}\frac{{{\partial }^{2}}F\left( x \right)}{\partial {{x}^{2}}} \right|}_{f=kx}}\]

(4)

可通过以下变量代换将詹金斯单元刚度$k$消去^[20]

\[\varphi =f/k,\rho \left( \varphi \right)={{k}^{2}}r\left( f \right)\]

(5)

于是，伊万模型数学表达式可改写为仅含有 $\rho (\varphi )$的形式

\[F\left( x \right)=\int_{0}^{x}{\varphi \rho \left( \varphi \right)}\text{d}\varphi +\int_{x}^{\infty }{x\rho \left( \varphi \right)}\text{d}\varphi \]

(6)

其中

\[\rho \left( \varphi \right)={{\left. -\frac{{{\partial }^{2}}F\left( x \right)}{\partial {{x}^{2}}} \right|}_{\varphi =x}}\]

(7)

2 六参数非均匀密度函数

文献^[15]采用均匀密度函数并引入对宏观滑移下残余刚度的描述. 文献^[20]提出了含截断幂律分布和单脉冲的非均匀密度函数.本文在文献^[20]提出的非均匀密度函数模型中增加一个新的脉冲函数来描述连接结构发生宏观滑移后的残余刚度，得到了含截断幂律分布和双脉冲的非均匀密度函数. 其示意图如图3所示.

其表达式为

\[\begin{align} & \rho \left( \varphi \right)=R{{\varphi }^{\alpha }}\left[ H\left( \varphi -{{\varphi }_{1}} \right)-H\left( \varphi -{{\varphi }_{2}} \right) \right]+ \\ & {{K}_{2}}\delta \left( \varphi -{{\varphi }_{2}} \right)+{{K}_{\infty }}\delta \left( \varphi -{{\varphi }_{\infty }} \right) \\ \end{align}\]

(8)

式(8)中$H$($\varphi $)是海维塞德单位阶跃函数，$\delta $($\varphi $)是狄拉克单位脉冲函数.$\varphi_{1}$表示微观滑 移起始点，$\varphi_{2}$表示宏观滑移起始点，$K_{2}$表示发生宏观滑移前一时刻接触界面的切向刚度，$K_{\infty}$表示发生宏观滑移后接触界面的残余切向刚度，$R$和$\alpha $为描述幂律分布的两个参数，$\alpha$是一个小于0的数，实验发现一般取值介于$-0.5<\alpha <0$之间，$\varphi _{\infty }$为宏观滑移后无穷远处的一点.式(8)中含有$R$,$\alpha $,$\varphi_{1}$,$\varphi_{2}$,$K_{2}$和$K_{\infty}$共6个有效参数，称之为六参数密度函数. 式(6)和式(8)共同构成六参数伊万模型.

当$\varphi_{1}$和$K_{\infty }$等于0时，式(8)变为

\[\rho \left( \varphi \right)=R{{\varphi }^{\alpha }}\left[ H\left( \varphi \right)-H\left( \varphi -{{\varphi }_{2}} \right) \right]+{{K}_{2}}\delta \left( \varphi -{{\varphi }_{2}} \right)\]

(9)

式(9)即为文献^[20]提出的非均匀密度函数.

当 $\alpha $和$K_{2}$等于0时，式(8)变为

\[\rho \left( \varphi \right)=R\left[ H\left( \varphi -{{\varphi }_{1}} \right)-H\left( \varphi -{{\varphi }_{2}} \right) \right]+{{K}_{\infty }}\delta \left( \varphi -{{\varphi }_{\infty }} \right)\]

(10)

式(10)即为文献^[15]提出的均匀密度函数.

3 六参数伊万模型力-位移关系 3.1 骨线方程

伊万模型的骨线是指在单调外载作用下模型的力-位移关系曲线.将密度函数式(8)代入式(6)进行积分，可得到伊万模型的骨线方程

\[F\left( x \right)=\left\{ \begin{array}{*{35}{l}} \frac{R\left( \varphi _{2}^{\alpha +1}-\varphi _{1}^{\alpha +1} \right)}{\alpha +1}x+{{K}_{2}}x+{{K}_{\infty }}x, 0\text{ }\le x<{{\varphi }_{1}} \\ \left( \frac{R\varphi _{2}^{\alpha +1}}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }} \right)x-\frac{R{{x}^{\alpha +2}}}{\left( \alpha +1 \right)\left( \alpha +2 \right)}- \\ \qquad \frac{R\varphi _{1}^{\alpha +2}}{\alpha +2},{{\varphi }_{1}}\text{ }\le x<{{\varphi }_{2}} \\ \frac{R\left( \varphi _{2}^{\alpha +2}-\varphi _{1}^{\alpha +2} \right)}{\alpha +2}+{{K}_{2}}{{\varphi }_{2}}+{{K}_{\infty }}x, x\text{ }\ge {{\varphi }_{2}} \\ \end{array} \right.\]

(11)

式(11)为分段函数. 其中，第1部分表示伊万模型中所有詹金斯单元均未发生屈服，此时伊万模型等价于一个线性弹簧；第2部分表示微观滑移阶段. 在此阶段中随着位移幅值的增加，伊万模型中的詹金斯单元逐渐发生屈服，外力与位移幅值之间呈现非线性关系；第3部分表示宏观滑移阶段. 此时伊万模型中所有的詹金斯单元均发生了屈服，仅有残余刚度$K_{\infty}$作用，外力与位移幅值呈线性关系.

将式(11)对位移$x$求导，可得到单调外载作用下，伊万模型切向刚度-位移关系

\[K\left( x \right)=\left\{ \begin{array}{*{35}{l}} \frac{R\left( \varphi _{2}^{\alpha +1}-\varphi _{1}^{\alpha +1} \right)}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }}, 0\text{ }\le x<{{\varphi }_{1}} \\ \frac{R\left( \varphi _{2}^{\alpha +1}-{{x}^{\alpha +1}} \right)}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }},{{\varphi }_{1}}\text{ }\le x<{{\varphi }_{2}} \\ {{K}_{\infty }}, x\text{ }\ge {{\varphi }_{2}} \\ \end{array} \right.\]

(12)

由式(12)可知，伊万模型切向刚度在$(0,\varphi_{2})$范围内连续. 由于密度函数中存在脉冲函数，因此在$x = \varphi_{2}$位置，切向刚度由$K_{2}+K_{\infty}$突然减小为$K_{\infty }$，这与文献^[5]的实验现象一致.

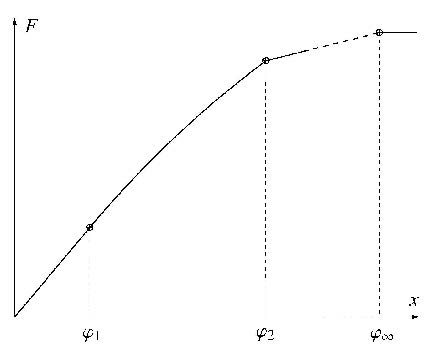
伊万模型骨线示意图如图4所示.

3.2 微观滑移情况下的卸载力

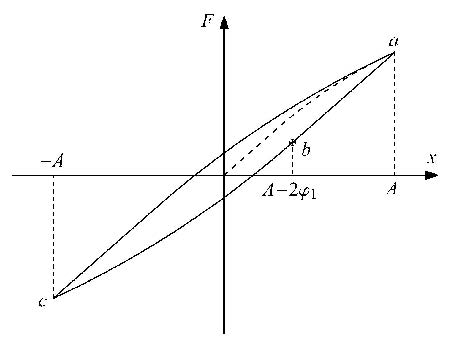
微观滑移情况如图5所示，其中最大位移幅值$A$的取值范围为 $\varphi_{1} ≤ A ≤ \varphi_{2}$. 卸载过程的力-位移曲线如图中$a$---$b$---$c$所示.

$a$---$b$阶段位移幅值$x$的取值范围是$A -2 \varphi_{1} ≤ x ≤A$. 伊万模型的力积分表达式为^[10]

\[{{F}_{u}}\left( x \right)=\int_{0}^{A}{\left( x-A+\varphi \right)\rho \left( \varphi \right)\text{d}\varphi }+\int_{A}^{\infty }{x\rho \left( \varphi \right)\text{d}\varphi }\]

(13)

式(13)左端的下标$u$表示卸载(unloading)过程.

用下标 mic 表示微观滑移(microslip)阶段. 将式(8)代入上式积分得到

\[\begin{align} & {{F}_{u,\text{mic}}}\left( x \right)=\left[ \frac{R\left( \varphi _{2}^{\alpha +1}-\varphi _{1}^{\alpha +1} \right)}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }} \right]x+ \\ & \frac{RA\varphi _{1}^{\alpha +1}}{\alpha +1}-\frac{R\varphi _{1}^{\alpha +2}}{\alpha +2}-\frac{R{{A}^{\alpha +2}}}{\left( \alpha +1 \right)\left( \alpha +2 \right)}, \\ & A-2{{\varphi }_{1}}\le x\le A \\ \end{align}\]

(14)

由式(14)可知，在$a$---$b$阶段力-位移关系为线性关系，伊万模型中的所有詹金斯单元在此阶段均未发生屈服，伊万模型等价为一个线性弹簧.

$b$---$c$阶段位移幅值$x$的取值范围是$- A ≤ x ≤ A -2 \varphi_{1}$. 伊万模型的力积分表达式为^[10]

\[\begin{align} & {{F}_{u}}\left( x \right)=\int_{0}^{\tfrac{\left( A-x \right)}{2}}{-\varphi \rho \left( \varphi \right)\text{d}\varphi }+ \\ & \int_{\tfrac{\left( A-x \right)}{2}}^{A}{\left( x-A+\varphi \right)\rho \left( \varphi \right)\text{d}\varphi }+\int_{A}^{\infty }{x\rho \left( \varphi \right)\text{d}\varphi } \\ \end{align}\]

(15)

将式(8)代入上式进行积分得到

\[\begin{align} & {{F}_{u,\text{mic}}}\left( x \right)=\frac{R{{\left( A-x \right)}^{\alpha +2}}}{{{2}^{\alpha +1}}(\alpha +1)(\alpha +2)}+ \\ & \left( \frac{R\varphi _{2}^{\alpha +1}}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }} \right)x+ \\ & \frac{R\varphi _{1}^{\alpha +2}}{\alpha +2}-\frac{R{{A}^{\alpha +2}}}{(\alpha +1)(\alpha +2)},-A\le x<A-2{{\varphi }_{1}} \\ \end{align}\]

(16)

式(16)中含有位移的一次项和 $\alpha + 2$次项，因此在$b$---$c$阶段力-位移关系为非线性关系. 随着外载荷的增加，伊万模型中的詹金斯单元逐渐发生屈服.

式(14)和式(16)即微观滑移情况下伊万模型的卸载方程.

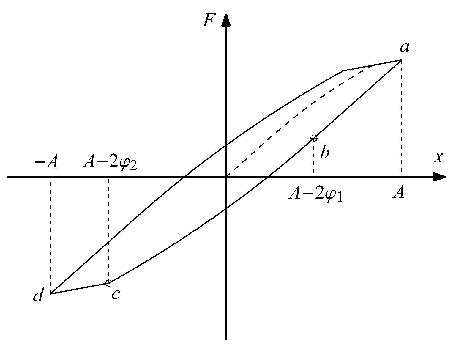
3.3 宏观滑移情况下的卸载力

宏观滑移情况示意图如图6所示，最大位移幅值$A$的取值范围为$A > \varphi_{2}$.卸载过程的力-位移曲线如 图中$a$---$b$---$c$---$d$所示.

$a$---$b$阶段位移幅值$x$的取值范围是$A-2\varphi_{1} ≤ x ≤ A$，伊万模型的力积分表达式即式(13).

将式(8)代入式(13)积分，用下标 mac 表示宏观滑移(macroslip)阶段，得到

\[\begin{align} & {{F}_{u,\text{mac}}}\left( x \right)=\left[ \frac{R\left( \varphi _{2}^{\alpha +1}-\varphi _{1}^{\alpha +1} \right)}{\alpha +1}+{{K}_{2}}+{{K}_{\infty }} \right]\left( x-A \right)+ \\ & \frac{R\left( \varphi _{2}^{\alpha +2}-\varphi _{1}^{\alpha +2} \right)}{\alpha +2}+{{K}_{2}}{{\varphi }_{2}}+{{K}_{\infty }}A, A-2{{\varphi }_{1}}\le x\le A \\ \end{align}\]

(17)

由式(17)可知，$a$---$b$阶段为线性段，即伊万模型中所有的詹金斯单元均没有发生屈服，模型等效为一个线性弹簧.

$b$---$c$阶段位移幅值$x$的取值范围是$A -2 \varphi_{2} ≤ x ≤ A -2 \varphi_{1}$，伊万模型的力积分表达式即式(15). 将式(8)代入式(15)积分得到

\[\begin{align} & {{F}_{u,\text{mac}}}\left( x \right)=\frac{R{{\left( A-x \right)}^{\alpha +2}}}{{{2}^{\alpha +1}}(\alpha +1)(\alpha +2)}+{{K}_{2}}\left( x-A \right)+ \\ & \frac{R\varphi _{2}^{\alpha +1}\left( x-A \right)}{\alpha +1}+\frac{R\left( \varphi _{2}^{\alpha +2}+\varphi _{1}^{\alpha +2} \right)}{\alpha +2}+ \\ & {{K}_{2}}{{\varphi }_{2}}+{{K}_{\infty }}x,A-2{{\varphi }_{2}}\le x<A-2{{\varphi }_{1}} \\ \end{align}\]

(18)

$b$---$c$阶段为非线性段，伊万模型中部分詹金斯单元发生了屈服.

在$c$---$d$阶段，位移幅值$x$的取值范围是$-A ≤ x ≤ A-2\varphi_{2}$. 伊万模型的力积分表达式为^[10]

\[{{F}_{u}}\left( x \right)=\int_{0}^{A}{-\varphi \rho \left( \varphi \right)\text{d}\varphi }+\int_{A}^{\infty }{x\rho \left( \varphi \right)\text{d}\varphi }\]

(19)

将式(8)代入式(19)进行积分得到

\[\begin{align} & {{F}_{u,\text{mac}}}\left( x \right)=-\frac{R\left( \varphi _{2}^{\alpha +2}-\varphi _{1}^{\alpha +2} \right)}{\alpha +2}-{{K}_{2}}{{\varphi }_{2}}+{{K}_{\infty }}x, \\ & -A\le x<A-2{{\varphi }_{2}} \\ \end{align}\]

(20)

$c$---$d$阶段为线性段，表示伊万模型中所有的詹金斯单元均发生了屈服，仅有残余刚度$K_{\infty }$作用，模型发生宏观滑移.

式(17),(18)和(20)即宏观滑移情况下伊万模型的卸载方程.

4 六参数伊万模型能量耗散表达式

伊万模型满足马辛假定^[26]，因此模型的卸载力与反向加载力满足如下关系

\[{{F}_{r}}\left( x \right)=-{{F}_{u}}\left( -x \right)\]

(21)

式(21)中左端下标$r$表示反向加载力(reloading).

在周期载荷作用下，伊万模型每周期内的能量耗散等于加载-卸载封闭曲线所围成的面积，如图7所示. 即

\[D\left( A \right)=\int_{-A}^{A}{\left[ {{F}_{r}}\left( x \right)-{{F}_{u}}\left( x \right) \right]\text{d}x}\]

(22)

于是由式(17),(20)$\sim$(22)可以得到微观滑移和宏观滑移情况下能量耗散关于位移幅值的表达式

\[{{D}_{\text{mic}}}\left( A \right)=\frac{4R{{A}^{\alpha +3}}}{\left( \alpha +2 \right)\left( \alpha +3 \right)}-\frac{4RA\varphi _{1}^{\alpha +2}}{\alpha +2}+\frac{4R\varphi _{1}^{\alpha +3}}{\alpha +3}\]

(23)

\[\begin{align} & {{D}_{\text{mac}}}\left( A \right)=\frac{4RA\left( \varphi _{2}^{\alpha +2}-\varphi _{1}^{\alpha +2} \right)}{\alpha +2}+4{{K}_{2}}{{\varphi }_{2}}A- \\ & \frac{4R\left( \varphi _{2}^{\alpha +3}-\varphi _{1}^{\alpha +3} \right)}{\alpha +3}-4{{K}_{2}}\varphi _{2}^{2} \\ \end{align}\]

(24)

引入以下无量纲参数

\[M=\frac{A}{{{\varphi }_{2}}},{{\kappa }_{2}}=\frac{{{K}_{2}}}{R\varphi _{2}^{\alpha +1}},d=\frac{D}{R\varphi _{2}^{\alpha +3}},\beta =\frac{{{\varphi }_{1}}}{{{\varphi }_{2}}}\]

(25)

其中，$M$为无量纲最大位移幅值，$\kappa_{2}$为无量纲刚度，$d$为无量纲能量耗散，$\beta $ 为描述微观滑移起始位置的参数. 得到能量耗散关于最大位移幅值的无量纲表达式

\[d\left( M \right)=\left\{ \begin{array}{*{35}{l}} 0, 0<M\text{ }\le \beta \\ \frac{4{{M}^{\alpha +3}}}{\left( \alpha +2 \right)\left( \alpha +3 \right)}-\frac{4{{\beta }^{\alpha +2}}M}{\alpha +2}+\frac{4{{\beta }^{\alpha +3}}}{\alpha +3}, \\ \beta <M\text{ }\le 1 \\ 4\left( \frac{1-{{\beta }^{\alpha +2}}}{\alpha +2}+{{\kappa }_{2}} \right)M-4\left( \frac{1-{{\beta }^{\alpha +3}}}{\alpha +3}+{{\kappa }_{2}} \right), \\ \text{ }M>1 \\ \end{array} \right.\]

(26)

由式(26)可知，当$M ≤ \beta $ 时，伊万模型中的詹金斯单元均未发生屈服，模型等价为一个线性弹簧. 由于弹簧不是耗能元件，因此能量耗散恒等于0.

微观滑移情况下，$\beta < M ≤ 1$. 伊万模型中部分詹金斯单元发生屈服，模型能量耗散表达式含有最大位移幅值的 $\alpha +3$次项和一次项.

宏观滑移情况下，$M >1$. 伊万模型中所有詹金斯单元均发生屈服，能量耗散与最大位移幅值呈线性关系. 残余刚度对能量耗散没有影响.

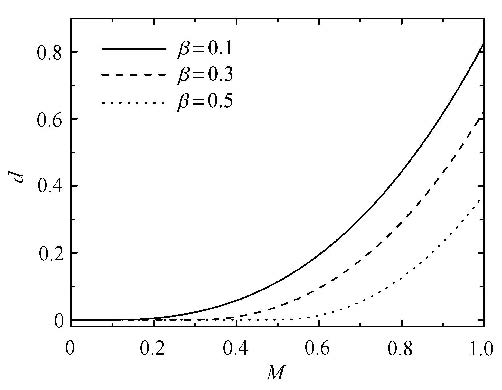
图8为 $\alpha =-0.3$时，伊万模型微观滑移阶段无量纲能量耗散与位移幅值之间的关系. 由图可知，能量耗散随着 $\beta $ 的 增大而减小.

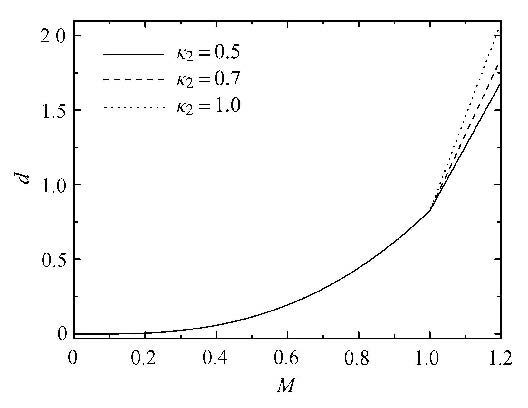
图9为 $\alpha =-0.3$，$\beta=0.1$时，伊万模型发生宏观滑移情况下的无量纲能量耗散曲线. 由图可知，在宏观滑移阶段，模型 能量耗散随着 $\kappa_{2}$的增大而增大.

特别地，当 $\beta =0$时,式(26)可简化为

\[d\left( M \right)=\left\{ \begin{array}{*{35}{l}} \frac{4{{M}^{\alpha +3}}}{\left( \alpha +2 \right)\left( \alpha +3 \right)}, & 0<M\le 1 \\ 4\left( \frac{1}{\alpha +2}+{{\kappa }_{2}} \right)M-4\left( \frac{1}{\alpha +3}+{{\kappa }_{2}} \right), & M>1 \\ \end{array} \right.\]

(27)

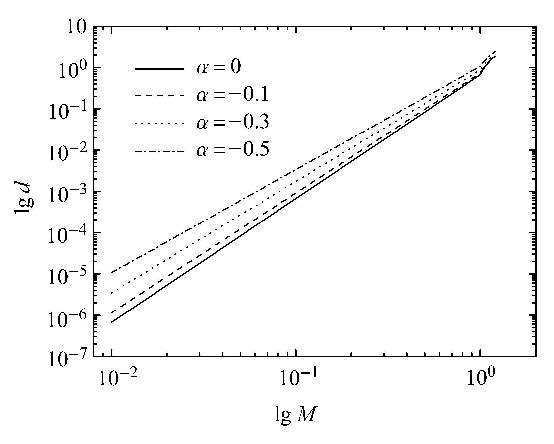
在双对数坐标系下，微观滑移阶段的无量纲能量耗散与无量纲最大位移幅值为线性关系，能量耗散-位移关系的斜率为 $\alpha +3$，如图10所示.

采用均匀密度函数代入伊万模型推导得到能量耗散-位移关系的斜率恒为3^[17]，而采用本文提出的密度函数， 斜率为 $\alpha +3$. 六参数伊万模型可以描述文献^[19]中的实验现象.

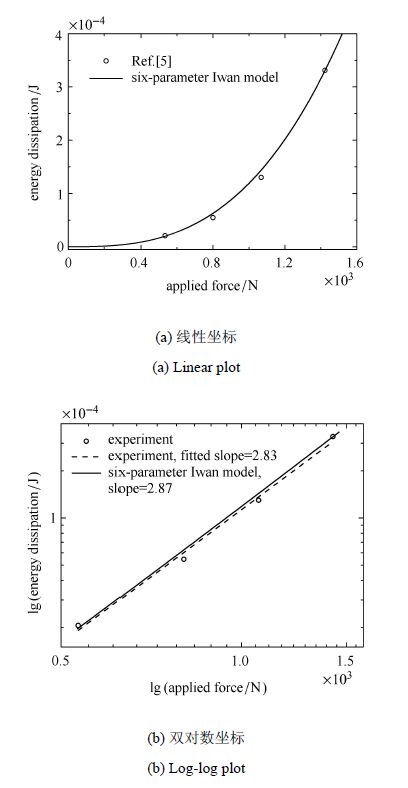
用六参数伊万模型来表征文献^[5]的螺栓连接结构实验，获得了不同加载力情况下的能量耗散结果. 如图11所示，在不同的加载力幅值情况下，计算结果的精度均较好.能量耗散幂次关系的实验结果为2.83，计算结果为2.87，计算结果与实验结果符合较好.

5 结 论

伊万模型常用于描述连接的能量耗散和阻尼特性，来研究复杂组合连接结构的非线性静动力学行为. 本文提出了一种截断幂律分布和双脉冲非均匀密度函数的六参数伊万模型. 推导得到了六参数伊万模型的骨线方程、卸载方程和能量耗散的解析表达式. 讨论了不同的模型参数对能量耗散的影响，并与已有的实验进行了对比分析. 结果表明：六参数伊万模型不仅可以描述微观滑移阶段能量耗散幂次关系，而且还可以反映宏观滑移阶段接触界面的残余刚度现象，与实验结果吻合较好. 六参数伊万模型与现有的伊万模型相比适用性更强.