引 言
绳系航天器是由两个或多个人造天体通过系绳连在一起飞行的空间组合体,由于其特殊的空间结构,使其在空间探索中可以实现诸多特殊任务,吸引了众多学者的关注[1]. 由于内在非线性,使得绳系航天器会表现出诸如瞬态混沌这样的复杂动力学现象[2, 3, 4].
许多学者研究了绳系航天器的动力学行为. 例如,文献[5]分析了由刚性系绳杆、质点卫星组成的两体绳系卫星发生混沌运动的可能性. 随后,文献[6]考虑到弹性系绳模型,利用梅尼科夫(Melnikov)方法和数值仿真预测了系绳摆动具有混沌行为. 文献[7]计入气动力和轨道偏心率等空间环境的作用,通过数值方法给出了发生混沌运动的参数区域. 然而,当卫星本体对于绳系系统具有影响时,则需要考虑卫星姿态的作用[8, 9]. 利用梅尼科夫方法,文献[10, 11]研究了在系绳张力作用下主星俯仰姿态运动,确定了消除混沌运动可能需要的阻尼. 文献[12]揭示了内共振情况下状态保持阶段绳系卫星的概周期运动规律. 近年来,人们通过物理仿真实验对绳系航天器开展地面试验研究[13]. 为模拟空间微重力环境,人们提出了多种实验方案,比如自由下落失重塔[14]、气浮平台[15]、坡面转台[16]等. 学者们利用地面实验系统对周期、概周期运动及释放和回收控制的算法进行了验证. 例如文献[17]实验揭示了绳系卫星系统的概周期运动. 关于绳系航天器混沌动力学的实验研究值得关注.
本文实验研究了两体绳系航天器面内俯仰运动与主星姿态相互耦合导致的混沌运动. 首先介绍了物理仿真实验系统的组成及工作流程,然后提出了两种天地动力学等效方案,指出了它们各自适用的实验情形. 最后通过对比试验与数值结果,实验验证了绳系航天器的混沌运动.
1 物理仿真系统
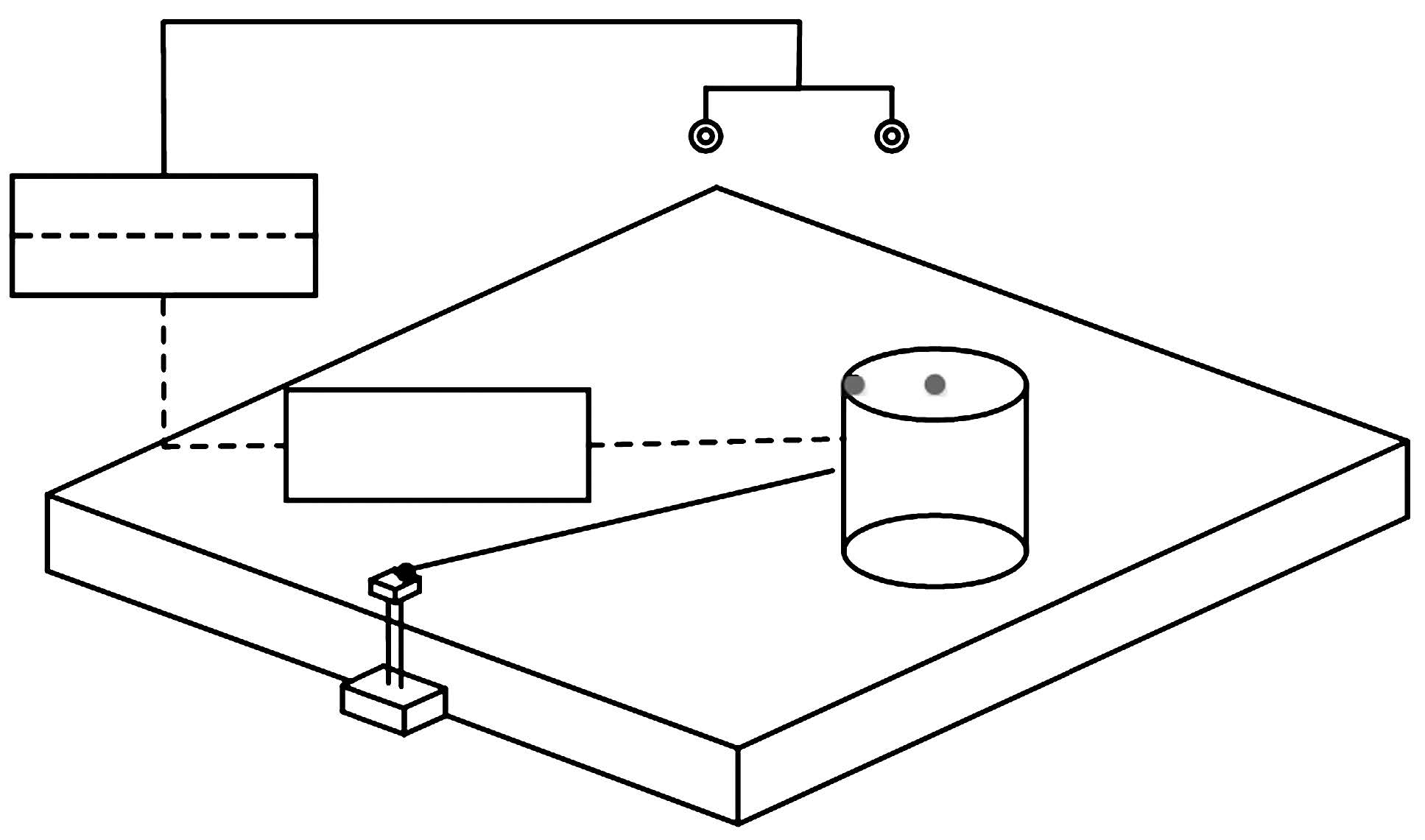
绳系航天器物理仿真实验系统由卫星仿真器、动态测量系统(DMS)、驱动和控制系统等组成,如图1所示. 动态测量系统将卫星仿真器位置及姿态信息发送到主控计算机,主控计算机根据给定的规则在线计算仿真器所需要的控制力和力矩,并由无线通讯模块发送指令至机载计算机来控制卫星仿真器上的驱动装置. 该物理仿真平台具有如下特点: 一是根据天地动力学相似原理,通过喷气力和动量轮力矩可以模拟空间动力学环境; 二是依据动力学等效可以模拟绳系航天器在椭圆轨道的运动.
实验所用系绳为"大力马"(Dyneema)高强度聚乙烯纤维,因质量很小以致在简化建模分析中忽略其影响. 卫星仿真器气瓶在满气时可装约1 kg高压二氧化碳液气混合体,经减压阀降压后分成两路: 一路为仿真器底部气浮轴承提供0.55 MPa压力以使仿真器几乎无摩擦地悬浮于平台; 一路输出至空气比例电磁阀以提供喷气力. 在满气状态可持续近400秒输出可控的喷气力. 比例电磁阀输出压力与输入电压之间有良好的线性关系,其控制压力范围为0$\sim$1.8 MPa. 经减压阀输入到控制阀的气压为0.55 MPa,仿真器喷嘴可输出喷气力最大约0.2 N.
采用德国GOM公司研制的PONTOS型三维动态测量系统进行仿真器状态测量,在全分辨率下最高采样频率60 Hz.该系统通过双目 视觉对仿真器上的荧光标志点进行位置捕捉,获取各点像素坐标后经计算转变为实际物理坐标,识别精度在60 μm以内. 在系绳端部和仿真器布置3个标志点以捕获系绳俯仰运动和仿真器姿态运动.若动态测量系统测得3个标志点位置为$(x_i ,y_i ),i = 1,2,3$,则系绳俯仰角为$\theta = \arctan [(y_2 - y_1 ) /(x_2 - x_1 )]$、仿真器姿态角为$\alpha = \arctan [(y_3 - y_2 ) / (x_3 - x_2 )]$,它们的角速度可由差分求得.仿真器状态信息通过美国DIGI公司研制的XBee型无线射频模块发出,并由卫星仿真器上的终端接收,其数据流根据IEEE802.15.4网络协议以8位浮点格式传输,传输速度可达57.6千字节每秒.
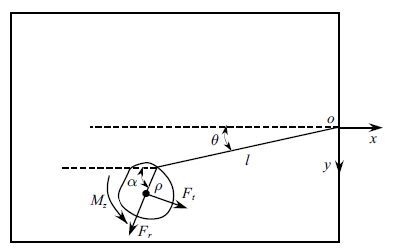
为建立天地动力学等效,首先要对地面实验系统进行动力学建模. 如图2所示,视卫星仿真器为刚体,忽略系绳质量与弹 性,以及仿真器与平台间摩擦力. 仿真器质量$m$,系绳长度$l$,系绳连接点至仿真器质心距离为$\rho$,这里$\rho \ll l$.位于仿真器侧面正交分布有四个喷嘴,产生的喷气力合力为$F_t $和$F_r $,动量轮产生的力矩为$M_z $.根据拉格朗日方程,该地面实验系统在固定坐标系\textit{oxy}中的动力学方程为
|
\[\left. \begin{array}{*{35}{l}}
\ddot{\theta }=-{{\beta }_{1}}{{{\dot{\alpha }}}^{2}}\sin (\theta -\alpha )-\frac{{{F}_{r}}}{ml}\sin (\theta -\alpha )+ \\
\left( \frac{{{F}_{t}}}{ml}-\frac{{{\beta }_{1}}{{M}_{z}}}{{{I}_{z}}} \right)\cos (\theta -\alpha ) \\
\ddot{\alpha }={{\beta }_{2}}{{{\dot{\theta }}}^{2}}\sin (\theta -\alpha )+\frac{{{F}_{t}}\rho }{{{I}_{z}}}(1-{{\cos }^{2}}(\theta -\alpha ))+ \\
\frac{{{F}_{r}}\rho }{2{{I}_{z}}}\sin 2(\theta -\alpha )+\frac{{{M}_{z}}}{{{I}_{z}}} \\
\end{array} \right\}\]
|
(1) |
式中$\beta _1 = \rho/l$,$\beta _2 = m\rho l/I_z $,$I_z $为仿真器绕其质心轴的转动惯量.
2 动力学等效
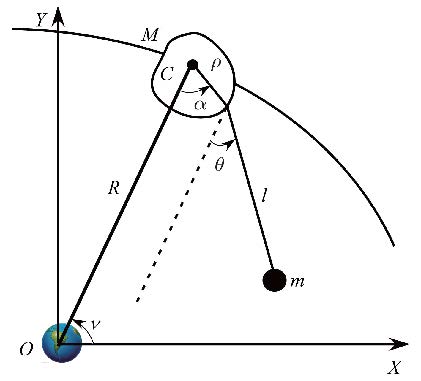
考虑沿赤道面内未扰开普勒圆轨道运动的绳系航天器系统,如图3所示. 将主航天器视为质量为$M$的刚体、主轴转动惯量为$I_x,I_y ,I_z $. 卫星视为质量$m$的质点. 主航天器质量远大于卫星质量以致绳系航天器系统的质心位于主航天器质心$C$. 主航天器轨道半径$R$、真近点角为$v$、动量轮提供的力矩为$M_z $. 建立固连于地心的惯性坐标系$OXY$,其中$OX$轴位于赤道面内并指向春分点. 定义系统的两个广义坐标为系绳俯仰角$\theta $和航天器姿态角$\alpha $. 根据Lagrange方程,系统动力学方程为
|
\[\left. \begin{array}{*{35}{l}}
\ddot{\theta }=-3{{{\dot{\nu }}}^{2}}\sin \theta \cos \theta -{{\beta }_{1}}[({{{\dot{\alpha }}}^{2}}+2\dot{\nu }\dot{\alpha })\sin (\theta -\alpha )+ \\
\qquad 3{{{\dot{\nu }}}^{2}}\cos \alpha \sin \theta -{{\beta }_{0}}{{{\dot{\nu }}}^{2}}\sin \alpha \cos \alpha \cos (\theta -\alpha )]- \\
\qquad \frac{{{\beta }_{1}}{{M}_{z}}}{{{I}_{z}}}\cos (\theta -\alpha ) \\
\ddot{\alpha }={{\beta }_{2}}[{{{\dot{\theta }}}^{2}}+2\dot{\nu }\dot{\theta }+3{{{\dot{\nu }}}^{2}}{{\cos }^{2}}\theta ]\sin (\theta -\alpha )- \\
{{\beta }_{0}}{{{\dot{\nu }}}^{2}}\sin \alpha \cos \alpha +\frac{{{M}_{z}}}{{{I}_{z}}} \\
\end{array} \right\}\]
|
(2) |
式中,$\beta _1 = \rho /l$,$\beta _2 = m\rho l/I_z $,$\beta _0 = 3(I_y - I_x )/I_z $.
对比方程(1)和(2)可以发现,若仅使用喷气力作为等效力,即$M_z = 0$,则等效喷气力为
|
\[{{F}_{r}}=\frac{{{I}_{z}}}{\rho }B\cot (\theta -\alpha )+Aml\frac{{{\cos }^{2}}(\theta -\alpha )-1}{\sin (\theta -\alpha )}\]
|
(3a) |
|
\[{{F}_{t}}=\frac{{{I}_{z}}}{\rho }B+Aml\cos (\theta -\alpha )\]
|
(3b) |
其中
|
\[\left. \begin{array}{*{35}{l}}
A=-\frac{3}{2}{{{\dot{\nu }}}^{2}}\sin 2\theta -{{\beta }_{1}}[2\dot{\nu }\dot{\alpha }\sin (\theta -\alpha )+ \\
\text{ }\qquad 3{{{\dot{\nu }}}^{2}}\cos \alpha \sin \theta -\frac{1}{2}{{\beta }_{0}}{{{\dot{\nu }}}^{2}}\sin 2\alpha \cos (\theta -\alpha )] \\
B=-\frac{1}{2}{{\beta }_{0}}{{{\dot{\nu }}}^{2}}\sin 2\alpha +{{\beta }_{2}}[2\dot{\nu }\dot{\theta }+3{{{\dot{\nu }}}^{2}}{{\cos }^{2}}\theta ]\sin (\theta -\alpha ) \\
\end{array} \right\}\]
|
(4) |
若使用喷气力与动量轮力矩的组合进行等效,则有
|
\[{{F}_{r}}=\frac{{{I}_{z}}}{\rho }B\cot (\theta -\alpha )+Aml\frac{{{\cos }^{2}}(\theta -\alpha )-1}{\sin (\theta -\alpha )}\]
|
(5a) |
|
\[{{F}_{t}}=\frac{{{I}_{z}}}{\rho }B+Aml\cos (\theta -\alpha )\]
|
(5b) |
|
\[{{M}_{z}}=-{{\beta }_{0}}{{{\dot{\nu }}}^{2}}{{I}_{z}}\sin \alpha \cos \alpha \]
|
(5c) |
其中
|
\[\left. \begin{array}{*{35}{l}}
A=-\frac{3}{2}{{{\dot{\nu }}}^{2}}\sin 2\theta -{{\beta }_{1}}[2\dot{\nu }\dot{\alpha }\sin (\theta -\alpha )+ \\
\text{ }\qquad 3{{{\dot{\nu }}}^{2}}\cos \alpha \sin \theta ] \\
B={{\beta }_{2}}[2\dot{\nu }\dot{\theta }+3{{{\dot{\nu }}}^{2}}{{\cos }^{2}}\theta ]\sin (\theta -\alpha ) \\
\end{array} \right\}\]
|
(6) |
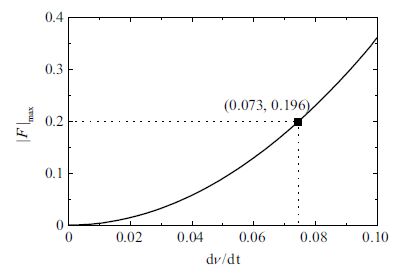
将上述仅使用喷气力进行等效的力学模型称为等效模型一、使用喷气力与动量轮力矩组合的等效模型为等效模型二.值得注意的是,绳系航天器轨道角速度$\dot {\nu }$很小,若将实际轨道角速度直接代入等效力模型中,则物理仿真实验中等效喷气力$F_t$和$F_r $太小,以致仿真器与平台之间的摩擦力、平台倾斜等外部干扰的影响变得突出,因而试验中考虑$\dot{\nu }$值高于实际轨道角速度. 为选择合适的轨道角速度,根据实验测得的系统参数值(如表1所示),以等效模型二为例进行数值仿真,得到$\dot{\nu }$与最大喷气力关系曲线如图4所示. 这里选择等效模型二进行数值仿真,是因为等效模型一的喷气力会在某些时刻出现极值,而等效模型二的喷气力曲线要光滑些. 考虑到本实验所研究的情况,初始条件采用实验中可能出现的最大初始角,即$(\theta_0 ,\dot {\theta }_0 ,\alpha _0 ,\dot {\alpha }_0 )=(0.5,0,- 1.5,0)$. 由于实验设备所能提供的最大喷气力为0.2N,根据图4可见,只要角速度$\dot {\nu}$小于$0.073$ rad/s,就可满足实验条件. 综上所述,实验中选$\dot {\nu } = 0.06$ rad/s.
表1(Table 1)

表1 物理仿真参数Table 1 Parameters of physical simulation
|
表1 物理仿真参数
Table 1 Parameters of physical simulation |
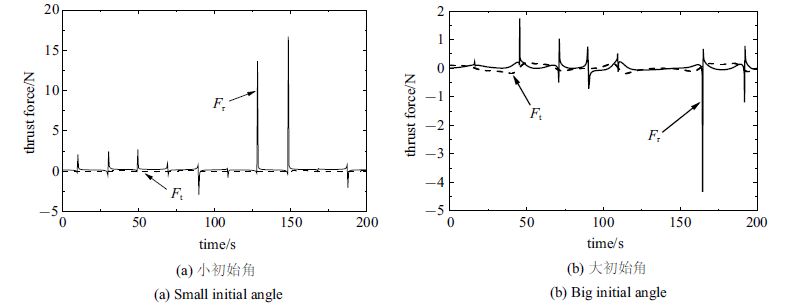
为研究两种等效模型在不同实验工况下的优劣,选取如表1所示系统参数,此时无量纲参数$\beta _1 = 0.0114$,$\beta _2= 1.376$. 考虑主航天器为形状不对称刚体,取参数$\beta _0 = 3$. 下面分别选取小角度和大角度为初始条件,对两种等效模型进行物理仿真. 图5给出了初始条件$(\theta _0 ,\dot {\theta }_0 ,\alpha _0 ,\dot {\alpha }_0)$分别取小初始角位移$(0.1,0,- 0.1,0)$ 和大初始角位移$(0.5,0,- 1.5,0)$时,等效模型一所需的喷气力时间历程.由图5可见,等效模型一的径向喷气力$F_r $在某些时刻会突然增大,出现极值且极值超出了实验设备所能提供的最大喷气力,但大多数时刻喷气力$F_r$变化平稳且量值合理.
在同样的参数下,图6给出了等效模型二的喷气力和动量轮力矩时间历程. 图6(a)和图6(c)表明,两种条件下喷气力的变化都在实验条件允许的范围内且曲线较光滑,没有出现极值. 从图6(b)和图6(d)可见,小初始角时的力矩曲线变化平稳,易于实现; 大初始角 时需要动量轮提供的力矩变化较复杂且过快,实验所用的动量轮难于实现. 因此,实验中大初始角时不能使用等效模型二.
综上所述,若主航天器为非对称刚体,即$\beta _0 \ne 0$,则当初始角的幅值较小时,由于等效模型二的喷气力和力矩变化平稳 且大小合适,此时选择等效模型二进行天地动力学等效;当初始角度的幅值较大时,利用等效模型二无法提供满足要求的等效动量轮力矩,等效模型二失效,所以此时选择等效模型一.
3 数值与实验结果
3.1 数值结果
选用表1中的参数对在轨绳系航天器系统进行数值仿真. 首先不考虑主航天器上动量轮的作用,即$M_z= 0$. 有研究表明,在不考虑系绳摆动而仅考虑系绳弹性对主星俯仰姿态的影响时,主星在未扰分离点附近会出现混沌运动[11]. 因而,猜测不考虑系绳弹性,仅考虑系绳的俯仰运动对主航天器姿态运动的作用,也可能会使主航天器的姿态运动进入混沌. 所以我们将数值仿真初始条件$(\theta_0 ,\dot {\theta }_0 ,\alpha _0 ,\dot {\alpha }_0 )$选择在主航天器姿态运动的未扰分离点附近,取为$(0.396,0,- 1.173,0)$.
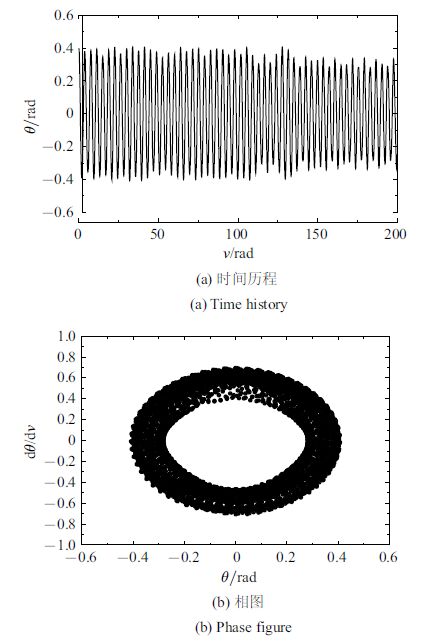
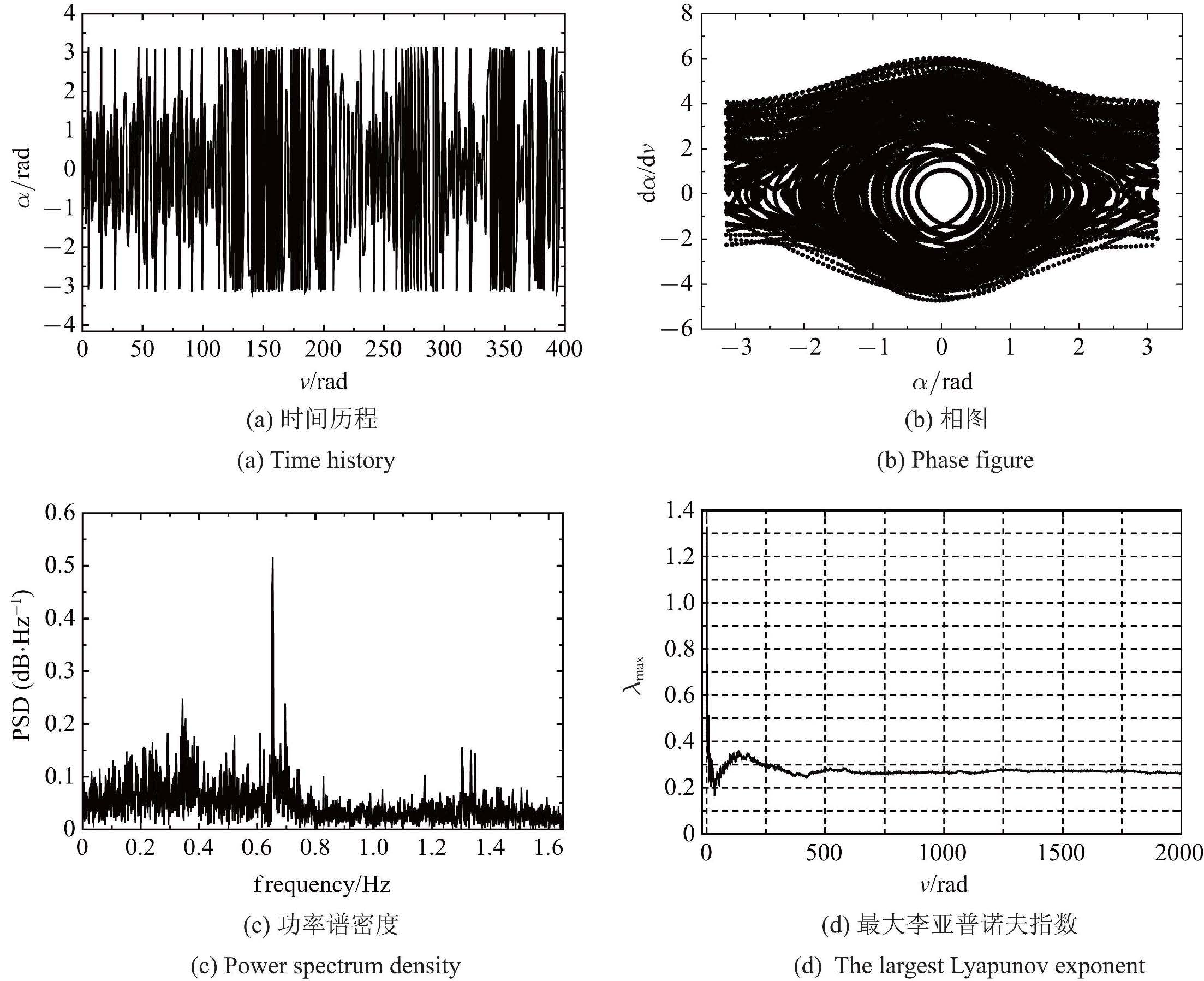
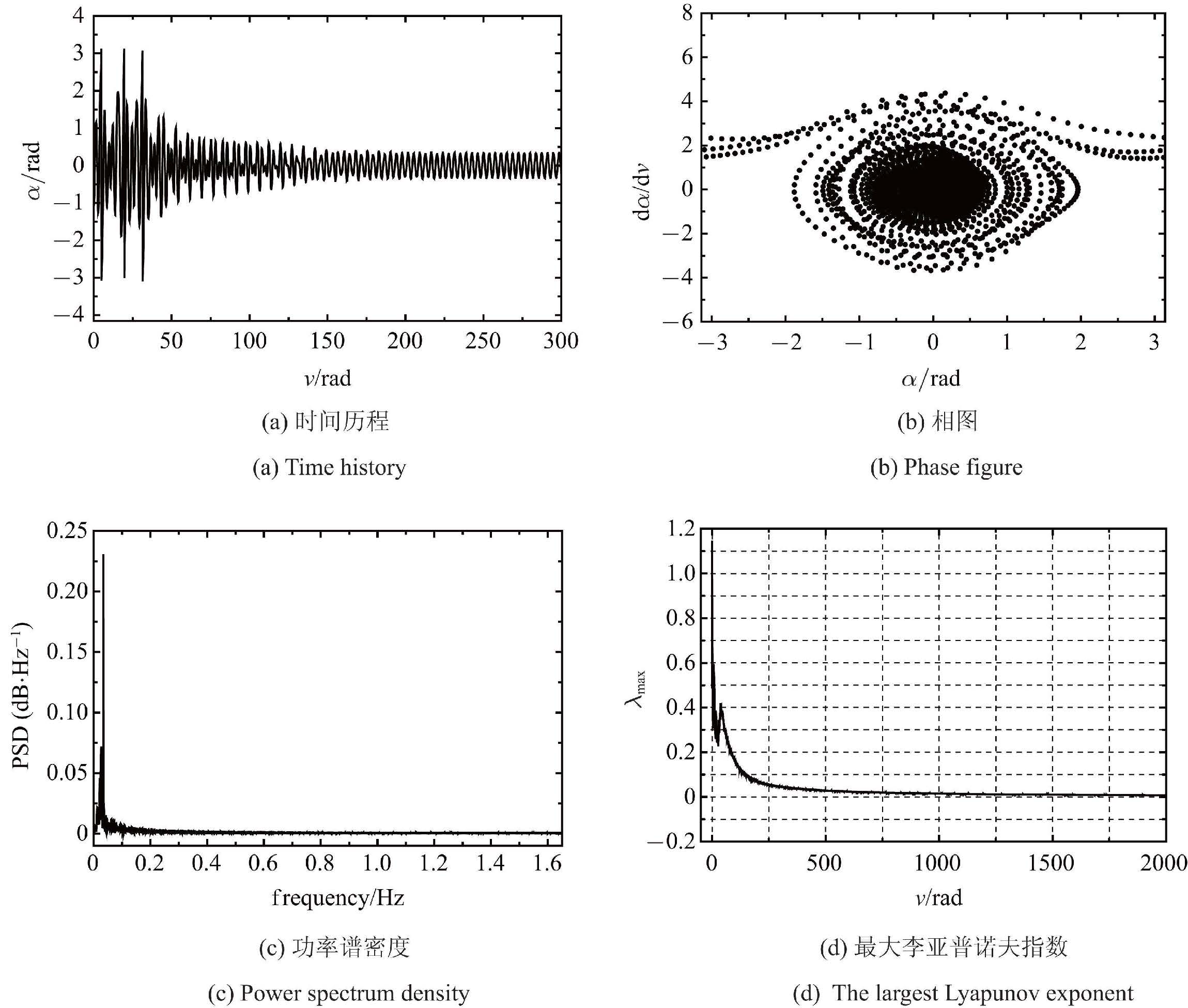
首先,研究系绳的俯仰运动,图7给出了系绳俯仰角$\theta $的时间历程图和相图. 从图7可见,系绳俯仰角作规则的概周期运动. 图8给出了主航天器姿态角$\alpha$的时间历程图、相图、功率谱、最大李亚普诺夫指数. 从图8(a)时间历程可以观察到主航天器俯仰角$\alpha$作不规律的运动,在相图8(b)中其表现为复杂的相轨迹,振动与旋转交替出现. 图8(c)表明该俯仰运动具有随机特性. 在图8(d)中最大李亚普诺夫指数逐渐稳定到一个正数. 所有这些特征都表明,主航天器的姿态运动在其未扰分离点附近发生了混沌.
如前所述,系绳摆动使主航天器姿态在其未扰分离点附近发生混沌,从而出现一些不期望的运动. 考虑主航天器上动量轮的作用,选取合适的输入力矩来避免这些混沌运动. 令力矩$M_z= - kI_z \dot {\alpha }$,即相当于给系统加入阻尼,这里$k$为阻尼系数. 令$k = 0.05$,对式(2)进行数值积分,初始条件仍然取在未扰分离点附近$(0.398,0,- 1.08,0)$,结果如图9所示. 从图9(a)和9(b)可见,加入阻尼力矩后,主航天器姿态运动初始表现为瞬态的混沌运动,而后逐渐变为规则有序的运动. 图9(c)所示功率谱密度只有一个单峰,表明系统呈现出周期特征,相应的最大李亚普诺夫指数逐渐趋近于零,如图9(d)所示. 表明阻尼力矩的加入有效地消除了混沌运动.
3.2 实验结果
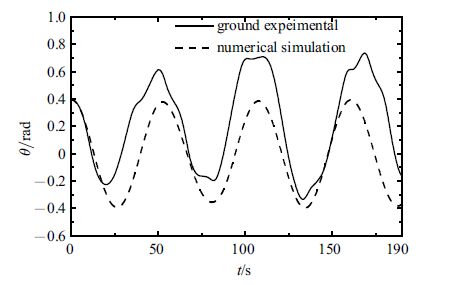
首先考虑不加入阻尼力矩的情况. 由仿真结果可知,此时主航天器姿态发生混沌运动,$\alpha$的幅值较大,所以在实验中选用等效模型一进行天地动力学等效,系统参数如表一所示. 多次实验均呈现类似结果,这里给出了在$(0.396,0,- 1.173,0)$初始条件下释放后,系绳俯仰角$\theta $的试验结果与数值仿真的对比,如图10所示. 从图10可见,实验所得系绳俯仰角与数值计算结果虽然在幅值上有一定差异但总体趋势是一致的. 实验结果整体偏移了一个正角度值,这可能是由于实验平台倾斜所致. 实验与数值结果都表明,系绳俯仰角作规则运动,等效模型一较好实现了天地动力学等效行为.
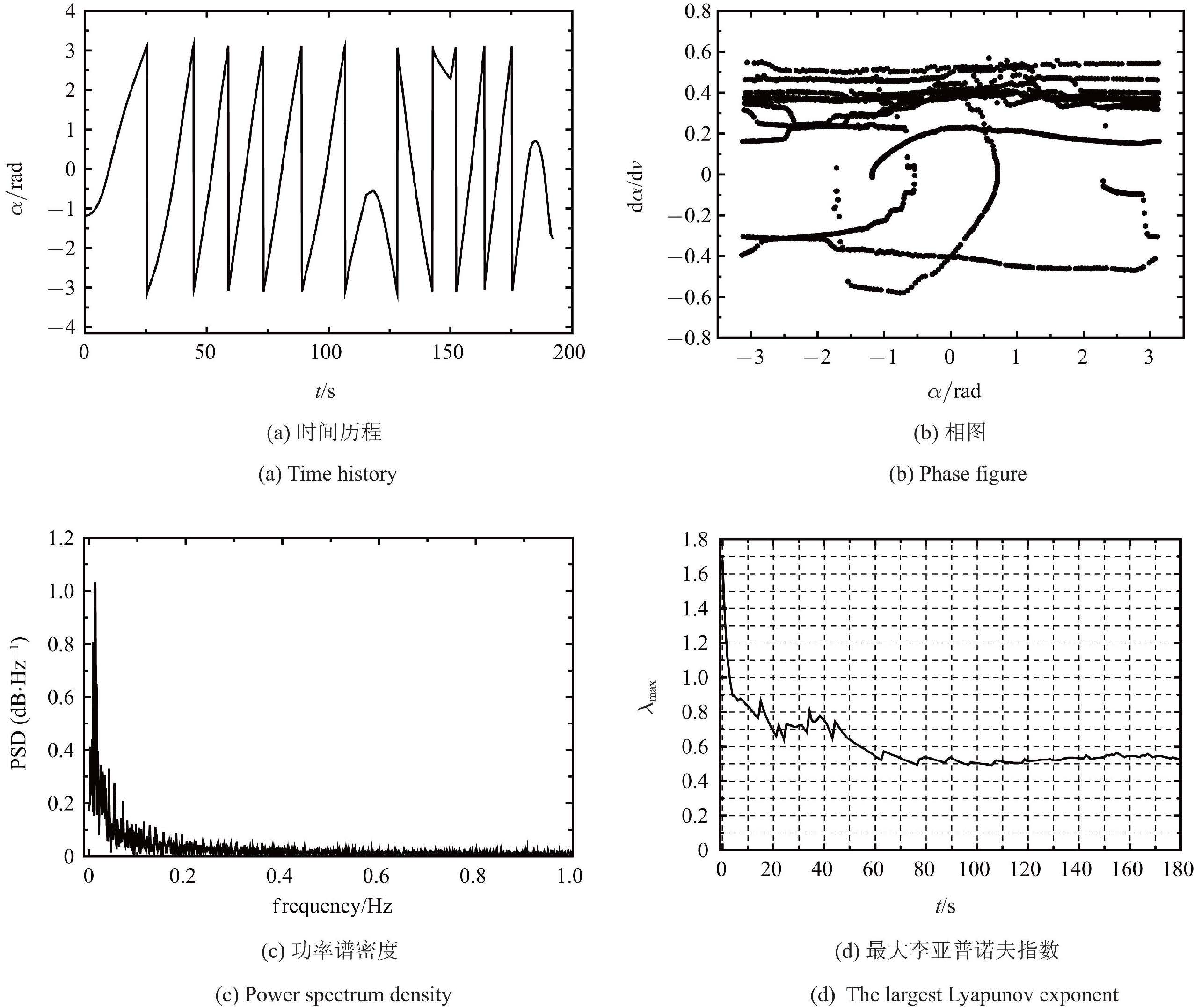
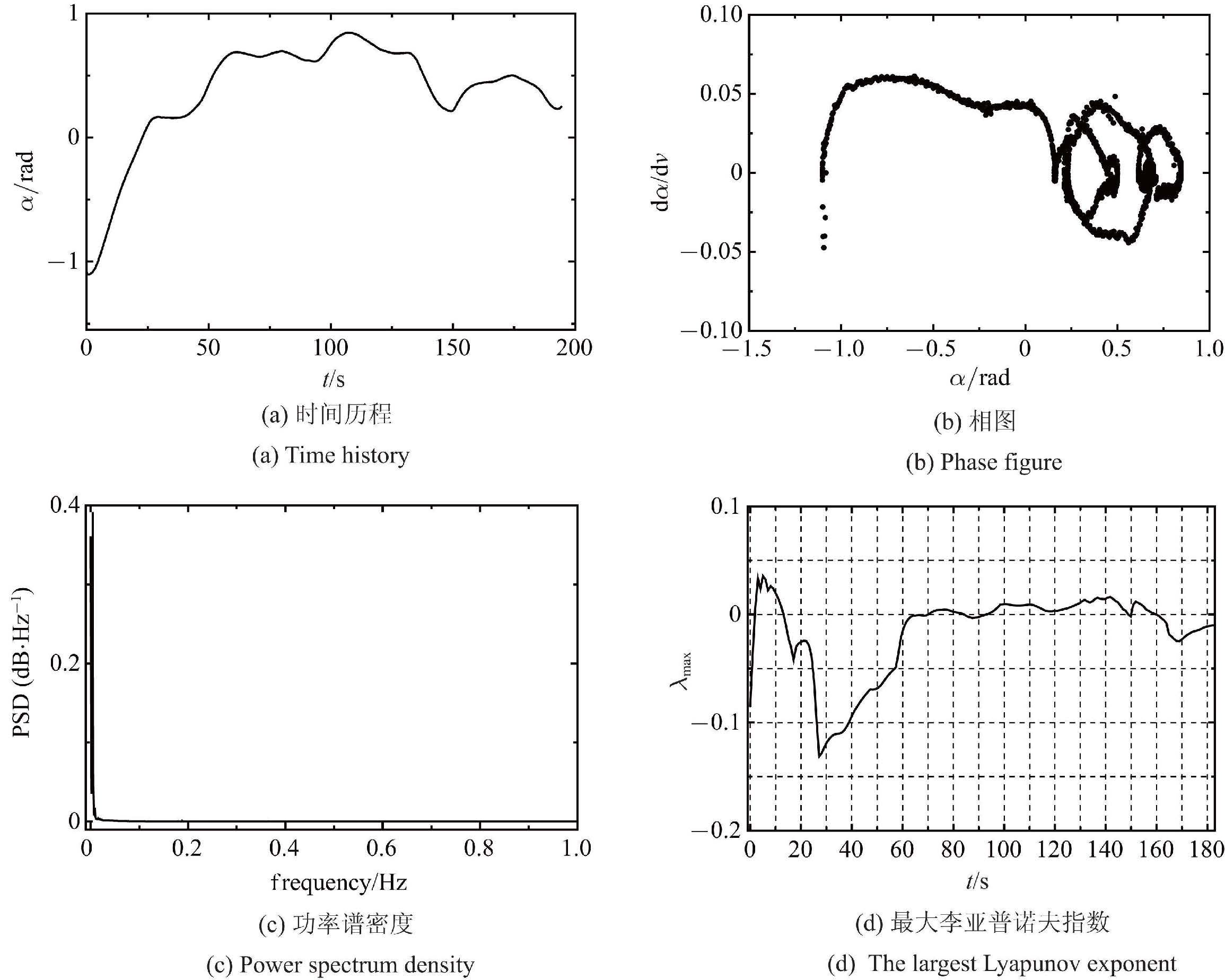
在同样的实验条件下,主航天器姿态运动如图11所示. 从时间历程和相图可见,姿态角$\alpha$ 作不规则的运动,多峰的功率谱密度和趋近于正常数的最大李亚普诺夫指数均表明,主航天器姿态呈现混沌现象,这与数值仿真分析所得结论一致. 综上可知,实验与仿真结果表明,在一定的参数与初始条件下,在系绳俯仰为规则运动的同时,主航天器姿态会出现混沌.
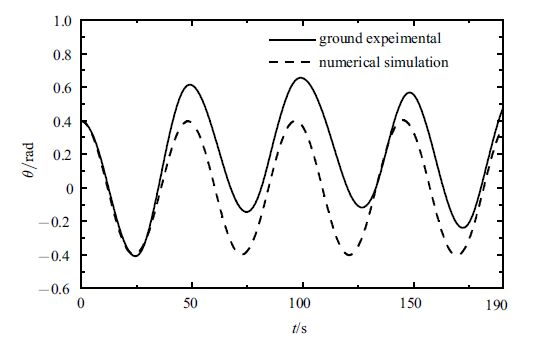
考虑加入阻尼力矩的情形,由数值仿真可知,姿态角$\alpha $的幅值很快由大变小并作小幅运动.所以实验中相应地选用等效模型 二进行天地动力学等效. 此时,地面试验系统动量轮力矩由两部分组成:一部分提供天-地等效所需的力矩,由式(5c)确定;一部分用于提供系统的阻尼力矩,令其大小为$- kI_z \dot {\alpha }$. 图12给出了在$(0.398,0,-1.08,0)$初始条件下释放后,系绳俯仰角$\theta $试验结果与数值仿真的对比. 从图12可见,实验所得的系绳俯仰角与数值结果在趋势上符合较好,在幅值方面仍然是实验曲线整体上偏移了一个正角度,较好实现了阻尼力矩情况下的天地动力学等效行为.
图13给出了主航天器姿态角$\alpha $的时间历程、相图、功率谱密度和最大李亚普诺夫指数. 从图13可见,系统不再存在混沌运 动特性,所以阻尼力矩的引入成功消除了系统的混沌运动,与数值仿真的结论一致.由于实验系统不可避免的外界干扰,使得姿态运动没有像数值仿真中那样在平衡位置附近振荡,而是在某一位置附近作往复振动.
综上所述,无论系统是否有阻尼力矩的作用,试验结果均证实了数值仿真的结论. 试验与数值仿真在量值上存在一定差异,但整 体趋势一致. 这些差异源于建模假设如系绳为无质量直杆、保持不会松弛等. 然而在验证混沌运动的试验中,系绳在某些时刻可能会发生短暂的瞬间松弛. 此外,实验平台的水平度、仿真器与平台间的些微摩擦等因素也可能引起这些差异.
4 结论
基于天地动力学相似原理,通过对仿真器施加喷气力和动量轮力矩可以再现绳系航天器的空间动力学环境. 针对是否提供动量轮力矩提出了两种等效方案. 数值仿真表明,当绳系航天器系统的初始角位移较小时,可以采用基于动量轮力矩的天地动力学等效模型; 当初始角位移较大时,则仅利用喷气力提供等效力进行物理仿真效果更好. 在一定的参数条件下绳系航天器发生周期或概周期运动,同时主航天器姿态呈现混沌,地面试验验证了这些运动的存在. 同时,试验表明加入阻尼力矩可有效避免混沌运动.
参考文献
| [1] |
Wen H, Jin DP, Hu HY. Advances in dynamics and control of tethered satellite systems. Acta Mechanica Sinica, 2008, 24(3): 229-241 |
| [2] |
Fujii HA, Ichiki W. Nonlinear dynamics of the tethered subsatellite system in the station keeping phase. Journal of Guidance, Control, and Dynamics, 1997, 20(2): 403-406 |
| [3] |
Steiner W. Transient chaotic oscillations of a tethered satellite system. Acta Mechanica, 1998, 127(1-4): 155-163 |
| [4] |
Misra AK, Nixon MS, Modi VJ. Nonlinear dynamics of two-body tethered satellite systems: Constant length case. Journal of the Astronautical Sciences, 2001, 49(2): 219-236 |
| [5] |
Nixon MS, Misra AK. Nonlinear dynamics and chaos of two-body tethered satellite systems. Advances in the Astronautical Sciences, 1993, 85(1): 775-794 |
| [6] |
Peng JH, Liu YZ. Chaotic motion of the tethered satellite system. Technishe Mechanik, 1996, 16(4): 327-331 |
| [7] |
Béda PB. On saddle-node bifurcation and chaos of satellites. Nonlinear Analysis: Theory, Methods and Applications, 1997, 30(8): 4881-4886 |
| [8] |
王晓宇, 金栋平. 计入姿态的绳系卫星概周期运动. 振动工程学报, 2010, 23(4): 361-365 (Wang Xiaoyu, Jin Dongping. Quasi-periodic motion of a tethered subsatellite with attitude. Journal of Vibration Engineering, 2010, 23(4): 361-365 (in Chinese)) |
| [9] |
金栋平, 庞兆君, 余本嵩. 绳系卫星系统周期运动的分岔与镇定. 南京航空航天大学学报, 2012, 44(5): 663-668 (Jin Dongping, Pang Zhaojun, Yu Bensong. Periodic motion bifurcation and stabilization of tethered satellite system. Journal of Nanjing University of Aeronautics and Astronautics, 2012, 44(5): 663-668 (in Chinese)) |
| [10] |
Aslanov VS. Orbital oscillations of an elastic vertically-tethered satellite. Mechanics of Solids, 2011, 46(5): 657-668 |
| [11] |
Aslanov VS, Ledkov AS. Chaotic oscillations of spacecraft with an elastic radially oriented tether. Cosmic Research, 2012, 50(2): 188-198 |
| [12] |
Jin DP, Wen H, Chen H. Nonlinear resonance of a subsatellite on a short constant tether. Nonlinear Dynamics, 2013, 71(3): 479-488 |
| [13] |
陈辉, 文浩, 金栋平, 等. 绳系卫星在轨试验及地面物理仿真进展. 力学进展, 2013, 43(1): 174-184 (Chen Hui, Wen Hao, Jin Dongping, et al. Experimental studies on tethered satellite systems. Advances in Mechanics, 2013, 43(1): 174-184 (in Chinese)) |
| [14] |
Takehara S, Terumichi Y, Nohmi M, et al. Numerical and experimental approaches on the motion of a tethered system. Journal of System Design and Dynamics, 2008, 2(5): 1106-1117 |
| [15] |
文浩, 金栋平, 胡海岩. 绳系卫星收放控制地面实验研究. 振动工程学报, 2010, 23(1): 7-11 (Wen Hao, Jin Dongping, Hu Haiyan. Ground-based experimental study on deployment and retrieval control of tethered satellite. Journal of Vibration Engineering, 2010, 23(1): 7-11 (in Chinese)) |
| [16] |
Kojima H, Fukukawa Y, Trivailo PM. Experimental verification of periodic libration of tethered satellite system in elliptic orbit. Journal of Guidance, Control, and Dynamics, 2011, 34(2): 614-618 |
| [17] |
Jin DP, Wang XY, Wen H. Quasi-periodic motion of a ground-based tethered sub-satellite with attitude. Advances in the Astronautical Sciences, 2012, 145: 1087-1096 |
EXPERIMENTAL VERIFICATION OF CHAOTIC ATTITUDE MOTIONOF TETHERED SPACECRAFT SYSTEM
Pang Zhaojun, Jin Dongping

State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Fund: The project was supported by the National Natural Science Foundation of China (11002068, 11202094) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Abstract: The paper studies chaotic motions of a tethered spacecraft by utilizing the ground-based experimental system. Based on the dynamics similarity principle, the dynamic equivalent model between the on-orbit tethered spacecraft and its ground experiment system are obtained. The space dynamics environment of the tethered spacecraft is simulated with the help of thrust forces and torque of momentum wheel on satellite simulator. Numerical simulations of the on-orbit tethered spacecraft show that the pitch motion of the tether is period or quasi-period one, while the attitude motion of the mother spacecraft behaves chaotic motion. The numerical results are verified based on the ground-based experimental system. The experiment shows that the torque of momentum wheel with a negative damping is able to suppress the chaotic motion.
Key words:
tethered spacecraft dynamics similarity ground-based experiment chaotic motion

 2015, Vol. 47
2015, Vol. 47