2. 石家庄铁道大学工程力学系, 石家庄050043
PMN-$x$PT($x$指晶体中PT的含量)是铌镁酸铅(PMN)和压电体钛酸铅(PT)的固溶体单晶,其压电性能与组份和单晶的切型密切相关,当组份材料铌镁酸铅的含量为67%,钛酸铅的含量为33%时,即PMN-0.33PT晶体的压电性能非常优异[1],这种单晶材料的压电常数、机电耦合系数和应变量均远远超出目前广泛应用的锆钛酸铅(PZT)系压电陶瓷,是制作新一代高效率、高灵敏度压电超声换能器、传感器、驱动器和致动器的理想材料,有望取代传统的多晶压电陶瓷[2, 3, 4].PMN-PT单晶的极化方向与其宏观对称性密切相关,在室温下,当PMN-PT沿[011]$_{\rm c}$方向极化时(c代表极化轴的方向),在宏观上呈现正交晶系(mm2对称性),当沿[001]$_{ \rm c}$方向极化时,在宏观上呈现四方晶系(4 mm对称性),当PMN-PT沿[111]$_{ \rm c}$方向极化时,在宏观上呈现三方晶系(3 m对称性).PMN-PT的许多潜在应用与弹性波的传播密切相关,这要求人们首先要弄清弹性波在PMN-PT压电材料中的传播规律,即晶体的极化方向、几何结构以及边界条件对传播特征的影响.Park[5]研究了弛豫型铁电单晶(1-$x)$Pb(Mg$_{1/3}$Nb$_{2/3})$O$_{3}-x$PbTiO$_{3}$(PMN-PT)的应变和压电行为,当PMN-PT压电晶体沿[001]$_{\rm c}$方向极化时,其压电系数超过传统压电陶瓷的4倍,机电耦合系数也远远的高于传统的铁电晶体或陶瓷材料;Wang等[6]研究了PMN-PT单晶圆板的振动问题,研究结果显示:当PMN-PT沿[001]$_{ \rm c}$方向极化时,其径向振动性能非常优异;Kook[7]研究了弛豫型正交各向异性铁电单晶PMN-PT表面声波的传播特性,该单晶的压电系数$d_{33}>2 000$ pC/N,力电耦合性能$k_{33}>90%$,可以作为宽带过滤器装置;Ren等[8]分析了PMN-PT单晶剪切模态的振动特点,在宽频率范围内获得了较大的输出功率;Chen 等[9, 10, 11]研究了PMN-PT单晶薄板中的导波,分析了传播方向以及晶体对称性对传播性能的影响; Li等[12, 13]和Zhang等[14]分析了表面声波在单晶PMN-0.33PT中的传播,沿[111]$_{\rm c}$方向极化时$x$向切割的单晶具有较低的相速度和较高的力电耦合系数,功率流角度(PFA)在特定的方向为零,可以大大提高表面声波器件的性能,理论研究结果显示:[111]$_{ \rm c}$方向极化$x$向切割的表面声波器件,在[111]$_{ \rm c}$方向倾覆5°为最佳方向;Chen等[15]研究了表面声波在PIN-PMN-PT晶体中传播时的力电耦合特性,发现SH型声表面波的力电耦合系数$K^{2}$较高,这一特性对于实现超宽带表面声波滤波器具有很大的吸引力.上述文献中大部分研究的是铁电单晶PMN-PT的导波和表面波的性质,对于由PMN-PT组成的复杂结构(层状结构)的声表面波特性的研究到目前为止还非常有限,本文研究PMN-PT层/弹性(金刚石)半空间结构中声表面波的传播性质,其中PMN-PT单晶沿不同的方向极化,分析PMN-PT层自由表面的电学边界条件以及极化方向对弹性波频散特性的影响.
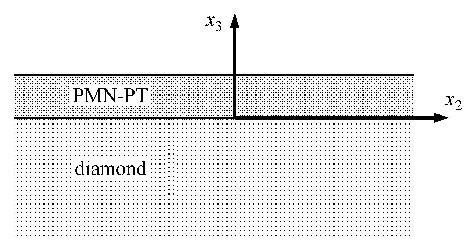
1 基本方程的描述如图1所示,考虑PMN-PT层/金刚石基底半空间结构中弹性波沿$x_{2}$方向传播. PMN-PT层的厚度为$h$,层和半空间在$x_{3}=0$的界面采用理想连接方式,即PMN-PT层与金刚石的位移、应力、电位移和电势在界面处是相等的,所有的场变量与坐标$x_{1}$无关.
|
图1 PMN-PT压电层/金刚石半空间结构 Fig.1 Geometry of the layered PMN-PT/diamond half space structure |
PMN-PT晶体沿[011]$_{ \rm c}$方向极化时,具有3个对称面,在宏观上具有mm2对称性,即呈现正交各向异性性质,有9个独立弹性参数$c_{ij}$,5个压电常数$e_{kl}$和3个介电常数 $\kappa _{mn}$
\[\left. \begin{array}{l}
c = \left[ {\begin{array}{*{20}{c}}
{{c_{11}}}&{{c_{12}}}&{{c_{13}}}&0&0&0\\
{{c_{12}}}&{{c_{22}}}&{{c_{23}}}&0&0&0\\
{{c_{13}}}&{{c_{23}}}&{{c_{33}}}&0&0&0\\
0&0&0&{{c_{44}}}&0&0\\
0&0&0&0&{{c_{55}}}&0\\
0&0&0&0&0&{{c_{66}}}
\end{array}} \right]\\
e = \left[ {\begin{array}{*{20}{c}}
0&0&{{e_{31}}}\\
0&0&{{e_{32}}}\\
0&0&{{e_{33}}}\\
0&{{e_{24}}}&0\\
{{e_{15}}}&0&0\\
0&0&0
\end{array}} \right],\kappa = \left[ {\begin{array}{*{20}{c}}
{{\kappa _{11}}}&0&0\\
0&{{\kappa _{22}}}&0\\
0&0&{{\kappa _{33}}}
\end{array}} \right]
\end{array} \right\}\]
(1)
弹性波在$x_{2}$-$x_{3}$平面内传播,所有量均与$x_{1}$方向无关,PMN-PT压电材料的本构方程为
\[\left. {\begin{array}{*{20}{l}}
{{\sigma _{22}} = {c_{22}}{u_{2,2}} + {c_{23}}{u_{3,3}} + {e_{32}}{\varphi _{,3}}}\\
{{\sigma _{33}} = {c_{23}}{u_{2,2}} + {c_{33}}{u_{3,3}} + {e_{33}}{\varphi _{,3}}}\\
{{\sigma _{32}} = {c_{44}}({u_{2,3}} + {u_{3,2}}) + {e_{24}}{\varphi _{,2}}}\\
{{D_2} = {e_{24}}({u_{2,3}} + {u_{3,2}}) - {\varepsilon _{22}}{\varphi _{,2}}}\\
{{D_3} = {e_{32}}{u_{2,2}} + {e_{33}}{u_{3,3}} - {\varepsilon _{33}}{\varphi _{,3}}}
\end{array}} \right\}\]
(2)
当PMN-PT晶体沿 [001]$_{\rm c}$方向极化时,在宏观上具有4mm对称性,有6个独立的弹性常数$c_{ij}$,3个独立的压电系数$e_{kl}$和2个独立的介电系数 $\kappa_{mn}$,电弹常数矩阵与[011]$_{ \rm c}$方向极化的电弹常数矩阵相似,在本文中令矩阵式(1)中$c_{22 }= c_{11}$,$ c_{23 }= c_{13}$,$ e_{32 }=e_{31}$,$ e_{24 }= e_{15}$,$\kappa_{22} = \kappa _{11}$可以得到PMN-PT晶体沿 [001]$_{\rm c}$方向极化时的材料常数,具体的材料参数在表1中列出.
不考虑体力和自由电荷的存在,在准静态电磁假设下,应力和电位移满足下面的方程
\[\left. {\begin{array}{*{20}{l}}
{\frac{{\partial {\sigma _{22}}}}{{\partial {x_2}}} + \frac{{\partial {\sigma _{23}}}}{{\partial {x_3}}} = \rho {{\ddot u}_2}}\\
{\frac{{\partial {\sigma _{32}}}}{{\partial {x_2}}} + \frac{{\partial {\sigma _{33}}}}{{\partial {x_3}}} = \rho {{\ddot u}_3}}\\
{\frac{{\partial {D_2}}}{{\partial {x_2}}} + \frac{{\partial {D_3}}}{{\partial {x_3}}} = 0}
\end{array}} \right\}\]
(3)
将式(2)代入式(3)得到压电材料平面问题的控制微分方程
\[\left. {\begin{array}{*{20}{l}}
{{c_{22}}{u_{2,22}} + {c_{44}}{u_{2,33}} + ({c_{23}} + {c_{44}}){u_{3,32}} + }\\
{\qquad ({e_{32}} + {e_{24}}){\varphi _{,23}} = \rho {{\ddot u}_2}}\\
{{c_{44}}{u_{3,22}} + {c_{33}}{u_{3,33}} + ({c_{44}} + {c_{23}}){u_{2,32}} + {e_{24}}{\varphi _{,22}} + }\\
{\qquad {e_{33}}{\varphi _{,33}} = \rho {{\ddot u}_3}}\\
{{e_{24}}{u_{3,22}} + {e_{33}}{u_{3,33}} + ({e_{24}} + {e_{32}}){u_{2,23}} - {\kappa _{22}}{\varphi _{,22}} - }\\
{\qquad {\kappa _{33}}{\varphi _{,33}} = 0}
\end{array}} \right\}\]
(4)
金刚石的本构方程为[16]
\[\left. {\begin{array}{*{20}{l}}
{{{\bar \sigma }_{22}} = {{\bar c}_{11}}{\varepsilon _{22}} + {{\bar c}_{12}}{\varepsilon _{33}}}\\
{{{\bar \sigma }_{33}} = {{\bar c}_{12}}{\varepsilon _{22}} + {{\bar c}_{11}}{\varepsilon _{33}}}\\
{{{\bar \sigma }_{32}} = {{\bar c}_{44}}{\gamma _{32}}}\\
{{{\bar D}_2} = {{\bar \kappa }_{11}}{E_2}}\\
{{{\bar D}_3} = {{\bar \kappa }_{11}}{E_3}}
\end{array}} \right\}{\rm{ }}\]
(5)
为了与PMN-PT材料的各个量相区分,相应于金刚石基底的各个量(位移$\bar { u}_i$,应力$\bar { \sigma }_{ij} $,电势$\bar {\varphi }$,电位移$\bar { D}_i$,弹性常数$\bar { c}_{ij} $以及介电常数$\bar {\kappa }_{11}$等)上方加"--"表示.
弹性半空间的控制方程为
\[\left. \begin{array}{*{35}{l}}
{{{\bar{c}}}_{11}}{{{\bar{u}}}_{2,22}}+{{{\bar{c}}}_{44}}{{{\bar{u}}}_{2,33}}+({{{\bar{c}}}_{12}}+{{{\bar{c}}}_{44}}){{{\bar{u}}}_{3,23}}=\bar{\rho }{{{\ddot{\bar{u}}}}_{2}} \\
({{{\bar{c}}}_{12}}+{{{\bar{c}}}_{44}}){{{\bar{u}}}_{2,23}}+{{{\bar{c}}}_{44}}{{{\bar{u}}}_{3,22}}+{{{\bar{c}}}_{11}}{{{\bar{u}}}_{3,33}}=\bar{\rho }{{{\ddot{\bar{u}}}}_{3}} \\
{{{\bar{\varphi }}}_{,22}}+{{{\bar{\varphi }}}_{,33}}=0 \\
\end{array} \right\}\]
(6)
对于所考虑的结构,压电层PMN-PT表面的边界条件包括机械边界条件和电学边界条件两种. 通常情况下,压电层的机械边界条件是应力为0,即$x_{3}=h$时,满足
\[{\sigma _{32}}({x_2},h) = 0,{\sigma _{33}}({x_2},h) = 0\]
(7)
自由表面的电学边界条件考虑电学短路和电学开路两种,电学开路边界条件满足介质表面的电荷密度为0,即
\[{D_3}({x_2},h) = 0\]
(8)
如果在压电介质表面覆有很薄的金属薄层(忽略其质量负载影响),表面电势为0,即为电学短路边界条件
\[\varphi ({x_2},h) = 0\]
(9)
在压电层和弹性半空间介质在界面处($x_{3} =0$)的位移、应力、电位移和电势是连续的,可以表示为
\[\left. {\begin{array}{*{20}{l}}
{{u_2}({x_2},0) = {{\bar u}_2}({x_2},0)}\\
{{u_3}({x_2},0) = {{\bar u}_3}({x_2},0)}\\
{{\sigma _{32}}({x_2},0) = {{\bar \sigma }_{32}}({x_2},0)}\\
{{\sigma _{33}}({x_2},0) = {{\bar \sigma }_{33}}({x_2},0)}\\
{\varphi ({x_2},0) = \bar \varphi ({x_2},0)}\\
{{D_3}({x_2},0) = {{\bar D}_3}({x_2},0)}
\end{array}} \right\}\]
(10)
考虑弹性波沿$x_{2}$方向传播,采用分离变量法,其控制方程(4)的解分为沿$x_{2}$方向的行波和沿$ x_{3}$方向的驻波,PMN-PT压电层中的解可以表示为
\[\left. {\begin{array}{*{20}{l}}
\begin{array}{l}
{u_2}({x_2},{x_3},t) = {A_1}{{\rm{e}}^{qk{x_3}}}\cos [k({x_2} - vt)]\\
{u_3}({x_2},{x_3},t) = {A_2}{{\rm{e}}^{qk{x_3}}}\sin [k({x_2} - vt)]\\
\varphi ({x_2},{x_3},t) = {A_3}{{\rm{e}}^{qk{x_3}}}\sin [k({x_2} - vt)]
\end{array}
\end{array}} \right\}\]
(11)
将式(11)代入控制方程(4)得到
\[\left. {\begin{array}{*{20}{l}}
\begin{array}{l}
({c_{44}}{q^2} - {c_{22}} + \rho {v^2}){A_1} + ({c_{23}} + {c_{44}})q{A_2} + \\
({e_{32}} + {e_{24}}){A_3}q = 0\\
({c_{44}} + {c_{23}})q{A_1} + ({c_{44}} - {c_{33}}{q^2} - \rho {v^2}){A_2} + \\
({e_{24}} - {e_{33}}{q^2}){A_3} = 0\\
({e_{24}} + {e_{32}})q{A_1} + ({e_{24}} - {e_{33}}{q^2}){A_2} + \\
({\kappa _{33}}{q^2} - {\kappa _{22}}){A_3} = 0
\end{array}
\end{array}} \right\}\]
(12)
\[\left| {\begin{array}{*{20}{c}}
{{c_{44}}{q^2} - {c_{22}} + \rho {v^2}}&{({c_{23}} + {c_{44}})q}&{({e_{32}} + {e_{24}})q}\\
{({c_{44}} + {c_{23}})q}&{{c_{44}} - {c_{33}}{q^2} - \rho {v^2}}&{{e_{24}} - {e_{33}}{q^2}}\\
{({e_{24}} + {e_{32}})q}&{{e_{24}} - {e_{33}}{q^2}}&{{\kappa _{33}}{q^2} - {\kappa _{22}}}
\end{array}} \right| = 0\]
(13)
\[{L_{1j}} = {A_{1j}}/{A_{3j}},{L_{2j}} = {A_{2j}}/{A_{3j}}(j = 1,2,3)\]
(14)
\[\left. {\begin{array}{*{20}{l}}
{{L_{1j}} = \frac{{\left| {\begin{array}{*{20}{c}}
{ - ({e_{32}} + {e_{24}}){q_j}}&{({c_{23}} + {c_{44}}){q_j}}\\
{ - ({e_{24}} - {e_{33}}q_j^2)}&{{c_{44}} - {c_{33}}q_j^2 - \rho {v^2}}
\end{array}} \right|}}{{\left| {\begin{array}{*{20}{c}}
{{c_{44}}q_j^2 - {c_{22}} + \rho {v^2}}&{({c_{23}} + {c_{44}}){q_j}}\\
{({c_{44}} + {c_{23}}){q_j}}&{{c_{44}} - {c_{33}}q_j^2 - \rho {v^2}}
\end{array}} \right|}}}\\
{{L_{2j}} = \frac{{\left| {\begin{array}{*{20}{c}}
{{c_{44}}q_j^2 - {c_{22}} + \rho {v^2}}&{ - ({e_{32}} + {e_{24}}){q_j}}\\
{({c_{23}} + {c_{44}}){q_j}}&{ - ({e_{24}} - {e_{33}}q_j^2)}
\end{array}} \right|}}{{\left| {\begin{array}{*{20}{c}}
{{c_{44}}q_j^2 - {c_{22}} + \rho {v^2}}&{({c_{23}} + {c_{44}}){q_j}}\\
{({c_{44}} + {c_{23}}){q_j}}&{{c_{44}} - {c_{33}}q_j^2 - \rho {v^2}}
\end{array}} \right|}}}
\end{array}} \right\}{\rm{ }}\]
(15)
将式(14)和式(15)代入式(11)可以得到PMN-PT层中的位移和电势的解为
\[\left. {\begin{array}{*{20}{l}}
{{u_2}({x_2},{x_3},t) = \sum\limits_{i = 1}^6 {{A_{3i}}{L_{1i}}{{\rm{e}}^{{q_i}k{x_3}}}\cos [k({x_2} - vt)]} }\\
{{u_3}({x_2},{x_3},t) = \sum\limits_{i = 1}^6 {{A_{3i}}{L_{2i}}{{\rm{e}}^{{q_i}k{x_3}}}\sin [k({x_2} - vt)]} }\\
{\varphi ({x_2},{x_3},t) = \sum\limits_{i = 1}^6 {{A_{3i}}{{\rm{e}}^{{q_i}k{x_3}}}\sin [k({x_2} - vt)]} }
\end{array}} \right\}\]
(16)
将式(16)代入方程(2)可得到应力和电位移
\[\left. {\begin{array}{*{20}{l}}
{{\sigma _{22}} = \sum\limits_{i = 1}^6 {( - {c_{22}}{L_{1i}} + {c_{23}}{q_i}{L_{2i}} + {e_{32}}{q_i})} {A_{3i}}k{{\rm{e}}^{{q_i}k{x_3}}} \cdot }\\
{\qquad \sin [k({x_2} - vt)]}\\
{{\sigma _{33}} = \sum\limits_{i = 1}^6 {( - {c_{23}}{L_{1i}} + {c_{33}}{q_i}{L_{2i}} + {e_{33}}{q_i})} {A_{3i}}k{{\rm{e}}^{{q_i}k{x_3}}} \cdot }\\
{\qquad \sin [k({x_2} - vt)]}\\
{{\sigma _{32}} = \sum\limits_{i = 1}^6 {({c_{44}}{q_i}{L_{1i}} + {c_{44}}{L_{2i}} + {e_{24}})} {A_{3i}}k{{\rm{e}}^{{q_i}k{x_3}}} \cdot }\\
{\qquad \cos [k({x_2} - vt)]}
\end{array}} \right\}\]
(17a)
\[\left. {\begin{array}{*{20}{l}}
{{D_2} = \sum\limits_{i = 1}^6 {({e_{24}}{q_i}{L_{1i}} + {e_{24}}{L_{2i}} - {\kappa _{22}})} {A_{3i}}k{{\rm{e}}^{{q_i}k{x_3}}} \cdot }\\
{\qquad \cos [k({x_2} - vt)]}\\
{{D_3} = \sum\limits_{i = 1}^6 {( - {e_{32}}{L_{1i}} + {e_{33}}{q_i}{L_{2i}} - {\kappa _{33}}{q_i})} {A_{3i}}k{{\rm{e}}^{{q_i}k{x_3}}} \cdot }\\
{\qquad \sin [k({x_2} - vt)]}
\end{array}} \right\}\]
(17b)
解控制方程(6),得到弹性介质中的位移和电势
\[\left. {\begin{array}{*{20}{l}}
{{{\bar u}_2}({x_2},{x_3},t) = {B_1}{{\rm{e}}^{\bar qk{x_3}}}\cos [k({x_2} - vt)]}\\
{{{\bar u}_3}({x_2},{x_3},t) = {B_2}{{\rm{e}}^{\bar qk{x_3}}}\sin [k({x_2} - vt)]}\\
{\bar \varphi ({x_2},{x_3},t) = {B_3}{{\rm{e}}^{\bar q'k{x_3}}}\sin [k({x_2} - vt)]}
\end{array}} \right\}\]
(18)
方程(6)最后一个与前两个方程不耦合,把式(18)中的最后一式代入方程(6)中最后一个,$B_{3}$不能为零,可以解出未知数${\bar{q}}'$为两个互为相反数的值(${\bar {q}}'_1 = - {\bar {q}}'_2 =1)$,正数和负数分别表示弹性半空间中电势的增强和衰减,我们只考虑半空间中的电势随$x_{3}$方向的衰减,因此只取正值,即${\bar{q}}' = 1$. 把式(18)中的前两式代入方程(6)中的前两式,得到
\[\left. {\begin{array}{*{20}{l}}
{({{\bar c}_{44}}{{\bar q}^2} + {v^2}\bar \rho - {{\bar c}_{11}}){B_1} + ({{\bar c}_{12}} + {{\bar c}_{44}})\bar q{B_2} = 0}\\
{ - ({{\bar c}_{12}} + {{\bar c}_{44}})\bar q{B_1} + \left( {{{\bar c}_{11}}{{\bar q}^2} + {v^2}\bar \rho - {{\bar c}_{44}}} \right){B_2} = 0}
\end{array}} \right\}\]
(19)
方程组(19)有非零解的充要条件是系数行列式的值为0,即
\[\left| {\begin{array}{*{20}{c}}
{{{\bar c}_{44}}{{\bar q}^2} + {v^2}\bar \rho - {{\bar c}_{11}}}&{({{\bar c}_{12}} + {{\bar c}_{44}})\bar q}\\
{({{\bar c}_{12}} + {{\bar c}_{44}})\bar q}&{{{\bar c}_{44}} - {{\bar c}_{11}}{{\bar q}^2} - {v^2}\bar \rho }
\end{array}} \right| = 0\]
(20)
展开式(20)后得到关于$\bar {q}$的4次方程,给定相速度$v$,可以得到4个$\bar{q}$的值满足上式方程,每个值都是解的一部分,同样,为了满足半空间中位移的衰减条件,只取实部大于0的两个根,将求得的解代入式(20)中的任何一个,可以得到弹性介质中 波传播时的振幅比为
\[{B_{2i}} = {\lambda _i}{B_{1i}}\]
(21)
式(21)代入到式(18)中得到弹性半空间中的位移和电势为
\[\left. {\begin{array}{*{20}{l}}
{{{\bar u}_2}({x_2},{x_3},t) = \sum\limits_{i = 1}^2 {{B_{1i}}{{\rm{e}}^{{{\bar q}_i}k{x_3}}}\cos [k({x_2} - vt)]} }\\
{{{\bar u}_3}({x_2},{x_3},t) = \sum\limits_{i = 1}^2 {{B_{2i}}{{\rm{e}}^{{{\bar q}_i}k{x_3}}}\sin [k({x_2} - vt)]} }\\
{\bar \varphi ({x_2},{x_3},t) = {B_3}{{\rm{e}}^{\bar q'k{x_3}}}\sin [k({x_2} - vt)]}
\end{array}} \right\}\]
(22)
将式(22)代入式(5)得到弹性基底中的应力和电位移如下
\[\left. {\begin{array}{*{20}{l}}
{{{\bar \sigma }_{33}} = \sum\limits_{i = 1}^2 {({{\bar c}_{11}}{{\bar q}_i}k{B_{2i}} - {B_{1i}}{{\bar c}_{12}}k)} {{\rm{e}}^{{{\bar q}_i}k{x_3}}} \cdot }\\
{\qquad \sin [k({x_2} - vt)]}\\
{{{\bar \sigma }_{32}} = \sum\limits_{i = 1}^2 {({{\bar c}_{44}}{{\bar q}_i}k{B_{1i}} + {{\bar c}_{44}}k{B_{2i}})} {{\rm{e}}^{{{\bar q}_i}k{x_3}}} \cdot }\\
{\qquad \cos [k({x_2} - vt)])}\\
{{{\bar D}_2} = - {{\bar \kappa }_{11}}k{B_3}{{\rm{e}}^{\bar q'k{x_3}}}\cos [k({x_2} - vt)]}\\
{{{\bar D}_3} = - {{\bar \kappa }_{11}}\bar qk{B_3}{{\rm{e}}^{\bar q'k{x_3}}}\sin [k({x_2} - vt)]}
\end{array}} \right\}\]
(23)
将上面推导的解代入到式(10),应用电学边界条件,可得到开路或短路情况下关于待定系数$A_{3i}$,$B_{11}$,$B_{12}$和$B_{3}$的齐次线性方程组,其矩阵形式为
\[{S_{9 \times 9}}X = {\bf{0}}\]
(24)
附录中给出了矩阵${ S}_{9\times9}$和向量${ X}$中各个元素的具体数值. 方程组(24)有非零解的充分必要条件是其系数矩阵的行列式值为0,从而得到频散方程
\[\det S = 0\]
(25)
方程(25)是关于波速$v$和波数$k$的超越方程,也称为频散方程或频散关系. 本文主要研究瑞利型表面波,其主要特点是[17]:当频率较高时,能量主要集中在结构的覆层内,主要沿层的方向传播,当频率较低时,主要沿基底表面传播.
压电材料中机械能和电能相互耦合的程度用机电耦合系数($K^{2})$来衡量,$K^{2}$的大小用来确定声表面波器件的带宽,压电材料中的机电耦合系数越大,其表面波器件的功耗越低,带宽越大,但是对于由压电材料制作谐振器时,较小的机电耦合系数才能获得较大的频率稳定性,因此,机电耦合系数可以作为压电材料和器件的综合性能指标,有效机电耦合系数可以近似表示为[18]
\[{K^2} = \frac{{2({v_{{\rm{open}}}} - {v_{{\rm{short}}}})}}{{{v_{{\rm{open}}}}}}\]
(26)
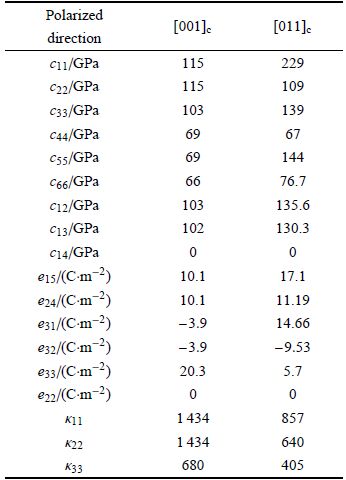
作为数值算例,利用上节得到的频散方程(25),本节分析PMN-PT压电层不同极化方向对频散性能、机电耦合系数以及结构中弹性位移和电势分布规律的影响,数值算例中弹性基底采用金刚石,材料参数见表2. 压电层采用PMN-PT单晶,密度为8.09 g/cm$^3$,PMN-PT不同极化方向时材料参数见表1.
弹性常数$\bar {c}_{ij} $单位为GPa,$\kappa _0 = 8.854 \times 10^{-12}$ C$^{2}$/(Nm$^2$) 为真空中的介电常数,密度$\bar {\rho }$的单位为kg/m.
图2给出了PMN-PT层/金刚石基底组成的复合结构短路条件下PMN-PT压电晶体分别沿[011]$_{\rm c}$方向和[001]$_{ \rm c}$方向 极化时前八阶模态的频散曲线,图中横坐标$K$为无量纲的波数,且$K = kh/(2\pi )$,纵坐标为相速度$v$.
图2给出的结果显示,第1阶模态(基本模态)的相速度均起始于金刚石半空间的瑞利波波速(10 937 m/s),随着无量纲波数$K$的增加,第1阶模态(基本模态)的相速度趋于PMN-PT压电层短路电学边界条件下沿相应极化方向时的瑞利波波速,即图2(a)中基本模态相速度趋于PMN-PT压电晶体沿[011]$_{ \rm c}$方向极化时的瑞利波波速(1 512.72 m/s),图2(b)中基本模态相速度趋于PMN-PT压电晶体沿[001]$_{\rm c}$方向极化时的 瑞利波波速(1 488.13 m/s),因此,第1阶模态(基本模态)是传统意义上的瑞利波,2阶及以上的高阶模态的相速度起始于金刚石基底的剪切体波波速(12 552 m/s),并且具有截止性质. 需要特别说明的是,当PMN-PT压电晶体沿[011]$_{ \rm c}$方向极化时,图2(a)中第3阶模态和第4阶模态发生了两次转化,在波数$K =0.6$附近第一次转化,在波数$K=1.3$附近第二次转化,说明能量在该频率附近发生了转化;当PMN-PT压电晶体沿[001]$_{ \rm c}$方向极化时,图2(b)中第3阶模态和第4阶模态在$K=0.6$附近虽然很接近,但是模态之间并没有发生转化,说明能量在该频率附近发生了集中.

|
图2 电学短路条件下PMN-PT层/金刚石基底结构中的前八阶模态的频散曲线 Fig.2 Dispersion curves of the first eight modes for PMN-PT layer/diamond half space under electrically shorted condition |
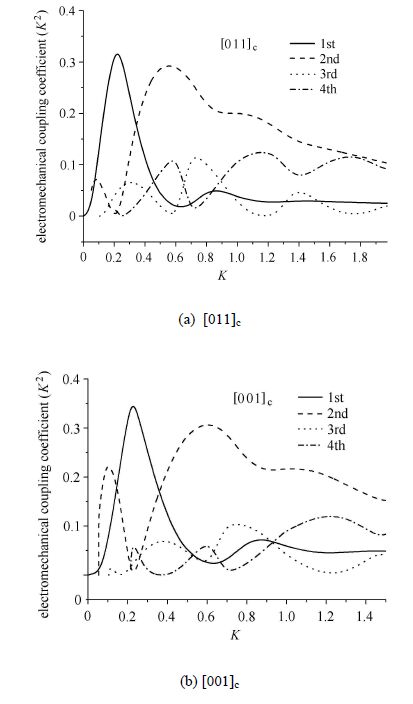
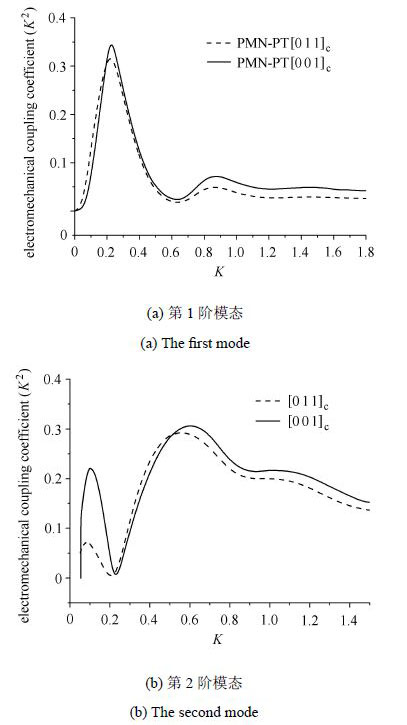
图3给出了当PMN-PT压电晶体沿[011]$_{ \rm c}$和[001]$_{ \rm c}$方向极化时,结构中前四阶模态的机电耦合系数随波数$K$的变化曲线,可以看出前两阶(瑞利波和西萨瓦波)的机电耦合系数明显大于其他阶的机电耦合系数.由图4可以看出,压电晶体PMN-PT的极化方向对机电耦合系数有一定的影响,PMN-PT压电层沿[001]$_{ \rm c}$方向极化时第1阶模态的机电耦合 系数第一个峰值略大于沿[011]$_{ \rm c}$方向极化时的第一个峰值,沿[001]$_{\rm c}$方向极化时第2阶模态的机电耦合系数的第一个峰值比沿[011]$_{ \rm c}$方向极化时的第一个峰值大很多,说明PMN-PT晶体沿[001]$_{ \rm c}$方向极化时压电性能比沿[011]$_{ \rm c}$方向极化时的压电性能好.
接下来分析PMN-PT压电覆层不同的极化方向对弹性位移和电势模态分布的影响. 其中横坐标为$kx_{3}$,代表结构深度方向位置的变化,在$kx_{3}=kh$时代表压电覆层自由表面的位置,$kx_{3}=0$代表压电覆层与半空间的交界面.
|
图3 PMN-PT层/金刚石基底结构中前四阶模态的机电耦合系数随无量纲波数变化曲线 Fig.3 Electromechanical coupling coefficient versus normalized wave number for the first four modes in a layered structure with PMN-PT on diamond |
|
图4 PMN-PT压电层不同极化方向时结构中前二阶模态的机电耦合系数变化曲线 Fig.4 Electromechanical coupling coefficient versus for the different polarization direction in a layered structure with PMN-PT on diamond |
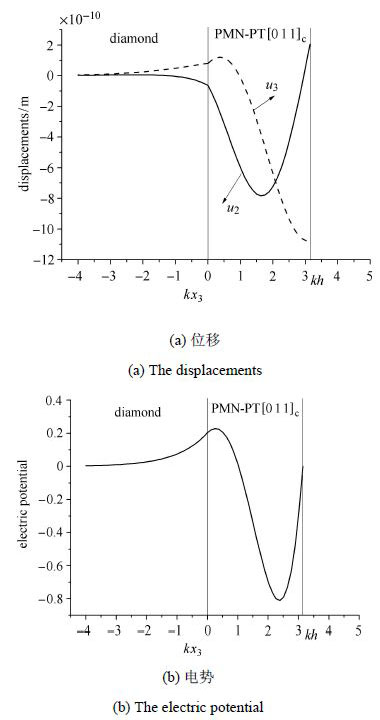
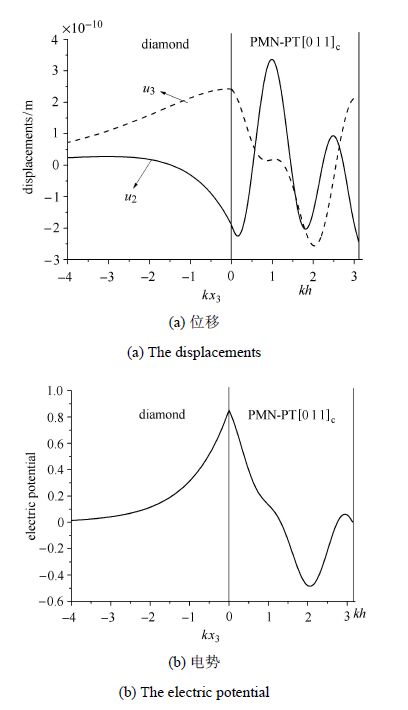
图5和图6绘出了PMN-PT电学短路沿[011]$_{ \rm c}$方向极化时压电层/金刚石结构中$u_{2}$和$u_{3}$以及$\varphi $随深度$kx_{3}$的变化曲线,其中,无量纲波数$K=0.5$. 图5是低阶模态(第1阶)的位移和电势,对应的相速度$v=1 986.1$ m/s,图6是相同波数时对应的高阶模态(第7阶)的位移和电势,相速度$v$的取值为10 656.8 m/s.
可以看到,随着深度的增加,位移和电势的值都是趋于零的,符合弹性波在半空间结构中的衰减性质,但是低阶模态的衰减速度要比高阶模态的衰减迅速.对比图5(b)和图6(b)看出,电势在自由界面$kh$处均为0,符合电学短路边界条件,当相速度取值足够精确,无论是位移还是电势在界面$kx_{3}=0$处都是连续的,满足式(10),也说明前面的数值计算结果是正确的.
|
图5 沿[011]$_{ \rm c}$极化时电学短路条件下PMN-PT层/金刚石基底结构中低阶模态的位移和电势分布 Fig.5 Variations of displacements and electric potential of the lower mode with $kx_{3}$ in the PMN-PT /diamond structure under electrically shorted condition |
|
图6 沿[011]$_{ \rm c}$极化时电学短路条件下PMN-PT压电层金刚石基底结构中高阶模态的位移和电势分布 Fig.6 Variations of displacements and electric potential of the higher mode with $ kx_{3}$ in the PMN-PT /diamond structure under electrically shorted condition |
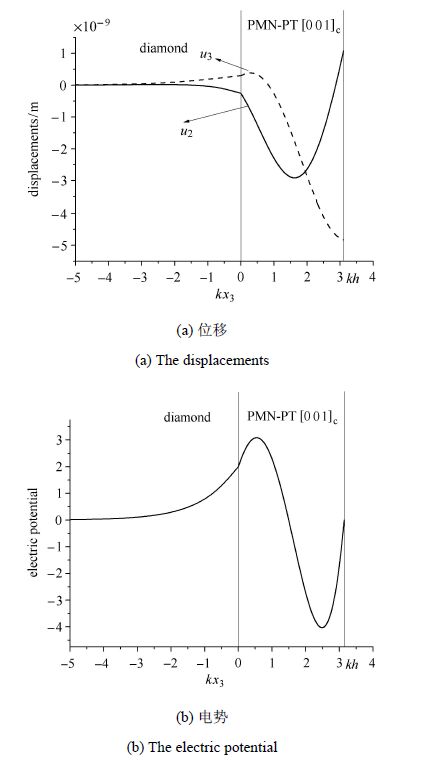
图7和图8绘出了PMN-PT电学短路沿[001]$_{\rm c}$方向极化时PMN-PT层/金刚石半空间结构中$u_{2}$和$u_{3}$以及$\varphi $ 随$kx_{3}$的变化曲线,计算过程中$K=0.5$. 图7是低阶模态(第1阶)的位移和电势,对应的相速度$v =1 930.9$ m/s,图8对应高阶模态(第7阶)的位移和电势,对应的相速度$v=10 657.6 $ m/s.比较图5(a)和图7(a)可以看出,结构中横向位移和纵向位移在PMN-PT压电晶体沿[001]$_{\rm c}$方向极化比沿[011]$_{ \rm c}$方向极化时大一个数量级,说明沿[001]$_{\rm c}$方向极化的波动性能较好,同时注意到弹性位移和电势无论是低阶模态还是高阶模态在基底中都很快衰减到零,大部分的能量集中在PMN-PT压电覆层中.
|
图7 沿[001]$_{\rm c}$极化时电学短路条件下PMN-PT压电层金刚石基底结构中低阶模态的位移和电势分布 Fig.7 Variations of displacements and electric potential of the lower mode with $kx_{3}$ in the PMN-PT /diamond structure under electrically shorted condition |

|
图8 沿[001]$_{\rm c}$极化时电学短路条件下PMN-PT压电层金刚石基底结构中高阶模态的位移和电势分布 Fig.8 Variations of displacements and electric potential of the higher mode with $kx_{3}$ in the PMN-PT /diamond structure under electrically shorted condition |
本文分析了PMN-PT层/弹性半空间结构中表面波的传播特性,得到了弹性波在结构中传播时的频散方程,数值表明了压电材料PMN-PT的极化方向对弹性波在结构中传播时的频散曲线、机电耦合系数以及位移的影响.研究结果为:(1)第1阶模态频散曲线的相速度起始于弹性半空间的瑞利波波速,随着波数的增大趋于PMN-PT的相应电学边界条件和晶体极化方向下的瑞利波波速,高阶模态的相速度起始于弹性半空间的剪切体波波速,并且具有相应的截止频率;(2)压电层PMN-PT沿[001]$_{ \rm c}$方向极化时的机电耦合系数比沿[011]$_{ \rm c}$方向时大,而且沿[001]$_{ \rm c}$方向极化时结构中的横向位移和纵向位移比沿[011]$_{ \rm c}$方向时相应的位移大一个数量级;(3)无论PMN-PT沿哪个方向极化,结构中弹性位移对相速度的数值都非常敏感.
| [1] | 许桂生,罗豪甦,王初评等. 新型压电材料-弛豫铁电单晶的研究. 无机材料学报,1997,12(5) :1 (Xu Guisheng, Luo Haosu, Wang Chuping, et al. Study of new piezoelectric material-Relaxor ferroelectric single crystal. Journal of Inorganic Materials, 1997,12(5):1 (in Chinese)) |
| [2] | 洪琳,赵丽艳,朱兴文等. 铌镁酸铋-钛酸铅压电陶瓷准同型相界附近的性能和相变温度研究. 无机材料学报,2012,27(7):735-740 (Hong Lin, Zhao Liyan, Zhu Xingwen, et al. Properties and Phase-transition temperature of (1-x) Bi(Mg2/3Nb1/3)O3-xPbTiO3 piezoelectric ceramics near the morphotropic phase boundary. Journal of Inorganic Materials, 2012, 27(7):735-740 (in Chinese)) |
| [3] | Service RF. Shape-changing crystals get shiftier. Science, 1997, 275(5308): 1878-1882 |
| [4] | Fu HX, Cohen RE. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature, 2000, 403: 281-283 |
| [5] | Park SE, Shrout TR. Ultrahigh strain and piezoelectric behavior in relaxor based ferroelectric single crystals. Journal of Applied Physics, 1997, 82: 1804-1811 |
| [6] | Wang FF, Zhou D, Luo LH, et al. Radial vibration mode of 0.71Pb (Mg1/3Nb2/3)O3-0.29PbTiO3 single crystal and its applications. Journal of Applied Physics, 2008, 103(5): 0541051-5 |
| [7] | Kook HC, Jin HO, Hyeong JK. Surface acoustic wave propagation properties of the relaxor ferroelectric PMN-PT single crystal. IEEE Ultrasonics Symposium, 2001, 161 |
| [8] | Ren B, Wang FF, Zhao XY, et al. Piezoelectric energy harvesting based on shear mode 0.71Pb (Mg1/3Nb2/3)O3-0.29PbTiO3 single crystals. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(6): 1419-1425 |
| [9] | Chen CW, Zhang R, Cao WW. Theoretical study on guided wave propagation in (1-x)Pb(Mg1/3Nb2/3)O3-x PbTiO3) (x =0.29 and 0.33) single crystal plates. Journal of Physics D: Applied Physics, 2009, 42 (9): 095411-6 |
| [10] | 陈传文, 项阳. 铌镁酸铅钛酸铅薄层中Lamb波的交叉特性. 物理学报,2012,61(10): 1077011-7 (Chen Chuanwen, Xiang Yang. Crossings of lamb modes in lead zinc niobate-lead titanate crystal plates. Acta Physica Sinica,2012,61(10): 1077011-7 (in Chinese)) |
| [11] | Chen CW, Zhang R, Cao WW. Theoretical study on guided wave propagation in (1-x)Pb(Mg1/3Nb2/3)O3-xPbTiO(3) (x =0.29 and 0.33) single crystal plates. Journal of Physics D: Applied Physics, 2009, 42: 095411 |
| [12] | Li XM, Zhang R, Huang NX, et al. Surface acoustic wave propagation properties in 0.67Pb(Mg1/ 3Nb2/3)O3-0.33PbTiO3 single crystal poled along [111] m c. Applied Physics Letters, 2009, 95: 242906 |
| [13] | Li XM, Zhang R, Huang NX, et al. Surface acoustic wave propagation in Y-and Z-cut 0.67PbMgNbO3-0.33PbTiO3 single crystals. Journal of Applied Physics, 2009, 106: 054110 |
| [14] | Zhang W, Li XM, Zhang R, et al. Numerical calculation of SWA propagation properties at the x-cut of ferroelectric PMN-33%PT single crystals. Journal of Physics Letters, 2009, 26: 064301 |
| [15] | Chen J, Wang HL, Hashimoto KY, et al. Theoretical analysis of ultrahigh electromechanical coupling surface acoustic wave propagation in Pb (In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 crystals. Journal of Applied Physics, 2011, 109 (5): 054104-3 |
| [16] | Glushkov E,Glushkova N, Zhang CZ. Surface and pseudo-surface acoustic waves piezoelectrically excited in diamond-based structures. Journal of Applied Physics, 2012, 064911-10 |
| [17] | Lardat C, Maerfeld C, Tournois P. Theory and performance of acoustical dispersive surface wave delay lines. Proceedings of the IEEE, 1971, 59: 355 |
| [18] | Liu JS, He ST. Propagaties of Love waves in layered piezoelectric structures. International Journal of Solids and Structures, 2010, 47: 169-174 |
| [19] | Benetti M, Cannatá D, Di Pietrantonio F, et al. Gigahertz-range electro-acoustic devices based on pseudo-surface-acoustic waves in AlN/diamond/Si structures. Applied Physics Letters, 2005, 87(3): 033504 |
2. Shijiazhuang Tiedao University, Department of Engineering Mechanics, Shijiazhuang 050043, China
 2015, Vol. 47
2015, Vol. 47