引 言
为了能够统一地处理岩土工程中的连续和非连续变形问题,石根华博士于1991年提出了数值流形方法[1].自1995年至今已召开 了11届关于数值流形法的国际会议.数值流形法在处理二维问题的连续和非连续变形分析方面已经取得了很多成功的应用,并已经发展了初步的三维数值流形法[2, 3, 4]. 近年来国内外学者更是将其改进和推广应用到裂纹扩展模拟中.文献[5, 6]基于线弹性断裂力学理论,首次将数值流形法应用到裂纹扩展问题中,不仅可以模拟单裂纹的受拉破坏,而且通过引入改进的拉格朗日乘子法处理材料界面的接触摩擦,也可模拟受压状态下的单裂纹扩展问题.文献[7]利用数值流形法和裂纹张开位移法成功地预测了非混合型的裂纹扩展.文献[8]结合数值流形法和虚裂纹扩展技术研究了混合型裂纹的扩展.文献[9]在传统数值流形法的位移函数中增加了用于捕捉裂纹尖端应力奇异性的附加函数,提出了考虑裂纹尖端场的数值流形法.它提高了传统数值流形法求解不连续的能力,尤其是不连续裂纹尖端解的精度,进而可更为准确地模拟岩体结构由连续到非连续的演化过程.文献[10]将扩展有限元中广为使用的基于面积积分的交互积分方法引入到数值流形法中研究了混合型裂纹扩展问题,证实交互积分法可以精确地预测裂纹尖端的应力强度因子.文献[11]建立了基于正六边形数学网格的数值流形法,同样在裂纹尖端附近扩展了位移函数,并对诸如分支裂纹、星型裂纹等复杂的裂纹问题进行了分析,以应力强度因子作为衡量标准,与参考解对比发现计算结果达到了很高的精度.文献[12]基于数值流形法,提出将裂纹尖端威廉姆斯解析解与其周边高阶多项式级数的数值解联合应用以求解应力强度因子的新方法.文献[13, 14, 15]发展了扩展的无网格流形法,并应用于二维裂纹模拟中,结果表明这种方法有着更高的精度.对于某一研究区域,由多个影响域来参与求解,若该区域被单条裂纹切割,则可以简单地通过将节点处的数学片一分为二来模拟不连续性;但对于复杂形状的多裂纹扩展问题,每个影响域被多条裂纹切割,情况极其复杂,尤其是在裂纹扩展过程中,因此亟需开发出严格通用的拓扑搜索技术来更新物理覆盖.它继承了无网格法可任意选择数学片的形状这一优势,但仍需考虑裂纹切割的拓扑问题.另外,此方法中无流形单元的概念,在进行类似于数值流形法中开-闭迭代式的接触模拟时,需要采取其他辅助措施,如在边界上布点等.文献[16]将流形法有限覆盖技术与无网格插值方式结合所提出的有限覆盖点插值方法应用于模拟简单的裂纹扩展问题中.文献[17, 18, 19]将数值流形法与边界元结合到一起用于模拟裂纹扩展问题,并达到了很好的效果.文献[20, 21, 22, 23]对摩擦型裂纹扩展,岩体含填充物时裂纹扩展行为,沉积岩动态破坏,弹塑性破坏分析等进行了深入的研究.文献[24]进一步发展了动载下裂纹应力强度因子求解的数值流形法.
在上述基于数值流形法的裂纹扩展研究中,很多情况下,扩展过程中裂纹尖端被强制地停留在单元边上,对网格表现了极大的依赖性.显然,当网格比较粗糙时,这将会引起很大的误差.
针对这些不足之处进行改进,当裂纹发生扩展后,将裂纹尖端所停留的流形单元细分,且保证细分后形成的新流形单元与细分前的流形单元所对应的插值点保持一致,这样就可以捕捉到位于流形单元内部的那段裂纹,使得裂纹尖端不必强制落在单元边上,克服了网格依赖性. 前述基于数值流形法的多裂纹扩展,并不成熟,比如每个时步内令几条裂纹同时扩展[25].因此,文中提出了一种直观的多裂纹扩展算法,在此基础上,实现了基于数值流形法的多裂纹扩展模拟.
1 数值流形法理论基础
数值流形法是一种基于"覆盖"和接触环路(contact loop)的数值方法. 它的覆盖包括数学覆盖(mathematicalcover,MC)和物理 覆盖(physical cover,PC). 其中,数学覆盖可视为一系列数学片(mathematicalpatch,MP)的并集,数学覆盖必须覆盖整个物理区域. 同样地,物理覆盖为物理区域内所有物理片(physicalpatch,PP)的并集. 物理片是物理区域各种元素(如边界,材料分界面或不连续面等)与数学片切割后形成的域.尽可能多的物理片的交集定义为流形单元. 接触环路主要用于表征接触面间的接触状态,以便于模拟不连续面间的接触行为.
1.1 物理覆盖与接触环路
为了便于理解,下面基于三角形网格对数值流形法的离散过程进行简要地介绍.
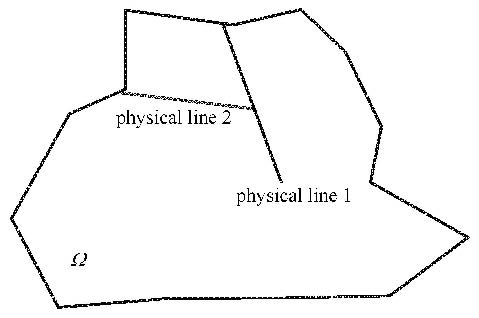
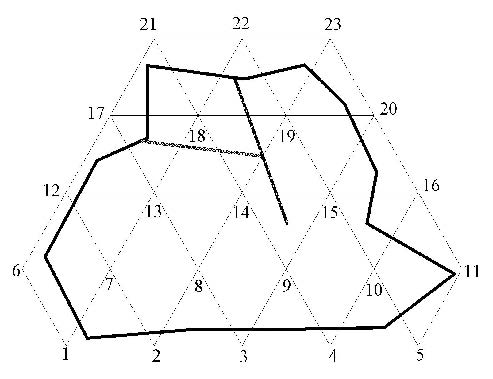
如图1所示,为一任意形状的物理区域$\Omega $,其内部的两条粗线定义为物理线. 在数值流形法中,物理线表示不连续面,如节理或裂纹等.
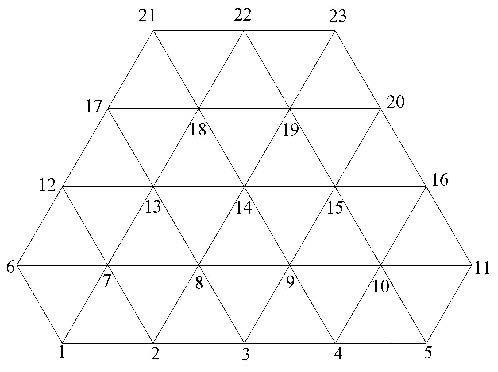
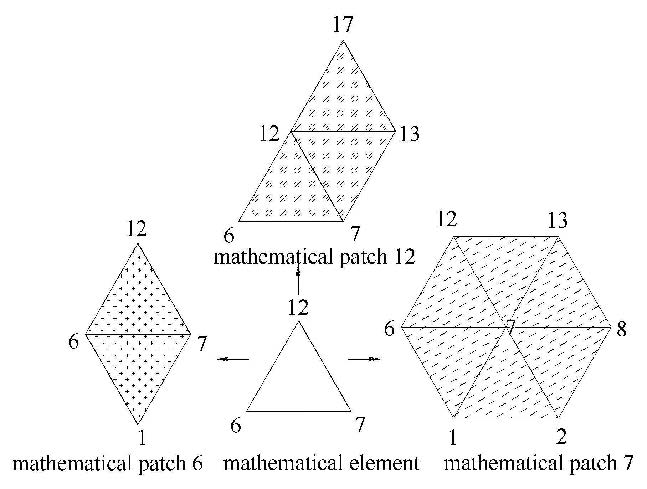
如图2,选用基于等边三角形网格的区域覆盖$\Omega$. 网格节点上的数字表示节点编号. 几个共用同一节点的三角形的并集定义为1个数学片. 如图3,正六边形1-2-8-13-12-6-1就表示数学片7,菱形1-7-12-6-1表示数学片6,梯形6-7-13-17-12-6表示数学片12. 这3个数学片的交集为三角形6-7-12-6,表示1个数学单元. 所有数学片的并集就是数学覆盖,图2所示区域实际上就是1个数学覆盖.
如图4所示,将物理区域$\Omega$的边界和2条物理线分别与图2中的各个数学片切割,会产生一系列的物理片. 物理片之间相互求交就形成流形单元.
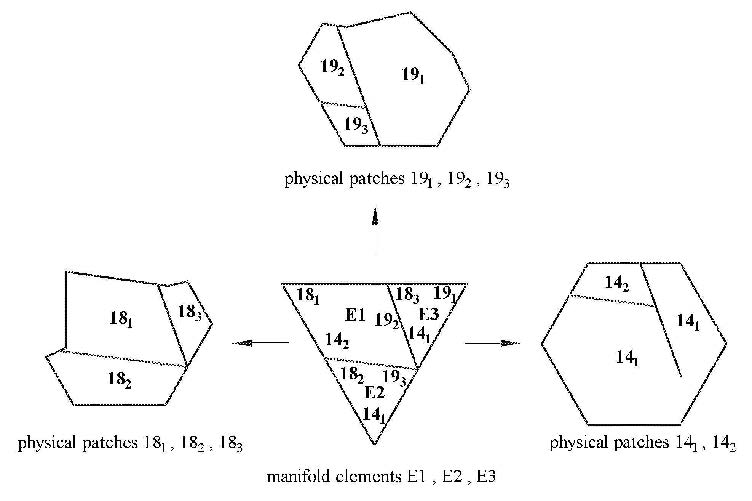
如图5所示,数学片19与物理区域边界和物理线切割后形成3个物理片19$_{1}$,19$_{2}$和 19$_{3}$. 同样地,数学片14切割为2个物理片14$_{1}$ 和14$_{2}$. 在物理片14$_{1}$中含有1个裂纹尖端,定义这种物理片为奇异物理片,而其他为非奇异物理片. 数学单元14-19-18-14被切割成3个流形单元,记为E1,E2和E3. 显然,流形单元E1是3个非奇异物理片18$_{1}$,14$_{2}$和19$_{2}$的交集. 同样地,E3为2个非奇异物理片18$_{3}$,19$_{1}$和1个奇异物理片14$_{1}$的交集. 所有物理片的并集为物理覆盖,它刚好覆盖整个物理区域$\Omega$.
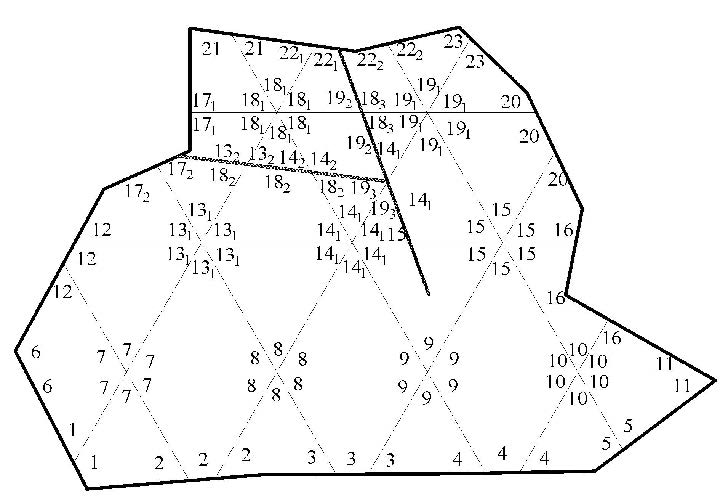
通过上述过程,即可形成如图6所示的流形单元和物理覆盖.
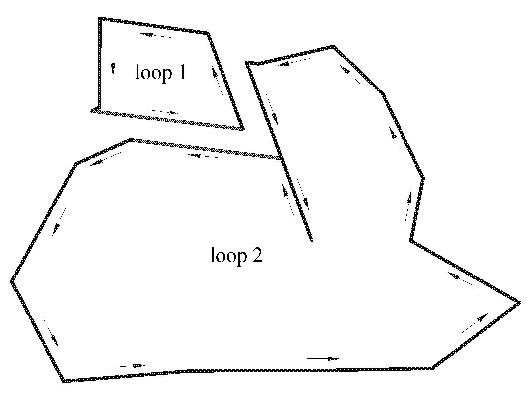
如图7所示,有2个接触环路,它们以位于其边界上的流形单元顶点编号沿逆时针方向排列来表示. 对于单连通体来说,箭头沿着逆时针方向前进时左手边构成的区域就是一个块体. 一般来说,接触环路主要用来表示块体间的接触状态. 裂纹扩展后接触环路的更新也是必不可少的.
1.2 单位分解函数
图6中的任一流形单元可记为$\Omega ^e$,覆盖它的3个物理片记为$\Omega^p_k$ ($k=1$,2,3). 它们分别来源于3个数学片,记为$\Omega _i^m $ ($i=1$,2,3). 对应的权函数为$w_i({ r})$ ($i = 1$,2,3),${ r}$表示位置矢量,满足
|
\[{w_i}(r) = 0(r \notin \Omega _i^m)\]
|
(1) |
|
\[0 \le {w_i}(r) \le 1(r \in \Omega _i^m)\]
|
(2) |
|
\[\sum\limits_{i = 1}^3 {{w_i}} (r) = 1(r \in {\Omega ^e})\]
|
(3) |
$\{ w_i ({ r}) \} $ 称之为对应于$\{ \Omega^m_i \}$的单位分解函数.
1.3 流形元空间
在每个物理片$\Omega^p_k$上定义一个函数空间,记为$V^p_k$. 将$V_k^p $与单位分解函数$ \{ w_k ( { r})\}$揉和到一起即可定义$\Omega^e$上的流形元空间$V(\Omega)$,表示为
|
\[V\left( {{\Omega ^e}} \right) = \sum {{w_k}} V_k^p \equiv \left\{ {v|v = \sum\limits_{k = 1}^3 {{v_k}} {w_k},{v_k} \in V_k^p} \right\}\]
|
(4) |
这里所构造的实际上是拉格朗日形式的流形元空间,适用于二阶问题的求解. 文献[26]建议了数值流形法的埃尔米特形式,并成功地将数值流形法应用于四阶问题的求解.
针对图5中存在的2种不同类型的物理片,包括非奇异物理片(如19$_{1}$)和奇异物理片(如14$_{1}$),将构造不同的局部函数空间.
1.3.1 非奇异物理片上的局部函数空间
在非奇异物理片上,一般选择多项式作为局部函数空间$V_k^p$. 如果是一阶多项式,定义其上的位移函数$u_k (x,y)$和$v_k(x,y)$采用如下形式
|
\[\left. \begin{array}{l}
{u_k} = a_k^0 + a_k^xx + a_k^yy\\
{v_k} = b_k^0 + b_k^xx + b_k^yy
\end{array} \right\}\]
|
(5) |
但这可能会引起总体刚度矩阵的亏秩和病态.
为了减少亏秩数,并改善刚度矩阵数值特性,$u_k(x,y)$和$v_k(x,y)$采用如下形式
|
\[{w_k} = T_k^0{d_k}\]
|
(6) |
首先,用${ w}^{\rm T}_k=(u_k,v_k)$来表示物理片上的局部位移函数. 基函数${ T}_k^0 $定义为
|
\[T_k^0 = \left| {\begin{array}{*{20}{c}}
1&0&{\frac{{x - {x_k}}}{{{l_k}}}}&0&{\frac{{y - {y_k}}}{{2{l_k}}}}&{\frac{{y - {y_k}}}{{2{l_k}}}}\\
0&1&0&{\frac{{y - {y_k}}}{{{l_k}}}}&{\frac{{x - {x_k}}}{{2{l_k}}}}&{\frac{{{x_k} - x}}{{2{l_k}}}}
\end{array}} \right|{\rm{ }}\]
|
(7) |
其中,$x_k $和$y_k $表示物理片所对应的插值点坐标;$l_k $表示数学片对应外接圆的最大直径. 自由度矢量${ d}_k $表示为
|
\[d_k^{\rm{T}} = ({\bar u^k}{\bar v^k}\bar \varepsilon _x^k\bar \varepsilon _y^k\bar \gamma _{xy}^k{\bar \omega ^k})\]
|
(8) |
这6个分量与位移同单位. $\bar u^k$和$\bar v^k$为$\Omega^p_k$平动位移分量;${ d}_k $的3到5个分量
|
\[\bar \varepsilon _x^k = {l_k}\varepsilon _x^k,\bar \varepsilon _y^k = {l_k}\varepsilon _y^k, \bar \gamma _{xy}^k = {l_k}\gamma _{xy}^k\]
|
(9) |
表示$\Omega _k^p $的变形引起的位移分量,其中,$\varepsilon^k_x,\varepsilon^k_y$和$\gamma^k_{xy}$为点$(x_k,y_k)$ 处的应变分量,即
|
\[\left. \begin{array}{l}
\varepsilon _x^k = \frac{{\partial {u_k}({x_k},{y_k})}}{{\partial x}}\\
\varepsilon _y^k = \frac{{\partial {v_k}({x_k},{y_k})}}{{\partial y}}\\
\gamma _{xy}^k = \frac{{\partial {u_k}({x_k},{y_k})}}{{\partial y}} + \frac{{\partial {v_k}({x_k},{y_k})}}{{\partial x}}
\end{array} \right\}\]
|
(10) |
${ d}_k$ 的第6个分量
|
\[{\bar \omega ^k} = {l_k}{\omega ^k}\]
|
(11) |
表示$\Omega _k^p $的刚体转动引起的位移分量,其中,$\omega ^k$为刚体转角,即
|
\[{\omega ^k} = \frac{{\partial {u_k}({x_k},{y_k})}}{{\partial y}} - \frac{{\partial {v_k}({x_k},{y_k})}}{{\partial x}}\]
|
(12) |
1.3.2 奇异物理片上的局部函数空间
为简单起见,仅考虑在奇异物理片$\Omega^p_k$中含1个裂纹尖端,如图5所示. 这种情况下,除了式(5)中的多项式形式,函数空间 $V^p_k$ 应该包含另外一个增强的局部位移函数来反应裂纹尖端附近位移的奇异性,即
|
\[{w_k} = T_k^0{d_k} + T_k^1{e_k}\]
|
(13) |
其中,${ e}_k $表示扩充的自由度,定义为
|
\[e_k^{\rm{T}} = \left( {e_1^k,e_2^k, \cdots ,e_8^k} \right)\]
|
(14) |
式(13)中的${ T}_k^1 $定义为
|
\[T_k^1 = \left[ {\begin{array}{*{20}{c}}
{{\Phi _1}}&0&{{\Phi _2}}&0&{{\Phi _3}}&0&{{\Phi _4}}&0\\
0&{{\Phi _1}}&0&{{\Phi _2}}&0&{{\Phi _3}}&0&{{\Phi _4}}
\end{array}} \right]{\rm{ }}\]
|
(15) |
其中
|
\[\begin{array}{l}
({\Phi _1}{\Phi _2}{\Phi _3}{\Phi _4}) = \\
(\sqrt r \cos \frac{\theta }{2}\sqrt r \sin \frac{\theta }{2}\sqrt r \cos \frac{{3\theta }}{2} \sqrt r \sin \frac{{3\theta }}{2})
\end{array}\]
|
(16) |
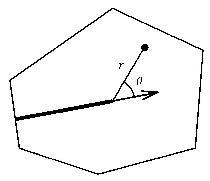
为裂纹尖端附近威廉姆斯位移级数的前两项[27],它与扩展有限元中广泛采用的形式虽无本质区别,但更为简洁.$\left( {r,\theta } \right)$为图8所示极坐标系.
2 多裂纹扩展控制算法
文献[28]已经实现了基于数值流形法的单裂纹扩展模拟.同样地,本文依然在线弹性断裂力学的理论范畴内,提出了一种直观的多裂纹扩展算法,尝试实现基于数值流形法的多裂纹扩展模拟.其中,裂纹尖端应力强度因子计算采用交互积分方法[29],并以最大周向应力准则[30]来判断裂纹的扩展方向.
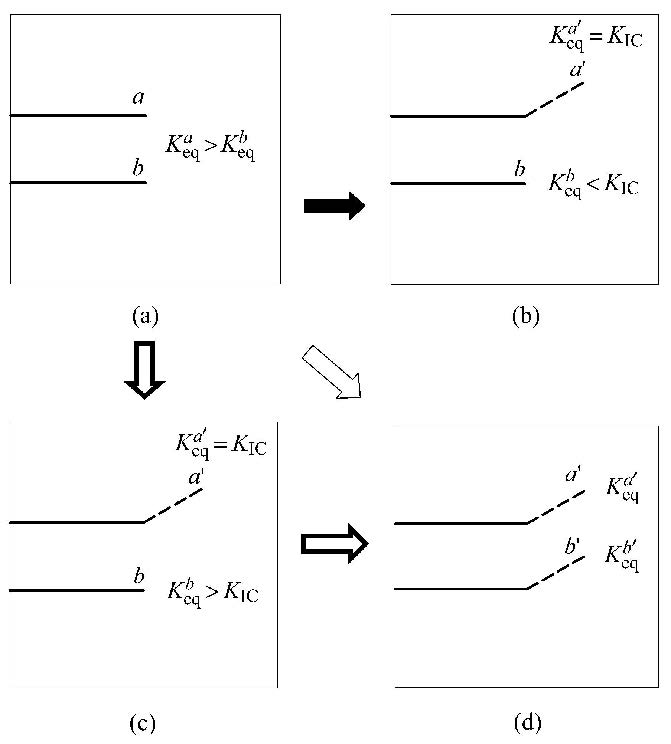
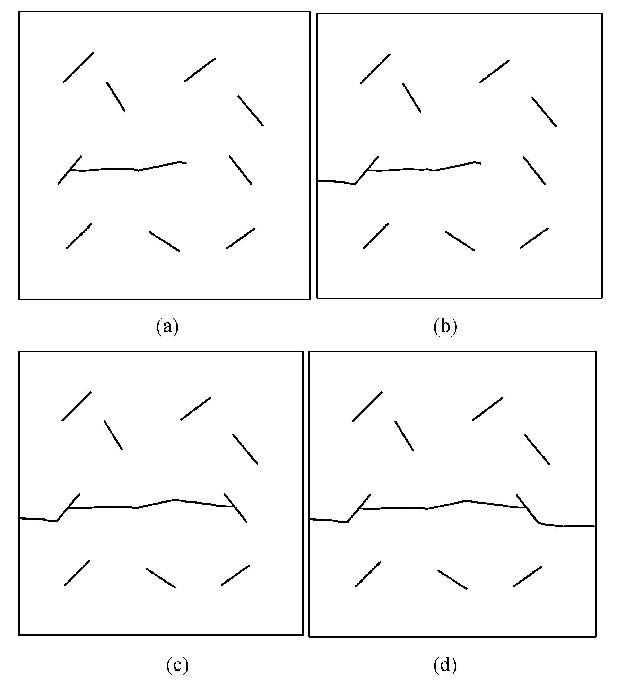
(1)如图9(a)所示,在一个正方形平板中含有两条单边裂纹,在顶部和底部受拉伸载荷$F$的作用,裂纹尖端分别记为$a$和$b$.经数 值计算后,若裂纹尖端$a$和$b$的等效应力强度因子与材料体断裂韧度有如下关系: $K^a_{\rm eq}> K^b_{\rm eq}$且$ K^a_{\rm eq}>K_{\rm IC}$,那么认为裂纹尖端$a$处达到破坏强度,并扩展长度$l_a $.
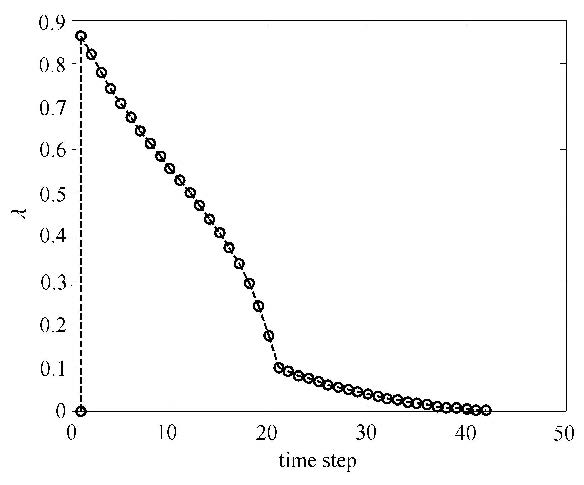
(2) 如图9(b)所示,$a$尖端扩展后,重新试算扩展后的尖端 $a'$和原来$b$尖端的等效应力强度因子,然后通过公式: $\lambda=K_{\rm IC}/K^{a'}_{\rm eq}$,调整载荷大小为$\lambda F$,使得$a'$尖端的等效应力强度因子等于材料的断裂韧度,即 $K^{a'}_{\rm eq}=K_{\rm IC}$.此时调整载荷乘子后$b$尖端的等效应力强度因子与材料的断裂韧度有如下关系:$K^b_{\rm eq}<K_{\rm IC}$,说明$a$尖端在扩展的过程中,$b$尖端始终未达到材料的破坏强度,并不会发生扩展,那么在这一步的扩展过程中,两个裂纹尖端的等效应力强度始终小于或等于材料的断裂韧度,并满足了力学上的平衡,因此认为这步扩展是正确的.
(3) 如图9(c),$a$尖端扩展后,若试算后的等效应力强度因子有如下关系: $K^b_{\rm eq}>K_{\rm IC}$. 很明显,在$a$扩展的过程中,$b$尖端也发生了破坏. 说明这步仅$a$尖端扩展存在问题.
(4) 对图9(c)存在的问题进行修正,认为这个时步内裂纹尖端$a$和$b$同时扩展,也即图9(a) $\to $图9(d).扩展后试算新裂纹尖端$a'$和$b'$ 的等效应力强度因子,并调整载荷乘子,$\lambda=K_{\rm IC}/\max (K^{a'}_{\rm eq},K^{b'}_{\rm eq})$,那么,这个时步内也始终满足力学平衡.
3 多裂纹扩展数值试验
加载边的位移$\bar u$定义为在外载荷${ t}$的作用下加载边上所有节点产生位移的平均值. $\bar u$和${t}$用来 描述材料体的整体响应. 在下面所有算例中,名义应力和名义应变均定义为
|
\[{\varepsilon ^{{\rm{nom}}}} = \frac{{\bar u}}{H}\]
|
(17) |
|
\[{\sigma ^{{\rm{nom}}}} = \left\| t \right\|\]
|
(18) |
其中,$H$表示材料体的高度.
3.1 裂纹交汇
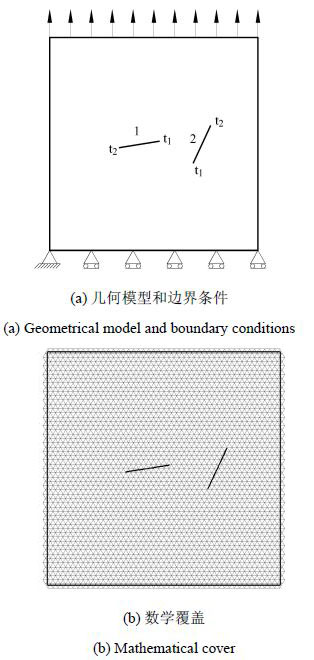
如图10(a)所示,宽度为5.08 cm的正方形平板,含有2条裂纹. 1#裂纹的中点坐标为($-0.355 6,0$),长度为0.977 1 cm,与水平方向的夹角为9°;2#裂纹的中点坐标为(1.168 4,0),长度为0.979 9 cm,与水平方向的夹角为64.8°. 数学覆盖如图10(b). 此算例主要用来测试裂纹的交汇问题. 板的顶部受到均布拉力的作用$\sigma =6.895$ MPa,底部左端点两个方向约束,底部的其他固定点仅约束竖直方向. 弹性模量为689.5 MPa,泊松比0.3,断裂韧度$K_{\rm IC} =8.79$ MPa$\cdot$cm$^{1/2}$.图11所示为文献[31]模拟的裂纹扩展路径.
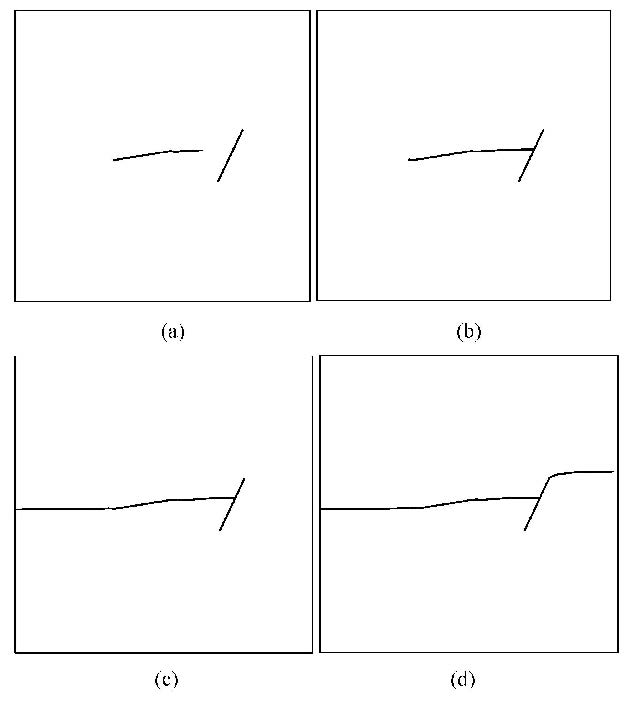
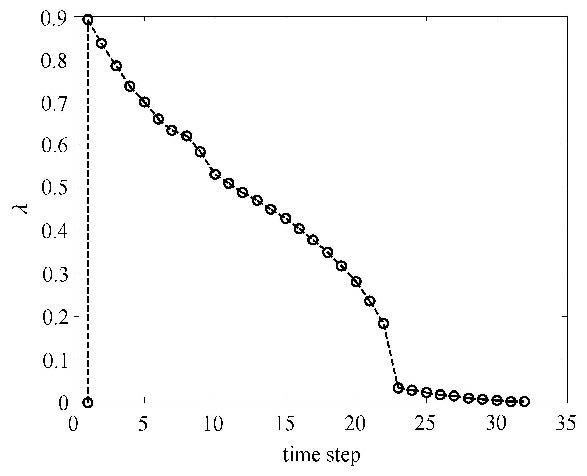
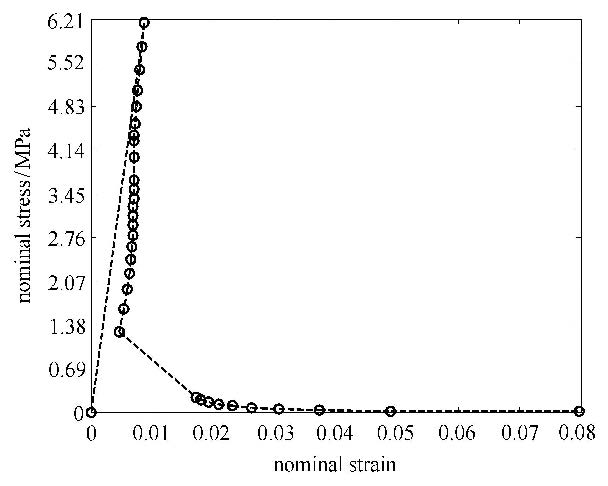
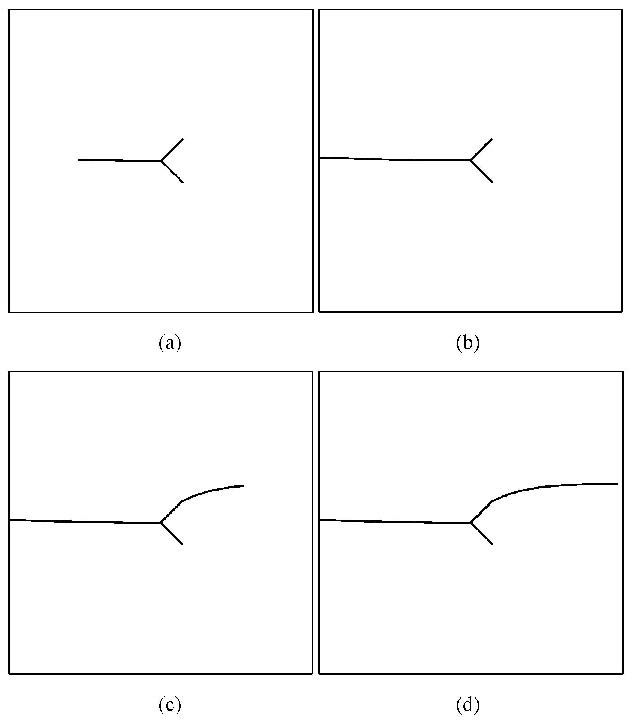
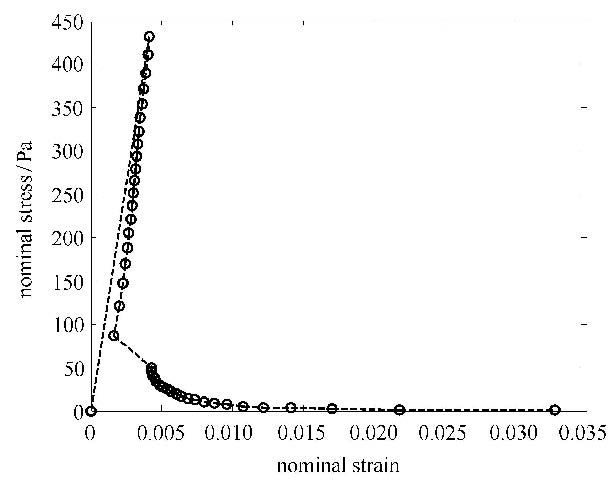
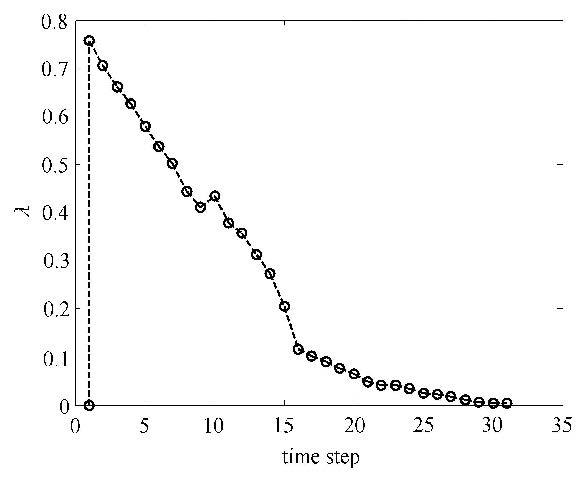
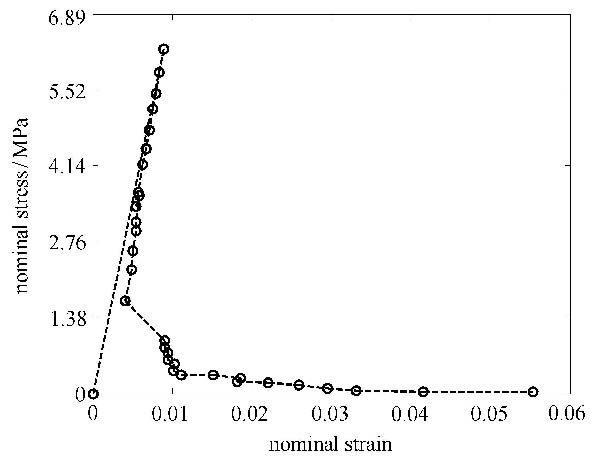
本文模拟的裂纹扩展过程如图12(a)$\sim $12(d)所示. 图12(a)1#裂纹t$_{1}$尖端首先发生扩展,并扩展一定长度;图12(b)1#裂纹t$_{1}$尖端与2#裂纹发生交割,此时一方面要保证不同裂纹尖端附近需要增加扩充位移函数的物理片之间相互不影响,另一方面在应用交互积分时不同裂纹尖端的面积积分路径也应互不影响,如此才能确保应力强度因子计算的正确性;这与载荷曲线图13中的第9时步相对应. 图12(c)1#裂纹t$_{2}$尖端向板左侧边界扩展,直到与板左侧边界交汇;与载荷曲线中的第22时步相对应.裂纹与左侧边界交割后,整体结构发生了较大的变化,所以载荷曲线自此也发生了转折,斜率变小,只需很小的载荷就可使结构继续破坏直至完全断开. 图12(d) 2#裂纹t$_{2}$尖端发生扩展,直到与板右侧边界交汇.名义应力-名义应变曲线如图14所示.
3.2 三条分叉裂纹
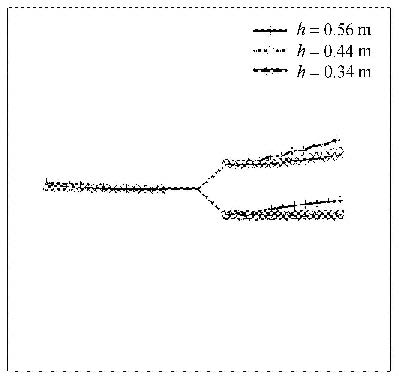
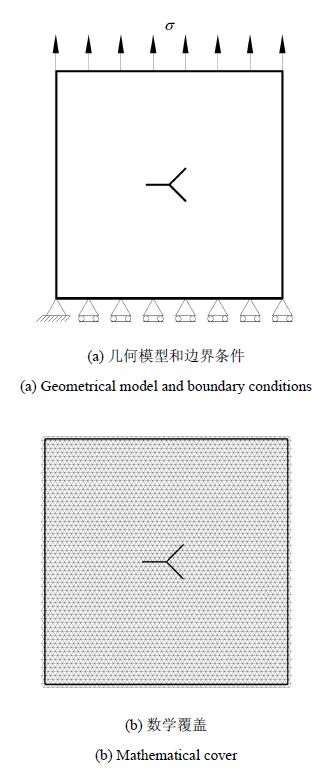
如图15(a)所示,宽度为10 m的正方形平板中,含有一个三分叉裂纹. 3条裂纹尺寸均为1.0 m,右边两条裂纹与水平方向夹角为$ \pm {\rm{ }}\pi /4$. 顶部受均布拉伸载荷作用,底部左端点固定,其他部分简支.弹性模量为0.1 MPa,泊松比为0.3,$\sigma =500$ Pa. 数学覆盖如图15(b).图16为文献[25]假定裂纹同时扩展时的模拟结果.其中,$h$表示每步扩展长度,当$h$取0.44 m或0.34 m时为最终收敛时的扩展路径.
如图17(a)$\sim $17(d)所示,为本文模拟的裂纹扩展路径. 图17(a) 左侧尖端首先发生扩展,并一直作为主导扩展裂纹.图17(b)左侧尖端扩展到板的左侧边界后,与边界交割,该尖端不再存在;这与载荷曲线图18中的第20时步相对应,此后观察到曲线斜率发生明显地转折,只需更小的载荷即可使得材料体继续破坏直至分离. 图17(c)右上尖端开始作为主导裂纹一直扩展. 图17(d) 右上尖端一直扩展到右侧边界.名义应力-名义应变曲线如图19.
3.3 含随机裂纹平板
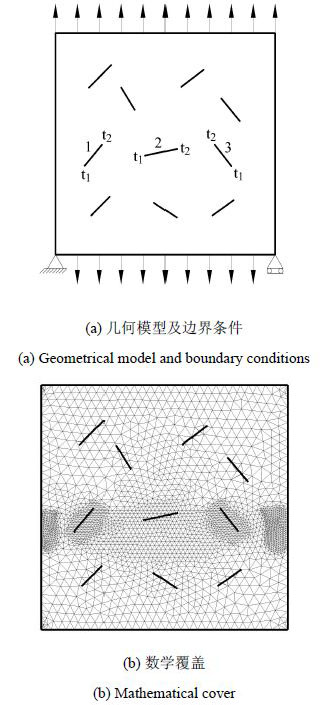
如图20(a)所示,长度为5.08 cm的正方形平板,包含10条随机裂纹. 板的顶部与底部受均布拉伸载荷的作用,左下角完全固定,右下角仅约束竖直方向位移. 弹性模量$E =689.5$ MPa,泊松比 $\upsilon =0.3$.加载大小为8.27 MPa,断裂韧度$K_{\rm IC} =8.79$ MPa$\cdot$cm$^{1/2}$. 数学覆盖如图20(b).此算例最初由文献[31]利用扩展有限元进行了多裂纹扩展模拟,结果如图21;然后文献[32]在裂纹尖端重新划分网格再次进行模拟,结果如图22.
如图23所示,为本文模拟的裂纹扩展路径. 其中,共发生4次裂纹之间或裂纹与边界间的交割. 图23(a)第2条裂纹的第1个裂纹尖端$t_{1}$与第1条裂纹发生了交割,与载荷曲线图24中的第1$\sim$10时步相对应,可见随着裂纹扩展,结构越来越容易破坏;图23(b)第1条裂纹的第1个裂纹尖端$t_{1}$与平板的左边界发生了交割,与载荷曲线中的11$\sim$15时步相应,此时结构整体性遭到破坏;图23(c) 第2条裂纹的第2个裂纹尖端$t_{2}$与裂纹3发生了交割. 图23(d)第3条裂纹的第1个裂纹尖端$t_{1}$与平板右边界交割,从而使得平板整体分离.名义应力-名义应变曲线 如图25.
由本文裂纹扩展最终构型图可见,仅1#、2#和3#裂纹发生了扩展,而其他7条裂纹保持稳定.需要特别注意,当裂纹与裂纹相割或裂纹与边界相割时,应力强度因子的计算需要满足两个要求:首先要保证两个裂纹尖端的扩展项不会发生相互影响,其次要保证交互积分的积分范围不会与裂纹发生交割.
这两种情况有一种发生都可能会导致应力强度因子的计算失误,进而使得整个扩展趋势发生偏转.文中通过调整网格,已避免这两种情况的发生. 本文结果与文献[32]的模拟结果几乎完全一致,如图22.与文献[31]的结果相比总体一致,但有些偏差,如图21.
4 结 论
本文提出了一种新的多裂纹扩展控制算法,基于数值流形法实现了多裂纹扩展模拟,且在每个时步中通过调整载荷来满足基本的力学平衡和断裂韧度条件.然后将其应用到3个典型的多裂纹扩展算例中,并给出裂纹扩展的过程图,模拟路径与文献结果基本一致.同时也给出了其载荷曲线与名义应力-名义应变曲线,很容易直观地了解加载体的受力和变形情况.需要注意的是,裂纹扩展过程中,考虑了裂纹的交汇和裂纹尖端间在施加增强函数和应用交互积分求解应力强度因子时的相互影响,保证了计算的准确性.所提出的多裂纹控制算法与每步同时扩展的裂纹数目相关,而且每步扩展中均假定了固定的扩展长度,下一步的研究中侧重于通过引入其他理论来确定真实的扩展长度.
参考文献
| [1] |
Shi GH. Manifold method of material analysis. In: Trans 9th Army Conf on Applied Mathematics and Computing. Minneapolis, Minnesota, 1991. 57-76 |
| [2] |
姜清辉,周创兵. 四面体有限单元覆盖的三维数值流形方法. 岩石力学与工程学报,2005,24(24):4455-4460 (Jiang Qinghui, Zhou Chuangbing. Three-dimensional numerical manifold method with tetrahedron finite element covers. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(24): 4455-4460 (in Chinese)) |
| [3] |
姜清辉,邓书申,周创兵. 三维高阶数值流形方法研究. 岩土力学,2006,27(9):1471-1474(Jiang Qinghui, Deng Shushen, Zhou Chuangbing. Study of three-dimensional high-order numerical manifold method. Rock and Soil Mechanics, 2006, 27(9): 1471-1474 (in Chinese)) |
| [4] |
姜清辉,王书法. 锚固岩体的三维数值流形方法模拟. 岩石力学与工程学报,2006,25(3):528-532(Jiang Qinghui, Wang Shufa. Three-dimensional numerical manifold method simulation of anchor bolt-supported rock mass. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 528-532(in Chinese)) |
| [5] |
王水林,葛修润. 流形元方法在模拟裂纹扩展中的应用. 岩石力学与工程学报,1997,16(5):7-12(Wang Shuilin, Ge Xiurun. Application of manifold method in simulating crack propagation. Chinese Journal of Rock Mechanics and Engineering, 1997, 16(5): 7-12 (in Chinese)) |
| [6] |
王水林,葛修润,章光. 受压状态下裂纹扩展的数值分析. 岩石力学与工程学报,1999,18(6):671-675 (Wang Shuilin, Ge Xiurun, Zhang Guang. Numerical analysis of crack propagation under compression. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(6): 671-675(in Chinese)) |
| [7] |
Tsay RJ, Chiou YJ, Chuang WL. Crack growth prediction by manifold method. Journal of Engineering Mechanics, 1999, 125(8): 884-890 |
| [8] |
Chiou YJ, Lee YM, Tsay RJ. Mixed mode fracture propagation by manifold method. International Journal of Fracture, 2002, 114(1): 327-347 |
| [9] |
李树忱,程玉民. 考虑裂纹尖端场的数值流形方法. 土木工程学报, 2005, 38(7): 96-101 (Li Shuchen, Cheng Yumin. Numerical manifold method for crack tip fields. China Civil Engineering Journal, 2005, 38(7): 96-101(in Chinese)) |
| [10] |
An XM. Extended numerical manifold method for engineering failure analysis. [PhD Thesis]. Singapore: Nanyang Technology University, 2010 |
| [11] |
张慧华,祝晶晶. 复杂裂纹问题的多边形数值流形方法求解. 固体力学学报,2013,34(1):38-46 (Zhang Huihua, Zhu Jingjing. Numerical manifold analysis of complex crack problems on polygonal elements. Chinese Journal of Solid Mechanics, 2013, 34(1): 38-46(in Chinese)) |
| [12] |
苏海东,祁勇峰,龚亚琦. 裂纹尖端解析解与周边数值解联合求解应力强度因子. 长江科学院院报,2013,30(6):83-89 (Su Haidong, Qi Yongfeng, Gong Yaqi. Compute stress intensity factors via combining analytical solutions around crack tips with surrounding numerical solutions. Journal of Yangtze River Scientific Research Institute, 2013, 30(6): 83-89 (in Chinese)) |
| [13] |
Li SC, Cheng YM. Enriched meshless manifold method for two-dimensional crack modeling. Theoretical and Applied Fracture Mechanics, 2005, 44(3): 234-248 |
| [14] |
Gao H, Cheng Y. A complex variable meshless manifold method for fracture problems. International Journal of Computational Methods, 2010, 7(1): 55-81 |
| [15] |
Zhu H, Zhuang X, Cai Y, et al. High rock slope stability analysis using the enriched meshless Shepard and least squares method. International Journal of Computational Methods, 2011, 8(2): 209-228 |
| [16] |
樊成,栾茂田,杨庆. 有限覆盖点插值无网格方法及其应用. 大连理工大学学报,2007,47(4):577-582 (Fan Cheng, Luan Maotian, Yang Qing. Element-free point-interpolation procedure based on finite covers and its application. Journal of Dalian University of Technology, 2007, 47(4): 577-582 (in Chinese)) |
| [17] |
赵妍,张国新,林易澍等. 基于数值流形元法的混凝土力学特性数值试验. 中国水利水电科学研究院学报,2011,9(2):88-95(Zhao Yan, Zhang Guoxin, Lin Yishu, et al. Numerical simulation of test of concrete mechanical properties based on numerical manifold method. Journal of Institute of Water Resources and Hydropower Research, 2011, 9(2): 88-95 (in Chinese)) |
| [18] |
Zhang GX, Sugiura Y, Hasegawa H. Application of manifold method to jointed dam foundation. In: Proc Third Int Conf Analysis of Discontinuous Deformation (ICADD-3). USA, Colorado, 1999. 211-220 |
| [19] |
Zhang GX, Zhu BF, Lu ZC. Cracking simulation of the Wuqiangxi ship lock by manifold method. In: Proc Sixth Int Conf Analysis of Discontinuous Deformation (ICADD-6). Norway, Trondheim, 2003. 133-140 |
| [20] |
Wu Z, Wong LNY. Modeling cracking behavior of rock mass containing inclusions using the enriched numerical manifold method. Engineering Geology, 2013, 162: 1-13 |
| [21] |
Wu Z, Wong LNY, Fan L. Dynamic study on fracture problems in viscoelastic sedimentary rocks using the numerical manifold method. Rock Mechanics and Rock Engineering, 2013, 46(6): 1415-1427 |
| [22] |
Wu Z, Wong LNY. Elastic-plastic cracking analysis for brittle-ductile rocks using manifold method. International Journal of Fracture, 2013, 180(1): 71-91 |
| [23] |
Wu Z, Wong LNY. Frictional crack initiation and propagation analysis using the numerical manifold method. Computers and Geotechnics, 2012, 39: 38-53 |
| [24] |
杨永涛,徐栋栋,郑宏. 动载下裂纹应力强度因子计算的数值流形元法. 力学学报,2014,46(5):730-738 (Yang Yongtao, Xu Dongdong, Zheng Hong. Evaluation on stress intensity factor of crack under dynamic load using numerical manifold method. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 730-738 (in Chinese)) |
| [25] |
Zhang HH, Li LX, An XM, et al. Numerical analysis of 2-D crack propagation problems using the numerical manifold method. Engineering Analysis with Boundary Elements, 2010, 34 (1): 41-50 |
| [26] |
Zheng H,Liu Z,Ge X. Numerical manifold space of Hermitian form and application to Kirchhoff's thin plate problems. International Journal for Numerical Methods in Engineering, 2013, 95(9): 721-739 |
| [27] |
Williams ML. On the stress distribution at the base of a stationary crack. Journal of Applied Mechanics, 1957, 24: 109-114 |
| [28] |
徐栋栋,郑宏,夏开文等. 高阶扩展数值流形法在裂纹扩展中的应用. 岩石力学与工程学报,2014,33(7):1375-1387 (Xu Dongdong, Zheng Hong, Xia Kaiwen, et al. Application of higher-order enriched numerical manifold method to crack propagation. Chinese Journal of Rock mechanics and Engineering, 2014, 33(7): 1375-1387 (in Chinese)) |
| [29] |
徐栋栋,郑宏. 数值流形法在处理强奇异性问题时的网格无关性. 岩土力学,2014,35(8):2385-2394 (Xu Dongdong, Zheng Hong. Mesh independence of numerical manifold method in treating strong singularity. Rock and Soil Mechanics, 2014, 35(8): 2385-2394 (in Chinese)) |
| [30] |
Erdogan F,Sih GC. On the crack extension in plate under in plane loading and transverse shear. Journal of Basic Engineering, 1963, 85(4): 519-525 |
| [31] |
Budyn E, Zi G, Moës N, et al. A method for multiple crack growth in brittle materials without remeshing. International Journal for Numerical Methods in Engineering, 2004, 61(10): 1741-1770 |
| [32] |
Azadi H, Khoei AR. Numerical simulation of multiple crack growth in brittle materials with adaptive remeshing. International Journal for Numerical Methods in Engineering, 2011, 85(8): 1017-1048 |
MULTIPLE CRACK PROPAGATION BASED ON THE NUMERICAL MANIFOLD METHOD
Xu Dongdong

, Zheng Hong, Yang Yongtao, Wu Aiqing
1. Key Laboratory of Geotechnical Mechanics and Engineering of Ministry of Water Resources, Yangtze River Scientific Research Institute, Wuhan 430010, China;
2. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Sciences, Wuhan 430071, China
Fund: The project was supported by the National Natural Science Foundation of China (11172313, 51179014), Key Project of Chinese National Programs for Fundamental Research and Development (973 Program) (2011CB710603).
Abstract: The numerical manifold method based on the two covers (mathematical cover and physical cover) and contact loop have been used to solve the continuum and discontinuum problems in a unified way. The mathematical cover is not enforced to coincide with the cracks when dealing with the discontinuous problem, facilitating the simulation of failure in rock mass. An enriched numerical manifold method is developed by adding the enriched displacement functions used for simulating the stress singularity to the physical patches around the crack tip. And on this base, a new algorithm of the multiple crack propagation is proposed; the overall response of the material is given during the crack propagation. Numerical examples with NMM for the classic linear elastic fracture mechanics problems are presented, suggesting that the proposed procedure is accurate and efficient.
Key words:
numerical manifold method physical cover mathematical cover contact loop multiple crack propagation randocracks three branch cracks
 2015, Vol. 47
2015, Vol. 47