引 言

复合材料的使用和研究结果表明，即使在冲击表面无任何征兆的情况下，低速冲击损伤仍严重威胁复合材料结构强度，使剩余强度急剧下降^{[1, 2]}.如何准确估算复合材料的低速冲击损伤，并根据冲击对复合材料造成的损伤形式，损伤严重程度与冲击能量、冲击方式、材料性能等因素的关系，采用一些适应复合材料特点的设计概念和方法，改善损伤阻抗和损伤容限特性，是提高复合材料结构设计水平的必经之路.鉴于此，复合材料结构的低速冲击损伤问题一直是国内外研究的焦点之一.

复合材料冲击损伤为多损伤耦合失效模式，损伤的萌生、累积、演变过程复杂.目前许多研究者把对复合材料冲击特性的研究集中在基于试验的理论分析与数值模拟上^[3]，本文认为在深入理解失效机理的基础上建立合理的分析模型是研究复合材料低速冲击损伤的关键，因此，基于连续介质损伤力学的分析方法被广泛用于复合材料冲击损伤特性的模拟中.

连续介质损伤力学方法包括损伤表征、损伤判定、损伤演化3部分.对应复合材料不同的损伤模式，损伤表征通过损伤状态变量的引入 从而建立损伤材料与完好材料间的本构关系.由失效准则判定复合材料的损伤萌生，一般采用哈辛(Hashin)失效准则.虽然哈辛准则能够区分复合材料不同的损伤形式，并考虑了材料主轴应力间的相互作用，但是无法解释横向压缩对剪切破坏的抑制效应以及不能确定材料的损伤断裂面角度^[4].对冲击后层合板截面的微观形貌研究^{[3, 5]}表明，在层合板厚度方向上存在许多明显的基体裂纹及断裂面，基体裂纹的扩展是导致其所处子层与相邻子层间产生分层的根本原因，因此如何在损伤模型中模拟基体裂纹的产生及不同断裂面角度对材料损伤的影响是合理模拟冲击损伤的关键.基于单层板破坏机理的卜克(Puck)失效准则^[6]考虑了断裂面角度对基体损伤的影响并能确定损伤后的断裂面角度值，该准则对大量复合材料典型试验[7- 8]的预测结果良好.}近年来已有学者尝试在低速冲击问题中应用部分简化的卜克准则预测复合材料基体压缩损伤的起始，取得了一定的进展^{[9, 10]}，但只是将断裂面角度简单假设为单轴压缩试验中的观测值，而非根据冲击条件下单层板的实际应力状态确定断裂面角度.针对材料损伤萌生后的演化规律，文献^{[11, 12]}认为损伤演化与损伤断裂面的有效应力分量有关，提出用威布尔分布函数表征损伤演化过程，文献^[13]采用上述指数型演化函数对复合材料冲击问题进行了研究. 文献^[14]基于材料的吉布斯自由能密度，推导出含损伤复合材料三维损伤本构关系，损伤演化函数包含热力学参量，较好地模拟了复合材料层合板的冲击损伤. 文献^{[9, 15, 16]}提出基于材料应变能释放的损伤线性软化模型，损伤程度经应变控制，通过引入单元特征长度，在一定程度上降低了损伤演化阶段网格的敏感性. 文献^[17]采用指数型损伤演化方法^[18]，对复合材料补片补强结构强度和损伤演化过程进行了研究. 文献^[19]等基于应变能耗散损伤演化思想，建立了损伤状态变量关于等效应变的损伤线性演化法则，有效预测了含开口复合材料层合板的面内拉伸强度.

在低速冲击问题中，层间分层是主要损伤形式，研究^[20]表明分层损伤是导致复合材料结构剩余强度大幅降低的因素之一，因此分层损伤的预测是复合材料冲击损伤分析中的关键部分.黏聚区模型(CZM)是研究复合材料界面损伤及扩展问题的一种有效方法，黏聚区模型将材料分成连续体以及连续体之间的黏聚层，层间失效由被粘接面的分离来表征，采用8节点三维粘接元能较好地模拟冲击载荷下的分层损伤^{[9, 10, 13, 21, 22]}，但粘接元的网格尺寸会严重影响黏聚区模型的预测精度，为确保计算结果正确，单元在裂纹起裂方向的长度应小于某一值，一般分层前缘黏聚区的长度小于1 mm时，相应的粘接元特征长度应小于0.5 mm^[23].另外，在所有铺层间均加入粘接元的方法会增加模型规模和计算时间^{[9, 24]}，对铺层总数较多的复合材料结构影响尤其明显.为克服黏聚区模型造成的模型规模增加和计算时间冗长等缺点，文献^[14]通过对粘接元使用质量缩放技术人为地增大材料密度，从而增大稳定极限值，节省了分析时间，但是材料密度的增加会增大动态分析的惯性效应，可能导致错误的分析结果. 文献^[25]通过调整铺层顺序，将相同铺层角的子层重叠，人为地增加单层厚度，从而对层合板进行简化处理，但是相关试验研究^[26]指出铺层重叠对分层面积与形状影响很大.显然，粘接元网格尺寸和数量的要求限制了黏聚区模型在实际复合材料结构损伤容限设计中的应用.

基于冲击载荷下复合材料层合板的损伤机理分析，本文认为：(1)复合材料基体裂纹将直接造成材料在断裂面上的承载能力下降，并间接影响材料主轴方向的承载，由此等效应力和损伤状态矩阵均需要在断裂面坐标系而非传统的材料主轴坐标系下定义，表示单层材料损伤主方向与材料主方向一般不重合(断裂面角度为0°时除外)；(2) 低速冲击下层合板子层内基体裂纹的扩展形成了子层间的分层，分层可以通过层内基体裂纹表征.因此，本文采用连续介质损伤力学方法分析低速冲击载荷下复合材料的损伤萌生和扩展，并认为损伤扩展是一个应变能释放的过程.根据复合材料低速冲击试验中损伤形式及分布情况，引入基体裂纹饱和密度参数表征材料的层间分层，建立了一种新的连续介质损伤力学分析模型. 模型中加入单元特征长度以考虑网格依赖性，并在"ABAQUS(阿巴克斯)"软件平台上通过自编材料子程序实现，完成了相关层合板低速冲击损伤响应参数的预测.

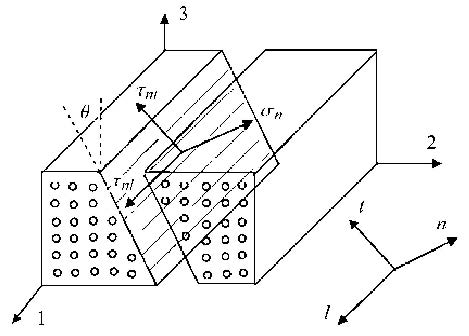
1 连续损伤本构模型 1.1 应力分析

基于摩尔-库伦断裂理论，认为复合材料基体的脆性断裂将会产生一个与层内纤维方向平行的断裂面，如图1所示.图中坐标系1-2-3为单层板的材料主轴坐标系，坐标系$l$-$n$-$t$为损伤断裂面坐标系.

当采用材料主轴坐标系时，无损伤正交各向异性单层复合材料的本构方程为

\[\varepsilon = {S_0}\sigma \]

(1)

其中，${ S}_0 $为材料主轴坐标系下的初始柔度矩阵，${\sigma} = \left[{\sigma _1 ,\sigma _2 ,\sigma _3 ,\tau _{23} ,\tau _{13} ,\tau _{12} } \right]^{\rm T}$为主轴坐标系下的应力，${\varepsilon }= \left[{\varepsilon _1,\varepsilon _2 ,\varepsilon _3 ,\gamma _{23} ,\gamma _{13} ,\gamma _{12} }\right]^{\rm T}$为主轴坐标系下的应变.

定义损伤断裂面角度为$\theta$ $( - 90^ \circ ≤ \theta ≤ 90^ \circ)$，材料主轴坐标系1-2-3绕纤维方向转动$\theta$得到断裂面坐标系为$l$-$n$-$t$，那么通过对材料主轴坐标系下的应力、应变进行坐标转换得到断裂面坐标系下的应力、应变

\[{\sigma ^{{\rm {fp}}}} = {T^{ - 1}}\sigma \]

(2)

\[{\varepsilon ^{{\rm {fp}}}} = {T^{\rm {T}}}\varepsilon \]

(3)

式中，${\sigma}^{\rm fp} = \left[{\sigma _l ,\sigma _n ,\sigma _t ,\tau _{nt} ,\tau _{lt} ,\tau _{nl} }\right]^{\rm T}$为断裂面坐标系下的应力，${\varepsilon }^{\rm fp} = \left[{\varepsilon _l ,\varepsilon_n ,\varepsilon _t ,\gamma _{nt} ,\gamma _{lt} ,\gamma _{nl} } \right]^{\rm T}$为断裂面坐标系下的应变，${T}$为标准坐标转换矩阵.

损伤断裂面坐标系下的本构方程定义为

\[{\varepsilon ^{{\rm {fp}}}} = S_0^{{\rm {fp}}}{\sigma ^{{\rm {fp}}}}\]

(4)

式中，${ S}_0^{\rm fp} $为断裂面坐标系下的初始柔度矩阵.将式(2)和式(3)代入式(4)，并与式(1)比较，可知断裂面坐标系 下的初始柔度矩阵由材料主轴坐标系下的柔度矩阵表示为

\[S_0^{{\rm {fp}}} = {T^{\rm {T}}}{S_0}T\]

(5)

1.2 损伤状态变量矩阵

一般认为，复合材料的面内损伤主要包括纤维损伤(fiber fracture,FF)与基体损伤(inter-fiber fracture,IFF)，纤维损伤断裂面 为纵向主应力作用面，基体损伤断裂面与横向主应力作用面的夹角为$\theta $，其中$\theta$为基体损伤的断裂面角度.区别断裂面法向载荷的作用方向，复合材料面内损伤具体分为纤维拉伸损伤(FFT)、纤维压缩损伤(FFC)、基体拉伸损伤(IFFT)、基体压缩损伤(IFFC) 4种损伤模式.

当复合材料单层板出现损伤后，引入损伤状态变量矩阵${ M}\left( { D}\right)$表示材料损伤后有效承载面积减 小的比例，用于量化各方向微裂纹的分布密度.基体损伤将直接导致材料在断裂面上承载能力的降低，因此需要在断裂面坐标系而非传统的材料主轴坐标系下定义等效应力.由连续介质损伤力学理论^[27]，将断裂面坐标系下的等效应力定义为

\[{\bar \sigma ^{{\rm {fp}}}} = {M^{{\rm {fp}}}}\left( D \right){\sigma ^{{\rm {fp}}}}\]

(6)

其中，${ M}^{\rm fp}\left( { D} \right)$为采用断裂面坐标系的损伤状态变量矩阵，其矩阵形式表示如下

\[\begin{array}{l} {M^{{\rm {fp}}}}\left( D \right) = {\rm {dig}}(\frac{1}{{1 - {d_l}}},\frac{1}{{1 - {d_n}}},\frac{1}{{1 - {d_t}}},\frac{1}{{1 - {d_{nt}}}},\\ \frac{1}{{1 - {d_{lt}}}},\frac{1}{{1 - {d_{nl}}}}) \end{array}\]

(7)

式中，$d_i$ $(i = l,n,t)$分别表征材料点在断裂面坐标系中沿$l$,$n$,$t$方向的损伤状态变量，$d_{ij}$ $(i,j = l,n,t)$为剪切损伤状态变量.

根据能量等价原理，只需将无损材料余能中的应力替换为等效应力便得到受损材料的弹性余能，无损材料与受损材料的余能函数形式相同，表示为

\[\begin{array}{l} {W_{\rm {d}}} = \frac{1}{2}{{\bar \sigma }^{{\rm {fp}}}}S_0^{{\rm {fp}}}{{\bar \sigma }^{{\rm {fp}}}} = \\ \frac{1}{2}{\sigma ^{{\rm {fp}}}}{M^{{\rm {fp}}}}{\left( D \right)^{\rm {T}}}S_0^{{\rm {fp}}}{M^{{\rm {fp}}}}\left( D \right){\sigma ^{{\rm {fp}}}} = \\ \frac{1}{2}{\sigma ^{{\rm {fp}}}}S_{\rm {d}}^{{\rm {fp}}}{\sigma ^{{\rm {fp}}}} \end{array}\]

(8)

由式(8)可知材料点在断裂面坐标系下的损伤柔度矩阵${ S}_{\rm d}^{\rm fp} $可表示为

\[S_{\rm {d}}^{{\rm {fp}}} = {M^{{\rm {fp}}}}{\left( D \right)^{\rm {T}}}S_0^{{\rm {fp}}}{M^{{\rm {fp}}}}\left( D \right)\]

(9)

将式(5)代入式(9)中，可得材料主轴坐标系下的损伤柔度矩阵

\[{S_{\rm {d}}} = {T^{{\rm { - T}}}}{M^{{\rm {fp}}}}{\left( D \right)^{\rm {T}}}{T^{\rm {T}}}{S_0}T{M^{{\rm {fp}}}}\left( D \right){T^{ - 1}}\]

(10)

定义材料主轴坐标系下的损伤柔度矩阵${ S}_{\rm d} $为如下形式

\[{S_{\rm {d}}} = M{\left( D \right)^{\rm {T}}}{S_0}M\left( D \right)\]

(11)

其中，${ M}\left( { D}\right)$为材料主轴坐标系下的损伤变量矩阵.对比式(10)，可知材料主轴坐标系下的损伤状态变量矩阵为

\[M\left( D \right) = T{M^{{\rm {fp}}}}\left( D \right){T^{ - 1}}\]

(12)

2 材料失效准则

复合材料的损伤分为纤维损伤与基体损伤，建立以应力分量组成的损伤函数$f_{\rm e}$表征的材料失效准则，当函数标量达到特定值，即满足失效准则后，定义为一种损伤模式. 本文采用三维卜克失效准则判断冲击载荷下层合板基体损伤的萌生，准则认为材料的基体损伤会产生一个断裂面，对于某一确定的应力状态，潜在断裂面是该应力状态作用下所有平面中最易发生断裂的作用面，也就是说基体的潜在断裂面承担了可能出现基体损伤最大的风险.设断裂面角度为$\theta $，那么基体损伤函数是关于潜在断裂面角度的函数，函数表示如下

基体拉伸损伤($\sigma _n ≥ 0)$

\[\begin{array}{l} {f_{{\rm {IFF}}}}\left( \theta \right) = \left[ {{{\left( {\frac{1}{{R_ \bot ^{\rm {t}}}} - \frac{{p_{ \bot \psi }^{\rm {t}}}}{{R_{ \bot \psi }^{\rm {A}}}}} \right)}^2}\sigma _n^2\left( \theta \right) + {{\left( {\frac{{{\tau _{nt}}\left( \theta \right)}}{{R_{ \bot \bot }^{\rm {A}}}}} \right)}^2} + } \right.\\ {\left. {{{\left( {\frac{{{\tau _{nl}}\left( \theta \right)}}{{{R_{ \bot \parallel }}}}} \right)}^2}} \right]^{\frac{1}{2}}} + \frac{{p_{ \bot \psi }^{\rm {t}}}}{{R_{ \bot \psi }^{\rm {A}}}}{\sigma _n}\left( \theta \right) \end{array}\]

(13)

基体压缩损伤($\sigma _n < 0)$

\[\begin{array}{l} {f_{{\rm {IFF}}}}\left( \theta \right) = \left[ {{{\left( {\frac{{p_{ \bot \psi }^{\rm {c}}}}{{R_{ \bot \psi }^{\rm {A}}}}{\sigma _n}\left( \theta \right)} \right)}^2} + {{\left( {\frac{{{\tau _{nt}}\left( \theta \right)}}{{R_{ \bot \bot }^{\rm {A}}}}} \right)}^2} + } \right.\\ {\left. {{{\left( {\frac{{{\tau _{nl}}\left( \theta \right)}}{{{R_{ \bot \parallel }}}}} \right)}^2}} \right]^{\frac{1}{2}}} + \frac{{p_{ \bot \psi }^{\rm {c}}}}{{R_{ \bot \psi }^{\rm {A}}}}{\sigma _n}\left( \theta \right) \end{array}\]

(14)

其中

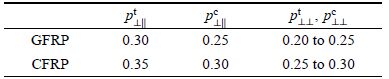
\[\left\{ \begin{array}{l} R_{ \bot \bot }^{\rm {A}} = \frac{{R_ \bot ^{\rm {c}}}}{{2\left( {1 + p_{ \bot \bot }^{\rm {c}}} \right)}}\\ \frac{{p_{ \bot \psi }^{{\rm {t}},{\rm {c}}}}}{{R_{ \bot \psi }^{\rm {A}}}} = \frac{{p_{ \bot \bot }^{{\rm {t}},{\rm {c}}}}}{{R_{ \bot \bot }^{\rm {A}}}}{\cos ^2}\psi + \frac{{p_{ \bot \parallel }^{{\rm {t}},{\rm {c}}}}}{{R_{ \bot \parallel }^{\rm {A}}}}{\sin ^2}\psi \\ {\cos ^2}\psi = \frac{{\tau _{nt}^2}}{{\tau _{nt}^2 + \tau _{nl}^2}},{\sin ^2}\psi = \frac{{\tau _{nl}^2}}{{\tau _{nt}^2 + \tau _{nl}^2}} \end{array} \right.\]

式中，$\sigma _n \left( \theta \right)$,$\tau _{nt} \left( \theta \right)$和$\tau _{nl} \left( \theta\right)$为断裂面上的应力，可由式(2)对材料主轴坐标系下的应力进 行坐标转换求得. $R_\bot ^{\rm t} $和$R_ \bot^{\rm c} $为单层板垂直于纤维方向的拉伸与压缩强度，$R_{ \bot\parallel } $为基体剪切强度. 考虑到潜在断裂面上的拉伸法向应力($\sigma _n≥ 0)$会促使基体拉伸损伤发生，同时压缩法向应力($\sigma _n <0)$会抑制基体压缩损伤的发生，引入斜率参数$p_{ \bot \parallel }^{\rm t} $,$p_{\bot \bot }^{\rm t} $,$p_{ \bot \parallel }^{\rm c} $和 $p_{ \bot \bot }^{\rm c}$分别表征潜在断裂面上拉压不同法向应力状态对损伤的影响，推荐取值见表1.

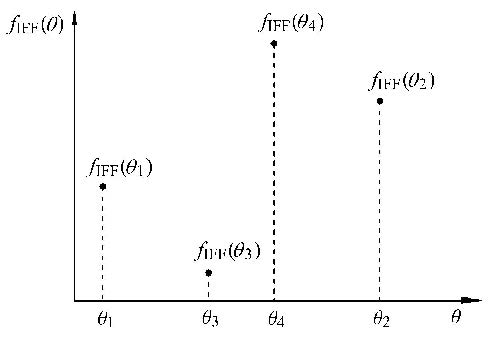
在多向应力的共同作用下，损伤函数的极大值对应的角度为潜在断裂面角度. 利用黄金分割快速搜索的数值算法^[29]求 解基体损伤函数$f_{\rm IFF} \left( \theta \right)$在区间$[- 90^ \circ ,90^ \circ]$内的极大值. 图2为黄金分割搜索算法示意图，首先已知点$\theta _1 $和 $\theta _2$ $(\theta _1 < \theta _2)$，则点$\theta _3 $及下一个点$\theta _4 $由式(15)确定

\[\frac{{{\theta _2} - {\theta _3}}}{{{\theta _3} - {\theta _1}}} = \frac{{{\theta _2} - {\theta _4}}}{{{\theta _4} - {\theta _3}}} = \varphi \]

(15)

式中$\varphi $为黄金分割比例，其值为1.618. 确定的两点$\theta _3 $和$\theta _4 $在原区间$[\theta _1 ,\theta _2]$内是对称的，比较损伤函数在$\theta _3 $和$\theta _4 $处的大小，当$f_{\rm IFF} \left( {\theta _3 } \right) >f_{\rm IFF} \left( {\theta _4 } \right)$，则下一个搜索区间为$[\theta _1 ,\theta _4]$，当$f_{\rm IFF} \left({\theta _3 } \right) < f_{\rm IFF} \left( {\theta _4 } \right)$，则下一个搜索区间为$[\theta _3 ,\theta _2]$.通过多次搜索，当区间小于规定的容差后，则停止迭代并求 得潜在断裂面角度$\theta $.

当损伤函数$f_{\rm IFF} \left( \theta\right)$的极大值大于1时，表示单层板发生基体损伤，此时的潜在断裂面为该材料点的真实基体损伤断裂面，潜在断裂面角度$\theta $为材料点的实际断裂面角度$\theta _{\rm fp} $.

判定纤维损伤时，忽略横向泊松效应的影响，采用最大应力准则，纤维失效准则如下

纤维拉伸损伤($\sigma _1 ≥ 0)$

\[{f_{{\rm {FF}}}} = \frac{{{\sigma _1}}}{{R_\parallel ^{\rm {t}}}}\]

(16)

纤维压缩损伤($\sigma _1 < 0$)

\[{f_{{\rm {FF}}}} = - \frac{{{\sigma _1}}}{{R_\parallel ^{\rm {c}}}}\]

(17)

其中$R_\parallel ^{\rm t} $和$R_\parallel ^{\rm c}$分别为沿纤维方向的拉伸与压缩强度. 当$f_{\rm FF} $的值大于1时，发生纤维损伤.

3 损伤演化

一旦材料出现损伤后，材料软化，宏观表现为弹性模量的退化和损伤区域内应力的下降，并在损伤阶段释放应变能，因此材料的损伤演化模型中考虑了损伤过程中的能量释放.

3.1 网格依懒性

有限元分析中，材料损伤后的应变软化会引起应变局部化问题，造成计算中的能量耗散严重依赖于网格尺寸^[15].由于损伤过 程中的能量耗散与单元尺寸成正比，所以采用裂纹带模型，引入单元特征长度$L^{\rm c}$，可以在一定程度上降低材料退化阶段对于网格尺寸的敏感性.

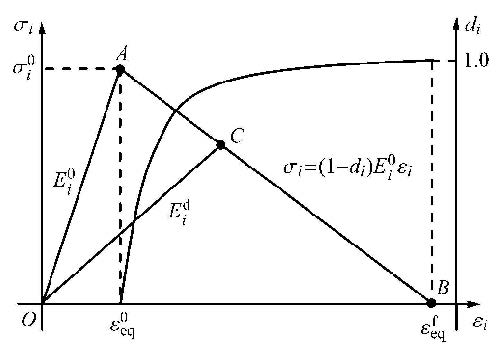
常规的损伤退化方法采用线性或指数形式函数对材料进行软化，假定损伤发生之后材料满足线性等效应变-软化行为(图3).复合材料的损伤过程实质为应变能释放的过程，材料点在损伤萌生后(点$A$)开始释放能量，在损伤过程中(点$C$)的应变能释放密度大小为点$O,A,C$所围的面积$S_{\rm OAC} $，当该应变能释放密度($S_{\rm OAC} )$等于材料点的临界断裂能密度($S_{\rm OAB})$时，表示该材料点完全失效.

如上所述，将材料完全破坏时的等效应变$\varepsilon _{\rm eq}^{\rm f} $定义为

\[\varepsilon _{{\rm {eq}}}^{\rm {f}} = \frac{{2{G_{\rm {c}}}}}{{\sigma _{{\rm {eq}}}^0{L^{\rm {c}}}}} = \frac{{2{g_{\rm {c}}}}}{{\sigma _{{\rm {eq}}}^0}}\]

(18)

式中，$\sigma _{\rm eq}^0 $为材料损伤萌生时的等效应力，$G_{\rm c} $为临界断裂能释放率，$g_{\rm c}$为弥散分布在特征长度内的临界断裂能密度，对应材料应力-应变曲线中的面积$S_{\rm OAB} $.

3.2 损伤状态变量

建立关于等效应变的损伤状态变量来描述材料从开始加载至完全失效过程中的损伤演化规律.考虑损伤后的线性软化行为，损伤 状态变量定义为

\[\begin{array}{l} {d^{\rm {I}}} = \max \left\{ {0,\min \left\{ {1,\varepsilon _{{\rm {eq}},{\rm {I}}}^{\rm {f}}\frac{{{\varepsilon _{{\rm {eq}},{\rm {I}}}} - \varepsilon _{{\rm {eq}},{\rm {I}}}^0}}{{{\varepsilon _{{\rm {eq}},{\rm {I}}}}\left( {\varepsilon _{{\rm {eq}},{\rm {I}}}^{\rm {f}} - \varepsilon _{{\rm {eq}},{\rm {I}}}^0} \right)}}} \right\}} \right\},\\ I \in \left( {{\rm {FFT}},{\rm {FFC}},{\rm {IFFT}},{\rm {IFFC}}} \right) \end{array}\]

(19)

其中，$d^{\rm I}$表示有限元计算中某一时刻与4种损伤模式对应的损伤状态变量，用于量化不同损伤模式下的微裂纹的分布密度.$\varepsilon_{\rm eq,I} $为当前等效应变，$\varepsilon _{\rm eq,I}^0 $和$\varepsilon _{\rm eq,I}^{\rm f}$分别代表材料损伤萌生和完全失效时的等效应变. $d^{\rm I}$以最大值函数形式表示用于微观损伤扩展的能量永远不会减少，并且损伤不可恢复. 当$d^{\rm I} =0$时，表示材料未出现损伤，当$d^{\rm I} = 1$时，表示材料完全破坏.

断裂面坐标系下的损伤变量矩阵${ M}^{\rm fp}\left( { D} \right)$中的$d_l$表征纤维损伤主轴($l$轴)，对于拉压两种损伤模式表示为^[24]

\[{d_l} = d_l^{{\rm {FFT}}} + d_l^{{\rm {FFC}}} - d_l^{{\rm {FFT}}}d_l^{{\rm {FFC}}}\]

(20)

$d_n$表征基体损伤主轴($n$轴)，当断裂面法向应力$\sigma _n \left( \theta\right)$为拉伸应力时使得基体裂纹张开而不能承载，但为压缩应力时却使基体裂纹闭合，此时材料仍然能够承受断裂面法向载荷，因此$d_n$表示为以下形式

\[{d_n} = d_n^{{\rm {IFFT}}}\]

(21)

损伤变量$d_t$表征的$t$损伤主轴始终垂直于纤维与基体损伤主轴($l$轴、$n$轴)，所以材料在损伤主轴$t$方向上不会出现纤维和基体损伤，即$d_t = 0$.

表征剪切损伤的变量$d_{ij}$ $(i,j = l,n,t)$分别为

\[{d_{nt}} = 1 - (1 - {d_m})(1 - {d_t})\]

(22)

\[{d_{nl}} = 1 - (1 - {d_m})(1 - {d_l})\]

(23)

\[{d_{lt}} = 1 - (1 - {d_l})(1 - {d_t})\]

(24)

其中，$d_m $表征基体损伤对剪切应力的影响

\[{d_m} = d_n^{{\rm {IFFT}}} + d_n^{{\rm {IFFC}}} - d_n^{{\rm {IFFT}}}d_n^{{\rm {IFFC}}}\]

(25)

3.3 等效应力应变

从材料的失效准则中可以看出，损伤断裂面上的应力$\sigma _n $,$\tau _{nl}$和$\tau _{nt} $造成了基体损伤，故对于基体损伤模式，其等效应力与应变定义为以下形式

\[{\sigma _{{\rm {eq}},{\rm {IFF}}}} = \sqrt {{{\left\langle {{\sigma _n}} \right\rangle }^2} + \tau _{nl}^2 + \tau _{nt}^2} \]

(26)

\[{\varepsilon _{{\rm {eq}},{\rm {IFF}}}} = \sqrt {{{\left\langle {{\varepsilon _n}} \right\rangle }^2} + \gamma _{nl}^2 + \gamma _{nt}^2} \]

(27)

式中$\left\langle x \right\rangle $是麦考利(McCauley)算子，定义$\left\langle x\right\rangle = \max \left( {0,x} \right)$.

同样对于纤维损伤模式，其等效应力与应变表示为

\[{\sigma _{{\rm {eq}},{\rm {FF}}}} = \sqrt {\sigma _1^2} \]

(28)

\[{\varepsilon _{{\rm {eq}},{\rm {FF}}}} = \sqrt {\varepsilon _1^2} \]

(29)

根据材料失效准则，损伤萌生时的等效应力与应变($\sigma _{\rm eq}^0 $和$\varepsilon _{\rm eq}^0)$对应于损伤函数$f_{\rm IFF} $或$f_{\rm FF} $等于1时的等效应力与应变. 材料完全破坏时的等效应变$\varepsilon_{\rm eq}^{\rm f}$由基于材料应变能释放密度的损伤演化准则确定，损伤演化准则为：当单元特征长度内应变能释放密度等于临界断裂能密度时，材料完全破坏，此时的等效应变即为$\varepsilon _{\rm eq}^{\rm f} $.纤维损伤发生后能量瞬间释放，$\varepsilon _{\rm eq,FF}^{\rm f}$与$\varepsilon _{\rm eq,FF}^0$非常接近，故认为纤维损伤后材料立刻完全破坏.

大量低速冲击试验^{[3, 5, 30, 31, 32, 33]}研究表明复合材料层合板的主要损伤是基体损伤，表现为层间分层(90°基体断裂面角度)和层内基体开裂(非90°基体断裂面角度).冲击过程中某些铺层内首先发生基体开裂，形成多条基体裂纹，基体裂纹沿厚度方向转向沿层间界面扩展而形成分层，界面分层又引发其它相关铺层内的基体发生开裂，损伤间相互耦合.基于上述基体裂纹扩展机理，认为当材料点因基体损伤产生的基体断裂面角度等于90°时，该材料点即出现分层；当基体断裂面角度不等于90°时，材料点内部首先出现多条基体裂纹，当单位长度上的层内基体裂纹的个数达到某一最大值后将引发层间分层. 因此本文引入基体裂纹饱和密度参数$\rho_{\rm crack}$^{[38, 39, 40]}，表示单位长度上产生层间分层需要的层内基体裂纹个数，认为该参数不受铺层顺序和冲击能量的影响，对于同一批试件，基体裂纹饱和密度参数的值可通过逆方法求得^[34]：选取某一冲击能量下的试件，调整基体裂纹饱和密度参数的值使得有限元预测的冲击力-时间历程与试验值吻 合最佳.材料点在出现分层损伤后将不能够承受层间剪力，导致附近未损伤材料点承担更多载荷，又可能引发未损伤材料点出现损伤.

基于上述分析，本文对传统的只模拟单个基体裂纹的连续介质损伤力学模型进行改进，在每个单元内模拟多个层内基体裂纹、一个层间分层裂纹以及一个纤维断裂面，模型将裂纹弥散于单元内，在发生基体损伤材料点的损伤演化中考虑多个基体裂纹的能量耗散.建立含多个基体裂纹的能量混合模式损伤演化判据如下

\[{\left( {\frac{{{g_n}L_{{\rm {IFF}}}^{\rm {c}}}}{{{n_{{\rm {crack}}}}G_{{\rm {2c}}}^k}}} \right)^\zeta } + {\left( {\frac{{{g_{nl}}L_{{\rm {IFF}}}^{\rm {c}}}}{{{n_{{\rm {crack}}}}{G_{{\rm {12c}}}}}}} \right)^\zeta } + {\left( {\frac{{{g_{nt}}L_{{\rm {IFF}}}^{\rm {c}}}}{{{n_{{\rm {crack}}}}{G_{{\rm {23c}}}}}}} \right)^\zeta } = 1\]

(30)

式中，$g_n $,$g_{nl} $和$g_{nt} $分别为基体损伤演化时与应力$\sigma _n $，$\tau _{nl} $和$\tau _{nt}$有关的应变能释放密度. $G_{\rm 2c}^k $,$G_{\rm 12c} $和$G_{\rm 23c}$分别表示横向拉伸(压缩)、面内剪切和层间剪切临界断裂能释放率，其中$k$ $(k = t,c)$表示拉伸和压缩. $L_{\rm IFF}^{\rm c}$为基体损伤对应的单元特征长度. $\zeta $为材料参数，一般取值为2. $n_{\rm crack}$为一个单元内的层内基体裂纹饱和个数，当断裂面角度$\left| {\theta _{\rm fp} } \right| = 90^ \circ $时，$n_{\rm crack} = 1$；当$\left| {\theta _{\rm fp} } \right| \ne 90^ \circ $时，$n_{\rm crack} $表示为

\[{n_{{\rm {crack}}}} = {\rho _{{\rm {crack}}}}{l_y}\]

(31)

式中，$l_y $为单元在全局坐标系下沿坐标轴$y$方向的特征长度.

式(30)说明当单元内$n_{\rm crack} $个基体裂纹的断裂能量全部耗散后，此时$n_{\rm crack}$个基体裂纹已经完全形成，基体裂纹沿厚度方向扩展至层间而形成分层，由此通过单元内$n_{\rm crack}$个基体裂纹的完全形成来表征层间分层.

在"ABAQUS(阿巴克斯)"商业有限元软件中，实体单元的特征长度默认等于该单元体积的三次方根.显然该方法未考虑单元长宽比，对于立方体单元，能够有效降低网格依赖性，但对于长宽高尺寸差别较大的单元，消除网格依赖性的效果有限.根据文献 ^[15]，单元特征长度$L^{\rm c}$定义为

\[{L^{\rm {c}}} = \frac{{{V_{{\rm {el}}}}}}{{{A_ \bot }}}\]

(32)

其中，$V_{\rm el} $表示单元体积，$A_ \bot $为单元在垂直于裂纹方向上的面积. 基体损伤对应的单元特征长度具体表示为

\[L_{{\rm{IFF}}}^{\rm{c}} = \left\{ \begin{array}{l} {l_z},{\rm{for}}\left| {{\theta _{{\rm{fp}}}}} \right| = 90^\circ \\ {l_y}\cos \left( {{\theta _{{\rm{fp}}}}} \right),{\rm{for}}\left| {{\theta _{{\rm{fp}}}}} \right| \ne 90^\circ \end{array} \right.\]

(33)

式中，$l_z $为单元在全局坐标系下沿坐标轴$z$方向的尺寸.

材料因基体损伤而完全破坏时有

\[g_i^{\rm {f}} = \int_0^{\varepsilon _i^{\rm {f}}} {{\sigma _i}} {\rm {d}}\varepsilon \approx \frac{1}{2}\sigma _i^0\varepsilon _i^{\rm {f}} = \frac{1}{2}\sigma _i^0{\beta _i}\varepsilon _{{\rm {eq}}}^{\rm {f}}(i = n,nl,nt)\]

(34)

式中，$\sigma _i^0 $为基体损伤萌生时断裂面上各应力分量，有限元计算中可当损伤函数$f_{\rm IFF} $值等于1时储存在程序中. $\beta _i $为模式混合率，其中

\[{\beta _n} = \frac{{\left\langle {{\varepsilon _n}} \right\rangle }}{{{\varepsilon _{{\rm {eq}}}}}},{\beta _{nl}} = \frac{{{\gamma _{nl}}}}{{{\varepsilon _{{\rm {eq}}}}}},{\beta _{nt}} = \frac{{{\gamma _{nt}}}}{{{\varepsilon _{{\rm {eq}}}}}}\]

(35)

将式(33)和式(34)代入式(30)中，可得材料点因基体损伤而完全破坏时的等效应变

\[\varepsilon _{{\rm{eq}},{\rm{IFF}}}^{\rm{f}} = \left\{ \begin{array}{l} \frac{2}{{{l_z}}}\Delta , {\rm{for}}\left| {{\theta _{{\rm{fp}}}}} \right| = 90^\circ \\ \frac{{2{\rho _{{\rm{crack}}}}}}{{\cos \left( {{\theta _{{\rm{fp}}}}} \right)}}\Delta , {\rm{for}}\left| {{\theta _{{\rm{fp}}}}} \right| \ne 90^\circ \end{array} \right.\]

(36)

其中，$\Delta = \left[{\left( {\dfrac{\sigma _n^0 \beta _n }{G_{\rm2c}^k }} \right)^\zeta + \left( {\dfrac{\tau _{nl}^0 \beta _{nl} }{G_{\rm12c} }} \right)^\zeta + \left( {\dfrac{\tau _{nt}^0 \beta _{nt} }{G_{\rm23c} }} \right)^\zeta } \right]^{ -1/\zeta }$.

4 层合板低速冲击损伤响应参数预测

选择两种不同材料不同铺层的复合材料层合板进行半球形落锤冲击试验的有限元模拟，获取不同冲击能量下层合板的低速冲击响应和损伤情况，验证本文提出的连续介质损伤力学分析模型.

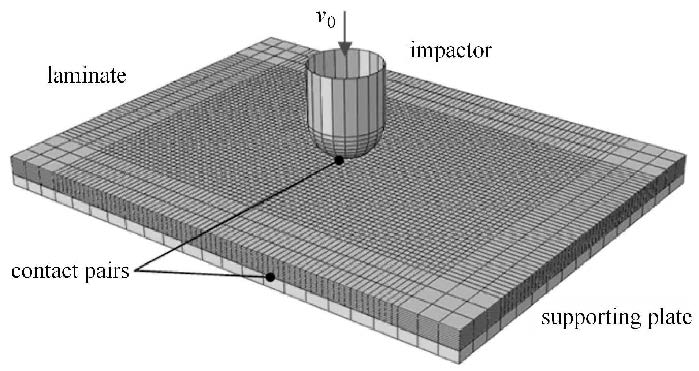
层合板的材料分别为HS300/ET223和T300/ NY9200Z，相应的铺层顺序分别为[0$_{3}$/45/$-$45]$_{\rm S}$和[45/0/$-$45/90]$_{\rm 4S}$，单层板材料属性见表2.有限元建模时层合板采用8节点减缩积分实体单元(C3D8R)模拟，厚度方向上将每一子层离散为一个单元，为减小计算时间，网格在冲击中心区域附近局部细化，并采用沙漏控制技术^[35].因为钢制冲头和支持夹具的刚度远大于层合板厚度方向的刚度，故不考虑二者的变形，将其视为刚体.考虑钢制冲头及夹具表面与试件表面的摩擦，滑动摩擦系数取为0.3^[10]. 复合材料层合板低速冲击有限元模型见图4.

4.1 [0$_{3}$/45/$-$45]$_{\rm S}$层合板

试验源自文献 ^[36]，矩形试件尺寸为65 mm× 87.5 mm × 3.2 mm，试验时被置于45 mm ×67.5 mm的矩形开 口简支支持夹具上.试验中通过改变落锤高度来调节冲击能量，冲头为直径12.5 mm的半球形钢球，质量为2.34 kg.试件铺层顺序为[0$_{3}$/45/$-$45]$_{\rm S}$，共10层，材料体系为HS300/ET223. 计算中基体裂纹饱和密度参数$\rho_{\rm crack} = 2.25$ mm$^{ -1}$. 由于断裂模式相同，横向拉伸临界断裂能释放率$G_{\rm 2c}^t$和面内剪切临界断裂能释放率$G_{\rm 12c} $分别用标准试验实测的I型和II型断裂能释放率$G_{\rm Ic} $,$G_{\rm IIc}$代替，大小分别为0.52 N/mm和0.92 N/mm^[36]. 层间剪切临界断裂能释放率$G_{\rm 23c} $取值与$G_{\rm 12c}$相同.模型根据试验时试件的真实夹持条件，将矩形开口简支夹具固支，同时限制冲头除冲击方向外的其余自由度，局部细化网格大小为1 mm×1 mm.

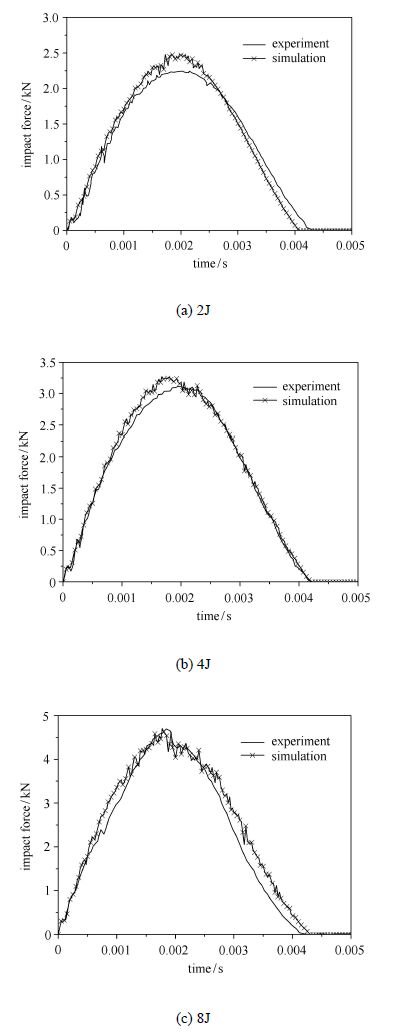
不同冲击能量下有限元预测与试验实测的冲击力-时间历程和冲击力-位移曲线见图5和图6.总体来说，3种能量下的 预测值与试验结果吻合良好.

图5的有限元结果表明，达到最大冲击力后冲击载荷出现较明显的突降现象，此时，层合板冲击背面子层发生了纤维拉伸断裂，试验曲线也显示出 类似的趋势，并且也在相同位置观察到纤维断裂.预测值与试验结果说明冲击背部的纤维损伤是导致层合板承受面外载荷能力突降的主要原因. 对应于2 J,4 J和8 J的冲击能量，试验测得的最大冲击力分别为2.3 kN，3.1 kN和4.6 kN，预测值分别为2.5 kN，3.3 kN和4.7 kN，有限元预测的误差分别为8.7%，6.4%和2.2%.

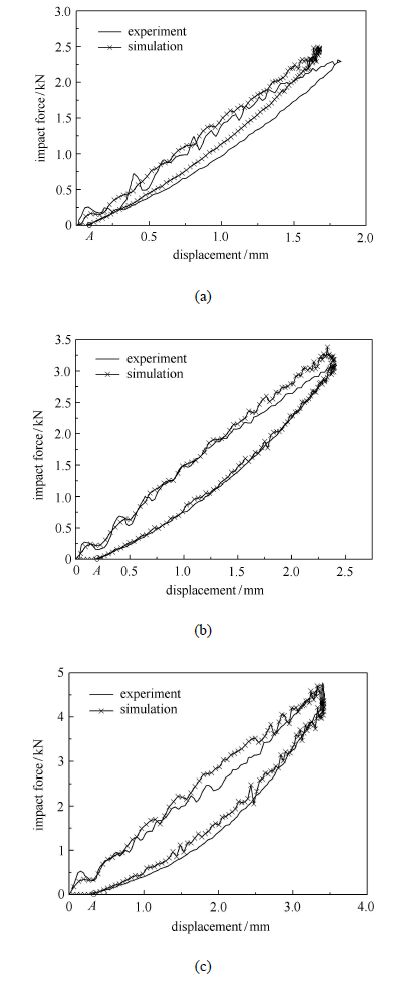
从图6可见，伴随层合板内部损伤萌生和扩展，损伤位置材料的局部软化，引起材料宏观刚度逐渐降低，导致冲击力-位移曲线出现波动.当冲头回弹后，由于损伤使得层合板的宏观刚度小于冲击前未损伤层合板的宏观刚度，并且冲击力与材料刚度成正比，所以相同位移下卸载阶段的冲击力小于加载阶段的冲击力，冲击力-位移曲线整体表现出非线性的特点.

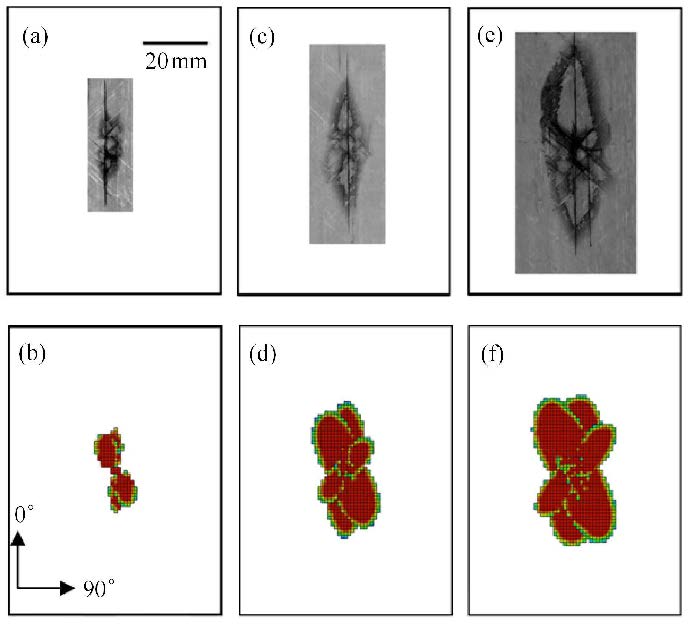
图7为不同冲击能量下层合板内部分层损伤投影形貌，有限元预测的分层投影形状大致呈椭圆形，其长轴沿着0°纤维方向，损伤特征与试验观测结果基本一致.当冲击能量增加时，分层投影长轴的预测值与测量值之间的误差有变大的趋势，这主要是由于模型中分层损伤是通过减缩积分单元中部积分点的应力值进行判断的，而非理想地由相邻子层间的应力值计算得到的，这一近似会降低模型对分层损伤的预测精度，但是从损伤投影面积的预测值和试验结果的对比曲线(图8)来看，分层投影面积的预测值和试验测量值比较接近，预测点和拟合曲线位于实测点围成的数据条带内.

从图8可见，层合板的损伤面积和吸收的能量随着冲击能量的增加而增加，且损伤面积和吸收能量与冲击能量近似呈线性关系.层合板吸收的能量为冲头损失的动能，大小等于图6中冲击力-位移曲线包裹的面积，包括损伤耗散能、板的变形能(凹坑变形、挠曲变形、压实变形)、板的振荡动能^[37].随着冲击能量的逐渐增加，材料的损伤程度变得愈来愈严重，这将使得更多的能量因损伤而耗散.由图6可见，卸载阶段冲击力开始为0时(图6中点$A$)的冲头位移随着冲击能量的增加不断变大，说明较高能量下板会产生更严重的残余变形.因此损伤耗散能和变形能的增加是导致高能量下层合板吸收能量增加的原因.

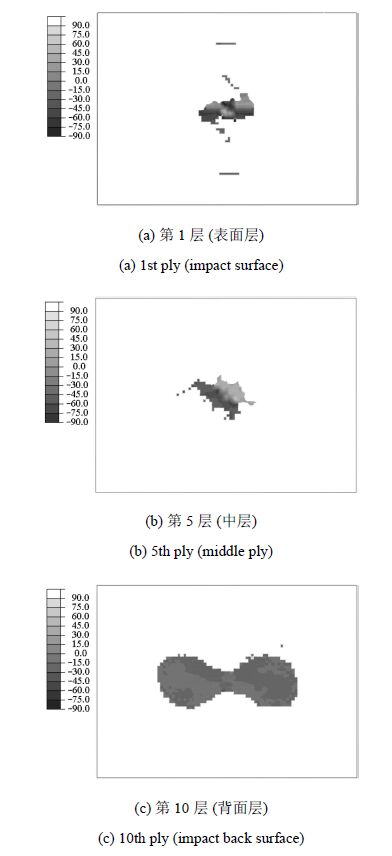
伴随着冲头的下压，所有能量下的层合板均在冲击背面首先出现沿纤维方向的基体拉伸损伤，随后由于损伤单元软化，载荷重新分配，损伤单元附近的完好单元的承载增大，基体损伤进一步扩展.以冲击能量为4J的试件为例，层合板在冲击后的基体损伤形貌多呈花生状. 图9为典型位置铺层的断裂面角度$\theta_{\rm fp} $ (用状态变量SDV8表示) 预测值的分布图，断裂面角度的参考坐标系为每个子层的材料主轴坐标系(见图1).计算结果表明，邻近冲击背面的铺层的断裂面角度大约为0°，接近面内横向拉应力单独作用时的角度，这主要是由于在冲击载荷作用下，层合板发生弯曲变形，冲击背面铺层的面内横向拉应力$\sigma_2 $导致基体拉伸损伤.冲击过程中层间剪应力沿板厚度方向呈抛物线状分布，层合板中部铺层承受的层间剪应力最大，因此，中部铺层的基体损伤主要是由层间剪应力所致，故其断裂面角度的大小在$\pm $45°附近.邻近冲击表面的铺层主要承受冲头的压力而使得材料发生基体压缩损伤，故冲头附近的基体断裂面角度均大于50°.上述有限元预测的基体断裂面角度大小及其沿厚度方向的分布情况与低速冲击试验[3,5,30 -33]观察到的基体裂纹分布规律一致.

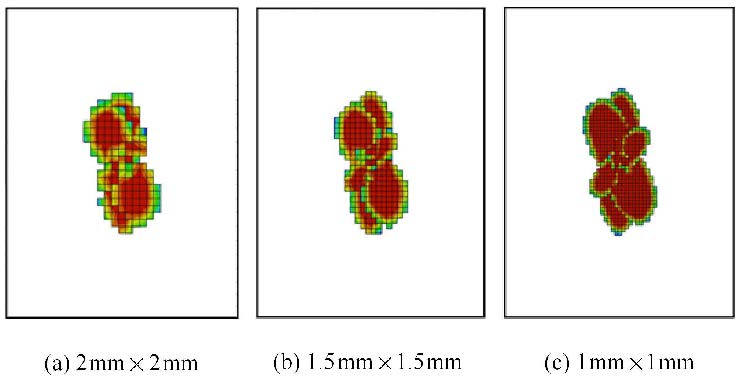
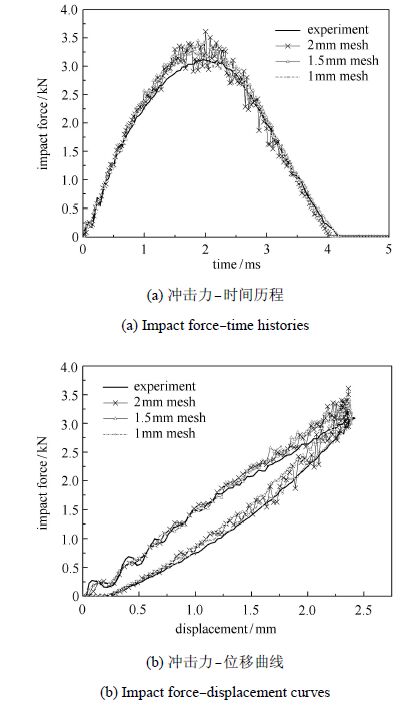
图10和图11分别给出了冲击能量为4J时，不同网格密度下的分层投影面积以及冲击力-时间历程与冲击力-位移曲线. 作为对比，在冲击中心区域局部细化的网格尺寸分别为2 mm×2 mm,1.5 mm×1.5 mm和1 mm×1 mm.结果表明对于不同的网格密度，预测的冲击力-时间历程与冲击力-位移曲线在趋势和数值上较为接近，分层投影区域的形状相似，大小基本一致，说明在本文的损伤演化模型中通过单元特征长度的引入在一定程度上降低了计算结果对网格的依赖性.但值得注意的是，虽然该方法可以使单元材料损伤造成的总耗散能与网格密度无关，但判断损伤起始的单元积分点上的应力仍然依赖于网格尺度，即不同的网格密度计算出的损伤区域不完全相同.对于低速冲击问题，试件与半球形冲头及支持夹具间的复杂接触响应也与网格密度密切相关，粗网格得到的冲击力曲线存在明显的震荡.因而引入单元特征长度的方法不可能完全消除网格敏感性.

4.2 [45/0/$-$45/90]$_{\rm 4S}$层合板

试验方法参考ASTM D7136标准. 试件长150 mm，宽100 mm，平均厚度为4 mm.采用均衡对称铺层，铺层顺序为[45/0/$-$45/90]$_{\rm 4S}$，铺层总数 共32层，材料体系为T300/NY9200Z.试验时将试件置于125 mm×75 mm的矩形开口简支支持夹具上，四周由4个夹子夹紧.试验中通过改变落锤质量来调节冲击能量，落锤高度保持在1.13 m，冲头为直径16 mm的半球形钢球，试件的分层面积由IUCS-II型便携式C扫描系统测得.

模型的边界条件为在简支夹具支持位置约束试件的$z$方向平动自由度，同时在试件拐角处约束$x$和$y$方向平动自由度，模拟夹子对试件的作用. 基体裂纹饱和密度参数为$\rho _{\rm crack} = 5.25$ mm$^{-1}$，I型和II型断裂能释放率$G_{\rm Ic}$和$G_{\rm IIc} $分别为0.175 N/mm和0.348 N/mm. 局部网格细化为1.5 mm×1.5 mm.

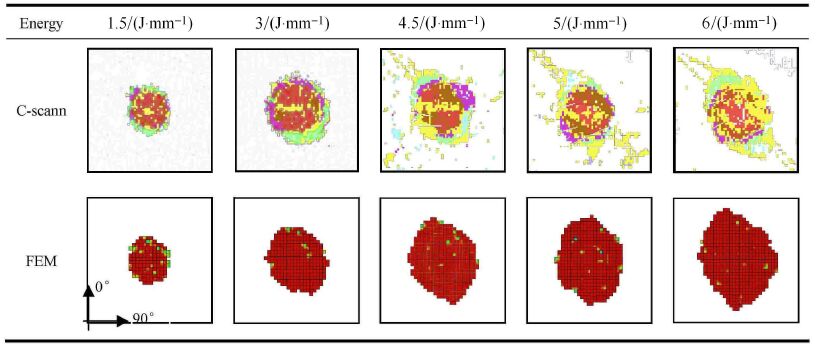
表3为不同冲击能量下，层间分层形状的预测值与试验结果的比较，表中截取的正方形区域大小为60 mm×60 mm.从中可见，有限元预测的分层投影形状与C扫描结果接近，冲击能量较低时，分层投影形状大致呈圆形，随着冲击能量的增加，形状变为椭圆形且长轴方向沿着冲击背面纤维铺设的方向.图12给出了预测的分层长度、宽度与测量值的比较，二者的总体趋势也比较一致.另外，断裂面角度沿厚度方向的分布情况与[0$_{3}$/45/--45]$_{\rm s}$层合板大致相同(见4.1节)，说明冲击载荷下，不同层合板的基体损伤机理是类似的.

5 结 论

本文基于冲击过程中基体裂纹的扩展机理引入基体裂纹饱和密度参数来表征层间分层的产生，建立了基于能量耗散原理的复合材料层合板面内渐进失效分析的连续介质损伤力学模型.采用该模型研究了两种不同材料和铺层的复合材料层合板的低速冲击响应问题，得到以下研究结果：

(1)复合材料基体裂纹直接造成材料在断裂面上的承载能力下降，损伤主轴与材料主轴一般不重合，采用连续介质损伤力学的分析方法推导了材料主轴坐标系下的损伤状态变量矩阵，并建立了基于应变能释放率的由断裂面上等效应变控制的线性连续损伤演化法则.

(2)采用基体裂纹饱和密度参数表征层间分层损伤的方法能够有效预测层合板的低速冲击响应参数，模型预测的冲击力-时间历程、冲击力-位移曲线、冲击中吸收的能量、分层投影大小与试验数据比较吻合，不同算例验证了本文连续介质损伤力学分析模型的有效性和普适性.

(3) 单元特征长度的引入在一定程度上降低了材料损伤演化阶段对网格密度的依赖性.

(4)基体损伤断裂面角度沿厚度方向的分布表明：邻近冲击表面的铺层受冲头压力而出现基体压缩损伤，断裂面角度大于50°；中部铺层的基体损伤主要是由层间剪应力所致，断裂面角度大约为45°；冲击背面的铺层因层合板弯曲产生的面内横向拉应力而出现基体拉伸损伤，基体裂纹面几乎垂直于板平面.