近年来,石墨烯、六方氮化硼($h$-BN)等二维原子晶体的奇异力学性能引起了研究者的关注[1, 2, 3, 4, 5, 6, 7]. 实验表明石墨烯和单层六方氮化硼的杨氏模量分别可达1.0 TPa[1]和0.776 TPa[2];文献[6]对单层石墨烯薄膜的分子动力学计算得到锯齿型单层石墨烯和扶手椅型单层石墨烯的杨氏模量分别约为1.03 TPa和1.06 TPa.然而,由于经典连续介质力学缺少描述物质粒子离散属性的内禀尺度参数,因而不能有效描述二维材料的一些力学行为,如尺度效应.现有的类石墨烯晶体理论模型基本上是通过等效途径建立 的[8, 9, 10, 11, 12, 13, 14].文献[10]提出的分子结构力学法得到了国内外研究人员的认可和应用,该方法核心思想是将共价键的谐和势能与经典结构力学中的典型单元(如杆、梁)的变形能进行均衡等效,从而确定等效单元的物理力学参数.文献[14]研究表明随着模型尺寸的增大,石墨烯逐渐表现出各向同性,且杨氏模量和泊松比分别趋于1.03 TPa和0.175,与已有的实验、理论值很接近.但基于分子结构力学法的模型在宏观上并非连续介质模型.
微态连续介质理论[15](简称微态理论)作为一种广义连续介质理论,假设物质是无数有限大小的可变形粒子(基元)的连续集 合.每个变形粒子除了3个宏观位移自由度外,还附加了描述粒子内部拉伸和旋转的9个微观变形自由度.由于假设基元粒子具有一定的体积,故其可承受偶应力作用,这也是微态理论与经典连续介质力学的本质区别.另外,可以在微态理论本构关系中可以引入材料内禀尺度参数,从而能够描述材料的尺度效应.各向同性线弹性微态模型的本构关系共含有18个材料常数,文献[16]提出了针对三维各向同性固体且不考虑基元旋转的特殊化微态理论,将材料常数减少到10个.文献[17]在线弹性、小变形及静态条件下,将微态材料常数减少到5个,研究了含约束薄膜的单轴拉伸行为.在小变形条件下,对于布拉维单胞中含有两个原子且具有三阶轴对称性的二维晶体[18],如石墨烯、单层$h$-BN,其力学行为具有各向同性性质,其布拉维单胞也可看作非刚性基元.故当特殊化微态理 论[16]简化为二维情况时,对类石墨烯二维晶体同样适用[19].另外,微态理论能够唯象地描述声子振动形式,通过给定谐波方程,一阶微态理论可给出12支声子色散关系[20].文献[16]利用微态形式的声子色散关系的久期方程拟合了单晶金刚石和硅的声子色散数据,计算了微态理论模型的材料常数.
本文首先根据微态理论基本方程和相关假设推导出类石墨烯二维原子晶体模型的主导方程,并给出简化的模型本构方程. 然后以石墨烯和单层$h$-BN为例,通过拟合其声子色散关系数据进而确定模型材料常数. 最后,将理论模型算例的等效杨氏模量与泊松比和已有的实验值进行对比、验证,并对所得模型本构常数进行了分析.
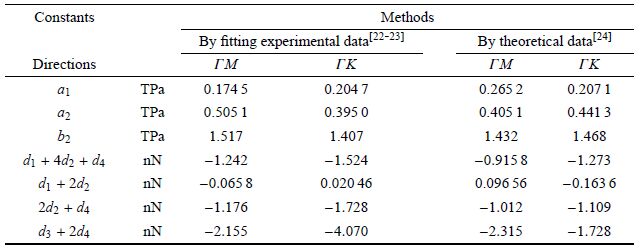
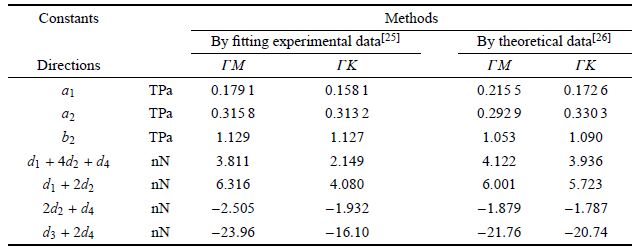
1 微态理论与声子色散关系 1.1 基元体类石墨烯二维原子晶体一般是指具有单原子层或多层的平面六角结构晶体[21],如石墨烯和$h$-BN,本文只研究其单原子层结构的面内弹性力学性能. 其中,单层$h$-BN由B和N原子依次交替排列形成,如图1(b). 由于它们的布拉维单胞不仅与其原胞等效,而且具有平移周期性,故可作为类石墨烯晶体的基元体,如图1所示.
|
图1
类石墨烯晶体结构及其布拉维单胞(菱形线框区域)[21] (a)石墨烯; (b)单层六方氮化硼 Fig.1 The structure of graphene-like crystals and their Bravais unit cells (within diamond)[21] (a) Graphene; (b) Monolayer $h$-BN |
根据微态理论基本方程[15]以及线弹性、小变形、不考虑体力和体力偶等[16]基本假设,可推导出在全局坐标系下以基元体宏观位移$u_{\alpha}$和微观变形$\varphi_{\alpha \beta } (=\varphi_{\beta \alpha })$表示的二维模型主导方程
\[\begin{array}{l}
\rho {{\ddot u}_\alpha } = {a_1}{u_{m,m\alpha }} + {a_2}({u_{\alpha ,\beta \beta }} + {u_{\beta ,\alpha \beta }}) + ({c_1} - {a_1}){\varphi _{mm,\alpha }} + \\
2({c_2} - {a_2}){\varphi _{\alpha \beta ,\beta }}
\end{array}\]
(1)
\[\begin{array}{l}
\rho j{{\ddot \varphi }_{\alpha \beta }} = ({a_2} - {c_2})({u_{\alpha ,\beta }} + {u_{\beta ,\alpha }}) + ({a_1} - {c_1}){\delta _{\alpha \beta }}{u_{m,m}} + \\
(2{c_1} - {a_1} - {b_1}){\delta _{\alpha \beta }}{\varphi _{mm}} + 2(2{c_2} - {a_2} - {b_2}){\varphi _{\alpha \beta }} + \\
2{d_1}({\varphi _{nn,\alpha \beta }} + {\delta _{\alpha \beta }}{\varphi _{rn,rn}}) + 4{d_2}({\varphi _{\alpha n,\beta n}} + {\varphi _{\beta n,\alpha n}}) + \\
{d_3}{\delta _{\alpha \beta }}{\varphi _{nn,rr}} + 2{d_4}{\varphi _{\alpha \beta ,rr}}
\end{array}\]
(2)
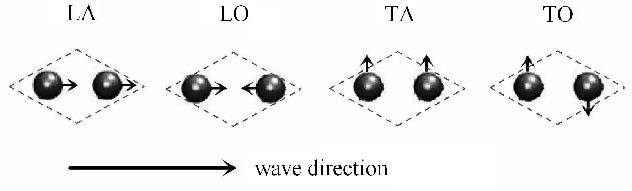
对于含有两个原子的类石墨烯晶体布拉维单胞,根据晶格动力学理论可知共有6支色散关系,其中有4支属于面内振动模式,即纵向声学支(LA)、纵向光学支(LO)、横向声学支(TA)和横向光学支(TO),如图2所示.
|
图2 含两个原子的布拉维单胞面内色散关系 Fig.2 The in-plane phonon dispersion relations of Bravais unit cells containing two atoms |
根据文献 [16]的相关分析,可知在纵向振动中被唯象激发的变形粒子的自由度只有$u_{1}$和 $\varphi_{11}$;在面内横向振动中被唯象激发的微态自由度为$u_{2}$和$\varphi _{12}$. 故由主导方程(2)展开得到
\[({a_1} - {c_1}){u_{1,1}} + (2{c_1} - {a_1} - {b_1}){\varphi _{11}} + (2{d_1} + {d_3}){\varphi _{11,11}} \equiv 0\]
(3)
\[\left. \begin{array}{l}
{u_\alpha } = {\rm{i}}{U_\alpha }\exp ({\rm{i}}kx - {\rm{i}}\omega t)\\
{\varphi _{\alpha \beta }} = {\Phi _{\alpha \beta }}\exp ({\rm{i}}kx - {\rm{i}}\omega t)
\end{array} \right\}\]
(4)
(1) LA,LO
\[\left| {\begin{array}{*{20}{c}}
{{A_{11}}{k^2} - \rho {\omega ^2}}&{{A_{12}}k }\\
{{A_{12}}k}&{{A_{22}}{k^2} + {B_{22}} - \rho j{\omega ^2}}
\end{array}} \right| = 0\]
(5)
(2) TA,TO
\[\left| {\begin{array}{*{20}{c}}
{{{\bar A}_{11}}{k^2} - \rho {\omega ^2}}&{{A_{12}}k}\\
{{A_{12}}k}&{{{\bar A}_{22}}{k^2} + 2{B_{22}} - 2\rho j{\omega ^2}}
\end{array}} \right| = 0\]
(6)
\[\left. \begin{array}{l}
{A_{11}} = {a_1} + 2{a_2},{{\bar A}_{11}} = {a_2},{A_{12}} = 2{a_2} - 2{c_2}\\
{{\bar A}_{22}} = 8{d_2} + 4{d_4},{A_{22}} = 2{d_1} + 8{d_2} + 2{d_4} \\
{B_{22}} = 2({a_2} + {b_2} - 2{c_2})
\end{array} \right\}\]
(7)
由于在同方向振动中,声学支和光学支微态方程的表达式相互耦合,使得久期方程(5)和(6)不能有效拟合声子色散关系数据. 故我们根据二维晶体声子色散关系特点,提出了一种解耦方法,即声学支在布里渊区中心附近区域时,其振动模式类似声波,可忽略光学支的耦合作用(本文中声学支色散关系数据取自于第一布里渊区的四分之一区域). 光学支色散关系数据应优先取自于第一布里渊区(简约区)的半区域内,其次是全区域内[16]. 由于石墨烯的面内横向光学支色散数据在第一布里渊区半区域内相对较少,为保证拟合的有效性及可行性,本文中石墨烯光学支色散数据均取自第一布里渊区的全区域. 由上述分析,可得待定材料常数关系$a_{2}=c_{2}$. 故简化的类石墨烯晶体面内声子色散关系,即频率与波矢($\omega $-$k$)的关系式,如方程(8)$\sim $(11). 声学支方程(8)和(10)中 $\omega $ 和$k$的线性关系,以及光学支方程(9)和(11)具有相同的截止频率,均与二维晶体声子色散特性相符,表明所得的简化方程具有一定的可行性.
\[{\omega _{{\rm{LA}}}} = k\sqrt {{A_{11}}/\rho } \]
(8)
\[{\omega _{{\rm{LO}}}} = \sqrt {({A_{22}}{k^2} + {B_{22}})/(\rho j)} \]
(9)
\[{\omega _{{\rm{TA}}}} = k\sqrt {{{\overline {A} }_{11}}/\rho } \]
(10)
\[{\omega _{{\rm{TO}}}} = \sqrt {({{\overline {A} }_{22}}{k^2} + 2{B_{22}})/(2\rho j)} \]
(11)
根据前文已得的材料常数之间关系及特殊化微态理论[16]的本构关系,可推导出类石墨烯晶体模型的二维本构方程
\[\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{t_{11}}\\
{t_{22}}\\
{t_{12}}\\
{s_{11}}\\
{s_{22}}\\
{s_{12}}
\end{array}
\end{array}} \right\} = \left| {\begin{array}{*{20}{l}}
{{a_1} + 2{a_2}}&{{a_1}}&0&{{a_1} + 2{a_2}}&{{a_1}}&0\\
{{a_1}}&{{a_1} + 2{a_2}}&0&{{a_1}}&{{a_1} + 2{a_2}}&0\\
0&0&{{a_2}}&0&0&{{a_2}}\\
{{a_1} + 2{a_2}}&{{a_1}}&0&{{a_1} + 2{b_2}}&{{a_1}}&0\\
{{a_1}}&{{a_1} + 2{a_2}}&0&{{a_1}}&{{a_1} + 2{b_2}}&0\\
0&0&{{a_2}}&0&0&{2{b_2}}
\end{array}} \right|\left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{\varepsilon _{11}}\\
{\varepsilon _{22}}\\
{\varepsilon _{12}} + {\varepsilon _{21}}\\
{\varphi _{11}}\\
{\varphi _{22}}\\
{\varphi _{12}}
\end{array}
\end{array}} \right\}\]
(12)
\[\begin{array}{l}
\left\{ {\begin{array}{*{20}{c}}
{{m_{111}}}\\
{{m_{222}}}\\
{{m_{211}}}\\
{{m_{122}}}\\
{{m_{112}}}\\
{{m_{212}}}
\end{array}} \right\} = \\
\left[ {\begin{array}{*{20}{c}}
{2{d_1} + 8{d_2} + 2{d_4}}&0&0&0&0&{2{d_1} + 4{d_2}}\\
0&{2{d_1} + 8{d_2} + 2{d_4}}&0&0&{2{d_1} + 4{d_2}}&0\\
0&0&{{d_3} + 2{d_4}}&0&{2{d_1} + 4{d_2}}&0\\
0&0&0&{{d_3} + 2{d_4}}&0&{2{d_1} + 4{d_2}}\\
0&{{d_1} + 2{d_2}}&{{d_1} + 2{d_2}}&0&{4{d_2} + 2{d_4}}&0\\
{{d_1} + 2{d_2}}&0&0&{{d_1} + 2{d_2}}&0&{4{d_2} + 2{d_4}}
\end{array}} \right] \cdot \\
\left\{ {\begin{array}{*{20}{c}}
{{\gamma _{111}}}\\
{{\gamma _{222}}}\\
{{\gamma _{211}}}\\
{{\gamma _{122}}}\\
{{\gamma _{112}}}\\
{{\gamma _{212}}}
\end{array}} \right\}
\end{array}\]
(13)
以石墨烯和单层$h$-BN为例,利用方程(8)$\sim$(11)分别沿 $\Gamma M$和 $\Gamma K$方向拟合了石墨面内/石墨烯声子色散关系的实验值[22- 23]及理论值[24],拟合曲线如图3,其中纵坐标频率用能量表示.图3中的光学支截止声子能量的拟合值198.0 meV和199.4 meV均与他们的实验值[22]或理论值[24]相符合.
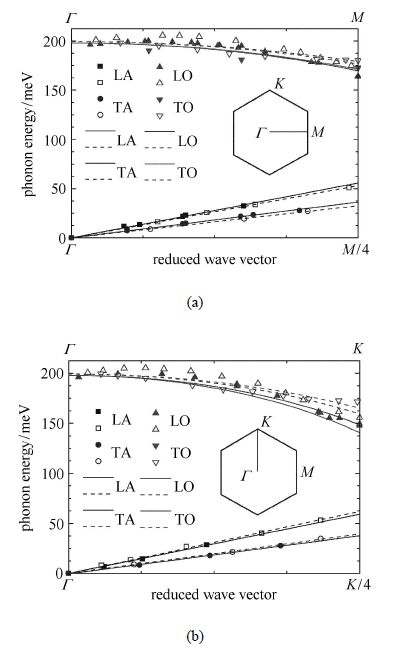
|
图3
石墨烯声子色散关系拟合曲线图 (a)沿 $\Gamma M$方向, (b)沿 $\Gamma K$方向,实心符号代表实验数据[22, 23],空心符号代表理论数据[24]. 曲线为拟合函数 Fig.3 The fitting curves of phonon dispersion relations of graphene. (a) Along $\Gamma M$ direction,(b) Along $\Gamma K$ direction,the solid symbols represent the experimental data[22, 23],the hollow symbols represent the theoretical data[24],the lines represent the fitting functions |
利用同样方法拟合了单层$h$-BN声子色散关系的实验值[25]及理论值[26],拟合曲线如图4. 图4中的光学支截止声子能量的拟合值171.4 meV和175.4 meV同样与它们的实验值[27]或理论值[26]相接近.每个模型算例计算得到的材料常数值(或其线性组合的值)基本上保持一致,见表1和2.由于在同一波矢位置,不同方法测得的声子能量存在差异,从而造成材料常数计算值上的差异.
为计算二维晶体模型的等效三维力学参数,石墨烯理论厚度取0.335 nm[28],单层$h$-BN取文献 [25, 26]中对应的值0.325 4 nm和0.365 nm.由表1可计算出石墨烯微态理论模型的等效杨氏模量和泊松比分别为1.05 TPa和0.197;由表2可得单层$h$-BN微态理论模型的等效杨氏模量和泊松比分别为0.766 TPa和0.225.其中,两个模型算例的等效杨氏模量分别与已有的实验值1.0 TPa[1]和0.776 TPa[2]符合较好,泊松比分别与实验值0.17[29]和0.208[2]较接近,从而表明本文构建的类石墨烯晶体微态理论模型具有一定的有效性.
另外,微态各向同性材料的稳定性可由两个独立的应变能密度函数均非负来保证[15],本文中可通过本构方程(12)和(13)中的常数矩阵的正定性来验证.分别把表1和表2中的4组材料常数的均值代入本构方程(12)和(13)中进行计算,得到方程(12)中本构矩阵的特征值均是正值,而方程中(13)本构矩阵的特征值并非都是正值,不能满足应变能密度函数均非负. 可以推测这主要因为方程中 (13)中的常数矩阵中存在较多(甚至全部)的负本构常数. 对于此问题,研究人员给出了不同的解释,如文献 [30]从晶格格点平衡的角度认为本构常数可以是负值;文献 [31]从周期单胞上应变能密度函数积分非负观点认为本构常数可为负值. 因而,本文计算所得的本构常数具有一定合理性.
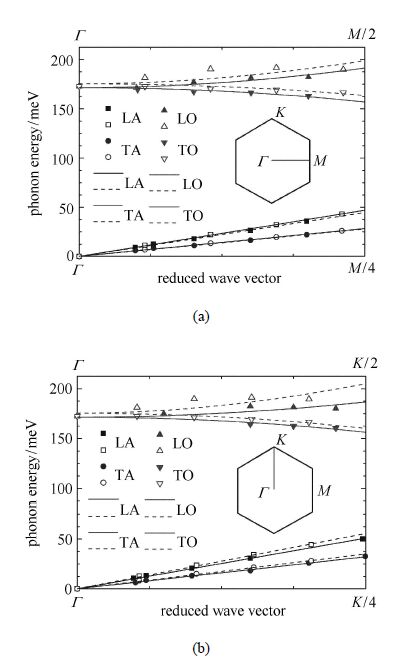
|
图4
单层$h$-BN声子色散关系拟合曲线图 (a)沿 $\Gamma M$方向,(b)沿 $\Gamma K$方向,实心符号代表实验数据[25],空心符号代表理论数据[26]. 曲线为拟合函数 Fig.4 The fitting curves of phonon dispersion relations of monolayer $h$-BN. (a) Along $\Gamma M $ direction,(b) Along $\Gamma K$ direction,the solid symbols represent the experimental data[25],the hollow symbols represent the theoretical data[26],the lines represent the fitting functions |
| 表1 石墨烯微态理论模型的材料常数 Table 1 The material constants of graphene micromorphic model |
| 表2 单层$h$-BN微态理论模型的材料常数 Table 2 The material constants of a micromorphic model of monolayer $h$-BN |
本文所构建的类石墨烯晶体微态理论模型只适合研究其面内力学行为,然而二维晶体的离面力学行为也是当前的热点研究方向.目前,已有研究者基于科瑟拉(Cosserat)连续介质理论、修正的偶应力理论和应变梯度理论研究了石墨烯或薄板的振动特性[32, 33, 34],而这些理论均可由微态理论经过适当简化、修正得到.另外,本文在求类石墨烯晶体的面内材料常数时,仅拟合了其面内声子色散数据,故我们推测其离面力学常数(如弯曲刚度)可以通过拟合其面外声子色散数据来确定. 因此,基于微态理论研究类石墨烯晶体的离面力学性能应该是可行的.
3 结 论本文给出了针对石墨烯、单层$h$-BN等二维六角原子晶体的微态理论模型. 首先,依据三维微态理论基本方程,推导了二维各向同性材料的主导方程,该模型考虑了有限大小基元粒子(布拉维单胞)的宏观位移和微观变形.然后针对布拉维单胞中含有两个原子的类石墨烯晶体,将布拉维单胞中原子振动特性与基元体自由度相联系,得到了二维情况下微态形式的声子色散关系久期方程,并根据二维晶体色散特性对其进行了简化,进而确定了类石墨烯模型的本构方程.最后,以石墨烯和单层六方氮化硼为例,利用简化得到的面内LA,LO,TA和TO四支色散关系式,拟合了已有的实验和理论色散关系数据,计算了两个模型的材料常数,其等效杨氏模量及泊松比与已有的实验值均相符合,表明本文提出的类石墨二维原子晶体的微态理论模型具有有效性和应用前景.
| [1] | Lee C, Wei X, Kysar JW, et al. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science, 2008, 321(5887): 385-388 |
| [2] | Bosak A, Serrano J, Krisch M, et al. Elasticity of hexagonal boron nitride: Inelastic x-ray scattering measurements. Physical Review B, 2006, 73(4): 041402 |
| [3] | Zhang B, Mei L, Xiao H. Nanofracture in graphene under complex mechanical stresses. Applied Physics Letters, 2012, 101 (12): 121915-121915. |
| [4] | Zhang B. Layered graphene structure of a hexagonal carbon. Physica B: Condensed Matter, 2013, 413: 73-75 |
| [5] | Zhang B, Yang G, Xu H. Instability of supersonic crack in graphene. Physica B: Condensed Matter, 2014, 434: 145-148 |
| [6] | 韩同伟, 贺鹏飞, 王建等. 单层石墨烯薄膜拉伸变形的分子动力学模拟. 新型碳材料, 2010, 25(4): 261-266 (Han Tongwei, He Pengfei, Wang Jian, et al. Molecular dynam ics simulation of a single graphene sheet under tension. New Carbon Materials, 2010, 25(4): 261-266 (in Chinese)) |
| [7] | 韩同伟, 贺鹏飞, 骆英等. 石墨烯力学性能研究进展. 力学进展, 2011, 41(3): 279-293 (Han Tongwei, He Pengfei, Luo Ying, et al. Research progress in the mechanical properties of graphene. Advances in Mechanics, 2011, 41(3): 279-293 (in Chinese)) |
| [8] | Alzebdeh KI. An atomistic-based continuum approach for calculation of elastic properties of single-layered graphene sheet. Solid State Communications, 2014, 177: 25-28 |
| [9] | Sakhaee-Pour A. Elastic properties of single-layered graphene sheet. Solid State Communications, 2009, 149 (1): 91-95 |
| [10] | Li C, Chou TW. A structural mechanics approach for the analysis of carbon nanotubes. International Journal of Solids and Structures, 2003, 40(10): 2487-2499 |
| [11] | Scarpa F, Adhikari S, Phani AS. Effective elastic mechanical properties of single layer graphene sheets. Nanotechnology, 2009, 20(6): 065709 |
| [12] | Boldrin L, Scarpa F, Chowdhury R, et al. Effective mechanical properties of hexagonal boron nitride nanosheets. Nanotechnology, 2011, 22(50): 505702 |
| [13] | 王飞, 庄守兵, 虞吉林. 用均匀化理论分析蜂窝结构的等效弹性参数. 力学学报, 2002, 34(6): 914-923 (Wang Fei, Zhuang Shoubing, Yu Jilin. Application of homogenization FEM to the equivalent elastic constants of honeycomb structures. Acta Mechanica Sinica, 2002, 34(6): 914-923 (in Chinese)) |
| [14] | 唐文来, 彭倚天, 倪中华. 基于有限元分析的石墨烯弹性性能和振动特性. 东南大学学报, 自然科学版, 2013, 43(2): 345-349 (Tang Wenlai, Peng Yitian, Ni Zhonghua. Analytical and numerical investigations for thin-film with constraint under uniaxial tension. Journal of Southeast University (Natural Science Edition), 2013, 43(2): 345-349 (in Chinese)) |
| [15] | Eringen AC. Microcontinuum Field Theories I: Foundations and Solids, 1999. New York: Springer |
| [16] | Chen Y, Lee JD. Determining material constants in micromorphic theory through phonon dispersion relations. International Journal of Engineering Science, 2003, 41(8): 871-886 |
| [17] | 张朝晖, 高原, 聂君锋等. 含约束薄膜的单轴拉伸的理论与数值研究. 工程力学, 2011, 28(11): 31-37 (Zhang Zhaohui, Gao Yuan, Nie Junfeng, et al. Analytical and numerical investigations for thin-film with constraint under uniaxial tension. Engineeing Mechanics, 2011, 28(11):31-37 (in Chinese)) |
| [18] | Berinskii IE, Borodich FM. On the isotropic elastic properties of graphene crystal lattice. Surface Effects in Solid Mechanics. Berlin Heidelberg: Springer, 2013: 33-42 |
| [19] | Zhang B, Yang G. A micromorphic model for monolayer hexagonal boron nitride with determined constitutive constants by phonon dispersions. Physica B: Condensed Matter, 2014, 451: 48-52 |
| [20] | Chen Y, Lee JD, Eskandarian, A. Atomistic viewpoint of the applicability of microcontinuum theories. International Journal of Solids and Structures, 2004, 41 (8): 2085-2097 |
| [21] | Miró P, Audiffred M, Heine T. An atlas of two-dimensional materials. Chemical Society Reviews, 2014, 43: 6537-6554 |
| [22] | Maultzsch J, Reich S, Thomsen C, et al. Phonon dispersion in graphite. Physical Review Letters , 2004, 92(7): 075501 |
| [23] | Mohr M, Maultzsch J, Dobardžić E, et al. Phonon dispersion of graphite by inelastic x-ray scattering. Physical Review B, 2007, 76(3): 035439 |
| [24] | Dubay O, Kresse G. Accurate density functional calculations for the phonon dispersion relations of graphite layer and carbon nanotubes. Physical Review B, 2003, 67(3): 035401 |
| [25] | Serrano J, Bosak A, Arenal R, et al. Vibrational properties of hexagonal boron nitride: inelastic X-Ray scattering and ab initio calculations. Physical Review Letters, 2007, 98(9): 095503 |
| [26] | Wirtz L, Rubio A, de La Concha RA, et al. Ab initio calculations of the lattice dynamics of boron nitride nanotubes. Physical Review B, 2003, 68(4): 045425. |
| [27] | Geick R, Perry CH, Rupprecht G. Normal modes in hexagonal boron nitride. Physical Review, 1966, 146: 543-547 |
| [28] | Al-Jishi R, Dresselhaus G. Lattice-dynamical model for graphite. Physical Review B, 1982, 26(8): 4514-4522 |
| [29] | Blakslee OL, Proctor DG, Seldin EJ, et al. Elastic constants of compression-annealed pyrolytic graphite. Journal of Applied Physics, 1970, 41(8): 3373-3382 |
| [30] | Bažant ZP, Christensen M. Analogy between micropolar continuum and grid frameworks under initial stress. International Journal of Solids and Structures, 1972, 8(3): 327-346 |
| [31] | Kumar RS, McDowell DL. Generalized continuum modeling of 2-D periodic cellular solids. International Journal of Solids and Structures, 2004, 41(26): 7399-7422 |
| [32] | Akgöz B, Civalek Ö. Free vibration analysis for single-layered graphene sheets in an elastic matrix via modified couple stress theory. Materials & Design, 2012, 42: 164-171 |
| [33] | 徐巍, 王立峰, 蒋经农. 基于应变梯度有限元的单层石墨烯振动研究. 固体力学学报, 2014, 35(5): 441-450 (Xu Wei, Wang Lifeng, Jiang Jingnong. Finite element analysis of strain gradient on the vibration of single-layered graphene sheets. Chinese Journal of Solid Mechanics, 2014, 35(5): 441-450 (in Chinese)) |
| [34] | 王晓明, 王飞, 赵学增等. 基于Cosserat理论的四边简支自由振动微平板尺度效应研究. 固体力学学报, 2012, 33(1): 63-68 (Wang Xiaoming, Wang Fei, Zhao Xuezeng, et al. On the size effects in a freely-vibrating micro-plate with the four edges simply-supported based on the cosserat theory. Chinese Journal of Solid Mechanics, 2012, 33(1): 63-68 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47