引 言
涡激振动问题是自然界中常见的现象,如高层建筑、海洋平台、海底管道等由于受到风或海流的作用,会因旋涡脱落而导致结构振动,在科学研究和实际工程中具有重要意义.涡激振动过程涉及湍流与漩涡、物体的运动与变形、流体与固体的耦合作用等复杂问题.该力学过程的难点在于流场的精确捕捉和运动物体的数值处理技术. 而振荡圆柱问题是该问题的典型算例.
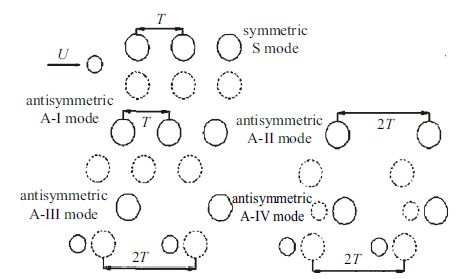
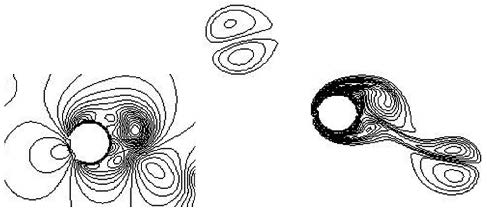
圆柱流向强迫振荡绕流是复杂的流固耦合现象,此研究方向以实验居多.文献[1]和文献[2]最早开展了流向振荡问题的实验研究.实验[3, 4, 5, 6, 7]重点研究了静止流体中强迫振荡圆柱的涡脱模式,并根据不同科勒冈-卡朋特(Keulegan-Carpenter) 数(简称科卡数)$KC$将流场划分为不同的流态区($KC=U_{m}T/D$,其中$U_{m}$和$T$分别表示振荡的最大速度和周期,$D$为圆柱直径). 文献[8]分析了流向振荡圆柱涡脱落形态,将涡脱落模态详细分为对称S模态和反对称A-I,A-II,A-III,A-IV模态,如图1所示,实线与虚线旋向相反.文献[9, 10, 11, 12, 13, 14]对流向振荡柱体尾流旋涡脱落模式进行了研究,分析了柱体受力以及不同涡脱模态的存在条件.随着计算机的快速发展,国内外学者采用不同的方法对该问题进行了研究.文献[9]和文献[15]利用文献[16]模拟了振荡圆柱引起的涡脱形态,得到了良好的结果.文献[17]通过共轭光谱傅里叶分析的方法研究了旋涡脱落的锁定模态.文献[18]的数值模拟表明由于尾流的准周期性振荡会引起尾流产生复杂的频谱.文献[19]应用运动网格技术计算了科卡数$KC$在不同流态区下的振荡圆柱流场,并分析了圆柱的受力情况.文献[20]采用动网格与静网格结构的方式,分析了振荡圆柱绕流中的涡脱情况.文献[21]采用任意拉格朗日-欧拉(简称任意拉欧)混合动网格方法对流向强迫振荡圆柱绕流问题进行了数值模拟,观察各个模态涡脱落现象.任意拉欧方法对于物体表面和远场边界描述观点的不同而使物体在运动中容易引起网格畸变[22],且柱体表面网格的正交性不易保持.
圆柱强迫振荡绕流会产生复杂的流体动力效应,其数值模拟的主要难度在于动边界的处理,而现在较为常用的动网格技术,由于需要不断地更新网格点的信息,使得计算耗时较大,不利于复杂问题的计算.本文拟采用自主研发的紧致插值曲线方法模型[23],在直角网格系统内,通过引入浸入边界方法,有效处理了流固耦合问题,可有效避免动态网格系统中的大量信息交换,保证模型的计算效率.紧致插值曲线作为一种高阶精度的离散方法,在水动力学的研究中有着广泛的应用.文献[24, 25]基于紧致插值曲线方法建立了适用于强非线性自由面问题的多相流数学模型,模拟了规则波与浮式结构的相互作用,得到了较好的结果.文献[26, 27]利用紧致插值曲线方法模型开展了畸形波与浮式结构物的相互作用的研究.文献[28]基于一种自适应紧致插值曲线方法模型开展了液面大变形问题的研究. 以紧致插值曲线模型为基础,文献[29]提出一种适用于自由面大变形流动的计算流体力学模型. 为了得到稳定的流场,本文采用了与传统差分格式不同的高阶差分紧致插值曲线方法对纳维-斯托克斯方程进行了离散,该方法通过对网格内结点函数值及其导数值联立方程,在一个网格内实现三阶精度的差分求解对流方程,具有格式稳定和低耗散性的特点. 本文将分别对静止流体中低科卡数$KC$振荡圆柱以及雷诺数$Re=200$时流向强迫振荡圆柱绕流进行数值模拟,模拟结果与文献结果进行比较,验证此方法处理复杂流动问题的准确性、高效性和有效性.
1 数学模型的建立
1.1 控制方程
本流场模型以二维纳维-斯托克斯方程为控制方程,其矢量形式为
|
\[\nabla \cdot u = 0\]
|
(1) |
|
\[\frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u = - \frac{1}{\rho }\nabla p + \frac{\mu }{\rho }{\nabla ^2}u + F\]
|
(2) |
为了把紧致插值曲线方法应用于对流方程,对方程(2)取空间导数,可得到下面的形式
|
\[\begin{array}{l}
\frac{{\partial ({\partial _i}u)}}{{\partial t}} + (u \cdot \nabla )({\partial _i}u) = \\
- {\partial _i}u \cdot \nabla u - {\partial _i}\left( {\frac{1}{\rho }\nabla p - \frac{\mu }{\rho }{\nabla ^2}u - F} \right)
\end{array}\]
|
(3) |
模型在直角笛卡尔系统下建立,采用多相流理论处理固-液的相互作用,满足下面的控制方程
|
\[\frac{{\partial {\phi _m}}}{{\partial t}} + u \cdot \nabla {\phi _m} = 0\]
|
(4) |
其中,$m = 1$,2,$\phi_1$为液体相,$\phi_2$为固体相,在一个网格内满足$\phi 1 + \phi_2 = 1$.固体相的处理基于浸入边界方法得到,将在下面的部分给出解释. 网格内的流体特性可用下式来表示
|
\[\lambda = \sum\limits_{m = 1}^2 {{\phi _m}{\lambda _m}} \]
|
(5) |
$\lambda $为密度$\rho $或黏性系数$\mu $.
1.2 数值方法
1.2.1 紧致插值曲线方法
紧致插值曲线 方法是文献[30]等于20世纪80年代中期提出并发展起来,用于求解双曲型偏微分方程的一种有效的数值计算方法. 其基本原理是基于 空间网格点的变量值及其空间导数值,利用三次多项式进行插值近似,反演出网格单元内部变量的真实信息,得到三阶精度的显式格式.为了更好地解释紧致插值曲线方法,考虑简单的常系数一维对流方程
|
\[\frac{{\partial f}}{{\partial t}} + u\frac{{\partial f}}{{\partial x}} = 0\]
|
(6) |
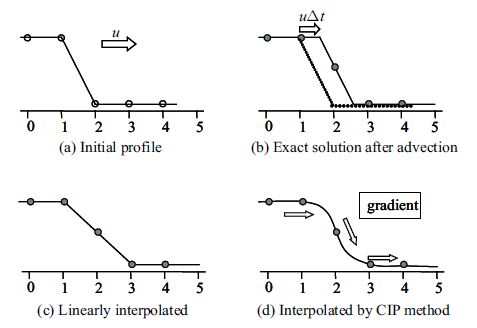
其中$u$为大于零的常数. 此类偏微分方程可用不同差分方法求解. 下面将给出紧致插值曲线方法的工作原理.图2(a)$\sim$图2(c)给出 了一阶迎风差分方法的工作原理,对于一阶差分格式来说,它利用直线的方式联立相邻两个节点的信息来工作,而忽略了网格内部的信息,导致较大的数值耗散.为了真实再现网格内部的信息,有必要求助高阶差分方法,而对于常规高阶差分的建立需要更多的网格点的信息.紧致插值曲线采用一种独特的方式,在一个网格内实现了高阶差分格式,通过利用空间网格点的变量值及其空间导数值,来描述该网格内的信息,可真实再现网格内的信息.
通过对方程(6)求关于$x$的偏导,得到如下的空间导数方程
|
\[\frac{{\partial g}}{{\partial t}} + u\frac{{\partial g}}{{\partial x}} = - g\frac{{\partial u}}{{\partial x}}\]
|
(7) |
其中$g=\partial f/\partial x$. 因对流速度$u$为常数,方程(7)右边项为0. 这样,方程(7)与方程(6)有相同的形式. 对于$u>0$的情况,在迎风向网格单元[$x_{i-1}$,$x_{i}$]内$n$时刻的剖面函数$f^{n}$可以近似为
|
\[F_i^n\left( x \right) = {a_i}{\left( {x - {x_i}} \right)^3} + {b_i}{\left( {x - {x_i}} \right)^2} + {c_i}\left( {x - {x_i}} \right) + {d_i}\]
|
(8) |
在$n+1$时刻的单元格剖面函数$f ^{n + 1}$可以通过将$n$时刻的剖面函数$f ^{n}$平移$-u\Delta t$得到,函数$f$和$g$的时间演变可以通过下面的拉格朗日变换得到
|
\[f_i^{n + 1} = F_i^n\left( {{x_i} - u\Delta t} \right),g_i^{n + 1} = {\rm{d}}F_i^n\left( {{x_i} - u\Delta t} \right)/{\rm{d}}x\]
|
(9) |
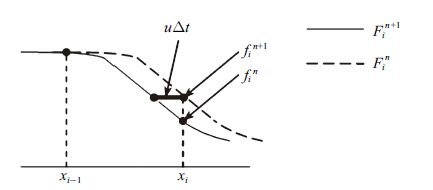
因此,从紧致插值曲线对流格式采用了拉格朗日常量解法(Lagrangian invariant solution)的角度来看,紧致插值曲线对流格式又称为半拉格朗日方法,如图3所示. 式(8)中的4个未知系数可由已知量$f_i^n$,$f_{i - 1}^n $,$g_i^n $和$g_{i - 1}^n $ 通过下列关系式来确定
|
\[\left. {\begin{array}{*{20}{l}}
{{a_i} = \frac{{g_i^n + g_{i - 1}^n}}{{\Delta {x^2}}} - \frac{{2\left( {f_i^n - f_{i - 1}^n} \right)}}{{\Delta {x^3}}},{c_i} = g_i^n}\\
{{b_i} = \frac{{2g_i^n + g_{i - 1}^n}}{{\Delta x}} - \frac{{3\left( {f_i^n - f_{i - 1}^n} \right)}}{{\Delta {x^2}}},{d_i} = f_i^n}
\end{array}} \right\}\]
|
(10) |
紧致插值曲线方法采用一种独特的方式,在一个网格内实现了高阶差分格式,使得本文的数值模型可以应用于复杂流动问题的模拟,这也是本文所采用的差分方法与其他方法的不同之处.
1.2.2 时间积分
采用分步算法对动量方程进行时间积分. 首先忽略扩散项和压力项,只考虑对流项的中间速度;其次求解扩散项;然后求解压力方程,计算下一时间步的压力;最后考虑压力梯度项,计算速度的最后值. 设$\Delta t$为时间步长,在$t=n \Delta t$到$t=(n+1)\Delta t$时刻的计算时间内,具体的时间积分过程如下
(1) 对流项(I)
|
\[\frac{{\partial u}}{{\partial t}} + \left( {u \cdot \nabla } \right)u = {\bf{0}}\]
|
(11a) |
|
\[\frac{{\partial \left( {{\partial _i}u} \right)}}{{\partial t}} + \left( {u \cdot \nabla } \right)\left( {{\partial _i}u} \right) = {\bf{0}}\]
|
(11b) |
通过紧致插值曲线方法[31]可得到方程的解
|
\[{u^ * } = X\left( {x - u\Delta t} \right)\]
|
(12a) |
|
\[{\left( {{\partial _i}u} \right)^ * }\left( x \right) = \frac{{\partial {X^ * }}}{{\partial {x_i}}}\left( {x - u\Delta t} \right)\]
|
(12b) |
其中"*"为对流项计算结束后的中间时间标志.
(2)非对流项(I)
下面进入扩散项的计算
|
\[\frac{{\partial u}}{{\partial t}} = \frac{\mu }{\rho }{\nabla ^2}u + F\]
|
(13a) |
|
\[\frac{{\partial ({\partial _i}u)}}{{\partial t}} = - {\partial _i}u \cdot \nabla u - {\partial _i}\left( {\frac{\mu }{\rho }{\nabla ^2}u + F} \right)\]
|
(13b) |
扩散项的时间离散采用显示格式,中间速度可表示为下面的形式
|
\[\frac{{{u^{**}} - {u^*}}}{{\Delta t}} = \frac{\mu }{\rho }{\nabla ^2}u + F\]
|
(14a) |
|
\[\frac{{{{({\partial _i}u)}^{**}} - {{({\partial _i}u)}^*}}}{{\Delta t}} = - {\partial _i}{u^*} \cdot \nabla {u^*} + {\partial _i}\left( {\frac{\mu }{\rho }{\nabla ^2}{u^*} + F} \right)\]
|
(14b) |
其中方程(14)的空间离散采用中心差分格式.
(3)非对流项(II)
下一步进入压力和速度的匹配
|
\[\frac{{\partial u}}{{\partial t}} = - \frac{1}{\rho }\nabla p\]
|
(15a) |
|
\[\frac{{\partial \left( {{\partial _i}u} \right)}}{{\partial t}} = - {\partial _i}\left( {\frac{1}{\rho }\nabla p} \right)\]
|
(15b) |
通过对方程 (15a)取散度,并引入连续方程,可得到如下形式的泊松方程
|
\[\nabla \cdot \left( {\frac{1}{\rho }\nabla {p^{n + 1}}} \right) = \frac{1}{{\Delta t}}\nabla \cdot {u^{ * * }}\]
|
(16) |
泊松方程的求解通过逐次超松弛迭代得到.
考虑动量方程的压力梯度项,计算速度的最终值,计算式为
|
\[{u^{n + 1}} = {u^{ * * }} - \frac{{\Delta t}}{\rho }\nabla {p^{n + 1}}\]
|
(17a) |
|
\[{\left( {{\partial _i}u} \right)^{n + 1}} = {\left( {{\partial _i}u} \right)^{ * * }} - \Delta t{\partial _i}\left( {\frac{1}{\rho }\nabla {p^{n + 1}}} \right)\]
|
(17b) |
根据式(4),(5)和(18)更新界面和网格内流体信息,然后返回到步骤1,这样就完成了整个计算过程,一直到设定的步骤结束.
1.3 固体边界处理
采用浸入边界方法 (immersed boundary method)[32]处理固体对流场的影响
|
\[{u^{n + 1}} = {\phi _2}U_{\rm{b}}^{n + 1} + \left( {1 - {\phi _2}} \right)u_{\rm{f}}^{n + 1}\]
|
(18) |
其中$ u_{\rm f}^{n +1}$为在欧拉坐标体系中通过式(17)计算得到的"局部"流场速度; $ U_{\rm b}^{n +1}$为通过拉格朗日方法得到的固体速度[25]; $ u^{n +1}$为二者耦合作用的"整体"速度,这样就得到了流固耦合流场的求解. 上述方法也可称为固体体积流固耦合处理方法. 基于浸入边界方法的流固耦合技术,采用固定网格,在计算过程中无需更新网格,可保证模型的高效率,使得模型在处理大位移的流固耦合计算中具有强大优越性. 本文采用的方法还具有较易实施的优势,方便模型向三维拓展.
2 算例及分析
2.1 主要参数定义
雷诺数: $Re=\rho UD/\mu$,其中,$U$为来流速度,$D$为柱体特征长度;
阻力系数: $C_{\rm d}=2F_{\rm d}/\rho U^{2}D$,其中,$F_{\rm d}$为流体作用于单位长度柱体上顺流速方向的分力;
升力系数: $C_{\rm l}=2F_{\rm l}/\rho U^{2}D$,其中,$F_{\rm l}$为流体作用于单位长度柱体上垂直流速方向的分力.
2.2 振荡圆柱
2.2.1 初始参数及计算模型
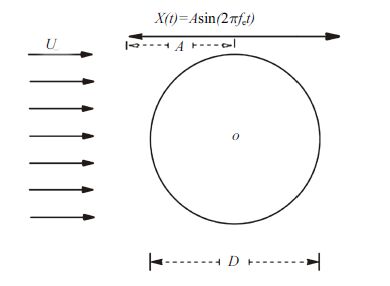
图4给出了静止流体中振荡圆柱全局网格及近壁网格划分示意图. 圆柱直径$D$为1 m,计算区域为30$D$×30$D$. 指定圆柱做水平简谐振荡\[X(t) = A\sin (2\pi {f_{\rm{e}}}t)\],$A$为圆柱振荡振幅,$f_{\rm e}$为圆柱振荡频率; 左右均为开边界,上下为自由滑移边界,柱体表面为无滑移边界.对于静止流体中的简谐振荡圆柱,描述圆柱振荡的无量纲数为$KC=U_{m}T/D$,$Re=U_{m}D/\nu$,其中$U_{m}$和$T$分别表示振荡的最大速度和振荡周期,$D$为圆柱直径,$\nu $为流体的运动黏性系数.
2.2.2 数值算例及结果分析
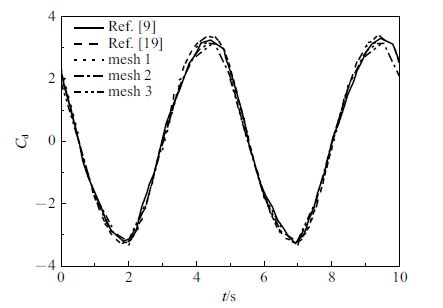
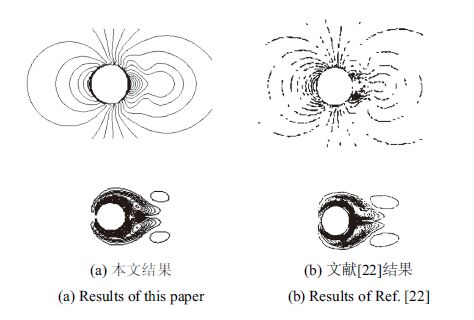
首先对$KC=5$,$Re=100$的静止流体中振荡圆柱进行了数值模拟. 选用三套网格,mesh 1,mesh 2和mesh3的最小尺寸分别为0.02 m,0.04 m和0.05 m,网格数分别为580×580,330×330和280×280.图5给出了计算得到的阻力系数时程曲线. 从图中可观察到三套网格的计算结果相差不大,说明网格已经收敛,同时与现有文献结果基本一致. 图6给出了相位角为90°时压力等值线和涡量等值线图,此时对称涡对将随着圆柱的前后振荡运动而脱离圆柱,与文献[19]的数值模拟结果吻合良好.
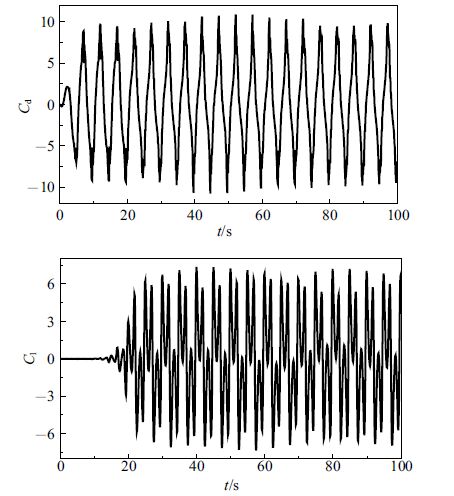
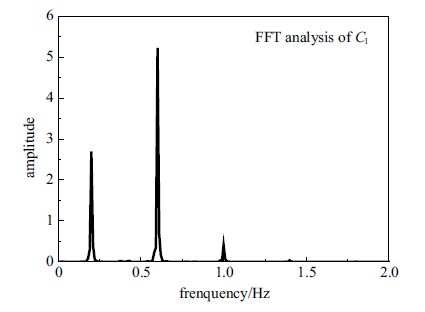
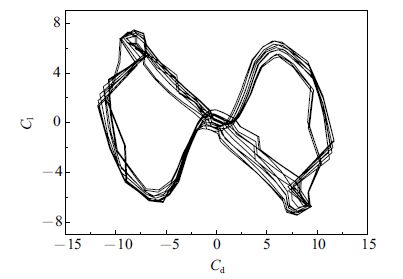
增大$KC$和$Re$,使得$KC=10$,$Re=200$. 由于振荡的加剧,此时流场更复杂. 图7给出了阻力系数和升力系数时程曲线,可以观察到 升力系数在一个周期内有多个峰值. 为了更能突出这一点,图8给出了升力系数的频谱分析,可发现升力存在3个频率,这是由于不同脱落频率的涡相互作用,并伴有涡的消逝以及涡的合并,使得旋涡脱落更加复杂.图9给出了10个周期内升力系数相对阻力系数的变化情况. 可以看出,此时涡脱落处在弱稳定状态,每个周期作用于圆柱上的力存在差异. 图10给出了相位角为90°时压力等值线和涡量等值线图.从图中可观察到与$KC=5$,$Re=100$时的涡脱结构有明显的不同,与文献[9]和文献[19]的结果基本一致.
2.3 振荡圆柱绕流
2.3.1 初始参数及计算模型
圆柱直径$D$为1 m,计算区域为30$D$×40$D$,网格划分与振荡圆柱网格类似. 圆柱距离入口边界15$D$,距离出口边界25$D$,距离上下边界分别为15$D$. 入口设置流速使$Re=200$,指定圆柱做水平简谐振荡\[X(t) = A\sin (2\pi {f_{\rm{e}}}t)\],图11给出了计算的物理模型. 左侧为入口边界,上下为自由滑移边界,右侧为出口开边界,柱体表面为无滑移边界.
2.3.2 数值算例及结果分析
为了得到圆柱绕流的涡脱频率,首先进行了静止圆柱绕流的数值模拟. 模拟得到的涡脱频率$f_{0}=0.192$,与文献[33]$f_{0}=0.195$以及文献[34]$f_{0}=0.187$的数模结果吻合良好,且与文献[35]$f_{0}=0.197$的实验结果基本一致.
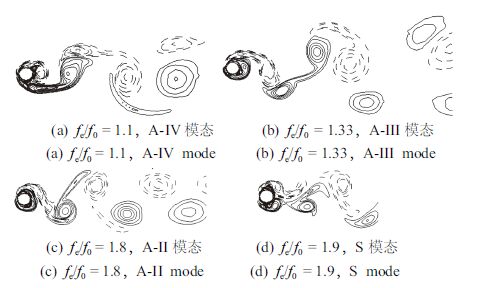
先对振幅比$A/D=0.1$,频率$f_{\rm e}/f_{0}=1.5\sim 2.2$的不同振荡问题进行模拟. 图12给出了$f_{\rm e}/f_{0}=1.5$和2.2时的涡量等值线图. 可发现0时刻和2$T$时刻的涡量等值 线图基本一致,可见此时涡脱周锁定在2$T$,并且两种振荡频率下旋涡脱落分别处于A-IV和A-II模态. 图13给出了$T$时刻A-IV模态向A-II模态转变的过程示意图,与文献[36]用格子玻尔兹曼方法的数值模拟结果基本一致.
增大振幅到$A/D=0.3$进行数值模拟. 图14给出了不同频率比$f_{\rm e}/f_{0}=1.1$,1.33,1.8,1.9时的$T$时刻涡量等值线图. 由于圆柱振荡幅值的增大,观察到了小振幅条件无法观察的对称S模态,同样捕捉到了小振幅和低阶精度算法[21]不能观察到的A-III模态,验证了本文数值方法的高阶精度.与文献[36]的结果吻合良好.
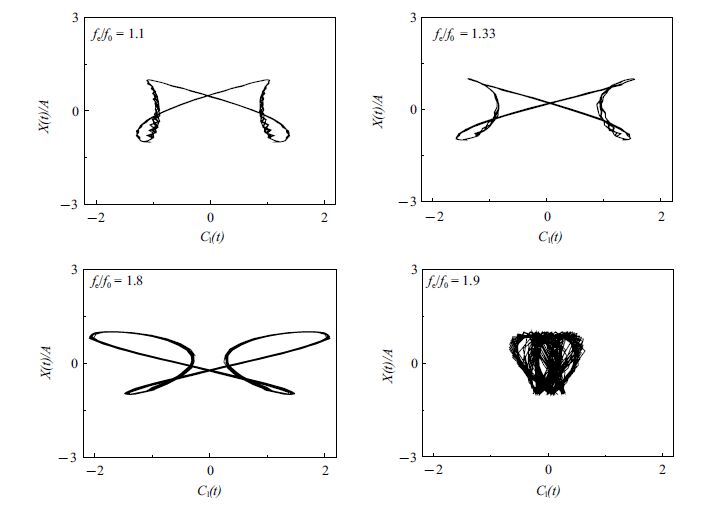
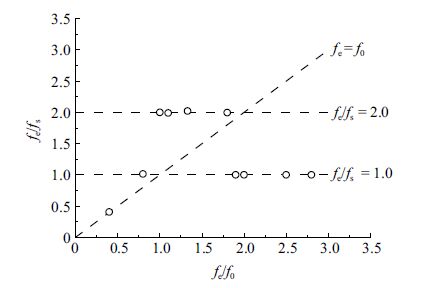
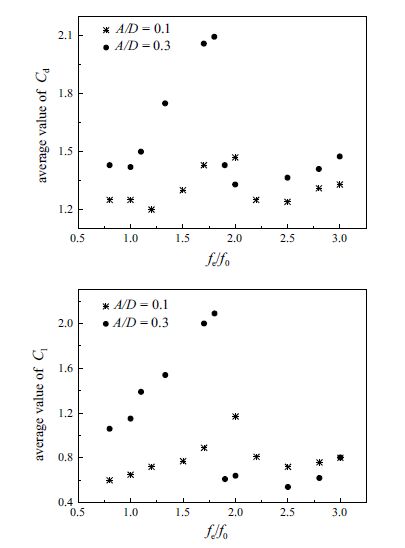
图15给出了$A/D=0.3$时李萨如图形[37]分析. 从图中可以看出在$f_{\rm e}/f_{0}=1.1$,1.33和1.8时,升力系数的变化随着圆柱的振荡具有明显的相位锁定,且升力系数随着强迫振荡频率的增大而增大,此时处在非对称涡脱模态;在$f_{\rm e}/f_{0}=1.9$时,可明显看出升力系数减小,此时已处在对称的S涡脱模态.图16给出了$A/D=0.3$时的实际涡脱频率,$f_{\rm s}$为实际旋涡脱落频率. 在低振荡频率时,$f_{\rm s}$涡脱频率与静止圆柱绕流涡脱频率$f_{0}$保持一致; 在$f_{\rm e}/f_{0}=1$附近时,$f_{\rm s}$涡脱频率与圆柱振荡频率相等; 随着$f_{\rm e}/f_{0}$进一步增大,$f_{\rm s}$涡脱频率锁定在圆柱振荡频率的二分之一; 一直到$f_{\rm e}/f_{0}=1.9$附近时,由于涡脱模态转变成对称S模态,$f_{\rm s}$涡脱频率锁定在圆柱振荡频率. 整体趋势与文献[21]的数值模拟结果基本一致,再一次验证了此方法的可靠性.图17给出了阻力系数$C_{\rm d}$均值、升力系数$C_{\rm l}$最大值与$f_{\rm e}/f_{0}$的关系.可看出两者均在锁定域内取得最大值,且$C_{\rm d}$均值随着振幅增大而增大; 由于S模态的出现,在$A/D=0.3$时,$f_{\rm e}/f_{0}=1.9$后的$C_{\rm l}$最大值较$A/D=0.1$的小.
3 结论
本文基于紧致插值曲线方法,以纳维-斯托克斯方程和连续性方程为控制方程,通过紧致插值高阶差分格式离散了对流方程,在直角坐标系里,利用浸入边界法处理运动边界,基于多相流的理论实现流-固耦合同步求解. 首先开展了静止流体中振荡圆柱的数值模拟,验证该数学模型对于求解此类问题的可行性; 然后又利用此数学模型对$Re=200$时,$A/D=0.1$和$A/D=0.3$两种振幅下振荡圆柱绕流进行了数值模拟,完整地再现了各涡脱模态.通过数值模拟与现有文献进行了定量和定性的比较,展现了良好的一致性,验证了紧致插值曲线模型的可靠性和准确性.该数学模型应用于流致振荡问题的研究,将是今后工作的重点.
参考文献
| [1] |
King R, Prosser M, Johns DJ. On vortex excitation of model piles in water. Journal of Sound and Vibration, 1973, 29(2): 169-188 |
| [2] |
Wootton L, Warner M, Cooper D. Some aspects of the oscillations of full-scale piles. In: Naudascher E, Flow-Induced Structural Vibrations. Berlin: Springer-Verlag, 1974, 587-601 |
| [3] |
Williamson CHK. Sinusoidal flow relative to circular cylinder. Journal of Fluid Mechanics, 1985, 155: 141-174 |
| [4] |
Bearman PW, Downie MJ, Graham MR, et al. Forces on cylinders in viscous oscillatory flow at low Keulegan-Carpenter numbers. Journal of Fluid Mechanics, 1985, 154: 337-356 |
| [5] |
Sarpkaya T. Force on a circular cylinder in viscous oscillatory flow at low Keulegan-Carpenter numbers. Journal of Fluid Mechanics, 1986, 165: 61-71 |
| [6] |
Obasaju ED, Bearman PW, Graham JMR. A study of forces, circulation and vortex patterns around a circular cylinder in oscillating flow. Journal of Fluid Mechanics, 1988, 196: 467-494 |
| [7] |
Williamson CHK, Roshko A. Vortex formation in the wake of an oscillating cylinder. Journal of Fluid Structure, 1988, 2(4): 355-381 |
| [8] |
Ongoren A, Rockwell D. Flow structure from an oscillating cylinder Part 2. Mode competition in the near wake. Journal of Fluid Mechanics, 1988, 191: 225-245 |
| [9] |
Dutsch H, Durst F, Becker S, et al. Low-Reynolds-number flow around an oscillating circular cylinder at low Keulegan-Carpenter numbers. Journal of Fluid Mechanics, 1998, 360: 249-271 |
| [10] |
Cetiner O, Rockwell D. Streamwise oscillations of a cylinder in a steady current. Part 1: locked-on stages of vortex formation and loading. Journal of Fluid Mechanics, 2001, 427: 1-28 |
| [11] |
Nishihara T, Kaneko S, Watanbe T. Characteristics of fluid dynamic forces acting on a circular cylinder oscillated in the streamwise direction and its wake patterns. Journal of Fluids and Structures, 2005, 20(4): 505-518 |
| [12] |
陈野军, 邵传平. 尾部喷射对流向振荡柱体尾流涡旋脱落的抑制. 中国科学 (G辑): 物理学, 力学, 天文学, 2012, 42(4): 406-420 (Chen Yejun, Shao Chuanping. Suppression of vortex shedding from an oscillating cylinder by base blowing. Scientia Sinica: Physica, Mechanica and Astronomica, 2012, 42(4): 406-420 (in Chinese)) |
| [13] |
王赛, 邵传平. 隔离板对流向振荡柱体绕流旋涡脱落的抑制. 力学学报, 2012, 44(4): 787-791 (Wang Sai, Shao Chuanping. Suppression of vortex shedding from an oscillating circular cylinder by a splitter plate. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4): 787-791 (in Chinese)) |
| [14] |
秦广素, 陈野军, 邵传平. 窄条控制件对流向振荡柱体尾流旋涡脱落的抑制. 中国科学 (G辑): 物理学, 力学, 天文学, 2014, 44(9): 1-20 (Qin Guangsu, Chen Yejun, Shao Chuanpin. Suppression of vortex shedding from an oscillating circular cylinder by a strip element. Scientia Sinica: Physica, Mechanica and Astronomica, 2014, 44(9): 1-20 (in Chinese)) |
| [15] |
Guilmineau E, Queutey P. A numerical simulation of vortex shedding from an oscillating circular cylinder. Journal of Fluids and Structures, 2002, 16(efeq6): 773-794 |
| [16] |
Morison JR, O'Brien MP, Johnson J W, et al. The force exerted by surface waves on piles. Transaction of American Institute of Mining, Metallurgical, and Petroleum Engineers, 1950, 2(5): 149-154 |
| [17] |
Al-Mdallal QM, Lawrence KP, Kocabiyik S. Forced streamwise oscillations of a circular cylinder: Locked-on modes and resulting fluid forces. Journal of Fluids and Structures, 2007, 23(5): 681-701 |
| [18] |
Leontini JS, Jacono DL, Thompson MC. A numerical study of an inline oscillating cylinder in a free stream. Journal of Fluid Mechanics, 2011, 688: 551-568 |
| [19] |
周林慧, 王志东. 静止水中振荡圆柱流场的数值模拟. 华东船舶工业学院学报, 2004, 18(5): 14-18 (Zhou Linhui, Wang Zhidong. Numerical simulation of oscillating cylinder in water. Journal of East Shipbuilding Institute, 2004, 18(5): 14-18 (in Chinese)) |
| [20] |
刘松, 符松. 流向振荡圆柱绕流中的涡脱落模态分析. 水动力学研究与进展, 2000, 15(4): 435-443 (Liu Song, Fu Song. Regimes of vortex shedding from an in-line oscillating circular in uniform flow. Journal of Hydrodynamics, 2000, 15(4): 435-443 (in Chinese)) |
| [21] |
张宇飞, 肖志祥, 符松. 流向强迫振荡圆柱绕流的涡脱落模态分析. 力学学报, 2007, 39(3): 408-416 (Zhang Yufei, Xiao Zhixiang, Fu Song. Analysis of vortex shedding modes of an in-line oscillating circular cylinder in a uniform flow. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(3): 408-416 (in Chinese)) |
| [22] |
Tnomurt. Finite element analysis of vortex-induced vibrations of bluff cylinder. Journal of Wind Engineering and Industrial Aerodynamics, 1993, 46: 587-594 |
| [23] |
Yabe T, Wang PY. Unified numerical procedure for compressible and incompressible fluid. Journal of the Physical Society of Japan, 1991, 60(7): 2105-2108 |
| [24] |
Hu CH, Kashiwagi M. A CIP-based method for numerical simulation of violent free-surface flows. Journal of Marine Science and Technology, 2004, 9(4): 143-157 |
| [25] |
Hu CH, Kashiwagi M. Two-dimensional numerical simulation and experiment on strongly nonlinear wave-body interactions. Journal of Marion Science and Technology, 2009, 14: 200-213 |
| [26] |
Zhao XZ, Hu CH. Numerical and experimental study on a 2-D floating body under extreme wave conditions. Applied Ocean Research, 2012, 35(1): 1-13 |
| [27] |
Zhao XZ, Ye ZT, Fu YN, et al. A CIP-based numerical simulation of freak wave impact on a floating body. Ocean Engineering, 2014, 87: 50-63 |
| [28] |
He GH. A new adaptive Cartesian-grid CIP method for computation of violent free-surface flows. Applied Ocean Research, 2013, 43: 234-243 |
| [29] |
赵西增. 一种自由面大变形流动的CFD模型. 浙江大学学报(工学版), 2013, 47(9): 1384-1392 (Zhao Xizeng. CFD modeling of distorted free surface flow. Journal of Zhejiang Univrsity (Engineering Science), 2013, 47(9): 1384-1392 (in Chinese)) |
| [30] |
Takewaki H, Nishiguchi A, Yabe T. Cubic interpolated pseudo-particle method (CIP) for solving hyperbolic-type equations. Journal of Computational Physics, 1985, 61(2): 261-268 |
| [31] |
Yabe T, Xiao F, Utsumi T. The constrained interpolation profile method for multiphase analysis. Journal of Computational Physics, 2001, 169(2): 556-593 |
| [32] |
Peskin CS. Flow patterns around heart valves. Journal of Computational Physics, 1972, 10(2): 252-271 |
| [33] |
Russel D, Wang ZJ. A Cartesian grid method for modeling multiple moving objects in 2D incompressible viscous flow. Journal of Computational Physics, 2003, 191(1): 177-205 |
| [34] |
Le DV, Khoo BC, Peraire J. An immersed interface method for viscous incompressible flows involving rigid and flexible boundaries. Journal of Computational Physics, 2006, 220(1): 109-138 |
| [35] |
Williamson CHK. Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers. Journal of Fluid Mechanics, 1989, 206: 579-627 |
| [36] |
龚帅, 郭照立. 流向振荡圆柱绕流的格子Boltzmann方法模拟. 力学学报, 2011, 43(1): 11-17 (Gong Shuai, Guo Zhaoli. Lattice Boltzmann simulation of the flow around a circular cylinder oscillating streamwisely. Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(1): 11-17 (in Chinese) ) |
| [37] |
韩新华. 李萨如图形特点的研究. 忻州师范学院学报, 2009, 25(5): 18-22 (Han Xinhua. Study on the feature of Lissajous figure. Journal of Xinzhou Teachers University, 2009, 25(5): 18-22 (in Chinese)) |
APPLICATION OF A CIP-BASED NUMERICAL SIMULATION OF FLOW PAST AN IN-LINE FORCED OSCILLATING CIRCULAR CYLINDER
Zhao Xizeng
1, 2, 3
, Fu Yingnan
1
, Zhang Dake
1, Cheng Du
1
1. Ocean College, Zhejiang University, Hangzhou 310058, China;
2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China;
3. Second Institute of Oceanography, SOA State Key Laboratory of Satellite Ocean Environment Dynamics, Hangzhou 310012, China
Fund: The project was supported by the National Natural Science Foundation of China (51209184, 51479175) and the Open Foundation of State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (2013490211).
Abstract: In this paper, A CIP-ZJU (Constrained Interpolation Profile method in Zhejiang University) model is developed to study a forced oscillating circular cylinder at low KC (Keulegan-Carpenter) in static fluid and flow past an in-line forced oscillating circular at Reynolds number of 200. The model was established in the Cartesian coordinate system, using the CIP method as the base flow solver to discretise the Navier-Stokes equations. The fluid-structure interaction is treated as a multiphase flow with liquid and solid phases solved simultaneously. An Immersed boundary method was used to deal with the boundary of solid body. Computations were compared with available results and good agreements were obtained, validating the reliability of the method to solve the problems of complex flow.
Key words:
flow past cylinder oscillating cylinder CIP method KC number immersed boundary method



 2015, Vol. 47
2015, Vol. 47