热毛细对流是由于表面张力不均匀而驱动的流动[1]. 热毛细对流中普遍关心的问题是,随着外加温差的增加,定常的对流如 何发展成振荡对流[2]. 所以对于热毛细对流转捩途径的研究是热毛细不稳定性研究的重要内容,也是对流体非线性研究的重要补充.
一直以来,前人对于热毛细对流的转捩途径的实验研究还不够充分.Gollub等[3]实验研究了Rayleigh-Bénard对流从层流转 变为湍流的各种转捩途径,作者通过改变各种不同的实验参数,包括模型的长高比、流体的普朗特数和平均流场,观察到4种不同的转捩途径,包括二频准周期-锁频-非周期状态、倍周期转捩、二频准周期-三频准周期-非周期状态和阵发性转捩途径.Mukutmoni等[4]数值模拟Rayleigh-Bénard对流转捩过程,观察到一种非典型的转捩途径: 定常-周期-准周期-定常状态. 作者认为,这种反常态的转变是由于转捩过程中对流的平均速度场和温度场的空间分布的变化.Bucchignani等[5, 6]数值模拟Rayleigh-Bénard对流的转捩过程,得到3种不同的转捩途径,其中识别出两种转捩机制,分别为倍周期转捩和三频准周期转捩.Bucchignani等[7, 8]对矩形液池热毛细对流转捩过程进行数值模拟,以Rayleigh数作为分岔的控制参数,观察到了周期状 态-二频准周期状态-三频准周期状态-混沌状态的转捩途径.胡文瑞等[9]通过半浮区液桥模型,实验和数值模拟研究了振荡热毛细对流从定常流动到振荡流动的转捩过程,得到了倍周期分岔的转捩途径. Zhu等[10, 11]对矩形液池热毛细对流转捩途径进行了初步的实验研究,发现了准周期分岔和倍周期分岔两种转捩途径,但还没有给出不同转捩途径发生的条件.
本文通过对矩形液池热毛细对流不稳定性进行研究,发现并总结转捩途径的规律,也将对其他流动转捩问题、混沌及湍流性质的研 究具有重要的参考和借鉴意义.
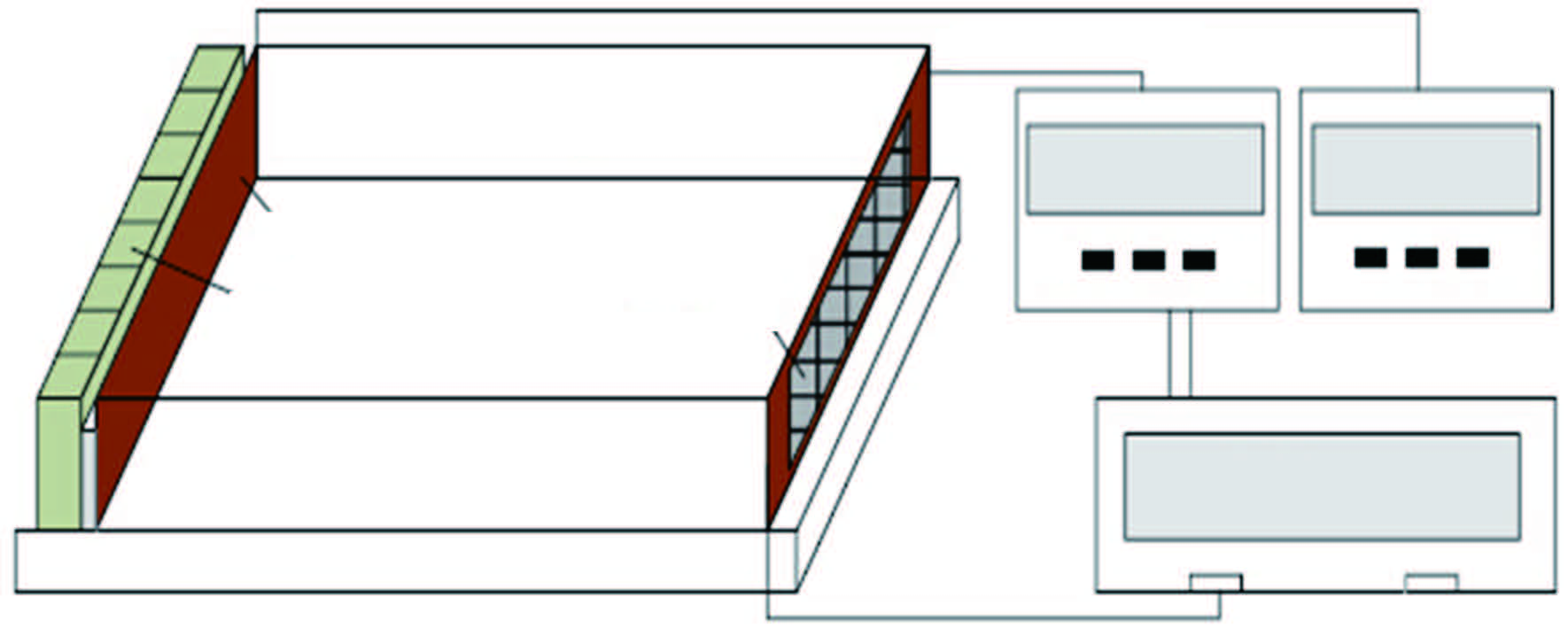
1 实验方法 1.1 热毛细对流控制系统为研究矩形液池中热毛细对流温度振荡特性,实验中首先搭建热毛细对流温度控制系统(图1).
|
图1 热毛细对流控制系统 Fig.1 Controlling system of thermocapillary convection |
矩形液池是用K9光学玻璃制成的,各壁面厚度是6 mm,液池的尺寸是52 mm × 36 mm × 6 mm,右壁面是贴有电热膜的铜块,左壁面是贴有半导体制冷片的同样大小的铜块. 两端分别通过热电偶与欧陆表连接,用于控制液池两端的温度.
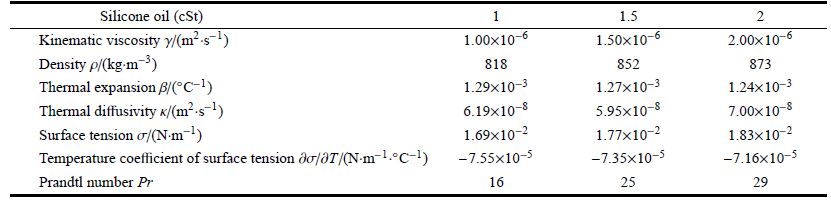
实验中使用信越公司的KF96系列硅油作为实验介质,1cSt,1.5cSt和2cSt的硅油物性参数如表1所示.
| 表1 硅油的物性参数 Table 1 Physical properties of silicone oil |
温度测量系统是由T型热电偶、Keithley纳伏表、及计算机组成.
热电偶是温度测量中常用的测温元件,精度高、测量范围广、使用方便. 纳伏表是一种非常灵敏的电压表,灵敏度可达1 pV,可 用于需要稳定、低噪声的电压和温度测量.
实验中将T型热电偶与Keithley (吉时利) 公司的2812A纳伏表 (图2) 相连,组成温度测量系统,从而实现高灵敏度的温度测量,温度测量灵敏度为0.001℃.

|
图2 纳伏表实物图 Fig.2 The picture of nanovoltmeter |
另外,为了对表面温度分布及波动情况进行观测,实验中采用了美国FLIR 公司E60 型号的红外热像仪 (图3).它具有320×240的热图像分辨率,60 Hz的帧频以及0.1℃的热灵敏度,具有较好 的表面波动观测效果.

|
图3 红外热像仪实物图 Fig.3 The picture of thermal infrared imager |
主要基于Labview软件开发实验数据处理程序,利用傅里叶变换获得时域信号的频谱图,利用小波分析提取原始信号当中的振荡信号 等,实现对微弱物理信号的数据分析.
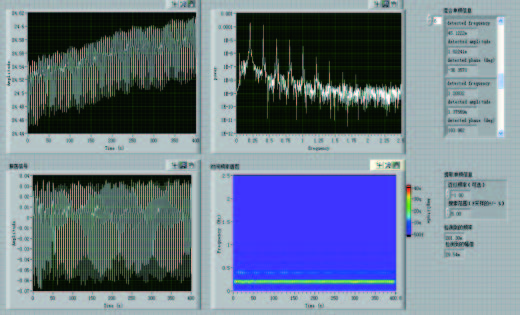
实验设计的Labview软件平台 (图4),主要包括显示原始信号、提取振荡信号、频谱测量、时频强度分析4部分. 在本实验中,主要 运用的是频谱测量功能模块,通过对采样频率进行设置,获取纳伏表测得的温度信号,对振荡信号进行快速傅里叶变换,从而进行频谱分析,得到反映不同频率相对强度的频谱图.这种频谱分析的方法在吴笛等[12]的文章中同样得到了广泛应用.
|
图4 Labview软件平台 Fig.4 Labview software platform |
实验中选取1cSt,1.5cSt和2cSt三种不同黏度的硅油,分别测量液层高度2 mm,2.5 mm,3 mm和3.5 mm各种不同工况在转捩 过程中的温度振荡,并选取较为典型的分岔,总结转捩途径的规律.
将硅油的黏度和液层高度无量纲化: 不同的黏度对应不同的普朗特数 (表1),定义长高比$\Gamma= L / H$,其中$L$表示液层的长度,$H$表示液层高度. 因此,通过计算可知$\Gamma$的变化范围是26到14.9.
2.2 转捩途径对于1cSt硅油 ($Pr=16$),各种不同的液高的转捩方式基本类似,以一种一般性的准周期分岔的途径为主,即当系统内有不同频率 的振荡互相耦合时,系统就会产生一系列新的耦合频率的运动,出现3个互不相约的频率之后,规则运动就很不稳定,然后进入混沌 (湍流)[13].
实验中通过功率谱只观察到二频准周期转捩,因为第三个频率即将出现时,如果存在一个奇异吸引子,那么同时就会出现一些 宽带噪声,在功率谱上仅能观察到两个独立的频率[14]. 以2.5 mm液高 ($\Gamma=20.8$) 为例,转捩过程依次经历了周期、二频准周期、非周期、混沌的转捩过程. 当温差为21℃时,温度周期振荡,在频谱图中观察到主频f1: 0.260和若干倍频0.520,0.775,1.035,1.295.温差继续增加到26℃时,功率谱中出现第二基频f2: 0.550,同时第一基频增大为0.293,另外其他分频均能用这两个不可约基频的线性组合表示: 0.258(2f1-f2),0.583(3f1-f2),0.653(2f1),0.845(2f2),0.875(4f1-f2). 继续增加温差,当温差为28℃时,出现宽频现象,振荡变为非周期; 进一步增加温差,到29℃时,功率谱逐渐连续,演变为混沌状态.
这种准周期分岔的形式在Zhu等[10]的实验中同样被观察到,与Gollub等[3]的实验和Bucchignani等[7, 8]对矩形液池热毛细对流转捩过程进行数值模拟的准周期分岔形式也类似. 结合本文的实验发现可以认为,准周期分岔的转捩形式是一种很主要的并且较为普遍的转捩途径.
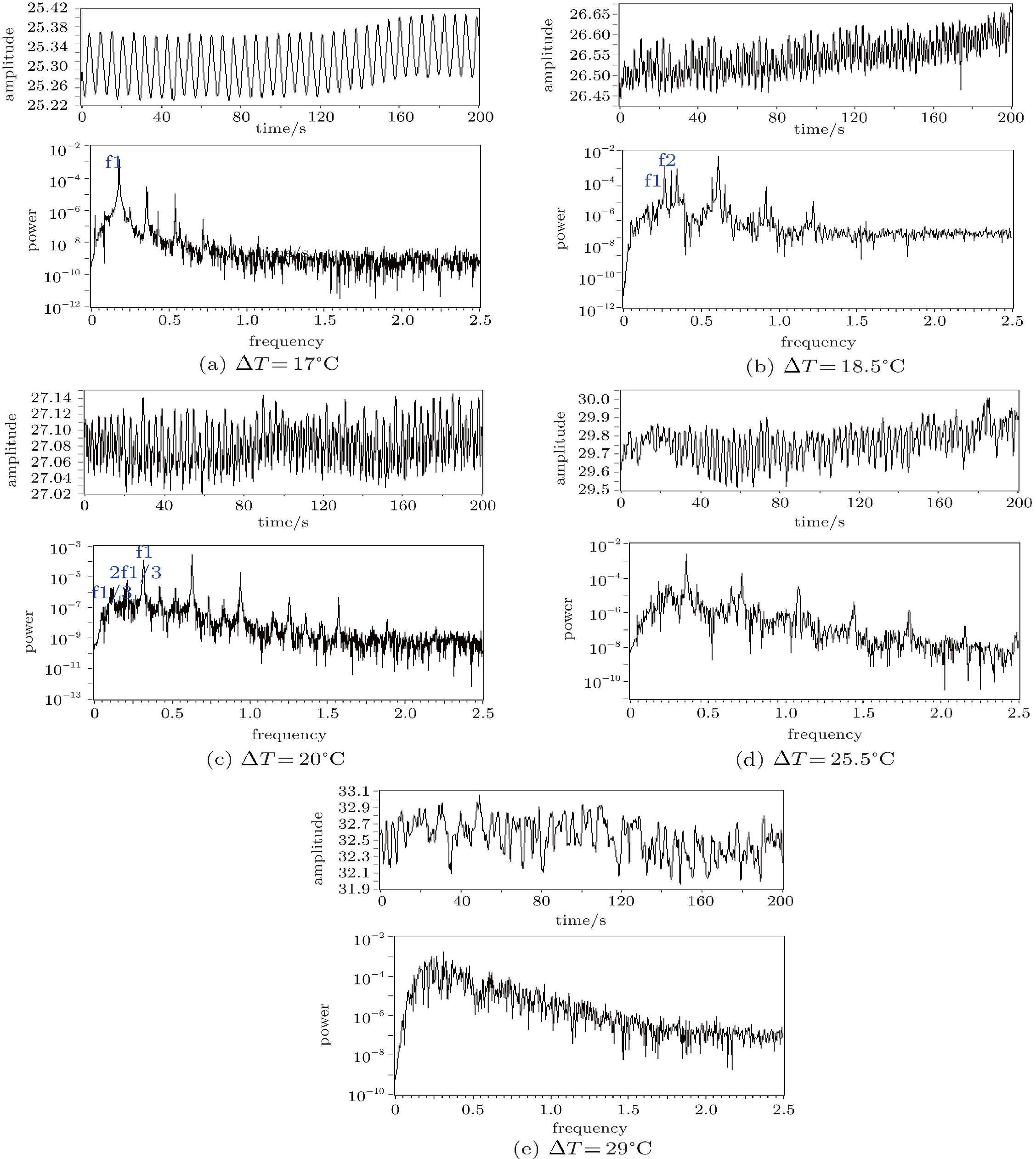
但并不是1cSt硅油所有工况都只是这种转捩方式,在3.5 mm液高 ($\Gamma =14.9$) 时,在准周期转捩的同时,还伴随有切分岔的出现,正如图5所示.
|
图5 不同温差时温度振荡信号和功率谱图 Fig.5 Time history of temperature and power spectra in various temperature differences |
切分岔即阵发混沌的道路,阵发混沌发生于切分岔起点之前,它随时间变化的基本特征是: 在基本上属于周期振荡的序列中,有时会突然出现一阵混沌运动,尔后又出现周期运动. 随着参数的减小混沌运动所占的时间比例越来越大,最后完全变为混沌.研究表明,凡是观察到倍周期分岔的系统都可以看到阵发混沌[15].
上图演化过程中,随温差的逐步增加,出现二频准周期分岔之后,出现切分岔,即出现一个更大的主频f1和它的分频f1/3及2f1/3,但这种切分岔不稳定,随后分频逐渐消失,变为周期运动,最后演化为混沌. 这种切分岔的形式在之前的实验中也都很少被观察到,而在本文实验中我们可以明显看到切分岔的出现.
对于1.5cSt ($Pr=25$) 硅油,转捩的方式比较复杂. 当液高为2 mm ($\Gamma=26$) 时,转捩途径与前面的类似,为一般性的准周期分岔途径,分别经历周期、二频准周期、非周期、混沌的转捩过程.
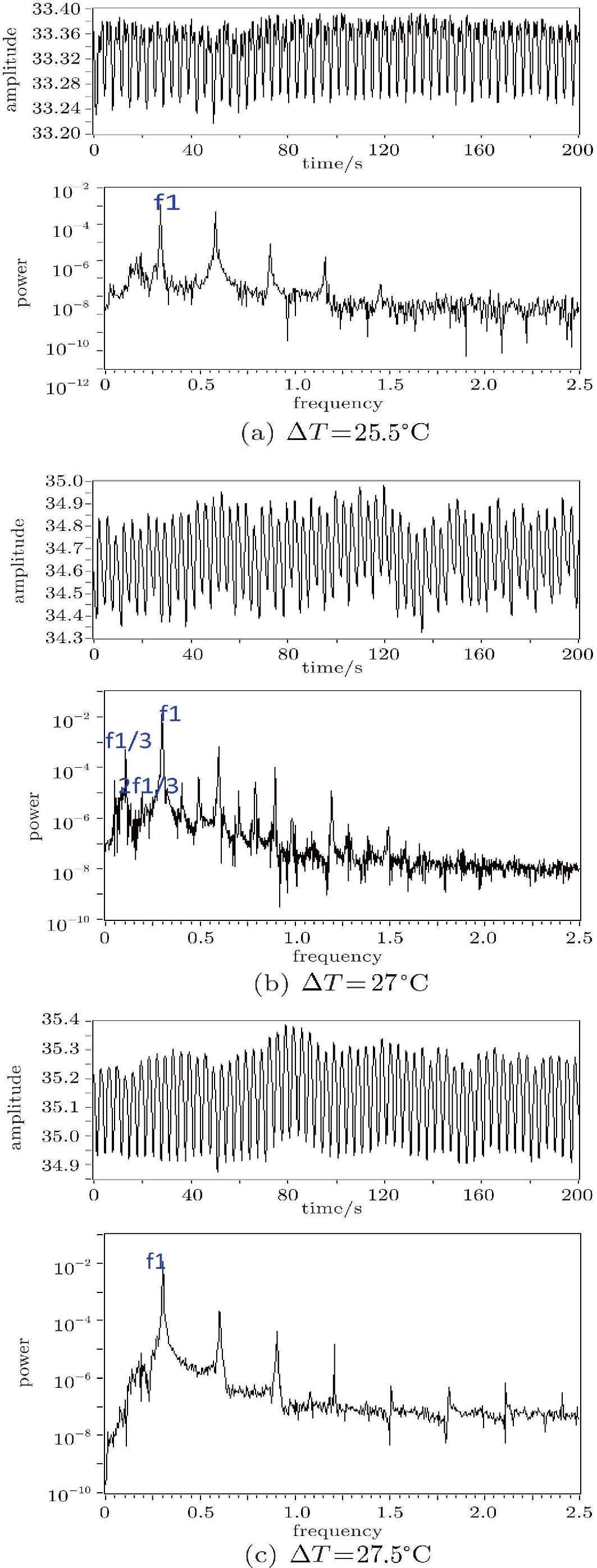
当液高为3 mm ($\Gamma =17.3$) 时,转捩途径为倍周期分岔途径,有时还会伴随有切分岔出现. 一般性的倍周期分岔转捩过程,即随温差的增加,依次经历周期、1/2倍周期分岔、1/4倍周期分岔、混沌的转捩过程,这种转捩途径在Zhu等[10]的实验中同样也被观察到,而且在胡文瑞等[9]的半浮区液桥模型中,用实验和数值模拟的方法也都得到了倍周期分岔的转捩途径; 而图6为倍周期分岔过程中伴随有切分岔的转捩过程,即周期分岔之后出现短暂的切分岔,随后由于切分岔不稳定,很快又变回周期分岔的形式.这种倍周期分岔与切分岔同时出现的形式在实验中还很少见.
|
图6 不同温差时温度振荡信号和功率谱图 Fig.6 Time history of temperature and power spectra in various temperature differences |
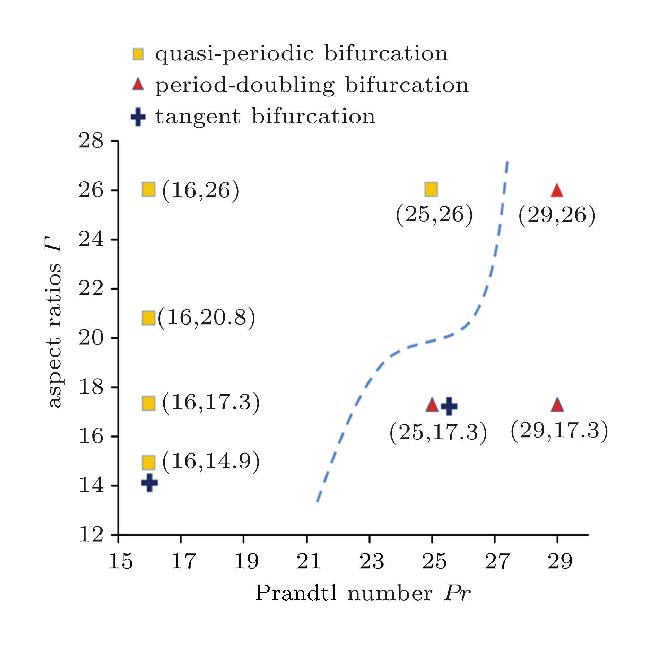
对以上转捩过程进行总结,主要观察到的转捩途径有4种: 一般性准周期转捩、一般性倍周期转捩、伴随有切分岔的准周期转捩和伴随有切分岔的倍周期转捩. 将这几种转捩途径与其对应的实验工况表示为一个散点图,如图7所示.
|
图7 不同工况的转捩途径分类 Fig.7 Transition routes to chaos in different experimental conditions |
用红外热像仪观测在转捩过程中液层表面温度扰动场的情况,发现随着温差的增加,扰动场由规则向不规则演化 (图8).

|
图8 1cSt硅油2 mm液高不同温差表面温度扰动场及其在转捩过程中的发展 Fig.8 Temperature perturbation and its evolution in transition process in liquid layer surface for various temperature differences for silicone oil 1cSt with the depth of 2 mm |
通过图8的演化过程可以看出,当温差为15℃时,表面波动形式较为规则,波动沿倾斜方向交叉传播;逐渐增加温差到20℃时,倾斜交叉方向的波动形式中夹杂一些不规则波动;继续增加温差到25℃时,波动形式已经非常混乱而变得无规则.
选取液层表面中心位置的一条竖直线$y$ (图9),观察这条直线上的各点在转捩过程中随时间的演化规律,对于不同的实验工况作对比,如图10.

|
图9 液层表面竖直线选取示意图 Fig.9 Diagram of the selection of vertical line in liquid layer surface |

|
图10 不同实验工况中间位置处竖直线各点在转捩过程中随时间演化图 Fig.10 The time evolution diagram of all points in the vertical line of middle position in the transition process in different experimental conditions |
通过对比可以清楚地看到: 液层表面在转捩中经历了从稳定状态到振荡状态的转变过程; 相同温差下,黏度越小的液层扰动越强烈; 同一黏度的液层越薄,振荡越剧烈; 在转捩过程中还观察到倾斜方向传播的热流体波.
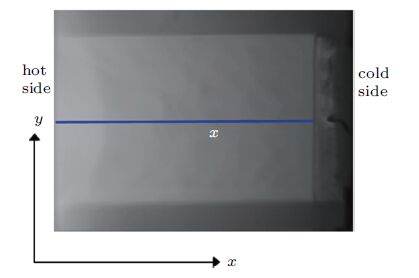
然后再取液层表面中心位置的一条水平线$x$ (图11),观察这条直线上的各点在转捩过程中随时间的演化规律,同样对于不同的实验工况作对比,如图12.
|
图11 液层表面水平线选取示意图 Fig.11 Diagram of the selection of horizontal line in liquid layer surface |

|
图12 不同实验工况中间位置处水平线各点在转捩过程中随时间演化图 Fig.12 The time evolution diagram of all points in the horizontal line of middle position in the transition process in different experimental conditions |
转捩过程中,液层中的流场结构经历了多种状态的转变,该过程会受到液层厚度的影响[16]. 通过图12的比较可以看出,转捩过程中,由于液层高度不同,导致流场结构不同,所以对流涡胞数目不同,液层越薄对流涡胞数量越多; 转捩过程中,观察到涡胞的振荡现象,在图中可以清楚地看到多条涡胞在转捩过程中振荡逐渐加强.
3 结论本文对矩形液池热毛细对流转捩途径进行了详细研究,发现其转捩途径呈现多样化趋势. 但在不同普朗特数、不同长高比的情况下具有一定的规律性,对转捩途径进行比较分类,可归纳为: 一般性的准周期分岔、一般性的倍周期分岔、伴随有切分岔的准周期分岔、伴随有切分岔的倍周期分岔以及还有其他一些不易识别的途径. 用红外热像仪对液层表面温度扰动场进行了观察,可以发现: 转捩过程中液层表面的温度扰动场由规则向不规则演化; 在液层表面有热流体波的传播和多涡振荡现象.
本文对于流动转捩问题的研究工作,是对非线性流体力学的一个重要补充,可以丰富非线性科学的内涵,为以后更加深入地探索流动转捩的本质提供很好的借鉴.
| [1] | 胡文瑞, 徐硕昌. 微重力流体力学. 北京: 科学出版社, 1999. 95-104 (Hu Wenrui, Xu Shuochang. Microgravity Fluid Mechanics. Beijing: Science Press, 1999. 95-104 (in Chinese)) |
| [2] | 胡文瑞, 等. 微重力科学概论. 北京: 科学出版社, 2010. 78-86 (Hu Wenrui, et al. An Introduction to Microgravity Science. Beijing: Science Press, 2010. 78-86 (in Chinese)) |
| [3] | Gollub JP, Benson SV. Many routes to turbulent convection. Journal of Fluid Mechanics, 1980, 100(3): 449-470 |
| [4] | Mukutmoni D, Yang KT. Thermal-convection in small enclosures-an atypical bifurcation sequence. International Journal of Heat and Mass Transfer, 1995, 38(1): 113-126 |
| [5] | Stella F, Bucchignani E. Rayleigh-Benard convection in limited domains: Part 1-Oscillatory flow. Numerical Heat Transfer Part A-Applications, 1999, 36(1): 1-16 |
| [6] | Bucchignani E, Stella F. Rayleigh-Benard convection in limited domains: Part 2 -Transition to chaos. Numerical Heat Transfer Part A-Applications, 1999, 36(1): 17-34 |
| [7] | Bucchignani E, Mansutti D. Horizontal thermal convection in a shallow cavity:oscillatory regimes and transition to chaos. International Journal of Numerical Methods for Heat & Flow, 2000, 10(2): 179-195 |
| [8] | Bucchignani E, Mansutti D. Horizontal thermocapillary convection of succinonitrile: steady state, instabilities, and transition to chaos. Physical Review E, 2004, 69(5): 056319 |
| [9] | 胡文瑞, 唐泽眉, 李凯. 浮区热毛细对流. 力学进展, 2009, 39(3): 360-377 (Hu Wenrui, Tang Zemei, Li Ka. Floating zone thermocapillary convection. Advances in Mechanics, 2009, 39(3): 360-377 (in Chinese)) |
| [10] | Zhu P, Duan L, Kang Q. Transition to chaos in thermocapillary convection. International Journal of Heat and Mass Transfer, 2013, 57: 457-464 |
| [11] | 朱鹏. 热毛细对流转捩问题研究. [博士论文]. 北京: 中国科学院大学, 2013. 53-64 (Zhu Peng. Study on the transition of thermocapillary convection. [PhD Thesis]. Beijing: University of Chinese Academy of Science, 2013. 53-64 (in Chinese)) |
| [12] | 吴笛, 张洋, 段俐等. Bénard-Marangoni对流温度振荡转捩实验研究. 力学学报, 2011, 43(6): 1054-1060 (Wu Di, Zhang Yang, Duan Li, et al. Experimental investigation of the transition of temperature oscillation in Bénard-Marangoni convection. Chinese Journal of Theoretical and Applied Mechani, 2011, 43(6): 1054-1060 (in Chinese)) |
| [13] | 陈滨. 混沌波形的相关性-相空间轨迹与混沌序列自相关特性. 西安: 西安电子科技大学出版社, 2011. 30-33 (Chen Bin. The Relativity of Chaotic Waveform-Phase Space Trajectory and the Chaotic Sequence Autocorrelation Properties. Xi'an: Xidian University Press, 2011. 30-33 (in Chinese)) |
| [14] | 舒斯特HG. 混沌学引论. 朱鋐雄, 林圭年 译. 第3版. 成都: 四川教育出版社, 2010. 152-152 (Schuster HG. A introduction to chaos. Zhu Hongxiong, Lin Guinian, translation. The third edition. Chengdu: Sichuan Educational Press, 2010. 152-152) |
| [15] | 陈瑞熊. 用混沌理论解释湍流现象. http://blog.sina.com.cn/s/blog_53d3accd0102e0f6.html. 2012-11-30 (Chen Ruixiong. Explain the turbulence phenomena with the chaos theory. http://blog.sina.com.cn/s/blog_53d3accd0102e0f6.html 2012-11-30 (in Chinese)) |
| [16] | 周彬, 朱鹏, 段俐等. 矩形液池内热毛细对流的流动不稳定性. 力学与实践, 2013, 35(3): 39-45 (Zhou Bin, Zhu Peng, Duan Li, et al. Flow instability of thermocapillary convection in rectangular pool. Mechanics and Engineering, 2013, 35(3): 39-45 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47