2. 南京理工大学智能弹药技术国防重点学科实验室, 南京210094
黏性流体经过钝体时会产生流动分离,导致阻力和升力的脉动,产生振荡、失稳和噪声等.流动控制按照有无能量输入的方式主要分为主动和被动控制方法. 主动控制方法指有能量输入的控制方法,比如合成射流.电磁力(Lorentz force)因其控制方法可适应各种工程实际条件而被广泛关注[1],被认为最有潜力的3种主动控制方法之一,并对其进行了大量的实验与理论研究.
Gailitis等[2]是较早利用电磁力进行流动控制研究的学者之一,他在1961年利用交错排布的电极和磁极制作了一个电磁激活板,对边界层的湍流转捩进行控制,发现电磁力可延缓湍流转捩,并可减少边界层厚度,减少阻力. Henoch等[3]利用Gailitis等[2]设计的电磁激活板,实验研究了平板湍流边界层的洛仑兹力控制,发现流向洛仑兹力会增加壁面的摩擦力,减少边界层的厚度,降低边界层的湍流强度. Berger等[4]对直接数值模拟了槽道湍流的洛仑兹力控制,研究了开环和闭环控制两种方式,研究结果显示理想壁面法向电磁力闭环控制能耗最小,且减阻率可达40%,但消耗的能量仍然比节省的能量大. Pang等[5]实验研究了展向振荡电磁力的湍流减阻,发现展向振荡的电磁力可减少湍流边界的摩擦阻力,减少幅度可达40%. Du等[6]基于直接数值模拟方法对壁湍流的控制进行了计算实验研究,展向行波电磁力可大幅度减少剪切力,减少幅度可达30%,相对于其他控制方式,展向行波电磁力可使边界层变的更稳定,且可消除近壁条带. Mutschke 等[7]利用谱方法,数值研究了翼型绕流分离的电磁力控制,强度足够大的稳定电磁力可完全抑制翼型的流动分离,振荡电磁力的频率与涡脱落的频率一致时,可提高电磁力控制的效果,优化升力的振荡幅度. 张辉等[8]对圆柱绕流的电磁力控制进行了研究,对圆柱绕流、圆柱剪切来流及其振动等问题的电磁控制进行了大量的研究.梅栋杰等[9]对槽道湍流的展向震荡电磁力控制机理进行了实验和数值研究,尹纪富等[10]研究了圆柱湍流绕流的控制,刘宗凯等[11] 研究了翼型绕流的电磁力优化控制.
电磁流动控制的研究取得了丰硕的成果,然而电磁力流动控制从1961年Gailitis[2]开始到现在已经过了半个世纪,对电磁力的控制机理进行了充分的研究,同时对各种电磁力在减阻、抑制流动分离、湍流转捩等方面进行了大量的研究,但这些研究都没有涉及到电磁力的控制效率问题. Berger等[4] (2000年)和Shatrov等[12](2007年)对电磁控制效率进行了研究,研究表明电磁力减阻的功耗比减阻收益大,Berger等[4]的计算结果甚至显示展向振荡电磁力减阻所需功耗比减阻收益大3个数量级,而Shatrov等[12]的研究也认为展向震荡电磁力控制功耗太高并不适合应用于流动控制,他研究结果显示流向电磁力对可移动平板的控制效率$\eta$最高可达0.8,但并没有对电磁控制能量损耗的原因进行研究.
作者曾在文献[13, 14]对翼型绕流的电磁力控制机理阐述,但并未对电磁力的控制效率问题进行讨论.为提高电磁力控制的效率,需要揭示电磁力控制能量损耗的原因,并基于该研究结果,探讨提高电磁力控制效率的方法.本研究基于翼型绕流的流向电磁力控制,利用Roger等[15]发展的双时间步Roe格式对电磁力的翼型绕流控制进行数值模拟,根据能量守能定律计算电磁力激活板的控制总能耗,基于翼型的升力和阻力推导电磁力控制后所节省的净能量,对电磁力控制效率进行分析,并分析焦耳热损耗及流体动能损耗,力图找出电磁力控制能量损耗的原因,基于该原因,探讨提高电磁力控制效率的方法,为控制效率提升及其优化提供理论依据及技术支持.
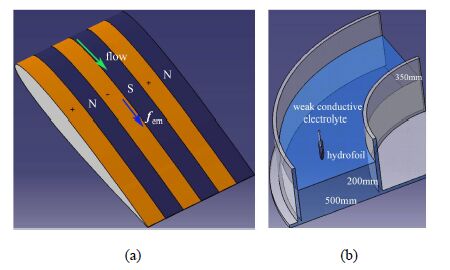
1 物理问题为研究电磁力控制效率问题,需要对电磁力控制过程中能量的损耗进行分析,寻找出损耗较大的部分,探讨避免损耗的方法.本研究将包覆有电磁激活板的翼型浸入到弱导电液体中,研究翼型绕流的电磁力控制效率,示意图如图1(a)所示,在翼型的表面包覆电磁激活板,产生的电磁力如图${ f}_{\rm em}$方向所示,其大小在壁面法向呈指数衰减[16],来流的方向如图1(a)中流动方向所示,电磁力弱导电液体的控制原理为电磁力作用在流体边界层上,增加壁面附近流体电磁力方向上的动量,当来流方向与电磁力方向相同时,可增强流体抵抗逆压梯度的能力,抑制流动分离,增升减阻,电磁力作用后流体流动的方向与电磁力的方向相同.
实验研究在如图1(b)所示的水槽中进行的,水槽的外径为2 m,内径为1 m,翼型绕流的流场用染色线显示,升阻力用压力传感器测量.
|
图1 包覆电磁激活板的翼型和实验水槽 Fig.1 Hydrofoil cover with Lorentz force actuator and water tank |
基于二维不可压缩N-S方程对翼型绕流的电磁力控制进行研究,基于翼型弦长$c$和来流速度$U_0 $对N-S方程进行无量纲化
\[\frac{{\partial u}}{{\partial t}} + (u \cdot \nabla )u = - \frac{1}{\rho }\nabla p + \frac{1}{{Re}}\Delta u + {f_{{\rm{em}}}}\]
(1)
\[\nabla u = 0\]
(2)
\[{f_{{\rm{em}}}} = N(j \times B)\]
(3)
为分析翼型绕流电磁力激活板的控制效率,需要对电磁力激活板控制下的翼型绕流的能量传递过程及其守恒进行分析. 根据能量守能定律
\[UIt = Q + {w_a} + {w_m}\]
(4)
分析式(4)可知,$w_a $为电磁力控制后能量的节省量,$UIt$为电磁力的控制所需要的总能耗,因此电磁力控制效率可定义为
\[\eta = \frac{{{w_a}}}{{UIt}}\]
(5)
\[{w_a} = \int_0^t F (t) \cdot S(t){\rm{d}}t\]
(6)
焦耳损耗率定义为
\[{\eta _1} = \frac{Q}{{UIt}}\]
(7)
由于电磁力对壁面流体加速导致翼面压力产生变化,导致升力增加,阻力减少,该部分的作用已体现在$w_a $中,因此$w_m $为控制区域内流体动能的增量,该部分能量可定义为损耗,因此,流体动能损耗率可定义为
\[{\eta _2} = \frac{{{w_m}}}{{UIt}}\]
(8)
由于实验研究电磁力控制效率存在较大技术难度,首先是压电传感器的力标定,其次升阻力做功的计算问题以及流体动能损耗的计算等,因此采用数值模拟的方法对电磁力控制效率进行研究,数值研究的第一步需要对数值模型、方法等进行验证.
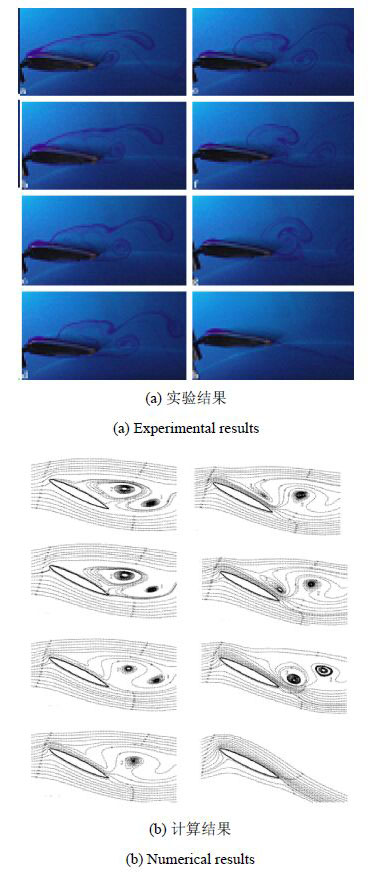
图2为电磁力控制下的翼型绕流流场控制结果,图2(a)为实验结果,图2(b)为数值模拟结果.图2的第一幅图为电磁力刚开始作用时的情形,此时的流场与无控制时类似,由前缘涡与后缘涡形成的涡对正准备离开翼型表面.正向电磁力作用后,前缘的流动分离点以一定的速度,沿壁面逐渐向翼型尾部移动,直至流动分离完全被抑制,整个过程如图2所示.电磁力的影响主要在近壁区域,随着分离点的后移,及脱体涡源的后移,边界层外缘的脉线从前缘往后缘逐渐消失,其后移速度小于壁面上分离点的后移速度.由图可知,在正向电磁力作用下,前缘涡与后缘涡脱落后,不再重新生成,流体分离完全被抑制,流场趋于稳定.数值模拟结果与实验的结果吻合的较好,呈现出一样的控制规律,验证了数值模拟程序.
|
图2 电磁力控制下的翼型流场 Fig.2 Flow field of hydrofoil under the control of Lorentz force |
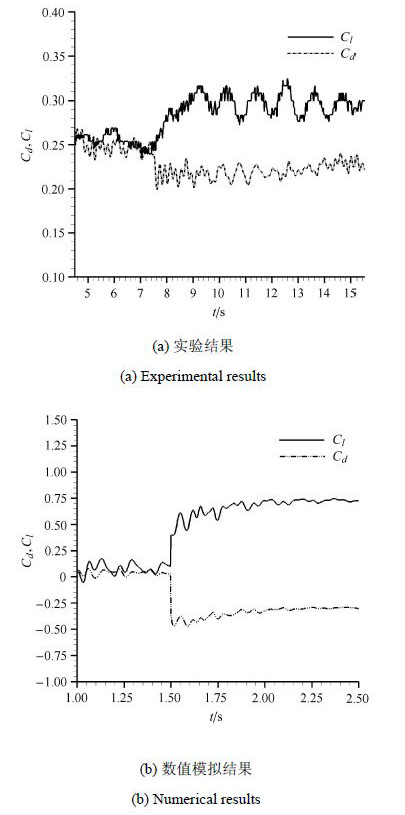
图3 为电磁力控制下的升力和阻力图,其中图3(a)为实验结果,图3(b)为数值模拟结果,图中显示电磁力开始作用时,升力有个阶跃的提升,并随着时间慢慢增加,最后稳定在某一个数值,而阻力则在电磁力开始作用后,有个阶跃的减小,而后随着时间慢慢增加,最后稳定在某一个数值. 数值模拟结果与实验结果吻合的较好,都呈现同一个规律,验证了数值模拟的升阻力计算.
|
图3 电磁力作用下的升力和阻力 Fig.3 Lift and drag under the action of Lorentz force |
将实验研究的参数代入到本研究中对电磁力的控制效率进行计算,具体的参数为电流密度$j_0 $为1 420 A/m$^{2}$,磁感应强度$B_0$为1.5 T,翼型弦长$c$为0.1 m,电极磁极的宽度为5 mm,电解液的密度$\rho$为1.1×10$^{3}$ kg/m$^{3}$,电解液的电导率为10 S/m.
图4为相同能量输入的电磁力控制翼型绕流流场图,图中显示,来流速度越低,翼型流动分离抑制的效果就越好,随着速度的增大,电磁力控制效果开始减弱,当速度来到0.5 m/s时,翼型的尾部出现了流动分离,表明随着来流速度的增加,电磁力对翼型绕流的控制效果减弱.

|
图4 相同能量输入的电磁力控制翼型绕流流场 Fig.4 Flow field of hydrofoil under the control of Lorentz force actuator with same power input |
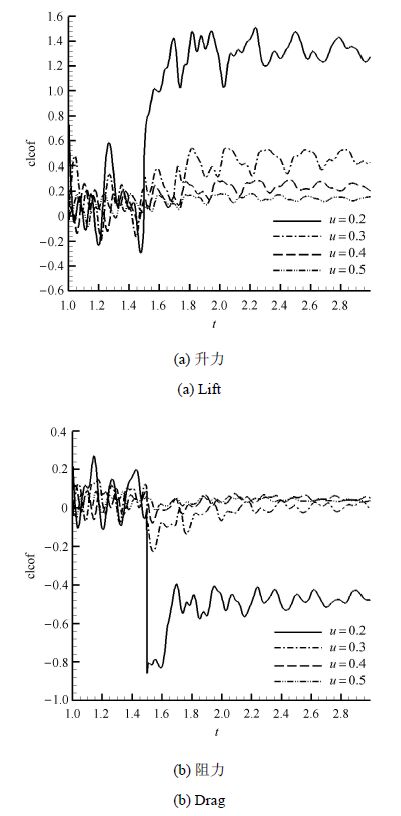
图5为相同能量输入的电磁力作用下不同来流速度的升阻力变化图,升力的增幅随着来流速度的增加而减小,当速度值达到0.5 m/s时,升力系数的增幅不到0.1 (图5(a) ),阻力的降幅则表现为阻力减少的幅度随着来流速度的增大而减小(图5(b) ).以上的结果显示相同能量输入的情况下,电磁力对翼型绕流的控制效果随着来流速度的增加而减弱.
|
图5 相同能量输入的电磁力作用下不同来流速度的升阻力系数 Fig.5 Hydrofoil lift and drag coefficient with different freestream velocity under the control Lorentz force actuator with same power input |
图6为电磁力控制效率随时间变化图,其中$\eta $为电磁力控制效率,$\eta _1 $为焦耳热损耗率,$\eta _2$为流体动能损耗率. 研究结果显示,在最初0.2 s内,输入的能量大部分损耗在流体动能损耗上,最高损耗率可达95%,其次损耗在焦耳热上,最高可达28%,该结果验证了Shatrov等[12]对震荡电磁力流动控制的研究结果,他的研究结果认为展向震荡电磁力控制功耗太高并不适合应用于流动控制.分析图4的结果,发现电磁力震荡的频率越大,能量的损耗就越高. 随着时间推移,流体动能损耗$\eta _2$下降,电磁力控制效率$\eta $及焦耳热损耗$\eta _1 $增加. 在速度较低时,电磁力控制效率$\eta$增加的幅度大于焦耳热损耗率$\eta _1$增加的幅度,因此可知,电磁激活板在一个方向上稳定工作时间越长,电磁力控制的效率就越高,其他损耗就越低.
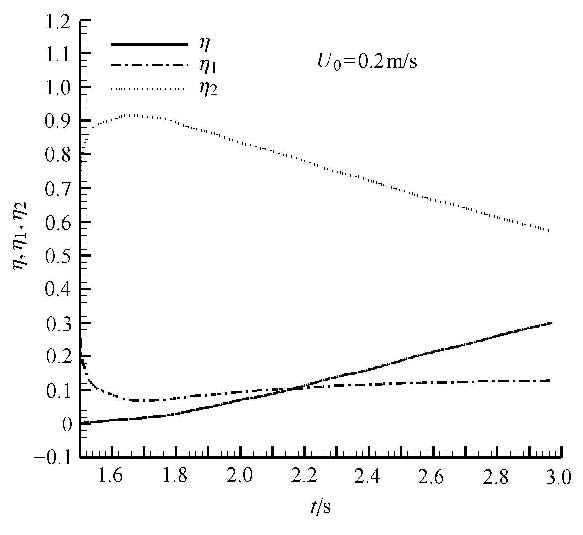
|
图6 电磁力控制效率随时间变化图 Fig.6 Diagram of Lorentz force control efficiency variation of with time |
图7为控制效率随速度变化图,图中显示电磁力控制效率与来流速度成反比例关系,来流速度越大,电磁力控制效率$\eta$越小,当来流速度为0.2 m/s时,电磁力的控制效率$\eta $可达30%,随着速度的增加,电磁力控制效率$\eta$的增幅及流动动能损耗率$\eta _2 $下降的幅度呈指数减少,当速度增加到0.5 m/s时,电磁力的控制效率$\eta$不到1%.而流体动能损耗率与来流速度成正比例关系,来流速度越大,流体动能损耗就越大,当来流速度达到0.5 m/s时,流体动能损耗率可达到87%.焦耳热的损耗$\eta _1 $与来流速度的关系不大,大约在10%$\sim $15%之间.
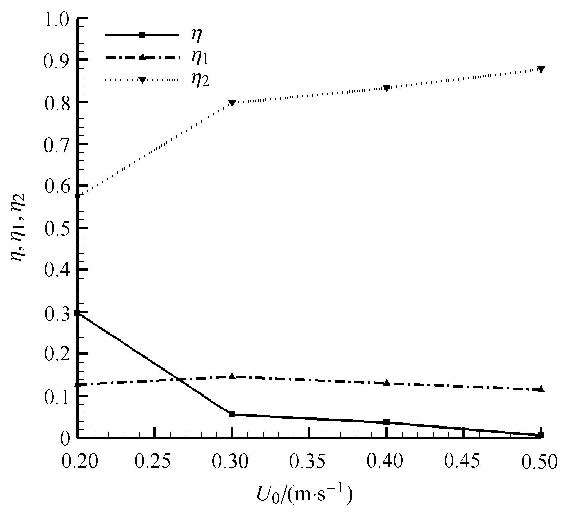
|
图7 控制效率随速度变化图 Fig.7 Diagram of Lorentz force control efficiency variation with velocity |
计算参数与上一节相同,来流速度设定为0.5 m/s,电流密度从1 420 A/m$^{2}$开始逐渐增加.根据电磁力激活板的尺寸,电解 液的电导率以及欧姆公式,电阻大约为2 $\Omega$,每增加1 000 A/m$^{2}$的电流密度,大约相当于增加0.5 A的输入电流.
图8为电磁力控制的翼型绕流流场,图中显示,当输入的电流密度为1 420 A/m$^{2}$时,翼型的背风面后缘还会产生流动分离,但随着电流密度的增加,翼型后缘的流动分离逐渐被抑制(图6(c) $\sim$图6(d)),结果表明增加电磁力激活板的能量输入,可以提高电磁力的控制效果.

|
图8 不同电磁力控制的翼型绕流流场 Fig.8 Flow field of hydrofoil under the control of different Lorentz force |
图9为不电磁力作用下翼型的升阻力系数图,结果显示,随着电磁力激活板能量输入的增加,翼型的升力逐渐增加(图9(a)),而翼型的阻力则无明显变化(图9(b)),原因为电磁力导致的阻力减小被电磁力产生的表面摩擦力所抵消.
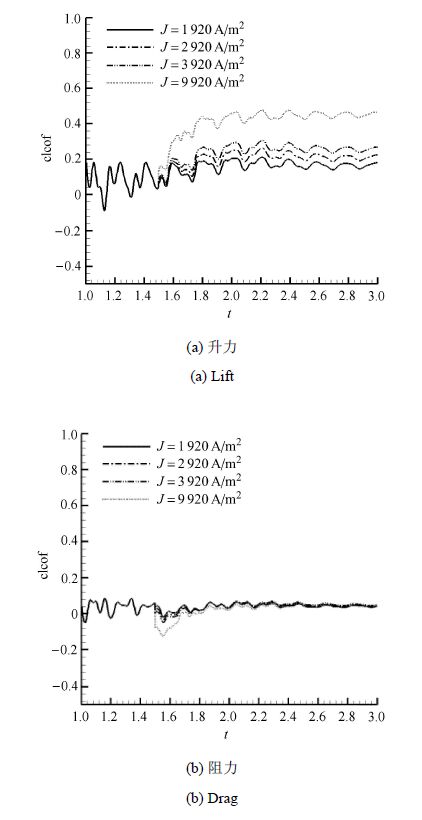
|
图9 不同电磁力作用下翼型的升阻力系数 Fig.9 Hydrofoil lift and drag coefficient under the control of different Lorentz force |
图10为电磁力控制效率$\eta$随输入电流密度变化图,图中显示在电流密度小于5 500 A/m$^{2}$时,随着电流密度的增加,电磁力控制效率有明显增加,但电磁力控制效率不超过5%;当电流密度超过5 500 A/m$^{2}$时,能量输入的增加导致的电磁力控制效率$\eta$的增加非常微小,在5 500 A/m$^{2}$到9 920 A/m$^{2}$之间的电磁力控制效率$\eta$的增加几乎为零.
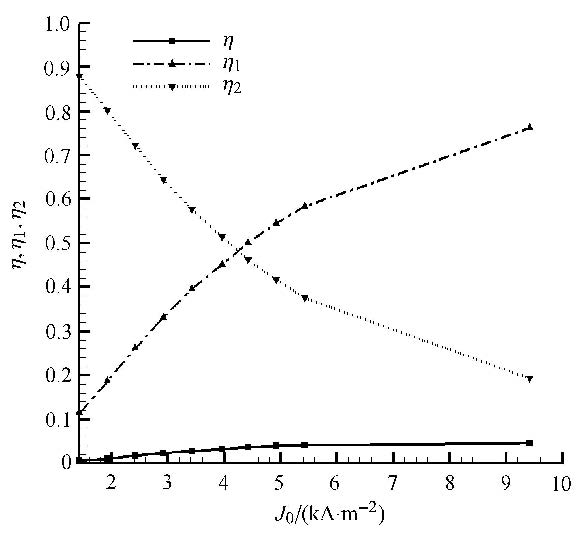
|
图10 电磁力控制效率随输入电流密度变化图 Fig.10 Diagram of Lorentz force control efficiency variation of with electric current density |
在翼型背风面流体边界层中形成的流向电磁力,可有效抑制流动分离,提高翼型的升力减小阻力. 阻碍其推广应用的瓶颈为较为低下的控制效率,为提高电磁力的控制效率,本文基于能量守恒定律,推导了电磁力控制效率计算公式,基于该公式研究了电磁力控制效率,分析电磁力损耗原因,发现了以下结论:
(1)电磁力控制开始阶段,电磁力激活板主要能耗为焦耳热及流体动能损耗,证明展向震荡电磁力能耗过高,该结论与Berger等[4]和Shatrov等[12]的研究结果相吻合,展向振荡电磁力能耗过高的原因为大部分电磁力的能量都用于改变流体的运动方向.
(2)电磁力控制效率随着时间增加而逐渐增长,电磁力稳定工作时间越长,电磁力控制效率越高.
(3)电磁力的控制效率随着来流速度的增加呈指数减小.
(4)增加电磁力激活板的能量输入,可有效增强电磁力的控制效果,但无法有效的提升电磁力的控制效率.
以上研究分析了电磁力控制效率低下的原因及其随着来流速度和时间的变化,下一步工作将研究如何提升电磁力的控制效率.
| [1] | Pulugundla G, Heinicke C, Karcher C, et al. Lorentz force velocimetry with a small permanent magnet. European Journal of Mechanics-B/Fluids, 2013, 41: 23-28 |
| [2] | Gailitis A, Lielausis O. On the possibility of drag reduction of a flat plate in an electrolyte. Appl Magnetohydrodyn Trudy Inst Fisiky AN Latvia SSR, 1961, 12: 143 |
| [3] | Henoch C, Stace J. Experimental investigation of a salt water turbulent boundary layer modified by an applied streamwise magnetohydrodynamic body force. Physics of Fluids, 1995, 7: 1371-1383 |
| [4] | Berger TW, Kim J, Lee C, et al. Turbulent boundary layer control utilizing the Lorentz force. Physics of Fluids, 2000, 12: 631-649 |
| [5] | Pang J, Choi K-S. Turbulent drag reduction by Lorentz force oscillation. Physics of Fluids, 2004, 16: L35 |
| [6] | Du Y, Symeonidis V, Karniadakis G. Drag reduction in wall-bounded turbulence via a transverse travelling wave. Journal of Fluid Mechanics, 2002, 457: 1-34 |
| [7] | Mutschke G, Gerbeth G, Albrecht T, et al. Separation control at hydrofoils using Lorentz forces. European Journal of Mechanics-B/Fluids, 2006, 25: 137-152 |
| [8] | Zhang H, Fan BC, Chen ZH, et al. Electro-magnetic control of shear flow over a cylinder for drag reduction and lift enhancement. Chinese Physics B, 2013, 22: 104701 |
| [9] | 梅栋杰, 范宝春, 陈耀慧 等. 槽道湍流展向振荡电磁力控制的实验研究. 物理学报, 2010, 59: 8335-8342 (Mei Dongjie, Fan Baochun, Chen Yaohui, et al. Experimental investigation on turbulent channel flow utilizing spanwise oscillating Lorentz force. Acta Physica Sinica, 2010, 59: 8335-8342 (in Chinese)) |
| [10] | 尹纪富, 尤云祥, 李巍 等. 电磁力控制湍流边界层分离圆柱绕流场特性数值分析. 物理学报, 2014, 63: 044701 (Yin Jifu, You Yunxiang, Li Wei, et al. Numerical analysis for the characteristics of flow control around a circular cylinder with a turbulent boundary layer separation using the electromagnetic force. Acta Physica Sinica, 2014, 63: 044701 (in Chinese)) |
| [11] | Liu ZK, Zhou BM, Liu HX, et al. Numerical investigation on feedback control of flow around an oscillating hydrofoil by Lorentz force. Fluid Dynamics Research, 2013, 45: 035502 |
| [12] | Shatrov V, Gerbeth G. Magnetohydrodynamic drag reduction and its efficiency. Physics of Fluids, 2007, 19: 035109 |
| [13] | 陈耀慧, 范宝春, 陈志华 等. 翼型绕流电磁控制的实验和数值研究. 物理学报, 2008, 57: 648-653 (Chen Yaohui, Fan Baochun, Chen Zhihua, et al. Experimental and numerical inve stigations on the electro-magnetic control of hydrofoil wake. Acta Physica Sinica, 2008, 57: 648-653 (in Chinese)) |
| [14] | 陈耀慧, 董祥瑞, 陈志华 等. 翼型绕流的洛仑兹力控制机理. 物理学报, 2014, 63: 034701 (Chen Yaohui, Dong Xiangrui, Chen Zhihua, et al. Control of flow around hydrofoil using the Lorentz force. Acta Physica Sinica, 2014, 63: 034701 (in Chinese)) |
| [15] | Rogers SE, Kwak D, Kiris C. Steady and unsteady solutions of the incompressible Navier-Stokes equations. AIAA Journal, 1991, 29: 603-610 |
2. Ministerial Key Laboratory of ZNDY, University of Science and Technology, Nanjing 210094, China
 2015, Vol. 47
2015, Vol. 47