高超声速飞行器的进气道需要利用人工转捩方法抑制激波边界层干扰产生的边界层分离,进而提高进气道的性能.由于高空飞行条件下雷诺数较低,人工转捩方法的有效性受到了很大限制,人们为找到可靠的低雷诺数人工转捩方法进行了大量的基础和应用研究.我们知道在风洞试验中,为了模拟边界层转捩,试验人员会在模型表面放置一个绊线,这种方法的一个主要问题是在低雷诺数情形下不能可靠的诱发转捩,所以人们基于三维扰动诱发转捩的思想,提出了多种形式的粗糙元(圆柱型、钻石型以及后掠斜坡型等)诱导人工转捩的方法.粗糙元诱导转捩的研究已经有半个世纪的历史,但是高超声速粗糙元诱导转捩的物理机制至今仍未完全研究清楚,这制约了人工转捩装置的设计,如形状、尺寸、位置、排列等.
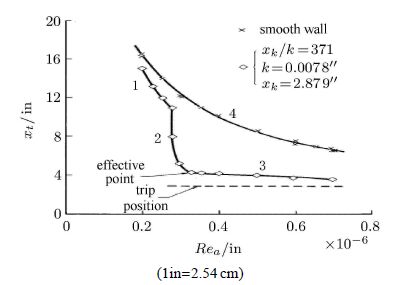
早在1961年,文献[1]就针对圆锥光滑表面及球形粗糙元表面的转捩情况就进行了研究. 在图1中,显示了4条曲线.曲线4显示的是光 滑壁面情形,此时转捩是随着单位雷诺数的增加而前移.在这个情形下,转捩完全是由于来流中的扰动引起的. 曲线1对应的粗糙元是非常小的,转捩也主要由于来流扰动引起.曲线2对应的是"临界条件",粗糙元诱导的扰动要比自由来流的扰动影响重要.此时随着单位雷诺数的进一步增加,边界层厚度持续减小.粗糙元的尺度足够诱发边界层转捩,自由来流的扰动起到的作用可以被忽略了,如曲线3所示.曲线2和曲线3的交叉点定义为"有效点",意味着粗糙元可以完全独立的诱导边界层转捩.
早期的粗糙元诱导转捩研究工作由于研究条件所限难以精细刻画流动细节. 随着精细试验手段的发展,流动细节的刻画越发清晰,粗糙元诱导转捩的物理机制的理解得到了明显的进步.
文献[2]利用一氧化氮平面激光诱导荧光的方法(NOPLIF),获得了半球和圆柱两种类型的粗糙元绕流的流动细节.文献[3]利用红外热图和油流技术,获得了钻石型、斜坡型、圆柱型及圆球型粗糙元绕流的流场转捩特征.文献[4]在静音风洞中,利用皮托探针、热线探针和壁面脉动压力传感器获得了圆柱型粗糙元绕流的非定常特征,发现了诱导马蹄涡失稳的主导频率大约为21 kHz.
在数值计算方面,高精度数值模拟方法的发展使得精细刻画流动细节成为可能.
文献[5]的直接数值模拟结果探索了粗糙元上游扰动的产生和扰动向下游的发展. 通过对流动细节的刻画他们发现大尺度和小尺度粗糙元的失稳区域大小是不一致的.
文献[6, 7]采用直接数值模拟方法针对圆柱和斜坡型粗糙元诱导的高超声速边界层转捩进行了研究. 针对圆柱型粗糙元,发现圆柱两侧的流动率先失稳,中心线处稍后失稳,并获得了诱导马蹄涡失稳的主导频率大约为19.23 kHz,与试验获得21 kHz基本吻合.针对斜坡型粗糙元,发现其失稳主要是出现在中心线处,并将计算结果与试验结果进行了定性上的对比,基本吻合.
综上所述,高超声速条件下不同类型的粗糙元诱导转捩的机理是不一致的,其诱导转捩的机理认识还十分欠缺. 在风洞试验方面,噪声度的影响及精细试验手段的限制等因素使得认识粗糙元诱导转捩物理机制十分困难.在数值计算方面,高精度数值方法及大规模并行计算技术的发展使得研究粗糙元诱导转捩物理机制成为了可能.
作者认为粗糙元为大扰动结构,从流动结构演化的思想出发,必然存在两种形式的失稳效应,一是拓扑结构失稳效应,二是边界层流动失稳效应. 这一观点尚未得到流动机理分析的证实.为此本文特别针对这一问题开展研究,选取同时存在这两种类型流动失稳效应的钻石型粗糙元外型,期望针对两种类型的失稳现象取得认识,为人工转捩装置的设计提供理论依据.
1 控制方程和数值方法控制方程为曲线坐标系下三维可压缩纳维-斯托克斯(Navier--Stokes)方程[8],采用高精度直接数值模拟方法求解 该方程.对于空间离散,无黏项采用五阶加权基本无振荡(WENO)格式[9],黏性项采用六阶中心差分.时间离散采用三阶总变差非增的龙格-库塔(TVD Runge-Kutta)方法[10].
壁面处采用等温无滑移边界条件,入口剖面的选取是通过二维平板直接数值模拟得到的,展向是周期边界条件,出口是超声速出口条件.
2 计算结果分析为了与试验结果进行比对,计算条件的选取是与文献[3]的试验状态一致.
具体的计算条件为 $$ M_\infty = 6 ,Re = 2.6\times 10^7 ,T_\infty = 70K ,T_{\rm W} = 300K $$ 其中,$Re$以1 m为特征长度.
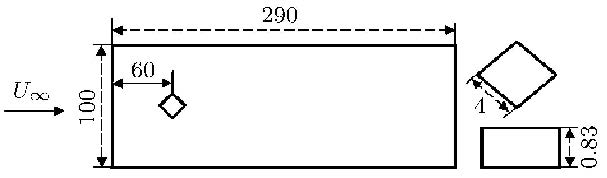
计算模型及尺寸的选取与文献[3]的试验模型一致,如 图2所示.
|
图2 计算模型尺寸图(单位mm) Fig.2 Sketch of the flat plate and the diamond roughness (unit:mm) |
本文选取的计算域入口为距平板前缘40 mm位置,其他计算域尺寸与试验模型一致,钻石型粗糙元的边长为4 mm,高度为0.83 mm,粗糙元位置处(60 mm)的边界层厚度为0.94 mm,粗糙元高度大约为当地边界层厚度的88%.计算网格的划分如图3所示. 壁面处第一层网格尺度为10 μm,$y^{ + }_{\rm wall}=0.8$,3个方向的网格数量分别为:1 321 (流向)×91 (法向)×481 (展向),总网格量约为5 700万.

|
图3 粗糙元附近网格示意图 Fig.3 The near-field grids around the diamond roughness |
下面针对直接数值模拟结果分别进行拓扑结构稳定性分析和边界层流动稳定性分析,揭示粗糙元诱导转捩的物理机制.
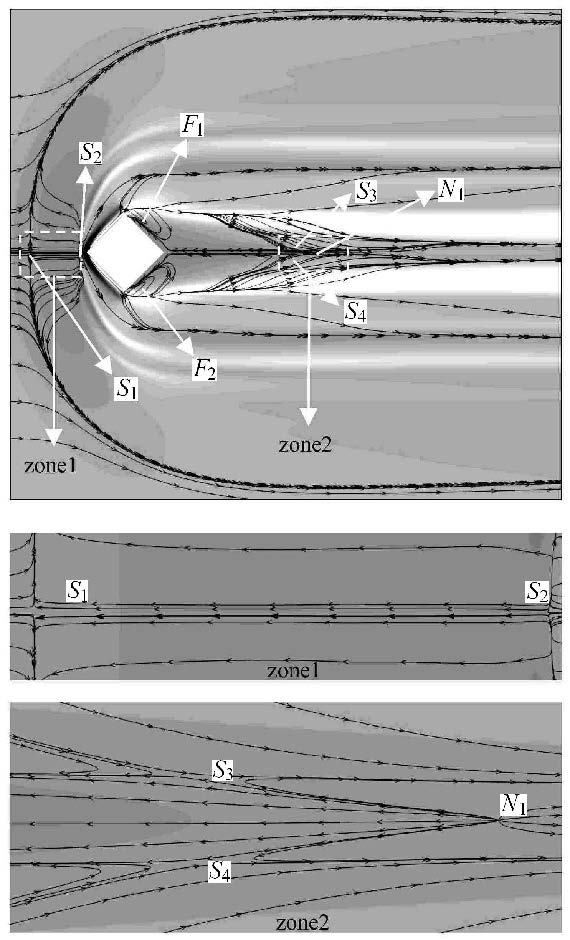
2.1.1 拓扑结构稳定性分析首先采用庞加莱(Poincare)的奇点理论对高超声速粗糙元绕流的流场拓扑结构进行分析. 图4显示的是钻石型粗糙元附近的摩擦力线和相应的奇点分布.在粗糙元的头部区域高超声速气流经过粗糙元会形成比较强的弓形激波,流动遇到粗糙元会向上游形成回流,此时会在粗糙元上游区域的中心线处形成鞍点$S_{1}$和鞍点$S_{2}$.图4中的zone1放大图清晰地显示了鞍点$S_{1}$和鞍点$S_{2}$附近的轨线分布.利用比索杜(Peixoto)定理可知,如果系统存在鞍点到鞍点的轨线,那么系统是结构不稳定的.由此可以得出在扰动存在的情况下,粗糙元两侧的流动结构会向着非定常、非对称的振荡结构发展.因此,粗糙元两侧的流动结构可能会失稳.在粗糙元的底部区域由于经过粗糙元两侧后气流开始膨胀,在压差的作用下其底部会出现分离,在拓扑结构上会出现两个对称的稳定焦点$F_{1}$和$F_{2}$.流动继续向粗糙元的近尾迹区发展,可以看出流动经过分离区后,由于两侧的压力高于中心线处压力,在压差的作用下流动再次被压缩,这样在拓扑结构上出现了两个关于中心线对称的鞍点结构($S_{3}$和$S_{4}$),同时在中心线处相应的出现了一个不稳定结点$N_{1}$. 这样3个奇点结构组合成了SNS轨线结构,图4中的zone2放大图清晰的显示了SNS轨线结构的构成.SNS轨线结构也是不稳定的[11],其在扰动存在的情况下同样会向着非定常、非对称的振荡结构发展.由此可以得出在扰动存在的情况下,粗糙元中心线附近的流动结构也有可能会失稳.
|
图4 粗糙元附近摩擦力线分布 Fig.4 Skin friction line around the roughness |
图5显示的是流动继续向粗糙元的远尾迹区发展的壁面摩擦力线分布. 可以看出粗糙元两侧的摩擦力线向中间汇聚并且出现结构失稳,摩擦力线在展向开始出现抖动,这预示着流动开始从壁面抬升,流动特征从大尺度开始向小尺度发展,更多小尺度结构的产生使得摩擦力线产生抖动.

|
图5 粗糙元转捩起始区域摩擦力线分布图 Fig.5 Skin friction line of wake-transition onset |
在图6中流动已经发展到了粗糙元的远尾迹区,可以看出中心线处的摩擦力线抖动越发剧烈,并且迅速向展向扩展,这预示着流动开始向壁面再附,更多小尺度结构激发出来,流动逐渐湍流化.

|
图6 粗糙元远尾迹区摩擦力线分布图 Fig.6 Skin friction line of wake-downstream |
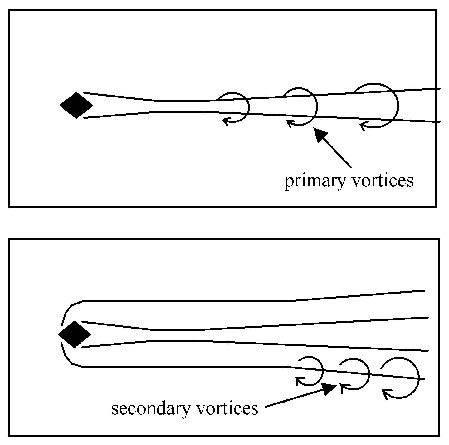
Moin等认为速度梯度张量第二不变量Q判据可以有效的识别涡结构. 图7为粗糙元速度梯度二阶不变量Q等值面图.图8 [6]和图9 [7]分别为圆柱型粗糙元和斜坡型粗糙元Q等值面图.从3张图的对比分析可以看出,不同类型粗糙元诱导转捩的机理是不一致的.图8中圆柱型粗糙元前缘会形成很强的弓形激波,粗糙元两侧的次涡结构会率先失稳,之后分离区后的主涡结构在流向涡的作用下也开始失稳.对于图8中圆柱型粗糙元其两侧的转捩优先于中线处.斜坡型粗糙元由于其前缘不存在弓形激波,其只存在主涡结构的失稳,所以其转捩也主要在中线处发生.对于钻石型粗糙元,图10给出了其尾迹区域涡系结构分布示意图,结合图7显示的结果可以看出,钻石型粗糙元分离区后的主涡结构在中线附近率先开始出现失稳,不同于平板自然转捩,其未经过线性发展阶段失稳后直接演化出流向涡及发卡涡.发卡涡在自诱导及平均流的作用下迅速形成发卡涡串、发卡涡包.与此同时粗糙元两侧的次涡结构也开始失稳,同样迅速发展出流向涡及发卡涡.主涡结构及次涡结构在展向区域相互作用使得流动结构向展向发展,最终在尾迹下游区域流动变为全湍流状态.

|
图7 粗糙元速度梯度二阶不变量Q等值面 Fig.7 Vortex structure by Q criterion |
|
图10 粗糙元涡结构示意图 Fig.10 Vortex structure in the wake region |
可以看出,钻石型粗糙元的转捩机理不同于圆柱型及斜坡型粗糙元. 斜坡型粗糙元失稳模式是主涡失稳模式,圆柱型和钻 石型粗糙元其失稳模式均包含主涡失稳模式及次涡失稳模式,其中圆柱型粗糙元次涡失稳早于主涡失稳,钻石型粗糙元主涡 失稳早于次涡失稳.
由于不同类型粗糙元的转捩机理存在差异,这就使得不同类型粗糙元具有各自的特点. 圆柱型和钻石型粗糙元由于存在两种失稳模式其诱导转捩能力要优于斜坡型粗糙元,但是由于圆柱型和钻石型粗糙元头部区域存在较强的弓形激波,导致粗糙元附近的阻力和热流急剧升高,这会产生较大的附加阻力和热流,其中由于圆柱型粗糙元存在而产生的附加阻力和热流要大于钻石型粗糙元.
针对飞行器对转捩的不同需求,需要合理利用不同类型粗糙元的各自特点. 飞行器表面布置粗糙元需要其附加的阻力和热流尽可能小,同时还需要其保持诱发转捩的作用. 基于此可以看出斜坡型粗糙元较圆柱型和钻石型粗糙元更有优势.但是需要注意的是斜坡型粗糙元只存在主涡失稳模式,在布置分布式斜坡型粗糙元时其相邻粗糙元的间距要尽可能小,以此来保证其诱导转捩的作用.
为了分析涡系结构随空间及时间的演化规律,图11将密度梯度的统计平均结果同瞬时结果进行了比对.可以看出涡系结构在初始 演化过程中尾迹结构是相似的. 这说明可以利用冻结时间的方法对涡系结构的空间发展开展研究.

|
图11 粗糙元密度梯度瞬时结果和统计结果 Fig.11 Instantaneous and average magnitude of density gradient |
针对涡系结构空间演化,选取多个流向剖面($X=80$,90,100,120,140,160,180,200 mm)进行研究,如图12所示.

|
图12 粗糙元尾迹区域不同流向截面的流线分布 Fig.12 Streamlines in the different streamwise location of wake region |
可以看出,在壁面附近低速流体"上抛"的影响下,在中心线位置处发卡涡(主涡)率先形成,在 图12(a)中,中心线位置处发卡涡的头部开始从近壁区抬起离开壁面进入更高速度的流层,在展向形成了一对反向旋转的诱导涡及一对反向旋转的发卡涡.从图12(b)及图12(c)中可以看出随着中心线位置处发卡涡涡脚之间的距离进一步缩小,在展向涡能量逐渐向中心线位置聚集,小尺度旋涡逐渐合并为大尺度旋涡,反向旋转的发卡涡越发明显.从图12(d)开始,中心线位置的发卡涡在强剪切的作用下,头部逐渐破碎,经过图12(e)$\sim$图12(g)中心线位置处的发卡涡完全破碎,更多小尺度旋涡出现,涡能量逐渐向展向传递,使得粗糙元两侧的发卡涡(次涡)开始失稳.在图12(h)中流动已经呈现随机化趋势,中心线位置处更多的小尺度结构出现,两侧的发卡涡(次涡)也已经破碎.
为了更加清晰形象地认识钻石型粗糙元诱导转捩的行为,采用密度梯度来对粗糙元流场结构进行刻画. 图13显示的是中心对称面处的密度梯度,从图中可以看出粗糙元附近的激波分布情况,流动在粗糙元前端经过压缩形成前缘激波,之后经过粗糙元,在粗糙元的后方流动出现膨胀和再压缩过程,形成相应的波系结构.随着流动向下游发展,可以清晰的看到由于高速气流和低速气流的剪切形成的流动失稳过程.

|
图13 粗糙元中心对称面处密度梯度图 Fig.13 Instantaneous magnitude of density gradient on the symmetric plane |
下面将直接数值模拟结果同理论及试验结果进行定性以及定量的比较,用以证实本文研究结果的可靠性.
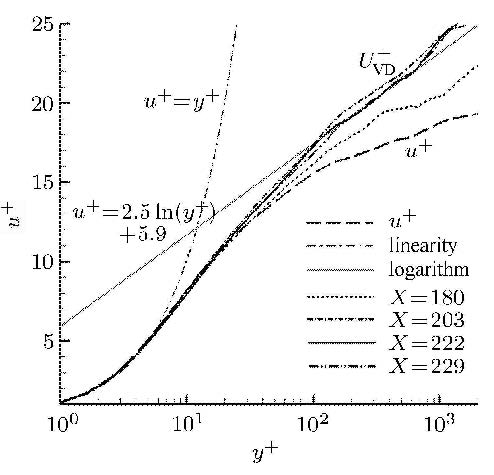
图14 给出了钻石型粗糙元中心线对称面不同流向位置处($X=180$,203,222,229 mm)的平均速度和范$\cdot $迪利斯特(Van Direst)变换后的平均流向速度剖面. 范$\cdot $迪利斯特变换的定义如下 \[U_{{\rm{VD}}}^ + = \int_0^{{u^ + }} ( \frac{{\bar \rho }}{{{\rho _{\rm{w}}}}}{)^{1/2}} {\rm{d}}{\bar u^ + }\]
|
图14 中心对称面处不同流向位置的平均流向速度和Van Direst 变换后速度剖面 Fig.14 Streamwise velocity profiles at different downstream locations on the centerline |
从图14中可以看出,当$0 < y^ + < 5.0$时平均流向速度剖面与壁面律:$u^ + = y^ + $吻合很好. 但是$u^ + $与$U_{\rm VD}^ + $有较大差别且所给出的对数律:$u^ + = 2.5\ln y^ + + 5.9$与不可压平板湍流的$u^ + = 2.5\ln y^ + +5.5$结果相比也有一定差别. 这表明在$Ma=6$情形下,有明显 的内在压缩性影响.这是由于来流马赫数较高时边界层内动能的耗散导致温度的升高,由此造成平均密度分布的改变,进而改变了流动的平均速度剖面.这与文献[12]的$Ma=6$平板边界层湍流研究结果一致.
另外从图14的不同流向位置的范$\cdot$迪利斯特变换后速度剖面还可以看出,随着流向距离的增加,速度剖面逐渐与对数律靠近,当$X=222$ mm时速度剖面与对数律完全吻合且随着流向距离的继续增加,速度剖面基本不变,说明流动已经进入完全湍流状态.
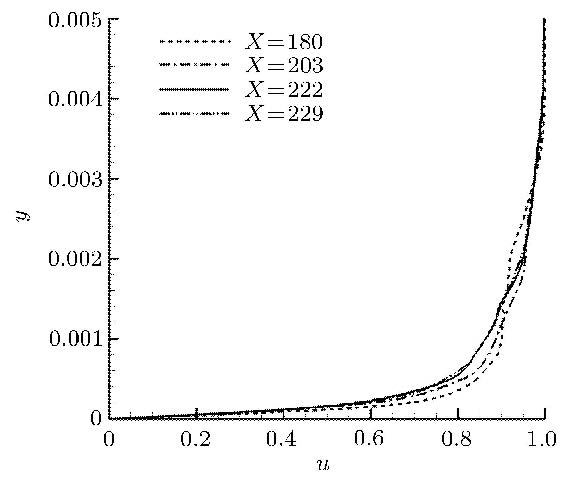
图15显示的不同流向位置处的流向速度沿壁面法向的分布,从图中可以看出:当$X>222$ mm后速度剖面基本重合,也说明流动已经完全湍流化.
|
图15 中心对称面处不同流向位置的速度剖面 Fig.15 Velocity profiles at different downstream locations on the centerline |
通过与理论的对比研究验证了本文数值模拟结果的可靠性. 下面将其与试验结果进行定量的对比分析. 层流及湍流的热流系数及摩阻系数的近似解是利用安德森(Anderson)的参考温度法得到的. 在参考温度法中雷诺比拟因子选为$s=1.0/1.16$.
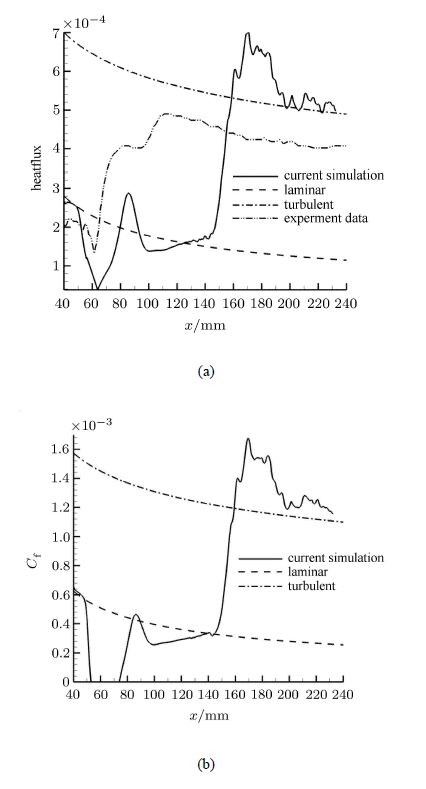
图16显示的分别为钻石型粗糙元中心对称面处的热流系数及摩阻系数分布曲线. 从热流系数分布曲线中,可以看出在粗糙元之前流动是层流状态与层流近似解基本吻合,流动经过粗糙元后由于涡系结构的相互作用,转捩开始出现,伴随着热流系数的急剧上升. 经过一段距离的发展,流动变为全湍流状态,此时热流系数与湍流的近似解基本吻合.摩阻系数的变化过程与热流系数的变化过程一致,直接数值模拟得到的摩阻系数曲线在层流区及湍流区与参考温度法得到的层流及湍流近似解基本吻合.
|
图16 钻石型粗糙元中心对称面处热流系数及摩阻系数分布的定量比较 Fig.16 Stanton number and skin friction coefficient distributions on the centerline |
从钻石型粗糙元诱导转捩的定量比较结果可以看出,试验结果(图16左图的双点划线)中转捩行为要早于本文的直接数值结果,这是由于转捩受来流噪声的影响很大.文献[3]对试验的噪声度进行了评估,其得出的结论是:对于本文选取的雷诺数条件,风洞的质量流量扰动为1.5%,其噪声度比"静风洞"及真实飞行情形下要高得多. 直接数值模拟研究存在的噪声度只由数值计算本身提供,它是十分微弱的.所以试验中转捩行为早于本文的直接数值模拟结果是合理的.
3 结 论本文采用直接数值模拟(DNS)的方法,针对钻石型粗糙元诱导的高超声速边界层转捩机理开展了研究,从拓扑结构稳定性和边界层流动稳定性两个角度分析了钻石型粗糙元诱导转捩的机理,同时通过对不同类型粗糙元(圆柱、斜坡及钻石型)的对比研究,揭示了粗糙元诱导转捩机理的异同,为高超声速人工转捩装置设计提供了基础理论支撑. 具体结论如下:
(1) 钻石型粗糙元同时存在拓扑结构失稳效应和边界层流动失稳效应两种类型失稳效应.
(2) 钻石型粗糙元头部区域和底部区域分别存在不稳定的鞍点--鞍点(SS)型轨线和鞍点--结点--鞍点(SNS)型轨线,在扰动的作用下其 会形成非定常、非对称的振荡结构.
(3) 不同类型的粗糙元诱导转捩的机理不同. 钻石型及圆柱型粗糙元失稳模式均包括主涡失稳模式及次涡失稳模式,斜坡型粗糙元的失稳模式只存在主涡失稳模式.
(4) 斜坡型粗糙元较圆柱型和钻石型粗糙元附加的阻力和热流小,其在飞行器表面布置粗糙元时更有优势. 但是在布置分布式斜坡型粗糙元时其相邻粗糙元的间距要尽可能小,以此来保证其诱导转捩的作用.
| [1] | Van Driest ER, Blumer CB. Boundary-layer at supersonic speeds-three dimensional roughness effects (spheres). North American Aviation, INC. Space and Information Systems Division Report, SID 61-275, 1961 |
| [2] | Danehy PM, Bathel BF, Ivey CB, et al. NO PLIF study of hypersonic transition over a discrete hemispherical roughness element. AIAA paper 2009-394, 2009 |
| [3] | Tirtey SC, Chazot O, Walpot L. Characterization of hypersonic roughness-induced boundary-layer transition. Experiments in Fluids, 2011, 50(2): 407-418 |
| [4] | Wheaton BM, Schneider SP. Roughness-induced instability in a hypersonic laminar boundary layer. AIAA Journal, 2012, 50(6): 1245-1256 |
| [5] | Bartkowicz MD, Subbareddy PK, Candler GV. Numerical simulations of roughness induced instability in the Purdue Mach 6 Wind Tunnel. AIAA paper 2010-4723, 2010 |
| [6] | Duan ZW, Xiao ZX, Fu S. Direct numerical simulation of hypersonic transition induced by a cylindrical roughness element. AIAA paper 2013-3112, 2013 |
| [7] | Duan ZW, Xiao ZX, Fu S. Direct numerical simulation of hypersonic transition induced by a ramp roughness element. AIAA paper 2014-0237, 2014 |
| [8] | 沈清,朱德华. 高超声速尾迹流场稳定性数值研究. 力学学报,2009, 41(1): 1-7 (Shen Qing, Zhu Dehua. Numerical study of the stability of hypersonic wake. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1):1-7 (in Chinese)) |
| [9] | Jiang GS, Shu CW. Efficient implementation of weighted ENO schemes. Journal of Computational Physics, 1996, 126: 202-228 |
| [10] | 张涵信,沈孟育. 计算流体力学:差分方法的原理和应用. 北京:国防工业出版社,2003 (Zhang Hanxin, Shen Mengyu. Computational Fluid Dynamics-Fundamentals and Applications of Finite Difference Methods. Beijing: National Defence Industry Press, 2003 (in Chinese)) |
| [11] | 朱德华,沈清,王强等. 钝头体高超声速绕流底部失稳特征数值模拟. 力学学报,2012,44(3): 465-472 (Zhu Dehua, Shen Qing, Wang Qiang, et al. Numerical study of the stability of hypersonic base flow over a blunt body and Apollo command module. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(3):465-472 (in Chinese)) |
| [12] | Li XL, Fu DX, Ma YW. Direct numerical simulation of a spatially evolving supersonic turbulent boundary layer at Ma=6. Chinese Phys Lett , 2006, 23(6): 1519-1522 |
 2015, Vol. 47
2015, Vol. 47