2. 福州大学土木工程学院, 福州350108
电化学沉积法是最近兴起的水环境下钢筋混凝土裂缝修复的新方法之一[1],当前关于该方法的探索,集中在以下两个方面:
一方面,围绕如何制备待修复试件展开. 实验室常采用加载预制法制备带裂缝试件,即对完好混凝土试件进行加载(如受压、受弯等)使其 产生裂 缝[2, 3]. 此外,文献[4, 5]制备了带干缩裂缝的混凝土试件 [4, 5];文献[6, 7]分别采用氯离子侵蚀[6]和人工预制[7]的方法生产带裂缝修复试件;文献[8]采用多孔混凝土 试件模拟带裂缝的混凝土试件.
另一方面,围绕该方法修复效果的评价指标及其影响因素进行. 电化学沉积试验常采用的评价指标是质量增加率、表面覆盖率、裂缝愈合 率、裂缝填充深度和渗透系数[9, 10, 11],超声波速度[8] ,抗弯强度等[7]. 影响修复效果的因素主要包括电解质溶液类型、溶液浓度、溶液温度、电流强度、电极类型和距离、混凝土自身参数以及添加剂 等[7, 11].
对于电化学沉积修复过程混凝土微观结构的演化及其与宏观性能的定量关系研究很少[12, 13],文献[12, 13]分别提出了 饱和与非饱和混凝土电化学沉积修复的细观力学模型,并采用森喜朗-田中(Mori-Tanaka)法对修复混凝土的有效模量进行预测. 区别于文献[12, 13]的成果,本文基于自洽法获取电化学沉积修复混凝土的有效性能. 自洽法作为一种应用广泛的细观力学方法,其在混凝土(未修复)、岩石等复合材料宏观性能预测方面已发挥重要作用,但是,其在电 化学沉积修复混凝土中的应用几乎没有. 针对这一情况,本文从修复饱和混凝土的(微)细观结构出发,给出了描述修复混凝土的细观力学模型,并基于自洽法对修复饱和混凝 土的有效性能进行多层次均匀化处理,定量连接了修复饱和混凝土的细观结构和宏观性能.
1 电化学沉积修复混凝土细观力学框架 1.1 电化学沉积修复饱和混凝土细观力学模型饱和混凝土是指混凝土中的孔隙由水充满[14]. 在细观层次,可以将电化学沉积修复后的饱和混凝土视为由水、电化学沉积产物、骨料、砂浆以及骨料和砂浆间的界面组成的多相复合材料. 进一步,为了考虑电化学沉积产物对混凝土性能的影响,可将混凝土中的固体相(骨料,砂浆以及两者间的界面)视为混凝土基体 相,而水和电化学沉积产物为夹杂相[12]. 为了建立描述修复混凝土的微观力学模型,文章作了如下假设:
(1)考虑饱和孔隙中的水能抑制混凝土变形,假设饱和孔隙的形状为球形[14].
(2)考虑较大的孔隙中有更多的电解质溶液,能产生更多的电化学沉积产物,假设电化学沉积产物数量和原孔隙体积成正比,且均匀分布在孔隙壁周边[12].
(3)尽管影响粘结界面的因素较多,但是当电流强度较小时,粘结效果较好. 简化起见,假设电化学沉积产物和混凝土基体的粘结界面完好[12].
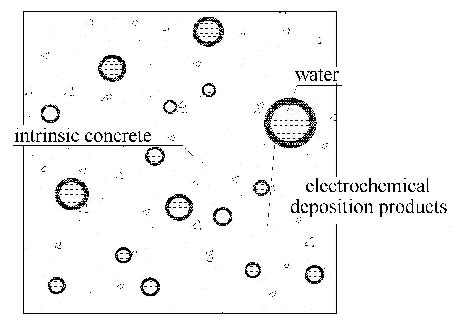
基于以上假设,文章提出了如图1所示的修复混凝土多相细观力学模型(包括水、电化学沉积产物和混凝土基体三相组分). 通过预测该模型的有效性能,便可以从理论上定量描述修复过程混凝土的有效性能.
|
图 1 饱和混凝土电化学沉积修复细观力学模型 Fig. 1 The micromechanical model for saturated concrete healed by the electrochemical deposition method |
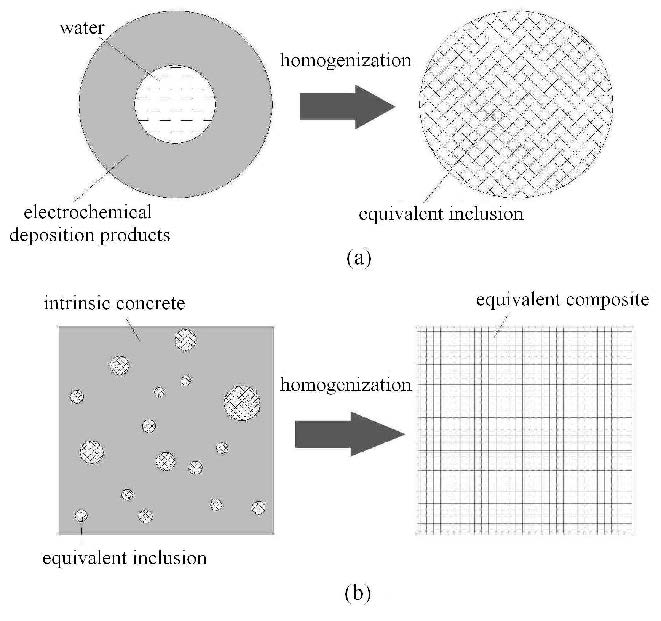
对于多相复合材料而言,常采取分步均匀化的思路获取其有效性能[12, 13]. 文章亦采用此思路获取电化学修 复后混凝土的有效性能,如图2所示.
|
图 2 多层次均匀化的思路:(a) 第1层次: 对水和电化学沉积产物进行均匀化;(b) 第2层次: 对混凝土基体和等效夹杂进行均匀化 Fig. 2 The multi-level homogenization scheme: (a) the first level: the homogenization of the deposition products and water, and (b) the second level: the homogenization of the intrinsic concrete and the equivalent inclusion |
(1)采用广义自洽方法获取等效夹杂(由水和电化学沉积产物组成)的有效性能,如图2(a)所示;
(2)采用自洽法 和沃伊特(Voigt)上限相结合的方式获取电化学沉积修复的饱和混凝土有效性能(由混凝土基体和等效夹杂组成),如图2(b)所示.
2 自洽法在所提细观力学模型中的应用 2.1 基于广义自洽模型的等效夹杂有效性能预测将电化学沉积产物视为基体相,将水视为夹杂相,那么由广义自洽模型可得[15]
| $ {K_{\rm{M}}} = {K_2} + \frac{{{\phi _{\rm{W}}}({K_1} - {K_2})(3{K_2} + 4{\mu _2})}}{{3{K_2} + 4{\mu _2} + 3(1 - {\phi _{\rm{M}}})({K_1} - {K_2})}} $ | (1) |
| $ A{(\frac{{{\mu _{\rm{M}}}}}{{{\mu _2}}})^2} + B(\frac{{{\mu _{\rm{M}}}}}{{{\mu _2}}}) + C = 0 $ | (2) |
式中,$A,B,C$定义参见文献[15]结果,$\phi_{\rm W} $是水占等效夹杂的体积含量;$K_1 $和$K_2 $是水和电化学沉积产物的体积模量;$\mu _2 $是电化学沉积产物的剪切模量;$K_{\rm M}$和$\mu _{\rm M} $是广义自洽模型预测的该两相材料的有效体积模量和剪切模量.
2.2 基于自洽模型的等效复合材料有效性能预测视电化学沉积修复饱和混凝土为由混凝土基体和等效夹杂(其性能由第1层均匀化处理获得)组成的两相材料. 那么,由自洽法可得[16]
| $ {K_{\rm{s}}} = {K_3} + \frac{{{\phi _{\rm{e}}}{K_{\rm{s}}}({K_{\rm{M}}} - {K_3})}}{{{K_{\rm{s}}} + 3{\gamma _{\rm{s}}}({K_{\rm{M}}} - {K_{\rm{s}}})}} $ | (3) |
| $\mu _{\rm s} = \mu _3 + \dfrac{\phi _{\rm e} \mu _{\rm s} (\mu _{\rm M} - \mu _3 )}{\mu _{\rm s} + 2\delta _{\rm s} (\mu_{\rm M} - \mu _{\rm s} )} $ | (4) |
| $\gamma _{\rm s} = \dfrac{K_{\rm s} }{3K_{\rm s} + 4\mu _{\rm s} } $ | (5) |
| $\delta _{\rm s} = \dfrac{3K_{\rm s} + 6\mu _{\rm s} }{15K_{\rm s} + 20\mu _{\rm s} } $ | (6) |
式中,$\phi _{\rm e} $是等效夹杂占饱和混凝土的体积含量; $K_3 $和$\mu _3 $是混凝土基体的体积模量和剪切模量;$K_{\rm s} $和$\mu _{\rm s} $是自洽法计算的修复后饱和混凝土的有效体积模量和剪切模量,可通过迭代求解获得. 那么,自洽法计算的材料弹性模量$E_{\rm s} $由下式可得
| $ E_{\rm s} = \dfrac{9K_{\rm s} \mu _{\rm s} }{3K_{\rm s} + \mu _{\rm s} } $ | (7) |
当夹杂的模量较低时,自洽法会高估夹杂的作用,使得预测的复合材料有效模量较实际值偏低. 对混凝土基体而言,等效夹杂(由水和电化学沉积产物组成)的有效模量往往较低. 为了减少这种误差,文章采用沃伊特上限[16]对自洽法计算结果进行修正. 即
| $K = 0.5 (K_{\rm s} + K_{\rm V} ) $ | (8) |
| $\mu = 0.5 (\mu _{\rm s} + \mu _{\rm V} ) $ | (9) |
| $E = 0.5 (E_{\rm s} + E_{\rm V} ) $ | (10) |
式中,$K,\mu $和$E$是本文方法计算的修复后饱和混凝土的有效体积模、剪切模量和弹性模量;$K_{\rm V} $,$\mu _{\rm V} $和$E_{\rm V} $分别是有效体积模、剪切模量和弹性模量的沃伊特上限值,详细结果请参考文献[16].
3 对比验证 3.1 与已有模型对比文献[12]提出了饱和混凝土电化学沉积修复的细观力学框架,该框架能较好的预测修复过程饱和混凝土宏观性能的变化. 为此,本节将本 文预测结果和文献[12]的结果进行对比. 根据文献[17]的试验数据取混凝土基体和水的材料参数,根据文献[12],取3种不同的电化学沉积产物,具体如表1所示.
| 表 1 混凝土基体、水和电化学沉积产物的性能 Table 1 Properties of the intrinsic concrete,water and the electrochemical deposition products (EDP) |
图3是本文和文献[12]方法所获有效剪切模量和弹性模量对比图. 从中可看出,两者预测结果较 为接近,尤其是修复的后期,两者几乎相同. 其中,$\max \left[{\left( {\mu - \mu ^\ast } \right) / \mu ^\ast } \right] < 3.5\% $,$\max \left[{\left( {E - E^\ast } \right) / E^\ast } \right] < 3.8\% $. 此处,$\mu ^\ast $和$E^\ast $是文献[12]方法计算的修复后饱和混凝土的剪切模量和弹性模量. 另外,从图中不难发现,对3种不同的沉积产物而言,随着电化学沉积产物性能的提高,修复后混凝土表现出更高的有效性能.

|
图 3 本文和文献[12]方法所获有效模量对比图(-1,-2,-3分别表示3种不同电化学沉积产物对应的计算结果) Fig. 3 The comparison between the results for the modulus obtained with the proposed method and the method in Ref.[12](-1,-2,-3 represent results obtained using three different kinds of deposition products, respectively) |
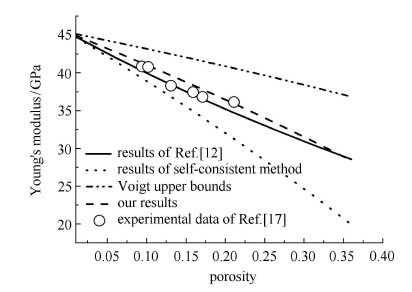
当未修复时,本文模型将退化为饱和混凝土细观力学模型. 考虑进一步水化和黏性的影响[12, 14],本文方法可预测饱和混 凝土的有效模量,结果如 图4所示.
|
图 4 不同模型预测的饱和混凝土弹性模量和文献[17] 试验数据对比图 Fig. 4 he comparison between the results obtained with different methods and those obtained experimentally for the Young's modulus saturated concrete in Ref.[17] |
从图4可知:单独用自洽法预测饱和混凝土(未修复)有效模量时,如孔隙含量在5%到10%时,其预测结果还可较好 的反应试验结果,但随着孔隙率的提高,其预测结果越来越偏离(小于)试验值和文献[12]结果;当采用本文方法时,其预测 结果和试验数据及文献[12]结果吻合较好.
4 结 论本文提出了含电化学沉积产物、水和混凝土基体三相组分的电化学沉积修复饱和混凝土细观力学模型. 为定量描述电化学沉 积产物的修复效果,文章基于自洽法对所提出的模型进行分层次均匀化处理. 对比试验和已有模型说明:本文所提出的电化学沉积修复饱和混凝土细观力学模型和基于自洽法的多层次均匀化方法能够从细观层 次定量描述电化学沉积产物对混凝土宏观性能的影响;当未修复时,本文模型和方法可以用来预测饱和混凝土的有效性能. 同时,基于本文模型和方法可发现,随着电化学沉积产物性能的提高,修复后饱和混凝土表现出更高的有效性能.
本文电化学沉积修复混凝土细观力学框架的建立是以文章的3个假设为前提,如果考虑孔隙形状、修复界面等的影响,那么,理论 预测的修复混凝土有效性能将小于本文预测的结果,定量的数值差别,有待于建立更通用的细观力学模型(如考虑修复界面性能的影 响)进行分析.
| [1] | 蒋正武,孙振平,王培铭.电化学沉积法修复钢筋混凝土裂缝的机理.同济大学学报(自然科学版), 2004, 32(11): 1471-1475 (Jiang Zhengwu, Sun Zhenping, Wang Peiming. Mechanism on rehabilitation of cracks in reinforced concrete using eiectrodeposition technique. Journal of Tongji University (Natural Science), 2004, 32(11): 1471-1475 (in Chinese)) |
| [2] | Ryu JS. New waterproofing technique for leaking concrete. Journal of Material Science Letters, 2003, 22(14): 1023-1025 |
| [3] | Ryou JS, Monteiro P. Electrodeposition as a rehabilitation method for concrete materials. Canadian Journal of Civil Enginereing, 2004, 31(5): 776-781 |
| [4] | Ryu JS. An experimental study on the repair of concrete crack by electrochemical technique. Materials and Structures, 2001, 34(241): 433-437 |
| [5] | Otsuki N, Ryu JS. Use of electrodeposition for repair of concrete with shrinkage cracks. Journal of Materials in Civil Engineering (ASCE), 2001, 13(2): 136-142 |
| [6] | Ryu JS, Otsuki, N. Crack closure of reinforced concrete by electro deposition technique. Cement and Concrete Research, 2002, 32(1): 159-264 |
| [7] | Chang JJ, Yeih WC, Hsu HM, et al. Performance evaluation of using electrochemical deposition as a repair method for reinforced concrete beams. Tech Science Press Structural Longevity, 2009, 1(2): 75-93 |
| [8] | Jiang ZW, Xing F, Sun ZP, et al. Healing effectiveness of cracks rehabilitation in reinforced concrete using electrodeposition method. Journal of Wuhan University of Technology, 2008, 23(6): 917-922 |
| [9] | Otsuki N, Hisada M, Ryu JS, et al. Rehabilitation of concrete cracks by electrodeposition. Concrete International, 1999, 21(3): 58-62 |
| [10] | Ryu JS, Otsuki N. Application of electrochemical techniques for the control of cracks and steel corrosion in concrete. Journal of Applied Electrochemistry, 2002, 32(6): 635-639 |
| [11] | Ryu JS. Influence of crack width,cover depth,water cement ratio and temperature on the formation of electrodeposition on the concrete surface. Magazine of Concrete Research, 2003, 55(1): 35-40 |
| [12] | Zhu HH, Chen Q, Yan ZG, et al. Micromechanical model for saturated concrete repaired by electrochemical deposition method. Materials and Structures, 2014, 47: 1067-1082 |
| [13] | Yan ZG, Chen Q, Zhu HH, et al. A multiphase micromechanical model for unsaturated concrete repaired by electrochemical deposition method. International Journal of Solids and Structures, 2013, 50(24): 3875-3885 |
| [14] | 王海龙,李庆斌. 饱和混凝土的弹性模量预测. 清华大学学报(自然科学版), 2005, 45(6): 761-763 (Wang Hailong, Li Qingbin. Saturated concrete elastic modulus prediction. Journal of Tsinghua University (Science and Technology), 2005, 45(6): 761-763 (in Chinese)) |
| [15] | Christensen RM, Lo KH. Solutions for effective shear properties in three phase sphere and cylinder models. Journal of the Mechanics and Physics of Solids, 1979, 27(4): 315-330 |
| [16] | Qu JM, Cherkaoui M. Fundamentals of Micromechanics of Solids. Hoboken, New Jersey: John Wiley & Sons, Inc., 2006 |
| [17] | Yaman IO, Hearn N, Aktan HM. Active and non-active porosity in concrete, part I: Experimental evidence. Materials and Structures, 2002, 35(3): 102-109 |
2. College of Civil Engineering, Fuzhou University, Fuzhou 350108, China
 2015, Vol. 47
2015, Vol. 47
