2. 大连理工大学, 航空航天学院, 大连116024
刚柔耦合系统在机械、航空航天等领域非常多见,从低速运动的机械手臂到高速旋转的直升机旋翼和涡轮发动机叶片等,大范围 运动对结构动力学特性的影响显得越来越重要,有必要对其进行研究.
刚柔耦合问题的研究先后经历了早期的运动弹性动力学方法和传统模型两阶段. 在1987年,文 献[1]通过对旋转运动悬臂梁变形的详 细描述而建立了比较精确的动力学模型,从而指出了传统模型的缺陷,并首次提出了``动力刚化''概念. 文献[2]探讨了关于惯性主轴等几种浮动坐标系的建模方法,详细分析了各自附带的约束条件及适用类型. 文献[3]深入研究了欧拉-伯努利梁的变形问题,充分考虑了横向弯曲变形对纵向变形的影响,给出了精确的非线性变形描述. 文献[4]总结了前人的相关工作,并针对横向变形如何对纵向变形产生影响以及几何刚度项如何产生等问题进行了对比探讨. 洪嘉振等[5]对刚柔耦合问题进行了全面的总结概括,并指出刚柔耦合问题的主要研究任务. 田强等[6]回顾了另一种建模方法-----绝对节点坐标法的研究进展,提出了值得进一步研究的问题. 蒋丽忠[7]和吴胜宝[8]分别研究了大范围运动悬臂梁动力学建模问题,建立了一次近似模型,并与传统模型之间的区别进行了探讨. 方建士等[9]和刘锦阳等[10]建立了大范围运动的中心刚体悬臂梁动力学模型,前者讨论了中心刚体半径与梁长比值对结构 动力学特性的影响,而后者讨论了扭转变形和截面转动惯量对结构动力学特性的影响. 焦小磊[11]通过拟变分原理探讨了作大范围转动的梁的振型问题. 陈思佳等[12]针对旋转运动的悬臂梁建立了一次近似模型,通过保留由动能得到的高次耦合项得到了高次耦合动力学模型.
当前很多研究大都采用了计入横向弯曲变形导致的纵向伸缩变形的一次近似模型. 该模型更多的关注了横向弯曲变形对纵向变形 的影响,特别是在动能中考虑比较充分;而对于轴向变形对横向变形的影响则有所忽视,如在应变能中仅保留了结构的轴向拉伸 应变能和横向弯曲应变能,而忽略了由轴向和横向变形所产生的应变能中的耦合项. 这种不加分析而人为忽略的方式是不够严谨、不够合理的,有必要探讨这些耦合项对结构动力学特性的影响.
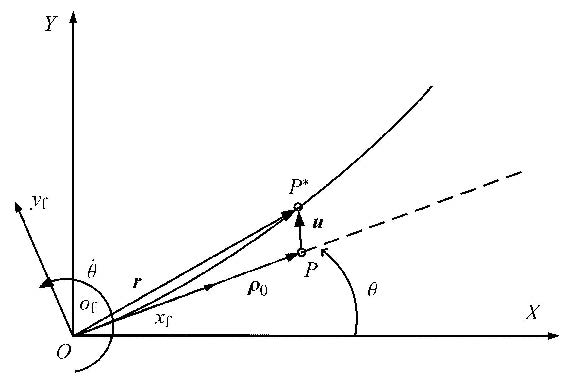
1 运动学描述 1.1 浮动坐标系如图1所示平面运动细长柔性悬臂梁,长度为$L$,密度为 $\gamma $,弹性模量为$E$,横截面积为$A$,截面惯性矩为$I$. $XOY$为全局惯性坐标系,$x_{\rm f}o_{\rm f}y_{\rm f}$为浮动坐标系,任意时刻柔性梁变形位置用实线表示;假想的未变形位置用虚线表示; $\theta $表示大范围转动; ${ \rho }_{0}$表示$P$点在浮动坐标系中的位置向量;${ u}$表示$P$点的变形位移;则$P^*$点的绝对位移${ r}$可表示为
|
图 1 平面梁的位移描述 Fig. 1 Displacement description of planar beam |
| $ r = B\left( {{\rho _0} + u} \right){\mkern 1mu} ,\;\;\;B = \left[\begin{array}{l} \cos \theta \;\;\;\;\; - \sin \theta \\ \sin \theta \;\;\;\;\;\;\;\cos \theta \; \end{array} \right] $ | (1) |
式中,${ \rho }_{0}=(x \ \ 0)^{\rm T}$,${ u}=(u_{1} \ \ u_{2})^{\rm T}$;${ B}$是旋转变换矩阵.
式(1)对时间求一阶导数,得到$P^*$点绝对速度表达式
| $v = \dot r = \dot B\left( {{\rho _0} + u} \right) + B\mathop u\limits^ \circ $ | (2) |
式中,``$ \cdot $''表示在惯性系下对时间求导;``$ \circ $''表示在浮动坐标系下对时间求导,不至混淆,后文统一用前者表示.
1.2 变形描述根据弹性梁的变形描述理论,选取如下形式[3]
| $ \begin{array}{l} u = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {u_1}\\ {u_2} \end{array} \end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {w_1} + {w_{{\rm{1r}}}} + {w_{\rm{c}}}\\ {w_2} + {w_{{\rm{2r}}}} \end{array} \end{array}} \right\} = \\ \;\;\;\;\;\left\{ {\begin{array}{*{20}{c}} {{w_1} - y\frac{{\partial {w_2}}}{{\partial x}} - \frac{1}{2}{{\int_0^x {\left( {\frac{{\partial {w_2}}}{{\partial \xi }}} \right)} }^2}d\xi {w_2} - \frac{1}{2}y{{\left( {\frac{{\partial {w_2}}}{{\partial x}}} \right)}^2}} \end{array}} \right\} \end{array} $ | (3) |
其中,$w_{1}$和$w_{2}$分别表示轴向伸缩和弯曲变形位移;$w_{\rm 1r}$和$w_{\rm 2r}$分别表示由于横截面转动引起的纵向和 弯曲变形位移,后文不计$w_{\rm 2r}$的影响;$w_{\rm c}$表示由于横向弯曲变形而产生的纵向伸缩量,是一次近似模型的关键项.
2 刚柔耦合动力学方程系统动能为
| $ T = \frac{1}{2}\int_V \gamma {\dot r^{\rm{T}}}\dot rdV $ | (4) |
利用连续介质力学中有限应变表达式
| ${\varepsilon _{xx}} = u_{\rm{1}}^, + \frac{1}{2}\left[ {u_1^{,2} + u_2^{,2}} \right]$ | (5) |
式中,上标``\,$'$\,''表示对横坐标$x$求一阶导数,后文中``\,$''$\,''表示对横坐标$x$求二阶导数,以此类推.
系统应变能完全描述为
| $ \begin{array}{*{20}{l}} {U = \frac{1}{2}\int_V E \varepsilon _{xx}^2dV = }\\ {\;\;\;\;\;\frac{1}{2}\int_L {} \left[ {EA\left( {\underline {w_1^{,2}} + w_1^{,3} + \frac{1}{4}w_1^{,4} + \frac{1}{{64}}w_2^{,8} + \frac{1}{4}w_1^{,2}w_2^{,4}} \right.} \right.}\\ {\;\;\;\; + \left. {\frac{1}{4}w_1^,w_2^{,4} - w_1^{,2}w_2^{,2} + \frac{1}{8}w_1^{,2}w_2^{,4} - \frac{1}{2}w_1^{,3}w_2^{,2} - \frac{1}{8}w_1^,w_2^{,6}} \right) + }\\ {\;\;\;\;EI\left( {\underline {w_2^{,,2}} + 3w_1^,w_2^{,,2} + \frac{3}{2}w_1^{,2}w_2^{,,2} - w_2^{.2}w_2^{,,2} + \frac{3}{8}w_2^{,4}w_2^{,,2}} \right. - }\\ {\;\;\;\left. {\left. {\frac{3}{2}w_1^,w_2^{,2}w_2^{,,2}} \right)} \right]dx + \frac{1}{2}\int_V E \frac{1}{4}{y^4}w_2^{,,4}dV} \end{array}$ | (6) |
当前研究中通常只选取两个下划线项而忽略了其他耦合项,忽略这些项是否合理只能通过进一步的分析之后才能做出回答.
利用哈密尔顿原理可以得到结构耦合动力学模型. 仅讨论大范围匀速运动情况(令$\ddot {\theta } =0$);对轴向仅保留$w_{1}$及其各阶导数的线性项;对横向仅保留$w_{2}$及其各阶导数的线性项;经过这些假设,考虑应变能耦合项后的模型(Model 1)如下
| $ \begin{array}{*{20}{l}} {\gamma A\left[ {{{\ddot w}_1} - {{\dot \theta }^2}\left( {x + {w_1}} \right) - 2\dot \theta {{\dot w}_2} - \ddot \theta {w_2}} \right] - }\\ {\;\;\;\;EA\left( {w_1^{,,} - w_2^{,2}w_1^{,,} + \frac{3}{8}w_2^{,4}w{{_1^{,,}}_1}} \right) - EI(\frac{3}{2}w_2^{,,2}w_1^{,,}) = 0} \end{array} $ | (7) |
| $ \begin{array}{*{20}{l}} {\gamma A({{\ddot w}_2} - {{\dot \theta }^2}{w_2} + {{\dot \theta }^2}{w_1}{w_2} + {{\dot \theta }^2}xw_2^, - }\\ {{{\dot \theta }^2}\frac{{{L^2} - {x^2}}}{2}w_2^{,,}) + \gamma I\left( {{{\dot \theta }^2}w_2^{,,} - \ddot w_2^{,,}} \right) + }\\ {6w_1^{,,}w_2^{,,,} + 6w_1^,w_1^{,,}w_2^{,,,} + 3w_1^{,,2}w_2^{,,} + 3w_1^{,,,}w_2^{,,} + }\\ {3w_1^,w_1^{,,,}w{{_2^{,,}}_2}) + EA(w_1^{,2}w_2^{,,} + \frac{1}{2}w_1^{,3}w_2^{,,} + }\\ {2w_1^,w_1^{,.}w_2^, + \frac{3}{2}w_1^{,2}w_1^{,,}w_2^,) = 0} \end{array} $ | (8) |
式(7)是轴向运动方程,观察到其中有静态离心力$\gamma A\dot {\theta }^2x$,因此轴向运动解被分解成两部分:定常解和振动解,通常求解弯曲振动频率时不考虑轴向振动的影响,故仅保留 式(7)中静力项并简化得
| $ \gamma {\dot \theta ^2}x + E{w''_1} = 0 $ | (9) |
对轴向静力变形方程(9)积分并利用边界条件得
| $ {w_1}\left( x \right) = \frac{{\gamma {{\dot \theta }^2}}}{{6E}}\left( {3{L^2}x - {x^3}} \right) $ | (10) |
将式(10)代入式(8),通过两个假设可将式(8)转化成横向振动广义特征方程:(1)假设$w_{2}$具有简谐形式的时变特性,即$w_2 \left( {x,\dot {\theta },t} \right) = \sigma \left( {x,\dot {\theta }} \right){\rm e}^{{\rm i}\omega t}$,$\omega $ 是结构频率,$\sigma $ 是与其对应的振型;(2)利用瑞利-里兹法,假设$\sigma \left( {x,\dot {\theta }} \right) = { \beta } \left( x \right) { h} \left( \dot {\theta } \right)$,其中${ \beta }$是无大范围运动悬臂梁弯曲振动振型函数行矢量. 式(8)左右同乘${ \beta }^{\rm T}$,并在整个结构上积分,就得到如下广义特征方程
| $ \left( {K - {\omega ^2}M} \right)h = 0 $ | (11) |
其中
| $ \begin{array}{*{20}{l}} {K = \int_L {} [\gamma A{{\dot \theta }^2}({w_1}{\beta ^{\rm{T}}}{\beta ^,} - {\beta ^{\rm{T}}}\beta + x{\beta ^{\rm{T}}}{\beta ^,} - }\\ {\;\;\;\;\;\qquad \frac{{{L^2} - {x^2}}}{2}{\beta ^{\rm{T}}}{\beta ^{,,}}) + \gamma I{{\dot \theta }^2}{\beta ^{\rm{T}}}{\beta ^{,,}} + }\\ {\;\;\;\;\;\;\;EI\left( {{\beta ^{\rm{T}}}{\beta ^{,,,,}} + } \right.\underline {3w_1^{,,}{\beta ^{\rm{T}}}{\beta ^{,,,,}}} + \underline {\frac{3}{2}w_1^{,,2}{\beta ^{\rm{T}}}{\beta ^{,,,,}}} + }\\ {\;\;\qquad \underline {6w_1^{,,}{\beta ^{\rm{T}}}{\beta ^{,,,}} + 6w_1^,w_1^{,,}{\beta ^{\rm{T}}}{\beta ^{,,,}} + 3w_1^{,,2}{\beta ^{\rm{T}}}{\beta ^{,,}}} + }\\ {\qquad \underline {3w_1^{,,,}{\beta ^{\rm{T}}}{\beta ^{,,}} + 3w_1^,w_1^{,,,}{\beta ^{\rm{T}}}{\beta ^{,,}}} ) + EA\left( {\underline {w_1^{,2}{\beta ^{\rm{T}}}{\beta ^{,,}}} + } \right.}\\ {\;\;\;\;\;\;\left. {\left. {\underline {\frac{1}{2}w_1^{,3}{\beta ^{\rm{T}}}{\beta ^{,,}}} + \underline {2w_1^,w_1^{,,}{\beta ^{\rm{T}}}{\beta ^,}} + \underline {\frac{3}{2}w_1^{,2}w_1^{,,}{\beta ^{\rm{T}}}{\beta ^,}} } \right)} \right]dx}\\ {\;\;M = \int_L {\left( {\gamma A{\beta ^{\rm{T}}}\beta - \gamma I{\beta ^{\rm{T}}}{\beta ^{,,}}} \right)dx} } \end{array}$ |
式(11)中去除下划线项即为不考虑应变能耦合项的一次近似模型 (Model 2).
3 动力学特性分析选取如下结构参数[3]:梁长$L =10$m,密度为 $\gamma =3 \times 10^{3}$\,kg/m$^{3}$,截面尺寸为0.02m$\times $0.02m,弹性模量$E =70$GPa.
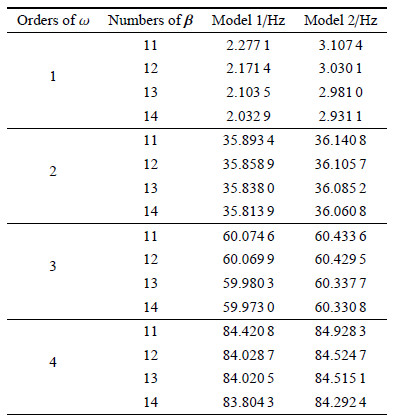
由式(11)可知:结构频率与转速有关,因此采用瑞利-里兹法 所选择的基本解组数也与转速有关,表1给出了当$\dot {\theta } =100$\,rad/s时分别选择前11至14阶振型${ \beta }$作为基本解组得到的前4阶频率值. 可以看到:各阶频率随着所选择振型数的增加而减小;不考虑应变能耦合项模型的1阶频率相对于考虑应变能耦合项模 型的1阶频率明显偏大,约为44%,而第2$\sim $4阶频率相差较小,可见应变能中的耦合项对结构基频影响较大,而结构基频直接关系到控制器带宽的确定,因此应慎重选择.
| 表 1 固有频率 Table 1 Natural frequencies |
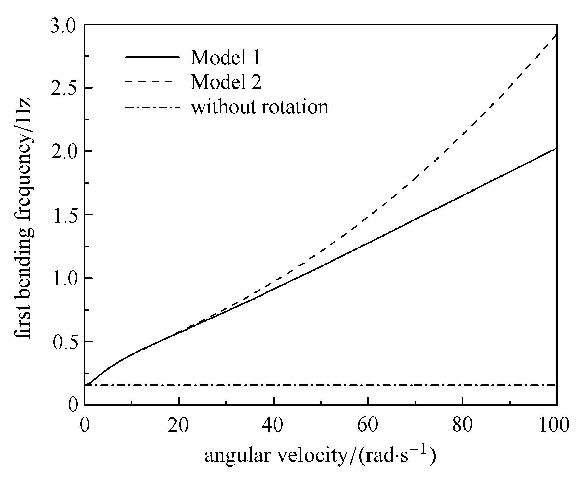
利用所选择的前14阶弯曲振型${ \beta}$作为基本解组,可得到对应与3种模型的结构一阶频率随转速增加的变化趋势对 比如图2所示. 可以看到:随着转动速度的增加,无大范围运动模型的一阶固有频率不发生变化;不考虑应变能耦合项模型和考虑应变能耦合项 模型的一阶固有频率都会增加,并且前者增加速度明显大于后者;在转速极低的情况下,两种模型的一阶固有频率可以近似认为相等.
|
图 2 一阶弯曲固有频率随转速变化 Fig. 2 Angular velocity and bending natural frequencies |
通过对大范围运动悬臂梁应变能的讨论,计入纵横向的耦合应变能,从而建立了结构耦合动力学模型,并对其横向弯曲振动动力学特 性进行了分析,得到以下结论:(1) 考虑应变能耦合项模型得到的一阶频率明显小于不考虑应变能耦合项模型的一阶频率,并且前者随转速增加的速度也明显小于后者;(2) 在转速极低的情况下,两种模型得到的一阶频率近似相等. 上述对比分析为作大范围运动悬臂梁的动力学特性分析奠定了基础,对工程应用具有重要的参考意义.
| [1] | Kane TR, Ryan RR, Banerjee AK. Dynamics of cantilever beam attached to moving base. Journal of Guidance, Control and Dynamics, 1987, 10(2): 139-151 |
| [2] | Nikravesh PE. Understanding mean-axes conditions as floating reference frames. Advances in Computational Multibody Systems. 2005, 2: 185-203 |
| [3] | Shi P, Mcphee J, Heppler GR. A deformation field for Euler-Bernoulli beams with applications to flexible multibody dynamics. Multibody System Dynamics. 2001, 5(1): 79-104 |
| [4] | Sharf I. Geometric stiffening in multibody dynamics formulations. Journal of Guidance, Control and Dynamics. 1995, 18(4): 882-890 |
| [5] | 洪嘉振, 蒋丽忠. 动力刚化与多体系统刚-柔耦合动力学. 计算力学学报, 1999, 16(3): 295-301 (Hong Jiazhen, Jiang Lizhong. Dynamic stiffening and multibody dynamics with coupled rigid and deformation motions. Chinese Journal of Computational Mechanics, 1999, 16(3): 295-301 (in Chinese)) |
| [6] | 田强, 张云清, 陈立平 等. 柔性多体系统动力学绝对节点坐标方法研究进展. 力学进展, 2010, 40(2): 189-202 (Tian Qiang, Zhang Yunqing, Chen Liping, et al. Advances in the absolute nodal coordinate method for the flexible multibody dynamics. Advances in Mechanics, 2010, 40(2): 189-202 (in Chinese)) |
| [7] | 蒋丽忠, 洪嘉振. 作大范围运动弹性梁的动力刚化分析. 计算力学学报, 1998, 15(4): 407-412 (Jiang Lizhong, Hong Jiazhen. Dynamics of an elastic beam in large overall motion. Chinese Journal of Computational Mechanics, 1998, 15(4): 407-412 (in Chinese)) |
| [8] | 吴胜宝, 章定国. 大范围运动刚体-柔性梁刚柔耦合动力学分析. 振动工程学报, 2011, 24(1): 1-7 (Wu Shengbao, Zhang Dingguo. Rigid-flexible coupling dynamic analysis of hub-flexible beam with large overall motion. Journal of Vibration Engineering, 2011, 24(1): 1-7 (in Chinese)) |
| [9] | 方建士, 章定国. 旋转悬臂梁的刚柔耦合动力学建模与频率分析. 计算力学学报, 2012, 29(3): 333-339 (Fang Jianshi, Zhang Dingguo. Rigid-flexible coupling dynamic modeling and frequency analysis of a rotating cantilever beam. Chinese Journal of Computational Mechanics, 2012, 29(3): 333-339 (in Chinese)) |
| [10] | 刘锦阳, 李彬, 洪嘉振. 作大范围空间运动柔性梁的刚-柔耦合动力学. 力学学报, 2006, 38(2): 276-282 (Liu Jinyang, Li Bin, Hong Jiazhen. Rigid-flexible coupling dynamics of a flexible beam with three-dimensional large overall motion. Chinese Journal of Theoretical and Applied Mechanics, 2006, 38(2): 276-282 (in Chinese)) |
| [11] | 焦小磊. 柔性梁大范围运动动力学特性的研究. [硕士论文]. 哈尔滨: 哈尔滨工程大学, 2013 (Jiao Xiaolie. Dynamics of large-scale movement of the flexible beam. [Master Thesis]. Harbin: Harbin Engineering University, 2013 (in Chinese)) |
| [12] | 陈思佳, 章定国, 洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型. 力学学报, 2013,45(2): 251-256 (Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam undergoing large deformation. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(2): 251-256 (in Chinese)) |
2. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China
 2015, Vol. 47
2015, Vol. 47