航天飞机以高马赫数再入大气层时,飞行数据表明,气动参数相比预测值产生了约0.03的俯仰力矩系数增量,这使得翼襟的配平转角 达到了地面预测值的两倍左右. 这种现象被称为"上仰异常"(pitch-up anomaly)现象[1]. 文献[2]认为高温真实气体效应带来较低的比热比并导致膨胀区压力降低是产生此现象的主要原因. 李康等[3]对"上仰异常"现象进行了数值研究,结果表明热化学非平衡效应所引起的流场气体比热比的不均衡分布才是其根本原因. 对于实际的流动来说,流动过程包含了多次压缩和膨胀过程,而目前对于压缩甚至再压缩流动中热化学非平衡的影响尚未达成一致的认识. Hirschel等[4]指出航天飞机的背风区流动与钝锥流动相近,且当膨胀区后存在再压缩效应时,膨胀区压力的降低现象不再出现,但 其研究并没有给出这种膨胀区压力的偏差是如何消失的. Kodera等[5]研究了HB2标准模型的气动力规律,其结果认为热化学非平衡条件下扩张裙体部分表面压力的升高是由边界层厚度的增 加引起的,这一结论与文献[6, 7]认为的黏性并不影响气动力规律的结论相矛盾. 综上可知,对于高焓热化学反应流动来说,当流动中存在再压缩效应时,仍有两个问题需要深入研究:(1)化学反应过程在其中扮演怎 样的角色,(2)化学非平衡过程对气动力规律是如何影响的.
1 数值方法及验证文献[6, 7]研究表明,黏性对气动力的影响较小,而黏性干扰的存在会使各相似参数相互影响,因此本文采用无黏流动模型. 数值求 解高温空气5组分热化学非平衡模型方程,详细的数值方法参考文献[3].
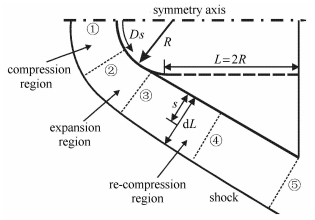
物理模型为钝锥,球头半径$R = 0.05$ m,锥的水平长度$L = 2 R$,如图1所示. $\theta $为激波层内的取值角,${\rm{d}}L$为$\theta $角方向激波层的厚度,$s$为离物面的垂直距离,$Ds$为物面上一点至驻点的距离,$\phi $为再压缩角. 图1中标出了①驻点线,② 45$^\circ$线,③锥体起始位置线,④锥体中间位置线和⑤锥体结束位置线. 再压缩角 考虑了0$^\circ$,5$^\circ$,20$^\circ$,25$^\circ$和30$^\circ$.
|
图 1 研究模型示意图 Fig.1 Schematic of physical model |
引入以下参数作为考察对象:一是钝锥半模沿$x$方向的压力积分系数$Cax = \int_{_{{\rm{wall}}}} {{P_{\rm{w}}} \cdot {n_y}} d\Gamma /(0.5{\rho _\infty }U_\infty ^2 \cdot {L_c}) - {P_\infty }/(0.5{\rho _\infty }U_\infty ^2)$,二是半模沿$y$方向的压力积分系数$Cax = \int_{_{{\rm{wall}}}} {{P_{\rm{w}}} \cdot {n_y}} d\Gamma /(0.5{\rho _\infty }U_\infty ^2 \cdot {L_c}) - {P_\infty }/(0.5{\rho _\infty }U_\infty ^2)$,式中$P_{\rm w} $为壁面压力分布,$n_x $,$n_y $为壁面切线方向单位矢量沿$x$,$y$方向的分量,$d\Gamma $为沿壁面的微元长度,$L_{ c} $为模型的特征长度. 来流参数选取$H = 60$ km高空的数据,马赫数为20.
图2给出了计算结果与风洞实验结果[6]的对比. 实验模型为球头半径分别为20 mm和50 mm的2个钝锥模型,来流总焓$H_0 = 7$ MJ/kg,其他尺寸及来流参数参见文献[6],对比显示计算结果与实验结果符合较好.

|
图 2 不同模型壁面压力计算与实验结果对比 Fig.2 Comparison between numerical and experimental results for different models |
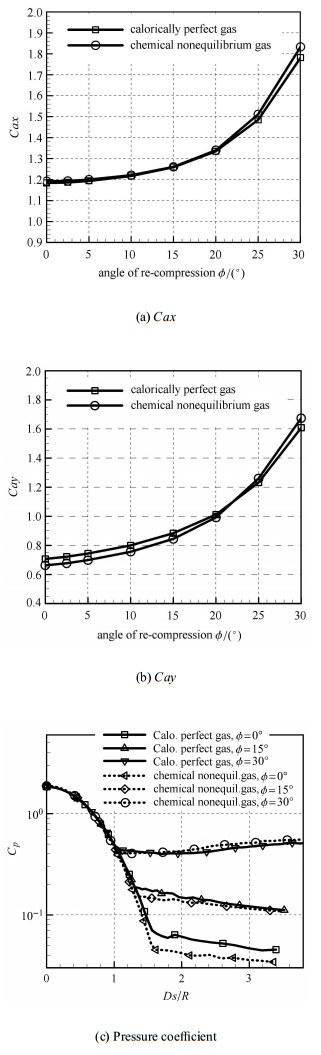
为求证高温真实气体效应下膨胀区压力偏低现象是否会受再压缩效应的影响而消失,图3(a),3(b)给出了气动力系数$Cax$,$Cay$随再压缩角$\phi $的变化规律. 由图3(a)可以看出,与量热完全气体模拟相比,热化学非平衡效应使得$Cax$增大,在$0^\circ < \phi < 15^\circ$范围内其 增量不明显,$15^\circ < \phi < 30^\circ$时,其增量随 $\phi $ 而显著增加. $Cay$的变化规律更为复杂,在$0^\circ < \phi < 20^\circ$范围内,热化学非平衡效应使得$Cay$变小,而在$20^\circ< \phi <30^\circ$范围内,则相反. 图3(c)给出了再压缩角为0$^\circ$,15$^\circ$和30$^\circ$的条件下压力系数沿物面的分布,显示了热化学非平衡效应使得膨胀区下游压力上升速率加快的过程. 显然,热化学非平衡效应对驻点压缩区的壁面压力影响甚微,其影响主要发生在膨胀区下游. $\phi = 0^\circ$时,热化学非平衡效应使得再压缩锥面压力降低,当在$\phi =15^\circ$时,锥面压力逐渐接近量热完全气体模拟值,当$\phi =30^\circ$时,反而高于后者. 上述现象体现了热化学非平衡效应对再压缩锥面压力的非线性影响.
|
图 3 气动力参数随再压缩角 φ 的变化及不同再压缩角壁面压力系数对比 Fig.3 The variation of aerodynamic data with angle of re-compression |
图4(a)和图4(b)分别给出了15$^\circ$和30$^\circ$压缩角情况下流场中的比热比分布. 在驻点线上和激波面附近,振动能的激发 降低了气体比热比$\gamma $;靠近驻点处随着气体离解程度的增加,$\gamma $逐渐增加,物面附近$\gamma \approx 1.44$. 上述 $\gamma $ 非单调变化反映了热非平衡与化学非平衡效应此消彼长的过程,因此,单纯用 $\gamma $ 的变小来表征高温真实气体效应是不妥当的.

|
图 4 流场中气体比热比的分布 (a), (b) 和锥体部分温度分布 (c) Fig.4 Distributions of (a),(b) specific heat ratio and (c) temperature |
图4(c)给出 $\phi =30^\circ$时锥体附近流场中的温度分布. 振动温度$T_{vib}$沿流向单调减小,而平动温度$T$则不同,在贴近锥面处,$T$沿流向先增后减,这表明此区域的化学反应先以放热复合反应主导,而后以吸热离解反应再次主导,体现 了膨胀与再压缩对化学反应流动的不同影响,也导致了 $\gamma $ 的非单调变化. 图4(a),4(b)在锥体部分的结果显示 $\phi =30^\circ$时流场 $\gamma $ 分布相比 $\phi =15^\circ$时在物面附近更为不均衡.
基于以上分析,下面建立气体比热比梯度与组分梯度的关系. $\gamma $ 为振动温度$T_{\rm vib}$和组分质量分数$c_{i}$的函数
| $\gamma = \gamma ({T_{{\rm{vib}}}},{c_i})$ | (1) |
对方程(1)取微分可得
| $\frac{{{\rm{d}}\gamma }}{{{\rm{d}}x}} = {(\frac{{\partial \gamma }}{{\partial {T_{{\rm{vib}}}}}})_{{c_i}}}\frac{{{\rm{d}}{T_{{\rm{vib}}}}}}{{{\rm{d}}x}} + {\rm{ }}{\sum\limits_{_{i = 1}} {(\frac{{{R_i}{C_v} - {C_{v,i}}R}}{{{{({C_v})}^2}}})} _{{T_{{\rm{vib}}}}}}\frac{{{\rm{d}}{c_i}}}{{{\rm{d}}x}}{\rm{ }}$ | (2) |
| $\frac{{{\rm{d}}\gamma }}{{{\rm{d}}y}} = {(\frac{{\partial \gamma }}{{\partial {T_{{\rm{vib}}}}}})_{{c_i}}}\frac{{{\rm{d}}{T_{{\rm{vib}}}}}}{{{\rm{d}}y}} + {\sum\limits_{_{i = 1}} {(\frac{{{R_i}{C_v} - {C_{v,i}}R}}{{{{({C_v})}^2}}})} _{{T_{{\rm{vib}}}}}}\frac{{{\rm{d}}{c_i}}}{{{\rm{d}}y}}$ | (3) |
本文研究中,$\gamma $ 的梯度定义为$\sqrt {{{({\rm{d}}\gamma /{\rm{d}}x)}^2} + {{({\rm{d}}\gamma /{\rm{d}}y)}^2}} $,$c_{i}$的梯度定义为$\sqrt {{{({\rm{d}}{c_i}/{\rm{d}}x)}^2} + {{({\rm{d}}{c_i}/{\rm{d}}y)}^2}} $. 对于空气组分来说,当流场中温度大于2 000 K时,振动温度所引起的 $\gamma $ 改变可以忽略. 因此,$\gamma $ 的不均衡性主要来源于组分梯度的贡献.
图5分别给出了 $\phi $ 为15$^\circ$和30$^\circ$条件下流场中 $\gamma $ 的梯度分布. 在锥体部分中间位置和结束 位置,$\phi=30^\circ$时的流场气体比热比梯度均比 $\phi =15^\circ$时大,且出现了明显的波动. 这表明 $\phi=30^\circ$再压缩角产生了更为剧烈的 $\gamma $ 不均衡性,验证了由化学反应引起 $\gamma $ 的不均衡分布是膨胀区下游壁面压力不同变化趋势的根本原因. 这也表明当再压缩效应较强时,锥体部分激波层内温度升高,化学反应速率加快,从而产生更剧烈的比热比分布不均衡性.

|
图 5 气体比热比梯度分布 Fig.5 γ gradient distributions |
针对高焓热化学非平衡流动中再压缩效应机理不明确的问题开展数值研究,通过对流场中比热比及其梯度的对比分析,得出了 高温真实气体中再压缩效应对气动力产生影响的机制,结论总结如下:
(1) 当流场中存在再压缩效应时,高温真实气体与量热完全气体下壁面压力分布偏差并不会消失. 再压缩角增大,锥体部分首先以 复合反应主导,而继续增大时,出口区域开始再次以离解反应主导,偏差再次逐渐增大.
(2) 高温真实气体效应与量热完全气体的偏差是由比热比的分布不均衡引起的.
目前尚有一些问题需要进一步开展. 本文并没有考察钝锥底部的压力分布,而只是将其设为来流压力分布. 另外,研究中黏性 也并未考虑. 这些问题的开展将对高超声速非平衡效应对气动力规律的影响有更大的应用价值.
| [1] | 姜宗林,李进平,赵伟等. 长试验时间爆轰驱动激波风洞技术研究. 力学学报, 2012, 44(5): 824-831 (Jiang Zonglin, Li Jinping, Zhao Wei, et al. Investigating into techniques for extending the test-duration of detonation-driven shock tunnels. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(5): 824-831 (in Chinese)) |
| [2] | Brauckmann GJ, Paulson JW, Weilmuenster KJ. Experimental and computational analysis of the Space Shuttle Orbiter hypersonic pitch-up anomaly. Journal of Spacecraft and Rockets, 1995, 32 (5): 758-764 |
| [3] | 李康,胡宗民,姜宗林. 高超声速流动上仰异常现象关键因素数值研究. 中国科学: 物理学·力学· 天文学,2014, doi: 10.1360/ SSPMA2014-00137 (Li Kang, Hu Zongmin, Jiang Zonglin. Numerical studies on the effect of the key parameter to hypersonic "pitch-up anomaly". Sci Sin-Phys Mech Astron, 2014, doi: 10.1360/ SSPMA2014-00137 (in Chinese)) |
| [4] | Hirschel EH, Weiland C. Selected Aerothermodynamic Design Problems of Hypersonic Flight Vehicles. Berlin Heidelbery: Springer-Verlag, 2009 |
| [5] | Kodera M, Tanno H, Takahashi M, et al. Comparison of re-entry flow computations with high enthalpy shock tunnel experiments. AIAA 2009-7305, 2009 |
| [6] | Kliche D, Mundt Ch, Hirschel EH. The hypersonic Mach number independence principle in the case of viscous flow. Shock Waves, 2011, 21(4): 307-314 |
| [7] | Miller JH. Computational aerothermodynamic datasets for hypersonic heat transfer on reentry vehicles. AIAA 2005-5911, 2005 |
 2015, Vol. 47
2015, Vol. 47
