某些真核细胞(eukaryotes),如盘基网柄菌细胞(dictyostelium discoideum)、中性粒细胞(neutrophils)、成纤维细胞(fibroblast)等能够感受 胞外环境中的化学或力学信号刺激,沿着信号场梯度方向发生定向运动[1].免疫反应、伤口愈合、神经发育及再生、癌转移等众多生理病理过程都与细胞的定向运动息息相关[2, 3, 4, 5].极化(polarization)是细胞运动前的准备阶段. 初生细胞受胞外梯度信号刺激后,会在其细胞骨架(cytoskeleton)前侧边缘生出伪足(pesudopod),后端发展为尾部,该过程称为初始极化(initial polarization)[6]. 高度极化的细胞受到反方向高强信号刺激后,其伪足会从原头部区域收回,再在之前的尾部区域重新生成. 因此,细胞原先的头部变成新的尾部、原先的尾部变成新的头部,这即为极性反转(repolarization)[7].
运动细胞具备``极性反转''的能力,这使得细胞可根据周边环境信号场的变化迅速调整运动方向,准确到达指定区域行使职能. 从分子 层面看,促成运动细胞``极性反转''的关键是胞内信号分子依据外信号刺激方向重新分布: 一些标志伪足形成的分子,例如,Rac小G蛋白(Rac GTPase)、磷酸激酶(PI3K)、肌动蛋白(F-actin)、磷脂酰肌醇--3,4,5--三磷酸(PIP3)会由之前伪足区域消失,再在后部重新积聚; 另一些标记尾部形成的分子,例如,磷酸酶(PTEN)、磷脂酰肌醇--4,5--双磷酸(PIP2)、肌浆球蛋白(Moysin-II)则需要由先前的尾部消失,重新积聚在头部[7, 8, 9]. 可以肯定,细胞在``极性反转''阶段所动用的胞内信号转导通路与``初始极化''阶段一致. 因此,为了揭示细胞``极性反转''的奥秘,无论是实验还是理论建模,都可从细胞极化相关分子的输运、调控、以及由此引发的时空效应等方面加以考察.
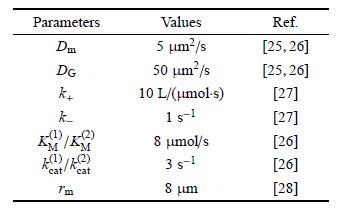
注意到,有些细胞``极性反转''实验采用微量吸液管(micropipette,释放趋化因子)或水槽装置(施加剪切力)制造精确反转信号场,并通过荧光成像技术实时观测各类细胞极性标记分子的时空演化特征,标定极性反转进程[7, 9].尽管实验所选取的模式细胞有所不同(例如,Dalous等[7]采用盘基网柄菌细胞,Gerisch等[10]采用中性粒细胞),但所揭示的细胞``极性反转''特征却是一致的. 以达卢实验为例(见图1),运动细胞``极性反转''的主要特征可归纳为以下3个方面: (1)运动细胞具有高效的极性反转能力,整个过程仅需~100s; (2)伪足从之前区域完全消失再到沿新方向开始形成,这之间存在着30~50s时间间隔;(3)极性反转前后,细胞仅维持单方面伪足.
|
图 1 采用盘基网柄菌细胞进行运动细胞极化反转现象[7]. 图中绿色 为细胞伪足,白色箭头标记外信号方向 Fig. 1 Actin relocalization after reversal of signal (derived from Ref.[7]) Green marks the pesudopod of the cell, and the white arrow indicates the direction of external signal } |
有关理论建模,则利用``激活-抑制''酶与底物的相互作用表征胞内级联转导,并通过考察底物输运、自催化(autocatalysis)、抑制自身衰减等机制构造包含反馈回路的非线性反应-扩散系统,模拟细胞极化[6, 11, 12].尽管已有数学模型能够从信号放大、自适应性(adaptation)等角度揭示极化机理,但始终未能为上述``极性反转''实验现象给出令人满意的解释. Meinhardt等[13]提出图灵类(Turing-type)模型,利用系统的非线性反应与线性扩散耦合产生空间定态斑图,实现信号放大效果. 然而,外信号只对斑图形成起诱导作用,图灵系统随后不再受外信号调控. Janetopoulos等[14]提出``局部激活-全局抑制''类模型(local excitation/global inhibition,LEGI)模型,考察外信号快速激发局部激活酶并稍慢激发全局抑制酶;局部激活与全局抑制的叠加效果是使得细胞过滤掉接收信号中的平均浓度信息,即实现自适应性;LEGI模型所针对是细胞骨架抑制剂(例如,Latrunculin A)处理的细胞,并不适用于已高度极化的细胞.Levine等[15]提出的平衡失活(balanced inactivation)模型,同样是考察外信号控制慢速扩散的激活酶和快速扩散的抑制酶,而在细胞后部,激活酶由等量抑制酶抵消,由此胞内信号沿细胞前、后呈``切换式''分布;平衡失活模型允许细胞对胞外信号进行实时响应,并不产生``延滞''现象.Mori等[16]提出的波桩(wave-pinning)模型,考察Rac在胞质失活态(快速扩散)与质膜激活态(慢速扩散)之间交换,同时,外信号引起活性态Rac浓度呈正反馈式放大,其分布以波的形式由前向后传播,并最终由于失活态Rac的消耗稳定;波桩模型允许细胞对超过一定阈值的反向信号进行响应,但其主要针对小G蛋白自身调控,无法单独表征极化.
此前,考察了由生化实验所定义的Rac-PIs(PIs包括PIP3和PIP2反馈回路(feedback loop)产生的空间效应,从胞内信号分子双向输运的角度构建细胞初始极化的数学模型[17]. 为细胞指定一个基准Rac活性梯度后,${\rm{PI3K}}\begin{array}{*{20}{c}}{{\rm{Rac + PI}}{{\rm{P}}_{\rm{2}}}}\\\mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \end{array}{\rm{PI}}{{\rm{P}}_{\rm{3}}}$构成短程正反馈回路、${\rm{PTEN}}\begin{array}{*{20}{c}}{{\rm{PI}}{{\rm{P}}_{\rm{3}}}}\\\mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \end{array}{\rm{PI}}{{\rm{P}}_{\rm{2}}}$构成长距离负反馈回路,二者分别驱动胞内``向前''与``向后''的分子输运. 在此基础上,本文通过引入时变的反转信号(胞内Rac活性梯度),进一步发挥Rac-PIs反馈回路的时间效应,探索运动细胞极性反转机理.
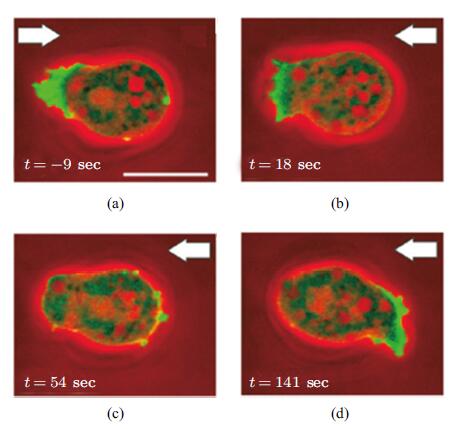
1 . 材料和方法 1.1 Rac-PIs反馈回路尽管负责调控运动细胞极化的信号转导通路所包含的分子机制错综复杂,但其主干结构比较清晰,可定义为Rac-PIs反馈回路[18, 19]. 该回路又可分为``上''、``下''两层(见图2),``上层"为Rac GTPase自身调控------胞外梯度信号首先引起PIP3极性分布,随后PIP3又通过鸟苷酸交换因子(guanine nucleotide exchange factors,GEFs)控制 Rac 活性梯度,为细胞提供胞内导向信号[20];``下层''为细胞骨架重组-----活性态Rac通过激活多类F-actin结合蛋白(actin binding protein,ABPs)参与F-actin合成[21]. 该过程中,PI3K经F-actin介导由胞质来到质膜,将PIP2磷酸化为PIP3;PTEN同样可由胞质来到质膜,并将PIP3去磷酸化为PIP2[22].
|
图 2 负责细胞极化的Rac-PIs反馈回路 Fig. 2 Rac-PIs feedback loop considered for studying reversal of cell polarity |
考虑到PIP3可通过为多种ABPs提供质膜结合点参与F-actin合成,加之实验已证实F-actin与PIP3时空演化特征基本一致[23],本文在建模时是将F-actin与PIP3归并一项,并以PIP3为代表(F-actin的合成与分布不分开专门讨论). 因此,一个简约的PIs-Rac反馈回路可只考察5种分子: Rac,PI3K,PTEN,PIP3和PIP2.
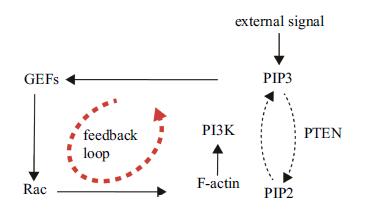
1.2 数学模型体外实验中,引导信号在胞外分布仅铺展为浅薄的一层,这使得细胞只有外侧一圈感受到信号刺激,其底部和背部并不接触到信号. 据此,本文所采用半径为rm的圆作为细胞的简化模型,以圆周代表细胞质膜,空腔代表细胞质(参见图3). PIP3/PIP2作为细胞极性标记物,只在质膜上扩散并通过质膜结合态PI3K/PTEN相互转换.PIP3/PIP2浓度随时间、空间变化可由如下的一对耦合的反应-扩散方程(极坐标形式)描述
| $\frac{{\partial {P_3}}}{{\partial t}} = \underbrace {{D_{\rm{m}}}\frac{1}{{r_{\rm{m}}^2}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}}{P_3}}_{{\rm{diffusion}}} + {\rm{ }}\underbrace {k_{{\rm{cat}}}^{({\rm{1}})}\frac{{RG_{\rm{m}}^{(1)}{P_2}}}{{K_M^{(1)} + {P_2}{\rm{ }}}} - k_{{\rm{cat}}}^{({\rm{2}})}{\rm{ }}\frac{{G_{\rm{m}}^{(2)}{P_3}}}{{K_M^{(2)} + {P_3}{\rm{ }}}}}_{{\rm{catalytic}}\;{\rm{effect}}},$ | (1a) |
| $\frac{{\partial {P_2}}}{{\partial t}} = \underbrace {{D_{\rm{m}}}\frac{1}{{r_{\rm{m}}^2}}\frac{{{\partial ^2}}}{{\partial {\varphi ^2}}}{P_2}}_{{\rm{diffusion}}} + \underbrace {k_{{\rm{cat}}}^{(2)}\frac{{RG_{\rm{m}}^{(2)}{P_3}}}{{K_M^{(2)} + {P_3}}} - k_{{\rm{cat}}}^{(1)}\frac{{RG_{\rm{m}}^{(1)}{P_2}}}{{K_M^{(1)} + {P_2}}}}_{{\rm{catalytic}}\;{\rm{effect}}},$ | (1b) |
| $\frac{{\partial {P_3}}}{{\partial n}} = 0,\quad \frac{{\partial {P_2}}}{{\partial n}} = 0.$ | (1c) |
|
图 3 运动细胞极性反转模型示意图 Fig. 3 Schematic diagram of cell model and stimulus |
式中出现的质膜结合态PI3K/PTEN浓度$(G_{\rm{m}}^{(i)},\;i = 1,2)$需要通过胞质游离态PI3K/PTEN浓度$(G_{\rm{c}}^{(i)} = G_{\rm{c}}^{(i)}(r,\varphi ,t),0 \le r \le {r_{\rm{m}}})$确定,$G_{\rm m}^{(i)} $满足: ${\partial G_{\rm m}^{(i)} }/{\partial t} = k_{\rm G}^ + P_{4 - i} G_{\rm c}^{(i)} - k_{\rm G}^ - G_{\rm m}^{(i)} $,其中,$k^ + $和$k^ - $为正、负交换系数. $G_{\rm c}^{(i)} $满足扩散方程,${\partial G_{\rm c}^{(i)} }/{\partial t} = D_{\rm G} \nabla ^2G_{\rm c}^{(i)} $,在边界处满足: $D_{\rm G} {\partial G_{\rm c}^{(i)} }/{\partial n} = - k_ + P_{4 - i} G_{\rm c}^{(i)} + k_ - G_{\rm m}^{(i)} $,其中,$D_{\rm G} $为蛋白小分子在胞质内扩散系数. $R$为Rac活性系数,$R = R(r_{\rm m},\varphi,t)$. 将质膜上两点$({r_{\rm{m}}},0)$和$({r_{\rm{m}}},\pm \pi )$标记为细胞前端和后端. 初始时,令这两点处$R$值分别为,$R_{\rm f}^{(1)} $和$R_{\rm b}^{(1)} $,$R_{\rm{f}}^{(1)} > R_{\rm{b}}^{(1)};$ 输入信号反转后则为$R_{\rm{f}}^{(2)}$与$R_{\rm b}^{(2)} $,$R_{\rm{f}}^{(2)} < R_b^{(2)}$. 本文暂不引入Rac在激活/失活之间的具体调控过程,故令活性态Rac总量保持守恒. 取${R_{{\rm{mid}}}}$为细胞中心处$R$值(Rac活性基准值),设定为常量. 由于细胞尺寸较小,$R(r_{\rm m},\varphi,t)$具体采用何种连续函数对于极化输出影响不大,可取为简单的余弦函数,见式(2).
| $\begin{array}{l} R({r_{\rm{m}}},\varphi ,t)\\ = \left\{ {\begin{array}{*{20}{l}} {{R_{{\rm{mid}}}} + \frac{{R_{\rm{f}}^{(1)} - R_{\rm{b}}^{(1)}}}{2}\cos \varphi \qquad (t \le {t_1})}\\ {{R_{{\rm{mid}}}} + \left[{\frac{{R_{\rm{f}}^{(1)} - R_{\rm{b}}^{(1)}}}{2} + (R_{\rm{f}}^{(2)} - R_{\rm{f}}^{(1)})\left( {\frac{{t - {t_1}}}{{{t_2} - {t_1}}}} \right)} \right]\cos \varphi \qquad ({t_1} < t \le {t_2})}\\ {{R_{{\rm{mid}}}} + \frac{{R_{\rm{f}}^{(2)} - R_{\rm{b}}^{(2)}}}{2}\cos \varphi \qquad (t > {t_2})} \end{array}} \right. \end{array}$ | (2) |
描述运动细胞极性反转的数学模型由式(1)、式(2)构成,可通过此前工作中开发的格子玻尔兹曼法(lattice Boltzmann method,LBM) +蒙特-卡洛(Monte--Carlo)法数值求解[17]. LBM-D2Q9求解包含两个基本步骤:(1)迁移------粒子从格子的一个结点以恒定的速度运动到相邻结点;(2)碰撞------从相邻结点运动到同一节点的粒子发生碰撞,随后根据质量、 动量和能量守恒的原则改变其速度,再以此速度迁移. 在两个LBM时间步之间,需要利用蒙特-卡洛法处理受配体分子结合/分离过程,并据此更新反应源项.受配体的结合过程是一个符合泊松分布(Poisson distribution)的随机过程. 以PI3K为例,利用Monte--Carlo法计算时需产生随机数$p_1 \in \left[{0,1} \right]$和$p_{ - 1} \in \left[{0,1} \right]$,当$p_1 $小于$1 - \exp ( - k_1 [{L}]\Delta t)$时,PI3K与PIP3结合的事件发生,其中$[{L}]$为游离态PI3K的浓度值; 当${p_{ - 1}}$小于$1 - \exp ( - k_{ - 1} \Delta t)$ 时,复合体分离成PI3K和PIP3的事件发生.
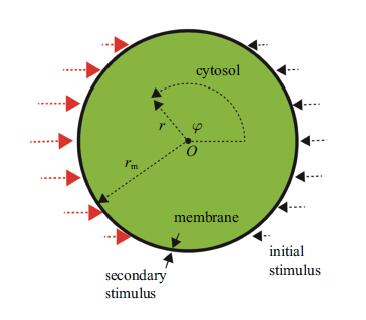
3 . 结 果初始时,所有的PI3K/PTEN均处于胞质游离态,[PI3K] = [PTEN] = 0.07 mol/L; PIP3/PIP2在质膜上均匀分布,[PIP3] = 0.1 mol/L,[PIP2] = 9.9mol/L,其他参数见表1; 随后,各组分通过计算程序的预运行获得应有的比例. 正式模拟计算主要考察: (I) ``极性反转''的基本过程和特征; (II)反转信号梯度对极性反转的影响.
| 表 1 参数取值 Table 1 Parameter values |
图4中为高梯度反转输入信号时程曲线图. 图中红色和绿色折线分别是细胞前端($\varphi = 0^ \circ $)和后端($\varphi = \pm 180^ \circ $)活性态Rac分数时程曲线. 质膜上其他各点Rac活性系数按式(2)变化. 初始阶段(t为0~230s),细胞上维持稳态梯度信号$(R_{\rm{f}}^{(1)} = 0.46,R_{\rm{b}}^{(1)} = 0.34);$ 在230~235s期间,细胞活性态Rac前端减少、后部增加,两者增减量始终相当,总的活性态Rac质量守恒; 在235s后,输入信号维持前低后高的稳态分布$(R_{\rm{f}}^{(2)} = 0.{\rm{12}},{\rm{R}}_{\rm{b}}^{({\rm{2}})}{\rm{ = 0}}.{\rm{68}})$.

|
图 4 细胞前、后活性态Rac分数时程曲线图(高梯度) Fig. 4 Fraction of activated Rac varying with time at the cell front and the back (high gradient) |
图5是质膜结合态、胞质游离态PI3K/PTEN分子总量时程曲线图. 图中显示,初始时刻(t=0s),绝大 部分PI3K ($\approx 87\% $)处于胞质游离态,而绝大部分PTEN($\approx 90\% $)处于质膜结合态,从而使得PIP3浓度极低(图6),细胞处于静息状态. 在0~230s这段时间,细胞处在初始极化阶段,胞质游离态PI3K通过Rac-PIs正反馈回路转变为质膜结合态; 观察到表征质膜态PI3K总量的曲线依次经历缓慢上升(0~30s)、加速上升(30~90s)、趋于 稳定(90~230s)三阶段,代表着极化强度由小渐大并直至饱和的过程. 在230~270s这段时间,随着细胞前端Rac活性分数降低(图4),Rac-PIs反馈强度也降低,大量PI3K由质膜上脱落,因此图中质膜结合态PI3K曲线迅速下降,而胞质游离态PI3K曲线则迅速升高. 在270~330s这段时间,表征质膜态PI3K总量的曲线又经历了与之前类似的上升、平缓过程,说明细胞沿新的方向极化. 整个过程中,质膜结合态PTEN曲线仅呈现平缓的下沉或上浮,这说明尽管有大量PIP2转变为PIP3,PIP2相对PTEN始终足量.
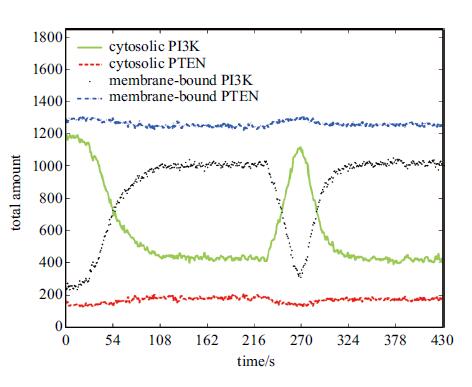
|
图 5 质膜结合态、胞质游离态PI3K/PTEN分子总量时程曲线图 Fig. 5 Total amount of cytosolic and membrane-bound PI3K/PTEN varying with time |

|
图 6 胞质游离态PTEN分子在t= 300 s时刻空间分布图 Fig. 6 Spatial distribution pattern of cytosolic PTEN t= 300 s |
图6为t=300s时游离态PTEN在胞质空间的分布(边缘与质膜接壤). 由图6可见,当质膜结合态PTEN从质膜脱离时,脱离点(位于 圆周)即为胞质中游离态PTEN的一个``源'',在``源''附近PTEN浓度显著升高(呈深红色); 当游离态PTEN与质膜结合时,结合点成为游离态PTEN的一个``汇'',``汇''附近PTEN浓度显著降低(呈深蓝色). PTEN与质膜的结合和分离具有随机性,因此,图6中``源''和``汇''的分布是随机的. 在远离质膜(圆周)的区域,PTEN浓度近似均匀,这是由于游离态PTEN扩散速率较快,消除了``源''和``汇''的影响. PTEN可通过胞质快速扩散到达细胞任何区域,又由于它与PIP2间的正反馈作用,总的游离态PTEN输运趋势是向着细胞后部. 与之类似,PI3K也通过胞质扩散,迅速到达细胞前端,帮助制造PIP3. 胞质游离态PI3K分布与图6类似,此处不再具体给出.
图7是细胞极性反转进程中PIP3时空调控图. 结合Rac输入信号设置(图4),可将该图划分为4个阶段. 第1阶段(0~230\;s),细胞前、后Rac活性与基准Rac活性的差值,经${\rm{PI3K}}\begin{array}{*{20}{c}} {{\rm{Rac + PI}}{{\rm{P}}_{\rm{2}}}}\\ \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over {\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} \end{array}{\rm{PI}}{{\rm{P}}_{\rm{3}}}$级联转导正反馈式放大,引起PIP3向细胞前端附近积聚; 稳态时,PIP3积聚在$\pm 45^\circ $区间,意味着伪足沿细胞前部伸出(对照图1a). 第2阶段(230~250s),由于Rac活性分布快速完成反转,PIP3绝对浓度降低,但PIP3依然能够维持之前空间分布,由此说明细胞伪足依然沿原先方向伸出,只是有部分回缩(对照图1b). 第3阶段(250~270s),细胞前部PIP3浓度始终处于极低的水平,至270s时,PIP3浓度已接近0,说明伪足已完全消失,细胞回到初始无极性状态(对照图1c). 第4阶段(270~430s),PIP3逐渐积聚并最终稳定分布在细胞后部$\pm 135^\circ $区间,意味着伪足沿细胞后部方向伸出(对照图1d).
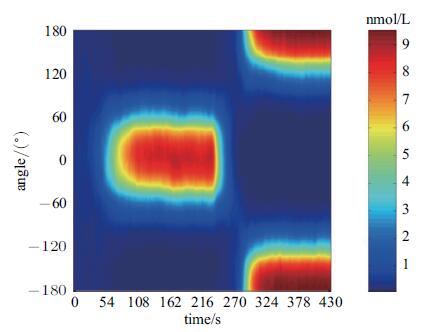
|
图 7 细胞反转极化进程中PIP3时空演化图 Fig. 7 Spatial-temporal evolution of PIP3 (upon high gradient reversal signal: Rf(2)=0.12, Rb(2)=0.68) |
图8是细胞前端(``angle 为 $0^\circ $'')与后端(``angle为$\pm {\rm{180}}^\circ $'') PIP3浓度时程曲线图. 由图8能够清楚看到,在输入信号反转后(t=230s),细胞前端PIP3时程曲线立刻降低,而后端PIP3时程曲线则在延滞30s后加速上升,整个极性反转所需的时间为100s. PIP2的分布特点与PIP3相反,此处不再具体给出.
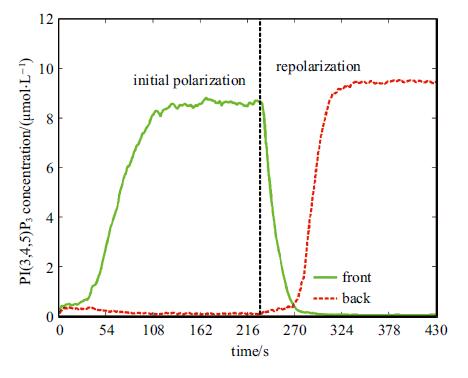
|
图 8 细胞前、后两端PIP3浓度时程曲线图 Fig. 8 Concentration of PIP3 varying with time at the cell front and the back |
图9是中等梯度($R_{\rm{f}}^{(2)} = 0.26,R_{\rm{b}}^{(2)} = 0.54$)的反转输入信号时程图. 初始阶段(0~230s)同样是给予细胞稳定的前高、后低活性态Rac输入信号;经历过信号反转后,235~430s阶段,所设定得稳定反向Rac活性梯度较之前图3 ($R_{\rm f}^{(2)}=0.12$,$R_{\rm b}^{(2)} =0.68$)明显的减弱.

|
图 9 中等梯度反转输入信号时程图 Fig. 9 Fraction of activated Rac varying with time at the cell front and the back (middle gradient) |
图10是与图9反转输入信号相应的PIP3时空演化图. 图中可见,在中等梯度的Rac反转信号作用下,细胞需要较长的 时间(~160s)才能完成极性反转,而稳态时的PIP3分布与此前采用高梯度反转信号时的情况一致.

|
图 10 中等梯度反转输入信号对应的PIP3时空演化图 Fig. 10 Spatial-temporal evolution of PIP3 (upon medium gradient reversal signal: Rf(2)=0.26, Rb(2)=0.54) |
类似地,图11是低梯度($R_{\rm{f}}^{(2)} = 0.34,R_{\rm{b}}^{(2)} = 0.46$)反转输入信号时程图. 图中显示,在235~430s阶段,反转后的活性态Rac梯度比图3和图9进一步降低.
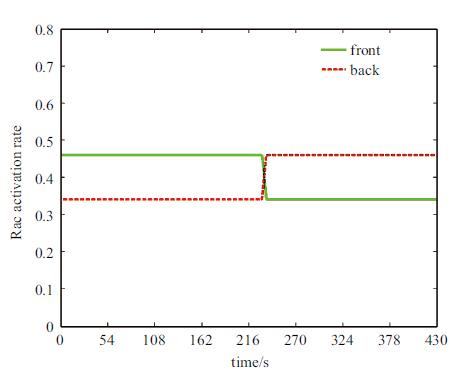
|
图 11 低梯度反转输入信号时程图 Fig. 11 Fraction of activated Rac varying with time at the cell front and the back (low gradient) |
图12是采用低梯度反转信号得到的PIP3时空演化图. 图中可见,由于细胞前部Rac活性降低,Rac-PIs回路的反馈强度 减弱,PIP3绝对浓度也由≅8 μmol/L降低到~5 μmol/L; 但是,由于反向梯度较小,不足以驱动细胞极性反转,PIP3积聚方位始终是维持在细胞前端,预示着细胞将长期处于图1(b)状态.
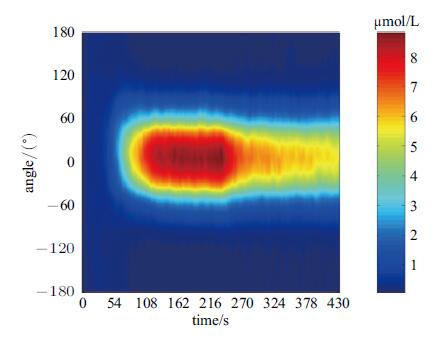
|
图 12 低梯度反转输入信号对应的PIP3时空演化图 Fig. 12 Spatial-temporal evolution of PIP3 (upon low gradient reversal signal:Rf(2)=0.34, Rb(2)=0.46) |
通过上述算例不难看出,如果细胞成功极性反转,那么新的伪足生成与先前的伪足消失之间必然存在着一定延滞时间. 此前,达卢 等认为这一``延滞''现象应通过LEGI机制解释[7]: 反向信号首先诱发快速扩散的全局抑制信号,促使胞内F-actin全面解离; 随即诱发慢速扩散的局部激活信号,抵消抑制信号,促进新的伪足形成. 达卢等同时推测,当反向信号较弱时,其发出的全局抑制信号也较弱,细胞因此无法消除已有极性,进而无法发生极性反转. 本文模拟结果则说明,这种``延滞''现象的产生是由细胞前端、后端对激活酶的``竞争''引起,对此不需要引入全局性抑制信号. 细胞接受反向信号刺激后,活性态Rac主要分布在细胞后端,而 PIP3则积聚在前端,这使得细胞前部大量的PIP3继续招聚PI3K,却由于缺少活性态Rac,无法引起PI3K激活; 细胞后部,尽管Rac活性较高,却由于缺少PIP3无法大量募集PI3K. 正是因为前、后两端对PI3K竞争,而短时期内一方无法取胜,制衡了Rac-PIs回路的反馈强度,从而在一段时期内,有效抑制细胞建立新的极性.
具体来说,依据反向信号梯度的高低,``竞争''的胜负结果可分为3种情况:
(1)反向信号梯度较高,这使得细胞前部伪足快速解离,尾部能在短时期内能够获得游离态激活酶,细胞得以在反方向迅速建立极性;
(2)反向信号梯度适中,细胞前部伪足需要较长时间解离,细胞极性建立较慢;
(3)反向信号梯度较弱,细胞前部长期维持一定量PIP3,细胞后部始终无法获得游离态激活酶,因此无法极性反转.
4 . 讨 论本文通过数学建模、数值模拟研究运动细胞``极性反转''行为,所得到的特征结果与已有实验结果一致. 图13是达卢等通过盘基网柄菌实验获得极性反转进程中细胞``前端''与``后端''的F-actin密度时程曲线(为多次试验所得平均结果). 图13中纵坐标``LimED-GFP''是F-actin荧光标记物,0点代表信号场反转时刻,黑色实心圆点标记细胞伪足F-actin密度,白色空心圆点则标记尾部. 本文以PIP3表征F-actin,相应的极性反转时程曲线与之一致(见图7,230~370s阶段).
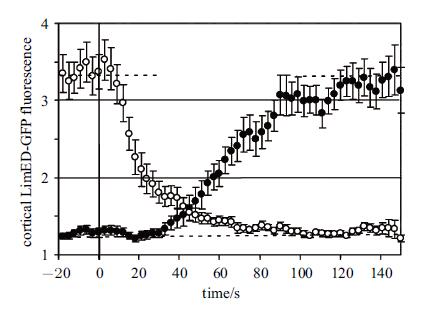
|
图 13 盘尼网柄菌极性反转实验所获得的细胞前后端 F-actin 时程曲线[7] Fig. 13 Concentration of F-actin varying with time at the cell head and the rear (derived from Ref.[7]) |
在运动细胞极化的研究领域中,数学模型已成为除生化实验外最为重要的研究手段. 此前,尽管有很多数学模型能够重现极化试 验现象,但能够定量地解释实验观测数据的模型还不多见. 本文为研究运动细胞``极性反转''所构建的模型仍属 ``激活-抑制''(activation-inhibition)类模型的范畴[11, 12, 13, 14, 15, 16] . 此类模型的共同特征是: 一类分子作为激活酶,能够在激活时对输入信号起正反馈作用; 另一类分子作为抑制酶,会对输入信号起负反馈作用,中止反应. 本文中,将分子的激活/抑制与实体单分子在胞质---质膜间的随机移置行为相结合,使得模型能兼具对信号处理与物质输运系统的特征. 尽管真实负责极化的级联转导十分复杂,但胞内分子间的基本作用形式以及物质运动形式总是有限的,据此可在生物系统``复杂''与模型``简约''之间寻求平衡.
本文在为运动细胞极性反转建立数学模型时,引入了一些必要的假设及简化,今后需着手开展以下3方面工作.
首先,本文是通过胞内信号分子的特征分布标记``极性反转''进程,其中并未考察细胞自身形态变化. 该假设的主要依据 来自myosin-II缺失细胞极性反转实验[7]. Myosin-II参与细胞骨架中张力纤维(stress fiber)的组装,myosin-II缺失既意味着细胞的力学性能发生改变. 实验发现myosin-II缺失细胞与正常细胞极化反转规律一致,说明力反馈回路与负责细胞极化的反馈回路之间并不耦合,因此不需要考虑力信号转导通路对于细胞极化的影响. 但是,考虑到已有研究显示,细胞自身几何形变能够使得信号分子的积聚更加陡峭[29],今后的研究中可以建立力-化耦合模型.
其次,本文所考察的Rac-PIs反馈回路仅为最简单的形式. 一些其他分子机制及中间信号转导环节,例如: PI3K质膜上的定位、F-actin合成、Rac自身调控等可以继续引入到现有模型框架中[23].
最后,``极性反转''只是运动细胞转向时所采取的几种方式中的一种. 有实验显示,细胞在接受方位与其初始头部较近的转向信号刺激时,更倾向于以固有伪足进行``U形''回转[10]. 显然,此时对细胞转向起主导作用的并非是由``双向分子输运''所介导的``极性反转''. 今后,为了更加准确的预测细胞转向行为可建立平行机制模型. 细胞最终转向方式,应由``双向分子输运''机制与其他机制(例如,伪足核心机制[30]之间的竞争获胜方决定.
5 . 结 论本文通过Rac-PIs反馈回路的时空效应驱动胞内双向分子输运,建立运动细胞极性反转数学模型. 数值模拟的结果重现了极性反转实验的主要现象,所得结论可归纳以下3个方面.
(1)理论计算得出的极性反转所需时间与实验观测一致,约为100s; 进一步提高反转信号梯度能够加快极性反转进程.
(2)细胞新的伪足延滞生成,这主要是由于细胞前端PIP3积聚对胞质游离态激活酶(例如: PI3K)展开竞争,使得激活因子无法有效到达细胞后部.
(3)反转信号梯度需要超过一定阈值才能引起细胞极性反转否则,细胞仍然维持之前极化方向.
| [1] | Wolf K, te Lindert M, Krause M, et al. Physical limits of cell migration: Control by ECM space and nuclear deformation and tuning by proteolysis and traction force. Journal of Cell Biology, 2013, 201(7): 1069-1084 |
| [2] | Wrighton KH. Wound healing: ESCRTs help repair membranes. Nature Reviews Molecular Cell Biology, 2014, 15(3): 151-151 |
| [3] | Muller WA. How endothelial cells regulate transmigration of leukocytes in the inflammatory response. American Journal of Pathology, 2014, 184(4): 886-896 |
| [4] | Polacheck WJ, Zervantonakis IK, Kamm RD. Tumor cell migration in complex microenvironments. Cellular and Molecular Life Sciences, 2013, 70(8): 1335-1356 |
| [5] | Tojima T, Itofusa R, Kamiguchi H. Steering neuronal growth cones by shifting the imbalance between exocytosis and endocytosis. Journal of Neuroscience, 2014, 34(21): 7165-7178 |
| [6] | Jilkine A, Edelstein-Keshet L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Computational Biology, 2011, 7(4): e1001121 |
| [7] | Dalous J, Burghardt E, Müller-Taubenberger A, et al. Reversal of cell polarity and actin-myosin cytoskeleton reorganization under mechanical and chemical stimulation. Biophysical Journal, 2008, 94(3): 1063-1074 |
| [8] | Chung CY, Funamoto S, Firtel RA. Signaling pathways controlling cell polarity and chemotaxis. Trends in Biochemical Sciences, 2001, 26(9): 557-566 |
| [9] | Yumura S, Mori H, Fukui Y. Localization of actin and myosin for the study of ameboid movement in Dictyostelium using improved immunofluorescence. Journal of Cell Biology, 1984, 99(3): 894-899 |
| [10] | Gerisch G, Keller HU. Chemotactic reorientation of granulocytes stimulated with micropipettes containing fMet-Leu-Phe. Journal of Cell Science, 1981, 52(1): 1-10 |
| [11] | Iglesias PA, Devreotes PN. Navigating through models of chemotaxis. Current Opinion in Cell Biology, 2008, 20(1): 35-40 |
| [12] | Simon CM, Vaughan EM, Bement WM, et al. Pattern formation of Rho GTPases in single cell wound healing. Molecular Biology of the Cell, 2013, 24(3): 421-432 |
| [13] | Meinhardt H. Orientation of chemotactic cells and growth cones: Models and mechanisms. Journal of Cell Science, 1999, 112(17): 2867-2874 |
| [14] | Janetopoulos C, Ma L, Devreotes PN, et al. Chemoattractant-induced phosphatidylinositol 3, 4, 5-trisphosphate accumulation is spatially amplified and adapts, independent of the actin cytoskeleton. Proceedings of the National Academy of Sciences, 2004, 101(24): 8951-8956 |
| [15] | Levine H, Kessler DA, Rappel WJ. Directional sensing in eukaryotic chemotaxis: A balanced inactivation model. Proceedings of the National Academy of Sciences, 2006, 103(26): 9761-9766 |
| [16] | Mori Y, Jilkine A, Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophysical Journal, 2008, 94(9): 3684-3697 |
| [17] | Feng S, Zhu W. Bidirectional molecular transport shapes cell polarization in a two-dimensional model of eukaryotic chemotaxis. Journal of Theoretical Biology. 2014, 363(21): 235-246 |
| [18] | Lin B, Holmes WR, Wang CC, et al. Synthetic spatially graded rac activation drives directed cell polarization and locomotion. arXiv preprint arXiv: 1204.5517, 2012 |
| [19] | Weiner OD, Neilsen PO, Prestwich GD, et al. A PtdInsP3-and Rho GTPase-mediated positive feedback loop regulates neutrophil polarity. Nature Cell Biology, 2002, 4(7): 509-513 |
| [20] | Bos JL, Rehmann H, Wittinghofer A. GEFs and GAPs: critical elements in the control of small G proteins. Cell, 2007, 129(5): 865-877 |
| [21] | Infante E, Ridley AJ. Roles of Rho GTPases in leucocyte and leukaemia cell transendothelial migration. Philosophical Transactions of the Royal Society B: Biological Sciences, 2013, 368(1629): 20130013 |
| [22] | Huang YE, Iijima M, Parent CA, et al. Receptor-mediated regulation of PI3Ks confines PI (3, 4, 5) P3 to the leading edge of chemotaxing cells. Molecular Biology of the Cell, 2003, 14(5): 1913-1922 |
| [23] | Charest PG, Firtel RA. Feedback signaling controls leading-edge formation during chemotaxis. Current Opinion in Genetics & Development, 2006, 16(4): 339-347 |
| [24] | Goldbeter A. Oscillatory enzyme reactions and Michaelis-Menten kinetics. FEBS Letters, 2013, 587(17): 2778-2784 |
| [25] | Postma M, Van Haastert PJM. A diffusion-translocation model for gradient sensing by chemotactic cells. Biophysical Journal, 2001, 81(3): 1314-1323 |
| [26] | Gamba A, de Candia A, Di Talia S, et al. Diffusion-limited phase separation in eukaryotic chemotaxis. Proceedings of the National Academy of Sciences, 2005, 102(47): 16927-16932 |
| [27] | Ueda M, Shibata T. Stochastic signal processing and transduction in chemotactic response of eukaryotic cells. Biophysical Journal, 2007, 93(1): 11-20 |
| [28] | Ma L, Janetopoulos C, Yang L, et al. Two complementary, local excitation, global inhibition mechanisms acting in parallel can explain the chemoattractant-induced regulation of PI(3,4,5)P3. Biophysical Journal, 2004, 87(6): 3764-3774 |
| [29] | Marée AFM, Grieneisen VA, Edelstein-Keshet L. How cells integrate complex stimuli: The effect of feedback from phosphoinositides and cell shape on cell polarization and motility. PLoS Computational Biology, 2012, 8(3): e1002402 |
| [30] | Neilson MP, Veltman DM, van Haastert PJM, et al. Chemotaxis: a feedback-based computational model robustly predicts multiple aspects of real cell behaviour. PLoS Biology, 2011, 9(5): e1000618 |
 2015, Vol. 47
2015, Vol. 47