壳体作为一种优越的空间结构形式,其重量小承载大的巨大优势将应用于越来越多的领域[1]. 其中曲面壳体已在土木、水利、汽车、航空航天等领域得到广泛的应用[2, 3]. 工程中提出很多有关多尺度问题的求解方法[4, 5, 6],壳单元作为一种为了解决多尺度问题而衍生出来的单元类型,一直是有限元研究领域的重要课题. 对于一般的三维空间壳体而言,由于几何描述的复杂性以及涉及到具体的壳体理论选择,很难直接构造位移和转动各自独立插值的曲壳单元[7].
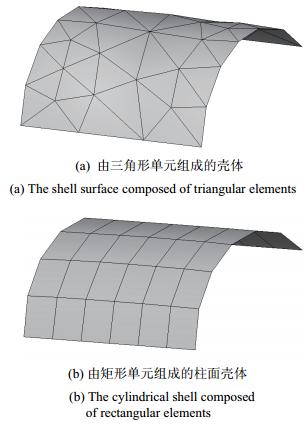
目前工程中提出了很多种壳体单元,包括平面壳元[7, 8]、超参数壳元[7, 8, 9]、相对自由度壳元[7]以及应用于复合材料的层合板壳单元[10, 11]等. 平面壳元在表达格式上比较简单,可以看作是平面应力问题和平板弯曲问题的叠加组合. 因此,有限元法中可以用折板代替壳体,利用平面壳元的理论基础近似计算,通常采用三角形或者四边形平面近似代替曲面壳体(图1),但此种方法只是在柱状单曲薄壳的计算时精度较好,且计算中需要将网格合理加密,以达到更好的近似,而且当曲面壳体曲率较大时,误差较大. 研究者们也在平面壳元的基础上做了大量工作,提出了很多不同的方法[12, 13, 14, 15]来解决不同的壳体问题. 工程实际中比较常用的是超参数壳元和相对自由度壳元,计算精度较高,但其表达格式复杂.
|
图 1 用折板代替曲面壳体 Fig.1 Folded plate simulating curved surface shells |
本文将介绍一种新的计算曲面壳体等效节点热载荷的方法,该方法将在平面壳元的理论基础上,结合本文提出的理论公式进行计算,并能达到和超参数壳元同样的精度. 目前比较常用的超参数壳元在计算曲面壳体的等效节点热载荷时,先得到坐标转换矩阵,将整体坐标系下的单元节点坐标转换到局部坐标系,在局部坐标系下计算所需的单元等效节点热载荷数值积分. 本文提出的方法将在壳单元切平面上建立局部坐标系,能有效适应壳单元的曲面形状,能直接利用平面壳元理论公式,在整体坐标系下计算局部坐标系下的单元等效节点热载荷数值积分,最后得到坐标转换矩阵,将局部坐标系下的单元节点热载荷转换到整体坐标系,并能达到较好的计算精度.
1 曲面壳体结构的等效节点热载荷计算根据热应力问题的基本理论[16],工程结构的热应力问题中,将增加一项以初应变形式出现的温度载荷项. 在用壳单元分析时,重要的是将壳单元的等效节点热载荷计算出来. 本文采用平面壳元计算曲面壳体的等效节点热载荷. 在平面壳元的热问题中,等效节点热载荷只引起单元内的变形,不产生弯曲变形,因此,平面壳元热问题的等效节点热载荷和平面应力问题的等效节点热载荷是一样的,只不过是处理整个曲面壳体结构在位于三维空间中的曲面模型,在单元的局部坐标系下按照平面应力问题计算完成后,将其转换到整体坐标下即可.
1.1 平面应力问题的等效节点热载荷为了避免混乱,在这里使用局部坐标标识$({x}',{y}',{z}')$讨论平面应力问题,单元为四节点四边形等参单元,平面应力问题的等效节点热载荷[17]可以表示为
| $P_{{\varepsilon _0}}^e = \int \int {} {B^{\rm{T}}}D{\varepsilon _0}t{\rm{d}}x'{\rm{d}}y'$ | (1) |
式中,$t$为壳的厚度,$B$为应变矩阵,其表达式为
| $B = \left[{{B_1}\;\;{B_2}\;\;{B_3}\;\;{B_4}} \right]$ | (2) |
| ${B_i} = \left[{\begin{array}{*{20}{c}} {\frac{{\partial {N_i}}}{{\partial x'}}}&0\\ 0&{\frac{{\partial {N_i}}}{{\partial y'}}}\\ {\frac{{\partial {N_i}}}{{\partial y'}}}&{\frac{{\partial {N_i}}}{{\partial x'}}} \end{array}} \right]$ | (3) |
四节点四边形等参单元形函数$N_i $为
| ${N_i}\left( {\xi ,\eta } \right) = \frac{1}{4}\left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right)$ | (4) |
式中,$i = 1\;,\;2\;,\;3\;,\;4$; $\xi$和$\eta $为四边形单元的自然坐标,$\xi _i$和$\eta _i $为4个角节点的自然坐标值,其值为
| $\left[{\begin{array}{*{20}{c}} {{\xi _1}}&{{\eta _1}}\\ {{\xi _2}}&{{\eta _2}}\\ {{\xi _3}}&{{\eta _3}}\\ {{\xi _4}}&{{\eta _4}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} { - 1}&{ - 1}\\ 1&{ - 1}\\ 1&1\\ { - 1}&1 \end{array}} \right]$ | (5) |
$D$为平面应力问题的弹性刚度矩阵,其表达式为
| $D = \frac{E}{{1 - {\mu ^2}}}\left[{\begin{array}{*{20}{c}} 1&\mu &0\\ \mu &1&0\\ 0&0&{\frac{{1 - \mu }}{2}} \end{array}} \right]$ | (6) |
式中,$E$为材料的弹性模量,$\mu $为泊松比.$ \varepsilon _0$为温度变化引起的初应变,其表达式为
| ${\varepsilon _0} = \alpha \Delta T{\left[{1\;\;1\;\;0} \right]^{\rm{T}}} = \alpha \left( {T - {T_0}} \right){\left[{1\;\;1\;\;0} \right]^{\rm{T}}}$ | (7) |
式中,$\alpha $为材料的热膨胀系数,$\Delta T$为温度场变化量,$T_0 $为结构的初始温度场,$T$为结构的稳态或瞬态温度场. $T$可由温度场分析得到的单元的节点温度$T_i $ 通过插值求得,即为
| $T = \sum\limits_{i = 1}^n {{N_i}} \left( {\xi ,\eta } \right){T_i}$ | (8) |
将式(2)~(7)代入式(1),可得到[17]
| $\begin{array}{l} \left\{ {{P_{{\varepsilon _0}}}} \right\}_i^e = \left\{ {\begin{array}{*{20}{l}} {{P_{{\varepsilon _0}x'}}}\\ {{P_{{\varepsilon _0}y'}}} \end{array}} \right\}_i^e = \\ \qquad \frac{{E\alpha }}{{1 - \mu }}\int \smallint \left\{ {\begin{array}{*{20}{l}} {{N_{i,x'}}}\\ {{N_{i,y'}}} \end{array}} \right\}t\Delta T{\rm{d}}x'{\rm{d}}y' = \\ \qquad \frac{{E\alpha }}{{1 - \mu }}\int_{ - 1}^1 {\int_{ - 1}^1 {\left\{ {\begin{array}{*{20}{l}} {{N_{i,x'}}}\\ {{N_{i,y'}}} \end{array}} \right\}} } t\Delta T\left| {{\rm{ }}J} \right|{\rm{d}}\xi {\rm{ d}}\eta \end{array}$ | (9) |
在传统方法中[18],计算$N_{i,x} $,$N_{i,y} $和$\left| J \right|$ 时是采用复合函数求导法则并进一步求逆推导出来的,即
| $\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial \xi }}\\ \frac{{\partial {N_i}}}{{\partial \eta }} \end{array} \right\} = \left\{ {\begin{array}{*{20}{c}} {\frac{{\partial x'}}{{\partial \xi }}}&{\frac{{\partial y'}}{{\partial \xi }}}\\ {\frac{{\partial x'}}{{\partial \eta }}}&{\frac{{\partial y'}}{{\partial \eta }}} \end{array}} \right\}\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial x'}}\\ \frac{{\partial {N_i}}}{{\partial y'}} \end{array} \right\} = J\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial x'}}\\ \frac{{\partial {N_i}}}{{\partial y'}} \end{array} \right\}$ | (10) |
从而有
| $\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial x'}}\\ \frac{{\partial {N_i}}}{{\partial y'}} \end{array} \right\} = {J^{ - 1}}\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial \xi }}\\ \frac{{\partial {N_i}}}{{\partial \eta }} \end{array} \right\}$ | (11) |
| $\left| J \right| = \left| {\begin{array}{*{20}{c}} {\frac{{\partial x'}}{{\partial \xi }}}&{\frac{{\partial y'}}{{\partial \xi }}}\\ {\frac{{\partial x'}}{{\partial \eta }}}&{\frac{{\partial y'}}{{\partial \eta }}} \end{array}} \right|$ | (12) |
但在计算曲面壳体结构时,建立在平面假设基础上的传统的折板代替曲面壳体的方法将产生较大的误差,因此需要对计算式(9)中的$N_{i,{x}'}$,$N_{i,{y}'} $ 和$\left| J \right|$的传统方法进行改进.
1.2 计算壳单元等效节点热载荷的新方法 1.2.1 建立壳单元局部坐标系以柱面壳体为例,单元为四节点矩形等参单元,传统的用折板代替曲面壳体的方法[7]是以单元的中心点为原点以柱壳母线方向为局部 坐标轴方向建立局部坐标系(图2),再将式(11)和式(12)代入式(9)计算等效节点热载荷,用这种方法计算的结果会产生较大的误差,因此很多工程软件会采用超参数单元或者相对自由度单元才能达到比较好的精度.
|
图 2 传统方法矩形单元的总体和局部坐标系 Fig.2 Local orthogonal set of axes over a rectangular element and global orthogonal set of axes in the traditional way |
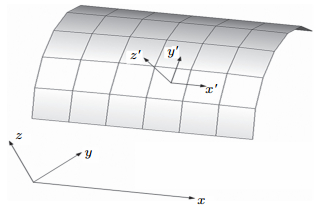
本文介绍一种新的计算式(9)的方法,首先以自然坐标系的原点为局部坐标系的原点,以自然坐标系的$\xi$的切线方向为局部 坐标系的${x}'$方向,以单元面的法线方向为${z}'$方向,再根据右手定则确定${y}'$方向,由此建立的局部坐标系[19] (图3)适用于不在同一个平面上的曲面单元,其${x}'$,${y}'$轴会与单元的曲线边界切线方向平行. 为了表示的方便,将局部坐标的 $\left({x}',{y}',{z}'\right)$的坐标标识写成$\left( {{x}'_1 ,{x}'_2 ,{x}'_3 } \right)$,整体坐标系的 $\left( {x,y,z} \right)$的坐标标识写成$\left( {x_1 ,x_2 ,x_3 } \right)$,自然坐标的坐标标识依然是$\left( {\xi ,\eta } \right)$.
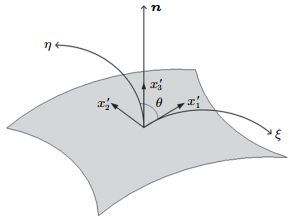
|
图 3 新方法建立的单元的局部坐标系 Fig.3 Local orthogonal set of axes over a surface element in the new way |
正如2.1节所提出的要想计算出式(9)的积分值,需要求出式中$N_{i,{x}'} $,$N_{i,{y}'} $ 和$\left| J \right|$的值,采用复合函数求导法则可知
| $\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial x'}}\\ \frac{{\partial {N_i}}}{{\partial y'}} \end{array} \right\} = \left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial x{'_1}}}\\ \frac{{\partial {N_i}}}{{\partial x{'_2}}} \end{array} \right\} = \left[{\begin{array}{*{20}{c}} {\frac{{\partial \xi }}{{\partial {{x'}_1}}}}&{\frac{{\partial \eta }}{{\partial x{'_1}}}}\\ {\frac{{\partial \xi }}{{\partial {{x'}_2}}}}&{\frac{{\partial \eta }}{{\partial x{'_2}}}} \end{array}} \right]\left\{ \begin{array}{l} \frac{{\partial {N_i}}}{{\partial \xi }}\\ \frac{{\partial {N_i}}}{{\partial \eta }} \end{array} \right\}$ | (13) |
| $\left. {\begin{array}{*{20}{l}} {\frac{{\partial \xi }}{{\partial {{x'}_1}}} = \frac{1}{{\left| {{m_1}} \right|}}}\\ {\frac{{\partial \xi }}{{\partial {{x'}_2}}} = \frac{{ - \cos \theta }}{{\left| {{m_1}} \right|\sin \theta }}}\\ {\frac{{\partial \eta }}{{\partial {{x'}_1}}} = 0}\\ {\frac{{\partial \eta }}{{\partial {{x'}_2}}} = \frac{1}{{\left| {{m_2}} \right|\sin \theta }}} \end{array}\;\;\;} \right\}$ | (14) |
式中,$\theta $为图3中所示自然坐标系下$x'_1 $轴和$\eta $轴的夹角,并且有
| $\left. {\begin{array}{*{20}{l}} {\left| {{m_1}} \right| = \sqrt {{{\left( {\frac{{\partial {x_1}}}{{\partial \xi }}} \right)}^2} + {{\left( {\frac{{\partial {x_2}}}{{\partial \xi }}} \right)}^2} + {{\left( {\frac{{\partial {x_3}}}{{\partial \xi }}} \right)}^2}} }\\ {\left| {{m_2}} \right| = \sqrt {{{\left( {\frac{{\partial {x_1}}}{{\partial \eta }}} \right)}^2} + {{\left( {\frac{{\partial {x_2}}}{{\partial \eta }}} \right)}^2} + {{\left( {\frac{{\partial {x_3}}}{{\partial \eta }}} \right)}^2}} } \end{array}\;\;\;} \right\}$ | (15) |
| $\cos \theta = \frac{1}{{\left| {{m_1}} \right|\left| {{m_2}} \right|}}\frac{{\partial {x_i}}}{{\partial \xi }}\frac{{\partial {x_i}}}{{\partial \eta }}\;\;(i = 1,3)$ | (16) |
式({15})和式({16})中的坐标值都是整体坐标系下的坐标值,将式({14})$\sim$({16})代入式({13})后即可得到$N_{i,{x}'}$和$N_{i,{y}'} $ 的值,因此,利用在整体坐标系下的单元节点坐标即可求出形函数对局部坐标的导数.
1.2.3 壳单元中从局部到自然坐标系积分转换的雅可比计算式以壳单元在整体坐标下的坐标转换为例,求出整体坐标到自然坐标积分转化的$\left| J \right|'$的值[19]. 如图4所示,$ r_\xi $和$ r_\eta $为相切于自然坐标的向量,$ n^\ast$为单元面的法向量,其表达式为
| $\left. {\begin{array}{*{20}{l}} {{r_\xi } = \frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \xi }}i + \frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \xi }}j + \frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \xi }}k}\\ {{r_\eta } = \frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \eta }}i + \frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \eta }}j + \frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \eta }}k} \end{array}\;\;\;} \right\}$ | (17) |
| $\begin{array}{l} {n^ * } = {r_\xi } \times {r_\eta } = \\ \;\left( {\frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \eta }} - \frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \eta }}} \right)i + \\ \;\left( {\frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \eta }} - \frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_3}\left( {\xi ,\eta } \right)}}{{\partial \eta }}} \right)j + \\ \;\left( {\frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \eta }} - \frac{{\partial {x_2}\left( {\xi ,\eta } \right)}}{{\partial \xi }} \cdot \frac{{\partial {x_1}\left( {\xi ,\eta } \right)}}{{\partial \eta }}} \right) \end{array}$ | (18) |

|
图 4 单元面的法向量 Fig.4 Normal vector to a surface element |
其中$ i$,$ j$,$ k$为整体坐标系下的单位方向向量.
从整体坐标$\left( {x_1 ,x_2 ,x_3 } \right)$到自然坐标$\left( {\xi ,\eta } \right)$转换的雅可比数值$\left| J \right|^\prime $为
| ${\left| J \right|^\prime } = \left| {{n^ * }} \right| = \left| {{r_\xi } \times {r_\eta }} \right|$ | (19) |
单元面的单位法向量为
| $n = \frac{{{n^ * }}}{{\left| {{n^ * }} \right|}} = {n_1}i + {n_2}j + {n_3}k$ | (20) |
式(9)中的$\left| J \right|$是从局部坐标转换到自然坐标的雅可比行列式,从整体坐标到自然坐标的雅可比行列式等于从局部坐标到自然坐标的雅可比行列式,即为$\left| J \right| = \left| J \right|^\prime $.
1.3 壳单元局部到整体坐标系转换矩阵计算法当把单元等效节点热载荷求出以后,需要将单元节点热载荷转换到整体坐标系,这时就需要一个将局部坐标系下的坐标、位移及载荷和整体坐标系下的坐标、位移及载荷相互转换的关系矩阵$ L$[19].
局部坐标系下位移及载荷可以用整体坐标系下的位移和载荷分别表示为
| $\left. {\begin{array}{*{20}{c}} {u{'_i} = {L_{ij}}{u_j}}\\ {P{'_i} = {L_{ij}}{P_j}} \end{array}\;\;(i,j = 1,3)} \right\}$ | (21) |
这里的$u_j$和$P_j$可以用单元节点的值通过形函数插值得到:
| $\left. {\begin{array}{*{20}{l}} {{u_j}\left( {\xi ,\eta } \right) = \sum\limits_{\alpha = 1}^M {{N_\alpha }\left( {\xi ,\eta } \right)} u_j^\alpha }\\ {{P_j}\left( {\xi ,\eta } \right) = \sum\limits_{\alpha = 1}^M {{N_\alpha }\left( {\xi ,\eta } \right)} P_j^\alpha } \end{array}\;\;\left( {j = 1,3} \right)} \right\}$ | (22) |
式中,$M$为壳单元节点数,$L_{ij} $为整体坐标系和局部坐标系坐标轴夹角的方向余弦值,其计算表达式为
| ${L_{1j}} = \frac{1}{{\left| {{m_1}} \right|}}\frac{{\partial {x_j}}}{{\partial \xi }}\;\;\left( {j = 1,3} \right)$ | (23) |
| $\left. {\begin{array}{*{20}{l}} {{L_{21}} = {n_2}{L_{13}} - {n_3}{L_{12}}}\\ {{L_{22}} = {n_3}{L_{11}} - {n_1}{L_{13}}}\\ {{L_{23}} = {n_1}{L_{12}} - {n_2}{L_{11}}} \end{array}\;\;\;} \right\}$ | (24) |
| ${L_{3j}} = {n_j}\;\;(j = 1,3)$ | (25) |
其中,$n_1 $,$n_2 $,$n_3 $为单元面在局部坐标原点单位法向量的分量,由式(18)$\sim$(20)确定.
由表达式(21)$\sim$(25)可求出从整体坐标系到局部坐标系的转换矩阵$ L$,并有关系$ L^{\rm T} = L^{ - 1}$. 局部坐标系和整体坐标系下的位移、载荷转换关系为
| $\left. {\begin{array}{*{20}{c}} {{{U'}^e} = L{U^e}}&{{U^e} = {L^{\rm{T}}}{{U'}^e}}\\ {{{P'}^e} = L{P^e}}&{{P^e} = {L^{\rm{T}}}{{P'}^e}} \end{array}\;\;\;} \right\}$ | (26) |
结合本文所述方法,采用FORTRAN90编制了采用新方法计算壳单元等效节点热载荷的计算程序FEALS,并对其计算结果和有限元商用软件ANSYS计算结果进行比较分析,验证本文所述计算方法的正确性. 为了进一步验证本文所述方法的优越性,在折板代替曲面壳体的方法的理论基础上,同样采用Fortran90编制了计算壳单元等效节点热载荷的计算程序FPLATE,待计算完成后,分别列出以上3种方法的计算结果进行比较分析.
使用商用软件ANSYS14.0版本进行计算,选用单元类型中的SHELL181单元. SHELL181单元是建立在超参数单元理论基础上的四节点四边形壳单元,可以用其对本文计算结果进行对比,验证本文所论述方法的正确性和精确性.
算例1: 柱面壳体等效节点热载荷计算
取柱壳模型进行计算分析(图5),模型曲面半径为4 m,长度为10 m,角度范围为$180^\circ$,壳体厚度为0.05 m,材料参数中 弹性模量为4 MPa,热膨胀系数为$2.5\times 10^{-5}$,令模型整体温度升高100$^\circ$C.

|
图 5 柱面壳体模型 Fig.5 The cylindrical shell body |
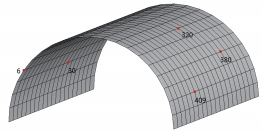
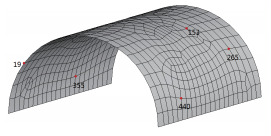
为了验证不同的方法对不同的网格类型的适用性,分别采用映射划分网格(图6)和自由划分网格(图7)的方式对柱壳模型进行网格划分,单元为四边形四节点单元. 其中以映射方式划分的单元为四节点矩形单元,单元数为400个,节点数为441个,以自由方式划分的单元为自由四边形四节点单元,单元数为506个,节点数为550个.
|
图 6 映射方式划分矩形网格 Fig.6 Meshing model in mapped method |
|
图 7 自由方式划分自由网格 Fig.7 Meshing model in free method |
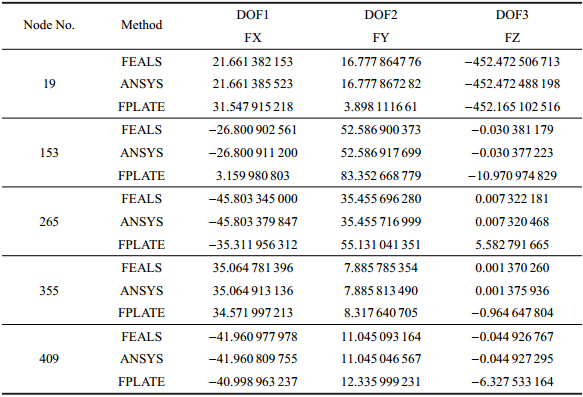
分别用计算程序FEALS、商用软件ANSYS14.0以及计算程序FPLATE的方法对这2种不同方式划分的网格模型进行计算,计算出柱面壳体模型的等效节点热载荷结果,由于转角自由度方向的结果都为0,因此只列出$x$,$y$,$z$三个位移自由度方向的计算结果. 随机选几个节点(图6、图7中标注的节点)的结果值进行对比(表1和表2).
| 表 1 映射方式划分柱壳网格的计算结果对比 Table 1 The comparison of the results of the Cylindrical shell elements meshing in mapped method |
| 表 2 自由方式划分柱壳网格的计算结果对比 Table 2 The comparison of the results of the Cylindrical shell elements meshing in free method |
可以看出,不论采取哪种方式划分网格,FEALS和ANSYS14.0的计算结果都非常接近. 当用映射方式划分网格时,用折板代替曲面壳体的方法计算出的结果与前两者也非常接近,当用自由方式划分网格时,用折板代替曲面壳体的方法计算出的结果与前两者相差较大. 说明传统的用折板代替曲面壳体方法只适用于用映射方式划分的矩形柱壳单元,本文所述的方法不仅适用于映射方式划分的矩形柱壳单元,同样适用于自由方式划分的自由四边形四节点柱壳单元,其应用更加自由和广泛,证明了本文所述方法的正确性和必要性.\vskip 3mm
算例2: 不规则四边形曲壳体等效节点热载荷计算
取一个扭转的四边形不规则曲面(图8),其可由如图9所示的一个1 m×1 m的规则四边形拉拽而成. 首先将图9所示模型中的2号点向$Z$轴负方向移动0.4 m,3号点向$Z$轴正方向移动0.3 m,4号点向$Z$轴负方向移动0.2 m; 然后再将整个模型沿$x$轴正方向旋转30$^\circ$,沿$y$轴正方向旋转$45^\circ$,沿$z$轴正方向旋转$60^\circ$; 最后将模型坐标原点由$\left( {0,0,0} \right)$移动到$\left( {1,2,3} \right)$,最终得到如图8所示的任意不规则四边形曲面模型. 厚度为0.05 m,材料参数中弹性模量为4 MPa,热膨胀系数为$2.5\times 10^{-5}$,令模型整体温度升高100$^\circ$C.

|
图 8 任意不规则四边形曲面模型单元 Fig.8 The formed irregular surface shell elements |

|
图 9 平面壳体模型单元 Fig.9 The plane shell elements |
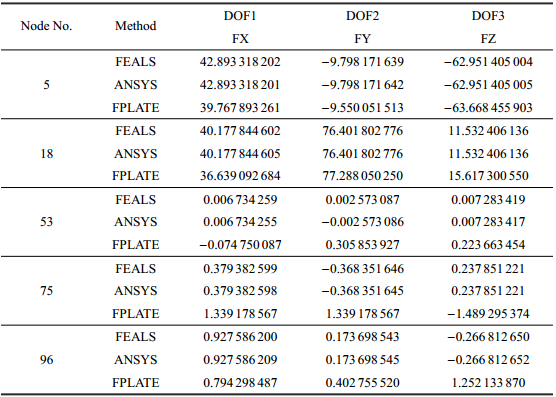
同样用四边形四节点单元对模型进行网格划分,单元数为100个,节点数为121个. 分别用计算程序FEALS、商用软件ANSYS14.0以及计算程序FPLATE的方法计算出柱面壳体模型等效节点热载荷结果,同样只列出$x$,$y$,$z$三个位移自由度方向的计算结果,随机选几个节点(图8中标注的节点)的结果值进行对比(表3).
| 表 3 不规则四边形曲面壳体模型的计算结果对比 Table 3 The comparison of the results of the formed irregular surface shell elements |
从表2的计算结果可以看出,利用本文介绍的计算壳单元等效节点热载荷积分的方法和成熟的商业软件ANSYS的计算结果非常接近,用折板代替曲面壳体的方法计算结果误差较大. 表明本文所用方法是正确的,其计算结果是可靠的.
3 结 论本文介绍了一种新的计算壳单元等效节点热载荷积分的方法. 在平面壳元的理论基础上,通过在壳单元的切平面建立局部坐标系,能有效适应曲面壳体形状,利用整体坐标系下的坐标值直接计算壳单元等效节点热载荷方程中的积分函数值,从而避免了折板壳元计算曲面壳体的误差和局限性,也避免了利用超参数壳单元计算曲面壳体时的理论基础和表达式的复杂性. 通过和商用软件ANSYS的计算结果的对比分析,证明了本文所述方法的正确性和可行性.
| [1] | 孙博华. 壳体简史. 力学与实践, 2013, 35(5): 104-106 (Sun Bohua. A brief history of shell. Mechanics in Engineering, 2013, 35(5): 104-106 (in Chinese)) |
| [2] | 张志田, 葛耀君. 悬索桥静动力特性分析的有限板壳单元法. 结构工程师, 2003, (4): 21-25 (Zhang Zhitian, Ge Yaojun. Static and dynamic analysis of suspension bridges based on an orthotropic shell finite element method. Structural Engineers, 2003, (4): 21-25 (in Chinese)) |
| [3] | 高铁军, 王忠金, 高洪波, 等. 涡扇发动机异形曲面壳体零件整体成形工艺. 推进技术, 2007, 28(4):437-440 (Gao Tiejun, Wang Zhongjin, Gao Hongbo, et al. Integral forming for special-shaped curved surface shell parts of turbofan engine. Journal of Propulsion Technology, 2007, 28(4): 437-440 (in Chinese)) |
| [4] | Lü Jun, Zhang Hongwu, Yang Dongsheng. Multiscale method for mechanical analysis of heterogeneous materials with polygonal microstructures. Mechanics of Materials, 2013(56): 38-52 |
| [5] | 吕军, 张洪武, 陈飙松. 基于扩展多尺度有限元法的含液闭孔材料拓扑优化. 固体力学学报, 2013, 34(4): 342-351 (Lü Jun, Zhang Hongwu, Chen Biaosong. Topology optimization of closed liquid cell materials based on extended multiscale finite element method. Acta Mechanica Solida Sinica, 2013, 34(4): 342-351 (in Chinese)) |
| [6] | 张洪武, 王鲲鹏. 材料非线性微-宏观分析的多尺度方法研究. 力学学报, 2004, 36(3): 359-363 (Zhang Hongwu, Wang Kunpeng. Multiscale methods for nonlinear analysis of composite materials. Acta Mechanica Sinica, 2004, 36(3): 359-363 (in Chinese)) |
| [7] | 王勖成. 有限单元法. 北京: 清华大学出版社, 2003 (Wang Xucheng. Finite Element Method. Beijing: Tsinghua University Press, 2003 (in Chinese)) |
| [8] | Clough R W, Johncon C P. A finite element approximation for the analysis of thin shell. Int. J. Solids Structures, 1968(4): 43-60 |
| [9] | Ahmad S, Irons B M, Zienkiewicz O C. Analysis of thick and thin shell structures by curved elements. Int. J. Numer. Methods. Eng, 1970(2): 419-451 |
| [10] | 白瑞祥, 郭兆璞, 陈浩然, 等. 复合材料层合板、壳胶-铆混合连接件有限元分析. 大连理工大学学报, 2000, 40(3): 280-284 (Bai Ruixiang, Guo Zhaopu, Chen Haoran, et al. Finite element analysis of adhesive-bolted joint for composite plate and rotary shell structures. Journal Of Dalian University of Technology, 2000, 40(3): 280-284 (in Chinese)) |
| [11] | 张志峰, 陈浩然, 白瑞祥. 一种分析AGS结构的三角形加筋板壳单元. 工程力学, 2006, 23(1): 203-208 (Zhang Zhifeng, Chen Haoran, Bai Ruixiang. A new triangular stiffened plate/shell elment for composite grid structure analysis. Engineering Mechanics, 2006, 23(1): 203-208 (in Chinese)) |
| [12] | 许磊平, 秦顺全, 马润平. 基于平面壳单元的分阶段成形结构平衡方程.西南交通大学学报, 2013, 48(5): 857-862 (Xu Leiping, Qin Shunquan, Ma Runping. Equilibrium equation derivation of structures formed by stages based on plane shell element. Journal of Southwest Jiaotong University, 2013, 48(5): 857-862 (in Chinese)) |
| [13] | 高蕊, 曹汝龙, 王岩, 等.板式结构体系的箱形平板薄壳单元.济南大学学报, 2013, 27(3): 315-319 (Gao Rui, Cao Rulong, Wang Yan, et al. A new box-type plate and shell element used in panel structures. Journal of University of Jinan, 2013, 27(3): 315-319 (in Chinese)) |
| [14] | 尹进, 杨东生, 张盛, 等. 几种基于组合方法的复合材料层合板壳单元.航空学报, 2013, 34(1): 86-96 (Yin Jin, Yang Dongsheng, Zhang Sheng, et al. Laminated composite plate and shell elements based on combination method. Acta Aeronautica et Astronautica Sinica, 2013, 34(1): 89-96 (in Chinese)) |
| [15] | 文颖, 戴公连, 曾庆元.基于带面内转角自由度四节点平板壳单元的板壳非线性分析.中南大学学报, 2013, 44(4): 1525-1531 (Wen Ying, Dai Gonglian, Zeng Qingyuan. 4-node flat shell element with drilling degrees of freedom for nonlinear analysis of plates and shells. Journal of Central South University, 2013, 44(4): 1525-1531 (in Chinese)) |
| [16] | 李维特, 黄保海, 毕仲波. 热应力理论分析及应用. 北京: 中国电力出版社, 2004 (Li Weite, Huang Baohai, Bi Zhongbo. The Theory Analysis and Application of Thermal Stress. Beijing: China Electric Power Press, 2004 (in Chinese)) |
| [17] | 邵红艳. 结构温度场和温度应力场分析. [硕士论文].西安: 西北工业大学, 2001 (Shao Hongyan. The structure temperature field and thermal stress field analysis. [Master's Thesis]. Xi'an: Northwestern Polytechnical University, 2001 (in Chinese)) |
| [18] | 侯建国, 安旭文. 有限单元法程序设计. 第二版.武汉: 武汉大学出版社. 2012 (Hou Jianguo, An Xuwen. Finite Element Method Program Design. Second edition. Wuhan: Wuhan University Press. 2012 (in Chinese)) |
| [19] | Gao XW, Davies TG. Boundary Element Programming in Mechanics. London: Cambridge University Press, 2002 |
| [20] | Lachat JC. A further development of the boundary integral technique for elastostatics. [PhD Thesis]. UK: University of Southampton, 1975 |
| [21] | Lachat JC, Watson JO, et al. A second generation boundary integral program for three dimensional elastic analysis. In: Cruse TA, Rizzo FJ eds. Boundary Integral Equation Method: Computational Applications in Applied Mechanics. New York: ASME, 1975 |
| [22] | Becker AA. The Boundary Element Method in Engineering. London: McGraw -Hill Book Co, 1992 |
 2015, Vol. 47
2015, Vol. 47