2. 石家庄铁道大学机械工程学院, 石家庄050043
动力吸振器(dynamic vibration absorber,DVA)是一种附加在受激励的主系统上以抑制其振动的控制装置. 自1909年弗拉姆发明第一个动力吸振器[1]以来,人们对它的研究已有上百年的历史. 然而该动力吸振器只考虑了在单自由度主系统上附加无阻尼动力吸振器的情况. 1928年,邓哈托等[2]发现在动力吸振器中加入阻尼能够有效抑制主系统振幅,并拓宽减振频率,这种含有阻尼的动力吸振器就是 目前广为所知的沃伊特型动力吸振器. 同时,邓哈托等[2]发现该动力吸振器的频率响应曲线存在两个与阻尼系数无关的固定点,并据此提出了动力吸振器设计的固定点理论. 其他学者根据该理论分别在1932年和1946年得到了动力吸振器的最优频率比[3]和最优阻尼比[4]. 目前根据固定点理论得到的结果已经成为国内外振动工程教科书[5, 6]中的经典结论,然而实际上该结果是沃伊特型动力吸 振器的近似最优解而非精确解. 文献[7, 8]中给出了阻尼动力吸振器最优参数的级数解,发现根据固定点理论推导的结果与级数解非常接近,而且形式简单,因此邓哈托 等的近似解公式在工程实际中仍然有重要的应用价值. 为了进一步提高吸振器的减振效果,文献[9]提出了一种新型的接地式动力吸振器,发现接地式动力吸振器仍然存在类似的固定点,并 且通过调整接地阻尼可以改善振动控制效果. 文献[10]采用另外一种方法也得到了和文献[9]类似的结果. 赵艳影 等[11, 12]研究了时滞对动力吸振器的影响,给出了如何利用时滞提高振动控制效果的思想. 申永军 等[13, 14]研究了4种半主动动力吸振器的近似解析解,并分析了半主动动力吸振器的参数设计和时滞对半主动控制效 果的影响.
随着对振动控制系统的深入研究,众多学者发现含有负刚度弹簧的振动系统具有固有频率低、承载能力大、减振效果好等优点,因此近年 来负刚度元件在减振方面的应用越来越多. 文献[15]提出将负刚度元件应用于隔振器当中. 彭献等[16]对含有负刚度弹簧的系统进行了能量分析,表明负刚度系统具有较好的减振效果. 彭解华等[17]对正负刚度并联系统的稳定性问题进行了研究. 文献[18]提出将正负刚度元件串联形成零功率磁悬浮主动减振器并进行了实验研究,证明了该模型在抵抗直接干扰方面具有很好的 效果[19, 20, 21, 22]. 帕克等[23]对正负刚度并联系统的最优设计从理论和实验方面进行了探讨. 纪晗等[24]针对长周期结构隔振效果差的问题,提出了在隔振层中附加负刚度阻尼装置的思想,并对其减振效果进行了分析. 文献[25]提出了含负刚度的无阻尼自适应动力吸振器,发现该系统能够很好地降低主系统振幅.
本文通过在经典沃伊特型动力吸振器中附加接地负刚度弹簧元件得到了一种新的动力吸振器模型. 利用固定点理论对该吸振器的刚度 和阻尼项进行了最优参数设计,并在保证系统稳定性的情况下得到了负刚度项的最优值. 通过与两种传统被动式动力吸振器模型的对比,证明负刚度模型在减振方面具有很大优势,能够极大地降低共振幅值,同时拓宽减 振频率,为设计新型的动力吸振器提供了一种选择.
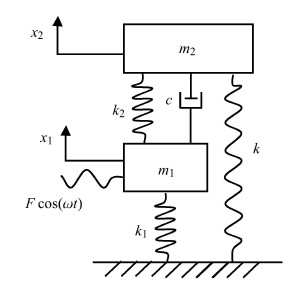
1 动力吸振器模型及参数优化图1所示为本文所提出的含有负刚度的动力吸振器模型,其中接地弹簧$k$为负刚度弹簧元件;$m_1$,$m_2 $,$k_1 $,$k_2 $分别表 示主系统和动力吸振器的质量和刚度系数;$c$表示吸振器阻尼系数;$\omega $表示激励力频率;$x_1 $,$x_2 $分别代表主系统和动力吸振器的位移.
|
图 1 动力吸振器模型 Fig. 1 The dynamical model of dynamic vibration absorber |
根据牛顿第二定律可以得到该系统的动力学方程为
| $ \left.\!\! m_1 \ddot {x}_1 + k_1 x_1 + k_2 (x_1 - x_2 ) + \\ \qquad c(\dot {x}_1 - \dot {x}_2 ) = F\cos (\omega t) \\ m_2 \ddot {x}_2 + k_2 (x_2 - x_1 ) + c(\dot {x}_2 - \dot {x}_1 ) + kx_2 = 0 \!\!\right\} $ | (1) |
引入以下参数
| $ \mu = \dfrac{m_2 }{m_1 }\,,\quad \omega _1 = \sqrt {\dfrac{k_1 }{m_1 }} \,,\quad \omega _2 = \sqrt {\dfrac{k_2 }{m_2 }} \\ \xi = \dfrac{c}{2m_2 \omega _2 }\,,\quad \alpha = \dfrac{k}{k_2 }\,,\quad f = \dfrac{F}{m_1 } $ |
式(1)可化为
| $\left. \begin{array}{l} {{\ddot x}_1} + 2\mu {\omega _2}\xi {{\dot x}_1} + (\omega _1^2 + \mu \omega _2^2){x_1} - \\ \qquad 2\mu {\omega _2}\xi {{\dot x}_2} - \mu \omega _2^2{x_2} = f\cos (\omega t)\\ {{\ddot x}_2} + 2{\omega _2}\xi {{\dot x}_2} + (\alpha \omega _2^2 + \omega _2^2){x_2} - \\ \qquad 2{\omega _2}\xi {{\dot x}_1} - \omega _2^2{x_1} = 0 \end{array} \right\}$ | (2) |
利用拉氏变换,式(2)可化为
| $ \left. \begin{array}{l} \left[ {{s^2} + 2\mu {\omega _2}\xi s + (\omega _1^2 + \mu \omega _2^2)} \right]{X_1} - \\ \qquad 2\mu ({\omega _2}\xi s + \omega _2^2){X_2} = f{{\rm{e}}^{{\rm{j}}\omega t}}\\ ({s^2} + 2{\omega _2}\xi s + \alpha \omega _2^2 + \omega _2^2){X_2} - \\ \qquad (2{\omega _2}\xi s + \omega _2^2){X_1} = 0 \end{array} \right\} $ | (3) |
设$X_1 = H({\rm j}\omega )_{x_1 } {\rm e}^{{\rm j}\omega t}$,$X_2 = H({\rm j}\omega )_{x_2 } {\rm e}^{{\rm j}\omega t}$,并令$s = {\rm j}\omega $,${\rm j}=\sqrt{-1}$则有
| $ \left. \begin{array}{l} {B_1}H{({\rm{j}}\omega )_{{x_1}}} - \mu {B_2}H{({\rm{j}}\omega )_{{x_2}}} = f\\ {B_3}H{({\rm{j}}\omega )_{{x_2}}} - {B_2}H{({\rm{j}}\omega )_{{x_1}}} = 0 \end{array} \right\} $ | (4) |
其中
| $ B_1 = - \omega ^2 + 2{\rm j}\mu \omega _2 \xi \omega + \omega _1^2 + \mu \omega _2^2 \\ B_2 = = 2{\rm j}\omega _2 \xi \omega + \omega _2^2 \\ B_3 = - \omega ^2 + 2{\rm j}\omega _2 \xi \omega + \alpha \omega _2^2 + \omega _2^2 $ |
这样可以得到
| $ \left.\!\! H({\rm j}\omega )_{x_1 } = \dfrac{B_3 f}{B_1 B_3 - \mu B_2^2 } \\ H({\rm j}\omega )_{x_2 } = \dfrac{B_1 f}{B_1 B_3 - \mu B_1 B_2 } \!\!\right\} $ | (5) |
因此主系统和动力吸振器振幅分别为
| $ \bar {X}_1 = \left| {H({\rm j}\omega )_{x_1 } } \right|\,, \quad \bar {X}_2 = \left| {H({\rm j}\omega )_{x_2 } } \right| $ | (6) |
为了便于推导,引入主系统振幅放大因子,定义如下
| $ A_1 = \left| {\dfrac{X_1 }{X_{st} }} \right| = \sqrt {\dfrac{A^2 + B^2\xi ^2}{C^2 + D^2\xi ^2}} $ | (7) |
其中
| $ A = \lambda ^2 - (1 + \alpha )\nu ^2\,,\ \ B = 2\lambda \nu \\ C = \lambda ^4 - (1 + \nu ^2 + \alpha \nu ^2 + \mu \nu ^2)\lambda ^2 + \\ \qquad (1 + \alpha + \alpha \mu \nu ^2)\nu ^2 \\ D = 2\lambda \nu \left[{1 + \alpha \mu \nu ^2 - (1 + \mu )\lambda ^2} \right] \\ \nu = \dfrac{\omega _2 }{\omega _1 }\,,\ \ \lambda = \dfrac{\omega }{\omega _1 }\,,\ \ X_{st} = F / k_1 $ |
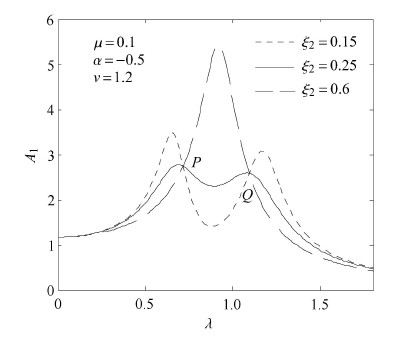
由式(7)通过简单推导,可以证明其归一化的幅频曲线都将通过2个独立于阻尼比的点,这2个点称作动力吸振器主 系统幅频曲线的固定点. 为了直观说明该结论图2给出了不同阻尼比情况下的归一化幅频曲线,从图2中可以清楚的看出曲线均通过$P$和$Q$两点.
|
图 2 不同阻尼比下归一化幅频响应曲线 Fig. 2 The normalized amplitude-frequency curves for different damping ratios |
根据固定点理论,为了使两固定点处纵坐标等值,只需使阻尼比趋于零和趋于无穷时的响应值相等,即$A/C=B/D$,则有
| $ [\lambda ^2 - \nu ^2(1 + \alpha )]\big / \big[\lambda ^4 - \lambda ^2(1 + \nu ^2 + \alpha \nu ^2 + \mu \nu ^2) + \\ \qquad \nu ^2(1 + \alpha + \alpha \mu \nu ^2)\big] = \\ \qquad \big[1 + \alpha \mu \nu ^2 - \lambda ^2(1 + \mu )\big]^{-1} $ | (8) |
化简得到
| $ (2 + \mu )\lambda ^4 - 2\lambda ^2\left[{1 + \nu ^2(1 + \alpha )(1 + \mu )} \right] + \\ \qquad 2\nu ^2(1 + \alpha ) + \alpha \mu \nu ^4(2 + \alpha ) = 0 $ | (9) |
假设式(9)存在2个根$\lambda _P $和$\lambda _Q $,则根据韦达定理可得
| $ \lambda _P^2 + \lambda _Q^2 = \dfrac{2\left[{1 + \nu ^2(1 + \alpha )(1 + \mu )} \right] }{2 + \mu } $ | (10) |
同时根据固定点理论可知,在最优频率比条件下$\lambda _P $和$\lambda _Q $两点处的响应值应该相等,即
| $ \dfrac{1}{1 + \alpha \mu \nu^2 - \lambda _P^2 (1 + \mu )} = \\ \qquad \dfrac{ - 1}{1 + \alpha \mu \nu ^2 - \lambda _Q^2 (1 + \mu )} $ | (11) |
从而可以得到
| $ \lambda _P^2 + \lambda _Q^2 = \dfrac{2 + 2\alpha \mu \nu ^2}{1 + \mu } $ | (12) |
联立式(10)和式(12)并化简可得到关于$\nu $的方程
| $ \left[{\alpha + (1 + \mu )^2} \right] \nu ^2 - 1 = 0 $ | (13) |
求解可以得到最优频率比为
| $ \nu _{\rm opt} = \sqrt {\dfrac{1}{\alpha + (1 + \mu )^2}} $ | (14) |
将最优频率比代入到方程(9)中可以求得2个固定点处横坐标
| $\lambda _P^2 = \dfrac{1 + \alpha + \mu - (1 + \mu )\sqrt {\dfrac{\mu }{2 + \mu }} }{\alpha + (1 + \mu )^2} $ | (15a) |
| $\lambda _Q^2 = \dfrac{1 + \alpha + \mu + (1 + \mu )\sqrt {\dfrac{\mu }{2 + \mu }} }{\alpha + (1 + \mu )^2} $ | (15b) |
在该优化条件下,可以得到2个固定点处响应值即纵坐标为
| $ \left. {A_1 } \right|_{(\lambda _P ,\lambda _Q )} = \dfrac{\alpha + (1 + \mu )^2}{(1 + \mu )^2}\sqrt {\dfrac{2 + \mu }{\mu }} $ | (16) |
通过上述求解所得到的最优频率比,使得2个固定点$P$和$Q$被调整到了相等的高度,即纵坐标相等. 根据固定点理论可 知,无论阻尼$\xi $取多少,所有的幅频曲线都会通过$P$和$Q$两点,即振幅最高点不会低于$P$和$Q$两点的纵坐标. 因此为了获得最优的减振效果,必须设法使$P$和$Q$两点成为幅频曲线的最高点. 根据极值条件,只有使曲线在2个固定点横坐标处的导数分别满足下式,才可使$P$和$Q$成为曲线的最高点
| $ \dfrac{\partial A_1^2 }{\partial \lambda ^2} = 0 $ | (17) |
为了求解该式,记
| $ A_1^2 = \frac{p}{q} = \frac{A^2 + B^2\xi ^2}{C^2 + D^2\xi ^2} $ | (18) |
则有
| $ \dfrac{\partial A_1^2 }{\partial \lambda ^2} = \dfrac{\partial }{\partial \lambda ^2}\left( {\dfrac{p}{q}} \right) = \dfrac{{p}'q - p{q}'}{q^2} = 0 $ | (19) |
其中${p}' = \partial p / \partial \lambda ^2$,${q}' = \partial q / \partial \lambda ^2$.
因此可以得到
| ${p}' = 2\lambda ^2 - 2\nu ^2(1 + \alpha - 2\xi ^2) $ | (20a) |
| $\begin{array}{l} q' = 4{\nu ^2}{\xi ^2}\left[{1 + \alpha \mu {\nu ^2} - 3\lambda (1 + \mu )} \right] \cdot \\ \;\;\;\;\;\;\left[{1 + \alpha \mu {\nu ^2} - \lambda (1 + \mu )} \right] + \\ \;\;\;\;\;\;2\left[{2\lambda - 1 - {\nu ^2}(1 + \alpha + \mu )} \right] \cdot \\ \;\;\;\;\;\;\left\{ {{\lambda ^2} - \lambda + \alpha \mu {\nu ^4} - {\nu ^2}\left[{(1 + \alpha )(\lambda - 1) + \mu \lambda } \right]} \right\} \end{array}$ | (20b) |
在最优频率比条件下可以得到
| $ \dfrac{p}{q} = \dfrac{1}{[1 + \alpha \mu \nu ^2 - \lambda ^2(1 + \mu )]^2} $ | (21) |
将最优频率比和两固定点横坐标$\lambda _P $,$\lambda _Q $分别代入,可得到
| $\xi _P^2 = \dfrac{\mu \left[{2\mu + 3 - \sqrt {\mu (2 + \mu )} } \right] }{4[(2 + \mu )(1 + \mu + \alpha ) - (1 + \mu )\sqrt {\mu (2 + \mu )}]} $ | (22a) |
| $\xi _Q^2 = \frac{{\mu \left[{2\mu + 3 + \sqrt {\mu (2 + \mu )} } \right]}}{{4[(2 + \mu )(1 + \mu + \alpha ) + (1 + \mu )\sqrt {\mu (2 + \mu )}]}}$ | (22b) |
上式说明,适当地选择$\xi $值时,仅仅能使曲线在$P$或者$Q$其中一点取得极值. 因此,为了得到较好的优化效果, 取$\xi_P^2 $和$\xi_Q^2 $的平均值作为最优阻尼比
| $ \xi _{\rm opt} = \sqrt {\dfrac{\mu (3 + 3\alpha + 3\mu + 2\alpha \mu )}{8(1 + \mu )^2 + 4(2 + \mu )[\alpha ^2 + 2\alpha (1 + \mu )]}} $ | (23) |
至此已经得到了最优频率比和最优阻尼比,但是由于本文模型中含有负刚度项,因此还必须对负刚度项进行优化. 根据负刚度 的特性,当振动控制元件承受预加荷载时,才能表现出负刚度性质. 而预加荷载会使系统产生预加位移,不恰当的负刚度值将会使得系统出现不稳定现象. 通过研究发现当预加荷载使系统产生位移等于固定点处响应值时,系统将处于稳定状态,而上文根据固定点理论得到的最优阻 尼比使得固定点值近似成为幅频曲线的最高点,因此可以认为此时系统取得最优控制效果,即令
| $ \left. {A_1 } \right|_{\lambda = 0} = \left. {A_1 } \right|_{(\lambda _P ,\lambda _Q )} $ | (24) |
也就是
| $ \sqrt {\dfrac{(1 + \alpha )^2\left[{\alpha + (1 + \mu )^2} \right]^2}{\left[{\alpha ^2 + (1 + \mu )^2 + \alpha (1 + \mu )(2 + \mu )} \right]^2}} = \\ \qquad \sqrt {\dfrac{(2 + \mu )\left[{\alpha + (1 + \mu )^2} \right]^2}{\mu (1 + \mu )^4}} $ | (25) |
求解该式得到所有可能的最优负刚度比值
| $\alpha _1 = - (1 + \mu )^2 $ | (26a) |
| $\alpha _{2,\;3} = - 1 - \mu \pm (1 + \mu )\sqrt { {\mu }/(2 + \mu)} $ | (26b) |
| $\alpha _{4,\;5} = - 1 - \mu (2 + \mu )\pm (1 + \mu )\sqrt {\mu (2 + \mu )} $ | (26c) |
然而,将几组可能最优值代入上述优化参数及主系统振幅放大因子中发现只有$\alpha_4 $能够在保证系统稳定状态下取得最优减振效果,而其他四组均会引起系统失稳,这显然是不符合要求的,因此选择$\alpha_4 $作为 最优负刚度比,即
| $ \alpha _{\rm opt} = - 1 - \mu (2 + \mu ) + (1 + \mu )\sqrt {\mu (2 + \mu )} $ | (27) |
为了验证前文得到结果的正确性,选取系统参数$\mu = 0.1$,$F = 1$\,kN,并根据式(14)、式(23)和式(27)得到$\nu = 1.408\,5$,$\xi = 0.356\,2$,$\alpha = - 0.705\,9$. 利用4阶龙格库塔法,选取计算时间800\,s,可以得到给定激励频率下系统响应的数 值解. 略去瞬态响应,取稳态解的最大值为响应幅值可以得到归一化的幅频曲线图,如图3中圆圈所示. 同时根据式(7),在图3中用实线画出了系统解析解的曲线. 从图中可以明显看出,与图2未优化结果相比,通过优化使2个固定点处于近似相等高度,并且使其处于峰值位置. 数值解与解析解吻合良好,也证明了求解过程和结果的正确性.

|
图 3 数值解和解析解比较 Fig. 3 The comparison between the amplitude-frequency curves of the analytical and numerical solution |
为了证明负刚度吸振器的减振效果,将该模型与两种传统的动力吸振器模型(即文献[2]和文献[9]中的模型)优化结果进行了对比,其 幅频曲线如图4所示. 从图中可以清楚看出,在相同初始参数(即质量比)条件下,负刚度动力吸振器能够大幅降低系统共振区振幅,同时也拓宽了减振频率.

|
图 4 与其他形式动力吸振器模型的对比 Fig. 4 The comparison with other DVAs |
由于在实际工程中系统所受的激励一般多为随机激励,因此本文进一步研究了随机激励下主系统的响应.
设该系统受均值为零功率谱密度为$S(\omega ) = S_0 $的白噪声激励,则负刚度模型与另外两种传统吸振器模型绝对位移响应的功率谱密度函数分别为
| $S_N (\omega ) = \left| {H_{Nx_1 } ({\rm j}\omega )} \right|^2S_0 $ | (28a) |
| $S_V (\omega ) = \left| {H_{Vx_1 } ({\rm j}\omega )} \right|^2S_0 $ | (28b) |
| $S_R (\omega ) = \left| {H_{Rx_1 } ({\rm j}\omega )} \right|^2S_0 $ | (28c) |
其中下脚标$N$,$V$和$R$分别代表负刚度模型、邓哈托的沃伊特模型和文献[9]中的接地型动力吸振器模型. 三类动力吸振器 模型的主系统位移均方值分别为
| $\begin{array}{l} \sigma _N^2 = \int_{ - \infty }^\infty {{S_N}(\omega )d\omega = } {S_0}\int_{ - \infty }^\infty {|{H_{N{x_1}}}({\rm{j}}\omega ){|^2}{\rm{d}}\omega = } \\ \;\;\;\;\;\;\;\frac{{\pi {S_0}}}{{2\omega _1^3\mu \xi \nu (1 + \alpha + \mu \alpha {\nu ^2}){{(\alpha {\nu ^2} - 1)}^2}}} \cdot \\ \;\;\;\;\;\;\{ (1 + \alpha )\{ {[{\nu ^2}(1 + \alpha ) - 1]^2} + \\ \;\;\;\;\;\;4{\nu ^2}{\xi ^2}\} + \mu {\nu ^2}[4{\xi ^2}(1 + \alpha ) + \\ \;\;\;\;\;\;2{\nu ^2}(1 + \alpha + 2\alpha {\xi ^2}) - 1] + {\mu ^2}{\nu ^4}(1 + 4\alpha {\xi ^2})\} \end{array}$ | (29a) |
| $\begin{array}{l} \sigma _V^2 = \int_{ - \infty }^\infty {{S_V}(\omega ){\rm{d}}\omega = {S_0}} \int_{ - \infty }^\infty {|{H_{V{x_1}}}({\rm{j}}\omega ){|^2}{\rm{d}}\omega = } \\ \;\;\;\;\;\;\frac{{\pi {S_0}}}{{2\omega _1^3\mu \xi \nu }}[1 + {\nu ^4}{(1 + \mu )^2} + \\ \;\;\;\;\;\;{\nu ^2}(4\mu {\xi ^2} + 4{\xi ^2} - \mu - 2)] \end{array}$ | (29b) |
| $ \begin{array}{l} \sigma _R^2 = \int_{ - \infty }^\infty {{S_R}(\omega ){\rm{d}}\omega = {S_0}} \int_{ - \infty }^\infty {|{H_{R{x_1}}}({\rm{j}}\omega ){|^2}{\rm{d}}\omega = } \\ \;\;\;\;\;\;\frac{{\pi {S_0}}}{{2\omega _1^3\mu \xi {\nu ^5}}} \cdot [1 + {\nu ^4} + (\mu + 4{\xi ^2} - 2)] \end{array} $ | (29c) |
假设三类系统中吸振器与主系统质量的比值均取$\mu =0.1$,则根据负刚度动力吸振器优化结果以及现有文献[3, 4, 5, 6, 7, 8, 9]中的优化公式,可以得到3种情况下主系统响应的均方值分别为
| $\sigma _N^2 = \dfrac{3.302\pi S_0 }{\omega _1^2 } $ | (30a) |
| $\sigma _V^2 = \dfrac{6.401\pi S_0 }{\omega _1^2 } $ | (30b) |
| $\sigma _R^2 = \dfrac{5.780\pi S_0 }{\omega _1^2 } $ | (30c) |
可以发现,当主系统参数相同时,负刚度模型在随机激励下仍然具有较好的减振效果.
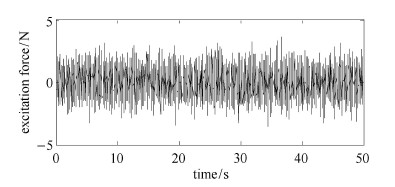
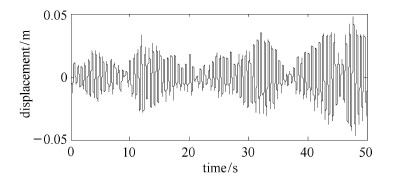
同时为了更真实地模拟工程实际,本文构建了50\,s均值为0方差为1的随机力激励,其时间历程如图5所示. 选取系统参数如下,主系统质量$m_1 =1$\,kg,主系统刚度$k_{1} =100$\,N/m,吸振器质量$m_2 =0.1$\,kg,其余最优参数根据文献[3, 4, 5, 6, 7, 8, 9]及上述推导得到. 为了验证负刚度吸振器模型在减振方面的优势,图6给出了不含吸振器时主系统时间位移响应,图7 $\sim$图9给出了主系统在附加3种不同吸 振器时其时间位移响应. 由于主系统位移方差往往与系统振动能量相关,因此在表1中总结了主系统位移方差及其衰减比.
|
图 5 随机激励时间历程 Fig. 5 The time history of the random excitation |
|
图 6 不含吸振器的主系统时间历程 Fig. 6 The time history of the primary system without DVA |
|
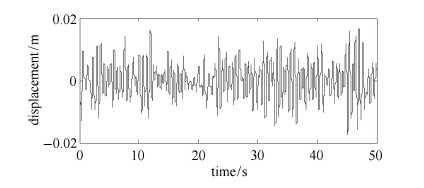
图 7 含沃伊特型吸振器的主系统时间历程 Fig. 7 The time history of the primary system with Voigt DVA |
|
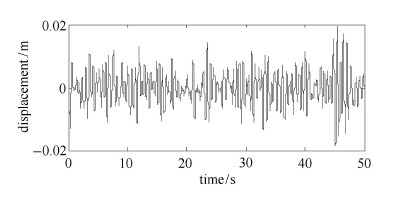
图 8 含接地型吸振器的主系统时间历程 Fig. 8 The time history of the primary system with the DVA by Ren |
|
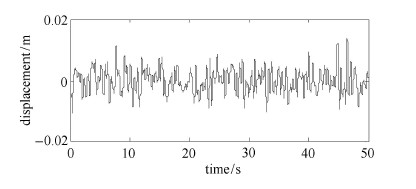
图 9 含负刚度吸振器的主系统时间历程 Fig. 9 The time history of the primary system with the DVA in this paper |
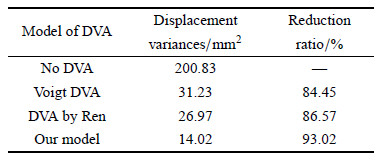
| 表 1 主系统位移方差及衰减率 Table 1 The variances and reduction ratios of the primary system |
从图6 $\sim$图9以及表1中可以明显看出,负刚度吸振器与另外2种传统形式动力吸振器相比取得了更好的减振效果,能够在整个频 率范围内大幅降低主系统振动能量.
3 结 论提出了一种含有负刚度元件的改进动力吸振器模型,并对其参数优化过程进行了详细研究. 通过固定点理论得到了负刚度吸振器 的最优频率比和最优阻尼比,同时根据负刚度弹性元件的特性通过使静位移与固定点相等的思想得到了在保证系统稳定情况下的最优负刚度比. 数值解与解析解的对比证明了求解过程和结果的正确性. 与2种传统动力吸振器模型的对比说明负刚度模型能够大幅降低系统响应的振幅并且拓宽了减振频带. 最后对随机激励情况下3种模型的减振效果分别进行了解析研究和数值验证,均说明负刚度模型具有较大优势,这些结果为以后提 出设计新型动力吸振器模型提供了参考和依据.
| [1] | Frahm H. Device for damping vibrations of bodies. U.S. Patent 989, 958. 1911 |
| [2] | Ormondroyd J, Den Hartog JP. The theory of the dynamic vibration absorber. Journal of Applied Mechanics, 1928, 50: 9-22 |
| [3] | Hahnkamm E. The damping of the foundation vibrations at varying excitation frequency. Master of Architecture, 1932, 4: 192-201 |
| [4] | Brock JE. A note on the damped vibration absorber. Journal of Applied Mechanics, 1946, 13(4): A-284 |
| [5] | Den Hartog JP. Mechanical vibrations. New York: McGraw-Hall Book Company 1947 |
| [6] | 倪振华. 振动力学. 西安:西安交通大学出版社,1989 (Ni Zhenhua. Vibration Mechanics. Xi'an: Xi'an Jiaotong University Press, 1989 (in Chinese)) |
| [7] | Nishihara O, Asami T. Close-form solutions to the exact optimizations of dynamic vibration absorber (minimizations of the maximum amplitude magnification factors). Journal of Vibration and Acoustics, 2002, 124: 576-582. |
| [8] | Asami T, Nishihara O, Baz AM. Analytical solutions to H_∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems. Journal of Vibration and Acoustics, 2002, 124(2): 284-295. |
| [9] | Ren MZ. A variant design of the dynamic vibration absorber. Journal of Sound and Vibration, 2001, 245(4): 762-770. |
| [10] | Liu KF, Liu J. The damped dynamic vibration absorbers: revisited and new result. Journal of Sound and Vibration, 2005, 284(3): 1181-1189 |
| [11] | 赵艳影, 李昌爱. 时滞反馈控制扭转振动系统的振动. 物理学报,2011, 60(10): 114305 (Zhao Yanying, Li Chang'ai. The delayed feedback control to suppress the vibration in a torsional vibrating system. Acta Physica Sinica, 2011, 60(10): 114305 (in Chinese)) |
| [12] | Zhao YY, Xu J. Effects of delayed feedback control on nonlinear vibration absorber system. Journal of Sound and Vibration, 2007, 308: 212-230. |
| [13] | Shen YJ, Wang L, Yang SP, et al. Nonlinear dynamical analysis and parameters optimization of four semi-active on-off dynamic vibration absorbers. Journal of Vibration and Control, 2013, 19(1): 143-160. |
| [14] | Shen YJ, Ahmadian M. Nonlinear dynamical analysis on four semi-active dynamic vibration absorbers with time delay. Shock and Vibration, 2013, 20(4): 649-663. |
| [15] | Platus DL. Negative-stiffness-mechanism vibration isolation systems. International Society for Optics and Photonics, 1992: 44-54 |
| [16] | 彭献, 陈树年, 宋福磐. 负刚度的工作原理及应用初探. 湖南大学学报, 1992, 19(4): 89-94 (Peng Xian, Chen Shunian, Song Fupan. Research on theory of negative stiffness and its application. Journal of Hunan University , 1992, 19(4): 89-94 (in Chinese)) |
| [17] | 彭解华, 陈树年. 正负刚度并联结构的稳定性及应用研究. 振动、测试与诊断. 1995, 15(2): 14-18 (Peng Jiehua, Chen Shunian. The stability and application of a structure with positive stiffness element and negative stiffness element. Journal of Vibration, Measurement & Diagnosis, 1995, 15(2): 14-18 (in Chinese)) |
| [18] | Mizuno T. Proposal of a vibration isolation system using zero-power magnetic suspension. In: Proceedings of the Asia-Pacific Vibration Conference, Hangzhou, China, 2001, 2: 423-427 |
| [19] | Mizuno T. Vibration isolation system using zero-power magnetic suspension. In: Proc. of the 15th Triennial World Congress, Barcelona, Spain, 2002: 955-960 |
| [20] | Mizuno T, Takemori Y. A transfer-function approach to the analysis and design of zero-power controllers for magnetic suspension systems. Electrical Engineering in Japan, 2002, 141(2): 67-75. |
| [21] | Mizuno T, Takasaki M, Kishita D, et al. Vibration isolation system combining zero-power magnetic suspension with springs. Control Engineering Practice, 2007, 15(2): 187-196. |
| [22] | Mizuno T, Toumiya T, Takasaki M. Vibration isolation system using negative stiffness. JSME International Journal Series C, 2003, 46(3): 807-812. |
| [23] | Park ST, Luu TT. Techniques for optimizing parameters of negative stiffness. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2007, 221(5): 505-510. |
| [24] | 纪晗, 熊世树, 袁涌. 基于负刚度原理的结构隔振效果分析. 华中科技大学学报(自然科学版), 2010, 38(2): 76-79 (Ji Han, Xiong Shishu, Yuan Yong. Analyzing vibration isolation effect of structures using negative stiffness principle. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2010, 38(2): 76-79 (in Chinese)) |
| [25] | Acar MA, Yilmaz C. Design of an adaptive-passive dynamic vibration absorber composed of a string-mass system equipped with negative stiffness tension adjusting mechanism. Journal of Sound and Vibration, 2013, 332(2): 231-245. |
2. Department of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China
 2015, Vol. 47
2015, Vol. 47