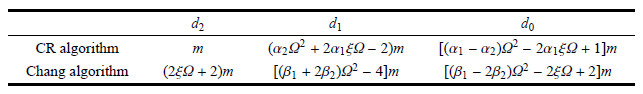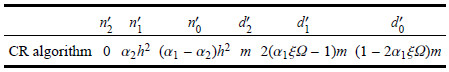结构动力学分析需要求解微分运动方程,其中直接积分法以适用性广、编程方便而被普遍使用. 直接积分法分为显式算法和隐式算法两类[1, 2, 3, 4]. 如果结构下一时刻的位移响应可由当前与之前时刻的位移、速度、加速度响应确定,则算法是显式的,否则是隐式算法. 而且,直接积分算法还可分为条件稳定和无条件稳定两类[1, 2, 3, 4]. 显式算法通常是条件稳定的,即积分步长小于某一特定值时才不会产生自由振动数值解的无界增大,如中心差分法,该类算法通常用于求解高频振动问题. 条件稳定的显式算法采用较小的时间步长,其计算步数较多,但无需迭代运算,从而每步效率高,总的计算花费较少. 隐式算法通常是无条件稳定的,即取任意时间步长所得到的解都不会无界地增长,如纽马克(Newmark)常平均加速度法、HHT-$\alpha $法、CH-$\alpha $法[5]等,隐式算法一般用于求解低频振动问题. 一般而言,条件稳定算法的时间步长需根据稳定性条件来选取,选取的时间步长是其上限,且在满足上限的前提下,可以根据精度要求选取. 事实上,条件稳定算法的积分步长与结构的最高固有频率成反比,对于大规模多自由度系统,由于其高阶频率较大,从而导致算法需选取很小的步长,这样使得计算时间增加. 无条件稳定算法可根据感兴趣的高阶振型的精度需求选取较大的步长,同时可获得高精度解. 所以,对于大规模多自由度系统,采用无条件稳定算法,可显著减小计算代价,提高计算效率.
尽管许多隐式算法是无条件稳定的,但是最近由于结构拟动力试验与实时子结构试验进行快速、精确动力学计算的需要,一些无条件稳定的显式算法倍受青睐[6, 7, 8, 9]. 例如,常氏(Chang)提出了两种无条件稳定的显式算法[6, 7],使得显式算法的稳定性由传统的条件稳定转变为无条件稳定,但对于算法中系数的取值是根据经验得到的,并没有给出推导过程. 而从离散控制论的角度,文献[8]提出了无条件稳定的CR显式算法,算法系数经过严格的推导给出,并分析了常氏算法[6]与CR算法以及纽马克常平均加速度算法之间的联系. 最近,文献[9]同样采用离散控制理论,结合CH-$\alpha $算法和CR算法,建立了无条件稳定的KR-$\alpha $显式算法.
离散控制理论作为结构动力学算法设计的一种新方法,使得算法的设计与推导过程更加理性和方便. 本文基于离散控制理论的基本原理,采用CR算法和常氏算法的位移、速度递推式,根据Z变换得到的传递函数的极点条件推导了递推格式系数的具体表达式,并引入了一个可以控制算法精度的变量$s$,从而设计了一种新的无条件稳定显式算法. 而且,从理论上分析了新算法的线性稳定性、精度和超调性质,并确定了非线性刚度硬化系统的稳定性界限. 最后,几个线性和非线性动力学多自由度系统算例展示了新算法的有效性与精度可控特性.
1 显式算法的设计方法这里以线弹性单自由度(SDOF)系统为例设计一种新的无条件稳定显式算法. 在$i$时刻的SDOF系统运动方程可表达为
| $ \label{eq1} m\ddot{x}_i+c\dot{x}_i+kx_i=f_i $ | (1) |
其中,$m$,$c$,$k$分别为系统的质量、阻尼和刚度,$\ddot{x}_i $,$\dot{x}_i $,$x_i $,$f_i $ 分别为$i$时刻的加速度、速度、位移和外载荷. 先介绍两类显式算法: CR算法和常氏算法. CR算法速度、位移的递推式[8]如下所示
| $ \label{eq2} \dot{x}_{i + 1} = \dot{x}_i + \alpha _1 h\ddot{x}_i,\ \ x_{i + 1} = x_i + h\dot{x}_i + \alpha _2 h^2 \ddot{x}_i $ | (2) |
其中
| $ \label{eq3} \alpha _1 = \alpha _2 = 4 / (\varOmega ^2 + 4\xi \varOmega + 4 ) $ | (3) |
式中,$\varOmega =h\omega$,$h$为积分步长,{$\omega $}为系统的固有频率,$\xi =c/2m$为系统的阻尼比. 常氏两种算法的位移、速度递推式为
| $ \left.\begin{array}{l} \dot{x}_{i + 1} = \dot{x}_i + 0.5h ( \ddot{x}_i + \ddot{x}_{i + 1} )\\ x_{i + 1} = x_i + \beta _1 h \dot{x}_i + \beta _2 h^2 \ddot{x}_i \end{array}\right\} $ | (4) |
式中,系数$\beta _{1}$和$\beta _{2}$的取值不同,分别对应两种不同的常氏算法. 对于常氏算法一[6]
| $ \left.\begin{array}{l} \beta _1 = 4(1 + \xi \varOmega ) / (\varOmega ^2 + 4\xi \varOmega + 4)\\ \beta _2 = 2 / (\varOmega ^2 + 4\xi \varOmega + 4) \end{array}\right\} $ | (5) |
而对于常氏算法二[7]
| $ \left.\begin{array}{l} \beta _1 = 2(1 + \xi \varOmega ) / (\varOmega ^2 + 2\xi \varOmega + 2) \\ \beta _2 = (1 - \xi \varOmega ) / (\varOmega ^2 + 2\xi \varOmega + 2) \end{array}\right\} $ | (6) |
CR算法递推式中的系数是通过离散控制论推导出的,而常氏算法中的系数是依据经验试凑得到的.
实际上,结构动力学直接积分算法的稳定性、振幅衰减率、周期延长率可以通过两类方法进行分析. 第1类是通过求单自由度无阻尼系统转换矩阵的特征值进行分析[1],即$ X_{i+1}={AX}_i$,$ X_{i}=\left\{ {x_i ,h\dot{x}_i ,h^2\ddot{x}_i} \right\}^{\rm T}$,$ A$称为转换矩阵. $ A$的特征值$\lambda $满足
| $ \label{eq7} \lambda^3-2A_1\lambda^2+A_2\lambda-A_3=0 $ | (7) |
其中,$A_{1}$为$A$的迹的一半,$A_{2}$为$A$的二阶主子式之和,$A_{3}$为$A$的行列式值.
第2类是通过离散控制理论建立直接积分算法的传递函数, 从而求得算法相应的开环或闭环系统的极点进行分析[8, 9]. 离散控制理论中系统的极点与转换矩阵$ A$的特征值是等价的. 相比于第1类方法转换矩阵与特征值的求解,利用离散控制理论获得系统的传递函数和极点简单方便, 尤其是对于隐式算法更能体现出这一优点,因此本文采用第2类方法进行算法分析.
传递函数$G(z)$定义为: 系统输出量(位移响应)与输入量(外载荷)的$Z$变换之比. 利用$Z$变换的定义及性质[10]得到$i$时刻、$i+1$时刻的加速度、速度、位移、外载荷的$Z$变换
| $ \label{eq8} \left.\begin{array}{l} Z(\ddot{x}_i)=\ddot{X}(z),\ \ Z(\dot{x}_i)=\dot{X}(z)\\ Z({x}_i)={X}(z),\ \ Z(f_i)=F(z) \\ Z(\ddot{x}_{i+1})=z\ddot{X}(z),\ \ Z(\dot{x}_{i+1})=z\dot{X}(z) \\ Z({x}_{i+1})=z{X}(z),\ \ Z({f}_{i+1})=zF(z) \end{array}\right\} $ | (8) |
式中,$F(z)$和$X(z)$分别为系统输入量、输出量的$Z$变换. 将式(8)代入式(1),式(2)和式(4), 可分别得到CR算法、常氏算法递推公式对应开环系统的传递函数
| $ \label{eq9} G(z) = \frac{X(z)}{F(z)} = \frac{n_2 z^2 + n_1 z + n_0 }{d_2 z^2 + d_1 z + d_0 } $ | (9) |
其中的系数$d_{2}$,$d_{1}$,$d_0$见表1[8]. 由控制理论可知,传递函数$G(z)$的分母为零对应的方程叫做系统的特征方程,即$d_{2}z^{2}+d_{1}z+d_0=0$,特征方程的根叫做系统的极点$p_{1,2}$. 分子为零对应的方程$n_{2}z^{2}+n_{1}z+n_0=0$的根叫做系统的零点$z_{1,2}$.
| 表 1 开环系统传递函数的系数 Table 1 Coefficients of transfer function of open-loop system |
由于算法的稳定性、振幅衰减率和周期延长率都与其转换矩阵的特征值相关,如果两个算法具有相同的特征值,即相同的传递函数极点,则这两个算法就具有相同的稳定性、振幅衰减率和周期延长率[9]. 注意到CR算法、常氏算法一以及纽马克常平均加速度算法具有相同的极点[8],它们都是无条件稳定算法,且该极点为
| $ p_{1,2} = \frac{4 - \varOmega ^2\pm 4\varOmega \sqrt {\xi ^2 - 1} }{\varOmega^2 + 4\xi \varOmega + 4} $ |
由于常氏算法二相比于常氏算法一,非线性稳定性区间增大,因此本文算法设计时利用CR算法的速度、位移递推式(2),并使之和常氏算法二具有相同的极点
| $ p_{1,2} = \frac{2\pm \varOmega \sqrt {4\xi ^2 - 4 - \varOmega ^2} }{\varOmega ^2 + 2\xi \varOmega + 2} $ |
为了保证基于CR算法递推式的新算法与常氏算法二具有相同的极点,两者特征方程的系数需满足以下关系式
| $ \label{eq10} d_1^{{\rm CR}}= d_{\rm 1}^{{\rm Chang}} d_2^{{\rm CR}}/d_{\rm 2}^{{\rm Chang}}, \ \ d_0^{{\rm CR}}=d_0^{{\rm Chang}} d_2^{{\rm CR}}/d_{\rm 2}^{{\rm Chang}} $ | (10) |
将式(6)代入表1,根据式(10)可求得系数$\alpha_{1}$和$\alpha_{2}$
| $ \label{eq11} \alpha _1 = \alpha _2 = 2 / (\varOmega ^2 + 2\xi \varOmega + 2 ) $ | (11) |
比较式(3)和式(11)可见系数$\alpha_{1}$和$\alpha _{2}$不同之处在于常系数,前者为4,后者为2. 于是,引入一个变量$s$,得到广义的系数$\alpha_{1}$和$\alpha_{2}$
| $ \label{eq12} \alpha _1 = \alpha _2 = s / (\varOmega ^2 + s\xi \varOmega + s) $ | (12) |
这样就获得了一种新的结构动力学直接积分显式算法,即速度、位移递推公式采用式(2),其中的系数$\alpha_{1}$, $\alpha_{2}$如式(12)所示,而平衡方程仍采用式(1). 当$s=4$时,系数$\alpha_{1}$,$\alpha_{2}$对应式(3),即CR算法; $s=2$时,系数对应式(11). 下节将从理论上分析引入变量$s$的新算法的稳定性、精度、超调以及非线性稳定性等.
2 新显式算法性能分析 2.1 线性系统的稳定性分析稳定性分析通常以单自由度无阻尼自由振动系统为对象. 离散控制理论采用开环系统分析线性系统的稳定性[10],开环系统的结构图如图1所示.
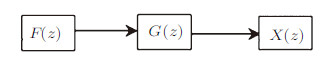
|
图 1 开环系统的结构图 Fig. 1 Block diagram of open-loop system |
图1中$G(z)$为开环系统的传递函数,即式(9)所示. 上节已指出,离散控制理论中单自由度系统直接积分算法传递函数的极点与其转换矩阵的特征值是等价的. 若转换矩阵的谱半径$\rho\leqslant 1$,则算法是稳定的. 本文含变量$s$的新显式算法对应传递函数的极点如下式所示
| $\begin{array}{l} {p_{1,2}} = \frac{{2{\Omega ^2}/s - {\Omega ^2} + 2 \pm \Omega \sqrt {{\Omega ^2} - 4 - 4{\Omega ^2}/s} }}{{2 + 2{\Omega ^2}/s}} = \\ \qquad \;P \pm Qi \end{array}$ | (13) |
其中
| $ \label{eq14} P = \frac{2\varOmega ^2 / s - \varOmega ^2 + 2}{2(1 + \varOmega ^2 / s)},\ \ Q = \frac{\varOmega \sqrt {4\varOmega ^2 / s - \varOmega ^2 + 4} }{2(1 + \varOmega ^2 / s)} $ | (14) |
一般而言,$h/T_{n} \leqslant 1/20$[1],即$\varOmega \leqslant 0.1\pi $. 当$s>0$时,$4\varOmega ^{2}/s-\varOmega^{2}+4>0$. 从而,$P^{2}+Q^{2}=1$,所以该极点相应的谱半径恒等于1,即: $\rho = \max (\left| {p_i } \right|) = 1$. 因此,$s>0$时,本文算法是无条件稳定的.
2.2 非线性稳定性分析离散控制理论采用闭环系统分析非线性系统的稳定性[11]. 直接积分算法闭环系统的结构图如图2所示.
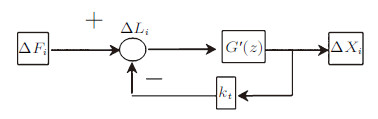
|
图 2 闭环系统的结构图 Fig. 2 Block diagram of closed-loop system |
将单自由度系统运动方程式(1)写成增量形式 $m\Delta\ddot{x}_i+c\Delta\dot{x}_i=\Delta f_i-\Delta r_i=\Delta L_i$. 其中$\Delta r_{i}=k_{t}\Delta x_{i}$,$k_{t}$为$i$+1时刻非线性系统的切线刚度,其每一时刻都会发生变化.
闭环系统的闭环传递函数可写为
| $ \label{eq15} G(z)=\frac{\Delta X(z)}{\Delta F(z)}=\frac{G'(z)}{1+k_tG'(z)} $ | (15) |
其中
| $ \label{eq16} {G}'(z) = \frac{X(Z)}{L(Z)} = \frac{\Delta X(z)}{\Delta L(z)} = \frac{{n}'_2 z^2 + n_1 ^\prime z + {n}'_0 }{d_2 ^\prime z^2 + d_1 ^\prime z + {d}'_0 } $ | (16) |
$G'(z)$为闭环系统的开环传递函数,其极点为$p'_{1,2}$,零点为$z'_{1,2}$. 式(15)中$G(z)$分母为零对应的特征方程为
| $ \label{eq17} 1 + k_t {G}'(z) = 1 + k_t \frac{{n}'_2 z^2 + n_1 ^\prime z + {n}'_0 }{d_2 ^\prime z^2 + d_1 ^\prime z + {d}'_0 } = 0 $ | (17) |
式(17)的根叫做闭环系统闭环传递函数的极点,记为$p_{1,2}^{\rm nl}$. 对于新算法, 式(16)和式(17)的具体系数见表2[11].
| 表 2 闭环系统传递函数的系数 Table 2 Coefficients of transfer function of closed-loop system |
当闭环系统的$k_{t}=k$时,即对应于线性系统,式(15)可写为
| $ \label{eq18} G(z) = \frac{{G}'(z)}{1 + k{G}'(z)} $ | (18) |
式(18)的极点记为$p_{1,2}^{\rm l}$,即线性系统对应的极点. 将表2中的系数代入式(18),并将表1中的系数代入式(9),经简单运算可知相应的式(18)与式(9)是完全一样的. 因此,线性问题可以采用开环或闭环系统等价地表示,且二者的传递函数相同.
考虑工程中常见的两种非线性问题,即刚度软化($0 < k_{t} < k)$和刚度硬化($k_{t}>k)$问题. 把$k_{t}$作为变量,$k_{t}$从0变化到$\infty$,闭环系统特征方程(17)的根$p_{1,2}^{\rm nl}$在平面上移动的轨迹称为根轨迹图. 当$k_{t}=0$时,由式(17)可知,$p_{1,2}^{\rm nl}= p' _{1,2}$;$k_{t}=\infty$时,$p_{1,2}^{\rm nl}=z'_{1,2}$; $k_{t}=k$时,$p_{1,2}^{\rm nl}=p_{1,2}^{\rm l}$. 非线性刚度软化问题的根轨迹起始于$p'_{1,2}$终止于线性根$p_{1,2}^{\rm l}$,而非线性刚度硬化问题的根轨迹起始于$p_{1,2}^{\rm l}$终止于$z'_{1,2}$. MATLAB控制工具箱命令能够轻易地画出根轨迹图,从而可方便地判断算法的非线性稳定性. 若根轨迹位于单位圆内或圆上,则该算法求解非线性问题是稳定的. 取$s=10$,$m=1$,$h=0.1$ s,$\xi =0$,$\omega =2\pi$,利用表2中的系数,可画出新算法特征方程的根轨迹图(图3).
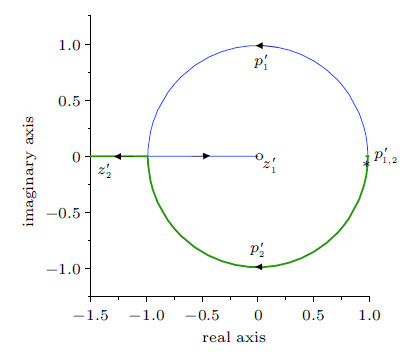
|
图 3 新算法特征方程的根轨迹 Fig. 3 Root-locus of characteristic equation of new algorithm |
由图3可知,新算法特征方程有2条根轨迹,第1条根轨迹起始于$p'_{1}=1$终止于$z'_{1}=0$, 第2条根轨迹起始于$p'_{2}=1$终止于$z'_{2}=\infty$,2条根轨迹分别经过$p_{1}^{\rm l}$,$p_{2}^{\rm l}$. 对于非线性刚度软化问题,根轨迹起始于$p'_{1,2}$终止于$p_{1,2}^{\rm l}$,且$p_{1,2}^{\rm l}$位于单位圆上, 所以新算法对于刚度软化问题是无条件稳定的.
对于非线性刚度硬化问题,根轨迹起始于$p_{1,2}^{\rm l}$终止于$z'_{1,2}$,其一条根轨迹在$z= -1$处穿越单位圆. 因 此将$z=-1$代入式(17),可得到非线性硬化问题的稳定性区间
| $ k_t \leqslant 4k / s + 4m / h^2\ \ {\rm or}\ \ k_t / k \leqslant 4 / s + 4 / \varOmega ^2 $ | (19) |
其中$k$为初始刚度. 式(19)表明,非线性刚度硬化问题的稳定性区间随着$s$的增大而减小. 需要注意的是,当$s=4$时, 由(19)可 知稳定性区间为 $k_{t}\leqslant k+4m/h^{2}$, 其与文献[11]分析的CR算法的非线性硬化问题的稳定性区间完全一致.
由上面的分析可知,利用开环、闭环系统分别进行直接积分显式算法的线性和非线性稳定性分析, 都对应有各自的传递函数和特征 方程,然后利用MATLAB控制工具箱可以方便地画出传递函数的根轨迹图. 如果特征方程的根的模小于等于1,即根位于单位圆内或单位圆上,则算法是稳定的.
2.5 精度分析
| $ \label{eq19} \tau = h^{{\rm - }2}[x(i + 1) - 2A_1 x(i) + A_2 x(i - 1)] $ | (20) |
将$x(i+1)$,$x(i-1)$在$i$时刻泰勒展开,并利用$i$时刻的平衡方程$m\ddot{x}_i + c\dot{x}_i + kx_i = 0$. 经计算, 可得新算法的截断误差为
| $ \label{eq20} \tau = \left( - \frac{\omega ^4}{s}x_i - \frac{2\xi \omega ^3}{s}\dot{x_i} + \frac{s\xi \omega }{3}{x}"'_i + \frac{1}{12}{x}""_i \right)h^2 \nonumber\\ +\; o(h^3) $ | (20) |
由式(21)可知,$h \to 0$时,$\tau\to0$. 所以$s>0$时,新算法具有二阶精度,或者说新算法具有二次收敛率.
另一方面,一个直接积分算法的精度还可以由振幅衰减率$AD$(或数值耗散)和周期延长率$PE$(或数值色散)这两方面予以衡量. 新显式算法对应开环系统的极点可表示成
| $ \label{eq21} p_{1,2} = P\pm Q{\rm i} = \exp \left[\bar {\varOmega }\left( - \bar {\xi }\pm {\rm i}\sqrt {1 - \bar {\xi }^2} \right)\right] $ | (22) |
其中,$P$,$Q$如式(14)所示,$\bar {\xi } = - \ln (P^2 + Q^2) / (2\bar {\varOmega })$,$\bar {\varOmega } = \tan ^{ - 1}(Q / P) / \sqrt {1 - \bar {\xi }^2} $.
而且,振幅衰减率$AD$和周期延长率$PE$的定义[8, 15]如下
| $ \label{eq22} AD = 1 - \exp ( - 2\pi \bar {\xi }),\ \ PE = \varOmega / \bar {\varOmega } - 1 $ | (23) |
由于$P^{2}+Q^{2}=1$,$\bar {\xi } = 0$,所以$AD=0$. $PE$是变量$s$和$\varOmega $的函数,当$s=2\sim20$时,画出新算法$PE$随$h/T_{n}$的变化图,如图4所示. 其中,NCAA为纽马克常平均加速度算法,$T_{n}$为系统的最小自振周期.
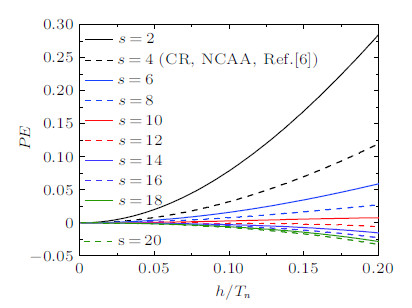
|
图 4 不同的s值对应的PE值 Fig. 4 PE values corresponding to different s |
图4表明,周期延长率$PE$与$s$的变化密切相关,随着$s$的增大,$PE$的绝对值先减小后增大. $s$在$10\sim12$之间取值,$PE$很小,因而新算法的精度较高. 图5表示$s$从10变化到12时的周期延长率,可以更清楚地观察到$PE$的变化情况,且周期延长率$PE$的绝对值小于0.008,显著小于纽马克常平均加速度算法、CR算法和常氏算法一的$PE$值(其最大值约为0.12). 值得说明的是,文献[8]曾指出: 选择不同的极点可减小CR算法的$PE$值,但将破坏算法的无条件稳定性. 然而,本文提出的新显式算法,既可以维持无条件稳定性,又能减小周期延长率$PE$,从而提高算法精度.
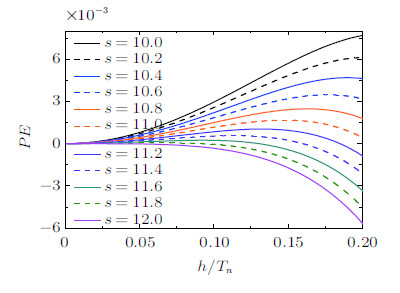
|
图 5 $s$取$10\sim 12$时$PE$值 Fig. 5 $PE$ values corresponding to $s$ with $10\sim 12$ |
对于非零初始条件的SDOF系统,可能会由于步长较大而在计算初始阶段出现系统响应被放大的现象,称为超调. 研究一个直接积分算法的超调特性,通常分析系统在无外载荷、初始位移和速度非零的情况下, 位移和速度在第一个时间步随$\varOmega$的变化趋势[13, 14].
新算法第一个时间步的位移和速度表达如下
| $ \label{eq23} x_1 = c_{11} x_0 + c_{12} v_0 h,\ \ v_1 = c_{21} x_0 / h + c_{22} v_0 $ | (24) |
经计算
| $ c_{11} = 1 - \dfrac{\varOmega ^2}{\varOmega ^2 / s + \varOmega + 1} ,\ \ c_{12} = 1 - \frac{2\varOmega \xi}{\varOmega ^2 / s + \varOmega + 1}\\ c_{21} = - \frac{\varOmega^2}{\varOmega ^2 / s + \varOmega + 1},\ \ c_{22} = 1 - \frac{2\varOmega \xi }{\varOmega ^2 / s + \varOmega + 1} $ |
上述分子中$\varOmega $的最高次数都等于分母中$\varOmega$的最高次数,这样位移、速度在第一时间步不会出现位移和 速度响应的放大. 因此$s>0$时,本文的显式算法是无超调的.
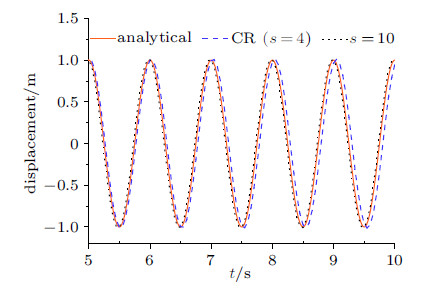
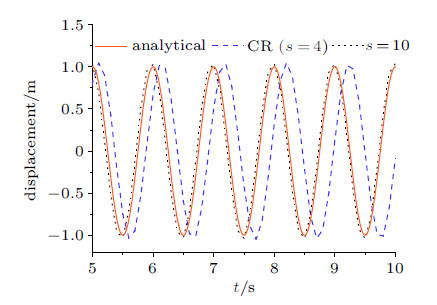
3 算例分析算例1 单自由度无阻尼自由振动系统的运动方程为$\ddot{x} + \omega ^2x= 0$,其中自振频率$\omega =2\pi $,初始位移为1、初始速度为0. 其位移响应的解析解为$x(t)=\cos(2\pi t)$[15]. 分别取步长$h=0.01$ s,0.05 s,0.1 s,将CR算法($s=4$)、新算法($s=10$)计算结果与解析解对比,如图6 $\sim $图8所示.
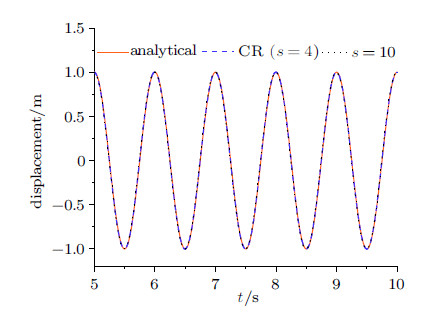
|
图 6 步长$h=0.01$ s时位移响应时程曲线 Fig. 6 Time histories of displacement response with $h=0.01$ s |
|
图 7 $h=0.05$ s时位移响应时程曲线 Fig. 7 Time histories of displacement response with $h=0.05$ s |
|
图 8 $h=0.1$ s时位移响应时程曲线 Fig. 8 Time histories of displacement response with $h=0.1$ s |
观察5$\sim $10 s位移时程曲线的对比图,随着步长$h$的增大,相比于$s=10$求得的结果,CR算法逐渐表现出了周期延长, 也 就是相位的偏移,在图8中最明显,这与图4中$PE$值随$s$的变化是一致的, 即$s=10$求得的位移响应的精度高于$s=4$时的精度.
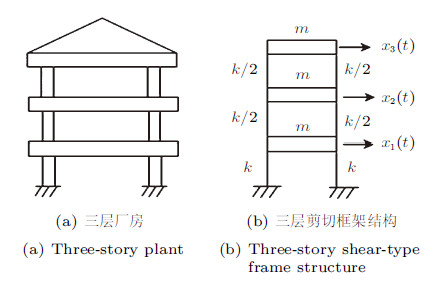
算例2 如图9(a)所示的3层厂房,可简化为9(b)所示的三自由度剪切结构. 瑞利阻尼$ C=\alpha M+\beta K$,系统初始静止. $k=1$,$m=1$,$\alpha =0.015$,$\beta =0.02$,$T=3.25$ s (结构的最小自振周期). 求结构底部在水平正弦加速度sin$t$作用下的顶部位移响应.
|
图 9 Fig. 9 |
分别取步长$h=T/100$,$T/20$,$T/10$,将本文算法($s=10$)与CR ($s=4$)算法、纽马克常平均加速度算法 ($\gamma=0.5$,$\beta =0.25$)和CH-$\alpha$算法($\rho =1$,无数值阻尼)得到的顶层位移结果进行比较,如表3所示. 新算法$s=10$得到的位移响应精度高于CR算法($s=4$). 在以上算 法中, $s=10$对应的算法求得的位移响应最大相对误差要小于其他无条件稳定的二阶精 度算法(CR算法、纽马克常平均加速度算法和CH-$\alpha$算法),其精度最高.
| 表 3 不同算法求解算例2顶层位移响应的比较 Table 3 Comparison of displacement responses of top story for Example 2 solved by different algorithms |
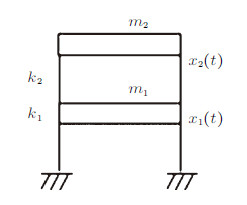
算例3 一个双层的无阻尼剪切结构如图10所示,初始静止,$k_{1}=k_{01}[1+\alpha_{1}(\Delta u)^{2}$], $k_{2}=k_{02}[1+\alpha_{2}(\Delta u)^{2}$],$\Delta u$为层间位移[7],为非线性刚度硬化问题. 考虑两种工况: (1) 底部施加水平正弦加速度$100\sin(\pi t)$,结构参数取$m_{1}=10$ t,$m_{2}=1$ t, $k_{01}=100$ MN/m,$k_{02}=100$ kN/m,$\alpha_{1}=100$,$\alpha_{2}=0.1$. (2) 底部施加El Centro地震动, 最大加速度峰值为3.417\;m/s$^{2}$,结构参数取$m_{1}=m_{2}=10$ t,$k_{01}=k_{02}=1$ MN/m,$\alpha_{1}=0.1$, $\alpha_{2}=100$. 将步长$h=1$\;ms时纽马克显式算法(NEM,\,$\gamma=0.5$,\,$\beta =0$,条件稳定)求得的结果作为"精确"解,以与本文的算法结果对照.
|
图 10 双层剪切框架结构 Fig. 10 Two-story shear-type frame structure |
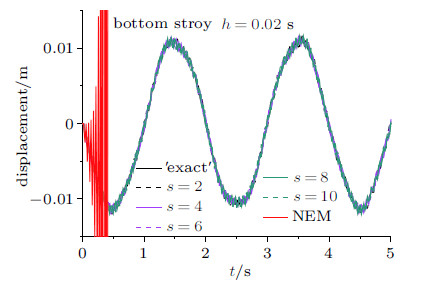
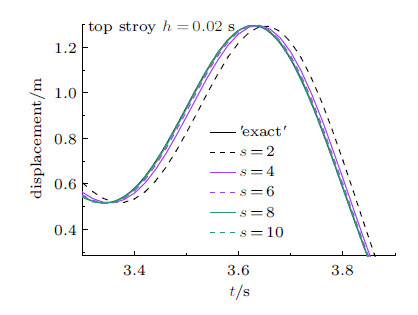
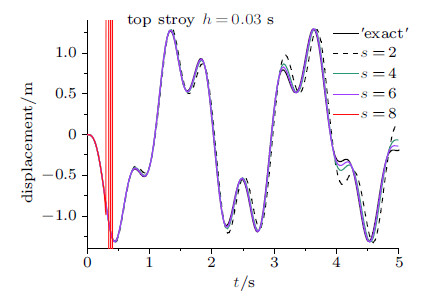
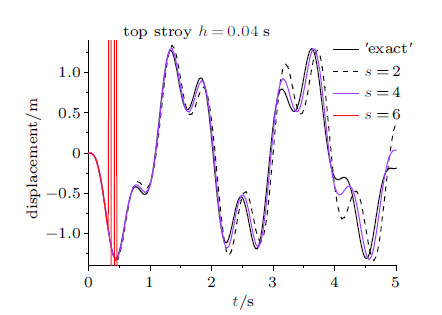
前文的理论分析已指出变量$s$是控制算法精度的一个指标. 图11和图12表明,当步长$h=0.02$ s时,纽马克显式算 法出现了失稳,而本文的算法仍得到正确解,且具有可控的精度. 图13表明,随着$s$的增大,位移时程与"精确"解接近, 即$s=10$求得的结果精度最高. 图14表明当$h=0.03$ s时,$s=2$,4,6时,算法的精度不断提高,逐渐靠近"精确"解, $s=8$时,算法失稳,这与理论分析随着$s$的增大,非线性稳定性界限区间减小是一致的. 当$h=0.04$ s (图15)时, $s=4$得到的结果要好于$s=2$,而$s=6$时算法失稳.
|
图 11 算例3底层位移时程曲线 ($h=0.02$ s) Fig. 11 Displacement time histories of bottom story for Example 3 ($h=0.02$ s) |

|
图 12 算例3顶层位移时程曲线 ($h=0.02$ s Fig. 12 Displacement time histories of top story for Example 3 ($h=0.02$ s) |
|
图 13 顶层位移时程局部放大图 ($h=0.02$ s) Fig. 13 Local zooming view for displacement time histories of top story ($h=0.02$ s) |
|
图 14 顶层位移时程曲线 ($h=0.03$ s) Fig. 14 Displacement time histories of top story ($h=0.03$ s) |
|
图 15 顶层位移时程曲线 ($h=0.04$ s) Fig. 15 Displacement time histories of top story ($h=0.04$ s) |
(1) 取$h=0.02$ s,0.03 s,0.04 s,$s=2$,4,6,8,10分别得到结构的位移响应与"精确解"对比(图11 $\sim $图15).
(2) 取$h=0.01$ s,$s=2$,4,10分别得到第2种工况下结构的位移地震响应与"精确解"对比.
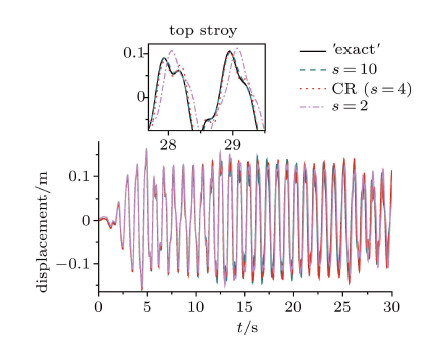
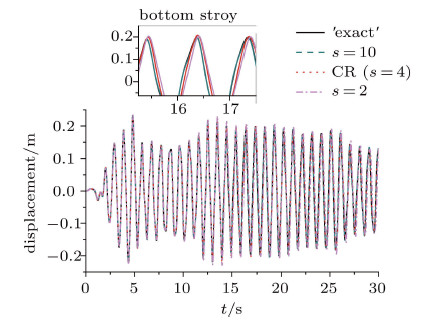
图16和图17的计算结果表明,剪切结构顶层和底层位移的局部放大图都反应了随着$s$的增大,算法的精度有所提高.
|
图 16 顶层位移时程曲线 Fig. 16 Displacement time histories of top story |
|
图 17 底层位移时程曲线 Fig. 17 Displacement time histories of bottom story |
算例4 一个8层的剪切结构,初始静止,从下到上各层的质量分别为 (3.442,3.278,3.056,2.756,2.739,2.739,2.739,2.739)$\times$100 t,各层层间侧移初始 刚度分别为(3.9,3.8,3.8,3.8,3.5,3.5,3.5,3.5)$\times$100 MN/m. 各层的刚度采用以下非 线性刚度硬化模型: $k_{i}=k_{0i}[1+\alpha_{i}(\Delta u)^{2}$],$i=1$,2,\ldots,8. $k_{0i}$为各层 的初始刚度,$\alpha_{i}$为非线性刚度的控制系数,$\alpha_{1}=100$,$\alpha_{i}=0.1$, $i=2,3,$ \ldots,8. $\Delta u$为层间位移. 底部受水平正弦加速度$100\sin(\pi t)$. 同样将$h=0.001$ s时纽马 克显式算法求得的结果作为"精确"解.
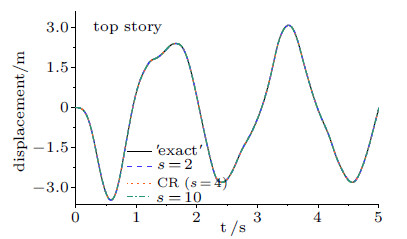
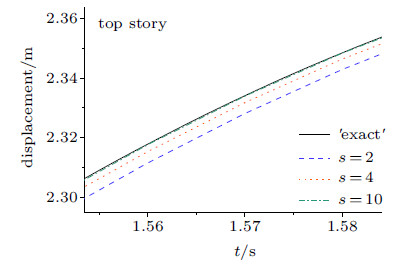
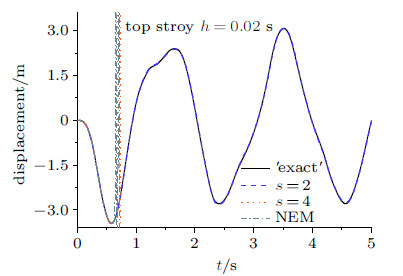
图18和图19中步长$h=0.01$ s,结果再次表明随着$s$的增大,算法的精度得到提高. 图20表明8层剪切结构非线性刚度硬化系统的稳定性区间随着$s$的增大而减小,当$h=0.02$ s时,纽马克显式算法以及CR ($s=4$)算法出现了数值失稳,而新算法$s=2$还可以求得正确解.
|
图 18 算例4顶层位移时程曲线($h=0.01$ s) Fig. 18 Displacement time histories of top story for Example 4 ($h=0.01$ s) |
|
图 19 顶层位移局部放大图($h=0.01$ s) Fig. 19 Local zooming view for displacement time histories of top story ($h=0.01$ s) |
|
图 20 顶层位移时程曲线($h=0.02$ s) Fig. 20 Displacement time histories of top story ($h=0.02$ s) |
本文引入变量$s$提出了一种新的结构动力学直接积分显式算法,具有二阶精度、零振幅衰减率、无超调、可控的周期延长率和自起步性质, 且CR算法是新算法的一个特例($s=4$). 新算法对于线性问题和非线性刚度软化问题是无条件稳定的, 而对于非线性刚度硬化问题是条件稳定的. 算例分析验证了$s$是一个控制精度及非线性刚度硬化系统的稳定性界限的指标, 与理论分析吻合. 而且,变量$s$通过调节周期延长率来控制精度,随着$s$的增大,算法精度逐渐提高($s \leqslant 10$), 但非线性刚度硬化系统的稳定性界限区间减小.
最后需要说明的是,本文提出的算法没有引入数值阻尼,但数值耗散也是算法进行多自由度系统动力分析所需的一个特性,在新算法中引入数值阻尼以及与含可控数值阻尼的广义$\alpha $法的计算比较工作还有待进一步研究.
| [1] | 张雄, 王天舒. 计算动力学. 北京:清华大学出版社, 2007 (Zhang eXiong, Wang Tianshu. Computational Dynamics. Beijing: Tsinghua University Press, 2007 (in Chinese)) |
| [2] | Chopra AK. Dynamics of Structures, 4th edn. Upper Saddle River, New Jersey: Prentice Hall, 2011 |
| [3] | 刘章军, 陈建兵. 结构动力学. 北京:中国水利水电出版社, 2012 (Liu Zhangjun, Chen Jianbing. Dynamics of Structures. Beijing: China Water Power Press, 2012 (in Chinese)) |
| [4] | 张伟伟, 金先龙. 统一格式的显式与隐式任意混合异步算法. 力学学报, 2014, 46(3): 436-446 (Zhang Weiwei, Jin Xianlong. An arbitrarily mixed explicit-implicit asynchronous integration algorithms based on uniform discretization format. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 436-446 (in Chinese)) |
| [5] | Chung J, Hulbert GM. A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-alpha method. Journal of Applied Mechanics, 1993, 60(2): 371-375. |
| [6] | Chang SY. Explicit pseudodynamic algorithm with unconditional stability. Journal of Engineering Mechanics, 2002, 128(9): 935-947. |
| [7] | Chang SY. An explicit method with improved stability property. International Journal for Numerical Methods in Engineering, 2009, 77(8): 1100-1120. |
| [8] | Chen C, Ricles JM. Development of direct integration algorithms for structural dynamics using discrete control theory. Journal of Engineering Mechanics, 2008, 134(8):676-683. |
| [9] | Kolay C, Ricles JM. Development of a family of unconditionally stable explicit direct integration algorithms with controllable numerical energy dissipation. Earthquake Engineering and Structural Dynamics, 2014, 43(9): 1361-1380. |
| [10] | 刘春生, 吴庆宪. 现代控制工程基础. 北京:科学出版社, 2011 (Liu Chunsheng, Wu Qingxian. Fundamentals of Modern Control Engineering. Beijing: Science Press, 2011 (in Chinese)) |
| [11] | Chen C, Ricles JM. Stability analysis of direct integration algorithms applied to nonlinear structural dynamics. Journal of Engineering Mechanics, 2008, 134(9):703-711. |
| [12] | Hughes TJR. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis. Mineola, New York: Dover Publications Inc, 2000 |
| [13] | 于开平,邹经湘.结构动力响应数值算法耗散和超调特性设计.力学学报, 2005, 37(4):467-476 (Yu Kaiping, Zou Jingxiang. Two time integration algorithms with numerical dissipation and without overshoot for structural dynamics. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(4):467-476 (in Chinese)) |
| [14] | Yu KP. A new family of generalized-α time integration algorithms without overshoot for structural dynamics. Earthquake Engineering and Structural Dynamics, 2008, 37(12):1389-1409. |
| [15] | 张立红, 刘天云, 李庆斌, 等. 结构动力问题的高精度组合差分时程积分法.计算力学学报, 2013, 30(4):491-495 (Zhang Lihong, Liu Tianyun, Li Qingbin, et al. A high accurate combination-difference time integration scheme for problems in structural dynamics. Chinese Journal of Computational Mechanics, 2013, 30(4): 491-495 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47