车辆是具有多自由度的复杂多体系统,近年来,车辆动力学建模与仿真成为车辆研究中重要的领域之一[1]. 车辆纵向动力学涉及到车辆的动力性、通过性、行驶平顺性、安全性及噪声等方面的问题[2]. 特别是车辆垂向振动与传动轴扭转振动的相互耦合,使得驱动轮的动力学特性更为复杂[3].
文献[2]为分析车辆的振动特性,建立了带悬架的车辆纵向动力学的简化模型, 并假设运动过程中4个车轮与地面始终保持接触,为评价车辆的动力性提供了理论依据. 文献[3, 4, 5, 6, 7]分别建立了不同类型车辆的传动系统及其纵向动力学的等效力学模型; 采用经验模型计算车轮与地面或车轮与轮轨间的摩擦力与滚阻力偶. 文献[3]未考虑传动系统扭振动与车身垂向振动的耦合效应. 文献[4, 5, 6]在分析传动系统的扭转自激振动以及车身的跳跃现象时,假设车身匀速直线平移, 未考虑车身与车轮的运动耦合效应. 文献[7]的力学模型忽略了车身的纵向运动. 文献[8, 9]运用非光滑多体系统动力学的方法研究火车的纵向动力学问题,将车厢视为质点, 车厢之间通过弹簧和阻尼器连接; 轮轨间的摩擦采用库伦干摩擦模型,用试算法求解其动力学方程.
车辆在运动过程中,由于车轮与路面 (或轮轨)之间存在摩擦力与滚阻力偶,导致车辆纵向多体系统的动力学方程是非光滑的,在黏滞与滑移转换时,其动力学方程是不连续的[10],会给方程的求解带来诸多困难. 文献[11]针对含摩擦与滚阻的平面非光滑多体系统,应用非光滑多体系统动力学方法,建立了其动力学方程,给出了相应的数值计算方法,为分析该类多体系统的动力学特性提供了一种新途径,但该算法互补维数较大,求解的计算成本较高.
为分析车辆的动力学特性,提供更为有效的数值算法,本文结合前人关于车辆动力学建模的工作基础,应用非光滑多体系统动力学方法,建立一种含滑动摩擦与滚动摩阻且考虑传动系统扭转振动的车辆纵向动力学的建模方法和数值计算方法. 用系统的位形坐标作为广义坐标,利用局部方法[12]分别列写系统的单/双边约束方程,由第一类拉格朗日方法导出该系统的动力学方程; 通过建立车轮角加速度与滚阻力偶余量,车轮与路面接触点相对切向加速度与摩擦力余量,以及接触定律的互补条件,将非光滑事件 (黏滞与滑移现象的切换)的判断转化为维数较低的线性互补方程的求解. 最后,通过数值仿真分析了不同工况下车辆纵向动力学特性.
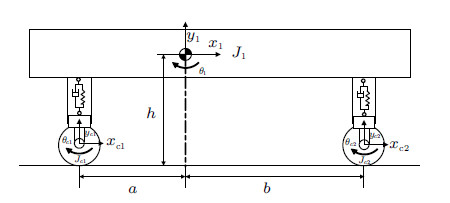
1 系统的描述及其动力学方程设车辆是由车身、车轮、传动轴及减振器等组成的平面多刚体系统[1],如图1所示. 其中,车身视为刚体,车轮近似为刚体 (考虑车轮与路面接触点的局部变形),两者通过含减振器的滑移铰连接,通常情况该滑移铰与车身不垂直. 车轮与水平路面之间存在滑动摩擦与滚动摩阻,其中滚动摩阻是由于车轮与路面接触点附近的局部变形所致.
|
图 1 车辆纵向多体系统力学模型 Fig. 1 Model of the longitudinal multi-body system of the vehicle |
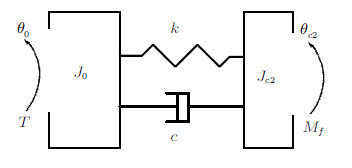
考虑传动系统的扭转振动[4],车轮与传动系统的力学模型,如图2所示. 其中,$J_0$ 为传动轴的转动惯量; $J_{\rm c2} $为前轮对传动轴的转动惯量; $k$和$c$分别为传动轴的等效扭转刚度系数和等效扭转阻尼系数; $T$为发动机的输出扭矩.
设${{ q}} = [x_1 \;y_1 \;\theta _1 \;x_{c1} \;y_{c1} \;\theta _{c1} \;x_{c2} \;y_{c2} \;\theta _{c2} \;\theta _0]^{\rm T}$为系统的广义坐标,其中$(x_1 ,y_1 ,\theta _1 )$为车身质 心坐标与俯仰角,$(x_{c1} ,y_{c1} ,\theta _{c1} )$,$(x_{c2} ,y_{c2} ,\theta _{c2})$分别为车后轮和前轮的质心坐标及 其转动角,$\theta _0 $扭矩输出轴的转角.
设$f_i ({{ q}}) = 0$ $(i = 1,2)$为前后车轮与车身之间滑移铰的约束方程,其矩阵表达式为
| $ {{ \varPhi }}({{ q}}) = [f_1 ,f_2]^{\rm T} = 0 $ | (1) |
设$g_{Ni} (x_{ci} ,y_{ci} ) \geqslant 0\ (i = 1,2)$为后轮和前轮受到地面法向的单边约束方程,其矩阵表达式为
| $ {{ g}}_N ({{ q}}) = \left[{g_{N1} ,g_{N2} } \right]^{\rm T} \geqslant 0 $ | (2) |
由第一类拉格朗日(Lagrange)方程可得到该系统的动力学方程
| $ \left.\begin{array}{l} M\ddot{ q}= Q+\varPhi^{\rm T}_q\lambda+ W_N\lambda_N+ Q^{\rm f}\\ \varPhi( q)=[f_1,f_2]^{\rm T}= 0\\ g_N=[g_{N1},g_{N2}]^{\rm T}\geqslant 0\\ \end{array}\right\} $ | (3) |
其中,${{ M}}$为系统的广义质量矩阵; ${{ Q}}$为主动力的广义力; ${{ \varPhi }}_{q} $为${{ \varPhi }}$的雅可比(Jacobi)矩阵; ${{ \lambda }}$为对应于约束方程 (1)的拉格朗日乘子列向量; ${{ W}}_{N} $为${{ g}}_N $的雅可比矩阵的转置; ${{ \lambda }}_{N} $为对应于约束方程 (2)的拉格朗日乘子列向量; ${{ Q}}^{\rm f}$为摩擦力与滚阻力偶的广义力列向量.
根据库伦摩擦定律与滚阻定律,作用于车轮$i$上的摩擦力$F_{\rm fi} $和滚阻力偶$M_{\rm fi} $ 与地面法向约束力$F_{Ni} $之间的关系式可表示为
| $ F_{\rm fi} = \left\{ \begin{array}{ll} - \mu _i F_{Ni} {\rm Sgn}(v_{ri} ),v_{ri} \ne 0 \\ - \mu _{0i} F_{Ni} {\rm Sgn}(\dot{v}_{ri} ),v_{ri} = 0 \\ \end{array} \right. $ | (4a) |
| $ M_{\rm fi} = \left\{ \begin{array}{ll} - \delta _i F_{Ni} {\rm Sgn}(\dot{\theta }_{ci} ),& \dot{\theta }_{ci} \ne 0 \\ - \delta _i F_{Ni} {\rm Sgn}(\ddot{\theta }_{ci} ),& \dot{\theta }_{ci} = 0 \\ \end{array} \right. $ | (4b) |
其中,集值函数
| $ {\rm{Sgn}}(x) = \left\{ {\begin{array}{*{20}{l}} {1,}&{x > 0}\\ {[- 1,1],}&{x = 0}\\ { - 1,x}&{lt;0} \end{array}} \right. $ |
$\mu _i$和$\mu _{0i}$分别为车轮与路面之间的动、静摩擦系数; $\delta _i$为车轮与路面间的滚阻系数. $v_{ri}$与$\dot{v}_{ri}$ 分别为车轮与路面接触点的速度和切向加速度. $\dot{\theta }_{ci}$与$\ddot{\theta }_{ci}$分别为车轮的角速度和角加速度.
采用笛卡尔坐标描述系统的位形,并通过局部方法列写的约束方程,可以得到约束力与拉格朗日乘子一一对应的关系[11],当车轮与水平路面接触时,其约束方程为$g_{Ni}(x_{ci} ,y_{ci} ) = y_{ci} - R = 0$ ($R$为车轮半径),对应的拉格朗日乘子为$\lambda _{Ni} $. 由此可得到法向约束力与拉格朗日乘子的关系[13]
| $ F_{Ni} = \lambda _{Ni}\ \ (i = 1,2) $ | (5) |
设$F_{fi} $,$M_{fi} $分别为作用在车轮$i$上的摩擦力和滚阻力偶,对应于的位形坐标$\left( {x_{ci} ,y_{ci} ,\theta _{ci}} \right)$的广义力为[10]
| $ \left[{{\begin{array}{*{20}c} {Q_{x_{ci} }^{\rm f} } \\ {Q_{y_{ci} }^{\rm f} } \\ {Q_{\theta _{ci} }^{\rm f} } \\ \end{array} }} \right] = \left[{{\begin{array}{*{20}c} {\dfrac{\partial g_{Ni} }{\partial y_{ci} }} & 0 \\[3mm] { - \dfrac{\partial g_{Ni} }{\partial x_{ci} }} & 0 \\ {R_i } & 1 \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {F_{fi} } \\ {M_{fi} } \\ \end{array} }} \right] \ \ (i = 1,2) $ |
为便于计算,将摩擦力与滚阻力偶的广义力用下列矩阵形式表示为
| $ Q^{\rm f} = W_{{T}} {{ \lambda }}_{{T}} $ | (6) |
其中
| $\begin{array}{l} {Q^{\rm{f}}} = {[Q_{{x_1}}^{\rm{f}}\;Q_{{y_1}}^{\rm{f}}\;Q_{{\theta _1}}^{\rm{f}}\;Q_{{x_{c1}}}^{\rm{f}}\;Q_{{y_{c1}}}^{\rm{f}}\;Q_{{\theta _{c1}}}^{\rm{f}}\;Q_{{x_{c2}}}^{\rm{f}}\;Q_{{y_{c2}}}^{\rm{f}}\;Q_{{\theta _{c2}}}^{\rm{f}}\;Q_{{\theta _0}}^{\rm{f}}]^{\rm{T}}}\\ {W_T} = {\left[{\begin{array}{*{20}{c}} 0&0&0&1&0&{ - R}&0&0&0&0\\ 0&0&0&0&0&{ - 1}&0&0&0&0\\ 0&0&0&0&0&0&1&0&{ - R}&0\\ 0&0&0&0&0&0&0&0&{ - 1}&0 \end{array}} \right]^{\rm{T}}}\\ {\lambda _T} = {[\begin{array}{*{20}{c}} {{F_{{\rm{f1}}}}}&{{M_{{\rm{f1}}}}}&{{F_{{\rm{f2}}}}}&{{M_{{\rm{f2}}}}} \end{array}]^{\rm{T}}} \end{array}$ |
因此,动力学方程 (3)中的第一式可写成
| $ \label{eq3} M\ddot{ q} = Q + \varPhi _{q}^{\rm T} \lambda + W_{N} \lambda_{{N}} + {{ W}}_{T} {{ \lambda }}_{{T}} $ | (7) |
由于摩擦力和滚阻力偶存在,使得该方程在非光滑点处$(v_{ri} = 0$或$\dot{\theta }_{ci} = 0)$ 是不连续的.
2 动力学方程的算法由于方程 (7)的右端向量场在非光滑点处不连续,给方程的数值求解带来了困难. 其难点在于非光滑 事件--黏滞滑移 (stick-slip)的判断. 应用非光滑动力学方法,可将车辆纵向动力学中非光滑事件的判断转化为线性互补问题的求解. 为此, 需要建立相关物理量的互补关系.
2.1 互补条件(1)与摩擦和滚阻相关物理量的互补条件: 静滑动摩擦力的正向与负向摩擦余量分别定义为[14]
| $ \label{eq4} \left. {\begin{array}{l} F_{fi}^ + = \mu _{0i} F_{Ni} + F_{fi} \\ F_{fi}^ - = \mu _{0i} F_{Ni} - F_{fi} \\ \end{array}} \right\} $ | (8) |
接触点的相对切向加速度$\dot{v}_{ri} $的正向与负向分别定义为[14]
| $\left. {\begin{array}{*{20}{l}} {\dot v_{ri}^ + = \frac{{(\left| {{{\dot v}_{ri}}} \right| + {{\dot v}_{ri}})}}{2}}\\ {\dot v_{ri}^ - = \frac{{(\left| {{{\dot v}_{ri}}} \right| - {{\dot v}_{ri}})}}{2}} \end{array}} \right\}$ | (9) |
滚阻力偶的正向与负向滚阻余量分别定义为[11]
| $\left. {\begin{array}{*{20}{l}} {M_{fi}^ + = {\delta _i}{F_{Ni}} + {M_{fi}}}\\ {M_{fi}^ - = {\delta _i}{F_{Ni}} - {M_{fi}}} \end{array}} \right\}$ | (10) |
前后车轮角加速度$\ddot{\theta }_{\rm ci} $的正向与负向分别定义为
| $ \left. {\begin{array}{*{20}{l}} {\ddot \theta _{ci}^ + = \frac{{(\left| {{{\ddot \theta }_{ci}}} \right| + {{\ddot \theta }_{ci}})}}{2}}\\ {\ddot \theta _{ci}^ - = \frac{{(\left| {{{\ddot \theta }_{ci}}} \right| - {{\ddot \theta }_{ci}})}}{2}} \end{array}} \right\} $ | (11) |
将式(8)与式(10)定义的摩擦余量和滚阻力偶余量统一表示成
| $ \left. {\begin{array}{*{20}{l}} {\lambda _{Hi}^ + = \mu _i^ * {\lambda _{Ni}} + {\lambda _{Hi}}}\\ {\lambda _{Hi}^ - = \mu _i^ * {\lambda _{Ni}} - {\lambda _{Hi}}} \end{array}} \right\} $ | (12) |
其中,若$\lambda _{Hi} = F_{fi} $,则$\mu _i^\ast = \mu _{0i} $; 若$\lambda _{Hi} = M_{fi} $,则$\mu _i^\ast = \delta _i $.
将式 (9)与式 (11)统一表示成
| $ \label{eq5} \left. {\begin{array}{l} \ddot{g}_{Hi}^ + = \dfrac{(\left| {\ddot{g}_{Hi} } \right| + \ddot{g}_{Hi} )}{2} \\[3mm] \ddot{g}_{Hi}^ - = \dfrac{(\left| {\ddot{g}_{Hi} } \right| - \ddot{g}_{Hi} )}{2} \\ \end{array}} \right\} $ | (13) |
其中,$\ddot{g}_{H1} = \dot{v}_{r1} ,\ddot{g}_{H2} = \ddot{\theta }_{c1} ,\ddot{g}_{H3} = \dot{v}_{r2} ,\ddot{g}_{H4} = \ddot{\theta }_{c2} $. 由此,$\lambda _{Hi}^ + $ 与$\ddot{g}_{Hi}^ + $,$\lambda _{Hi}^ - $与$\ddot{g}_{Hi}^ - $,构成下列互补关系
| $ \label{eq6} \left. {\begin{array}{l} \ddot{g}_{Hi}^ + \geqslant 0,\ \ \lambda _{Hi}^ + \geqslant 0,\ \ \ddot{g}_{Hi}^ + \lambda _{Hi}^ + = 0 \\ \ddot{g}_{Hi}^ - \geqslant 0,\ \ \lambda _{Hi}^ - \geqslant 0,\ \ \ddot{g}_{Hi}^ - \lambda _{Hi}^ - = 0 \\ \end{array}} \right\} $ | (14) |
互补条件式(14)的适用条件为$\dot{g}_{Ti} = 0$. 其中,$\dot{g}_{T1} = v_{r1}$,$\dot{g}_{T2} = \dot{\theta }_{c1}$, $\dot{g}_{T3} = v_{r2}$,$\dot{g}_{T4} = \dot{\theta }_{c2} $.
(2)接触定律的互补条件
单边约束的法向约束力$\lambda _{Ni} $与$\ddot{g}_{Ni} $满足的互补条件[14]
| $ \label{eq7} \ddot{g}_{Ni} \geqslant 0,\lambda _{Ni} \geqslant 0,\ \ \ddot{g}_{Ni} \lambda _{Ni} = 0 $ | (15) |
互补条件式(15)的适用条件为$g_{Ni} = \dot{g}_{Ni} = 0$.
2.2 动力学方程算法将式 (4)代入式 (6),摩擦力与滚阻力偶的广义力可表示成如下形式
| $\begin{array}{l} {Q^{\rm{f}}} = {W_T}{\lambda _T} = \\ \;\;\;\;{W_T}S\left[ {\begin{array}{*{20}{c}} { - {\mu _{01}}{\rm{Sgn}}({{\ddot g}_{T1}})}&{amp;}\\ { - {\delta _1}{\rm{Sgn}}({{\ddot g}_{T2}})}&{amp;}\\ {}&{amp; - {\mu _{02}}{\rm{Sgn}}({{\ddot g}_{T3}})}\\ {}&{amp; - {\delta _2}{\rm{Sgn}}({{\ddot g}_{T4}})} \end{array}} \right]{\lambda _N} + \\ \;\;\;{W_T}(E - S)\left[ {\begin{array}{*{20}{c}} { - {\mu _1}{\rm{Sgn}}({{\dot g}_{T1}})}&{amp;}\\ { - {\delta _1}{\rm{Sgn}}({{\dot g}_{T2}})}&{amp;}\\ {}&{amp; - {\mu _2}{\rm{Sgn}}({{\dot g}_{T3}})}\\ {}&{amp; - {\delta _2}{\rm{Sgn}}({{\dot g}_{T4}})} \end{array}} \right]{\lambda _N} \end{array}$ |
其中
| $ \begin{array}{l} S = {\rm{diag}}[1 - \left| {{\rm{Sgn}}\left( {{{\dot g}_{T1}}} \right)} \right|,1 - \left| {{\rm{Sgn}}\left( {{{\dot g}_{T2}}} \right)} \right|,1 - \left| {{\rm{Sgn}}\left( {{{\dot g}_{T3}}} \right)} \right|,\\ \quad 1 - \left| {{\rm{Sgn}}\left( {{{\dot g}_{T4}}} \right)} \right|] \end{array} $ |
将式 (12)摩擦余量与滚阻力偶余量代入上式中的广义静摩擦力部分 (包括静摩擦力和静滚阻力偶),可得
| $ \begin{array}{l} {Q^{\rm{f}}} = {W_T}S\left[ {\begin{array}{*{20}{c}} {\lambda _{H1}^ + - {\mu _{01}} \cdot {\lambda _{N1}}}\\ {\lambda _{H2}^ + - {\delta _1} \cdot {\lambda _{N1}}}\\ {\lambda _{H3}^ + - {\mu _{02}} \cdot {\lambda _{N2}}}\\ {\lambda _{H4}^ + - {\delta _2} \cdot {\lambda _{N2}}} \end{array}} \right] + \\ \quad {W_T}(E - S)\left[ {\begin{array}{*{20}{c}} { - {\mu _1}{\rm{Sgn}}({{\dot g}_{T1}})}&{amp;0}\\ { - {\delta _1}{\rm{Sgn}}({{\dot g}_{T2}})}&{amp;0}\\ 0&{amp; - {\mu _2}{\rm{Sgn}}({{\dot g}_{T3}})}\\ 0&{amp; - {\delta _2}{\rm{Sgn}}({{\dot g}_{T4}})} \end{array}} \right]\\ {\lambda _N} = \quad {W_H}\lambda _H^ + + {W_T}\left\{ {S\left[ {\begin{array}{*{20}{c}} { - {\mu _{01}}}&{amp;{\rm{0}}}\\ { - {\delta _1}}&{amp;{\rm{0}}}\\ {\rm{0}}&{amp; - {\mu _{02}}}\\ {\rm{0}}&{amp; - {\delta _2}} \end{array}} \right] + } \right.\\ \left. {\quad (E - S)\left[ {\begin{array}{*{20}{c}} { - {\mu _1}{\rm{Sgn}}({{\dot g}_{T1}})}&{amp;0}\\ { - {\delta _1}{\rm{Sgn}}({{\dot g}_{T2}})}&{amp;0}\\ 0&{amp; - {\mu _2}{\rm{Sgn}}({{\dot g}_{T3}})}\\ 0&{amp; - {\delta _2}{\rm{Sgn}}({{\dot g}_{T4}})} \end{array}} \right]} \right\}{\lambda _N} = \\ \quad {W_H}\lambda _H^ + - {W_T}\mu {\lambda _N} \end{array} $ |
其中,${{ W}}_H = {{ W}}_T {{ B}}$,${{ B}}$由${{ S}}$中非零的列向量构成; ${{ \lambda }}_{H}^+$是由${{ S}} \cdot \left[{{\begin{array}{*{20}c} {\lambda _{H1}^ + } & {\lambda _{H2}^ + } & {\lambda _{H3}^ + } & {\lambda _{H4}^ + } \end{array} }} \right]^{\rm T}$中非零的元素构成的列向量; 设
| $ {{ \mu }} = {{ S}}\left[{{\begin{array}{*{20}c} {\mu _{01} } & {\rm 0} \\ {\delta _1 } & {\rm 0} \\ {\rm 0} & {\mu _{02} } \\ {\rm 0} & {\delta _2 } \\ \end{array} }} \right]{\rm + }({{ E - S}})\left[ {{\begin{array}{*{20}c} {\mu _1 {\rm sgn}(\dot{g}_{T1} )} & 0 \\ {\delta _1 {\rm sgn}(\dot{g}_{T2} )} & 0 \\ 0 & {\mu _2 {\rm sgn}(\dot{g}_{T3} )} \\ 0 & {\delta _2 {\rm sgn}(\dot{g}_{T4} )} \\ \end{array} }} \right] $ |
则该系统的动力学方程式 (7)可写成如下形式
| $ \label{eq8} M\ddot{ q} = Q + \varPhi_{q}^{\rm T} \lambda + W_{N} {{ \lambda }}_{N} + {{ W}}_{H} {{ \lambda }}_{H}^{+} - {{ W}}_{T} {{ \mu \lambda }}_{N} $ | (16) |
引入包姆加藤 (Barmgarte)违约修正公式[15](3),式中的双边约束方程改写为
| $ \label{eq9} {{ \varPhi }}_q {{\ddot{ q}}} + {{\dot{ \varPhi }}}_q {{\dot{ q}}} + \alpha {{ \varPhi }}_q {{\dot{ q}}} + \beta{{ \varPhi }} = 0 $ | (17) |
由系统动力学方程式(16),可得
| $ \begin{array}{l} \ddot q = {M^{ - 1}}Q + {M^{ - 1}}\Phi _q^{\rm{T}}\lambda + {M^{ - 1}}({W_N} - {W_T}\mu ){\lambda _N} + \\ \quad {M^{ - 1}}{W_H}\lambda _H^ + \end{array} $ | (18) |
将式 (18)代入式 (17)可得
| $ \begin{array}{l} {{ \lambda }} = {{ D \varPhi }}_q {{ M}}^{ - 1}({{ W}}_{N} - {{ W}}_T {{ \mu }}){{ \lambda }}_{N} + {{ D \varPhi }}_q {{ M}}^{ - 1}{{ W}}_H {{ \lambda }}_{H}^+ + {{ A}} \\ {{ D}} = [- {{ \varPhi}}_q {{ M}}^{ - 1}{{ \varPhi }}_{q}^{\rm T}]^{ - 1} \\ {{ A}}^\ast = {{ \varPhi }}_q {{ M}}^{ - 1} Q + \dot{ \varPhi}_q {{\dot{ q}}} + \alpha {{ \varPhi }}_q {{\dot{ q}}} + \beta {{ \varPhi }} \\ {{ A}} = {{ D A}}^\ast \\ \end{array} $ |
再将${{ \lambda }}$代入动力学方程 (18)可得
| $ \label{eq10} \ddot{ q} = M^{ - 1}{{ Q}} + {{ M}}^{ - 1}{{\tilde{ W}}}_N {{ \lambda }}_{N} + M^{ -1}{{\tilde{ W}}}_H {{ \lambda }}_{H}^{+} + {{ M}}^{ - 1}{{ \varPhi }}_{q}^{\rm T} {{ A}} $ | (19) |
其中
| $ \begin{array}{l} {{\tilde{ W}}}_N = {{ \varPhi }}_{q}^{\rm T} {{ D \varPhi }}_q {{ M}}^{ - 1}({{ W}}_{N} - {{ W}}_T {{ \mu }}) +{{ W}}_{N} - {{ W}}_T {{ \mu }} \\ {{\tilde{ W}}}_H = {{ \varPhi }}_{q}^{\rm T} {{ D \varPhi }}_q {{ M}}^{ - 1}{{ W}}_H + {{ W}}_H\\ \end{array} $ |
车轮与路面法向约束的加速度关系式
| $ \label{eq11} {{\ddot{\pmb g}}}_N = {{ W}}_N^{\rm T} {{\ddot{ q}}} $ | (20) |
将式 (19)代入式 (20)可得
| $ \label{eq12} {{\ddot{\pmb g}}}_N = {{ W}}_N^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_N {{ \lambda }}_{N} + {{ W}}_N^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_H {{ \lambda }}_{H}^{+} + {{ C}} $ | (21) |
其中,${{ C}} = {{ W}}_N^{\rm T} {{ M}}^{ - 1}({{ Q}} + {{ \varPhi }}_{q}^{\rm T} {{ A}})$.
前后车轮与水平路面接触点的相对切向加速度及角加速度关系式为
| $ \label{eq13} {{\ddot{\pmb g}}}_T = {{ W}}_T^{\rm T} {{\ddot{ q}}} $ | (22) |
当前后车轮与地面接触点的相对速度为零或车轮角速度为零时,式 (22)可写成如下形式
| $ \label{eq14} {{\ddot{\pmb g}}}_H = {{ W}}_H^{\rm T} {{\ddot{ q}}} $ | (23) |
其中,${{\ddot{\pmb g}}}_H = {{\ddot{\pmb g}}}_T {{ B}}$; 将式 (13)及式 (19)代入式 (23)可得
| $ \label{eq15} {{\ddot{\pmb g}}}_{H }^ + - {{\ddot{\pmb g}}}_{H }^ - = {{ W}}_H^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_N {{ \lambda }}_{N} + {{ W}}_H^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_H {{ \lambda }}_{H}^{+} + {{ L}} $ | (24) |
其中,${{ L}} = {{ W}}_H^{\rm T} {{ M}}^{ - 1}({{ Q}} + {{ \varPhi }}_{q}^{\rm T} {{ A}})$.
式 (12)中的两式相加可得
| $ \label{eq16} {{ \lambda }}_{H}^{{ + }} + {{ \lambda }}_{H}^ - = 2{{ \mu }}_H {{ \lambda }}_{N} $ | (25) |
其中
| $ {{ \mu }}_{H} = ({{ \mu }}_0 {{ B}})^{\rm T} \,,\ \ \ \ {{ \mu }}_0 = \left[ {{\begin{array}{*{20}c} {\mu _{01} } & {\delta _1 } & { 0} \\ { 0} & {\mu _{02} } & {\delta _2 } \\ \end{array} }} \right] $ |
由此,当车轮与路面接触点相对速度或车轮转速为零时,车轮与路面接触点处的摩擦力与滚阻力偶的计算问题转化为求解线性互补问题 (LCP). 将式 (21),式 (24)与式 (25)合写成如下矩阵形式
| $ \label{eq17} \left[{{\begin{array}{*{20}c} {\ddot{\pmb g}_N } \\ {\ddot{\pmb g}_{H}^{{ + }} } \\ {{{ \lambda }}_H^ - } \\ \end{array} }} \right] = \left[{{\begin{array}{*{20}c} {{{ W}}_N^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_N } & {{{ W}}_N^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_H } & 0 \\ {{{ W}}_H^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_N } & {{{ W}}_H^{\rm T} {{ M}}^{ - 1}{{\tilde{ W}}}_H } & E \\ {2{{ \mu }}_H } & { - E} & 0 \\ \end{array} }} \right]\left[{{\begin{array}{*{20}c} {{{ \lambda }}_N } \\ {{{ \lambda }}_{H}^{{ + }} } \\ {\ddot{\pmb g}_H^ - } \\ \end{array} }} \right] + \left[{{\begin{array}{*{20}c} C \\ L \\ 0 \\ \end{array} }} \right] $ | (26) |
其中
| $ \begin{array}{l} [\begin{array}{*{20}c} {\ddot{\pmb g}_N } & {\ddot{\pmb g}_H^ + } & {{{ \lambda }}_{H}^{{ - }} } \\ \end{array}]^{\rm T} \geqslant 0,\ \ {}[{{\begin{array}{*{20}c} {{{ \lambda }}_N } & {{{ \lambda }}_{H}^{{ + }} } & {\ddot{\pmb g}_H^ - } \\ \end{array} }}]^{\rm T} \geqslant 0 \\ {} [\begin{array}{*{20}c} {\ddot{\pmb g}_N } & {\ddot{\pmb g}_H^ + } & {{{ \lambda }}_{H}^{{ - }} } \\ \end{array}][\begin{array}{*{20}c} {{{ \lambda }}_N } & {{{ \lambda }}_{H}^{{ + }} } & {\ddot{\pmb g}_H^ - } \\ \end{array}]^{\rm T} = 0\\ \end{array} $ |
应用线性互补的相关求解算法,如莱姆克(Lemke)算法,求解上式,可以得到${{ \lambda }}_{H}^ + $和${{ \lambda }}_{N} $代入式 (16),用求解常微分方程的数值方法求解动力学方程.
当车轮与路面接触点的相对速度以及车轮的角速度均不等于零时,即车轮相对于地面既滑又滚时,动力学方程中摩擦力和滚阻力偶的大小和方向是确定的,将式 (4)中的滑动摩擦和滚动滚阻代入式 (7),利用求解常微分方程的数值计算方法求解动力学方程.
3 数值仿真仿真算例的系统如图1和图2所示,设车身与滑移铰轴线垂直,系统参数分别为[16] $m_1 = 1 400$ kg,$J_1 = 1\,200$ kg$\cdot$m$^2$,$m_{2} = 30$ kg,$J_2 = 2$ kg$\cdot$m$^{2}$,$m_{3} =30$ kg,$J_{3} =2$ kg$\cdot$m$^{2}$,$J_{0} =250$ kg$\cdot$m$^{2}$,$k_1 =25$ kN/m,$c_1 =3.5$ kN$\cdot$s/m,$k =30$ kN$\cdot$m/rad,$c =30$ N$\cdot$m$\cdot$s/rad,$a =1$ m,$b =1$ m,$h= 0.6$ m,$R = 0.25$ m.
|
图 2 车辆传动系统扭转振动力学模型 Fig. 2 Model of torsional vibration of the vehicle |
系统初始条件 $\dot{\theta }_{0} = 0$,$\dot{\theta }_{1} = 0$,$\dot{x}_{1} = \dot{x}_2 = R\dot{\theta }_{{c1}} = R\dot{\theta }_{{c2}} =0\; {\rm m/s}$; $x_1 = a$,$ y_1 = h$,$ \theta _1 = 0$,$x_{c1} = 0$,$ y_{c1} = R$,$\theta _{c1} = 0$,$x_{c2} = (a + b)$,$ y_{c2} = R$,$\theta _{c2} = 0$,$\theta _0 = 0$; 包姆加藤违约修正参数 $\alpha = 30$,$\beta = 30$.
情形一
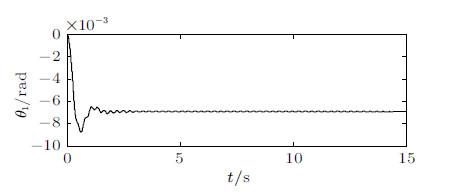
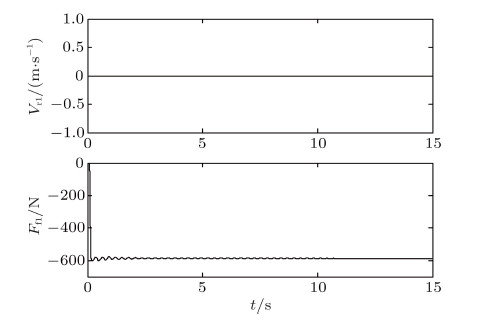
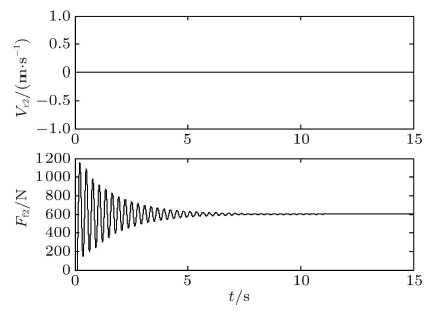
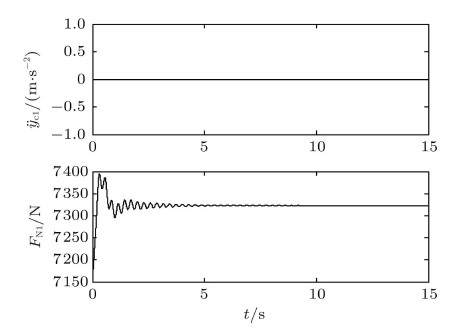
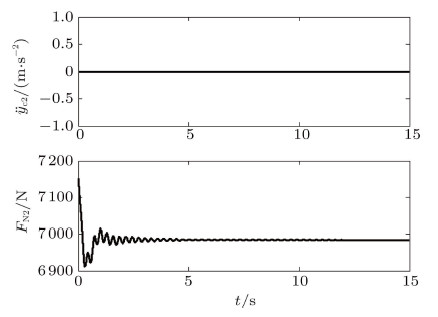
车辆在干燥的沥青路面上行驶,车轮与路面间的静、动摩擦系数为$\mu _{{01}} =\mu _{{02}} = 0.8$,$\mu _{1}= \mu _2 = 0.75$,滚阻系数$\delta = 0.02$ m,设输出扭矩$T = 300$ N$\cdot$m. 图3$\sim$图5分别给出了车身俯仰角$\theta _{1}$,后轮 与水平路面接触点的速度$V_{\rm r1}$ 和摩擦力$F_{\rm f1}$,以及前轮与水平路面接触点的速度$V_{\rm r2}$ 和摩擦力$F_{\rm f2}$的时间历程图. 由计算结果可知,前后车轮在地面上纯滚动; 由于减振器的作用, 车身经过一段时间的振动后,最终达到稳定的平衡位置; 受传动系统扭转振动的影响, 前后车轮与地面之间的摩擦力的大小初始阶段波动之后最终达到常值. 图6和图7分别给出了后轮和前轮质心垂直方向的加速度及与地面接触点的法向约束力的时间历程图. 结合图3, 可得知前后车轮与地面始终处于接触状态 (前后轮的法向约束力始终大于0); 车身的振动导致了地面作用在前后车轮上法向约束力的大小在初始阶段呈现波动现象,最终达到常值, 且前轮的法向约束力小于后轮的法向约束力. 这一结果与定性分析的结果吻合.
|
图 3 $\theta _{1}$的时间历程 Fig. 3 Time history of $\theta _{1}$ |
|
图 4 $V_{\rm r1} $和$F_{\rm f1} $的时间历程 Fig. 4 Time history of $V_{\rm r1} $ and $F_{\rm f1}$ |
|
图 5 $V_{\rm r2} $和$F_{\rm f2} $的时间历程 Fig. 5 Time history of $V_{\rm r2} $ and $F_{\rm f2} $ |
|
图 6 $\ddot{ y}_{{\rm c1}} $和$F_{{\rm N1}} $的时间历程 Fig. 6 Time history of $\ddot{ y}_{\rm c1}$ and $F_{{\rm N1}}$ |
|
图 7 $\ddot{ y}_{{\rm c2}} $和$F_{{\rm N2}}$的时间历程 Fig. 7 Time history of $\ddot{ y}_{{\rm c2}}$ and $F_{{\rm N2}} $ |
情形二
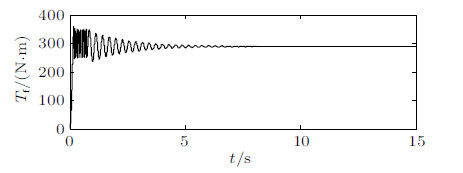
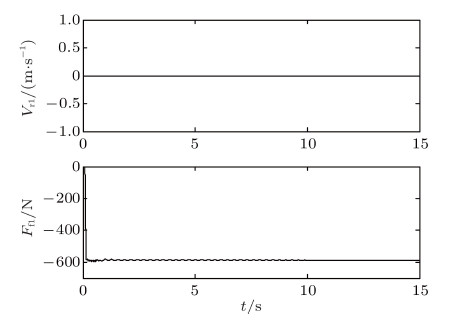
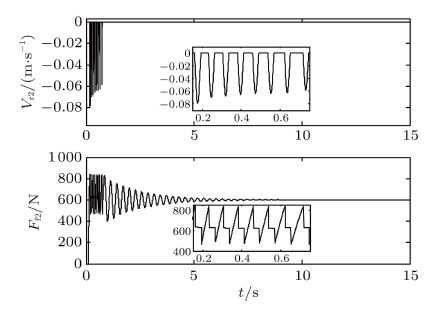
车辆在压紧的冰雪地面上行驶,车轮与路面的静、动摩擦系数$\mu _{{01}} =\mu _{{02}}= 0.12$,$\mu _1 = \mu _2 = 0.09$,滚阻系数$\delta = 0.02$ m,设输出扭矩$T = 300$ N$\cdot$m. 图8为 传动系统输出到前轮扭矩的时间历程图; 图9和图10分别给出了后轮与路面接触点的速度$V_{\rm r1}$与摩擦 力$F_{\rm f1}$,以及前轮与路面接触点的速度$V_{\rm r2}$与摩擦力$F_{\rm f2}$的时间历程. 数值结果表明,后轮始终 作纯滚动,但初始阶段,前轮在地面上纯滚动, 随着输出扭矩的增加,前轮相对于地面打滑,经过一段时间的黏滞滑移运 动之后,由于传动系统扭转阻尼的作用, 输出到前轮的扭矩最终达到常值 (如图8所示),车轮与地面接触点的相对速度逐步趋 于零,最终前轮在地面上又作纯滚动.
|
图 8 $T_{\rm f}$的时间历程 Fig. 8 Time history of $T_{\rm f} $ |
|
图 9 $V_{\rm r1}$和$F_{\rm f1}$的时间历程 Fig. 9 Time history of $V_{\rm r1}$ and $F_{\rm f1} $ |
|
图 10 $V_{\rm r2}$和$F_{\rm f2} $的时间历程 Fig. 10 Time history of $V_{\rm r2} $ and $F_{\rm f2} $ |
情形三
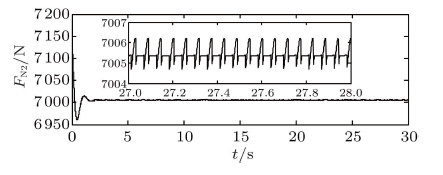
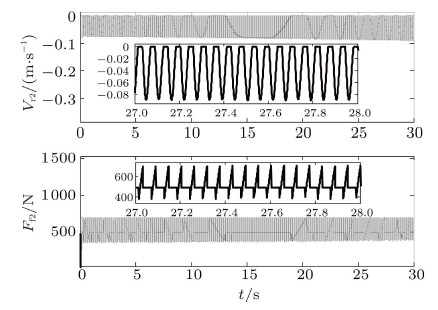
车辆在冰面上行驶,车轮与路面的静、动摩擦系数分别为$\mu _{{01}} =\mu _{{02}}= 0.1$,$\mu _1 = \mu _2 = 0.07$, 滚阻系数$\delta = 0.02$ m. 若发动机输出扭矩为$T = 268$ N$\cdot$m时,图11 $\sim$图13分别给出了作用于前轮的扭矩$T_{\rm f} $,车身俯仰的角加速度$\ddot{\theta}_1 $ 及前轮与地面接触点的法向约束力$F_{\rm N2}$的时间历程. 图14为前轮与路面接触点的速度$V_{\rm r2}$与摩擦力$F_{ \rm f2}$ 的时间历程. 由仿真结果可以得知,车身呈现抖动现象,前轮发生了持续的黏滞滑移运动现象. 该现象的产生 不仅与摩擦系数的减小有关,还与传动系统的扭振和车身振动等因素有关. 传动系统的扭振导致作用在前轮的驱动力矩呈现周期性变化, 车身的振动导致地面作用在车轮上的法向约束力呈现周期性变化,又由于动、静摩擦系数的不同,导致了车轮出现黏滞 滑移运动状态; 摩擦力周期变化,又进一步激发车身的振动以及传动系统的扭振. 这种相互耦合作用使得车辆在工况三的情况下出现持续的黏滞滑移运动状态.

|
图 11 $T_{\rm f}$的时间历程 Fig. 11 Time history of $T_{\rm f}$ |

|
图 12 $\ddot{\theta }_1$的时间历程 Fig. 12 Time history of $\ddot{\theta }_1 $ |
|
图 13 $F_{{\rm N2}}$的时间历程 Fig. 13 Time history of $F_{{\rm N2}} $ |
|
图 14 $V_{\rm r2} $和$F_{\rm f2} $的时间历程 Fig. 14 Time history of $V_{\rm r2} $ and $F_{\rm f2} $ |
图15为约束方程二次范数$\left\| {{ \varPhi }} \right\|$的时间历程,未加违约修正时,$\left\| {{ \varPhi }} \right\|$随时间递增,采用违约修正后,$\left\| {{ \varPhi }} \right\|$ 始终保持在很小的范围内 ($\left\| {{ \varPhi }} \right\| < 1 \times 10^{ - {\rm 5}}$ m).

|
图 15 约束方程二次范数$\left\| {{ \varPhi }} \right\|$的时间历程 Fig. 15 Time history of $\left\| {{ \varPhi }} \right\|$ |
本文应用非光滑多体系统动力学方法研究车辆纵向动力学问题, 将车辆视为由车身、车轮、减振器、传动系统构成的具有双边理想约束和 单边非理想约束的多刚体系统, 考虑车轮与路面之间的摩擦与滚动摩阻,由第一类拉格朗日方程导出了该系统的动力学方程. 由于摩擦和滚动摩阻的存在致使动力学方程不连续,为此建立了相关的物理量的互补关系,引入包姆加藤违约修正, 并结合动力学方程,将车轮与地面间非光滑事件 (接触分离、黏滞滑移)的判断问题转化为线性互补问题的求解, 并给出了相应的算法. 最后,通过数值仿真,分析了在不同路况以及不同输出扭矩条件下车辆的动力学特性, 揭示了当系统参数取某组特定值时,由于传动系统的扭振、车身的振动以及地面摩擦力的耦合效应,导致驱动轮 (前轮)与地面的接触点会持续出现黏滞滑移运动状态切换.
本文给出的方法不同于传统的方法,可有效地反映车轮与路面间的干摩擦和滚动摩阻的非光滑力学特性,便于分析车辆的非 光滑动力学行为. 本文给出的方法不仅适用于前驱车辆的动力学分析,也适用于后驱或全驱车辆的动力学分析.
| [1] | Pacejka HB. Tyre and Vehicle Dynamics (2nd edn.). Cornwall:MPG Books Ltd., 2002 |
| [2] | Stone MR, Demetriou MA. Modeling and simulation of vehicle ride and handling Performance. IEEE, 2000. 85-90 |
| [3] | 姚远, 张红军, 罗赟等. 黏滑振动理论及其在铁路机车中的应用. 机械工程学报, 2010, 46 (24): 75-82 (Yao Yuan, Zhang Hongjun, Luo Yun, et al. Theory of stick-slip vibration and its application in locomotive. Journal of Mechanical Engineering, 2010, 46(24): 75-82 (in Chinese)) |
| [4] | 贾建章, 邵明亮. 高滑转率下车辆动力传动系的失稳与稳定性判据.农业机械学报, 1999, 30 (1):1-4 (Jia Jianzhang, Shao Mingliang. Stability criterion of vehicle power-train under high slipping rate. Transactions of the Chinese Society for Agricultural Mchinery, 1999, 30(1): 1-4 (in Chinese)) |
| [5] | 任少云, 包继华. 牵引车在大负荷拖载工况下传动系自激振动建模与仿真研究. 振动与冲击, 2005, 24 (6):95-101 (Ren Shaoyun, Bao Jihua. Modeling and simulation of the self-excited torsional vibration of driving for SZG 4031 towing tractor under heavy load. Journal of Vibration and Shock, 2005, 24(6): 95-101 (in Chinese)) |
| [6] | 喻进军, 杨明忠. 车辆发生跳跃现象的传动系自激振动研究. 机械研究与应用, 2006, 19 (2):46-48 (Yu Jinjun, Yang Mingzhong. Study on self-excited vibration of vehicle transmission in jumping phenomenon. Mechanical Research and Application, 2006, 19(2): 46-48 (in Chinese)) |
| [7] | 葛剑敏, 王佐民, 郑联珠. 轮式车辆传动系自激扭转振动仿真计算研究. 农业机械学报, 2003, 34 (3): 1-4 (Ge Jianmin, Wang Zuomin, Zheng Lianzhu. Simulation of self-excited vibration on vehicle power train. Transactions of the Chinese Society for Agricultural Machinery, 2003, 34(3): 1-4 (in Chinese)) |
| [8] | Oprea RA. Longitudinal dynamics of trains——a non-smooth approach. Nonlinear Dyn, 2012, 70: 1095-1106. |
| [9] | Oprea RA. A constrained motion perspective of railway vehicles collision. Multibody Syst Dyn, 2013, 30: 101-116. |
| [10] | Albert CJ, Brandon CG. Stick and non-stick periodic motions in periodically forced oscillators with dry friction. Journal of Sound and Vibration, 2006, 291(1/2): 132-168. |
| [11] | 曹洁, 吕敬, 王琪. 含滚阻摩擦平面多体系统的建模与数值方法. 北京航空航天大学学报, 2012, 38 (3): 410-415 (Cao Jie, Lü Jing, Wang Qi. Modeling and simulation of planar multi-body systems with rolling resistance and coulomb friction. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(3): 410-415 (in Chinese)) |
| [12] | 洪嘉振. 计算多体系统动力学. 北京:高等教育出版社, 1999 (Hong Jiazhen. Computational Dynamics of Multi-body Systems. Beijing: Higher Education Press, 1999 (in Chinese)) |
| [13] | 彭慧莲, 郭易圆, 王琪. 用第一类Lagrange方程求解平面多体系统约束力的方法. 工程力学, 2008, 25 (12):65-71 (Peng Huilian, Guo Yiyuan, Wang Qi. A method for solving constrained force of planar multi-body system via the first kind of Lagrange's equation. Engineering Mechanics, 2008, 25(12): 65-71 (in Chinese)) |
| [14] | Pfeiffer Friedrich. On non-smooth dynamics. Meccanica, 2008, 43(5): 533-554. |
| [15] | Pfeiffer F, Foerg M, Ubrlch H. Numerical aspects of non-smooth multibody dynamics. Computer Methods in Applied Mechanics and Enginee ring, 2006, 195(50/51): 6891-6908 |
| [16] | Andrzejewski R, Awrejcewicz J. Nonlinear Dynamics of A Wheeled Vehicle. New York: Springer, 2005 |
 2015, Vol. 47
2015, Vol. 47