2. 浙江工业大学机械工程学院, 杭州310014
随着新材料的研制和发展,仪器化压入测试在薄膜/涂层、非晶合金、生物材料、微机电系统等相关领域得到广泛应用,逐渐成为微/纳 米尺度材料力学参数识别的通用测试技术. 现有的测试技术是基于室温工况而建立的,为了掌握材料在不同温度下的力学性能,需要研究非室温下的压入测试技术. 仪器化压入测试的压入深度通常在几十纳米至几微米[1],测试条件的不稳定较易引起位移测量误差. 高温仪器化压入测试中,室温压头与热试样的非等温接触导致压头和部分压杆热胀冷缩,引起测量位移的热漂移,降低测试的准确性. 因此,必须研究高/低温仪器化压入测试中热接触对位移测量漂移的影响.
近年来,由于仪器设备、材料种类和温度范围各异,在高温仪器化压入测试研究领域主要出现以下2种不同的研究方向:
(1)稳态热接触研究. Schuh等[2]和Trenkle等[3]基于Hysitron公司的 Triboindenter®纳米压入系统: 室温压头和热试样首先在1μN或2μN的设定载荷下接触75min,压头 和试样的温度场达到各自的稳态后,开始进行压入测试. Schuh等[2]和Trenkle等[3]从实验和理论两方面分析,研究压头和试样稳态热接触后的传热引起设备构件的热胀冷缩对位移测量的影响,理论分析时未考虑压头和热试样接触面间接触热阻对温度场的影响. Lee等[4]在Schuh 等[2]研究的基础上,同样假设压头与试样接触面间接触热传导系数为无穷大,进行有限元模拟分析. 其研究表明,热漂移率受压头基托材料、试样种类和接触时间的影响,可以达到几个数量级的差异; 对较软的金属试样应严格控制压入深度,以减小热接触时间和面积.
(2)等温接触研究. Everitt等[5]基于Micro Materials公司的NanoTest® 纳米压入测试系统: 采用两个单独的加热装置,分别加热压头和试样,温度每升高100K,整个系统需平衡1h,以保证压头与试样接触面温度相同,然后进行压入测试. Everitt等[5]从有限元模拟和实验两方面对比分析,研究等温和非等温接触压入测试中位移漂移率的变化情况. 其研究表明,压头和试样等温接触,可以比较有效地减小位移漂移量; 非等温接触时,对于热传导率较大的金属试样,位移漂移量会超过设定阈值,建议采用快速加载方式以避免出现较大的热漂移[6, 7]. 因此,现有的研究很少研究高温下快速压入测试的情况,考虑压头与试样接触面间导热性质的瞬态热传导情况也较少,通常不考虑固体接触热阻对温度场的影响[8, 9, 10].
目前,Agilent 公司推荐Nano Indenter®G200采取快速测试(fast testing)的方式: 加卸载过程各1s,无预先热接触和热平衡过程,最大压入载荷300mN,加载速率为300mN/s. 压头与试样间存在接触热阻,为非等温接触,且接触面间传热为瞬态热传导. 因此,本文将针对Agilent 公司的Nano Indenter® G200的高温压入装置,重点研究压头和热试样接触面间热传导性质对基托内温度场的影响机制,分析压头基托热膨胀引起的位移测量漂移量,探讨如何优化测试程序,以便获得可靠的压入载荷- 深度曲线.
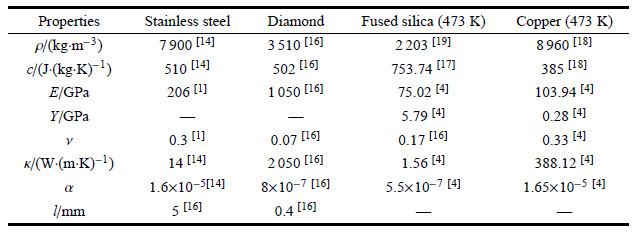
1 热传导理论分析分析对象为纳米压入仪的核心活动部件-----压头. 其由两部分组成: 前部为金刚石压尖(diamond tip),用于压入试样; 后部为不锈钢基托(stainless steel holder),用于固定压头前部和连接仪器压杆[1]. 其侧视图如图1所示.
|
图 1 压头的侧视图 Fig.1 Side elevation of the nanoindenter |
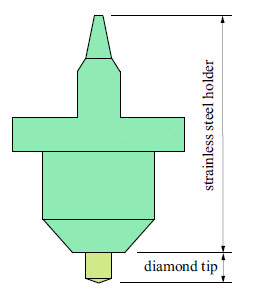
为了便于分析,简化压头模型(参见图2(a)): 基托部分根据等效体积法简化为圆柱体,选择相同的高度计算出等效半径; 正三棱锥尖端简化为等效半锥角为70.3$^\circ$的圆锥体. 简化后的热压入模型局部放大示意参见图2(b).
|
图 2 热压入的简化模型示意图 Fig.2 Illustration of the simplified model of hot nanoindentation |
(1) 待测试样温度保持恒定. 压头压入试样前,先通过热台(hot stage)将待测试样加热到特定温度,试样温度均匀后开始测试. 试样尺寸相对于压头足够大,可等效成半无限大体,如图2(a)所示. 采用快速测试的方式,即压头与试样从接触到分离仅经历数秒时间,所以暂不考虑压头对试样表面局部温度的影响.
(2)压头前部的金刚石瞬间达到热平衡. 在传热学中,可以通过热传导特征时间表征不同的材料的导热性能. 热传导特征时间[11]表示为
| $t_{\rm h.c.}\approx \frac{\rho cl^2}{\kappa}$ | (1) |
式中,$\rho $为密度,kg/m3; $c$为比热容,J/(kg$\cdot$K); $\kappa $为热传导率,W/(m$\cdot$K); $l$为特征长度,表征压头的金刚石压尖和不锈钢基托两部分的竖向几何高度尺寸. 根据式(1),结合表1所列的参数进行估计,金刚石和不锈钢的热传导特征时间分别约为$1\times10^{-4}$s和7s,两者热传导特征时间相差5个量级. 由此假定,压头和热试样接触后,压头前部的金刚石压尖瞬间达到热平衡[12, 13]. 金刚石压尖的几何特征仅导致热传导通道的横截面积大小,由实际接触面积$A_{\rm c}$ 过渡到基托横截面积$A_{\rm H} $,如图2所示.
| 表 1 材料属性参数表 Table 1 Materials' properties used in this study |
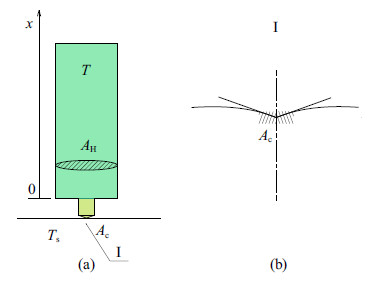
(3)压头与试样之间的热接触属于非理想接触. 接触面的局部放大示意图参见图3,由于实际接触面的粗糙不平,接触面间的热传递为两固体材料接触点的固体导热与空气间隙导热的复合[14]. 而空气 的导热系数远低于固体材料,温度场的求解不容忽视固体接触热阻的客观存在,因此接触的两表面间具有温度差.
|
图 3 接触面的局部放大示意图 Fig.3 Illustration of the local amplification of contacting surface |
(4)不锈钢基托和金刚石压尖在压入过程中只发生理想弹性变形,且假定其不受温度的影响. 基于假设(1)中待测试样温度 保持恒定,本文中试样的属性参数直接采用所研究的测试温度(473K)下的数值,如表1所示.
基于以上假设,高温仪器化压入测试中的热接触问题可以简化为,考虑固体接触热阻的半无限大热试样与室温压头接触时的一维瞬态 热传导问题.由于压头和热试样的初始温度不同,两者接触后,压头及其上部压杆温度会发生变化,产生热胀冷缩,引起位移测量漂移. 压头部分的温度场变化尤为关键,而金刚石压尖瞬间达到热平衡,分析最邻近的不锈钢基托内的温度场变化成为主要任务: 通过热传导理论分析,研究热接触后基托内温度场的变化情况,近似确定不同试样组合下基托热膨胀引起的位移漂移量,以便确定相应的热压入测试条件,优化高温压入测试程序,提高测试的可靠性.
1.2 接触面间的热传导分析压头与热试样之间为非理想热接触,即受固体接触热阻的影响,接触面间具有温度差. 为研究高温仪器化压入测试中热接触对位移测量漂移的影响,必须首先分析接触面间的热传导性质及其对压头基托内温度场的影响机制. 固体接触热阻和接触热传导系数成倒数关系
| $R = \frac{{1}}{k}$ | (2) |
式中,$R$为固体接触热阻,$k$为接触热传导系数. 相互接触的两固体表面之间一般通过直接接触点的传热、间隙气体对流传热和辐射传热3种 方式传热[21, 22, 23, 24],所以接触热传导系数包含如下3部分
| $k = k_{\rm c} + k_{\rm g} + k_{\rm r}$ | (3) |
式中,$k_{\rm c} $为直接接触导热系数,$k_{\rm g} $为间隙气体对流传热系数,$k_{\rm r} $为两物体间的辐射传热系数. 3种传热方式的贡献大小不等,且随着接触情况的不同而变化. 其中,直接接触导热系数$k_{\rm c}$[22]可以表示为
| $k_{\rm c} \approx \frac{p_{\rm 0} \kappa _{\rm r} }{E_{\rm r} u_0 }$ | (4) |
式中,$p_0 $为两接触面间的挤压压强,$\kappa _{\rm r} $为折合热传导率,$E_{\rm r} $为折合弹性模量,$u_0 \approx R_{{\rm RMS}}$[22],$R_{{\rm RMS}} $为表面均方根粗糙度(root-mean-square surface roughness). $1/{\kappa _{\rm r} } = 1/{\kappa _{\rm s} + }1/{\kappa _{\rm i} }$,$1/{E_{\rm r} } = 1/{E_{\rm s} } + 1/{E_{\rm i} }$,$\kappa $为热传导率,$E$为弹性模量,下角标s和i分别表示试样材料和压尖材料. 对于熔融石英和铜试样,$k_{\rm c}$的数量级分别为106W/(m2·k)和108W/(m2·k). 间隙气体对流传热系数[22]可表示为
| $k_{\rm g} = \kappa _{{\rm gas}} \langle \left( {d + \Lambda }\right)^{ - 1}\rangle$ | (5) |
式中,$d$为接触面的间隙距离,$\Lambda $为气体的平均自由程,$\left\langle \right\rangle $表示取总体平均值. 在大气压强和室温下$\kappa _{{\rm gas}} \approx0.02$W/(m·K),$\Lambda \approx 65$nm,$d$取为10nm量级,所以$k_{\rm g} \approx 1\times10^5$W/(m2·K). 辐射传热系数[13]可表示为
| $k_{\rm r} = \sigma \frac{T_{\rm s}^{4} - T_0^4 }{T_{\rm s} - T_0 }$ | (6) |
式中,$\sigma = 5.669\times 10^{ - 8}$W/(m2·K4)[13]为斯蒂芬-玻尔兹曼常数(Stefan-Boltzmann constant),$T_{\rm s} $为待测试样所需加热到的温度,$T_{\rm 0} $为室温压头的初始温度. 当$T_{\rm s} = 473$K,$T_{\rm 0} = 293$K时,估算得到$k_{\rm r} \approx 13$W/(m2·K).
经上述分析,3种传热系数之间存在数量级上的差异,表明压头与试样的直接接触传热占主导部分. 而且,实际的压入测试是在密闭箱内进行的,其内部空气流动接近静止,空气对流传热影响较小,可以忽略. 当温度低于773K时,辐射传热也可以忽略[3]. 故有近似关系
| $k \approx k_{\rm c} \approx \frac{p_0 \kappa _{\rm r} }{E_{\rm r} u_0 }$ | (7) |
压尖材料为金刚石,试样材料可选. 由式(7)可知,压头与热试样间的接触热传导系数随被测试样及其接触情况的不同而改变. 被测试样的导热性能越好,挤压压强越大,表面粗糙度越低,接触面间的传热性能就越好. 熔融石英(fused silica)和纯铜(copper)是热性能差异显著的两种材料,熔融石英可视为热绝缘性材料,而铜则为良导热性材料,两者的接触热传导系数数量级分别为106W/(m2K)和$10^8$W/(m$^{2}$$\cdot$K),相差2个数量级. 接触面间热传导性质又影响压头基托内温度场的重新分布,以及热膨胀引起的位移漂移,详见1.3节.
1.3 热传导方程的建立及其求解为了尽可能降低压头与试样间的温度差对位移测量的影响,Agilent公司的Nano Indenter® G200纳米压入系统推荐高温压入采取快速测试的方式,压入时间仅为数秒. 短时间内,热试样与室温压头接触所传递的热量尚未均匀分布,压头基托内温度场改变,且随时间发生变化,为瞬态热传导.
基于1.1节的简化模型和基本假设,列出相应的导热微分方程,并确定边界条件和时间条件,进而导出压头基托内温度场分布的解析解.
常物性一维温度场的非稳态导热微分方程[24]为
| $ \label{eq8} \frac{\partial ^2\vartheta \left( {x,t} \right)}{\partial x^2} = \frac{1}{a}\frac{\partial \vartheta \left( {x,t} \right)}{\partial t},\ \ 0 < x < \infty ,t > 0$ | (8) |
式中,$a = \kappa /{\rho c}$为基托的热扩散率,m2/s; 表征热传导过程中物体内温度场趋于一致的能力; $x$为自压头基托下端沿轴线的距离,如图2(a)所示; $\theta \left( {x,t}\right) = T\left( {x,t} \right) - T_0 $为温度的变化量,$T\left( {x,t} \right)$为压头基托内温度场分布.
求解上述微分方程,需要确定出定解条件. 本文研究问题中的定解条件包含两部分: 温度边界条件和时间初始条件,表示如下
| $\begin{array}{l} \kappa {A_{\rm{H}}}\frac{{\partial \vartheta \left( {x,t} \right)}}{{\partial x}} + {k_{\rm{c}}}{A_{\rm{c}}}\left( {\vartheta \left( {x,t} \right) - {\theta _0}} \right) = 0{\mkern 1mu} ,x = 0,t > 0\\ \vartheta \left( {x,t} \right) = 0{\mkern 1mu} ,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x \to \infty ,t > 0\\ \vartheta \left( {x,t} \right) = 0{\mkern 1mu} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} x \ge 0,t = 0 \end{array}$ | (9) |
式中,$\vartheta _0 = T_{\rm s} - T_0 $,定解条件式(9)中第1式为非理想接触情况接触面上的边界条件,把固体接触热阻的影响考虑在内,即相接触的两表面间存在温度差. 得到压头基托内温度场分布的解析解为
| $ \begin{array}{l} T\left( {x,t} \right) = {\vartheta _0}{\rm{erfc}}\left( {\frac{x}{{\sqrt {4at} }}} \right) + {T_0} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\vartheta _0}{e^{Gx + {G^2}at}} \cdot {\rm{erfc}}\left( {G\sqrt {at} + \frac{x}{{\sqrt {4at} }}} \right) \end{array}$ | (10) |
式中,为了简化解析解的表达形式,令$G \equiv {k_{\rm c} A_{\rm c} }/({\kappa A_{\rm H} })$,式(10)为简化后的表达式.
如果不考虑固体接触热阻的影响,假设压头与热试样是理想热接触,较容易推出基托内温度场分布的解析解[25]
| $T\left( {x,t} \right) = {\vartheta _0}{\rm{erfc}}\left( {\frac{x}{{\sqrt {4at} }}} \right) + {T_0}$ | (11) |
对比式(10)和(11)可以发现,非理想热接触的解析解表达式比理想热接触的解析解表达式多出一部分,该部分表示接触面间热传导性质对压头基托内温度场的影响. 对于非理想热接触,受接触热阻的影响,接触的两表面上具有温度差,即$x=0$时,式(10)简化为$T - T_{\rm s}= - \theta _0 e^{G^2at} \cdot \mbox{erfc}\left({G\sqrt {at} } \right) \le 0$; 对于理想热接触,接触面间传热系数为无穷大,接触的两表面上不具有温度差,即任意时刻,$x=0$,式(11)简化为$T = T_{\rm s} $.
分析理想和非理想热接触压头基托内的温度场分布情况. 设定分析条件: 被测试样熔融石英的温度为473K,压头及其周围环境温度为293K,采取快速加载的方式,加卸载过程各1s. 对于同种压入试样的理想和非理想热接触情况,压头基托内 温度场的分布情况如图4(a)所示,卸载结束,即$t=2$s时,基托内各点的温度变化量均达到3个数量级的差异. 对于同种压入试样两种不同热接触情况,压头基托上端边界处温度随时间的变化情况如图4(b)所示,任意时刻压头基托顶部温度的变化量均达到约3个数量级的差异. $t<0.3$s时,非理想热接触温升约为10$^{- 5}$量级,理想热接触温升约为10$^{-2}$量级,温升量非常小,为了能在同一图中表示两种热接触情况的温度改变量,图中从0.3s开始. 因此,研究高温仪器化压入测试中热接触对位移测量漂移的影响时,固体接触热阻对温度场的影响不容忽视,接触面间的热传导性质显著影响压头基托内温度场的分布.

|
图 4 理想和非理想热接触 Fig.4 Perfect and imperfect thermal contact |
分析不同试样材料在理想和非理想热接触时压头基托内的温度场分布情况,分析条件设定同上. 对于理想热接触,由于式(11)中仅含 基托材料的属性参量,表明压头基托内温度场的变化不受待测试样材料性质的影响,如图5(a)所示,卸载结束,即$t=2$s时,熔融石英和铜试样对应的压头基托内温度场分布情况是重合的. 对于非理想热接触,式(7)中同时含有基托材料和待测试样的属性参量,表明压头基托内温度场的变化不仅与基托材料性质相关,也与试样材料属性有关,如图5(b)所示,卸载结束,即$t=2$s时,熔融石英和铜试样分别对应的基托相同位置处温度的变化量达到2个数量级的差异. 因此,研究高温仪器化压入测试中热接触对位移测量漂移的影响时,不同的试样材料,接触面间传热效果的不同会显著影响压头基托内温度场的分布.

|
图 5 卸载结束时压头分别与熔融石英和铜热接触时基托内的温度场分布 Fig.5 Temperature distribution along the of the holder at the end of unload respectively when indenting on fused silica and copper |
分析热膨胀引起的位移漂移量. 设定分析条件: 被测试样温度为473K压头及其周围环境温度为293K.传感器位移测量差异量主要是压头基托长度的变化,积分基托内温度场的变化量,可得压头基托部分热膨胀引起的位移漂移量
| $ U = \int_0^l {\alpha _l \vartheta \left( {x,t} \right)}d x = f(\alpha _l ,\vartheta _0 ,a,G,x,t)$ | (12) |
式中,$\alpha _l $为基托的(线)热膨胀系数. 对于非理想热接触,式(12)中含有参量$G$,$G$与接触热传导系数$k$相关,而不同试样与压头接触面间接触热传导系数不同,表明测试条件相同时,位移漂移量$U$会随试样而改变. 对于熔融石英和铜试样,基托热膨胀引起的位移漂移量分别约为6.67nm和680nm,平均热漂移率分别约为3.33nm/s和340nm/s,达到2个数量级的差异. 因此,高温仪器化压入测试中待测试样的材料种类对位移测量漂移有显著影响.
另外,通过理论分析的解析结果可说明压头上部连接压杆的热膨胀效应可忽略不考虑. 如图5(b)所示,对于标准试样熔融石英,压头基托 最上端边界处温升约为0.02K,上部连接压杆的温升假定为均匀的0.02K,特征长度设为10mm,材料殷钢的热膨胀系数为$\alpha = 1.2\times 10^{ - 6}$K$^{ - 1}$,则压杆热膨胀量约为0.24nm远远小于压头不锈钢基托热膨胀量6.67nm,故假定可忽略压杆的热膨胀效应对位移测量漂移的的影响.
对于标准试样熔融石英,Agilent公司在G200的使用手册中指出,采用快速测试的方法进行大量试验得到热漂移率在5nm/s以内[20],本文研究中设定的测试条件参考使用手册中所给建议,且研究结果与其一致. 对于导热性能较好的铜试样,热漂移率较大,会造成测量数据的严重偏差. Everitta等[4]也指出对于导热性能性能较好的金属试样,压入过程中会引起基托较大的热膨胀量,超过可接受范围,本文的研究结果与之一致.
2 热压入的有限元模拟为验证上述理论分析的准确性,本文借助商业有限元软件ABAQUS模拟高温仪器化压入测试过程.热压入模型简化为一变形体压头(包括金刚石压尖和不锈钢基托)压入半无限大热试样,试样大小设定为最大接触半径的10倍以上,以便试样可近似为半无限大体,忽略边界效应的影响. 为便于分析,简化方法同第1节,有限元分析模型的示意图如图6所示,具体尺寸参考Micro Star Technologies[16]中提供的实际压头的尺寸简化等效得到.
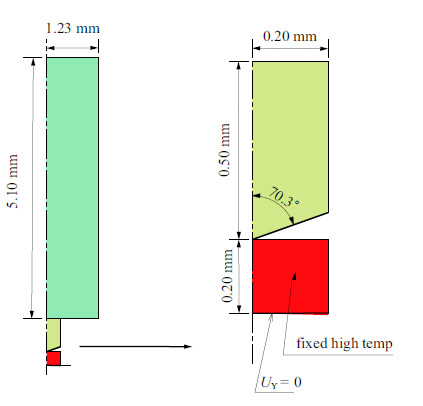
|
图 6 热压入有限元分析模型示意图 Fig.6 Illustration of the finite element model of hot nanoindentation |
本文有限元分析模型采用轴对称二维变形体模型,压头由不锈钢基托和金刚石压尖构成. ABAQUS模拟热压入过程,应选用温度-位移耦合(coupled temp--displacement)分析模块,模型中所有单元均采用4节点热耦合的轴对称四边形单元(CAX4T)[3]. 属性参量设置: 在材料属性(property)模块中分别设置基托材料不锈钢、压尖材料金刚石、试样材料(铜和熔融石英)的弹性模量、泊松比、密度、热传导率、比热容和热膨胀系数; 在接触(interaction)模块中设置接触面热传导系数(thermal conductance),理想热接触时为无穷大,模拟中分别设置为1$\times$10$^{6}$,1$\times$10$^{7}$,1$\times$10$^{8}$和无穷大进行分析. 设定数值模拟条件: 被测试样温度为473K,压头及其周围环境温度为293K; 采取位移控制的方式,压深为1000nm,加卸载过程各1s.
通过有限元模拟,可以得到温度场的实时变化情况,以及压头基托热膨胀引起的位移测量漂移量. 将得到的数值结果($T_{\rm FEM})$与1.3节的解析结果($T_{\rm AM})$对比分析,以验证解析解的准确性. 数值模拟中压头与热试样的接触面积由零逐渐变化,理论模型中热接触面积假设为常量,因此解析结果比数值结果偏大. 如图7(a)所示,对于熔融石英试样,压头基托内温度场分布的数值解与解析解的相对误差在$\pm$0.02%以内,表明两者吻合较好. 因此,有限元模拟验证了理论分析的正确性.

|
图 7 Fig.7 |
图7(b)为压头与不同材料的试样热接触后引起位移测量漂移量的数值结果,有限元模拟所用到的试样材料属性参数直接采 用常温下的数值,如表2所示. 图中材料大致分为两类: $\kappa< 10$W/(m$\cdot$K),主要为玻璃; 10W/(m$\cdot$K) $< \kappa < 500$W/(m$\cdot$K),主要为纯金属及其合金. 可以看出,位移测量漂移量随被测试样热传导率的增大而变大; 对于两类试样,压头基托的热膨胀量最高可达到约两个数量级的差异. 合金的硬度一般比其组分中任一纯金属的硬度大,热传导率和弹性模量一般与合金的组成元素相当[27],结合式(7),易得合金试样与压头接触面间传热性能优于纯金属试样. 如图7(b)所示,卸载结束,即$t=2$s时,合金试样引起的位移测量漂移量高于对应的纯金属试样,表明不同试样接触面间的传热效果会显著影响位移测量漂移量. 因此,有限元模拟的数值结果与理论分析的结论保持一致.
| 表 2 材料属性参数表 Table 2 Materials' properties used in FEM |
针对高温仪器化压入测试中压头与高温试样接触传热引起测量位移漂移的问题,本文从研究室温压头与热试样接触面间的 热传导性质出发,探讨固体接触热阻对压头基托内温度场的影响. 采用理论分析和有限元模拟的技术途径,并以数值模拟验证理论分析的准确性. 研究发现,压头与热试样间的接触热阻对压头基托内温度场的重新分布有不可忽视的作用,显著影响基托的热膨胀量,导致压入深度的测量误差. 不同材料属性的被测试样与压头接触面间的接触热阻不同,引起的位移测量漂移量可以达到几个数量级的差异. 本文所研究的1000nm压深的高温测试,对于热传导率较差的熔融石英,理论分析和数值模拟获得的位移测量热漂移率均在5nm/s以内,说明对于导热性差的被测试样,在一定测试条件下可以保证位移测量数据的可靠性,同时校核了G200使用手册中建议熔融石英经验性测试条件[20]的可靠性. 对于热传导率良好的铜试样,位移测量漂移量能够达到数百纳米,导致测量数据偏差较大. 因此,对于导热性好的金属及合金试样,压入测试时,可采取缩短压入时间等措施,尽可能减小热接触引起的位移测量漂移量. 本文的研究结果将有助于确定高温仪器化压入测试条件,优化测试程序,以便获得可靠的高温压入载荷-深度曲线及其材料力学性能.
| [1] | 张泰华. 微/纳米力学测试技术及其应用——仪器化压入的测量、分析、应用及其标准化.北京: 科学出版社, 2013 (Zhang Taihua. Micro/nano-mechanics Testing Technology and Its Application —— Measurement, Analysis, Application and Standardization of Instrumented Indentation. Beijing: Science Press, 2013 (in Chinese)) |
| [2] | Schuh CA, Packard CE, Lund AC. Nanoindentation and contact-mode imaging at high temperatures. Journal of Materials Research, 2006, 21(efeq3):725-736 |
| [3] | Trenkle JC, Packard CE, Schuh CA. Hot nanoindentation in inert environments. Review of Scientific Instruments, 2010, 81(7): 073901 |
| [4] | Lee H, Chen Y, Claisse A, et al. Finite element simulation of hot nanoindentation in vacuum. Experimental Mechanics, 2013, 53(efeq7):1201-1211 |
| [5] | Everitt NM, Davies MI, Smith JF. High temperature nanoindentation ——- the importance of isothermal contact. Philosophical Magazine A-Physics of Condensed Matter Structure Defects and Mechanical Properties, 2011, 91(7-9):1221-1244 |
| [6] | Guillonneau G, Kermouche G, Bec S, et al. A simple method to minimize displacement measurement uncertainties using dynamic nanoindentation testing. Tribology International, 2014, 70:190-198 |
| [7] | Korte S, Stearn RJ, Wheeler JM, et al. High temperature microcompression and nanoindentation in vacuum. Journal of Materials Research, 2012, 27(01): 167-176 |
| [8] | Wheeler JM, Michler J. Elevated temperature, nano-mechanical testing in situ in the scanning electron microscope. Review of Scientific Instruments, 2013, 84(efeq4): 045103 |
| [9] | Wheeler JM, Brodard P, Michler J. Elevated temperature, in situ indentation with calibrated contact temperatures. Philosophical Magazine, 2012, 92(25-27):3128-3141 |
| [10] | Wheeler JM, Michler J. Invited Article: Indenter materials for high temperature nanoindentation. Review of Scientific Instruments, 2013, 84(efeq10):101301 |
| [11] | 谈庆明.量纲分析.合肥: 中国科学技术大学出版社, 2005 (Tan Qingming. DimensionalAnalysis. Hefei: University of Science and Technology of China Press, 2005 (in Chinese)) |
| [12] | Cui JB, Amtmann K, Ristein J, et al. Noncontact temperature measurements of diamond by Raman scattering spectroscopy. Journal of Applied Physics, 1998, 83(12): 7929-7933 |
| [13] | Beake BD, Smith JF. High-temperature nanoindentation testing of fused silica and other materials. Philosophical Magazine A, 2002, 82(10): 2179-2186 |
| [14] | 岳丹婷. 工程热力学和传热学. 大连: 大连海事大学出版社, 2009 (Yue Danting. Engineering Thermodynamics and Heat Transfer. Dalian: Dalian Maritime University Press, 2009 (in Chinese)) |
| [15] | Chrobak D, Kim KH, Kurzydlowski KJ, et al. Nanoindentation experiments with different loading rate distinguish the mechanism of incipient plasticity. Applied Physics Letters, 2013, 103(7): 072101 |
| [16] | Micro Star Technologies. http://www.microstartech.com |
| [17] | Bhakhri V, Wang J, Ur-rehman N, et al. Instrumented nanoindentation investigation into the mechanical behavior of ceramics at moderately elevated temperatures. Journal of Materials Research, 2012, 27(1): 64-74 |
| [18] | Carderelli F. Materials Handbook: A Concise Desktop Reference. New York: Springer, 2008 |
| [19] | Korte S, Clegg WJ. Micropillar compression of ceramics at elevated temperatures. Scripta Materialia, 2009, 60(9): 807-810 |
| [20] | Agilent Technologies. Localized high temperature stage user's guide .Part number G2A-13192-© Agilent Technologies, Inc. 201 |
| [21] | Abuzeida OM, Alnumanb N. Thermal contact conductance of elastically deforming nominally flat surfaces using fractal geometry. Industrial Lubrication and Tribology , 2013, 65(efeq6): 390-398 |
| [22] | Persson BNJ, Lorenz B, Volokitin AI. Heat transfer between elastic solids with randomly rough surfaces. European Physical Journal E, 2010, 31(efeq1): 3-24 |
| [23] | Bahrami M, Culham JR, Yananovich MM, et al. Review of thermal joint resistance models for nonconforming rough surfaces. Applied Mechanics Reviews, 2006, 59(1-6):1-12 |
| [24] | Johnson KL. Contact Mechanics. Cambridge :Cambridge University Press, 1985 |
| [25] | Crank J. The Mathematics of Diffusion. Clarendon: Oxford, 1979 |
| [26] | David WH, Necati OM. Heat Conduction. John Wiley and Sons, 1979 |
| [27] | Adelbert Phillo Mills. Materials of Construction: Their Manufacture and Properties. John Wiley and Sons, 1979 |
| [28] | Vin Karola. http://www.vinkarola.com/pdf. © Vin Karola Instruments, 2003 |
| [29] | http://www.azom.com/article.aspx?ArticleID=6652,2014.08.08http://www.azom.com/article.aspx?ArticleID=6652,2014.08.08 |
| [30] | Material Properties Database. http://www.makeitfrom.com,2014.08.08 |
2. College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China
 2015, Vol. 47
2015, Vol. 47