2. 成都飞机设计研究所, 成都610091
连续纤维增强陶瓷基复合材料是由高强度的纤维,高模量和抗氧化性能优良的基体,以及保证材料在多重损伤机制下表现出良好的韧性破坏的界面层材料组成,因而其具有耐高温、抗氧化、高比强、高比模和显著的韧性破坏等优异的力学性能,并在航空航天领域具有广阔的应用前景[1]. 新型材料的设计、使用和改良都必须以了解和掌握各材料组分的性能为基础,例如基体开裂应力、热残余应力、界面脱粘能和界面滑移力等,以上都是控制材料力学行为和性能的重要参数[2].
Domergue等[3, 4, 5]首先提出并建立了连续纤维增强陶瓷基复合材料迟滞行为与组份力学 性能参数间的计算关系; 在基体裂纹均匀分布假设下,计算分析了具有单向、0/90°叠层和平纹编织3种纤维结构的SiC/CAS和SiC/SiC 复合材料组份力学性能参数. Ahn等[6]考虑了基体的随机开裂过程,依据裂纹间距大小将基体碎块分为长、中、短3种并区别对待;在不考虑界面脱粘能的条件下分析 计算了单向SiC/CAS复合材料的组份力学性能参数. Li等[7]依据界面是否完全脱粘和脱粘区域能否发生完全反向滑移,分4种情况研究了单向SiC/CAS复合材料的迟滞力学行为并计算得到了界面剪切力随循环加载次数的变化规律. Wang等[8]研究了2D-C/SiC复合材料的迟滞力学行为,并运用文献[3]中的理论结果计算得到了材料的界面滑移力和纤维径向热残余应力.
本文基于剪滞理论,考虑界面脱粘能和基体碎块长度,并结合2D-SiC/SiC复合材料自身特点,建立了其加卸载理论模型. 通过循环加卸载试验获得了2D-SiC/SiC复合材料的迟滞力学行为. 通过计算得到了4个表征材料组份性能的参数: 基体开裂应力、热残余应力、界面脱粘能和界面滑移力. 最后考虑基体短碎块的存在,分析了其对所得数值精准性的影响. 得到的材料组份性能参数能够有效的表征材料整体的力学行为.
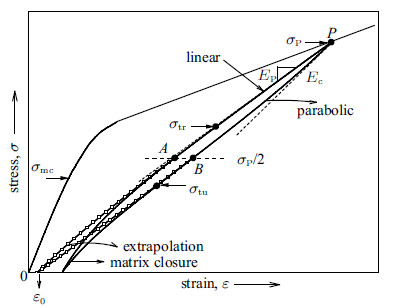
1 2D-SiC/SiC复合材料迟滞-应力应变行为2D-SiC/SiC复合材料的典型拉伸迟滞应力-应变曲线如图1所示. 在拉伸应力达到$\sigma _{\rm mc}$之前,材料表现为线弹性. 卸载和重加载过程对应应力-应变曲线分别由直线段和二次曲线组成,两者间的应力边界值分别定义为卸载临界应力$\sigma_{\rm tu}$和重加载临界应力$\sigma _{\rm tr}$; 曲线切线模量的最大值和最小值分别定义为含裂纹的材料拉伸模量$E_{\rm c}$和平台模量$E_{\rm P}$[3]. 图中方形点划线部分是依据迟滞环对称特点得到的去除裂纹闭合效应影响的应力-应变曲线,$\varepsilon_0$为残余应变.
|
图 1 2D-SiC/SiC复合材料迟滞应力-应变行为 Fig.1 Schematic of the hysteresis stress-strain behavior of 2D SiC/SiC |
对于2D-SiC/SiC复合材料,拉伸载荷主要由纵向(加载向)纤维束承担,单轴拉伸力学行为也主要由纵向纤维束决定[9]. 拉伸过程中 纵向纤维束内发生的基体横向开裂、界面脱粘和滑移等损伤机制是控制材料迟滞力学行为的主要因素. 同时, 材料内部SiC纤维的弯曲角度很小,最大倾斜角约为13$^\circ$,拉伸力学行为与竖直纤维束近似. 研究发现, 2D-SiC/SiC复合材料和1D-SiC/SiC复合材料的拉伸应力-应变曲线具有典型的1/2对应关系[10]. 在相同的拉伸损伤机制下,可以利用一维迟滞力学模型从宏观上对2D-SiC/SiC复合材料迟滞力学行为及 材料组份性\linebreak 能[5, 8]进行分析计算. 通过上述方法得到的计算结果并不是材料组分的真实就位力学性能, 但是可以用来表征材料整体的力学性能和迟滞行为. 上述计算方法避开了材料复杂的平纹编织几何结构, 显著降低了计算难度.
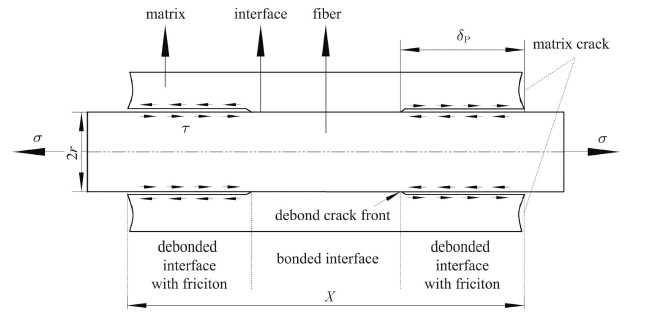
2 一维迟滞力学模型复合材料的拉伸损伤主要发生在应力区间($\sigma _{\rm mc}$,$\sigma _{\rm s} $)内,而迟滞应力-应变行为的研究 也主要集中在这一应力区间,其中$\sigma _{\rm s} $为基体裂纹饱和应力. 在上述应力区间内, 假设材料只发生基体开裂、界面脱粘和滑移,但是纤维保持完好,那么材料整体与纤维具有相同的轴向变形. 通过如图2所示的剪滞理论模型,可以求得加卸载过程中纤维轴向平均应力与施加应力的对应关系, 并进一步得到材料的迟滞应力-应变行为. 剪滞模型中$r$为纤维半径,$\delta _{\rm P} $为界面脱粘长度, $\tau$为界面滑移力,$x$为相邻基体裂纹间距,即基体碎块长度.
|
图 2 剪滞模型单胞示意图 Fig.2 The unit cell of shear-lag mode |
当施加应力$\sigma $达到卸载峰值应力$\sigma _{\rm P} $时,基体裂纹两侧的界面脱粘长度$\delta _{\rm P} $为
| $\delta _{\rm P} = \frac{r}{2\tau }[\alpha (\sigma _{\rm P} + \sigma _{\rm th} ) - \gamma]$ | (1) |
其中
| $\alpha = (V_{\rm m} E_{\rm m} ) / (V_{\rm f} E)$ | (2) |
$\sigma _{\rm th}$为材料热残余应力,$V_{\rm m}$和$V_{\rm f}$分别为基体和纤维体积分数, $E_{\rm m}$和$E$分别为基体拉伸模量和复合材料初始拉伸模量. $\gamma$为界面脱粘尖端处纤维内部轴向应力的突变数值,具体形式[3, 11]如下
| $\gamma = \sigma _{\rm{f}}^ - - \sigma _{\rm{f}}^ + = \frac{{1 - {a_1}{V_{\rm{f}}}}}{{{V_{\rm{f}}}{c_1}}}\sqrt {\frac{{{E_{\rm{m}}}{\rm{ }}{\Gamma _i}}}{r}} $ | (3) |
其中$\Gamma _i $为界面脱粘能,$a_1 $和$c_1 $为无量纲系数[11].
由于2D-SiC/SiC复合材料具有较大的界面脱粘能,加卸载过程中正向和反向滑移会在整个界面脱粘区域发生[3],所以只需将不同长度基体碎块划分为长、短两类. 本文中,对于给定的$\sigma_{\rm P} $,当基体碎块长度$x > 2\delta _{\rm P} $时,其在加载过程中只发生部分脱粘,称之为长碎块,当$x \le 2\delta _{\rm P} $时,其包裹界面发生完全脱粘,称之为短碎块. 加卸载过程中长、短碎块包裹纤维的轴向应力分布具有不同形式,需要区别对待.
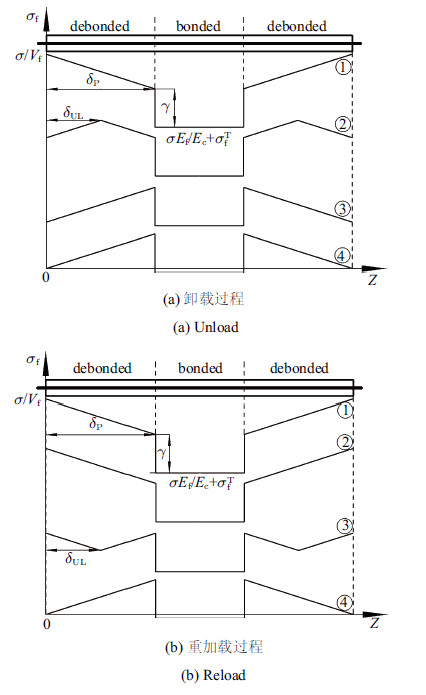
2.1 长碎块包裹纤维的轴向应力分布加卸载过程中,依据剪滞模型得到长碎块包裹纤维的轴向应力分布曲线如图3所示. 在图3(a)中,状态①对应卸载初始时刻, 即施 加应力$\sigma= \sigma _{\rm P} $,此时长碎块包裹纤维的轴向平均应力为
| $\sigma _{\rm UL} = \frac{\delta _{\rm P}}{x} [\alpha (\sigma _{\rm P} + \sigma _{\rm th} ) + \gamma] + \left(\sigma _{\rm P} \frac{E_{\rm f} }{E_{\rm c} } - \alpha \sigma _{\rm th} \right)$ | (4) |
|
图 3 加卸载过程中长基体碎块包裹纤维轴向应力分布图 Fig.3 The distributions of axial stress within fibers wrapped by long fragment during load-unload cycle |
考虑到热残余应力的影响,为使计算应变与实测应变一致,求得的纤维轴向平均应力都需要加上$\alpha \sigma _{\rm th} $,故式(4)变为
| $ \sigma _{\rm UL} = \frac{\delta _{\rm P}}{x} [\alpha (\sigma _{\rm P} + \sigma _{\rm th} ) + \gamma ] + \sigma _{\rm P} \frac{E_{\rm f} }{E_{\rm c} }$ | (5) |
随着$\sigma $的减小,界面脱粘区域由裂纹面向内开始发生界面反向滑移,反向滑移长度$\delta _{\rm
| $\delta _{\rm U} = \frac{r\alpha }{4\tau }(\sigma _{\rm P} - \sigma )$ | (6) |
在发生完全反向滑移之前(状态②),纤维的轴向平均应力为
| ${\sigma _{{\rm{UL}}}} = [{\delta _{\rm{P}}}\alpha ({\sigma _{\rm{P}}} + {\sigma _{{\rm{th}}}}) + {\delta _{\rm{P}}}\gamma - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{r{\alpha ^2}}}{{4\tau }}{({\sigma _{\rm{P}}} - \sigma )^2}]\frac{1}{x} + \sigma \frac{{{E_{\rm{f}}}}}{{{E_{\rm{c}}}}}$ | (7) |
卸载过程中反向滑移长度不断增加,当反向滑移到达界面脱粘尖端时,$\delta _{\rm U} $ 达到最大值并且$\delta _{\rm U} = \delta _{\rm P} $,此时界面脱粘区域正好发生完全反向滑移,对应的卸载临界应力为
| $\sigma _{\rm tu}^{\rm L} = 2(Y - \sigma _{\rm th} ) - \sigma _{\rm P}$ | (8) |
其中$Y = \gamma / \alpha $. 分析可知材料能够发生完全反向滑移的条件为
| $\gamma \ge \frac{\alpha }{2}(\sigma _{\rm P} + 2\sigma _{\rm th} )$ | (9) |
完全反向滑移发生后(状态③),反向滑移长度不再增加,此时纤维的轴向平均应力为
| $ \sigma _{\rm UL} = \frac{\delta _{\rm P}}{x} [\alpha (2\sigma + \sigma _{\rm P} ) + 3\alpha \sigma _{\rm th} - \gamma] + \sigma \frac{E_{\rm f} }{E_{\rm c} }$ | (10) |
当卸载到0时(状态④),纤维的轴向平均应力为
| $\sigma _{\rm UL}^0 =\frac{ \delta _{\rm P}}{x} [\alpha \sigma _{\rm P} + 3\alpha \sigma _{\rm th} - \gamma]$ | (11) |
重加载过程中长碎块包裹纤维的轴向应力分布曲线如图3(b)所示. 此阶段,界面脱粘区域纤维相对于基体再次发生正向滑移,正向滑移距离为
| $\delta _{\rm R} = \frac{r\alpha }{4\tau }\sigma$ | (12) |
当$\delta _{\rm R} < \delta _{\rm P} $时(状态②),纤维的轴向平均应力为
| $ \sigma _{\rm RL} = \sigma \frac{E_{\rm f} }{E_{\rm c} } + \bigg\{\delta _{\rm P} [\alpha (\sigma _{\rm P} + 3\sigma _{\rm th} ) - \gamma] + \frac{r\alpha ^2\sigma ^2}{4\tau }\bigg\} / x$ | (13) |
当$\delta _{\rm R} = \delta _{\rm P} $时,正向滑移到达界面脱粘尖端,此时的重加载临界应力为
| $\sigma _{\rm tr}^{\rm L} = 2[\sigma _{\rm P} - (Y - \sigma _{\rm th} )]$ | (14) |
完全正向滑移发生后(状态③),纤维的轴向平均应力为
| $ \sigma _{\rm RL} = \sigma \frac{E_{\rm f} }{E_{\rm c} } + \frac{\delta _{\rm P}}{x} [2\alpha \sigma + \alpha (\sigma _{\rm th} - \sigma _{\rm P} ) + \gamma]$ | (15) |
当施加应力重新达到$\sigma _{\rm P}$时,纤维轴向平均应力表达式与式(5)相同.
2.2 短碎块包裹纤维的轴向应力分布卸载和重加载过程中,短碎块包裹纤维的轴向应力分布曲线在图4中给出. 当$\sigma = \sigma _{\rm P} $时,短碎块包裹纤维与基体间界面会发生完全脱粘.

|
图 4 短基体碎块加卸载过程中纤维轴向应力分布图 Fig.4 The distributions of axial stress within fibers wrapped by short fragment during load-unload cycle |
卸载过程中,在界面脱粘区域未发生完全反向滑移之前(状态②),短碎块包裹纤维的轴向平均应力为
| $\sigma _{\rm US} = \left[\alpha (\sigma _{\rm P} + \sigma _{\rm th} ) + \sigma \frac{E_{\rm f} }{E_{\rm c} }\right] - \frac{\tau }{2r}x - \frac{r\alpha ^2}{4\tau x}(\sigma _{\rm P} - \sigma )^2$ | (16) |
当$\delta _{\rm U} = x / 2$时,界面脱粘区域发生完全反向滑移,对应卸载临界应力为
| $\sigma _{\rm tu}^{\rm S} = \sigma _{\rm P} - \frac{2\tau x}{r\alpha }$ | (17) |
完全反向滑移发生后(状态③),纤维轴向平均应力为
| $ \sigma _{\rm US} = \frac{\sigma }{V_{\rm f} } + \alpha \sigma _{\rm th} + \frac{\tau }{2r}x$ | (18) |
当$\sigma = 0$时(状态④),纤维轴向平均应力为
| $\sigma _{US}^00 = \alpha {\sigma _{{\rm{th}}}} + \frac{\tau }{{2r}}x$ | (19) |
重加载过程中,当$\delta _{\rm R} < x / 2$时(状态②),轴向平均应力为
| $ \sigma _{\rm RS} = \sigma \frac{E_{\rm f} }{E_{\rm c} } + \alpha \sigma _{\rm th} + \frac{\tau x}{2r} + \frac{r\alpha ^2\sigma ^2}{4\tau x}$ | (20) |
当$\delta _{\rm R} = x / 2$时,界面脱粘区域刚好发生完全正向滑移,对应重加载临界应力为
| $\sigma _{\rm tr}^{\rm S} = 2\frac{\tau x}{r\alpha }$ | (21) |
完全正向滑移发生后(状态③),轴向平均应力为
| $ \sigma _{\rm RS} = \frac{\sigma }{V_{\rm f} } + \alpha \sigma _{\rm th} - \frac{\tau x}{2r}$ | (22) |
加卸载过程中,如果材料基体开裂所形成的基体碎块全为长碎块,通过纤维轴向平均应力随施加应力的变化关系式$F(\sigma)$可以得到材料整体的迟滞应力-应变行为如下式所示
| $\varepsilon = \frac{\sigma _{\rm R,U} }{E_{\rm f} } = \frac{F(\sigma )}{E_{\rm f} }$ | (23) |
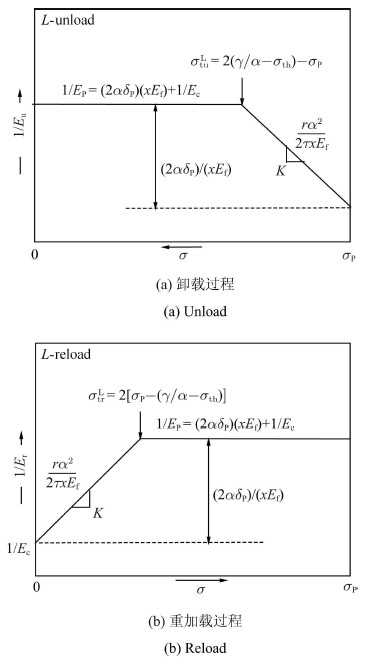
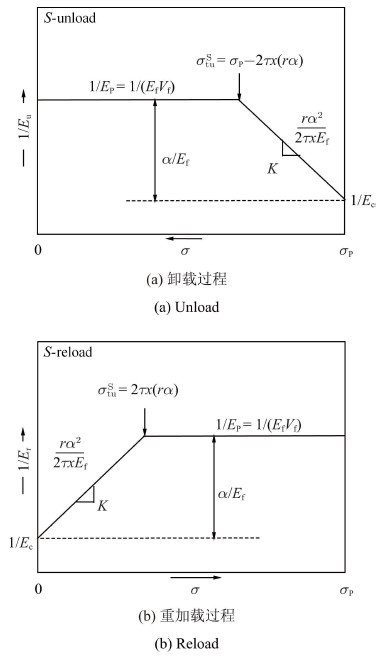
其中,$\varepsilon $为纤维轴向应变,即材料整体的拉伸应变; $E_{\rm f} $为纤维拉伸弹性模量. 将式(23)两端分别对$\sigma $求导,得到卸载和重加载过程中应力-应变曲线切线模量的倒数$E_{\rm u}^{- 1} $和$E_{\rm r}^{ - 1} $随施加应力$\sigma $的变化关系曲线如图5中所示. 同理,如果加卸载过程中材料基体开裂全部形成短碎块,对应的$E_{\rm u}^{-1} $和$E_{\rm r}^{ - 1} $随施加应力$\sigma $的变化曲线如图6所示.
|
图 5 长碎块切线模量倒数随加载、卸载应力变化示意图 Fig.5 Relation curves between inverse tangent moduli $E_{\rm u}^{ - 1} $ and unloading stress $\sigma _{\rm u} $, $E_{\rm r}^{ - 1}$ between reloading stress $\sigma_{\rm r} $ for long fragment |
|
图 6 短碎块切线模量倒数随加载、卸载应力变化示意图 Fig.6 Relation curves between inverse tangent moduli $E_{\rm u}^{ - 1} $ and unloading stress $\sigma _{\rm u} $, $E_{\rm r}^{ - 1}$ and reloading stress $\sigma _{\rm r} $ for short fragment |
由图5和图6可以看出,卸载过程中以$\sigma _{\rm tu} $为分界点,$E_{\rm u}^{ - 1} $随$\sigma $的减小首先线性增加而后保持不变; 重加载过程中以$\sigma _{\rm tr}$为分界点,$E_{\rm r}^{ - 1} $随$\sigma $的增大首先线性增加而后保持不变. 这是因为加卸载过程中界面发生了反向和正向滑移,改变了纤维和基体间的载荷传递方向和基体的载荷承担比例,并最终影响了材料整体的迟滞应力-应变行为. 界面脱粘区域反向和正向滑移长度随施加应力的变化是材料加卸载应力-应变曲线形状发生分段变化的原因.
2.4 材料组份性能参数计算2D-SiC/SiC复合材料的拉伸强度小于基体裂纹饱和应力,拉伸过程中界面不会出现完全脱粘,绝大部分基体碎块只在两端发生部分脱粘,属于长碎块. 较大的界面脱粘能是2D-SiC/SiC复合材料具有上述拉伸损伤特性的主要原因. 但是由于材料内部孔洞的存在,再加上SiC基体的制备缺陷,在应力集中作用下,材料内部也会出现开裂间距较小的基体裂纹,进而形成基体短碎块. 综上所述,拉伸过程中2D-SiC/SiC复合材料内部的基体碎块由绝大多数的长碎块和少量短碎块共同组成. 所以下面通过长碎块对应的推导结果获得材料组份性能参数的计算方法. 最后考虑少量短碎块的影响,对所得计算结果的精准性进行进一步分析.
首先由图5可得
| $K = \frac{r\alpha ^2}{2\tau xE_{\rm f} }$ | (24) |
其中,$K$值由试验曲线拟合得到,在$x$数值已知的条件下,可求得界面滑移力$\tau $值. 此外由图5可得
| $ \frac{1}{E_{\rm P} } - \frac{1}{E_{\rm c} } = \frac{2\alpha \delta _{\rm P} }{xE_{\rm f} }$ | (25) |
由式(11)和式(23)可得
| $\varepsilon _0 = \frac{\alpha \delta_{\rm P}}{xE_{\rm f} }[\sigma _{\rm P} + \alpha \sigma _{\rm th} - \gamma / \alpha]$ | (26) |
综合式(24)~式(26),可得到热残余应力$\sigma _{\rm th} $和界面脱粘尖端纤维轴向应力突变$\gamma $值; 将$\gamma $值代入式(3),可以求得材料界面脱粘能$\Gamma _i $值; 通过基体损伤参数$D$与$\sigma _{\rm P} $的关系曲线可求得基体开裂应力$\sigma _{\rm mc} $.
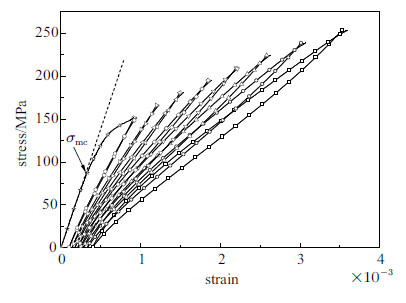
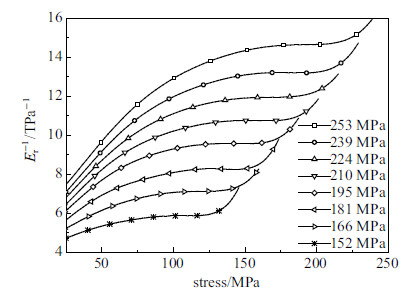
3 分析计算 3.1 试验及数据处理拉伸加卸载试验在Instron 5567试验机上进行,加载速率为0.2mm/min. 试验所得应力-应变曲线如图7所示. 由重加载过程对应的应力-应变曲线得到的$E_{\rm r}^{-1}$随施加应力$\sigma $的变化曲线如图8所示. 图8中试验结果与图5中理论推导结果基本一致,都是由线性上升段和平台段两部分组成.
|
图 7 2D-SiC/SiC复合材料迟滞应力-应变曲线 Fig.7 Hysteresis stress--strain curve of 2D-SiC/SiC composites |
|
图 8 重加载过程中$E_{\rm r}^{ - 1} $随$\sigma $数值变化曲线 Fig.8 Relation curves of $E_{\rm r}^{ - 1} $ and $\sigma $ in reloading processes |
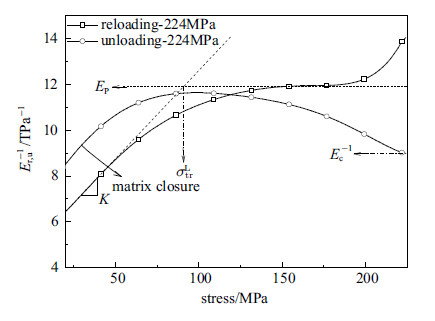
以$\sigma =224$MPa为例,在图9中同时给出了$E_{\rm r}^{ - 1} $和$E_{\rm u}^{ - 1} $ 随$\sigma $的变化曲线. 对比发现,卸载过程对应试验曲线与推导结果相差较大,曲线没有明显的平台段; 在低应力水平下,由于裂纹闭合效应的影响,$E_{\rm u}^{- 1} $ 数值出现明显下降. 造成上述差异的原因是因为材料内部界面脱粘能和剪切滑移力数值分布具有一定的分散性,卸载过程中两者的数值在不断调整变化减小分散性,并在后续重加载过程中具有较好的统一性,所以重加载过程对应试验曲线和理论曲线呈现出较好的一致性[4]. 同时,由于低应力水平下应变数据测量相对误差较大,同时又受到裂纹闭合现象的影响,所以高应力水平下的试验数据具有更好的可用性. 综上所述,并参照图5中的理论曲线,确定计算所需参数值在试验曲线中的选取方案如图9所示,$E_{\rm P}^{-1} $和$K$由重加载曲线获得,$E_{\rm c}^{ - 1} $由卸载曲线获得. 如图1所示,依据迟滞环的对称特点,残余应变可由下式求得
| $\varepsilon _0 = \varepsilon _{\rm B} + \varepsilon _{\rm A} - \varepsilon _{\rm P}$ | (27) |
|
图 9 计算所需参数值在试验曲线中的选取示意图 Fig.9 Selections of the needed parameters in calculation from experimental curves |
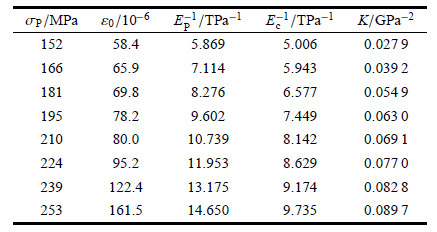
其中$\varepsilon _{\rm A} $,$\varepsilon _{\rm B} $和$\varepsilon _{\rm P} $分别为$A$,$B$和$P$点对应的拉伸应变. 计算过程中所需余下材料组份性能参数在表1中列出.
| 表 1 2D-SiC/SiC复合材料组份性能参数 Table 1 Parameters of material components in 2D-SiC/SiC composites |
依据试验曲线得到的$\varepsilon _0 $,$E_{\rm P}^{ - 1} $,$E_{\rm c}^{ - 1} $和$K$随$\sigma _{\rm P} $的数值变化一并在表2中给出. 上述试验数据是否具有较好的可用性,可以利用滑移参数$\upsilon$来检验,具体形式如下[4]
| $\upsilon = \frac{1}{2}k(E / E_{\rm c} - 1)^{ - 1}$ | (28) |
| 表 2 不同加卸载循环中计算所需试验数据列表 Table 2 Values of the needed parameters in calculation in each load-unload cycle |
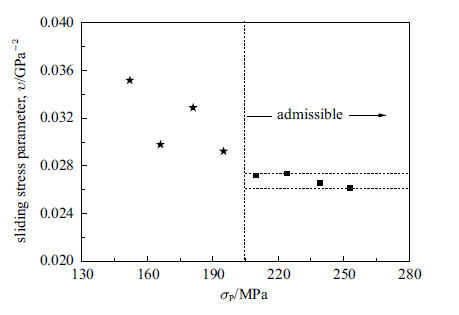
其中$E=279$GPa,为材料初始拉伸模量. 不同加卸载循环对应的$\upsilon $随$\sigma _{\rm P} $ 的数值变化规律在图10中给出. 可以看出,除去前4个循环,余下4个循环对应数据都具有较好的可用性. 这是因为在高卸载峰值应力水平下,应变数据采集具有较小的相对误差,材料的拉伸损伤也比较均匀和充分,所以高卸载峰值应力水平下材料的拉伸迟滞力学行为和试验数据具有更好的准确性和可用性. 在后续计算过程中,继续给出前4个循环对应计算结果,但是不再计入材料组分性能参数计算.
|
图 10 滑移参数$\upsilon $随$\sigma _{\rm P}$的数值变化规律 Fig.10 Variation of sliding stress parameter $\upsilon $with $\sigma _{\rm P} $for 2D-SiC/SiC composites |
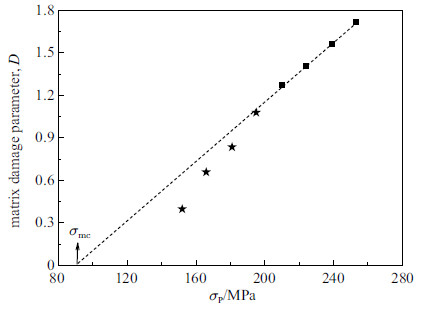
基体损伤参数$D$随卸载峰值应力$\sigma _{\rm P} $的数值变化规律在图11中给出,$D$定义为[4]
| $D = E / E_{\rm c} - 1$ | (29) |
|
图 11 基体损伤参数$D$随$\sigma _{\rm P}$的数值变化规律 Fig.11 Variation of matrix damage parameter $D$ with $\sigma _{\rm P} $for 2D-SiC/SiC composites |
当$D=0$时,其对应的$\sigma _{\rm P} $值即为材料基体开裂应力$\sigma _{\rm mc} $值,按上述方法求得$\sigma _{\rm mc} $约为90MPa,与图7中的试验结果吻合很好.
将表2中的试验数据代入计算分别得到了2D-SiC/SiC复合材料热残余应力和界面脱粘能随$\sigma _{\rm P} $的数值变化规律,并在图12中一起给出. 因为上述组分性能参数是材料的固有特性,所以数值不随$\sigma _{\rm P} $变 化,通过对可用数据求平均值,可以得到材料的热残余应力和界面脱粘能分别约为19MPa和3.1Jm$^{2}$. 分析可知,较低的热残余应力与材料在加卸载过程中表现出较小的残余应变是相对应的;求得的界面脱粘能数值与以往研究工作中给出的取值范围是相符的,同时也说明了2D-SiC/SiC复合材料属于大脱粘能材料,在理论分析过程中必须考虑其界面脱粘能的存在.

|
图 12 热残余应力和界面脱粘能随$\sigma _{\rm P} $的数值变化规律 Fig.12 Variations of residual stress $\sigma _{\rm th} $and debond energy $\Gamma _i $ with $\sigma _{\rm P} $ for 2D-SiC/SiC composites |
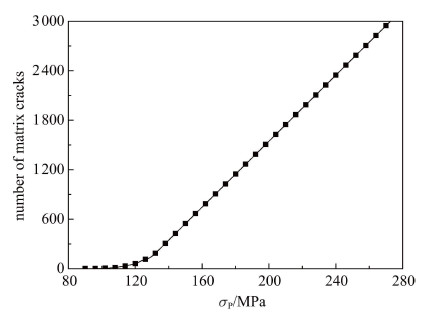
利用已有试验数据不能直接求得界面剪切力$\tau $的数值,还需要得到基体碎块平均长度随施加应力$\sigma $的变化关系. 直 接对试件材料进行基体裂纹观测并统计得到基体裂纹平均长度具有很大困难,所以这里运用Guillaumat和Lamon[13, 14]建立的基体随机开裂理论模型,并通过Matlab编程计算,得到了材料基体开裂数目随拉伸应力的变化曲线如图13所示. 最终获得界面剪切力$\tau$随$\sigma _{\rm P} $的数值变化规律如图14所示,并求得材料的界面剪切力$\tau $约为74MPa.
|
图 13 材料基体开裂次数随拉伸应力增长曲线 Fig.13 Relation curve between matrix cracks' number and $\sigma _{\rm P} $for 2D-SiC/SiC composites |

|
图 14 界面剪切力随卸载峰值应力数值变化规律 Fig.14 Variation of sliding stress $\tau $ with $\sigma _{\rm P} $for 2D-SiC/SiC composites |
上述计算过程没有考虑少量短基体碎块的存在,而是假设材料基体完全由长碎块构成,如此假设等效于将短碎块``合并''为长碎块. 分析可知,同一加卸载循环内,相比于基体全部开裂成长碎块,短碎块的出现会使得残余应变$\varepsilon_0$ 数值增大,试验曲线对应的斜率$K$值和含裂纹材料拉伸模量倒数$E_{\rm c}^{ - 1} $ 值也会增大. 对于平台模量倒数$E_{\rm P}^{ - 1}$,在低卸载峰值应力水平下,短碎块的出现会使其数值增大; 在高卸载峰值应力水平下,短碎块的出现会使其数值减小. 结合材料组份性能参数的计算方法可知,在``全为长碎块''假设下得到的界面剪切力$\tau$ 值相比于真实情况偏小,界面脱粘能$\Gamma _i $值偏大,热残余应力$\sigma _{\rm th} $ 值偏大,而基体开裂起始应力$\sigma _{\rm mc}$值不受其影响. 上述数值偏差程度受长、短基体碎块数量的比值影响. 当短 基体碎块所占比例较小时,``全为长碎块''假设下计算所得数值的偏差很小,所以可以在计算过程中忽略短基体碎块的存在.
4 结 论(1) 基于剪滞理论,建立了单向纤维增强陶瓷基复合材料的加卸载理论模型; 结果表明基体长碎块和短碎块对材料迟滞力学行为具 有不同的影响.
(2) 加卸载过程中界面反向和正向滑移的发生,改变了纤维和基体间的载荷传递方向和基体的载荷承担比例. 界面脱粘区域反向和 正向滑移长度随施加应力的变化是材料加卸载应力-应变曲线形状发生分段变化的原因.
(3) 将2D-SiC/SiC复合材料拉伸加卸载试验数据代入加卸载理论模型,计算得到了表征平均意义上材料组份性能的4个参数: 基体 开裂应力约为90MPa,热残余应力约为19MPa、界面脱粘能约为3.1Jm$^{2}$,界面滑移力约为74MPa.
(4) 考虑短基体碎块的存在,在``全为长碎块''假设下计算所得2D-SiC/SiC复合材料界面剪切力$\tau $值相比于实际情况偏小,界面脱粘能$\Gamma _i $值偏大,热残余应力$\sigma _{\rm th} $值偏大,而基体开裂 应力$\sigma _{\rm mc} $值不受影响.
| [1] | Zhu S, Mizuno M, Kagawa Y, et al. Monotonic tension, fatigue and creep behavior of SiC-fiber-reinforced SiC-matrix composites: A review. Composites Science and Technology, 1999, 59: 833-851 |
| [2] | 杨成鹏. 陶瓷基复合材料的力学特性和氧化损伤模拟研究. [博士论文]. 西安: 西北工业大学, 2011 (Yang Chengpeng. Mechanical characterization and oxidation damage modeling of ceramic matrix composites. [PhD Thesis]. Xi'an: Northwestern Polytechnical University, 2011 (in Chinese)) |
| [3] | Vagaggini E, Domergue JM, Evans AG. Relationship between hysteresis measurements and the constituent properties of ceramic matrix composites: I, Theory. J Am Ceram Soc , 1995, 78(10): 2709-2720 |
| [4] | Domergue JM, Vagaggini E, Evans AG. Relationship between hysteresis measurements and the constituent properties of ceramic matrix composites: II, Experimental studies on unidirectional materials. J. Am. Ceram. Soc., 1995, 78(10): 2721-2731 |
| [5] | Domergue JM, Heredia FE, Evans AG. Hysteresis loops and the inelastic deformation of 0/90 ceramic matrix composites. J Am Ceram Soc , 1996, 79(1): 161-170 |
| [6] | Ahn BK, Curtin WA. Strain and hysteresis by stochastic matrix cracking in ceramic matrix composites. J Mech Phys Solids, 1996, 45(2): 177-209 |
| [7] | Li LB, Song YD. An approach to estimate interface shear stress of ceramic matrix composites from hysteresis loop. Applied Composite Materials, 2010, 17: 309-328 |
| [8] | Wang YQ, Zhang LT, Cheng LF, et al. Characterization of tensile behavior of a two-dimensional woven carbon/silicon carbide composite fabricated by chemical vapor infiltration. Material Science and Engineering A, 2008, 497: 295-300 |
| [9] | 杨成鹏, 矫桂琼, 王波.2D-C/SiC复合材料的单轴拉伸力学行为及其强度. 力学学报, 2011, 43(2): 330-337 (Yang Chengpeng, Jiao Guiqiong, Wang Bo.Uniaxial tensile stress-strain behavior and strength of plain woven C/SiC composite.Chinese Journal of Theoretical and Applied Mechanics, 2011, 43(2): 330-337 (in Chinese)) |
| [10] | Evans AG, Zok FW. The physics and mechanics of fiber-reinforced brittle matrix composites. Journal of Materials Science, 1994, 29: 3857-3896 |
| [11] | Hutchinson JW, Jensen HM. Models of fiber debonding and pullout in brittle composites with friction. Mechanics of Materials, 1990, 9: 139-163 |
| [12] | 李崇俊. SiC/SiC复合材料及其应用. 高科技纤维与应用, 2013, 38(3): 1-7 (Li Chongjun. SiC/SiC composites and application.Hi-Tech Fiber & Application, 2013, 38(3): 1-7 (in Chinese)) |
| [13] | Solti JP, Mall S, Robertson DD. Modeling damage in unidirectional ceramic-matrix composites. Composites Science and Technology, 1995, 54(1): 55-66 |
| [14] | 李潘, 王波, 甄文强 等.2D-SiC/SiC复合材料拉伸加卸载行为. 复合材料学报, 2014, 31(3): 676-682 (Li Pan, Wang Bo, Zhen Wenqiang, et al.Tensile loading/unloading stress-strain behavior of 2D-SiC/SiC composites.Acta Materiae Composites Sinica, 2014, 31(3): 676-682 (in Chinese)) |
2. Chengdu Aircraft Design and Research Institute, Chengdu 610091, China
 2015, Vol. 47
2015, Vol. 47