颗粒材料作为典型的离散介质广泛地存在于实际的工程中,如土石坝堆料[1]、路基填料[2]、颗粒阻尼器[3]. 它在静力加载下的应力应变关系[4, 5]、组构张量的演化[6, 7]、循环加载[8, 9] 下的力学特性等数值和模型试验已经存在很多相关的研究,而对于颗粒材料的动力学特性[10, 11],尤其是系统内部能量的关系却很少涉及. 近年来,堆石坝由于其取料方便、施工简单、抗震性能强等特性,在我国的经济建设中尤其是地震较为频繁的地区得到越来越多的应用,因此对于离散介质的动力学响应以及其耗能机制的研究有着极其重要的意义. 传统的有限元方法在讨论岩土材料的动力学特性时,一般采用设置阻尼系数来研究结构内部的能量耗散. 这种方法虽然简便,然而对其物理机制的描述却很模糊. 事实上,离散介质内部能量耗散的形式主要体现在颗粒表面相互滚动和滑动导致的摩擦耗能,以及颗粒间非弹性碰撞引起的阻尼耗能. 文献[12]以二维圆形颗粒为模型研究了无黏性土在动力载荷下系统能量的耗散,指出在各种外界激励下摩擦耗能占据内部能耗的绝大部分; 文献[3]通过研究两种阻尼器模型,从数值模拟的角度研究阻尼和摩擦耗能的关系,然而其模型的基本单元局限在等直径圆形颗粒; 文献[13]通过研究非阻碍性颗粒阻尼(non-obstructive particle damping)时发现颗粒摩擦耗能与碰撞阻尼耗能处于同一等级,并且随着颗粒半径的减小摩擦耗能在系统能耗中增加,但是在讨论颗粒粒径的对于耗能的影响时,所研究的颗粒的数目并不是固定的; 黄俊宇等[14]通过改变外界加载应变率的变化讨论了脆性颗粒材料的应变率效应,却没有明确指出阻尼和摩擦的影响. 事实上,在实际的工程中颗粒材料往往不是规则的圆形,并且在外界激励下尤其是粗粒料往往会发生破碎,引起系统内颗粒级配的改变,从而显著的影响结构强度、内部结构等特性[15, 16, 17, 18, 19],这些变化对系统能量的吸收和耗散的影响是一个值得关心的课题.
本文采用离散元的方法,通过设置连接键将若干基本颗粒绑定为一个具有不规则外形的整体,以此为模型模拟了二维颗粒体随外界循环动力载荷的破碎过程,并从微观的角度探讨颗粒体破碎对于系统耗能的影响. 具体的,第1节对颗粒体连接键的设置、破碎率的定义以及能量的组成部分作简要介绍; 第2节给出数值试验的模型和参数,以及外加动力载荷的模式; 第3节在给定的细观参数以及加载方式下进行一系列数值试验,并对结果加以解释; 第4节总结本文得出的结论.
1 基本原理离散元方法(discrete element method)首先由文献[20]提出,假设最基本单元是一个个能够产生局部变形的刚性小球,通过局部接触模型和牛顿第二定律来研究物体的运动和变形. 与传统的有限元相比,它更贴近实际物理模型并且能从微观的角度提供更多的信息来解释宏观的力学行为. 关于颗粒流离散元的基本原理在文献[21, 22]中已经做出了详细的介绍,不再赘述. 这里给出的基本概念包括: 颗粒体连接键、能量以及破碎率.
1.1 颗粒体连接键传统的离散元方法对颗粒做出了刚性假设,允许颗粒间接触发生重叠但颗粒本身无法变形以及破碎. 为了实现颗粒的破碎过程,一般设置具有一定强度的连接键将若干基本颗粒绑定为一个整体. 本文的重点在于描述颗粒破碎对于能量耗散的影响,简单起见,采用与文献[15, 23, 24]类似的方法,粗略地将样本中原始粒径超过细沙范围的颗粒等质量地替换为7个颗粒绑定的颗粒体,如图1所示. 颗粒间连接键设置有两种,接触键和平行键[22]. 其中接触键不允许绑定的颗粒间发生滚动,其接触集中在一个点,如果超过接触力临界值接触键断裂,但是这种接触模型无法记录接触键的弹性变形以及能量的变化; 平行键相当于颗粒间的黏结物质(比如混凝土中粗骨料间的水泥砂浆),允许其在一定界限内发生弹性变形并储存弹性能,超出强度极限即发生脆断,连接键失效,但是这种连接键允许颗粒间接触``脱落'',并且颗粒间可以发生相对滑动.
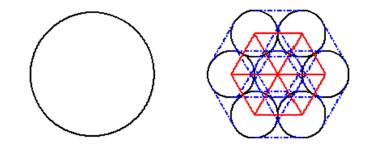
|
图 1 颗粒体代替单个颗粒示意图(红线表示接触键,蓝线表示平行键) Fig. 1 Schematic picture of the repalcement of single particle by cluster.(Red line stands for contact bond, and blue line stands for paralleled bond) |
本文采用两种键混合的形式来实现颗粒破碎前颗粒体内部不发生相对滑动, 同时记录断裂前能量的变化和颗粒破碎消耗的能量. 这 种混合键的形式在很多研究中均得到了采用,但是, 大多的数值模拟关于两种键参数的设定并不严谨: 其中一个键的失效并不能同时保证另外一个键的失效. 事实上, 在颗粒破碎后,脱离原集合体的颗粒变为``自由颗粒'',从而不再与``本体''有键的连接. 为了保证使数值模拟的过程更加贴近实际情况,本文中涉及的计算均设定当接触键失效的同时设定平行键强度参数为零,即平行键失效.
1.2 破碎率破碎率是衡量颗粒破碎程度的重要指标,刘汉龙等[19]总结了多种根据粒径级配曲线变化的定义,指出这类方法只能反映某个粒径下颗粒数目的变化,不能从整体上反映系统颗粒破碎的情况. 在实际的数值模拟中,颗粒体是由事先定义好的小粒径颗粒连接组成,所以初始设定组成等效颗粒体中小颗粒的直径对于破碎后的颗粒粒径的分布有很大的影响,从而影响到破碎程度判断. 本文采用刘君等[15]的定义,即通过断裂的连接键与初始设定的总连接键的比值来定义破碎率
| ${B_{\rm{r}}} = \frac{{{N_{{\rm{br}}}}}}{{{N_{{\rm{ini}}}}}}$ | (1) |
其中,${N_{{\rm{br}}}}$,${N_{{\rm{ini}}}}$分别是断裂的连接键数目和初始连接键的数目.
1.3 能量重力做功${E_{\rm{b}}}$
| ${E_{\rm{b}}} = \sum\limits_{t = 0}^t {\sum\limits_{p = 1}^{{N_p}} {\rm{ }} } {m_p}g{\rm{d }}{u_p}{\rm{d }}t$ | (2) |
其中,${N_p}$,${m_p}$,$g$,${\rm{d }}{u_p}$分别为颗粒数,颗粒的质量,重力加速度和颗粒质心的位移增量.
边界施加的外力功${E_{\rm{w}}}$
| ${E_w} = \sum\limits_{t = 0}^t {\sum\limits_{w = 1}^{{N_w}} {\left( {{f_w}{\rm{d}}{u_w} + {t_w}{\rm{d}}{\theta _w}} \right)} } {\rm{ d}}t$ | (3) |
其中,${N_w}$是边界的数目,${f_w}$和${t_w}$分别为外力和外力矩,${\rm{d}}{u_w}$,${\rm{d}}{\theta _w}$为相应的位移增量和角度增量.
颗粒平移和旋转的动能${E_k}$
| ${E_k} = \frac{1}{2}\sum\limits_{p = 1}^{{N_p}} {\left( {{m_p}\dot u_p^2 + {I_p}\omega _p^2} \right)} $ | (4) |
其中,${I_p}$和${\omega _{{\rm{ }}p}}$分别为转动惯量和相应的角速度.
数值模拟中颗粒假设为不可变形的刚体,其等效应力通常由颗粒表面各接触点的接触力获得[4, 5, 6],颗粒的应变也集中在接触点并由接触弹簧的变形来体现. 于是,颗粒接触应变能${E_{\rm{s}}}$等效为接触部分的法向与切向弹簧变形能之和,其表达式为
| ${E_{\rm{s}}} = \frac{1}{2}\sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left( {\frac{{f_{\rm{n}}^2}}{{{k_{\rm{n}}}}} + \frac{{f_{\rm{t}}^2}}{{{k_{\rm{t}}}}}} \right)} $ | (5) |
其中,${N_{\rm{c}}}$为接触数,${f_{\rm{n}}}$和${f_{\rm{t}}}$分别为接触力的法向和切向分量,${k_{\rm{n}}}$和${k_{\rm{t}}}$为相应的接触刚度.
颗粒摩擦耗能${E_{\rm{f}}}$是指由于颗粒间的相互滚动和滑动使得接触表面产生摩擦力而耗散的能量,其表达式为
| ${E_{\rm{f}}} = \sum\limits_{t = 0}^t {\sum\limits_{c = 1}^{{N_{\rm{c}}}} {{f_{\rm{t}}}d{u_{{\rm{slip}}}}{\rm{d}}} } t$ | (6) |
其中${\rm{d}}{u_{{\rm{slip}}}}$是扣除弹性变形后的位移增量.
颗粒碰撞阻尼耗能${E_{\rm{d}}}$是指颗粒间的非弹性碰撞耗散的能量,其表达式为
| ${E_{\rm{d}}} = \sum\limits_{t = 0}^t {\sum\limits_{c = 1}^{{N_{\rm{c}}}} {\left[{\left( {{c_{\rm{n}}}{{\mathop u\limits^. }_{\rm{n}}}} \right){\rm{d}}{u_{\rm{n}}} + \left( {{c_{\rm{t}}}{{\mathop u\limits^. }_{\rm{t}}}} \right){\rm{d}}{u_{\rm{t}}}} \right]} } {\rm{d}}t$ | (7) |
其中,${c_{\rm{n}}}$和${c_{\rm{t}}}$分别为法向和切向的阻尼系数.
连接键弹性能${E_{{\rm{pb}}}}$
| ${E_{{\rm{pb}}}} = \frac{1}{2}\sum\limits_{c = 1}^{{N_{{\rm{pb}}}}} {\left( {\frac{{f_{{\rm{pbn}}}^2}}{{{A_{{\rm{pb}}}}{k_{{\rm{pbn}}}}}} + \frac{{f_{{\rm{pbt}}}^2}}{{{A_{{\rm{pb}}}}{k_{{\rm{pbt}}}}}} + \frac{{t_{{\rm{pb}}}^2}}{{{I_{{\rm{pb}}}}{k_{{\rm{pbn}}}}}}} \right)} $ | (8) |
其中,${N_{{\rm{pb}}}}$表示连接键数目,${f_{{\rm{pbn}}}}$,${f_{{\rm{pbt}}}}$和${t_{{\rm{pb}}}}$ 分别表示连接键所受法向力、切向力以及扭矩,${k_{{\rm{pbn}}}}$和${k_{{\rm{pbt}}}}$ 分别为连接键法向刚度和切向刚度,${A_{{\rm{pb}}}}$和${I_{{\rm{pb}}}}$分别表示连接键的横截面积以及转动惯量. 连接键失效瞬间,记录该时刻${E_{{\rm{pb}}}}$作为外界激励使该连接键失效所需要的能量$E_{{\rm{bp}}}^{\max }$,于是颗粒体破碎所消耗的能量${E_{{\rm{br}}}}$可以表示为
| ${E_{{\rm{br}}}} = \sum\limits_{{c_{{\rm{br}}}} = 1}^{{c_{{\rm{br}}}}} {E_{{\rm{bp}}}^{\max }{\rm{d}}{c_{{\rm{br}}}}} $ | (9) |
其中,${c_{{\rm{br}}}}$为失效的连接键的数量.
上述能量分量中,施加在边界墙上的载荷为外界激励,重力势能、颗粒动能、摩擦耗能、阻尼耗能、颗粒间以及连接键间的应变能为内部的能量. 由能量守恒,可得
| ${E_w} = {E_{\rm{b}}} + {E_k} + {E_{\rm{s}}} + {E_{\rm{f}}} + {E_{\rm{d}}} + {E_{{\rm{pb}}}} + {E_{{\rm{br}}}}$ | (10) |
本文研究的对象为粒径在2.0~15.0mm范围的二维无黏性颗粒. 样本生成的过程是: 首先将底部和左右两侧的边界固定,接 着在较大区域内均匀生成上述粒径范围内的颗粒, 并且将粒径大于6mm的颗粒用同等质量的颗粒体代替,如下图2所示,其中绿色颗粒表示的为小于6mm的颗粒, 蓝色表示的为等效的颗粒体. 颗粒体中颗粒间连接键用球心间红色连线表示,若连接键失效红线也随之消除. 接着施加重力使颗粒沉降同时检测底部边界受力,当其受力稳定后即认为系统平衡,删除高出范围的颗粒, 使样本的尺寸为360mmx360mm; 继续循环直至底部边界受力再次稳定,样本生成完毕. 由1.1节的假设可知在设置颗粒体破碎准则时,只用定义接触键的极限值. 接触键的强度是影响颗粒体破碎的重要参数, 其值的大小直接影响到颗粒体破碎的程度. 黄俊宇等[26]在研究颗粒体时设定平行键强度法向强度为30MPa, 对应于本文不同粒径的颗粒体连接键极限值范围约为485~3000N. 本文的研究重点在于颗粒体破碎对于系统耗能的影响,故不区分接触键拉伸破坏或剪切破坏. 考虑到连接键极限值过低, 系统在加载至初始固结应力下会过早的发生颗粒体破碎,故设置5组不同强度的接触键其值分别为1kN,1.5kN,2.0kN, 3.0kN,5.0kN以模拟在相同加载条件下系统颗粒体不同程度的破碎. 其余微观参数参照文献[12, 25]对石英沙土的取值, 即颗粒间法向和切向刚度均取10MN/m,颗粒间摩擦系数为0.5,法向阻尼系数比例为0.1,颗粒密度取2650kg/m3.
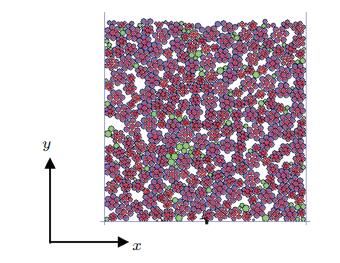
|
图 2 样本示意图 Fig. 2 2D computational model |
为了模拟样本在循环动力载荷下的运动过程,采用土工试验中动三轴双向激振的方法. 在初始应力为${\sigma _x} = 70\;{\rm{kPa}}$,${\sigma _y} = 100{\rm{kPa}}$的状态下,固定底部边界和左边边界,同时对顶部边界和右边边界分别施加速度激励,速度激励形式为
| $\left. \begin{array}{l} {{\dot u}_x}\left( t \right) = \frac{{{v_p}}}{2}\sin \left( {{\alpha _p}t} \right),0 \le t \le T\\ {{\dot u}_y}\left( t \right) = {v_p}\sin \left( {{\alpha _p}t + \pi } \right),0 \le t \le T \end{array} \right\}$ | (11) |
其中,${\alpha _p} = 2\pi f$,$f$为加载频率取${\rm{4Hz}}$. ${v_p}$为速度激励幅值取0.674m/s,这样样本在竖直方向达到最大压缩时,其工程应变正好为15%.
3 结果和讨论本节主要对颗粒体在外加动力载荷下的破碎过程进行数值模拟,同时探讨该过程中系统微观结构的变化以及能量耗散的机理.
3.1 颗粒体破碎及系统耗能在外界激励下,颗粒不断与周围颗粒或者边界碰撞,通过相互间的摩擦和挤压,颗粒体中连接键受力达到极限值时失效,颗粒体逐渐破碎并分解为粒径较小的颗粒,如图3所示.

|
图 3 颗粒体破碎情况随时间变化示意图: 由(a)到(d)加载时间分别为0,1/4,3/4,1个周期, (e)到(h)为相应红圈区域放大图(颗粒间有效连接键由红线表示) Fig. 3 The progress of cluster breakage: the loading time of the snippets from (a) to (d) are 0,1/4,3/4,1 period, respectively; and the snippets from (e) to (f) are the zooming pictures of the area circled with red lines, vskip -1mm respectively (The red lines indicate the effective contact bonds) |
图4(a)显示的是颗粒体破碎率随时间的变化,可以看出加载阶段在A点0.035s前破碎率增加较慢,随后颗粒体加速破碎, B点0.125s即1/2周期开始卸载,破碎率增加减缓,到C点约0.22s颗粒体破碎率不再增加, D点0.25s完成一个加载循环后外界停止速度激励. 在这个过程中,系统内应力的竖向方向分量随时间的变化如图 4(b)所示. 虽然在加载初期已有少部分连接键失效,但是颗粒体其他连接键的约束以及颗粒表面摩擦阻力使得颗粒之间没有 较大的相对运动,系统内部结构没有较大的变化,整体表现为弹性变形,于是应力稳定变化. E点0.043s后破碎率继续增加,颗粒 的内部连接减弱,颗粒之间的相互运动使原有的结构发生变化,使得系统的承载力有所下降,应力出现跌落. 随后系统又形成新的构型, 系统接触数目增加,颗粒排列更加紧密使应力回升,如此反复使得应力在加载阶段出现较大波动. B点后底部边界向下运动,卸载过程中颗粒几乎不再破碎,系统内部结构相对稳定,于是应力曲线变化较为光滑. 同时, 由于内部颗粒的排列发生变化,经过一个周期的运动回到初始状态时, 系统内平均应力竖直方向分量由初始100kPa减小到约30kPa.
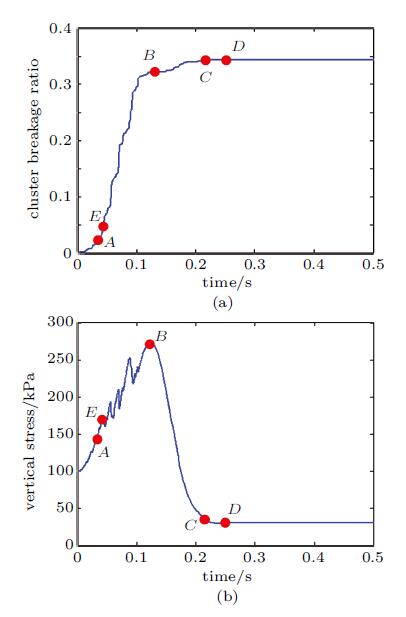
|
图 4 系统破碎率(a) 与竖向应力分量(b) 随时间变化曲线 Fig. 4 The cluster breakage ratio (a) and the vertical stress component (b) time histories |
在能量方面,图5(a)表明外部输入的能量与内部吸收耗散的能量大致相等,保证整个计算过程能量守恒. 图5(b)显示了各 能量组成部分随时间变化的过程,其中颗粒间摩擦耗能在加载阶段约为卸载阶段的2倍, 阻尼耗能只是在加载阶段增加随后保持不变,应变能由于初始应力场在加载前不为零, 在经历一段与应力同样的波动达到峰值随后减小. 由前面的讨论可知,加载阶段颗粒体发生破碎,颗粒间的相对运动加剧, 并且颗粒接触表面积增加,促进了系统内摩擦和阻尼耗能; 0.125s系统达到最大形变后卸载,与加载阶段相比, 系统内力降低,颗粒几乎不再发生破碎,系统内部结构稳定减少了颗粒间的相对运动,整体表现为弹性变形, 摩擦和阻尼耗能增量也随之降低. 同时可以发现,经过一个循环的加载, 由于系统内部颗粒体的破碎使得颗粒间的排列更加紧凑,相同宏观应变的情况下系统内部的应力减小, 系统的应变能相对于加载之前有所降低.
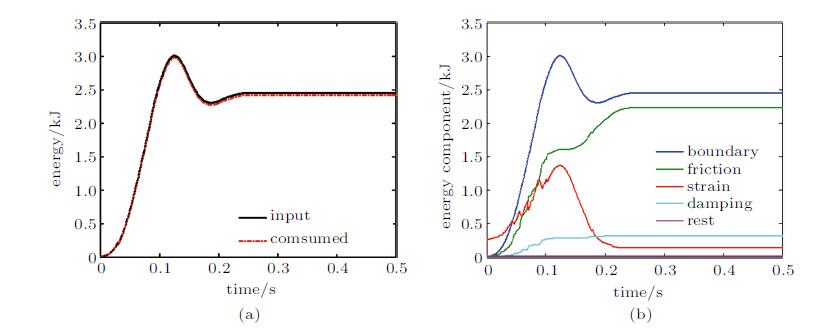
|
图 5 外界输入能量(a) 以及内部消耗能量(b) 随时间变化示意图 Fig. 5 Input (a) and consumed (b) energy time histories |
为进一步探讨颗粒体的破碎程度对系统耗能的影响,在保证其他参数相同的情况下将连接键强度分别设置为1.5kN,2.0kN,3.0kN,5.0kN. 图6表明不同连接键强度下,系统能量各分量随时间变化的情况大致相同. 随着连接键强度的增加,边界输入的能量和应变能也随之增加,并且应变能在加载阶段逐渐变得光滑. 这是由于,连接键强度越高,颗粒体越难以破碎,系统内部结构越稳定,内部扰动引起的卸载现象就越难以发生,宏观上应变能波动就越小.
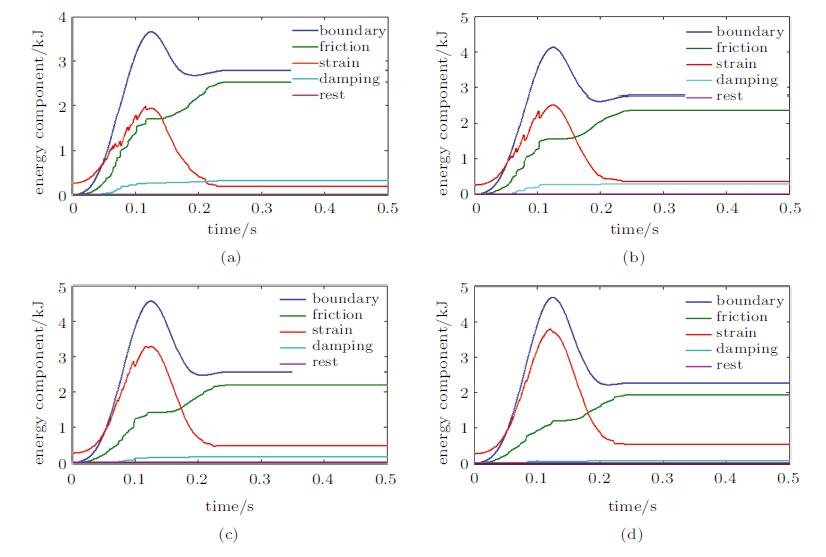
|
图 6 不同连接键强度下系统能量各组成部分随时间的变化(由(a) 到(d) 连接键强度分别为1.5, 2.0, 3.0, 5.0 kN) Fig. 6 Energy components time histories of different contact bond values (The bond strengths from (a) to (d) are 1.5, 2.0, 3.0, 5.0 kN, respectively) |
同时,由于破碎率的降低,颗粒间的相对运动受到限制,颗粒间的阻尼耗能逐渐减少,应变能峰值也随着连接键强度的增加而逐渐超过摩擦耗能. 这说明颗粒破碎率的变化改变了系统储能以及耗能的比例. 为了量化这一现象,引入能量耗散率的概念,即系统耗散的能量与外界输入能量的比值. 图7显示的是外界累计输入能量达到最大值时能量耗散率随连接键强度的变化情况,可以看出,连接键强度为5.0kN时,系统内部颗粒没有发生破碎,外界输入的能量只有大约26%被颗粒间相互摩擦消耗,其余约74%的能量储存为应变能; 连接键强度减小至1.0kN时破碎率提高到32%时,摩擦和阻尼消耗的能量占据外部输入能量的比值提高至62%. 也就是说,颗粒体破碎程度越严重系统消耗的能量的越多,储存为系统的应变能就相对减少. 而对于具体的结构来说,系统储存的应变能越高其稳定性越低. 颗粒体破碎提高了系统的能量耗散能力,进而提高了其稳定性,使得结构更加安全.
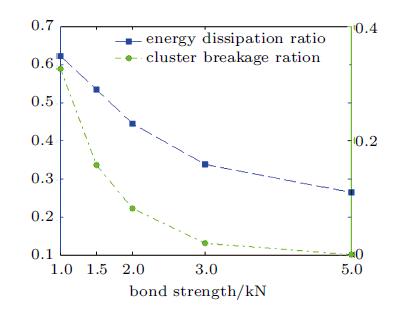
|
图 7 外界累计最大输入能量时连接键强度对能量耗散率和破碎率的影响 Fig. 7 The influence of contact bond value on energy dissipation ratio and cluster breakage ratio |
为讨论循环加载对于破碎率的变化及其对系统能耗的影响,在相同的条件下将载荷激励时间延长至8s. 图8显示的是连接键强度为1.0kN时颗粒体破碎率随时间变化的过程,可以看出,破碎率是随时间单调增加的,并且在加载初期不规则的颗粒外形使得应力集中现象较为严重,颗粒体破碎速率较快; 随后由于大的颗粒体逐渐分解为小的颗粒,系统颗粒级配分布更加合理,接触点的应力集中现象得到了缓解,颗粒间接触力分布更加均匀,使得连接键足以抵抗外界的激励,破碎率逐渐减缓. 该结果与文献[27]在动力三轴试验仪下观察的颗粒在循环加载初期阶段发生大多数破碎的现象相吻合.
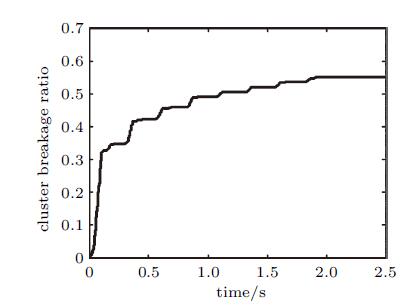
|
图 8 循环载荷下破碎率随时间的变化 Fig. 8 Cluster breakage ratio time history under cyclic loading |
本文采用离散元的方法,模拟出颗粒体在外界动力激励下的破碎过程,并以此探讨颗粒体破碎对于系统能量耗散的影响. 结果表明,在动力载荷下外部输入的能量主要转化为应变能以及被颗粒间的摩擦和碰撞阻尼所消耗,并且在相同载荷条件下系统内颗粒破碎率越高,能量耗散率越高; 在循环载荷下,颗粒在加载初期破碎较为剧烈,系统能量耗散率较高,随后颗粒破碎速率降低,能量耗散率也随之降低,进一步说明了颗粒破碎程度与系统耗能能力成正相关关系. 本文仅对一组微观参数和加载模式下进行数值分析,而颗粒材料的微观参数(如刚度、阻尼系数、密度、摩擦系数),以及加载模式(加载周期、频率、振幅等)对于颗粒材 料耗能特性的影响将会在接下来的研究中做进一步探讨.
| [1] | Deluzarche R, Cambou B. Discrete numerical modelling of rockfill dams. International Journal for Numerical and Analytical Methods in Geomechanics, 2006, 30(11): 1075-1096 |
| [2] | 石云, 郑月秀. 大粒径填石路堤碾压试验研究. 公路交通技术, 2011, 6: 13-15 (Shi Yun, Zheng Yuexiu. Experimental research on rolling compaction of large particle size rock filling roadbed. Technology of Highway and Transport, 2011, 6: 13-15 (in Chinese)) |
| [3] | Bai XM, Keer L, Wang QJ, et al. Investigation of particle damping mechanism via particle dynamics simulations. Granular Matter, 2009, 11(6): 417-429 |
| [4] | Bagi K. Stress and strain in granular assemblies. Mechanics of Materials, 1996, 22(3): 165-177 |
| [5] | Li X, Yu HS, Li XS. Macro-micro relations in granular mechanics. International Journal of Solids and Structures, 2009, 46(25-26): 4331-4341 |
| [6] | Li X, Li XS. Micro-macro quantification of the internal structure of granular materials. Journal of Engineering Mechanics, 2009, 135(7): 641-656 |
| [7] | Millet O, Gu S, Kondo D. A 4th order fabric tensor approach applied to granular media. Computers and Geotechnics, 2009, 36(5): 736-742 |
| [8] | Sitharam TG. Discrete element modelling of cyclic behaviour of granular materials. Geotechnical & Geological Engineering, 2003, 21(4): 297-329 |
| [9] | Ng T, Dobry R. Numerical simulations of monotonic and cyclic loading of granular soil. Journal of Geotechnical Engineering, 1994, 120(2): 388-403 |
| [10] | 孔宪京, 刘君, 韩国城. 面板堆石坝模型动力破坏试验与数值仿真分析. 岩土工程学报, 2003, 25(1): 26-30 (Kong Xianjing, Liu Jun, Han Guocheng. Dynamic failure test and numerical simulation of model concrete-faced rockfill dam. Chinese J. Geot. Eng., 2003, 25(1): 26-30 (in Chinese)) |
| [11] | 杨庆华, 姚令侃, 杨明. 地震作用下松散堆积体崩塌的颗粒流数值模拟. 西南交通大学学报, 2009, 44(4): 580-584 (Yang Qinghua, Yao Lingkan, Yang Ming. Particle flow numerical simulation of landslip of loose slope under seismic loading. Journal of Southwest Jiaotong University, 2009, 44(4): 580-584 (in Chinese)) |
| [12] | Huang JJ, Qi Y, Chen MX, Micromechanical response of granular geomaterials subjected to earthquake ground motions. In: Proc. of International Conference on Science and Technology of Heterogeneous Materials and Structures, Wuhan. 2013. |
| [13] | Chen T, Mao K, Huang X, et al., Dissipation mechanisms of nonobstructive particle damping using discrete element method. Smart Structures and Materials: Damping and Isolation, 2001.4331: 294-301. |
| [14] | 黄俊宇, 徐松林, 胡时胜. 脆性颗粒材料的应变率效应机理研究. 固体力学学报, 2013, 34(3): 247-250 (Huang Junyu, Xu Songlin, Hu Shisheng. Inverstifation on the intrinsic mechanisms of strain rate effects of brittle granular materials. Chinese Journal of Solid Mechanics, 2013, 34(3): 247-250 (in Chinese)) |
| [15] | 刘君, 刘福海, 孔宪京. 考虑破碎的堆石料颗粒流数值模拟. 岩土力学, 2008, 29(增1): 107-112 (Liu Jun, Liu Fuhai, Kong Xianjing. Particle flow code numerical simulation of particle breakage of rockfill. Rock and Soil Mechanics, 2008, 29(sup.1): 107-112 (in Chinese)) |
| [16] | 马刚, 周伟, 常晓林, 等. 考虑颗粒破碎的堆石体三维随机多面体细观数值模拟. 岩石力学与工程学报, 2011, 30(8): 1671-1682 (Ma Gang, Zhou Wei, Chang Xiaolin, et al. Mesoscopic numeiacal simulation of rockfill considering particle breakage by using three-dimensional stochatic polyhedrons. Chinese Journal of Rock Mechancs and Engineering, 2011, 30(8): 1671-1682 (in Chinese)) |
| [17] | Huang J, Xu S, Hu S. Effects of grain size and gradation on the dynamic responses of quartz sands. International Journal of Impact Engineering, 2013, 59: 1-10 |
| [18] | Huang JY, Xu SL, Hu SS. Influence of particle breakage on the dynamic compression responses of brittle granular materials. Mechanics of Materials, 2014, 68: 15-28 |
| [19] | 刘汉龙, 孙逸飞, 杨贵, 等. 粗粒料颗粒破碎特性研究述评. 河海大学学报(自然科学版), 2012, 40(4): 361-369 (Liu Hanlong, Sun Yifei, Yang Gui, et al. A review of particle breakage characteristics of coarse aggregates. Journal of Hohai University (Natural Sciencesm ), 2012, 40(4): 361-369 (in Chinese)) |
| [20] | Cundall PA, Strack ODL, A discrete numerical model for granular assemblies. G Technique, 1979, 29: 47-65. |
| [21] | Cho N, Martin CD, Sego DC. A clumped particle model for rock. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(7): 997-1010 |
| [22] | Potyondy DO, Cundall PA. A bonded-particle model for rock. International Journal of Rock Mechanics and Mining Sciences, 2004, 41(8): 1329-1364 |
| [23] | Jensen R, Edil T, Bosscher P, et al. Effect of particle shape on interface behavior of DEM —— simulated granular materials. International Journal of Geomechanics, 2001, 1(1): 1-19 |
| [24] | Jensen R, Plesha M, Edil T, et al. DEM simulation of particle damage in granular media —— structure interfaces. International Journal of Geomechanics, 2001, 1(1): 21-39 |
| [25] | El Shamy U, Denissen C. Microscale characterization of energy dissipation mechanisms in liquefiable granular soils. Computers and Geotechnics, 2010, 37(7-8): 846-857 |
| [26] | 黄俊宇, 徐松林, 王道荣, 等. 脆性颗粒材料的动态多尺度模型研究. 岩土力学, 2013, 34(4): 922-932 (Huang Junyu, Xu Songlin, Wang Daorong, et al. Investigation of dynamic multiscale model for brittle granular materials. Rock and Soil Mechanics, 2013, 34(4): 922-932 (in Chinese)) |
| [27] | Lackenby J, Indraratna B, McDowell G, et al. Effect of confining pressure on ballast degradation and deformation under cyclic triaxial loading. G Technique, 2007, 57: 527-536 |
 2015, Vol. 47
2015, Vol. 47