在交通流模型研究的早期,主要研究对象是速度、流量(或者车头时距)、密度(或者车头间距)以及它们之间的关系[1, 2, 3]. 此后,随着研究的深入,人们开始逐渐关注车流加速度,其模型则可以粗略地分为微观和宏观两大类.
首先发展起来的是微观车辆跟驰(car following,CF)模型,这一概念最早由Reuschel[4]和Pipes[5]提出,Pipes认为后车的期望安全车头时距为1.02s左右,这是实施加速或减速的依据.Chandler,Gazis等在此基础上提出了不同的CF模型[6, 7],其中最著名的是非线性的GM模型[8],它把此前一系列研究的成果都概括起来,得到了一个形式相当一般的CF模型.多年来有许多研究对GM模型进行了补充和扩展,如Herman和Rothery[9]指出加速和减速行为的概率并不相同,Bexelius等[10]提出多车跟驰模型等.根据GM类模型,一般需要考虑3种可能影响后车加速度的因素: 后车速度、后车与前车间距以及后车与前车速度差.但也有一些学者认为只需要考虑这3种因素中的一部分,如Newell[11]认为速度是车间距的函数,Kometani和Sasaki等[12, 13]认为加速度是速度差的函数,Bando等[14]则认为加速度主要与速度和车间距有关.Bando引进了期望速度的概念,把后车加速度看作其速度与期望速度之差的函数,而期望速度又与它和前车之间间距有关,因此得到了不同于GM模型的另一类CF模型.Treiber等[15]及Helbing等[16]则认为加速度除了受到期望速度的影响之外,还应受到期望最小车间距的影响.Toledo[17]对CF模型的发展历史做过一个比较完整的综述.
另一方面,Payne最早把加速度方程引入交通流的宏观流体力学模型,建立了"二阶模型"方程组,并编写了FREFLO软件提供实 际应用[18, 19].根据Payne模型,车流加速度主要与车流速度和平衡速度之差有关,也与车流密度梯度有关,而平衡速度也是密度的函数. 20世纪90年代,吴正[20]针对中国城市低速混合交通特征提出的"一维管流模型",则把车流加速度主要看作密度梯度的函数,同时可以考虑相邻车道(包括非机动车或行人)的影响,其形式与Payne模型很接近.Daganzo[21]指出,Payne模型为代表的二阶交通流宏观流体力学模型,存在着"类气体行为",在一定条件下其数值解可能出现车辆倒退的不合理结果. 因此,又出现了各种具有"各向异性"特征的二阶模型[22, 23],以Jiang等[23]的模型为例,其中加速度不再是密度梯度的函数,而变成了速度梯度的函数.还有许多与宏观模型中加速度有关的研究,由于与本文关系不大,所以不再一一论述.
交通流模型研究,无论是模型建立,参数标定,还是模型比较和评判,都需要实测数据作依据,上述各种模型的提出、改进和发展过程都是和实际测量紧密相连的.交通流的实测和数据采集方法也经历着不断发展的过程,从早期的定点记录流量、跟车测速、浮动车测速等方法,到20世纪80年代以后,环形线圈检测器、微波检测器、超声波检测器、视频检测装置等许多新技术新设备,被成功应用于检测道路的车流量、车型、车速、占有率等数据.在这些数据采集方法中,视频检测方法具有独特的优势,它能够完整记录所拍摄的整个路段在一段时间内各个瞬间的交通状态,从而在微观交通流数据和宏观交通现象之间架起桥梁,有利于深刻理解数据所反映的事实真相及其背后的机理. 美国联邦公路管理局(FHWA)实施的NGSIM (The Next GenerationSimulation Program)项目,通过视频检测得到大批车辆轨迹信息,进一步计算得到车速、流量、加速度、换道比例等各种实测参数[24].Moridpour等[25, 26, 27]利用NGSIM数据中的货车轨迹研究了相关的换道规律;Aghabayk等[28]则通过车流中跟驰的不同车辆对(客-客,客-货,货-客,货-货)的车头间距、速度差、加速度数据,对CF模型进行了一系列新的研究.
我们课题组从2008年起,也提出了一种基于视频检测的交通流数据采集方法[29, 30],在中国几个大中城市的快速路和城际高速公路上拍摄了数百小时具有不同特征的交通录像,从中采集大量"车头间距-车速"数据对,分析不同路况的交通特点以及驾驶员行为对交通的影响[31, 32],并进行各种交通流速-密、流-密关系模型的比较研究[33, 34, 35]. 在此基础上,本文进一步尝试从这些视频中获得大量"加速度-速度差-车头间距-车速"实测数据对,开展与车流加速度有关的各种统计分析,并对GM模型为代表的CF模型进行比较研究.由于注意到有关CF模型的文献一般都没有区分不同密度条件下加速度的差异,以及它与速度差、车头间距、车速等影响因素之间关系的差异,本文将着重揭示不同密度条件(或者说交通状态)下加速度数据的变化规律,为相应的理论研究提供基础.
本文的结构为:第1节介绍测量方法、测量对象和获得的数据;第2节分别讨论加速度与速度、车头间距、速度差之间关系,着重揭示不同密度条件下这些关系的差异;第3节以GM模型和Bando模型为代表,进行CF模型比较研究; 第4节是全文的总结.
1 测量方法和实测加速度数据 1.1 测量方法及样本简介本文以上海延安高架的视频资料为基本研究对象,拍摄地点是市中心陕西路西侧西向东方向100m的路段,该路段与进、出口匝道距离在300m以上,路北侧是上海展览馆,在路南侧居民楼12层高处固定架设摄像机进行长时间连续拍摄. 仍采用文\linebreak 献[30, 31, 32]介绍的基本方法,将视频资料按0.8s间隔截取成系列图片,通过课题组自编软件并辅以人工干预,准确确定每一幅截图上车辆位置,进而计算得到车头间距d,车速v,加速度a和速度差dv.由于本文主要关心加速度数据,而且是CF模式下(即没有换道)的加速度数据,所以在一段时间内(连续若干幅截图上)总是选定位于同一车道上的一个CF车对进行采集,分别记录该车对在不同时刻下不同的位置,直至该车对驶出截图,这样可以得到该车对的轨迹线,以及相应的d,v(位置关于时间一阶差分),a(位置关于时间二阶差分)和dv(前车速度减去本车速度)等信息. 在数据采集中,个别CF车对中前车曾经发生换道,但所有后车都未换道,并且没有任何其他车辆插入两车之间.
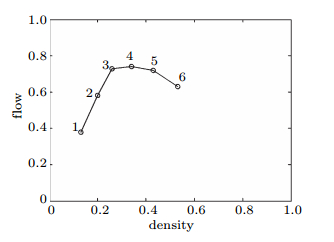
为了考察不同密度条件下的加速度变化规律,本文在该路段拍摄的几十个小时交通录像中,挑选了2008年7月21日(周一,晴天)、2008年7月27日(周日,晴天)和2008年12月29日(周一,雨天)三个上午,分别提取了20min数据,组成6个样本,如表1所示. 表1中样本编号的次序是根据实测得到的平均密度从小到大排列的. 图1给出了这6个样本流量-密度关系曲线,其中横坐标是每隔30s测得该路段4条车道车辆总数换算成密度之后的平均值,纵坐标是每30s内流量(通过该路段下游截面的车辆数)的平均值,再分别除以密度和流量的最大值(无量纲化). 根据图1,样本1,2可以看作是低密度交通流的代表,样本3,4和样本5,6分别是中等密度和高密度的代表.
| 表 1 本文实测样本及其编号 Table 1 Empirical data samples and their serial numbers |
|
图 1 各样本平均密度-平均流量关系 Fig. 1 Dimensionless flow-density diagram |
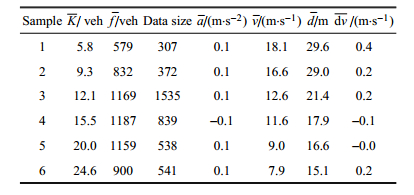
表2给出了6个样本的统计信息:其中,K为画面上的车辆数(除以路段长度后就是密度),f为流量.考虑到车辆性能及道路交通状况,本文中将实测数据的合理取值范围限定为: v ∈ (0, 25] m·s-1,d > 7 m,a ∈ [-4, 4] m·s-2. 已经指出[32],这样的测量方法能够保证测速误差控制在3km/h(即0.83m/s)以内.
| 表 2 各样本的变量平均值 Table 2 Mean values of the parameters in each sample |
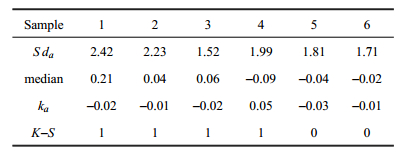
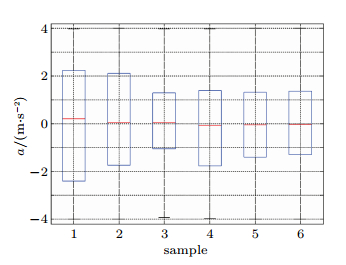
图2以样本6为例给出了加速度a的频率直方图,图中实线表示均值为0、标准差为2的正态分布,两者吻合程度较高.表3则显示了 各样本中加速度数据的标准差 Sda,中位数、偏度系数ka以及K-S检验结果,可以看出(除样本3外):密度越小(样本编号越小)时,Sda越大,说明a的波动越大; 密度越大时,Sda越小,说明a的分布更加集中、平稳. 这一点也可以从表3中K-S检验结果得到证明:样本5,6的检验结果为0,表示在显著性水平0.05下接受服从均值为0、标准差为2的正态分布假设,说明在密度较大的同步流或拥挤流中,a分布更加集中、平稳,|a|较大的数据发生频率降低,|a|较小的数据发生频率上升;而样本1,2,3,4的检验结果为1,表示拒绝该假设,说明在密度较低的自由流中,a更加具有随机性,容易产生|a|较大的数据。通过ka以及图3还可以看到,各样本的a分布基本均关于a = 0对称,说明在各种交通密度状态下,加速和减速的概率都是相近的.

|
图 2 样本6的加速度频率分布 Fig. 2 Frequency distribution of the acceleration in sample 6 |
| 表 3 各样本加速度的统计信息 Table 3 Statistical information of the acceleration in each sample |
|
图 3 各样本加速度的箱线图 Fig. 3 Boxplots of the acceleration in each sample |
6个样本的平均速度$\bar v$随着交通流密度增大而下降,速度数据集中于$\bar v$附近,关于$\bar v$具有比较明显的对称性. K-S假设检验发现,除样本4外,其他5个样本速度变量均服从正态分布,与已知结论一致[32].
6个样本的车间距数据分布则关于均值$\bar d$明显不对称,右侧具有长尾,顶点偏向左边,具有对数正态分布的特征[32].
速度差的分布在以前的研究中尚未涉及. 图4给出了6个样本dv的箱线图,可以看到,dv的平均值也在0附近,并且其数据分布也有一定的对称性. 总体而言,具有正速度差(记为dv+)的数据量比具有负速度差(记为dv-)的数据量要大一些,表明驾驶员更愿意跟驰速度比较大的前车. 需要指出,由于存在不大于0.83m/s的可能测速误差,所以在dv=0附近的数据很可能因为这种误差而被改变了正负号.为了能够准确指出d$v$的正负对加速度的影响,本文以下涉及这一概念时均把|dv| < 0.5m/s的数据剔除.

|
图 4 各样本dv的箱线图 Fig. 4 Boxplots of dv in each sample |
图5给出了各样本v–a关系曲线,做法是: 将横坐标a的数据范围等分成16组,计算每一组的$\bar a$和$\bar v$,即可得到 该样本的v–a关系曲线. 同理,如果要得到a-v关系曲线,则需要以v的大小为依据来进行分组,其余变量两两之间的关系以此类推.

|
图 5 各样本v–a关系曲线 Fig. 5 v–a diagrams |
通过图5可以看到,6个样本的v–a关系曲线均呈现"左高右低"的形态,表明正加速度(记作 a+)主要出现于v较低的 时候,而减速度(记作a-)主要出现于v较高的时候.如果以v–a曲线平均斜率的绝对值来衡量,则是密度较低的样本2最大,密度较高的样本5最小. 这又说明,在密度较低的自由流中,本车速度对驾驶员的变速行为有较大影响,慢车容易选择加速,快车则会考虑减速;而在密度较高的同步流或拥挤流中,本车速度影响下降,驾驶员的变速行为更多受到其他因素影响.
图6给出了6个样本的dv–a关系曲线. 图中直线为各曲线的线性拟合函数. 在样本3~6中,dv–a曲线可拟合为经过零 点的线性单增函数,a+主要出现在dv+区域,a-主要出现在dv-区域. 在样本1、2中则没有这种明显的趋势. 这表明,在密度较低的自由流中,前车速度对驾驶员的变速行为不易产生影响; 而在密度较高的同步流或拥挤流中,本车与前车的速度差是决定驾驶员变速行为的主要因素,平均加速度的正负与平均速度差的正负一致,平均加速度的大小与平均速度差的大小基本成正比.

|
图 6 各样本dv–a关系曲线 Fig. 6 dv–a diagrams |
图7分别给出了6个样本的a–v,a–d及a–dv关系曲线,其中上、下两条曲线分别为a+和a-数据,直线为各 曲线的线性拟合函数.

|
图 7 各样本 a–v, a–d 及 a–dv 关系曲线 Fig. 7 a–v, a–d and a–dv diagrams |
一般认为,a–v拟合直线斜率为负,a–d和a–dv拟合直线斜率为正. 但图7所示,样本3、5、6的a+部分,a–v拟合直线斜率为正; 样本1的a+部分,a–dv拟合直线斜率为负;而总共12条a–d拟合直线中,斜率为正和为负的大致各占一半. 这说明了实际交通现象的复杂性,驾驶员的行为是多个因素共同作用的结果,而且具有较大的随机性,现有的理论模型仍难以完整描述这样的非线性过程,具有明显的局限性.
另一方面,拟合直线斜率的绝对值越大,说明这个变量对加速度的影响也越大,反之亦然. 从图7可以看到,在样本1,2中,斜率最大的是a–v曲线,说明低密度交通流中对加速度影响最大的是本车速度这个因素; 在样本5,6中,斜率最大的是a–dv曲线,说明高密度交通流中对加速度影响最大的是前车与本车的速度差这个因素; 而在样本3,4中,三者规律不明显,a–d曲线斜率相对较大,说明中等密度交通流比较复杂,车头间距这个因素可能对加速度产生影响,同时也不排除另外2个因素的影响.
总的来讲,3种变量对加速度的影响体现了驾驶员对于理想驾驶状态的追求,即: 保持理想车速、理想车间距以及零速度差的跟驰状态.这里的理想车速可以认为是$\bar v$,而理想车间距可以认为是各样本车间距分布曲线的顶点位置,即样本的众数. 尝试根据上述分析,对这种影响进行定量描述:假定某一因素对a+(或a-)具有最大影响记作3,具有一般影响记作2,具有较小影响记作1,将对a+和a-的影响合计,得到结果如表4所示. 根据定量的描述,表4也给出了各个因素影响程度的定性结论.
| 表 4 不同密度下$a$的影响因素 Table 4 Levels of impact on the acceleration under different densities |
非线性GM模型的一般形式为[8]
| ${a^{GM}}(t) = \alpha \frac{{{v^\beta }(t)}}{{{d^\gamma }(t - \tau )}}v(t - \tau )$ | (1) |
这一模型综合反映了v, d 和 dv 3个因素对加速度的影响,其中 τ则体现了信息影响的滞后效应,由于本文实测数据中各个变量是同步的,所以本节取τ=0. 式(1)中,α, β 和 γ 为3个待定的模型参数,在不同文献中有不同取值(α > 0). 本节将实测得到的v, d 和 dv数据代入(1),计算得到aGM并与实测数据a进行比较, 寻找最优的 α, β 和 γ 取值取值.参数优化时采用的判断标准是下式定义的样本平均误差达到最小
| ${e_{GM}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left( {\frac{{{a_i}}}{{a_i^{GM}}} - 1} \right)}$ | (2) |
其中ai为某一样本中第i组实测加速度数据,aiGM为将该组3个影响变量实测值代入式(1)计算得到的理论加速度值,N为该样本数据量(|dv| < 0.5的数据剔除之后). 参数优化结果如表5所示.
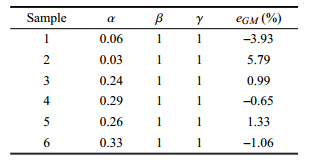
| 表 5 实测数据拟合GM模型结果 Table 5 Fitting results for GM model |
从表5可以看到6个样本的平均误差都在6%以下,显示GM模型与本文实测数据之间拟合效果都很不错,两者能够相互印证合理性.又注意到拟合结果对参数β和γ的取值并不敏感,说明参数β和γ取值大小对GM模型的影响不大.因此,可以取β=γ=1[36],将式(1)简化为
| $a = \alpha \frac{v}{d}{\rm{d}}v$ | (3) |
其中,α值随着密度增大而增大(这并不意味着在同样的速度和密度下,一定的速度差会产生更大加速度,而是因为随着密度增大,速度除以密度的值变小,所以系数会大一些).式(3)形式简单,实测数据证明它具有很好的平均拟合效果,不过其拟合结果中有少量数据的绝对值大于4m/s2,这可能与测量数据误差有关,也可能与个别驾驶员行为导致数据异常有关.
3.2 Bando模型Bando模型的一般形式为[14]
| ${a^{Bd}}{\rm{ }} = \lambda \left[ {DV(d) - \frac{v}{{{v_{\max }}}}} \right] = \lambda \left[ {\tanh (d - 2) + \tanh 2 - \frac{v}{{{v_{\max }}}}} \right]$ | (4) |
其中,DV(d)称为期望速度,它是车间距d的函数,整个模型则反映了v和d两个因素对加速度的影响.式(4)中,λ是待定参数(λ>0).
按照前文分析,认为Bando模型存在2个较大的缺陷:(1)没有考虑本车与前车速度差对加速度的影响,而在密度较高的同步流或拥挤流中这一因素具有重要的地位;(2)根据式(4)计算,减速度最大值为-1(d=0,v=vmax),而加速度最大值为1+tanh2≈1.964(d→∞,v=0),也就是说无论λ如何取值待定,得到的加速度分布都会有很强的不对称性,与实测数据不一致.
为了克服不对称性,提出如下改进形式的Bando模型
| ${a^{Bd}}{\rm{ }} = \lambda \left[ {DV(d) - \frac{v}{{{v_{\max }}}}} \right] = \lambda \left[ {\tanh (d - \mu ) + \theta - \frac{v}{{{v_{\max }}}}} \right]$ | (5) |
其中, μ 和 θ 是2个新的待定参数. 利用实测得到的dmin 和 dmax,可有
| $\left. \begin{array}{l} a_{\min }^{Bd} = \lambda [\tanh ({d_{\min }} - \mu ) + \theta - 1] < 0\\ a_{\max }^{Bd} = \lambda [\tanh ({d_{\max }} - \mu ) + \theta - 0] > 0 \end{array} \right\}$ | (6) |
为了保证加速度数据值域的对称,又有
| $ - a_{\min }^{_{^{Bd}}}{\rm{ }} = a_{\max }^{_{^{Bd}}}{\rm{ }}\mathop {\rm{ = }}\limits^\Delta {\rm{ }} = {a_{\max }}{\rm{ }} \Rightarrow {\rm{ }}\left\{ {\begin{array}{*{20}{c}} {\theta = \frac{1}{2}[1 - \tanh ({d_{\min }} - \mu ) - \tanh ({d_{\max }} - \mu )]}\\ {\lambda = \frac{{2{a_{\max }}}}{{1 - \tanh ({d_{\min }} - \mu ) + \tanh ({d_{\max }} - \mu )}}} \end{array}} \right.$ | (7) |
这里amax可取 4 m/s2,也可以取实测加速度最大值. 将 λ 和 θ表达式(7)代入式(5),最后得到一个依赖于单参数 μ 的模型.
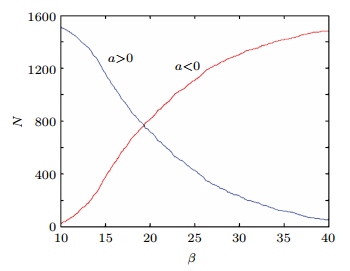
图8以样本3为例,给出不同μ值时按式(5)计算的加速度大于0和小于0的车辆数(分别记作NBd+和NBd-)变化曲线,2条曲线交点表示NBd+=NBd-对应的μ值(此时aBd中位数为0),记为μ0.这一样本中有μ0=19.3m,它恰好与该样本车间距的众数重合.其他5个样本的μ0值依次为:26.9,26.9,16.5,15.0,14.4,它们都具有与样本车间距众数重合的特征,说明式(5)中的参数μ体现了加速度对称分布前提下车间距的期望值,当与此相应的期望速度DV>v/vmax时车辆加速,反之减速.
|
图 8 样本3的NBd+和NBd- Fig. 8 NBd+和NBd- of sample 3 |
仍采用3.1节所述方法,对改进的Bando模型式(5)进行参数优化(其中vmax=25m/s,amax=25m/s2),结果如表6所示. 从表6同样可以看到6个样本的平均误差都在6%以下,显示Bando模型与本文实测数据之间拟合效果也很不错,也能够相互印证合理性. 表6中μ值都与上段给出的μ0值很接近,这又说明在式(5)中用μ=μ0代入计算也是可行的
| 表 6 实测数据拟合Bando模型结果 Table 6 Fitting results for Bando model |
(1)本文采用6个不同密度下的交通流样本,从视频中提取总共4132个CF车对的车头间距d,车速v,加速度a和速度差dv数据.统计分析发现,a的值域关于0点具有对称性;在密度较大的同步流或拥挤流中,a能接受正态分布假设;在密度较低的自由流中,a分布具有更强随机性,容易产生|a|较大的数据.
(2)v,d和dv是影响加速度的3个主要因素,但在不同密度条件下三者的重要性是不同的,并且在同样条件下对加速度和减速度的影响也是不同的.从统计平均角度看,三者对交通流加速度影响的重要程度可归纳为表4.
(3) 利用实测数据对GM模型进行参数优化,结果发现参数β和γ取值大小对GM模型的计算结果影响不大. 据此提出一种GM模型的简化形式,它与本文实测数据之间拟合效果很好,6个样本的平均误差都在6%以下.
(4) 通过实测数据的分析比较,提出一种改进的Bando模型,克服了原模型中加速度值域关于0点不对称的缺点,其中主要参数μ的实际意义是d分布的众数. 利用实测数据对改进的Bando模型进行参数优化,结果也能很好拟合本文实测数据,6个样本的平均误差都在6%以下.
| [1] | Greenshields BD. A study of traffic capacity. Highway Research Board Proceedings, 1934, 14: 448-477 |
| [2] | Lighthill MJ, Whitham GB. On kinematic waves II: A theory of traffic flow on long crowded roads.roc of the Loyal Society of London A, 1955, 229(1178): 317-345 |
| [3] | Richards PI. Shock waves on the highway. Operations Research, 1956, 4: 42-51 |
| [4] | Reuschel R. Fahrzeugbewegungen in der Kolonne. Osterreichisches Ingenieur Archiv, 1950, 4: 193-215 |
| [5] | Pipes LA. An operational analysis of traffic dynamics. Journal of Applied Physics, 1953, 24(3): 274-281 |
| [6] | Chandler R, Herman R, Montroll EW. Traffic dynamics: studies in car following. Operations Research, 1958, 6: 165-184 |
| [7] | Gazis D, Herman R, Potts B. Car following theory of steady-state traffic flow. Operations Research, 1959, 7: 499-505 |
| [8] | Gazis D, Herman R, Rothery RW. Nonlinear follow-the-leader models of traffic flow. Operations Research, 1961, 9: 545-567 |
| [9] | Herman R, Rothery RW. Car following and steady-state flow. In: J. Almond ed. Proceedings of the 2nd International Symposium on the Theory of Traffic Flow. Organization for Economic Co-operation and Development (OECD), Paris. 1965. 1-11 |
| [10] | Bexelius S. An extended model for car following. Transportation Research, 1968, 2: 13-21 |
| [11] | Newell G. Nonlinear effects in the dynamics of car following. Operations Research, 1961, 9: 209-229 |
| [12] | Kometani E, Sasaki T. On the stability of traffic flow. Journal of Operations Research——Japan, 1958, 2: 11-26 |
| [13] | Kometani E, Sasaki T. Dynamic behaviour of traffic with a nonlinear spacing-speed relationship. In: Proceedings of the Symposium on Theory of Traffic Flow. New York, NY: Elsevier, 1959.105-119 |
| [14] | Bando M, Hasebe K, Nakayama A. Dynamical model of traffic congestion and numerical simulation. Physical Review E, 1995, 51: 1035-1042 |
| [15] | Treiber M, Hennecke A, Helbing D. Congested traffic states in empirical observation and numerical simulations. Physical Review E, 2000, 62: 1805-1824 |
| [16] | Treiber M, Helbing D. Memory effects in microscopic traffic models and wide scattering in flow-density data. Physical Review E, 2003, 68: 046119 |
| [17] | Toledo T. Driving Behaviour: Models and challenges. Transport Reviews, 2007, 27(1): 65-84 |
| [18] | Payne HJ. Models of freeway traffic and control. Simulation Council Proc, 1971, 1: 51-61 |
| [19] | Payne HJ. FREFLO: A macroscopic simulation model of freeway traffic. Transpn Res R, 1979, 772: 68-75 |
| [20] | 吴正. 低速混合型城市交通的流体力学模型. 力学学报, 1994, 26(1): 149-157 (Wu Zheng. A fluid dynamics model for the low speed traffic systems. Acta Mechanica Sinica, 1994, 26(1): 149-157 (in Chinese)) |
| [21] | Daganzo CF. Requiem for second-order approximations of traffic flow. Transpn Res B, 1995, 29: 277-286 |
| [22] | Zhang HM. A nonequilibrium traffic model devoid of gas-like behavior. Transpn Res B, 2002, 36: 275-290 |
| [23] | Jiang R, Wu QS, Zhu ZJ. A new continuum model for traffic flow and numerical tests. Transpn Res B, 2002, 36: 405-419 |
| [24] | Cambridge Systematics. NGSIM BHL Data Analysis, Summary Report, Federal Highway Administration. http://ngsim.casys.com/.2004 |
| [25] | Moridpour S, Rose G, Sarvi M. Effect of surrounding traffic characteristics on lane changing behavior. J Transpn Eng, 2010, 136(11): 973-985 |
| [26] | Moridpour S, Rose G, Sarvi M. Influence of the surrounding traffic characteristics on lane changing decision of heavy vehicle drivers. Road and Transport Res, 2012, 21(3): 19-33 |
| [27] | Moridpour S, Sarvi M, Rose G. Lane changing models——A critical review. Transpn Letter: Int J Transp Res, 2010, 2: 157-173 |
| [28] | Aghabayk K, Sarvi M, Young W. Understanding the dynamics of heavy vehicle interactions incar-following. J Transpn Eng, 2012, 138(12): 1468-1475 |
| [29] | 吴正, 朱辉, 贾楠. 基于快速路交通录像的交通流模型参数测量方法研究. 复旦学报(自然科学版), 2008, 47(2): 147-152 (Wu Zheng, Zhu Hui, Jia Nan. Measuring Method Study of the Traffic Flow Model Parameters Based on Video Recording of Expressway Traffic. Journal of Fudan University (Natural Science), 2008, 47(2): 147-152 (in Chinese)) |
| [30] | Zheng X, Wu Z, Xu S, et al. Video-based measurement and data analysis on traffic flow of urban expressway. Acta Mech Sinica, 2011, 27(3): 346-353 |
| [31] | 林展熙, 吴正, 杨朝晖等. 基于上海延安高架录像资料的交通流实测研究. 水动力学研究与进展A, 2010, 25(5): 683-693 (Lin Zhanxi, Wu Zheng, Yang Chaohui, et al. A study on traffic flow models based on measure video of Yanan Expressway of Shanghai. Journal of Hydrodynamics, 2010, 25(5): 683-693 (in Chinese)) |
| [32] | 吴胜春, 郑贤清, 郭明旻等. 国内典型大城市快速路交通流实测. 中国科学:物理学、力学、天文学, 2011, 41(6): 791-800 (Wu Shengchun, Zheng Xianqing, Guo Mingmin, et al. Survey report on urban freeway traffic flow of several typical cities in China. Scientia Sinica Physica, Mechanica & Astronomica, 2011, 41(6): 791-800 (in Chinese)) |
| [33] | 吴正, 郭明旻, 郑贤清等. 大城市高架路实测数据分析与交通流模型研究. 力学学报, 2010, 42(4): 789-797 (Wu Zheng, Guo Mingmin, Zheng Xianqing, et al. Measured data analysis of urban expressway and research on traffic flow models. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(4): 789-797 (in Chinese)) |
| [34] | 林展熙, 郭明旻, 郑贤清等. 基于实测数据的交通流模型比较研究. 力学学报, 2010, 42(5): 848-855 (Lin Zhanxi, Guo Mingmin, Zheng Xianqing, et al. A comparative study on traffic flow models based on mesured data. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(5): 848-855 (in Chinese)) |
| [35] | 吴正, 郭明旻, 许谦. 城市快速路交通流速密关系模型优化研究. 力学学报, 2012, 44(4): 709-717 (Wu Zheng, Guo Mingmin, Xu Qian. Study on optimization of traffic flow velocity-density models for urban freeway. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(4): 709-717 (in Chinese)) |
| [36] | Helly W. Simulation in bottlenecks in single-lane traffic flow. In: Proceedings of the Symposium on Theory of Traffic Flow. New York, NY: Elsevier, 1961.207-238 |
 2015, Vol. 47
2015, Vol. 47