颗粒在湍流边界层中的运动和分布是典型的两相流问题,广泛存在于各种自然现象和工程实际中,如河床的冲淤演变[1]、非平衡输沙[2]、管流的分离净化[3]、浮游生物和污染物扩散[4]等. 然而,由于边界层中湍流拟序结构的复杂性,及其与颗粒运动之间的高度耦合,此方面的研究面临较大的挑战.
颗粒运动与湍流拟序结构之间存在双向耦合作用.Shao等[5]采用直接数值模拟和浸入边界法模拟了颗粒在渠道中的输运,研究了颗粒粒径、固体体积比(颗粒总体积与水体体积的比值)和颗粒沉降效应对湍流统计特征的影响. 其结果表明:当颗粒的沉降效应较弱时,与单相流相比,顺流向流速的湍动在缓冲区减弱,而在核心区和黏性底层增强,竖向和展向流速的湍动在整个断面内增强,这与颗粒的存在部分地破坏了湍流拟序结构,以及颗粒之间的随机碰撞使得湍动趋向于各向同性有关. 当沉降效应较强时,颗粒沉积在底部,顺流向流速的湍动在近壁区减弱,而在核心区增强,这与颗粒表面的泄涡抬升进入核心区有关.Kidanemariam等[6]采用类似的方法研究了低固体体积比、小粒径颗粒的起动和输移,发现颗粒的顺流向流速及其湍动低于流体的顺流向流速及其湍动,而颗粒的竖向和展向速度的湍动高于流体相应方向速度的湍动; 与单相流相比,由于颗粒的固体体积比较小且数量较少,颗粒对湍流统计特征的改变可以忽略. Soldati等[7]开展了湍流直接数值模拟和大涡模拟,并结合颗粒离散元法,模拟湍流边界层中颗粒的运动,提出了两种颗粒沉降和再悬浮机理,指出颗粒的沉降和再悬浮主要受控于湍流拟序结构的喷发(ejection)和扫掠(sweep)过程,以及颗粒自身惯性大小.
颗粒在近壁区的分布也受到湍流拟序结构的影响.研究者从实验[8, 9, 10, 12]和数值模拟[5, 6, 7, 11]的角度 对颗粒局部浓度和分布进行了研究.Shao等[5]指出颗粒倾向于在低流速带聚集,与湍流拟序结构形成的流向涡对有关.Kidanemariam等[6]同样也发现颗粒在湍流拟序结构的作用下向低流速带聚集的趋势,并应用Voronoi分析方法,给出了颗粒聚集所产生条带结构的统计特征. Monchaux等[12]通过风洞实验观察颗粒在湍流壁面边界层中的分布,对不同雷诺数和颗粒Stokes数条件下的颗粒分布进行Voronoi分析,并指出Voronoi分析在研究颗粒动力特性和分布特征方面有很大潜力.本文作者也对颗粒在近壁区的分布进行了数值模拟研究. Ji等 [13, 14]: 颗粒在床面并非均匀分布,这些条带结构的形状、长度和持续时间随颗粒粒径、密度以及水流条件的不同而变化. 颗粒粒径较小时,条带状分布明显;而粒径较大时,条带状分布不明显,颗粒趋于随机分布. 显然,作者以往的研究 [11, 13, 14],较难考察不同因素(如颗粒粒径、固体体积分数和水流条件等)对颗粒分布特征的影响,需要对颗粒分布特征进行定量描述,而基于颗粒瞬时位置的Voronoi分析就是这么一种描述颗粒分布特征的简单且有效的定量方法.
本文应用直接数值模拟和点球浸入边界法,并与颗粒离散元相结合,模拟了明渠湍流边界层中颗粒的运动与分布. 首先,对单 相流和两相流中液相和固相的平均流速、湍动强度和雷诺应力进行比较,研究颗粒运动对湍流统计特征的影响. 其次,观察瞬时流场和颗粒位置,定性分析颗粒运动和湍流拟序结构之间的关系. 最后,基于颗粒瞬时位置进行Voronoi分析,定量描述颗粒在湍流边界层内的分布特征,及其随时间间隔的自相关特性.
1 数值方法颗粒在明渠湍流边界层中输运的数值模型包括两个子模型: 基于直接数值模拟和点球浸入边界法的水动力模型和基于颗粒离散元的颗粒运动模型.
1.1 水动力模型流动的控制方程为Navier-Stokes方程,采用基于有限体积法的高效能湍流并行计算程序------CgLES对明渠湍流进行直接数值模拟,此程序具有二阶的时间和空间精度,其可靠性和计算效率在作者课题组以往的研究 [11, 13, 14, 15]中得到了充分的验证.湍流和颗粒之间的相互作用通过点球浸入边界法模拟. 基本思想是,采用固定的笛卡尔网格对计算域进行空间离散,将颗粒模化为位于颗粒中心、随颗粒一起运动的浸入边界点,将颗粒与湍流之间的相互作用转化为施加在浸入边界点上的附加体积力,并通过插值函数将此体积力映射到笛卡尔网格点上,最终附加到流体动量方程中,从而达到颗粒与流体的双向耦合.
采用具有二阶时间精度的Adams-Bashforth格式对基于浸入边界法的流体控制方程进行离散,可得
| ${u^{n + 1}} = {u^n} + \delta t\left( {\frac{3}{2}{h^n} - \frac{1}{2}{h^{n - 1}} - \frac{3}{2}\nabla {p^n} + \frac{1}{2}\nabla {p^{n - 1}}} \right) + {f^{n + 1/2}}\delta t$ | (1) |
| $\nabla \cdot {u^{n + 1}} = 0$ | (2) |
式中,u为速度矢量,p为压强,$h = \nabla \cdot ( - uu + \nu (\nabla u + \nabla {u^t}))$ 包含对流项和 扩散项,v为运动黏滞系数,δt为时间步长,∇为梯度算子,上标t表示矩阵转置,上标n表示 时间步.f为附加体积力项,表示为
| ${f^{n + 1/2}} = D\left( {{F_D}} \right)$ | (3) |
式中,D为分布函数,将物理量从浸入边界点向笛卡尔网格映射,FD为颗粒受到的流体拖曳力,通过经验公式确定.
1.2 颗粒运动模型颗粒运动模型基于牛顿第二定律,将颗粒假设为均匀刚性球体,应用颗粒离散元研究颗粒在自身重力、流体力以及颗粒与颗粒之间、颗粒与壁面之间相互作用下的运动特性.控制方程为颗粒的轨迹方程和动量方程,如下所示
| $\frac{{{\rm{d}}X}}{{{\rm{d}}t}} = V$ | (4) |
| $m\frac{{{\rm{d}}V}}{{{\rm{d}}t}} = F$ | (5) |
式中,X,V为单个颗粒的位移矢量和速度矢量,F为作用在颗粒上的合力矢量,m为颗粒的质量. 本模型中,作用在颗粒上的力包括颗粒自身的有效重力,水流拖曳力和颗粒与颗粒之间、颗粒与壁面之间的法向接触力和切向摩擦力,模型不考虑颗粒转动和变形,F的表达式如下
| $F = {F_G} + {F_D} + {F_n} + {F_s}$ | (6) |
式中,FG=πd3(ρp-ρf)g/6为颗粒所受有效重力,d为颗粒粒径,ρp和ρf分别为颗粒和流体密度,g为重力加速度.FD为水流拖曳力,与颗粒和水流相对速度的平方成正比,表示为
| ${F_D} = {C_D}\frac{\pi }{8}{d^2}{\rho _{\rm{f}}}\left( {U - V} \right)\left| {U - V} \right|$ | (7) |
式中,U= I(u)为颗粒中心位置的水流速度矢量,I为线性插值函数,将物理量从笛卡尔网格向浸入边界点映射,CD为拖曳力系数,是颗粒雷诺数Rep=|U-V|d/v 的函数. Morsi等[16]通过实验研究近似给出CD与Rep之间的关系,表达式如下
| ${C_D} = {a_0} + \frac{{{a_1}}}{{R{e_{\rm{p}}}}} + \frac{{{a_2}}}{{R{e_{\rm{p}}}}}$ | (8) |
式中,a0,a1,a2的取值取决于Rep,具体参考文献[16].
模型中,颗粒之间、颗粒与壁面之间的相互作用通过弹簧-阻尼系统模拟[17],并考虑颗粒与颗粒(壁面)之间的碰撞能量耗散. 颗粒与颗粒(壁面)接触判断条件为
| $r = {\left\{ {{{\left( {{x_i} - {x_j}} \right)}^2} + {{\left( {{y_i} - {y_j}} \right)}^2} + {{\left( {{z_i} - {z_j}} \right)}^2}} \right\}^{1/2}} \le d$ | (9) |
式中,r为颗粒与颗粒(壁面)之间间距,(xiyizi)和xiyizi分别为第i个颗粒和第j个颗粒(或壁面)的坐标. 定义法向向量n和切向向量s分别为平行和垂直于颗粒中心连线的单位向量,颗粒与颗粒(壁面)之间的法向接触力和切向摩擦力计算如下
| ${F_n} = \left[ {{k_n}{{({d_i} + {d_j} - r)}^{3/2}} - {\gamma _n}{m_e}(V \cdot n)} \right] \cdot n$ | (10) |
| ${F_s} = \left[ { - {\rm{sign}}\left( {{\delta _s}} \right)\min \left( {{k_s}{\delta _s},\mu \left| {{F_n}} \right|} \right) - {\gamma _s}{m_e}\left( {Vs} \right)} \right]s$ | (11) |
式中,V=Vi-Vj为颗粒与颗粒(壁面)相对速度,颗粒与壁面相互作用时,Vj=0.me=mimj/(mi+mj)为等效质量,颗粒与壁面相互作用时,mj→∞,me=mi.kn,ks为法向和切向弹簧系数,γn,γs为法向和切向阻尼系数,u为静摩擦系数.
1.3 点球浸入边界法的适用性探讨常规的浸入边界法采用精细的网格来刻画颗粒(网格边长远小于颗粒粒径),通过满足颗粒表面的无滑移边界条件来计算颗粒受到的 流体力,所有尺度的涡旋运动通过网格全解析,是一种处理有限尺寸颗粒输运的精确方法.本文采用的点球浸入边界法基于浸入边界法发展而来. 将颗粒当作"点球"处理,颗粒粒径小于网格长度,颗粒所受的流体力通过经验模型来计算,湍流通过直接数值模拟求解,颗粒运动与周围流场之间通过在流体控制方程中增加附加体积力实现双向耦合. 由于网格精度不足,点球浸入边界法对于单个颗粒周围的流场无法准确刻画,比如颗粒周围流线的弯曲和颗粒背流侧的流线分离(当颗粒雷诺数较大时)等,但是对于多个颗粒的群体行为在统计意义上是可以准确预测的. 首先,对于单个颗粒受到的流体力问题,众多研究者进行了大量的理论、实验和数值模拟研究,拟合出了颗粒雷诺数适用范围较广(Rep < 1 000)的经验公式(式(6)),其精度较高. 对于泥沙颗粒运动来说,由于粒径较小,水流速度不大,因此符合经验公式的适用范围,因此本文依据式(6)计算单个颗粒受到的流体力是具有相当精度的.
其次,网格结点上的流速是其控制体范围内的平均流速,当网格的边长大于颗粒粒径时,在一个结点控制体内可能包含多个颗粒,因 此该结点的流速实际上受到位于控制体内的多个颗粒对流动影响的平均作用,即网格起到了低通滤波的作用. 另一方面,颗粒粒径较小,颗粒对流场的影响仅局限在局部很小的范围内,当网格边长大于颗粒粒径时,颗粒仅会改变紧邻网格结点上的流速,而对以外结点的流速几乎没有影响. 可见,虽然点球浸入边界法无法准确模拟单个颗粒周围的局部流动,但是在描述多个颗粒对流动的影响时,具有平均意义上的准确性.
最后,点球浸入边界法可以大体上模拟邻近颗粒之间通过局部流场引起的相互作用,即颗粒之间的遮蔽效应-上游颗粒的尾流对处在其中的下游颗粒的受力产生影响. 这是由于:上游颗粒的存在降低了紧邻结点上的流速,而下游颗粒在计算所受流体力时,需要用到此结点流速,因此下游颗粒的受力发生改变.当然,这种影响也可以是由下游颗粒向上游颗粒或者是周边颗粒施加的.这里需要指出的是:点球浸入边界法仅能大体上模拟颗粒之间通过局部流场发生的相互作用,由于网格不足以解析局部流场,因此当颗粒(粒径较大)的尾流存在泄涡时,尾流会对下游颗粒及其自身的受力产生高频的脉动,这种现象是点球浸入边界法无法模拟的. 然而,本文关心的是大量颗粒的群体行为,此高频振荡在进行统计平均时将被过滤掉. 此外,本文研究颗粒的粒径较小,难以在颗粒表面产生泄涡.因此,点球浸入边界法在模拟小粒径相邻颗粒的遮蔽效应时具有一定的可信性.
虽然点球浸入边界法存在以上不足,然而其优势也非常突出.全解析颗粒输运直接数值模拟,从微观尺度上研究离散颗粒的输运问题,得到的结果精度高,又称为"数值实验".然而,此方法要求颗粒粒径至少为10倍的网格长度,其计算量巨大,以现有的计算能力,仅能研究几千个颗粒的输运问题.传统的采用浓度概念描述颗粒分布的方法,通过求解颗粒浓度输运方程从宏观尺度上研究颗粒的输运问题,其计算量很小,适用于大尺度的颗粒输运研究.然而,此方法无法真实反映颗粒的起动以及输运的机理,仅是通过人为改变经验参数来"调节"模拟结果,所得结果的科学性和可靠性,以及模型的普适性不足.点球浸入边界法从介观尺度研究颗粒输运问题,跳过了颗粒周围局部流场和单个颗粒精确运动的求解,而研究更大尺度范围内大量颗粒的群体运动特性,其可模拟百万甚至千万量级的颗粒的运动,而所需的计算资源适中,适合研究较大空间尺度的颗粒输运过程.Nabi等 [18, 19, 20]应用点球浸入边界法数值模拟了明渠湍流中沙纹、沙垄和沙浪的发展和演变,以及桩柱周围的局部冲刷和淤积问题,得到沙纹尺寸和冲刷坑形态,与实验结果吻合良好. Zhou等[21]应用类似方法------直接数值模拟结合拉格朗日颗粒追踪法,模拟了湍流混合层中气状颗粒的凝结发展过程,讨论气状颗粒运动与湍流混合的关系.
2 验证算例 2.1 单个颗粒在静止流体中的自由沉降单个颗粒在静水中沉降,当颗粒受到的流体拖曳力与有效重力平衡时,颗粒达到最终沉降速度,根据前文中提到的流体拖曳力公式和有效重力公式,得到最终沉降速度公式如下
| ${\omega _s} = \sqrt {\frac{4}{3}\frac{{\left( {{\rho _p}/{\rho _f} - 1} \right)dg}}{{{C_D}}}}$ | (12) |
由式(8)可知拖曳力系数CD是ωs的函数,即式(12)为隐式方程,可应用迭代方法求解. 为了验证模型在颗粒受力方面的正确性,本文模拟了d= 0.025cm的单个颗粒在静止流体中的沉降过程,得到了沉降速度的时程曲线,如图1(a)所示,同式(12)的计算结果(图1(b))对比,吻合较好.

|
图 1 单颗粒在静水中自由沉降速度 Fig. 1 The settling velocity of a particle in a steady flow |
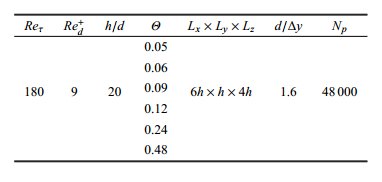
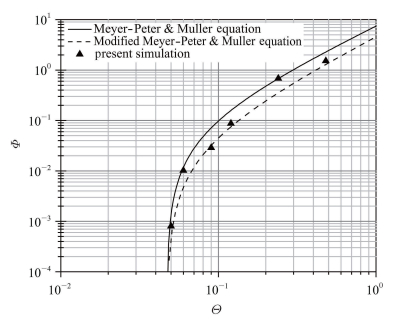
进一步,本文模拟了不同希尔兹数下大量颗粒在明渠湍流中的输移,得到不同希尔兹数对应的输沙率,相应的计算条件如表1所示. 需要说明: 本文通过改变颗粒的重力加速度来调节希尔兹参数,而水流条件不变,这样可以保证每个工况的泥沙颗粒雷诺数相同,得到的结果更具可比性.图2给出了无量纲的输沙率随希尔兹数变化的散点图,并与经典的Meyer-Peter和Muller公式ф= 8(θ - 0.047)1.5及修正的Meyer-Peter和Muller公式ф= 4.93(θ - 0.047)1.6进行了比较,数值模拟得到的输沙率在两个经验 公式结果之间,与经验值吻合良好.
| 表 1 输沙率验证算例的计算条件 Table 1 Simulation parameters of transport rate verification cases |
|
图 2 不同谢尔兹参数下的无量纲输沙率 Fig. 2 Normalized transport rate with different Shields numbers |
计算域大小为4πh×h×2πh(x×y×z),采用384×64×384的均匀网格进行空间离散.水流方向为$x$轴正方向,重力方向为$y$轴负方向,初始时颗粒均匀分布于壁面,如图3所示.边界条件设置为:顺流向(x轴方向)和展向(z轴方向)采用周期边界,底部壁面采用不可滑移边界,顶面采用可滑移边界.本文的计算域大小大于Kim等[22]建议的最小计算域尺寸6h×h×4h,满足周期边界的使用条件.

|
图 3 计算域及颗粒初始分布 Fig. 3 Computational domain and initial particle distribution |
基于明渠高度h和摩阻流速uτ的雷诺数Reτ= uτh/v= 180,基于体积流 速的雷诺数Reb = ubh /v= 2862,湍流耗散率ε = 15.9,无量纲Kolmogorov 长度尺度η+ = 1.8,无量纲垂向网格尺寸∆y+ = 2.8. 采用均匀粒径颗粒d /h = 0.05,颗粒雷诺数Red =uτd/v =9,颗粒数量为4096,固体体积分数为φ = 0.34% ,颗粒与流体的密度比为2.65,希尔兹数θ =uτρ2f}/[gd(ρp-ρf)]=0.5.
本文数值模拟在HP800高性能工作站上完成,处理器为8核2.3GHz,模拟耗时48 h. 在模拟过程中,首先进行单相明渠湍流的模拟,模 拟的无量纲时长30T,T = h / uτ为大涡回转时间,待湍流充分发展后,释放颗粒,在湍流作用下颗粒运动,此阶段的模拟时长为10T,待颗粒运动稳定后,开始记录颗粒的位置、速度以及周围流场,继续模拟20T,以得到流场和颗粒运动的统计特征.
3.2 颗粒对湍流统计特征的影响图4为顺流向平均速度剖面图,比较发现,两相流流速剖面与单相流几乎一致,都符合对数壁面法则,两相流的流速略低于单相流的,但两者相差不超过最大平均流速的2%,可以认为小粒径颗粒在低固体体积比条件下对平均流速剖面影响很小. 此外,图4还给出了颗粒的平均顺流向速度.可以发现: 颗粒的平均顺流向速度在整个明渠高度范围内均小于同高度上的平均流速,一方面是由于颗粒自身的惯性使得其速度小于当地流速; 另一方面,由于在湍流边界层中颗粒更易聚集于低流速带,在喷发结构作用下,低速颗粒被流向涡对挟带进入高速上部流体(如图5所示),造成颗粒速度低于同高度的平均流速.进一步观察发现: 颗粒速度与平均流速之间的速度差在y+ = 20~80的近壁区中最为明显,这主要是因为在此区域内,湍流拟序结构最强烈,流向涡对强度最大,造成颗粒沿竖向频繁穿梭于不同速度流体之间,使得速度差较大.在流动核心区以及更靠近壁面的底层,流体湍动较小,流向涡对减弱或消失,此时的速度差主要是由颗粒的惯性引起.这种速度滞后现象在Kidanemariam等[7]的直接数值模拟研究结果中,以及作者之前的研究中[11, 13]均有报道,同时也被Muste等[23]的实验结果证实.

|
图 4 平均顺流向速度剖面图 Fig. 4 Wall-normal profiles of the mean streamwise velocity |
|
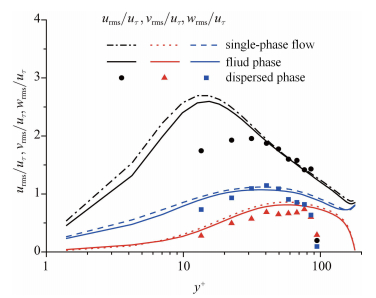
图 5 湍动强度剖面图 Fig. 5 Wall-normal profiles of the turbulence intensities |
图5给出了湍动强度沿高度的分布,图中urms/ uτ,vrms / uτ,wrms/ uτ分别为顺 流向、竖向和展向速度的无量纲湍动强度. 可以看出,由于颗粒运动,两相流的3个方向上的湍动强度均略小于单相流的情况,颗粒在3个方向上的湍动强度均小于或接近流体的湍动强度. 然而,Shao等[5]的全解析颗粒输运结果表明: 当颗粒的沉降效应可忽略时,颗粒分布在整个明渠断面内并跟随流体一起运动,与单相流相比,缓冲区内顺流向湍动强度略有降低,而核心区和黏性 底层内的顺流向湍动强度略有增大,竖向和展向的湍动强度在整个断面高度内均略有增大. 当沉降效应较强时,颗粒沉积在壁面附近,近壁区的3个方向的湍动强度大幅降低,而核心区的湍动强度大幅增大. 当沉降效应适中时,湍动强度沿高度的分布则是以上两种情况的组合. 显然,两组结果之间存在不同.
本文算例中,颗粒粒径小(d / h = 0.05),固体体积分数小(φ ≈ 0.34% ),颗粒沉降效应弱(λv ≈ 0.035). 为此,将本文结果与Shao等[5]的颗粒沉降效应较弱的算例(d / h = 0.05,φ ≈ 0.79\% ,λv = 0.05)进行对比.
从Shao等[5]的结果来看(见其图16(b)),与单相流相比,在缓冲区0.03 < y / H < 0.2内,两相流的顺流向湍动降低,这主要是由于颗粒的存在破环了此处的湍流拟序结构所致. 在流动核心区(y / H > 0.2)中,两相流的顺流向湍动增强,Shao等[5]指出这主要是由于从颗粒表面的脱落的涡旋抬升并向核心区发展造成的. 在黏性底层 (y / H < 0.03$)中,两相流的顺流向湍动增强,由于此处顺流向速度较小,不易在颗粒表面上产生泄涡,湍动增强主要是由于流体质点绕过颗粒表面引起的流线弯曲和流速波动所致. 此外,Shao等[5]的结果还表明:保持粒径不变,随着固体体积比的增加(即颗粒数量的增加),黏性底层区的湍动增强的趋势更加明显.这恰好说明了黏性底层湍动增强与颗粒周围流线弯曲有关------颗粒数量较多,流线更加曲折,湍动增强. 与单相流相比,两相流的竖向和展向湍动强度在整个明渠高度内较大. 这是由于: 在缓冲区内,颗粒的存在虽然部分破环了湍流拟序结构,使顺流向湍动强度降低,但是由于颗粒之间的碰撞及其反弹角度具有一定的随机性,导致湍动有向各项同性发展的趋势[11, 13],造成竖向和展向的湍动增强.核心区和黏性底层处竖向和展向流速湍动增强的原因与此处顺流向湍动增强的原因相同,不再赘述.
本文结果与Shao等[5]的结果不同的原因与点球浸入边界法的特点直接相关. 如前所述,点球浸入边界法无法模拟颗粒周围的局部流场,包括流动分离、流线弯曲以及涡旋脱落等,因此无法体现核心区和黏性底层导致湍动增强的机制. 然而,点球浸入边界法可以反映颗粒对湍流拟序结构的抑制作用,因此在缓冲区顺流向湍动强度减弱,这与Shao等[5]的结果趋势相同.
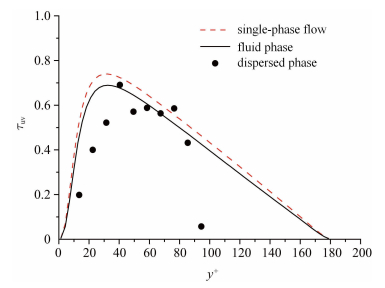
图6给出雷诺应力沿高度的分布,雷诺应力τ uv = 〈u'v’〉/uτ2表示顺流向脉动速度u'与竖向脉动速度v’的相关性. 图中可以看出,相比于单相流,两相流中湍动雷诺应力减小,在缓冲区(y+ = 30~ 80)减小最为显著,这是由于颗粒运动部分破坏了缓冲区中湍流拟序结构,具体过程有待进一步研究. 颗粒雷诺应力与流体雷诺应力变化趋势一致,在y+ < 40时逐渐增大,之后逐渐减小,同Chan-Braun等[24]的结果一致.
|
图 6 雷诺应力剖面图 Fig. 6 Wall-normal profiles of the Reynolds shear stress |
喷发和扫掠是湍流边界层中两种典型拟序结构: 湍流底部低速流体在逆向旋转涡对的作用下被抬升,远离壁面形成喷发.喷发现 象在壁面形成高于平均剪切应力的区域,能够将颗粒从床面带起,是颗粒起动的主要动力因素.扫掠现象是指上部高速流体向壁面的俯冲,并挟带外层流体中的颗粒向壁面运动.图7给出了顺流向瞬时流场和颗粒 Z-Y平面分布图,红色小球为远离壁面运动的颗粒,主要位于图中绿色低速喷发区域; 蓝色小球为向壁面运动的颗粒,主要位于图中橙色和黄色的高速扫掠区域.

|
图 7 顺流向速度瞬时云图和颗粒在Z-Y平面的分布图(红色颗粒远离壁面运动,蓝色颗粒向壁面运动) Fig. 7 The instantaneous contours of the streamwise velocity and the particles distribution in Z-Y plane (The red particles move away from the wall while the blue ones move towards the wall) |
图8(a)和图8(b)分别为瞬时流场涡旋结构和颗粒分布的透视图和俯视图,图中涡旋结构由λ2 = -400的等值面绘制(λ2是对称张量S2 + Ω2 的第二特征值,其中S和Ω分别是速度梯度张量∇u的对称和反对称部分,关于λ2的定义详见文献[6]),涡旋表面颜色代表顺流向涡量的正负,红色表示正值,蓝色表示负值,颗粒颜色代表颗粒顺流向速度大小. 从图中可看出,湍流涡旋结构与颗粒聚集区域重合,直观地说明了颗粒运动与湍流拟序结构关系密切. 除此之外,颗粒在湍流边界层中的运动与自身惯性也有关系.Soldati等[7]模拟明渠湍流中惯性较大颗粒(St = 2.0)和惯性较小颗粒(St = 0.1)的运动(St = τp/τf,为无量纲化的颗粒对流体的响应时间,其中,τp = ρpd2/18μ 为颗粒对流体的响应时间,τf = μ/ 〈τw 〉为流体特征时间尺度,〈τw 〉为壁面平均剪切应力),发现:颗粒惯性的增大削弱了颗粒与流动之间的跟随性,颗粒惯性越大,其运动与湍流拟序结构之间的相关性越不明显.

|
图 8 瞬时流场涡旋结构和颗粒分布透视图(a)和俯视图(b) Fig. 8 A perspective view (a) and a plan view (b) of the coherent structures and the particles distribution |
图9为顺流向瞬时流场和颗粒在X-Z平面内的分布图,颗粒颜色表示颗粒顺流向速度大小,可以发现:颗粒在壁面聚集形成顺流向条带状结构,这些条带结构与低流速区域重合,并且能在一定时间内保持连续和稳定,单个颗粒在随流体向下游输移的过程中,能够相对长的时间保持在同一条带结构中.

|
图 9 顺流向瞬时流场和颗粒X-Z平面分布图 Fig. 9 The instantaneous contours of the streamwise velocity and the particles distribution in X-Z plane |
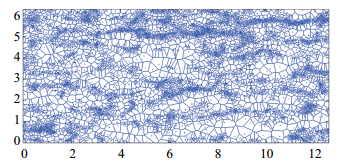
以上仅是直观地对颗粒在壁面上分布进行定性描述,为得到分布特征的定量描述,本文进一步应用Matlab开展了基于颗粒位置的Voronoi分析. Voronoi分析是描述颗粒分布和浓度的简单且有效的方法,它将二维区域划分成与每个颗粒相关的互不重合的独立单元,每个单元定义为到颗粒的距离小于到其余任一颗粒距离的点的集合,每个单元的面积AV的大小与颗粒所在位置的局部浓度成反比,即AV值越小说明颗粒局部浓度越大. 对球心高度位于0 < y+ < 9范围内的颗粒(即位于壁面上的颗粒)进行分析,将其球心向水平面进行投影,得到颗粒瞬时分布,具此得到其Voronoi图,如图10所示. 可以看出,Voronoi图可以清晰地反映颗粒的聚集情况. 需要指出的是: 由于计算域外部没有颗粒,因此在四周边界处会产生面积很大的Voronoi单元,这与真实情况不符,需要将其舍弃. 本文的处理方法是: 将任一结点位于计算域以外的Voronoi单元舍弃,仅分析剩余的Voronoi单元.
|
图 10 瞬时颗粒分布的Voronoi图 Fig. 10 The instantaneous particles distribution and the\\ corresponding Voronoi diagram |
为了说明颗粒在湍流边界层分布的非均匀性,本文将其同颗粒随机泊松分布(RPP)结果相比较. 根据Ferenc等[25]对颗粒随机泊松分布进行Voronoi分析研究,颗粒随机分布的Voronoi单元面积概率密度函数(PDF)的拟合公式为
| ${f_{2D}}\left( {{A^ + }} \right) = \frac{{343}}{{15}}\sqrt {\frac{7}{{2\pi }}} {A^{ + 5/2}}\exp \left( { - \frac{7}{2}{A^ + }} \right)$ | (13) |
式中,A+= AV/〈AV〉为无量纲Voronoi单元面积.无量纲Voronoi单元面积的标准差可以衡 量颗粒分布的不均匀性.本文取400个连续不同时刻的颗粒分布进行统计分析(相邻采样时刻间隔为0.05T,总采样时间长度为20T),得到无量纲Voronoi单元面积标准差σV = 1.19. 参考Ferenc等[25]的随机泊松分布的计算结果, σVRPP = 0.53,可得σV > σVRPP ,说明颗粒在湍流边界层分布不均匀(标准差更大表示Voronoi单元面积更加分散,即颗粒分布更不均匀),存在明显的高浓度区和低浓度区.
为进一步研究高浓度区和低浓度区中颗粒分布的形态结构,本文根据Monchaux等[12]提出的“簇”(cluster)和“空”(void)两 个概念,对瞬时颗粒分布的无量纲Voronoi单元面积进行统计. 将其概率密度曲线与随机泊松分布的概率密度曲线进行比较,如图11(a)所示. 两条曲线存在两个交点,对应于无量纲Voronoi单元面积分别为和νc和νv,这两个值可作为定义“簇”和“空”的临界值,其含义为: 颗粒的Voronoi单元面积小于νc的概率密度大于随机分布的概率密度,说明颗粒间距小于随机分布颗粒间距的概率更大,即: 颗粒聚集于“簇”;颗粒的Voronoi单元面积大于νc的概率密度大于随机分布的概率密度,说明颗粒间距大于随机分布颗粒间距的概率更大,即: 颗粒位于”空“区域; 介于两者之间的单元称为过渡单元.图11(b)中两种不同概率密度的比值曲线可以更直观地表示颗粒的分布特征. 图中PDFsimulation/PDFRPP = 1的虚线对应图11(a)中两条概率密度曲线的交点,无量纲Voronoi单元面积位于深灰色区域的颗粒位于“簇”,无量纲Voronoi单元面积位于浅灰色区域的颗粒位于“空”,中间白色区域对应于过渡单元.图11(c)是瞬时颗粒分布的Voronoi图,图中填充色为深灰色的区域为处于“簇”状态的Voronoi单元,填充色为浅灰色的区域为处于“空”状态的Voronoi单元,无填充色的区域为过渡单元,可以看出,颗粒聚集形成的“簇”呈顺流向条带状分布.

|
图 11 无量纲Voronoi单元面积的概率密度曲线(a),相对概率密度曲线(b)和瞬时颗粒分布Voronoi着色图(c) Fig. 11 The PDF of the normalized Voronoi cell areas(a),the ratio of the two PDFs versus the normalized Voronoi cell areas (b) and the colored visualization of clusters (dark gray) and voids (light gray) (c) |
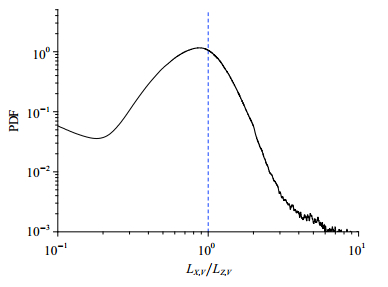
为进一步定量说明颗粒的条带状分布特征,取Voronoi单元的长宽比进行分析,即Voronoi单元顺流向最大长度与展向最大长度的比值 LXY/LZY,其值越小,说明Voronoi单元在顺流向越扁,颗粒在顺流向的间距越小,顺流向条带结构越明显. 图12给出了LXY/LZY的概率密度曲线,可见,LXY/LZY < 1的概率(曲线下位于竖线左侧的面积)明显大于LXY/LZY > 1的概率(曲线下位于竖线右侧的面积),F(LXY/LZY < 1) = 1.5,两者比值越大说明颗粒分布的顺流向条带特征越明显.
|
图 12 Voronoi单元长宽比的概率密度曲线 Fig. 12 The PDF of the Voronoi cell aspect ratio |
通过Voronoi分析可以得到不同时刻颗粒的局部浓度,从而实现对颗粒浓度的拉格朗日追踪. 颗粒的拉格朗日变量随时间自相关函数定义如下
| ${R_{L,{Q_V}}}(\Delta t) = \frac{{\langle Q_V^\prime (t)Q_V^\prime (t + \Delta t)\rangle }}{{\langle Q_V^\prime (t)Q_V^\prime (t)\rangle }}$ | (14) |
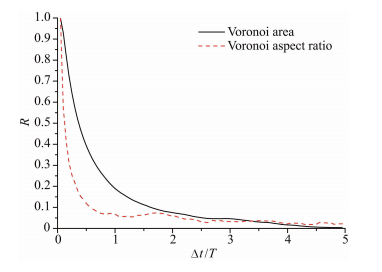
式中,QV(t)表示t时刻单个颗粒的拉格朗日变量(无量纲Voronoi单元面积或长宽比),Q'V(t)=QV(t)-〈QV〉表示拉格朗日变量的脉动量,式中〈〉符号表示针对所有时刻的所有颗粒取平均值. 图13为Voronoi单元面积和长宽比的拉格朗日随时间的自相关系数曲线. 图中可以看出,Voronoi单元面积和长宽比随时间的自相关系数逐渐趋于零,并且长宽比自相关系数的下降速度大于面积自相关系数的下降速度,说明了Voronoi单元的长宽比更加不易保持,这与Kidanemariam等[6]的结论相同.
|
图 13 Voronoi单元面积和长宽比自相关系数曲线 Fig. 13 The autocorrelation curves for the Voronoi area and the Voronoi cell aspect ratio |
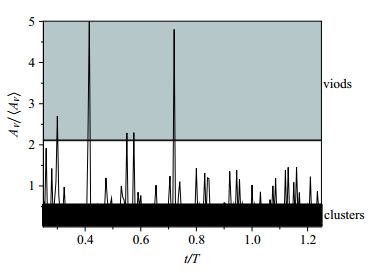
图14给出了一个颗粒的无量纲Voronoi单元面积(局部浓度)的拉格朗日追踪(实际上,本文对更多的颗粒进行了同样的分析,得到了与之类似结果,限于篇幅,此处未给出其他颗粒结果). 图中显示: 颗粒在大部分时间都保持在“簇”的状态中,偶尔跳跃到“空”状态,但能够很快重新聚集到颗粒密集区,此跳跃是该颗粒由一个条带结构跳跃到另外一个条带结构.
|
图 14 单个颗粒Voronoi单元面积的拉格朗日追踪 Fig. 14 Lagrangian tracking of the Voronoi area of a single particle |
本文利用直接数值模拟求解湍流场,利用颗粒离散元方法处理颗粒运动,将颗粒假设为均匀刚性球体,充分考虑颗粒与利时颗粒之间、颗粒与壁面之间的相互作用,通过点球浸入边界法实现了颗粒与流体之间的双向耦合,研究了颗粒运动对湍流统计特征的影响,颗粒在湍流边界层中的运动等,并对颗粒在湍流边界层中的分布进行了定量分析,得到了以下结论:
(1) 通过比较两相流与单相流的统计特征发现: 在明渠高度范围内,颗粒的顺流向平均速度均滞后于水流平均流速,由于颗粒对湍流拟序结构具有抑制作用,导致与单相流相比两相流的湍动强度略有减小,讨论了与他人结果之间的异同,并分析了其原因.
(2) 分析了湍流拟序结构对颗粒运动的影响,发现颗粒在喷发结构作用下远离壁面,在自身重力与扫掠结构作用下回到壁面.
(3) 研究了颗粒在湍流边界层中的分布,从定性和定量两个角度说明了颗粒沿顺流向呈条带状分布、颗粒更易聚集于低流速带的特征,分析了颗粒的拉格朗日变量随时间的自相关性.
| [1] | 王光谦. 河流泥沙研究进展. 泥沙研究, 2007, (2): 64-81 (Wang Guanqian. Advances in river sediment research. Journal of Sediment Research, 2007, (2): 64-81 (in Chinese)) |
| [2] | Floris R,van Thienen P. Experimental investigation of turbulent particle radial transport processes in DWDS using optical tomography. Drinking Water Engineering and Science, 2011, 4(1): 61-83 |
| [3] | 陈鑫, 余锡平. 基于两相紊流模型的非平衡输沙研究. 力学学报, 2012, 44(1): 65-70 (Chen Xin, Yu Xiping. A two-phase numerical model for non-equilibrium sediment transport. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(1): 65-70 (in Chinese)) |
| [4] | 吴修广, 沈永明, 郑永红, 等. 非正交曲线坐标下水流和污染物扩散输移的数值计算. 中国工程科学, 2003, 5(2): 57-61 (Wu Xiuguang, Shen Yongming, Zheng Yonghong, et al. Numerical computation of flow and pollutant diffusion-transportation with non-orthogonal curvilinear coordinates. Engineering Science, 2003, 5(2): 57-61 (in Chinese)) |
| [5] | Shao X, Wu T, Yu Z. Fully resolved numerical simulation of particle-laden turbulent flow in a horizontal channel at a low Reynolds number. Journal of Fluid Mechanics, 2012, 693: 319-344 |
| [6] | Kidanemariam A G, Chan-Braun C, Doychev T, et al. Direct numerical simulation of horizontal open channel flow with finite-size, heavy particles at low solid volume fraction. New Journal of Physics, 2013, 15, 025031 |
| [7] | Soldati A, Marchioli C. Sediment transport in steady turbulent boundary laryers: Potentials, limitations, and perspectives for Lagrangian tracking in DNS and LES. Advances in Water Resources, 2012, 48: 18-30 |
| [8] | Rashidi M, Hetsroni G, Banerjee S. Particle-turbulence interaction in a boundary layer. International Journal of Multiphase Flow, 1990, 16(6): 935-949 |
| [9] | Hetsroni G, Rozenblit R. Heat transfer to a liquid-solid mixture in a flume. International Journal of Multiphase Flow, 1994, 20(4): 671-689 |
| [10] | Yung B P K, Merry H, Bott T R. The role of turbulent bursts in particle re-entrainment in aqueous systems. Chemical Engineering Science, 1989, 44(4): 873-882 |
| [11] | Ji C, Munjiza A, Avital E, et al. Saltation of particles in turbulent channel flow. Physical Review E, 2014, 89(5), 052202 |
| [12] | Monchaux R, Bourgoin M, Cartellier A. Preferential concentration of heavy particles: A Voronoi analysis. Physics of Fluids, 2010, 22(10), 103304 |
| [13] | Ji C, Munjiza A, Avital E, et al. Direct numerical simulation of sediment entrainment in turbulent channel flow. Physics of Fluids, 2013, 25(5), 056601 |
| [14] | 及春宁, 陈威霖, 宋晓阳, 等. 明渠湍流中泥沙颗粒输移的大涡模拟研究. 泥沙研究, 2014, (4): 1-8 (Ji Chunning, Chen Weilin, Song Xiaoyang, et al. Large eddy simulation of sediment particles transport in turbulent open channel flow. Journal of Sediment Research, 2014, (4): 1-8 (in Chinese)) |
| [15] | 及春宁, 王元战, 王建峰. 虚拟区域法在流固耦合问题中的应用. 力学学报, 2009, 41(1): 49-59 (Ji Chunning, Wang Yuanzhan, Wang Jianfeng. Application of the fictitious domain method in fluid- structure interaction. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(1): 49-59 (in Chinese)) |
| [16] | Morsi S A, Alexander A J. An investigation of particle trajectories in two-phase flow systems. Journal of Fluid Mechanics, 1972, 55(2): 193-208 |
| [17] | Lee Jysoo, Herrmann HJ. Angle of repose and angle of marginal stability: molecular dynamics of granular particles. Journal of Physics A: Mathematical and General, 1993, 26(2): 373-383 |
| [18] | Nabi M, de Vriend H J, Mosselman E, et al. Detailed simulation of morphodynamics: 1. Hydrodynamic model. Water Resources Research, 2012, 48(12), W12523 |
| [19] | Nabi M, de Vriend H J, Mosselman E, et al. Detailed simulation of morphodynamics: 2. Sediment pickup, transport, and deposition. Water Resources Research, 2013, 49(8): 1-17 |
| [20] | Nabi M, de Vriend H J, Mosselman E, et al. Detailed simulation of morphodynamics: 3. Ripples and dunes. Water Resources Research, 2013, 49(9): 1-15 |
| [21] | Zhou K, Attili A, Alshaarawi A, et al. Simulation of aerosol nucleation and growth in a turbulent mixing layer. Physics of Fluids, 2014, 65, 065106 |
| [22] | Kim J, Moin P, Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number, Journal of Fluid Mechanics, 1987, 177: 133-166 |
| [23] | Muste M, Yu K, Fujita I, et al. Two-phase flow insights into open-channel flows with suspended particles of different densities. Environmental Fluid Mechanics, 2009, 9(2): 161-186 |
| [24] | Chan-Braun C, Garcia-Villalba M, Uhlmann M. Force and torque acting on particles in a transitionally rough open-channel flow. Journal of Fluid Mechanics, 2011, 684: 441-474 |
| [25] | Jarai-Szabo Ferenca, Zoltan Nedaa. On the size distribution of Poisson Voronoi cells. Physica A: Statistical Mechanics and its Applications, 2007, 385(2): 518-526 |
 2015, Vol. 47
2015, Vol. 47