在轨运行航天器的动力供应系统、生命系统等的正常运作都离不开空间水气管理和应用,系统中流体的形态及流动特性直接影响系 统整体运行效率及寿命. 因此,流体特性的研究在空间流体管理领域的重要性逐渐提高. 与地面常重力环境相比,微重力条件下[1]水气管理问题更具复杂性. 并且,气液两相流系统相比于单相流动系统,其传热性能、能量传输性能以及控制管理方面都具有重大优势. 对空间流体流型及流动特性进行深入研究,有利于我们更好地认识空间水气管理系统内部流动机理、提高空间水气管理系统的实用 性及安全性[2].
针对空间管路气液两相流动问题,特别是微重力环境下两相流流动[3],已有众多学者[4, 5, 6, 7, 8, 9, 10, 11, 12, 13]进行过实验研究,包括利用失重飞机、落塔设备等产生实验所需要的微重力环境以及利用在轨运行航天器的搭载实验研究等,提出了管内弹状流、环状流、弹$\!$-$\!$-$\!$环过渡流、环状流等不同流型,分析了不同重力条件下气液两相在流动过程中相对位置、管内截面空隙率大小和两相流体之间相互作用力等对流型转化的影响. Shephard等[14]还给出了流型转变的理论和模型分析.顾汉洋等[15]利用双平行探针技术对水平直管内气液两相流中单气泡的形态特征进行了实验研究,得出气泡头部和气泡体形态取决于气液混合弗劳德Fr数,而气泡尾部特征与气泡长度有关,且尾部特征变化决定弹状流与段塞流的转变.Bousman等[16]实验研究了微重力飞行器上不同管径直管段内气液两相流动特性,发现气液两相流型的转变受管径影响.Valota等[17]利用NASAKC-135失重飞机进行了竖直管内气液两相流空隙组分的可视化统计分析,结果表明方差和信噪比大小能更好地确定特征流型.Zhao等[18]对NASA KC-135失重飞机内气液两相实验流型数据进行了分析,得出管内弹状流过渡到弹-环状流再到环状流主要受韦伯数影响.赵建福等[19]在90°弯管流型分析中同样得出弹状流、弹-环状流、环状流3种不同流型,并在微重力气液两相流动与池沸腾传热方面的地基实验、飞行实验和理论研究等方面取得众多成果[20].
微重力环境下气液两相流型受管路结构、重力环境以及流体间的界面张力、惯性力、浮力等因素共同影响.而实验研究时间短、成本高、实验仪器精度低、甚至有些实验不能实现等,都会成为气液两相流实验研究的限制条件,而相应的数值模拟研究成本低、可控性好、对环境条件要求低等优点可以很好地弥补实验研究方法的不足.Clarke等[21]建立了二维模型,研究了微重力下垂直管内两相流的漂移速度,发现气相直径、气相径向位置、雷诺数及管道直径对漂移速度都有显著影响.Gabriel等[22]采用VOF方法模拟了竖直上升管内二维轴对称模型,对微重力和常重力下管内气弹周围流场进行分析,但只考虑了轴向和径向流场参数对气弹的影响,无法形成各周向参数对气弹的影响. 对不同重力下水平管的研究,刘向东等[23]建立了三维数值模型,采用VOF方法模拟分析气相单元径向空隙率、滑速比以及截面空隙率脉动等随重力条件的变化规律.然而空间流体管理是一个复杂多变的过程,上述研究仅是对于简单管路段内的分析研究,不能全面体现空间流体在复杂管路中流动特性.
本文综合考虑气液两相流体流动过程中,管形、重力条件以及流场轴向、径向和周向参数的影响,建立不同重力条件下90°弯管内气液两相流动的三维非稳态物理模型,利用计算流体软件FLUENT进行数值研究分析,考虑10-6g0,10-4g0,10-2g0,1g0(g0=9.8m/s2)不同重力环境对气液两相流流型的影响作用,研究不同工况下90°弯管内气液两相流的流型、流场分布情况,并对90°弯管内气液两相流过程的轴向空隙率,滑速比及气相尾部最大斜向角等随重力的变化规律进行分析和讨论.
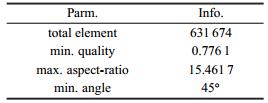
1 数值计算方法 1.1 计算模型由于模型的结构特点对整体管路系统两相流流动影响明显,本文所研究的计算模型取自于文献[19]的实验研究模型 中90°弯管部分,并且在数值计算过程中对模型入口进行处理. 整体物理模型的几何结构和尺寸如图1所示.
|
图 1 物理模型 Fig.1 Physical model |
气液两相主管路的设计参照文献[19],主管路入口垂直段长度为H1=500 mm,内径为D=12.7$\,mm,H2=58.4 mm,L=39.4 mm,90°弯管弯曲半径为R=76.5 mm. 模型对入口垂直管进行内径优化处理,并且,入口设置为十字形的气液混合段[23],采用垂直主管段方向的入口模型,有利于减小主管段气液两相流的扰动距离,有助于 气相混合稳定流动.模型主管段的垂直上升距离为H1,各入口支路长度为3.5D,内径为0.5D,结构如图1 所示.
模型中重力的方向与气液两相入口速度的方向垂直,气相采用空气,液相采用水,气液两相从底部十字形入口水平对冲进入 管内,在垂直管底部充分混合进入主管段,整个过程不考虑传热问题.
1.2 控制方程气液两相流在弯管内的流动情况比较复杂,两相界面[24, 25]难以捕捉. 然而,VOF方法[26]是处理复杂自由界面的有效方法. 在每个控制容积内,所有相的体积分数和为1.所有变量及其属性的区域被各相共享并且代表了容积平均值.
在气液两相流流动的数值模拟过程中,引入气相流体的容积比率记为αg,液相流体的容积比率记为α1,则αg+α1=1,且有以下3种可能情况:
(1)αg=0:气相流体在单元中是空的;
(2)αg=1:气相流体在单元中是充满的;
(3)0 < αg < 1:单元中包含了气相流体和液相流体的界面.
通过VOF方法可得到计算网格内各相的体积分数,并能完整捕捉气液两相分布情况.在整个流场计算区域内,描述流体运区性动的连续性方程和Navier-Stokes方程分别为
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \upsilon } \right) = 0{\rm{ }} $ | (1) |
| $ \frac{{\partial \upsilon }}{{\partial t}} + \left( {\upsilon \cdot \nabla } \right)\upsilon = - \frac{1}{\rho }\nabla \rho + \frac{1}{\rho }\nabla \cdot \left[ {\mu \left( {\nabla \upsilon + \nabla {\upsilon ^{\rm{T}}}} \right)} \right] + g + {F_{\rm{v}}} $ | (2) |
式(1)和式(2)中
| $ \rho = {\alpha _{\rm{g}}}{\rho _{\rm{g}}} + {\alpha _{\rm{l}}}{\rho _{\rm{l}}}{\rm{ }} $ | (3) |
| $ \mu = {\alpha _{\rm{g}}}{\mu _{\rm{g}}} + {\alpha _{\rm{l}}}{\mu _{\rm{l}}}{\rm{ }} $ | (4) |
式中,ρ为密度(kg/m3),t为时间(s),υ为速度矢量(m/s),μ为动力黏度(kg/(m·s)),Fυ为表面张力(N/m3).
流体体积由体积函数αg确定,体积函数的控制微分方程为
| $ \frac{{\partial {\alpha _{\rm{g}}}}}{{\partial t}} + \upsilon \cdot \nabla {\alpha _{\rm{g}}} = 0{\rm{ }} $ | (5) |
式中,下标g,l分别表示气相和液相.
1.3 网格划分由于管路复杂以及重力变化,对本文管路中的气液两相的流动对称性产生很大影响,相邻单元中气液两相的相互作用以及气液两相沿周 向方向的特征参数不可忽略. 因此,本文使用三维计算模型.
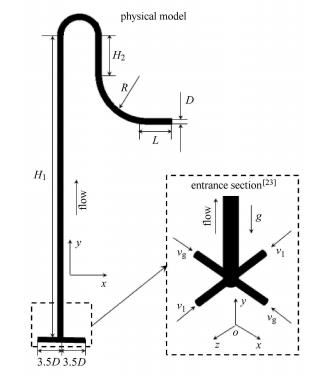
模型全部采用六面体结构化网格对模型进行分区划分,整体区域共分为两个:入口管段区域和主管段区域.考虑到气液两相界面准确捕捉问题,对整体网格进行合理加密,并对主管路壁面附近网格进行加密处理,加密网格如图2所示.整个计算域的总网格量为63万左右,具体网格参数如表1所示.通过对数值计算结果进行网格检验,网格数量符合独立性要求.
|
图 2 网格划分 Fig.2 Mesh division |
| 表 1 网格参数 Table 1 Mesh parameters |
采用VOF方法处理复杂自由表面的问题,可以只用一个函数来描述自由表面的各种复杂变化问题,有效捕捉气液两相间的界面运动情况.
针对不同重力环境下90°弯管内气液两相流模型,采用定入口速度边界条件(vg = 0.3m/s,vl = 0.5m/s)以及 壁面无滑移边界条件,速度场和压力场耦合采用临近校正和偏度校正的压力隐式算子分裂(PISO)方法[27],通过动量插值消除不合理的压 力场,非稳态求解.
2 计算结果与讨论 2.1 流型及模型验证为了验证本文所建立的数值模型的正确性,本文将对90°弯管内微重力气液两相流型进行分析讨论,并且将数值模拟所得到 的流型与可视化实验观测流型特征进行比较.
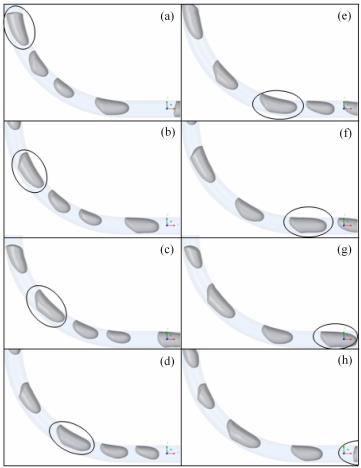
90°弯管气液两相流流动结构与直管道内相应流型有本质上的差异.气液两相经对冲的十字入口段进入主管路,受重力、惯性力及弯管结构等共同作用影响,在弯管内形成渐变的气液两相流型.图3给出了一组数值模拟微重力环境下气液两相在90°弯管内流动的流型渐变图,流动时间间隔为0.05\,s. 由图3(a)~图3(d)可知:气液两相在90°弯管入口段流动时其尾部斜向弯管内侧作用越来越强烈,当出口段流动时,尾部逐渐恢复 为光滑平坦状,如图3(e)~图3(h).
|
图 3 流型渐变图 Fig.3 Flow patterns transition diagram |
在微重力条件下,气液两相分别以恒定速度0.3 m/s,0.5 m/s流入系统,弯管内连续出现被液相分隔开的分散气相,定义为弹状流 流型. 气相头部轮廓呈子弹型在弯管内流动,子弹型气相尾部则斜向弯管内侧,形成一定斜面角度. 图4为1×10-4g0和1×10-2g0下气相流型对比,随着重力的增大,管内流型由流动均匀的弹状流过渡转变到浮力效应显著的长弹状流.微重力下,数值模拟得到的流型结果与可视化失重飞机实验(实验下重力条件为1×10-2g0~1×10-3g0[2])的实验观测结果一致性较好,由于实验只针对90°弯管气液两相流流型的定性研究分析,故本文只对微重 力下分布流型特征进行对比,并且,得到的结论规律与实验研究分析规律类似. 在常重力1g0条件下,气液两相工质受竖直方向上浮力作 用增强,流场扰动性增大,在90° 弯管内气相流型明显被拉长且形状较不规则,如图4(d)所示.
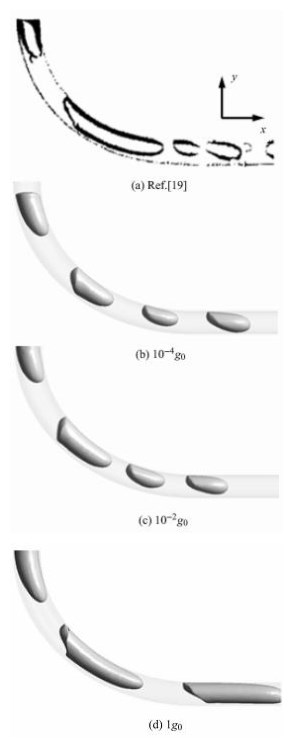
|
图 4 不同重力下90°弯管气液两相流型图 Fig.4 Gas-liquid two-phase flow patterns in 90° bend under different gravities |
90°弯管气液两相流动过程中,气相的相分布特性受到不同重力的影响作用显著. 另外,弯管作用、气液两相惯性力、黏性力、相互作用力、表面张力、气液两相界面剪切力、湍流脉动效应及接触角大小等因素协同影响气相轴向空隙率的分布. 气相截面空隙率表示气液两相流某一截面上,气相所占截面与总流道截面之比. 气液两相在90°弯管内流动过程中,定义αg为气液两相轴向空隙率,则
| $ {\alpha _{\rm{g}}} = \frac{{{A_{\rm{g}}}}}{{{A_{\rm{g}}} + {A_{\rm{l}}}}}{\rm{ }} $ | (6) |
式中,Ag,Al分别表示气相和液相所占流道截面的面积,单位(m2).
90°弯管内轴向截面空隙率随重力水平的变化分布如图5所示,为使所分析的空隙率数据符合统计规律,取流经弯管50个以上气相单元的数据统计进行分析,各截面数值取用平均值. 由图5可以看出,气相轴向空隙率峰值偏向于弯管内侧方向. 在弯管作用下,气相尾部向弯管内侧斜向变化导致轴向空隙率由弯管外侧到达空隙率峰值过程中,轴向空隙率呈现平缓递增趋势,并且微重力条件下递增趋势明显低于高重力条件.
气液两相流在90°弯管流动时由于离心力作用,密度较大的液相工质趋向于弯管外侧部分流动,密度较小的气相工质趋向于弯管内侧方向流动. 从图5中也可以看出,轴向空隙率整体偏向于弯管内侧方向,并且空隙率峰值出现在管路中心轴线偏上方向. 同时,气相轴向空隙率在峰值附近变化平缓说明气相在此区域集中度较高.
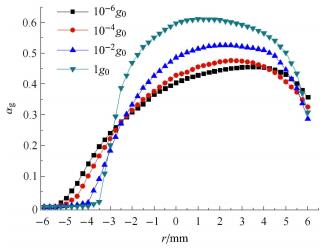
|
图 5 90°弯管轴向空隙率分布随重力变化 Fig.5 Curves of axial void fraction distribution versus gravity in 90° bend |
随着重力水平的不断提高,由重力引起的浮力作用逐渐增强,密度较小的气相工质进一步向弯管内侧聚集,密度较大的液相工质趋向于向弯管外侧聚集. 1g0时,弯管下壁面附近2 mm区域内几乎全为液相. 这是由于气液两相流在弯管内流动时离心力以及重力水平等产生不同大小的浮力等因素的影响,气相趋向于弯管内侧流动,液相趋向于弯管外侧流动现象明显.
2.3 重力对90°弯管内滑速比的影响由于气液两相在管路中流动过程中受作用力不同,其各相的流速不同,故在两相之间存在相对滑移速度. 滑速比S是表征气液两相流流动过程的一个重要特性参数,可以表示气液两相实际平均速度的相对大小
| $ S = \frac{{\beta \left( {1 - {\alpha _{{\rm{a}}v}}} \right)}}{{{\alpha _{{\rm{a}}v}}\left( {1 - \beta } \right)}} $ | (7) |
式中,αav和β分别为气液两相的平均截面含气率和容积含气率.
不同重力下气液两相流动过程中浮力大小不同,气液两相经过主管上升段后经U型弯管方向发生180°转变,再竖直下降进入90°弯管. 由图6可以看出,在90°弯管内,气相速度总大于液相速度大小. 重力水平较低时,气液两相速度相差不大,在10-6g0时,气液两相速度接近相等. 随着重力水平的提高,气液两相各相速度呈减小趋势,气相速度范围在0.35$\sim $0.45\,m/s,液相速度范围在0.25$\sim $0.45\,m/s,并且,液相速度减小的速度明显大于气相速度减小的速度.
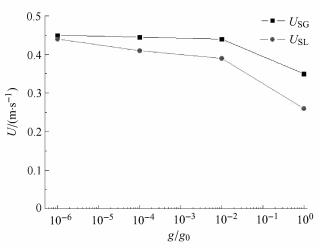
|
图 6 气液两相表观速度随重力变化 Fig.6 Curves of superficial velocity of gas-liquid two-phase flow versus gravity |
图7为气液两相滑速比随重力变化关系图,从图中可以看出:低重力水平下,水、气两相在90°弯管中流动过程中,两相的流速大小相差较小,滑速比接近为1. 随着重力水平的提高,重力导致的浮力效应在气液两相流中逐渐增强,气相速度增大趋势明显,促使两相滑速比呈递增趋势变化,滑速比范围为1.00~1.45之间. 气液两相在系统中的动量大小受重力、浮力、惯性力及弯管产生的离心力共同作用的影响,高重力环境下,两相速度变化剧烈,滑速比较大.
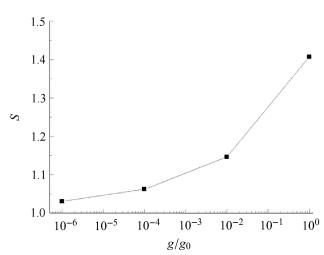
|
图 7 滑速比随重力变化 Fig.7 Slip ratio versus gravity |
气液两相流动过程中,由于竖直方向作用力不均衡,从而使气液两相流体的动量在管路流动过程中逐渐变化. 另外,由于弯管的结构特点,两相流在弯管内流动产生的离心力作用同样是影响滑速比变化的关键因素. 随着重力水平提高,在90°弯管内气液两相流惯性力增大,滑速比随之增大,弯管容积含气率增加(图8). 因此,不同重力环境影响两相流惯性力变化进而影响滑速比及含气率的变化.
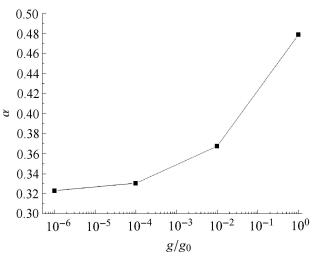
|
图 8 90°弯管容积含气率 Fig.8 Volume void fraction in 90° bend |
在两相弹状流和弹-环状流中,气相形成的气团会阻断单相弯管流动中对称的二次流通道,即不再是对称的二次涡旋,使 得两相二 次流谱出现明显不同,如图9(a). 截面速度矢量图9(b)可以看出,截面上速度分量远小于主流速度,气团在垂直主流方向的截面上由于速度不均匀而发生整体偏转旋转 流动,整体看来,气团是旋转前进[19],但单个气团的旋转方向是随机的.
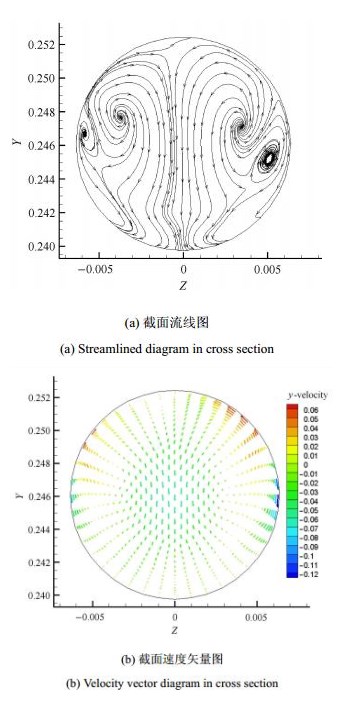
|
图 9 90°弯管出口处流线及速度图 Fig.9 Streamline and velocity in outlet of 90° bend |
在不同重力环境下,从气液两相流流经90°弯管的运动分析可以看出:气相运动形成子弹头型微尖的头部以及较 为平整的尾部,并且在弯管的作用下,平整的尾部斜向弯管内侧方向,在弯管内侧形成微凸的结构. 图10给出了弯管内气液两相流流动过程中气相典型单元结构,其中φ为尾部均平面与弯曲半径方向的夹角.
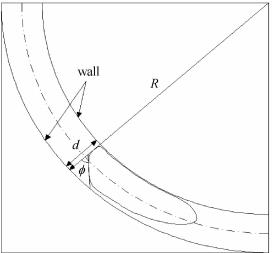
|
图 10 90°弯管内气液相单元结构图 Fig.10 Gas-liquid structures in 90° bend |
图11给出了90°弯管内气液两相流流动过程中速度矢量图,可以看出红色气相尾部运动受到弯管作用明显,尾部速度矢量方向 发生明显变化,向弯管中心方向指向偏转,导致气相尾部产生斜向角. 由连续的气液两相运动分析可以看出:气相进入弯管内部后尾部斜向角逐渐增大,达到弯管弯曲中心位置时弯管斜向作用效果达 到最大,斜向角达到最大值;逐渐流出弯管时,尾部斜向角逐渐减小,弯管作用减弱. 因此,气相尾部位于弯管中心45°位置时斜向角定义为最大斜向角.
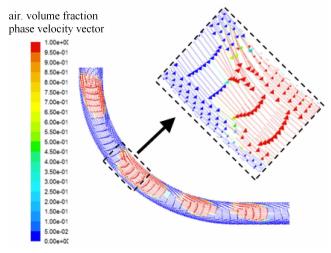
|
图 11 气液两相速度矢量图 Fig.11 Gas-liquid two-phase velocity vectors diagram |
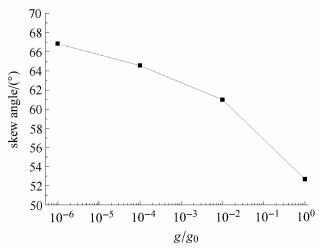
|
图 12 最大斜向角随重力变化 Fig.12 Maximum skew angle versus gravity |
不同重力环境下,最大斜向角随重力不同的变化如图12所示. 根据统计规律方法对最大斜向角大小进行数据分析. 由图12可以看出,随着重力水平的提高,气相在弯管内流动时最大斜向角逐渐减小,这主要是由于在微重力条件时,气相主要受到弯管作 用影响,气相尾部斜向弯管内侧的程度较大;随着重力水平的提高,重力的作用促使气相工质整体趋向于管上部流动,气相 向尾部聚集,均平面的面积减小,弯管作用减弱,最大斜向角减小.
3 结 论通过本文研究,得出如下结论:
(1)气液两相流在管路中的流型是多种外力共同作用的结果,重力水平的提高使竖直方向浮力效应增强,导致流体在竖直管路中流动时动量发生变化,90°弯管内气相单元上浮聚集合并,流型发生变化.
(2) 随着重力水平提高,90°弯管内气相轴向空隙率峰值受弯管影响减小,峰值增大且趋向于弯管中心方向移动.1g0时,弯管下壁面附近2 mm区域几乎全为液相.
(3)随着重力水平提高,在90°弯管内气液两相流惯性力增大,气液两相滑速比呈增大趋势,弯管容积含气率增加.
(4)气液两相在弯管内流动过程中,气相尾部受弯管作用影响十分明显. 气相单元流入弯管时尾部斜向角逐渐增大,流出弯管时斜向角减小至尾部变平缓,在90°弯管中心位置附近,最大斜向角最大. 随着重力水平提高,最大斜向角呈减小趋势.
| [1] | 庞明军,魏进家,宇波. 微重力量值对气液两相流相分布及液相湍流统计量影响的数值模拟. 空间科学学报,2012,32(2):368-375 (Pang Mingjun,Wei Jinjia,Yu Bo. Numerical investigation on influence of micro-gravity magnitude on phase distribution and liquid turbulence statistics in bubbly flow. Chinese Journal of Space Science, 2012, 32(2): 368-375 (in Chinese)) |
| [2] | 赵建福. 微重力条件下气/液两相流流型的研究进展. 力学进展,1999,29(3):368-382 (Zhao Jianfu. A review of two-phase gas-liquid flow patterns under microgravity conditions. Advances in Mechanics, 1999, 29(3): 368-382 (in Chinese)) |
| [3] | 王景涛. 微重力实验环境. 北京:中国学术期刊电子出版社,1998,27(7):392-398 (Wang Jingtao. Experimental Microgravity Environment. Beijing: China Academic Journal Electronic Publishing House, 1998, 27(7): 392-398 (in Chinese)) |
| [4] | Zhao JF, Xie JC, Lin H, et al. Experimental studies on two-phase flow patterns aboard the mir space station. International Journal of Multiphase Flow, 2001, 27: 1931-1944 |
| [5] | Zhao JF, Xie JC, Lin H, et al. Experimental studies on two-phase gas-liquid flow patterns at normal and reduced gravity conditions. Science in China, 2001, 44(5): 553-560 |
| [6] | 赵建福,解京昌,林海 等. 不同重力条件下气/液两相流实验研究. 工程热物理学报,2001,22(3):367-369 (Zhao Jianfu, Xie Jingchang, Lin Hai, et al. Experimental study on two-phase gas-liquid flow patterns at different gravity conditions. Journal of Engineering Thermophysics, 2001, 22(3): 367-369 (in Chinese)) |
| [7] | 赵建福,解京昌,林海 等. 部分重力条件下气液两相流型研究. 工程热物理学报,2004,25(1):85-87 (Zhao Jianfu, Xie Jingchang, Lin Hai, et al. Study on two-phase gas-liquid flow patterns at partial gravity conditions. Journal of Engineering Thermophysics, 2004, 25(1): 85-87 (in Chinese)) |
| [8] | Rezkallah KS, Zhao L. A flow pattern map for two-phase liquid-gas flows under reduced gravity conditions. Advances in Space Research, 1995, 16(7): 133-136 |
| [9] | Colin C, Fabre J. Gas-liquid pipe flow under microgravity conditions: influence of tube diameter on flow patterns and pressure drops. Advances in Space Research, 1995, 16(7): 137-142 |
| [10] | Zhao JF, Lin H, Xie JC. Pressure drop of bubbly two-phase flow in a square channel at reduced gravity. Advances in Space Research, 2002, 29(4): 681-686 |
| [11] | 赵建福,解京昌,林海等. 常重力和低重力条件下气液两相流实验研究. 中国科学,2002,32(4):491-495 (Zhao Jianfu, Xie Jingchang, Lin Hai, et al. Experimental study of gas liquid two phase flow in normal and low gravity conditions. Science in China, 2002, 32(4): 491-495 (in Chinese)) |
| [12] | Balasubramaniam R, Ramé E, Kizito J, et al. Two phase flow modeling: Summary of flow regimes and pressure drop correlations in reduced and partial gravity. National Center for Space Exploration Research, Cleveland, Ohio. NASA/CR, 2006, 214085 |
| [13] | Choi B, Fujii T, Asano H, et al. A study of the flow characteristics in air-water two-phase flow under microgravity (results of flight experiments). JSME International Journal, 2003, 46(2): 262-269 |
| [14] | Shephard AM, Kurwitz C, Best FR. Microgravity bubbly-to-slug flow regime transition theory and modeling. Microgravity Science Technology, 2013, 25: 167-177 |
| [15] | 顾汉洋,郭烈锦,张西民 等. 水平管内气液两相流中单气泡形态特征实验研究. 工程热物理学报,2006,27(3):433-436 (Gu Hanyang, Guo Liejin, Zhang Ximin, et al. The shape of isolated bubble in intermittent flows in horizontal straight tube. Journal of Engineering Thermophysics, 2006, 27(3): 433-436 (in Chinese)) |
| [16] | Bousman WS, Mcquillen JB, Witte LC. Gas-liquid flow patterns in microgravity: effects of tube diameter, liquid viscosity and surface tension. Elsevier Science, 1996, 22(6): 1035-1053 |
| [17] | Valota L, Kurwitz C, Shephard A, et al. Microgravity flow regime data and analysis. International Journal of Multiphase Flow, 2007, 33: 1172-1185 |
| [18] | Zhao L, Rezkallah KS. Gas-liquid flow patterns at microgravity conditions. International Journal of Multiphase Flow, 1993, 19(5): 751-763 |
| [19] | 赵建福,Gabriel KS. 微重力条件下90°弯管气液两相流型研究. 工程热物理学报,2004,25(5):801-803 (Zhao Jianfu, Gabriel KS. Flow patterns of two-phase gas-liquid flow in a 90° bend at microgravity. Journal of Engineering Thermophysics, 2004, 25(5): 801-803 (in Chinese)) |
| [20] | Zhao JF. Two-phase flow and pool boiling heat transfer in microgravity. International Journal of Multiphase Flow, 2010, 36(2): 135-143 |
| [21] | Clarke NN, Rezkallan KS. A study of drift velocity in bubbly two-phase flow under microgravity conditions. International Journal of Multiphase Flow, 2001: 1533-1554 |
| [22] | Gabriel KS. Microgravity Two-phase Flow and Heat Transfer. California: Springer, 2007, 132-140 |
| [23] | Liu XD, Chen YP, Shi MH. Influence of gravity on gas-liquid two-phase flow in horizontal pipes. International Journal of Multiphase Flow, 2012, 23-35 |
| [24] | 刘赵淼,刘丽昆,申峰. Y型微通道中两相界面特性变化分析. 机械工程学报,2014,50(8):189-196 (Liu Zhaomiao, Liu Likun, Shen Feng. Numerical analysis on two-phase flow characteristics at convection microfluidic Y-junctions. Journal of Mechanical Engineering, 2014, 50(8): 189-196 (in Chinese)) |
| [25] | 刘赵淼,刘丽昆,申峰. Y型微通道两相流内部流动特性. 力学学报,2014,46(2):209-216 (Liu Zhaomiao, Liu Likun, Shen Feng. Two-phase flow characteristics in Y-junction microchannel. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2): 209-216 (in Chinese)) |
| [26] | Hirt CW, Nichols BD. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 1981, 39: 201-225 |
| [27] | 李国杰,黄萌,陈斌. 基于PISO算法的非结构化网格VOF算法. 工程热物理学报,2013,34(3):476-479 (Li Guojie, Huang Meng, Chen Bin. VOF method on unstructured grid using PISO algorithm. Journal of Engineering Thermophysics, 2013, 34(3): 476-479 (in Chinese)) |
 2015, Vol. 47
2015, Vol. 47