层流向湍流的转捩是流体力学研究最具挑战性问题之一.从基础理论研究角度来看,转捩是一个连续演化的流动过程,是一种从简 单分层稳定状态向复杂多变湍流状态的过渡.从工程应用角度来看,湍流的气动加热以及摩擦阻力均高于层流,且热流峰值通常发生在转捩区,因此流动转捩位置及转捩区长度的准确预测对飞行器表面的防热和减阻设计至关重要.湍流具有强混合性且不易发生流动分离,吸气式高超声速飞行器通常控制在进气道入口之前转捩,从而减小进气道入口处激波边界层干扰产生的流动分离,利于进气道燃烧室燃料的充分燃烧,提高燃料利用率,保证超燃冲压发动机的正常启动.
影响边界层转捩的因素很多,例如:头部钝度、来流雷诺数、来流湍流度、攻角、壁温、噪声等. 针对边界层转捩众多影响因素,国内外学者进行了一系列的研究. Horvath等[1]通过风洞实验方法对圆锥、裙锥的边界层转捩进行了研究,得到了头部钝度、来流雷诺数和总温对转捩的影响规律. Fedorov等[2]通过实验、直接数值模拟 (direct numerical simulation, DNS)等多种方法分析了壁温对边界层转捩的影响. 李新亮等[3]和苏彩虹等[4]分别采用DNS方法和基于稳定性理论的eN方法对1°攻角圆锥进行了模拟,揭示了小攻角下边界层转捩机制. 沈清等[5]给出了高超声速圆锥边界层失稳结构与转捩攻角效应.
目前预测转捩的计算方法有:半经验的eN方法、基于雷诺平均的Navier-Stokes方程(RANS)的湍流/转捩模式、转捩 准则、DNS等. 其中转捩模式是在RANS方程基础之上,结合稳定性理论分析中得到的各种失稳模态以及实验中观察得到的“间歇现象”和非湍流脉 动概念所构造的一种可快速判断复杂外形流动转捩的工程预测方法. 现有文献公开发表的基于RANS方程的转捩模式已多达十几种. 如Langtry和Menter[6]的γ-Reθ模式,Papp[7]的k-kL-ε模式,王亮和符松[8, 9]的k-ω-γ模式等. 其中k-ω-γ转捩模式针对高超声速流动提出,经文献孔维萱[10]、周玲等[11]的检验和验证,能够较准确地反映高超声速三维边界层转捩. 然而,对于k-ω-γ转捩模式对各种转捩影响因素的预测能力,目前并没有系统的研究.
因此,本文拟采用k-ω-γ转捩模式,对5°圆锥的高超声速边界层转捩进行模拟. 通过计算不同头部钝度、来流雷诺数和来流湍流度三种影响因素下的转捩位置,验证该模 式对不同因素影响转捩位置的预测性能;同时通过分析k-ω-γ $转捩模式的构造参数,如:等效脉动动能、黏性系数等,给出了该模式反映不同因素影响转捩位置的原因,希望对于工程 转捩预测以及转捩模式的构造和改进具有一定的参考价值.
1. 计算方法 1.1 控制方程及空间离散方法[12]本文采用有限体积法求解雷诺平均N-S方程组,时间离散采用LU-SGS (lower-upper symmetric Gauss-Seidel)方法,无黏通量空间离散使用三阶上风Roe格式,黏性通量离散采用二阶中心差分格式.
1.2 k-ω-γ转捩模式[8, 9]k-ω-γ转捩模式以SST(shear-stress transport)湍流模型为基础,由关于等效脉动动能k、等效脉动动能比耗散率ω以及间歇因子γ的3个输运方程构成
| $ \left. \begin{array}{l} \\ \frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho {u_j}k)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}[(\mu + {\sigma _k}{\mu _{{\rm{eff}}}})\frac{{\partial k}}{{\partial {x_j}}}] + {P_k} - \varepsilon \\ \frac{{\partial (\rho \omega )}}{{\partial t}} + \frac{{\partial (\rho {u_j}\omega )}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}[(\mu + {\sigma _\omega }{\mu _{{\rm{eff}}}})\frac{{\partial \omega }}{{\partial {x_j}}}] + \\ {P_\omega } - {D_\omega } + C{d_\omega }\\ \frac{{\partial (\rho \gamma )}}{{\partial t}} + \frac{{\partial (\rho {u_j}\gamma )}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}[(\mu + {\mu _{{\rm{eff}}}})\frac{{\partial \gamma }}{{\partial {x_j}}}] + {P_\gamma } - {\varepsilon _\gamma }\\ \end{array} \right\}$ | (1) |
其中等效脉动动能k方程是以间歇因子为权重将Mayle和Schulz[13]提出并模化的非湍流脉动动能k的输运方程与湍动能kT方程统一而成.
k-ω-γ转捩模式构造有效涡黏性系数 μeff代替SST湍流模型中的涡黏性系数μt. 对μeff 的模化引用Warren的假设考虑非湍流脉动的影响,具体表达式如下
| $ {\mu _{{\rm{eff}}}} = (1 - \gamma ){\mu _{nt}} + \gamma {\mu _t}{\rm{ }} $ | (2) |
非湍流脉动黏性系数μnt通过构造扰动模态的时间尺度τnt进行模化
| $ {\mu _{nt}} = {C_\mu }\bar \rho k{\tau _{nt}}{\rm{ }} $ | (3) |
| $ {\tau _{nt}} = \left\{ \begin{array}{l} {\tau _{nt1}},|{M_{{\rm{rel}}}}| \le 1\\ {\tau _{nt1}} + {\tau _{nt2}},|{M_{{\rm{rel}}}}| > 1 \end{array} \right. $ | (4) |
其中,Mrel=(U-cr)/a为相对马赫数,a为当地声速,cr为扰动相速度. 根据稳定性理论,Mrel > 1的区域需考虑第二扰动模态. τnt1和τnt2分别表示第一、第二扰动模态时间尺度,由有效长度尺度ζ eff构造,具体表达式如下
| $ {\tau _{nt1}} = {C_2}[\zeta _{{\rm{eff}}}^{1.5}/\sqrt {{{(2{E_u})}^{0.5}}v} ]{\rm{ }} $ | (5) |
| $ {\tau _{nt2}} = {C_3}[2{\zeta _{{\rm{eff}}}}/U({y_s})]{\rm{ }} $ | (6) |
| $ {\zeta _{{\rm{eff}}}} = \min [\frac{{{d^2}\Omega }}{{\sqrt {2{E_u}} }},{C_1}\frac{{\sqrt k }}{\omega }]{\rm{ }} $ | (7) |
其中,Eu=0.5(U-Uw)i2为当地流体相对壁面的平均流动动能.Ω为平均涡量的模,d为物面距离,U(ys)为广义拐点ys处的速度. 关于k-ω-γ转捩模式的详细介绍参见文献[8, 9].
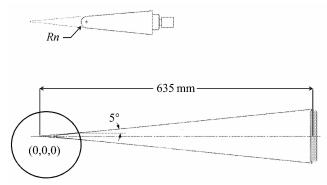
2 算例及结果分析本文算例采用Horvath[1]等在Ma6风洞进行的圆锥边界层转捩实验模型,如图1所示. 模型半锥角为5°,原点取在理论尖点,全长635 mm,头部钝度Rn分别为0.0025 mm,0.79 mm和1.58 mm. 针对不同头部钝度生成三套网格,无侧滑采用半模计算,其中法向150个网格单元,半模周向60个网格单元,在保证三套网格 相同流向位置处网格分布一致的基础上,头部钝度由小到大布置的网格单元数量分别为 240,170和140.
2.1 头部钝度影响算例本算例的计算条件参考Horvath[1]等的实验条件给出,来流马赫数Ma∞=6,来流温度T∞=63 K,来流压强P∞=2037.88 Pa,来流单位雷诺数Re∞=2.56×107/m,壁面温度Tw=273 K,攻角和侧滑角均为0°,取来流湍流度(free-steam turbulence intensities)FSTI=0.4%. 该方法具有2个可调参数C2,C3,需根据与计算外形相近的实验数据进行标定,本文以头部钝度Rn=0.79 mm工况进行标定,取C2=0.2,C3=0.1.
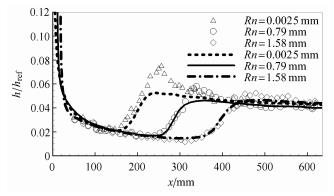
图2给出了计算得到的3种头部钝度工况下传热系数h/href分布. 其中,h=q/(Haw-Hw),这里q和H分别为壁面热流密度和焓值,脚标aw表示绝热壁,w 表示壁面,href由Fay Riddell热流计算公式求出的参考值,h/href是判别流动转捩的重要宏观物理量. 图2中点表示实验值[1],线表示计算值. 从中可以看到,随着头部钝度减小,转捩位置逐渐前移,转捩区长度逐渐减小. 湍流区的h/href值大约为层流区的3倍,而热流峰值处的h/href值几乎可达到层流区的4倍. 计算得到的全层流和全湍流区的h/href与实验值一致. 而转捩区,除了Rn=0.0025 mm 工况计算得到的转捩位置较实验结果略微靠后外,其他两种工况,计算得到的转捩起始位置以及转捩区长度均与实验值十分吻合.
|
图 2 不同头部钝度传热系数分布 Fig.2 Heat transfer coefficient distribution of different nose bluntness |
但对于图2中转捩区的热流峰值,计算与实验结果差异较大,且转捩位置越靠前,差异越明显. k-ω-γ模式提出者王亮在其博士论文[8]零攻角圆锥算例中发现了同样的缺陷. 针对这一问题,宋博等[14]分析认为这与间歇因子经验公式的选取有关. Papp等[7]在其构造的转捩模式中利用间歇因子耦合可压缩修正的方法进行峰值差异修正,虽然模拟出了热流过冲现象,但 是热流峰值具体位置与实验数据相比还是有所差异. 本文作者也参考Papp的方法进行了峰值修正尝试,但计算得到的全湍流区域传热系数值偏小,推测认为该修正方法并不适用于本 文所采用的转捩模式. 为此,我们只关心转捩位置、转捩区长度和层、湍流区数值,重点关注其中的变化规律,暂时回避热流峰值对比.
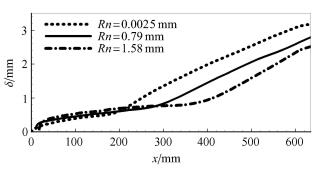
头部钝度直接影响头部弓形激波的位置,钝度越大,激波越脱体,头部附近的熵层越厚,导致边界层受熵层影响严重,甚至被熵 层吞没(即“熵吞”现象). 图3给出了不同头部钝度下边界层厚度变化曲线,其中横坐标x表示流向位置,纵坐标δ表示边界层厚度. 从中可以看到:头部钝度越小,层流区内边界层越薄,转捩发生位置(边界层厚度突然增大位置处)越提前.
|
图 3 不同头部钝度下边界层厚度 Fig.3 Boundary layer thickness of different nose bluntness |
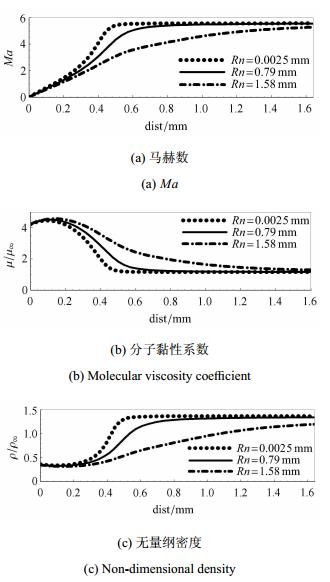
图4给出了层流区内流向站位x=100 mm处的马赫数Ma、分子黏性系数μ 和无量纲密度ρ/ρ∞沿壁面法向的分布,横坐标dist表示壁面距离. 从图4(a)中得到:随头部钝度减小,相同壁面距离位置处马赫数逐渐增大,导致对应的当地雷诺数增大,转捩提前发生. 从图4(a)中同样能够看到熵吞现象的影响. 由图3已知x=100 mm站位处Rn=0.002 5 mm,0.79 mm和1.58 mm的边界层外缘分别在δ=0.40 mm,0.45 mm和0.53 mm位置处. Rn=0.002 5 mm工况下在边界外缘附近马赫数很快达到波后马赫数,而随着头部钝度增大,在边界层外缘之后当地马赫数才逐渐达到波后马赫数,说明头部钝度越大,厚的熵层影响范围越大. 在高超声速边界层中,第一模态的不稳定扰动波由黏性引起,而被称为第二模态的Mack模态,主要以声波的形式在壁面和相对声速线间来回反射,且高马赫数的边界层比低马赫数情况更加不稳定.图4(b)给出了x=100 mm站位处的分子黏性系数分布,头部钝度越小,头部脱体激波越弱,波后温度越低,从而分子黏性系数越小.从式(5)易知,小的分子黏性系数对应的第一扰动模态时间尺度较大,利于转捩发生. 图4(c)给出了无量纲密度分布,可见,头部钝度越小,相同壁面距离位置处无量纲密度越大,由式(3)模式构造角度分析,非湍流脉动黏性μnt与密度成正相关,较大的边界层密度能够促进非湍流脉动的发展,进而导致等效脉动动能发展,促进转捩提前发生.
|
图 4 不同头部钝度下x=100 mm处参数分布 Fig.4 Parameters distribution of different nose bluntness on x=100 mm |
雷诺数对于转捩研究十分重要,转捩准则[15]方法以及Langtry[6]等提出的 γ-Reθ方法,都采用了动量厚度雷诺数Reθ相关量进行转捩预测,本文所采用的k-ω-γ方法在推导长度尺度时依据了Wilocx[16]提出的关于动量厚度雷诺数的关系式. 对于雷诺数对流动转捩的影响,计算以头部钝度Rn=0.79 mm作为对比算例,变换来流雷诺数进行了对比分析. 来流雷诺数分别取2.59×107/m,2.03×107/m,1.77×107/m,1.41×107/m和1.05×107/m.
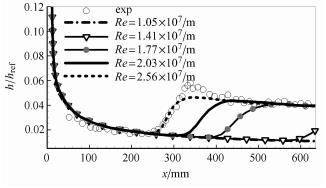
图5给出了不同来流雷诺数条件下的圆锥传热系数分布. 从图中可以看到,随着来流雷诺数从Re=2.59×107/m逐渐减小到1.41×107/m,圆锥壁面转捩起始位置逐渐延迟. Re=1.41×10/m工况转捩在模型尾段刚刚发生,而Re=1.05 ×10/m工况下转捩未发生.
|
图 5 不同来流雷诺数下传热系数分布 Fig.5 Heat transfer coefficient distribution of different free-steam Reynolds number |
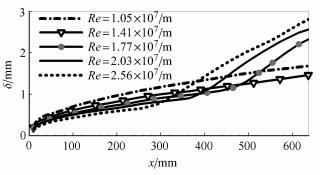
图6对应5种来流雷诺数工况下的圆锥流向边界层厚度变化. 对比图5,图6中边界层明显增厚的位置大约在图5中转捩区中 间位置,较转捩起始位置略有滞后. 由式(8)[17]可以看出,相同边界层外缘 马赫数的情况下,来流雷诺数越大,边界层厚度越小,图6中的结果很好地符合这一规律. 与头部钝度算例中边界层发展规律一致,边界层越薄,转捩位置靠前.
| $ \frac{\partial }{x} \propto \frac{{M_e^2}}{{\sqrt {Re} }}{\rm{ }} $ | (8) |
|
图 6 不同雷诺数下边界层厚度 Fig.6 Boundary layer thickness of different free-steam Reynolds number |
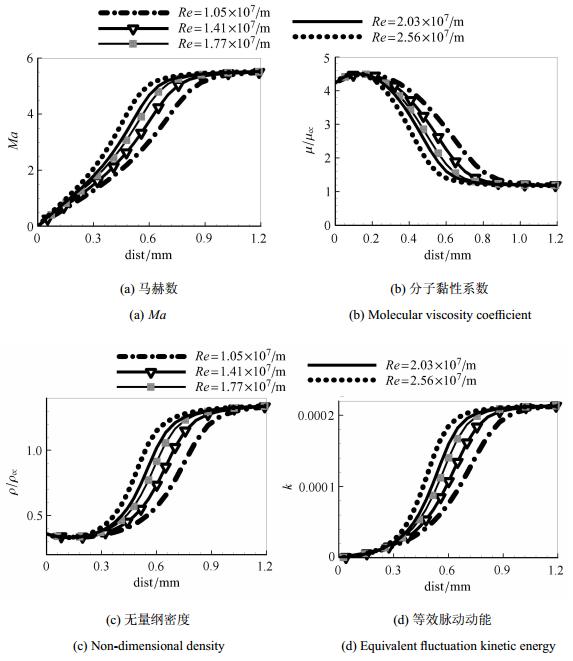
图7(a)~图7(d)分别给出了5种雷诺数工况下x=100 mm站位处马赫数、分子黏性系数、无量纲密度和等效脉动动能的分布.可以看到在边界层区域内,雷诺数越大,相同壁面距离位置处的马赫数越大、分子黏性越小、密度越大.同头部钝度算例中分析的规律一致,边界层内马赫数越大,当地速度也越大,对应的当地雷诺数越大,流动易于转捩;分子黏性与第一模态扰动时间尺度成负相关,来流雷诺数越大,分子黏性越小,第一模态扰动时间尺度越大,流动越容易转捩;边界层外密度一致,而高雷诺数下边界层较薄,导致边界层内的密度变化梯度大,相同位置处密度较大,而密度与等效脉动动能成正相关,因此边界层内密度增大导致等效脉动动能的发展,促进层流转捩为湍流.
|
图 7 不同来流雷诺数下x=100 mm处参数分布 Fig.7 Parameters distribution of different free-steam Reynolds number on x=100 mm |
来流湍流度FSTI可表征描述背景噪声或自由来流扰动的强度,是影响流动转捩的关键因素之一,其定义式如式(9)所示,正确评 估来流湍流度是准确预测边界层转捩的前提.一般情况下普通风洞中来流湍流度较大,可达到1%以上;静音风洞中来流湍流度较小,一般小于0.1%,接近高空湍流度水平.
| $ T{u_\infty } = \sqrt {\frac{{{{u'}_i}{{u'}_i}}}{3}} /U $ | (9) |
本算例基于头部钝度Rn=0.79 mm工况,依据单一变量原则,FSTI选取0.1%,0.2%,0.4%和0.8%进行研究.
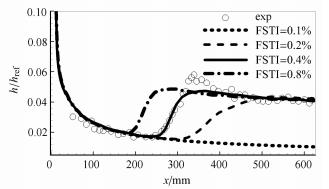
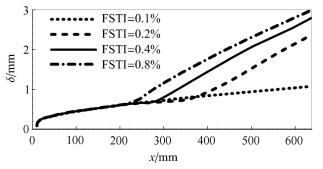
图8给出了不同湍流度工况下的热流分布曲线,可看到当来流湍流度为0.1%时边界层转捩未发生;随着来流湍流度增大,转捩发生并且转捩位置逐渐提前,转捩区长度逐渐变短. 同样对比不同来流湍流度下边界层厚度变化,如图9所示,可以看到边界层厚度在层流区完全一致,随着流动转捩发生,边界层逐渐变厚.
|
图 8 不同来流湍流度下传热系数分布 Fig.8 Heat transfer coefficient distribution of different FSTI |
|
图 9 不同来流湍流度下边界层厚度 Fig.9 Boundary layer thickness of different FSTI |
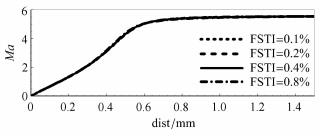
图10给出了x=100 mm站位处的Ma分布. 由于在层流区4种来流湍流度工况下边界层厚度相同,沿壁面法向Ma分布一致,说明 来流湍流度对层流区的流动没有影响.
|
图 10 不同来流湍流度下x=100 mm站位处Ma沿壁面法向分布 Fig.10 Mach number distribution of different FSTI on x=100 mm |
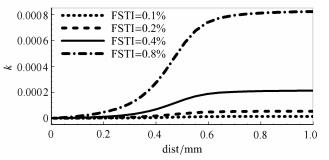
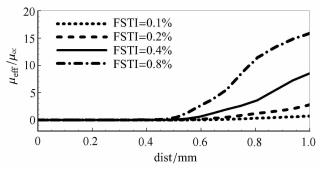
为探究来流湍流度影响过程,取x=100 mm站位处的等效脉动动能和涡黏性系数沿壁面法向的分布,如图11,图12所示.可见,随着来流湍流度增大,等效脉动动能逐渐增大,等效涡黏性系数随来流湍流度的变化规律与等效脉动动能一致.从模式构造角度进行分析,本文所使用的k-ω-γ模式等效脉动动能初值与来流湍流度直接相关,如下所示
| $ {k_0} = \frac{3}{2}FST{I^2}(u_0^2 + v_0^2 + w_0^2)/10000(10) $ | (10) |
|
图 11 不同来流湍流度下x=100 mm站位处等效脉动动能沿壁面法向分布 Fig.11 Equivalent fluctuation kinetic energy distribution of different FSTI on x=100 mm |
|
图 12 不同来流湍流度下x=100 mm站位处等效涡黏性系数沿壁面法向分布 Fig.12 Equivalent eddy viscosity coefficient distribution of different FSTI on x=100 mm |
来流湍流度表征外界扰动,外界扰动越大,边界层越容易发生流动失稳,转捩为湍流. 从模式构造角度来看,来流湍流度越大,等 效脉动动能初值越大,导致流动容易随着等效脉动动能的发展而转捩为湍流.
3 结 论通过k-ω-γ模式方法详细模拟了不同头部钝度、来流雷诺数和来流湍流度影响下的5°圆锥的高超声速边界层转捩,通过对模拟结果的分析可得出如下结论:
(1)k-ω-γ模式基本能够预测高超声速圆锥边界层转捩,能够准确地反映头部钝度、来流雷诺数和来流湍流度对高超声速边界层转捩的影响规律,即随着头部钝度减小、来流雷诺数增大、或者来流湍流度增大,转捩位置提前,转捩区长度变短;
(2)在高超声速边界层转捩中,相同来流马赫数情况下,头部钝度越小或者来流雷诺数越大,层流区边界层越薄,层流区边界层相同壁面法向位置处,分子黏性越小,对应第一模态时间尺度越大;同时边界层内当地马赫数越大,促进第二模态时间尺度的增长,导致转捩易于发生;
(3)来流湍流度表征了外界扰动的大小,外界扰动越大,来流湍流度越大,等效脉动动能初值越大,层流区内相同位置处的等效脉动动能越大,有效地猝发流动转捩;
(4)k-ω-γ模式不能精确模拟转捩后的热流峰值现象,推测认为与间歇因子输运方程构造有关,具体原因还需要进一步深入研究.
| [1] | Horvath TJ, Berry SA, Hollis BR, et al. Boundary layer transition on slender cones in conventional and low disturbance Mack 6 wind tunnels. AIAA Paper 2002-2743 |
| [2] | Fedorov A, Soudakov V, Egorov I. Numerical and experimental studies of high-speed boundary-layer stability on a sharp cone with localized wall heating or cooling. AIAA Paper 2014-1271 |
| [3] | Li XL, Fu DX, Ma YW. Direct numerical simulation of hypersonic boundary layer transition over a blunt cone with a small angle of attack.Physics of Fluids, 2010, 22: 025105 |
| [4] | Su CH, Zhou H. Transition prediction of a hypersonic boundary layer over a cone at small angle of attack-with the improvement of em N method. Science in China Series G: Physics, Mechanics & Astronomy, 2009, 52(1): 115-123 |
| [5] | 沈清,袁湘江,王强等. 可压缩边界层与混合层失稳结构的研究进展及其工程应用. 力学进展,2012, 42(3): 252-261 (Shen Qing, Yuan Xiangjiang, Wang Qiang. Review on the instability structure in compressible boundary layers and mixing layers and its application. Advances in Mechanics, 2012, 42(3): 252-261 (in Chinese)) |
| [6] | Langtry RB, Menter FR. Transition modeling for general CFD applications in aeronautics. AIAA Paper 2005-522 |
| [7] | Papp J, Dash SM. Modeling hypersonic laminar to turbulent transitional flows for 3D geometries using two-equation onset and intermittency transport models. AIAA Paper 2012-0449 |
| [8] | 王亮. 高超音速边界层转捩的模式研究. [博士论文]. 北京: 清华大学, 2008 (Wang Liang. Investigation of transition model for hypersonic boundary layer. [PhD Thesis]. Beijing: Tsinghua University, 2008 (in Chinese)) |
| [9] | 王亮,符松.一种适用于超音速边界层的湍流转捩模式.力学学报,2009, 41(2): 162-168 (Wang Liang, Fu Song. A new transition/turbulence model for the flow transition in supersonic boundary layer. Chinese Journal of Theoretical and Applied Mechanics, 2009, 41(2): 162-168 (in Chinese)) |
| [10] | 孔维萱,阎超,赵瑞.壁面温度条件对边界层转捩预测的影响.航空学报, 2013, 34(10): 2249-2255 (Kong Weixuan, Yan Chao, Zhao Rui. Effect of wall temperature on boundary layer transition prediction using transition model. Acta Aeronautica et Astronautica Sinica, 2013, 34(10): 2249-2255 (in Chinese)) |
| [11] | 周玲,阎超,孔维萱. 高超声速飞行器前体边界层强制转捩数值模拟. 航空学报,2014, 35(6): 1487-1495 (Zhou Ling, Yan Chao, Long Weixuan. Numerical simulation of forced boundary layer transition on hypersonic vehicle forebody. Acta Aeronautica et Astronautica Sinica, 2014, 35(6): 1487-1495 (in Chinese)) |
| [12] | 阎超.计算流体力学方法及应用. 北京: 北京航空航天大学出版社, 2006. 15-25 (Yan Chao. Computational Fluid Dynamic's Methods and Applications. Beijing: Beihang University Press, 2006. 15-25 (in Chinese)) |
| [13] | Mayle RE, Schulz A. The path to predicting bypass transition. Journal of Turbomachinery, 1997, 119: 405-411 |
| [14] | 宋博,李椿萱. 基于非湍流脉动动能方程的高超声速转捩预测. 北京航空航天大学学报,2010, 36(2): 244-247 (Song Bo, Li Chunxuan. Laminar to turbulent transition onset prediction onset prediction of hypersonic flows based on laminar kinetic energy equation. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(2): 244-247 (in Chinese)) |
| [15] | 孔维萱,张辉,阎超. 适用于高超声速边界层的转捩准则预测方法. 导弹与航天运载技术,2013, 5: 54-58 (Kong Weixuan, Zhang Hui, Yan Chao. Transition criterion prediction method for hypersonic boundary layer. Missiles and Space Vehicles, 2013, 5: 54-58 (in Chinese)) |
| [16] | Wilcox DC. Turbulence model transition prediction. AIAA Journal, 1975, 13(2): 241-243 |
| [17] | Anderson JD. Hypersonic and high temperature gas dynamics. McGraw-Hill Book Company, 1989. 301-307 |
 2015, Vol. 47
2015, Vol. 47