2. 航天飞行动力学技术国家级重点实验室,西安 710072
空间机动技术是实现空间操作任务的基础,具有重要的应用价值. 连续推力轨道机动容易控制、机动能力强,因此成为研究热点[1, 2, 3, 4]. 采用连续推力设计机动轨道存在一个很大的难点,即无法求其解析解.针对该问题,本文提出一种基于虚拟中心引力场(virtual central gravitational field,VCGF)的连续推力轨道设计新方法. 该方法是通过设计中心引力场来实现轨道机动.该方法包含两个步骤:第一步是设计满足任务约束的虚拟中心引力场;第二步是计算实现该虚拟中心引力场所需推力.该方法将航天器轨道设计问题转化为2个参数寻优问题,很大程度上简化了轨道设计过程,为航天器机动轨道设计提供新思路.
1 虚拟中心引力场的定义虚拟中心引力场是指引力场中心不在地心上,且其引力常数不等于地心引力常数的中心引力场. 该引力场可用参 数r0,μ2来定义,其中r0为虚拟引力场中心与地心相对位置矢量,称为虚拟引力场位置参数;μ2为虚拟引力场引力常数;在虚拟中心引力场中的轨道为虚拟圆锥曲线轨道.
2 轨道动力学建模与虚拟中心引力场设计 2.1 动力学建模设定地心引力场引力常数为μ1,航天器在地心惯性坐标系下位置矢量为r0,假定在航天器上施加推力加速度为at,则有
| $ \dfrac{d^2{\pmb r}_1 }{d t^2} + \dfrac{{\pmb\mu}_1 }{|{\pmb r}_1 |^3} \times {\pmb r}_1 = {\pmb a}_{\rm t} $ | (1) |
假设地心惯性坐标系为OXYZ,虚拟中心引力场坐标系为O'X'Y'Z'. 推力与地心引力场的合力形成的虚拟中心引力场参数为r0,μ2,则在虚拟中心引力场坐标系下有
| $ \dfrac{d^2({\pmb r}_1 - {\pmb r}_0 )}{d t^2} + \Big(\dfrac{{\pmb\mu}_2 }{ | {\pmb r}_1 - {\pmb r}_0 |^3}\Big) \times ({\pmb r}_1 - {\pmb r}_0 ) = {\bf 0} $ | (2) |
设r2=r1-r0,在特定虚拟中心引力场中,r0为定值,则(r0)' = 0,r'2 = r'1 - r'0 = r'1. 地心惯性坐标系下航天器位置和速度与虚拟中心引力场坐标系下位置和速度转化关系为
| $ {\pmb r}_2 = {\pmb r}_1 - {\pmb r}_0 \,,\ \ {\pmb v}_2 = {\pmb v}_1 $ | (3) |
由式(2)和式(3)可知,在虚拟中心引力场坐标系下,航天器运动方程可表示为如下形式
| $ \dfrac{d^2{\pmb r}_2 }{d t^2} + \dfrac{\mu _2 }{ |{\pmb r}_2 |^3} {\pmb r}_2 = 0 $ | (4) |
实现虚拟中心引力场所需推力可由下式得到
| $ {\pmb a}_{\rm t} = \dfrac{d^2{\pmb r}_1 }{d t^2} + \dfrac{\mu _1 }{ | {\pmb r}_1 | ^3}{\pmb r}_1 - \dfrac{d^2{\pmb r}_2 }{d t^2} -\dfrac{\mu _2 }{ |{\pmb r}_2 | ^3}{\pmb r}_2 = \dfrac{\mu_1 }{ |{\pmb r}_1 | ^3}{\pmb r}_1 - \dfrac{\mu _2 }{ | {\pmb r}_2 | ^3}{\pmb r}_2 $ | (5) |
由上述分析可知,通过调整推力,可形成一种虚拟中心引力场. 在该虚拟中心引力场中,航天器运动轨迹为虚拟圆锥曲线.若该虚拟圆锥曲线轨道满足轨道转移约束,则可实现轨道机动.
2.2 虚拟中心引力场设计如图 1所示,在地心引力场中,航天器在A点的速度、位置矢量、真近点角分别为${\pmb V}_{a1} = (V_{ax},V_{ay})$`,${\pmb r}_{a1} = (r_{ax},r_{ay} )$ fa1;在B点速度、位置矢量、真近点角分别为${\pmb V}_{b1} =(V_{bx} ,V_{by} )$,${\pmb r}_{b1} = (r_{bx}, r_{by} )$, fb1. 在虚拟中心引力场中,A点速度矢量为,${\pmb V}_{a2} = (V_{ax},V_{ay} )$,A点位移矢量为${\pmb r}_{a2} = {\pmb r}_{a1} + {\pmb r}_0 =(r_{ax} + r_{0x} ,r_{ay} + r_{0y} )$,真近点角为fa2; B点速度矢量为${\pmb V}_{b2} = {\pmb V}_b =(V_{bx} ,V_{by} )$,位置矢量为${\pmb r}_{b2} = {\pmb r}_{b1} + {\pmb r}_0 = (r_{bx} + r_{0x} ,r_{by} +r_{0y} )$,真近点角为fb2. 实现轨道转移,r0应该满足以下条件
| $\left. \begin{array}{l} {r_{a2}} = {r_{a1}} + {r_0}\\ {r_{b2}} = {r_{b1}} + {r_0}\\ {h_2} = {r_{a2}} \times {V_{a2}} = {r_{b2}} \times {V_{b2}} \end{array} \!\! \right\}$ | (6) |

|
图 1 在虚拟中心引力场中的转移轨道及受力分析 Fig. 1 Transfer orbit and force analysis using VCGF |
而虚拟引力常数μ2应满足以下条件
| $ \left. \begin{array}{l} {r_{a2}} = \frac{{h_2^2}}{{{\mu _2}}}\frac{1}{{1 + {e_2}\cos ({f_{a2}})}}\\ {r_{b2}} = \frac{{h_2^2}}{{{\mu _2}}}\frac{1}{{1 + {e_2}\cos ({f_{b2}})}}\\ {f_{b2}} = {f_{a2}} + \Delta f \end{array} \! \right\} $ | (7) |
求解方程组(7)需要确定2个参数值,r0,fa2,其中 $f_{a2} \in [0,2\pi]$;而r0的范围可以由方程(6)确定.在平面轨道设计问题中,${\pmb r}_0 = (r_{0x} ,r_{0y} )$,式(6)化为
| $ a_1 r_{0x}-b_1r_{0y}=c_1 $ | (8) |
其中,a1,b1,c1为常值系数.
如图 2所示, ${\pmb r}_0 = (r_{0x} ,r_{0y} )$的取值可以用一条直线来表示. 在圆锥曲线轨道上任何一点的矢径和其速度夹角小于180°,由此可知r0范围. 如图 1所示,虚拟中心引力场位置参数范围为$r_{0x}\in(x_a,x_b)$, 代入式(8)可知r0范围. 在三维轨道设计问题中,由式(7)约束条件亦可得到r0.
在虚拟中心引力场中,转移轨道就是虚拟圆锥曲线轨道,可以虚拟开普勒轨道要素来表示. 同样实现转移轨道消耗能量和时间也可以采用这些虚拟轨道要素表示. 这样,转移轨道设计可以转化为2个参数优化问题. 优化参数为x = (r0,fa2)$,其中优化参数r0的取值范围由式(6)确定;而优化参数$f_{a2}\in [0,2\pi]$;优化目标函数为采用虚拟轨道参数表示的能量消耗或转移时间.假定fE为虚拟圆锥曲线轨道(转移轨道)所消耗的能量,则目标函数为$F({\pmb x}) = \min (f_E ,{\pmb x })$. 当求出优化参数${\pmb x } = ({\pmb r}_0 ,f_{a2} )$,转移轨道就唯一确定了.求解优化问题,本文采用了粒子群优化算法,具体算法详见文献[9].
3 实现虚拟圆锥曲线轨道所需推力 3.1 二维平面轨道转移推力计算实现平面轨道转移所需推力可由式(9)求出
| $ \left. \begin{array}{l} {a_{ro}} = {\mu _1}/r_1^2\\ {{a'}_{ro}} = {\mu _2}/r_2^2\\ \alpha = \arccos ({{a'}_{ro}}/{a_{ro}})\\ {a_c} = {a_{ro}}\sin (\alpha ) \end{array} \!\! \right\} $ | (9) |
其中, $a_{ro},{a}'_{ro},a_c$分别为地心引力,虚拟中心引力,及控制力.
3.2 三维轨道转移推力计算虚拟引力场中A点速度和位置矢量为${\pmb v }_{a2} = [v_{ax} ,v_{ay} ,v_{az}]$:${\pmb r}_{a2} = {\pmb r}_{a1} + {\pmb r}_0$;B点位置矢量${\pmb r}_{b2} = {\pmb r}_{b1} + {\pmb r}_0$. 则在虚拟中心引力场中有:
| $ \left. \begin{array}{l} {r_{a2}} = \frac{{h_2^2}}{{{\mu _2}}}\frac{1}{{1 + {e_2}\cos ({f_{a2}})}}\\ {r_{b2}} = \frac{{h_2^2}}{{{\mu _2}}}\frac{1}{{1 + {e_2}\cos ({f_{b2}})}}\\ {h_1} = {r_{a2}} \times {v_{a2}}\\ {h_2} = {r_{b2}} \times {v_{b2}}\\ {h_1} = {h_2} \end{array} \! \right\} $ | (10) |
假定航天器在机动轨道上所受地心引力加速度为aMr1,在虚拟引力场引力加速度 aMr2,推力加速度为${\pmb T}_{\rm ac} = [T_{\rm acn} ,T_{\rm act}]$,其中,Tacn,Tact方向分别为法向和周向,则有
| $ \left. {\begin{array}{*{20}{l}} \begin{array}{l} \beta = \pi - \arccos (\frac{{|{h_2} \cdot {r_1}|}}{{|{h_2}||{r_1}|}})\\ {a_{{\rm{Mr1}}}} = \frac{{{\mu _1}}}{{r_1^2}}\\ {a_{{\rm{Mr2}}}} = \frac{{{\mu _2}}}{{r_2^2}}\\ \alpha = \arcsin (\frac{{{a_{{\rm{Mr2}}}}}}{{{a_{{\rm{Mr1}}}}\cos \beta }})\\ {T_{{\rm{act}}}} = {a_{{\rm{Mr1}}}}\cos \beta \sin \alpha \\ {T_{{\rm{acn}}}} = {a_{{\rm{Mr1}}}}\sin \beta \end{array} \end{array}} \! \right\} $ | (11) |
其中,β为r1与虚拟圆锥曲线轨道平面的夹角. α为周向力加速度Tacn与地心引力在虚拟圆锥曲线平面投影的夹角.
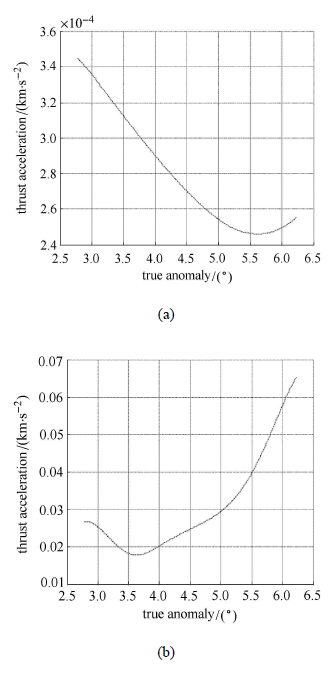
4 仿真分析 4.1 二维转移轨道设计初始点和终端点位置矢量和速度矢量分别为${\pmb r}_{a1} = [8\,491.2,133.9]$ km, ${\pmb r}_{b1} = [-9\,993,- 2\,913.3]$ km, ${\pmb v }_{a1} = [0,6.687\,2]$ km/s, ${\pmb v}_{b1} = [1.696\,0,-4.947\,8]$ km/s. 时间约束为10 402 s,实现轨道转移的虚拟中心引力场参数为${\pmb r}_0 = [734.5,108.7]$ km, $\mu _2 = 2.989\,46\times 10^5$. 仿真结果见图 2 和图 3,采用虚拟中心引力场方法实 现轨道转移所需要推力加速度小于 3.5×10-4 km/s2,整段轨道消耗能量$\Delta V=1.497\,3$ km/s. 而采用形状方法所需推力加速度小于7×10-2 km/s2,整段轨道消耗能量$\Delta V=10.472\,8$ km/s.

|
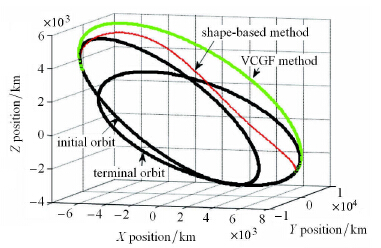
图 2 采用VCGF方法和形状方法的转移轨道 Fig. 2 Transfer trajectories using VCGF and SB methods |
|
图 3 采用VCGF(a)和形状方法(b)所需推力 Fig. 3 Thrust profiles using VCGF (a) and SB methods |
初始点和终端点的位置矢量和速度矢量分别为 ra1=[-7 032,-4 490,3 600] km, rb1=[7 572,305.8,0] km,va=[-2.457,4.618,2.533] km/s,vb=[-0.638 7,-6.644,0] km/s 时间约束为4 353 s. 虚拟中心引力场参数为r0=[-634,710.5,-691.7] km, μ2=3.188 80×105.
仿真结果图 4和图 5,采用VCGF方法其推力小于3.0 m/s2,能量消耗$\Delta V=5.46$ km/s. 采用形状方法实现转移轨道所需推力小于 60 km/s2,能量消耗$\Delta V=15.510\,6$ km/s.
|
图 4 三维空间机动轨道(VCGF和SB) Fig. 4 Transfer orbits using VCGF and SB method |

|
图 5 采用VCGF(a)和形状方法(b)所需推力 Fig. 5 Thrust profile using VCGF (a) and SB methods (b) |
本文针对连续推力航天器机动轨道设计问题,提出了虚拟中心引力场的轨道设计新方法. 并将其应用到转移轨道设计中,得到以下结论:
(1) 虚拟中心引力场方法将航天器转移轨道设计问题转化为2个参数寻优问题. 大大减少了轨道设计参数,简化了求解转移轨道设计过程;
(2) VCGF方法能够适用于一般情况,扩大了航天器机动范围. 在同样条件下,相比形状方法,虚拟中心引力场方法在实现轨道转移时所需推力以及所需能量较小.
| [1] | 李俊峰,蒋方华,连续小推力航天器的深空探测轨道优化方法综述,力学与实践,2011, 33(3): 1-6 (Li Junfeng, Jiang Fanghua. Survey of low-thrust trajectory optimization methods for deep space exploration. Mechanics and Engineering, 2011, 33(3): 1-6 (in Chinese)) |
| [2] | 汤国建,张洪波. 小推力轨道机动动力学与控制,北京:科学出版社,2013 (Tang Guojian, Zhang Hongbo. Dynamics and Control of Low-thrust Orbital Maneuver. Beijing: Science Press,2013 (in Chinese)) |
| [3] | Tisen H. Take-off from satellite orbit. Journal of the American Rocket Society, 1953, 23(4): 233-236 |
| [4] | Boltz FW. Orbit motion under continuous radial thrust. Journal of Guidance, Control, and Dynamics, 1991, 14(3): 667-670; |
| [5] | Petropoulos AE, Longuski JM. Automated design of low-thrust gravity-assist trajectories. Journal of Spacecraft and Rockets, 2004, 41(5): 787-796 |
| [6] | Bradley W. Shape-based approximation method for low-thrust trajectory optimization. AIAA 2008-6616, 2008. 1-9 |
| [7] | Wall BJ, Conway BA. Shape-based approach to low-thrust rendezvous trajectory design. Journal of Guidance, Control, and Dynamics, 2009, 32 (1): 95-101 |
| [8] | Hudson J, Scheeres D. Fourier coefficient selection for low-thrust control shaping. Journal of Guidance, Control, and Dynamics, 2013, 36 (6): 1783-1786 |
| [9] | 潘峰,李位星. 粒子群优化算法与多目标优化. 北京: 北京理工大学出版社, 2013(Pan Feng, Li Weixing. Particle Swarm Optimization Algorithm and Multiply Variables Optimization. Beijing: Beijing Institute of Technology Press, 2013 (in Chinese)) |
2. National Key Laboratory of Aerospace Flight Dynamics,Xi'an 710072,China
 2015, Vol. 47
2015, Vol. 47