2. 清华大学材料学院, 北京 100086
高速冲击下凝聚相含能材料的初始响应一直是爆轰学的核心内容之一,并且围绕此问题建立了很多经典理论.固体含能材料在冲击 载荷作用下会表现出各种现象,如形变或伴随着剧烈化学反应的相变等.凝聚相高能材料的冲击起爆或爆轰涉及高温、高压、较短的时间和空间尺度,并且其中还存在强烈的耦合问题,这给当前的实验技术和理论分析带来了很大的挑战.分子动力学技术可以提供多种时空尺度下的结构响应模拟,因此分子动力学是关联极端条件下含能材料微观或宏观响应的有力工具.冲击波诱导含能材料化学反应的模拟往往需要适当的势函数.加州理工学院Goddard小组提出的反应力场分子动力学(reactive force field moleculardynamics)方法可以模拟真实含能材料分子结构在极端条件下的微观响应过程,并相对量子力学来说具有较小的计算成本.反应力场势函数中包含调和能、二体拉伸、三体弯曲和四体扭转能函数,非成键作用则包括范德华和库伦能.原子电荷为动态变量,并会在每步中通过最小化静电能计算得出[1].当前ReaxFF-MD方法已经很好地应用于含能材料的热解[2]、燃烧[3]以及冲击响应[4]等问题.ReaxFF/lg势函数[5]是在ReaxFF势函数[1]的基础上增加了长程修正项(${{\text{E}}_{{\text{lg}}}}$)的描述,更适用于含能材料平衡 密度的计算,而含能材料的密度则与其爆轰宏观性质有着非常紧密的联系.当前ReaxFF/lg势函数已经在极端条件下含能材料的微观响应方面得到了较好的应用[6].本文采用大尺度原子/分子并行计算模拟器(large-scale atomic/ molecular massively parallel simulator,LAMMPS)分子动力学模拟程序包[7]同时结合ReaxFF/lg势函数进行梯恩梯(2,4,6-trinitrotoluene,TNT)高速冲击压缩的微观响应模拟,并分析了此过程中的压力$\!$-$\!$-$\!$体积变化、密度和粒子速度剖面以及具体化学反应细节等.
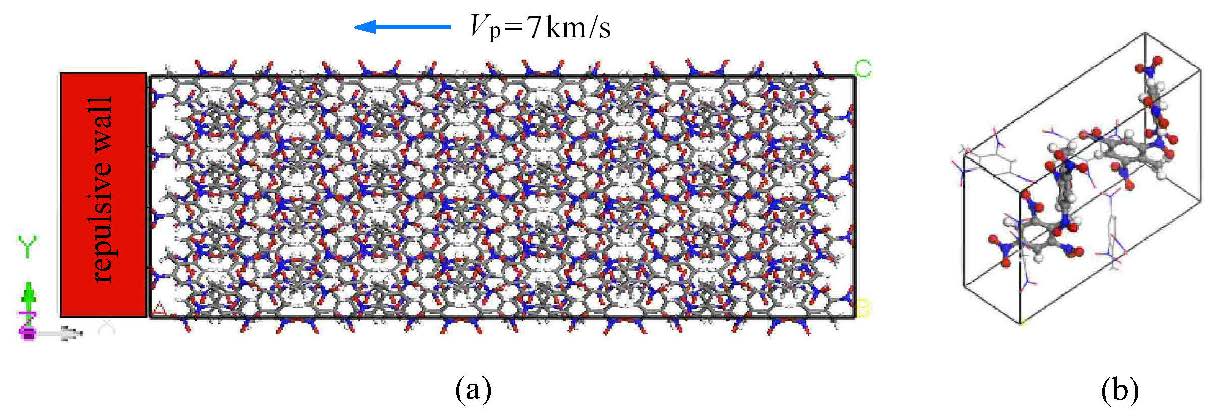
1 模拟及计算细节本文采用的梯恩梯初始单胞结构来自剑桥晶体数据库(cambridge crystallographic datacentre,CCDC),单胞中含有8个梯恩梯分子,每个梯恩梯分子含有21个原子. 首先通过结构优化得到最低能量的梯恩梯单胞结构. 为了得到较为理想的冲击图像,随后建立20$\times $4$\times$1正交超晶胞结构,共含640个梯恩梯分子,总计13 440个原子. 初始密度为1.704 g/cm$^{3}$.模拟过程中$y,z$方向采用周期边界条件,$x$方向采用非周期边界(shrink-wrapped)条件(如图1所示).首先使得最低能量结构的梯恩梯板结构低温平衡(5 K) 1 ps,其次快速升至常温(约300 K),随后梯恩梯板内粒子以$V_{\rm p}$(7 km/s)沿$x$一方向平面撞击固定壁面,壁面紧贴梯恩梯板左端. 时间步长为0.01 fs,整个模拟过程持续4 ps.
|
图 1 梯恩梯板内粒子以7 km/s 撞击固定壁面示意图(a) 及梯恩梯单胞(b) Fig.1 Schematic diagram of buttress-like TNT impact on mounting surface with 7 km/s (a) and unit cell (b) |
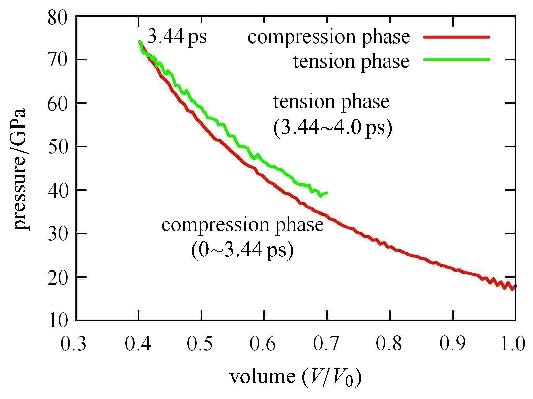
图2为梯恩梯冲击响应过程的$P$-$\!$-$V$曲线. 整个过程主要分为冲击压缩和反向稀疏拉伸两个阶段. 当梯恩梯与固定壁面发生撞击接触时,左端梯恩梯分子层受到绝热压缩,压力突跃至20 GPa.随着冲击波在梯恩梯板中的传播,系统内的压力逐渐上升,体积不断的受到压缩,当冲击压缩作用传播至梯恩梯板右端自由面时($t=3.44$ ps),系统内的压力达到峰值74 GPa,此时梯恩梯板的体积压缩至原体积的40{\%}.随后伴随着稀疏波反向拉伸梯恩梯,系统内的压力快速下降. 至4 ps时,系统内的压力下降至约38 GPa.
|
图 2 冲击压缩与稀疏拉伸过程的P-V 曲线 Fig.2 P-V relations of the process of shock compression and tension |
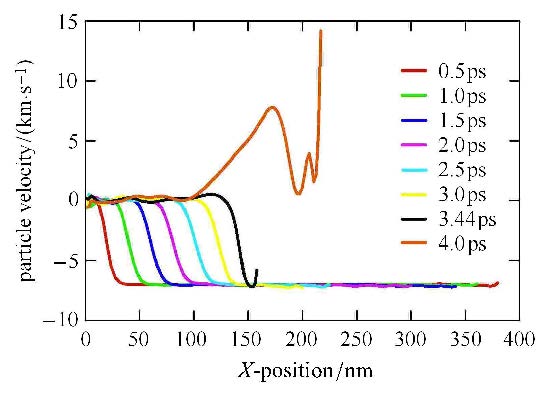
为了得到梯恩梯冲击压缩过程的密度以及粒子速度的时空分布,这里将梯恩梯沿$x$方向进行一维空间分层处理,每层厚度为0.1 nm,并随时间输出各层的密度以及粒子速度.图3和图4为冲击压缩过程中,不同时刻密度及粒子速度的一维空间分布.当梯恩梯板内粒子速度以7 km/s沿$x$一方向撞击固定壁面时,冲击压缩作用致受冲击部分的密度增加,且密度介于2.5$\sim$3.0 g/cm$^{3}$,而在不同时刻下固定壁面处的密度均较高(4.0$\sim$6.0 g/cm$^{3}$),至3.44 ps时,冲击压缩完全时,初始长度($x$方向)39.36 nm的梯恩梯板被压缩至约15.7 nm,随后稀疏作用致右端粒子高速飞溅至下游,且使得该处密度降低.

|
图 3 冲击压缩过程的一维密度剖面(续) Fig.3 1-D density profile in shock compression process (continued) |
|
图 4 冲击过程的一维粒子速度剖面 Fig.4 1-D particle velocity profile in shock process |
粒子速度剖面显示压缩波前后存在明显的粒子速度阶跃. 压缩波前方的粒子速度为$-7$ km/s,压缩波后方的高温高压区域内的粒子基本处于静止状态. 而压缩波区域内的粒子则存在明显速度梯度(0$\sim$7 km/s),3.44$\sim$4.0 ps之间,右端粒子开始向下游飞溅,并出现明显的沿$x$正向的粒子速度.
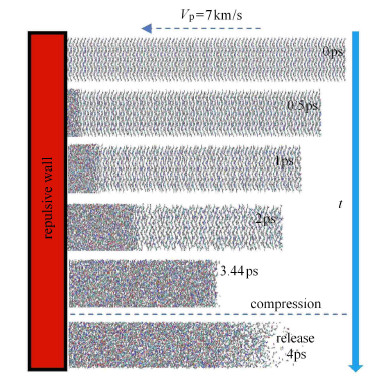
2.3 冲击压缩与稀疏拉伸过程的物理图像图5为梯恩梯板高速撞击固定壁面后,冲击波和拉伸波在梯恩梯内传播的物理图像.板状梯恩梯高速撞击固定壁面时,当压力波到达梯恩梯板的自由表面时会反射形成拉伸波,并会在右端自由表面的某处造成拉应力,并且一旦满足动态断裂准则后,会引起该处材料的破裂,并且碎片会以一定的动量飞出.当$t=3.44$ ps时,冲击波传播至梯恩梯板右端自由面,部分原子或分子基团飞出,随后3.44 ps至4 ps阶段,拉伸脉冲开始反向拉伸压缩态的梯恩梯板,并且右端出现大量的原子或分子基团飞溅至下游,同时伴随着压力的卸载.
|
图 5 冲击压缩与稀疏拉伸的物理图像 Fig.5 Physical picture of the process of shock compression and tension |
在产物分析中,当任意两个分子碎片中的彼此任意两个原子构成的原子对的键级大于0.3时,则认为化学键形成,两碎片视为新生成的分子[1].
图6为整个过程中梯恩梯分解的时间尺度以及主要产物分布情况. 图6(a)为压缩波在梯恩梯板中传播后的分解以及物种产生情况.在0.5 ps前,左端梯恩梯分子受到绝热压缩,分子动能增加,温度和压力升高,化学键断裂,H,O原子脱落,分子碎片间距变小而聚合形成较大的分子团簇.Dremin[8]认为此阶段受激发的分子将会出现显著的平动-振动模态,时间尺度为10$^{-13}\sim $10$^{-12}$ s.Nomura[4]结合ReaxFF-MD技术就黑索金(RDX)冲击后受激发分子的平动$\!$-$\!$-$\!$振动模态问题进行了详细的研究,其研究结果显示冲击压缩后的RDX分子由平动转化为振动模态的时间尺度为0.3 ps.对照图2,图6(a)和图7(a)的模拟结果显示,在前期冲击压缩的0.5 ps内,梯恩梯分子完成了由平动$\!$-$\!$-$\!$振动的弛豫过程.这在时间尺度上和Klimenko和Dremin以及Nomura的研究结论具有一致性.梯恩梯板左端分子在绝热压缩作用下,梯恩梯分子脱落H,O原子后,分子碎片聚合为大的团簇,同时伴随着分子平动$\!$-$\!$-$\!$振动模态的转换,因此0.5 ps前,并未在梯恩梯板内形成稳定的冲击波. 对照图3(e)和图6(a).当冲击波传播至右端自由面时,板内的640个梯恩梯分子完全分解,并且转化为$\sim $210种新物质.4 ps时,体系中的新物质增加至$\sim $260种.物种的增加,主要是由于稀疏波作用使得系统内的压力降低、体积膨胀所致.
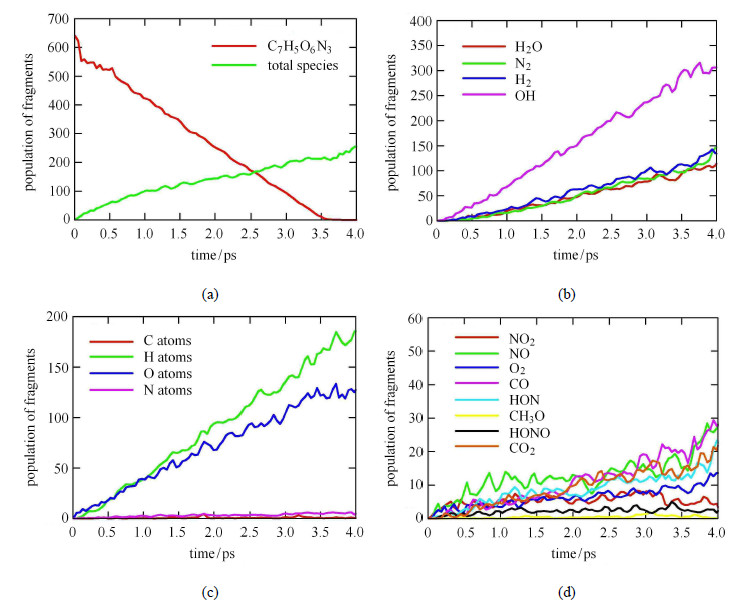
|
图 6 冲击过程中主要产物随时间演化情况 Fig.6 The time evolution of main products during the shock process |
在初始反应路径方面,在整个4 ps计算周期内,大量的H,O原子首先脱落,这主要来自于C--H,N=$\!$=O键的断裂. 随后O,H原子结合形成HO,H$_{2}$以及H$_{2}$O,并且有大量的H,O原子游离在体系中,而未参与任何反应.R--NO$_{2}$上的O原子发生脱落后,R--N键发生断裂,N原子聚合形成N$_{2}$.另外,H$_{2}$O,N$_{2}$和H$_{2}$几乎具有相同的产生速率.图6(d)显示整个计算周期内NO$_{2}$,NO,O$_{2}$,CO,HON,CH$_{3}$O,HONO,CO$_{2}$分子或基团则维持在一个较低的分布水平.
2.5 含碳团簇演化分布图7为针对结果进一步分析得到的冲击作用在梯恩梯板传播过程中形成的最大摩尔质量含碳团簇(${{\text{N}}_{{\text{cluster}}}}$)的分布以及团簇 中原子数量比的波动情况. 图7(a)为每时间步长内最大摩尔质量含碳团簇随时间的成长情况.在0.5 ps前,冲击压缩使得梯恩梯分子脱落掉部分原子,剩余部分在冲击压缩的作用下,分子间距变小而进一步键合形成较大的分子团簇.此过程中分子经历了平动$\!$-$\!$-$\!$振动弛豫过程.0.5 ps后,随着压缩波在梯恩梯板中的传播,波阵面后方压力的逐渐增加,含碳团簇的摩尔质量也呈现快速增大态势,当压缩波达到右端后,稀疏波开始反向拉伸压缩态的梯恩梯板后,含碳团簇开始裂解.图7(b)为最大摩尔质量含碳团簇中的原子数量比情况. 初始结构中原子数量比为O/C=0.857,H/C=0.714,N/C=0.429.在0.5 ps前,O/C,H/C,N/C的值呈现快速减小趋势.随着压缩波在梯恩梯板中传播,含碳团簇中O原子与C原子比维持在较稳定的状态(0.680),而H,N与C原子个数比则处于缓慢降低趋势,至模拟结束时(4 ps),H,N与C原子个数比分别为0.410,0.284.整个过程中,梯恩梯板中含碳团簇中原子个数比一直保持为O/C$>$H/C$>$N/C.
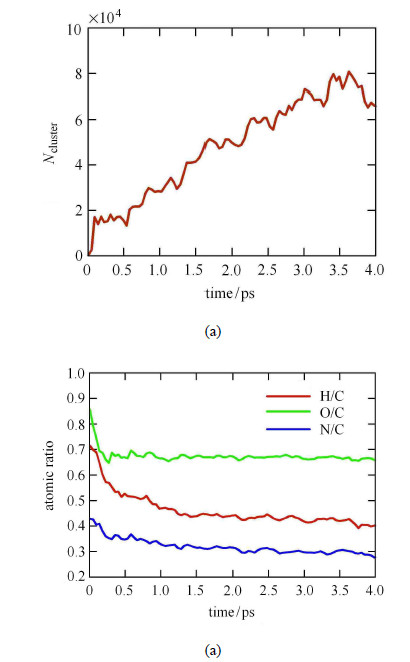
|
图 7 冲击过程中最大摩尔质量含碳团簇的演化分布(a)以及团簇中原子数量比的波动情况(b) Fig.7 Time evolution of the largest carbon-containing cluster formed (a) and fluctuations in the elemental composition (b) during the shock process |
本文利用ReaxFF分子动力学方法模拟了高能量密度材料梯恩梯的冲击响应问题.通过对模型进行空间分层研究了冲击压缩过程中密度及粒子速度的1维时空行为,密度及粒子速度剖面显示压缩波后方密度较大,且粒子基本处于静止状态,压缩波内存在较大的粒子速度梯度.为了分析其过程中的化学反应路径问题,利用原子对键级判断彼此间是否成键.结果显示冲击压缩过程中C--H,O=$\!$=N键断裂并进一步形成H$_{2}$,H$_{2}$O,HO以及N$_{2}$,残基则快速聚合形成较大的含碳团簇.冲击激发梯恩梯分子经历了平动$\!$-$\!$-$\!$振动模态的转换,并且此过程的时间尺度为0.5 ps.冲击压缩作用致含碳团簇的最大摩尔质量不断累积,并且含碳团簇中的原子数量比较初始结构逐渐降低.ReaxFF分子动力学技术的发展促进了我们对冲击起爆问题的认知,势函数往往决定着模拟结果的优劣,因此未来需要不断完善描述含能材料反应过程的势函数以及建立更大尺度的物理模型去研究近真实条件下含能材料的冲击起爆问题.
| [1] | Van Duin ACT, Dasgupta S, Lorant F, et al. ReaxFF: a reactive force field for hydrocarbons. J Phys Chem A, 2001, 105(41): 9396-9409 |
| [2] | Strachan A, Kober EM, van Duin ACT, et al. Thermal decomposition of RDX from reactive molecular dynamics. J Chem Phys, 2005, 122: 054502 |
| [3] | Agrawalla S, van Duin ACT. Development and application of a ReaxFF reactive force field for hydrogen combustion. J Phys Chem A, 2011, 115(6): 960-972 |
| [4] | Nomura K, Kalia RK, Nakano A, et al. Dynamic transition in the structure of an energetic crystal during chemical reactions at shock front prior to detonation. Phys Rev Lett, 2007, 99: 148303 |
| [5] | Liu LC, Liu Y, Zybin SV, et al. ReaxFF-lg: correction of the ReaxFF reactive force field for london dispersion, with applications to the equations of state for energetic materials. J Phys Chem A, 2011, 115(40): 11016-11022 |
| [6] | Wen YS, Xue XG, Zhou XQ, et al. Twin induced sensitivity enhancement of hmx versus shock: a molecular reactive force field simulation. J Phys Chem C, 2013, 117: 24368-24374 |
| [7] | Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comp Phys 1995, 117(1): 1-19 http://lammps.sandia.gov. |
| [8] | Dremin AN. Shock discontinuity zone effect: the main factor in the explosive decomposition detonation process. Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences, 1992, 339(1654): 355-364 |
2. School of Materials Science and Engineering, Tsinghua University, Beijing 100086, China
 2015, Vol. 47
2015, Vol. 47