引言

桩与连续梁组合形式被广泛应用于桥梁、码头这类建构筑物中，由于这类建构筑物基础通常有部分桩身出露于地表，容易遭受自然灾害或人为事故的破坏和损伤，在可能的桩身破坏和损伤发生后，需要对基础的安全性能进行检测和评估.另外，如果在桩顶用梁连接后对桩身质量存在疑问，也将涉及这类组合形式下桩基质量的检测问题.传统的单桩无损检测方法中以低应变动测法最为便捷，但检测时通常要求桩顶为自由端.对于在役基桩，由于其上部结构会对桩身应力波的传播产生非常复杂的反射、透射、折射等多重干扰，仍采用传统的低应变动测法检测缺乏有效的分析判断依据.已有的数值模拟和试验研究^{[1, 2, 3, 4]}表明，在上部结构存在时通过传统低应变动测法检测基桩质量的有效性将依赖于对上部结构－桩－土耦合振动特性的认知程度.但采用数值模拟分析时由于涉及高频动力分析，模型计算量较大，相关动力学参数较难确定，而通过试验研究得到的结果往往受限于所分析的试验模型，且全面的试验难以实现.

另一方面，基础的动力性能是动力基础设计中最为关心的内容.作为目前在深厚软土地区和高承载要求条件下广泛使用的基础形式，桩基础的动力特性备受关注.已有理论研究中，对于单桩振动和桩－土动力相互作用的研究相对较为成熟^{[5, 6]}，对于群桩振动的研究则主要集中于桩－土－桩之间的动力相互作用问题，且一般将承台假设为刚体^{[7, 8]}.而对于柔性承台下群桩振动问题的研究通常需结合数值模拟进行.针对桩与连续梁组合这一结构形式，本文推导了在梁上瞬时激振下梁和土层以上桩段的动力响应时域半解析解.然后，通过与有限元模拟结果对比验证理论解的合理性.在此基础上，讨论梁几何参数和桩身缺陷对梁－桩－土竖向耦合振动特性的影响.该工作将为梁－桩－土耦合情况下基桩完整性检测及类似动力基础形式的设计提供理论依据.

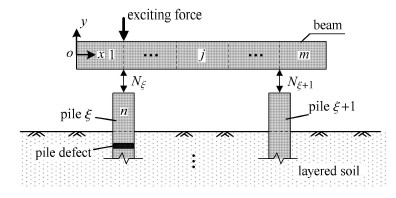
1 数学模型及求解 1.1 梁－桩－土动力系统几何模型

梁－桩－土动力系统几何模型如图1所示.对于桩侧土层及土层以下桩段，依据土层成层性和桩身截面 物理力学参数的变化情况从下到上共划分为$n-1$层，土层以上桩段仅考虑无截面物理力学参数变化的情况，为第$n$层桩段.梁根据桩位、激振力作用位置、梁截面物理力学参数变化情况由左至右共划分为$m$段.根据对桩－土体系和梁分别建立的坐标系统，$l_j $表示第$j$梁段右侧的坐标，$h_k$表示第$k$桩段顶部的坐标(桩底$z =0 $ m). 第$\xi $桩与梁的动力相互作用简化为竖向点载荷，用$N_\xi $表示.

采用的基本假设如下：土层上表面为自由边界，土层径向无穷远处位移、应力为0，桩与土完全接触；桩和梁均视为一维杆件，仅考虑桩与梁连接点竖向位移的连续；不考虑桩由于土层联系产生的动力相互作用，系统仅发生小变形振动.

1.2 梁－桩－土竖向振动控制方程及求解

根据Novak等提出的平面应变模型可求得桩与桩侧土界面上土体剪切复刚度为

${K_k} = 2\pi {r_{{\text{p}}k}}G_{{\text{s}}k}^*{{\text{K}}_1}\left( {{\zeta _k}{r_{{\text{p}}k}}} \right)/{{\text{K}}_0}\left( {{\zeta _k}{r_{{\text{p}}k}}} \right)$

(1)

式中，$k \in \left[{1,n - 1} \right]$；$G_{{\rm s}k}^ * = G_{{\rm s}k} \left( {1 + {\rm i}\beta _{{\rm s}k}} \right)$；${\rm K}_0 $和${\rm K}_1 $分别表示零阶和一阶第二类修正贝塞尔函数；$r_{{\rm p}k}$表示第$k$桩段半径；$\zeta _k = s/{\left( {v_{{\rm s}k} \sqrt {1 + {\rm i} \beta _{{\rm s}k} } }\right)}$，$s = i\omega $，${\rm i} = \sqrt { - 1} $，$\omega $为圆频率，$v_{{\rm s}k} = \sqrt {{G_{{\rm s}k}} /{\rho _{{\rm s}k} }} $；$v_{{\rm s}k} $,$G_{{\rm s}k} $,$\rho _{{\rm s}k} $,$\beta _{{\rm s}k}$分别为第$k$层土体剪切波速、剪切模量、质量密度和阻尼系数.

将桩视为一维黏弹性杆件，其纵向振动控制方程的拉普拉斯变换形式如下

$\chi _k \dfrac{\partial ^2W_k }{\partial z^2} - \left( {\rho _{{\rm p}k}A_{{\rm p}k} s^2 + K_k } \right)W_k = 0$

(2)

式中，$k \in \left[{1,n} \right]$；$\chi _k = E_{{\rm p}k} A_{{\rm p}k} + A_{{\rm p}k} \delta _{{\rm p}k}s$；$W_k $,$E_{{\rm p}k} $,$A_{{\rm p}k} $,$\delta _{{\rm p}k} $,$\rho _{{\rm p}k}$分别表示第$k$桩段的竖向位移、弹性模量、横截面积、黏性阻尼系数和质量密度；对于出露的桩段，$K_k = 0$.

由式(2)可求得桩竖向位移和轴力如下

$\left[{\begin{array}{*{20}{c}} \begin{gathered} {W_k} \hfill \\ N_{\text{p}}^k \hfill \\ \end{gathered} \end{array}} \right] = \left[\begin{gathered} \hfill \\ G_{11}^kG_{12}^k \hfill \\ G_{21}^kG_{22}^k \hfill \\ \end{gathered} \right]\left[{\begin{array}{*{20}{c}} \begin{gathered} m_1^k \hfill \\ m_2^k \hfill \\ \end{gathered} \end{array}} \right]$

(3)

式中，$G_{11}^k = \sin \left( {p_k z} \right)$，$G_{12}^k = \cos \left( {p_k z} \right)$，$G_{21}^k = \chi _k p_k G_{12}^k$，$G_{22}^k = - \chi _k p_k G_{11}^k $；$p_k = {\sqrt { - K_k -\rho _{{\rm p}k} A_{{\rm p}k} s^2} } / {\sqrt {\chi _k } }$.

根据桩底的动力支撑条件或桩段间的位移和轴力连续条件可确定式(3)中2个系数的关系如下

${m_2^k } /{m_1^k } = {\left( {G_{21}^k - Z_{k - 1}G_{11}^k } \right)}/{\left( {Z_{k - 1} G_{12}^k - G_{22}^k }\right)}$

(4)

式中，$Z=h_{k-1}$,$Z_{k-1}$表示第$k -1$桩段顶的竖向位移阻抗函数，$Z_{k - 1} = {N_{\rm p}^{k - 1} \left({h_{k - 1} } \right)}/ {W_{k - 1} \left( {h_{k - 1} } \right)}$. 而桩底的支撑刚度可表示为^[9]

${Z_{\text{b}}} = {G_0}{A_{{\text{p1}}}}\left( {4/{r_{{\text{p1}}}} + 3.2s/{v_{{\text{s}}0}}} \right)/{\text{ }}\left[ {\pi \left( {1 - {\mu _0}} \right)} \right]$

其中，$G_0 $,$\mu _0 $,$v_{{\rm s}0} $分别表示桩底土层的剪切模量、泊松比、剪切波速.

将梁视为Timoshenko梁，其竖向振动控制方程的拉普拉斯变换形式如下

$\left. {\begin{array}{*{20}{l}} \begin{gathered} {A_{{\text{b}}j}}{G_{{\text{b}}j}}{\mu _{{\text{b}}j}}\left( {\frac{{\partial {Y_j}}}{{\partial x}} - {\Theta _j}} \right) = - {E_{{\text{b}}j}}{I_{{\text{b}}j}}\frac{{{\partial ^2}{\Theta _j}}}{{\partial {x^2}}} + {\rho _{{\text{b}}j}}{I_{{\text{b}}j}}{s^2}{\Theta _j} \hfill \\ {A_{{\text{b}}j}}{G_{{\text{b}}j}}{\mu _{{\text{b}}j}}\left( {\frac{{{\partial ^2}{Y_j}}}{{\partial {x^2}}} - \frac{{\partial {\Theta _j}}}{{\partial x}}} \right) = {\rho _{{\text{b}}j}}{A_{{\text{b}}j}}{s^2}{Y_j} \hfill \\ \end{gathered} \end{array}} \right\}$

(5)

式中，$Y_j $,$\varTheta _j $,$A_{{\rm b}j} $,$G_{{\rm b}j} $,$\mu _{{\rm b}j} $,$E_{{\rm b}j} $,$I_{{\rm b}j} $,$\rho _{{\rm b}j}$分别表示第$j$梁段的竖向位移、弯曲变形角、横截面积、剪切模量、截面剪切形状系数、弹性模量、截面惯性矩以及质量密度；$A_{{\rm b}j} = h_{{\rm b}j} \times b_{{\rm b}j} $，$h_{{\rm b}j} $和$b_{{\rm b}j}$分别表示第$j$梁段的横截面高度和宽度；$j \in \left[{1,m} \right]$.

由式(5)解耦可求解得到梁竖向位移、弯曲变形角、剪力和弯矩的通解如下^[10]

$\left[{\begin{array}{*{20}{c}} \begin{gathered} {Y_j} \hfill \\ {\Theta _j} \hfill \\ Q_{\text{b}}^j \hfill \\ M_{\text{b}}^j \hfill \\ \end{gathered} \end{array}} \right] = \left[\begin{gathered} M_{11}^jM_{12}^jM_{13}^jM_{14}^j \hfill \\ M_{21}^jM_{22}^jM_{23}^jM_{24}^j \hfill \\ M_{31}^jM_{32}^jM_{33}^jM_{34}^j \hfill \\ M_{41}^jM_{42}^jM_{43}^jM_{44}^j \hfill \\ \end{gathered} \right]\left[{\begin{array}{*{20}{c}} \begin{gathered} {A_j} \hfill \\ {B_j} \hfill \\ {C_j} \hfill \\ {D_j} \hfill \\ \end{gathered} \end{array}} \right]$

(6)

根据桩段$n$顶部与梁竖向力的协调条件以及底部的位移和轴力的连续条件，可建立如下关系：$N_{\rm p}^n \left( {h_n } \right) = N_\xi $和$N_{\rm p}^n \left( {h_{n -1} } \right) = Z_{n - 1} W_n \left( {h_{n - 1} }\right)$. 根据桩与梁的竖向位移协调条件，可得$Y_j \left( {l_\xi }\right) = W_n \left( {h_n } \right)$，其中$l_\xi $表示第$\xi$桩桩顶反力作用梁段的左侧位置.

根据梁段交界面的竖向位移、弯曲变形角、剪力和弯矩连续条件，可建立如下矩阵方程

$\left[{\begin{array}{*{20}{c}} \begin{gathered} {Y_j} \hfill \\ {\Theta _j} \hfill \\ \end{gathered} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} \begin{gathered} {Y_{j - 1}} \hfill \\ {\Theta _{j - 1}} \hfill \\ \end{gathered} \end{array}} \right],\;\left[{\begin{array}{*{20}{c}} \begin{gathered} Q_{\text{b}}^j \hfill \\ M_{\text{b}}^j \hfill \\ \end{gathered} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} \begin{gathered} Q_{\text{b}}^{j - 1} + Q_{\text{w}}^j \hfill \\ M_{\text{b}}^{j - 1} + M_{\text{w}}^j \hfill \\ \end{gathered} \end{array}} \right]$

(7)

式中，$x = l_{j - 1} $，$j \in \left[{2,m} \right]$；$Q_{\rm w}^j $和 $M_{\rm w}^j$分别为梁段$j$左侧所受的外部竖向集中力与外部力矩作用. 例如，当半正弦激振力$q_0 = Q_{\max } \sin \left({\omega _0 t} \right)$ $(t \in \left[0,\pi / \omega _0 \right])$ 作用于$\xi $桩中心线对应的梁段$j$左侧，$Q_{\rm w}^j = N_\xi - Q_{\max } \omega _0 {\left( {{\rm e}^{ - {\rm i} \omega\pi /{\omega _0 }} + 1} \right)}/ {\left( {\omega _0^2 - \omega ^2} \right)}$.

根据以上条件可求解式(3),(6)中的系数. 然后借助离散傅里叶逆变换可获得梁及土层以上桩段动力响应的时域解答. 以梁竖向速度$v_{\rm b} $为例

${v_{\text{b}}}\left( t \right) \approx \frac{1}{{2\pi }}\sum\limits_{\eta = 1}^{{\eta ^*}} {{\text{i}}{\omega _\eta }{Y_j}\left( {{\omega _\eta }} \right){{\text{e}}^{{\text{i}}{\omega _\eta }t}}\Delta \omega }$

(8)

式中，$Y_j \left( {\omega _\eta } \right)$为在连续曲线$Y_j \left( \omega\right)$中按一定频率间隔$\Delta \omega $抽取的$\eta ^ *$个离散数据点，$\omega _1 = 0$. 上述求解过程可通过计算机编程实现.

2 半解析方法与有限元模拟对比

已有研究表明，桩侧土对桩顶动力响应的影响主要表现为对响应幅值的衰减作用，但对响应曲线的波动特征(如桩底、缺陷反射信号峰值时刻)影响较小^[6] }$ (成层土层间参数变化较大对曲线波动特征有一定影响)，而不计桩侧土影响时承台-桩竖向振动的数值模拟结果对于响应曲线的波动特征分析而言仍较为可靠^{[3, 4]}. 为简化分析并使半解析计算结果与数值模拟结果的对比更为清晰，仅考虑线弹性梁－桩整体结构的竖向振动(忽略桩－土－桩动力相互作用)，采用二维和三维有限元模拟(2-D和3-D FEM)，桩底为刚性支撑. 梁-桩体系的基本物理力学参数如下：$h_{\rm b}=b_{\rm b} =0.5$ m，$\rho _{\rm b} =\rho _{\rm p} =2 400$ kg/m$^{3}$，$E_{\rm b} =E_{\rm p} =36.1$ GPa，桩和梁材料泊松比为0.2；梁长度8 m；桩径0.6 m，桩长12 m，两桩中心线距梁两端各1.5 m；激振力为半正弦激振力，幅值$Q_{\max } =1$ N，激振力频率$\omega _0 = 4 000$ rad/s，激振力施加于左侧桩中心线对应的梁上侧. 拾振点位于桩身$z =11$ m处和梁跨中. 为便于对比，对曲线归一化处理.

图2对比了半解析计算和有限元模拟得到的桩身拾振点处的速度响应($v_{\rm p}^ *)$和轴力响应($N_{\rm p}^ * )$以及梁跨中的速度响应($v_{\rm b}^ *)$. 由图可知，半解析计算结果与有限元模拟结果在响应幅值和波动特征上总体较为吻合，这在一定程度上说明了本文解的合理性.

3 参数分析

下面将主要考察梁的几何参数及桩身缺陷对系统动力响应的影响. 计算参数如下：$\mu_{\rm b} =0.8$，土体泊松比0.4，$\rho _{\rm s} =1 800 $ kg/m$^{3}$，$v_{\rm s} =100$ m/s，$\beta _{\rm s} =0.005$，$\delta_{\rm p} =0.1 $ MN$\cdot $m$^{ - 3}\cdot $s；桩入土深度10 m，为摩擦桩；桩身缺陷段埋深2.5 m，长度0.5 m；梁上拾振点设置于激振点位置；其他相关参数与上节相同. 另外，对桩身和梁竖向速度响应按如下方式进行无量纲处理：${{\text{v}}_{\text{p}}} = {v_{\text{p}}}{A_{\text{p}}}\sqrt {{E_{\text{p}}}{\rho _{\text{p}}}} /{Q_{\max }},{\bar v_{\text{b}}} = {v_{\text{b}}}{A_{\text{p}}}\sqrt {{E_{\text{p}}}{\rho _{\text{p}}}} /{Q_{\max }}$.

图3分析了梁几何参数对梁和桩动力响应的影响，箭头所指为桩底一次反射信号峰值时刻.由图可知，随着梁截面高度的增加以及 梁中跨宽度($l_{2}-l_{1})$的减小，桩竖向速度、桩身轴力(${\text{(}}{{\text{N}}_{\text{p}}}{\text{)}}$以及梁竖向速度响应曲线中的桩底反射信号变得难以区分，且其峰值时刻与箭头所指时刻有所偏离，故此时无法准确计算桩长.对比而言，梁上拾振点处的速度响应曲线和桩身拾振点处的力响应曲线比桩身拾振点处的速度响应曲线更有利于对桩底反射信号的识别.

图4分析了缺陷程度对梁和桩动力响应的影响，箭头所指为缺陷一次反射信号峰值时刻，$E_{{\rm p2}} $为缺陷桩段弹性模量. 由图可知，随着缺陷程度的增加，缺陷引起的各拾振位置动力响应的变化更加明显.由于体系动力响应的复杂性，缺陷在不同位置、不同类型响应曲线上的表现差异较大. 此外，当桩身完整时，在$t=6$ ms时刻前(基本对应于桩底一次反射信号出现前)，桩身拾振位置的速度和力响应以及梁上拾振位置的速度响应曲线的波动特征较为相似，但受到缺陷的影响后，此时刻前3类曲线的波动特征以不同的方式改变，且缺陷程度越明显，受桩身缺陷影响后3类曲线波动特征的差异越大. 这一对比结果表明结合这3类曲线进行分析将有利于桩身缺陷的识别.

4 结论

随着梁截面高度增加和梁中跨宽度减小，桩身拾振位置速度响应曲线和力响应曲线以及梁上拾振位置速度响应曲线中的桩底反射信号变得难以区分.梁上拾振点处的速度响应曲线和桩身拾振点的力响应曲线比桩身拾振点处的速度响应曲线更有利于对桩底反射信号的识别.

桩身完整时，在桩底一次反射信号出现前，桩身拾振位置的速度和力响应以及梁上拾振位置的速度响应曲线的波动特征较为相似，但受到桩身缺陷影响后，此时刻前3类曲线的波动特征以不同的方式改变，且缺陷程度越明显，受桩身缺陷影响后3类曲线波动特征的差异越大. 这一对比结果表明结合这3类曲线进行分析将有利于桩身缺陷的识别.