2. 国防科技大学, 长沙 410073
众所周知,当表征气体稀薄程度的努森数较大时,基于连续流假设的NS方程将失效.因而求解稀薄过渡流域的问题时需要借助于蒙 特卡罗直接模拟法(direct simulation Monte Carlo method,DSMC)或者玻尔兹曼方程.DSMC方法的本质是在一个时间步长内解耦分子运动和碰撞,因此只有当时间步长小于分子平均碰撞时间,这种做法在物理上才是合理的.玻尔兹曼方程的碰撞项十分复杂,已提出了BGK模型、Shakhov模型、ES-BGK模型等多种简化形式.而直接采用传统CFD方法求解玻尔兹曼方程或其简化模型方程的方法,大多也是借鉴了DSMC将分子运动和碰撞解耦的做法,算法推进时间步长仍然受平均碰撞时间的约束. 费飞等[1]提出了一种扩散信息保存(diffusive information preservation,D-IP)方法,该方法避免了DSMC方法对时间步长的限制. 在求解玻尔兹曼模型方程这条路上,Xu等[2]提出和发展了UGKS (unified gas kineticscheme),该方法基于上述模型方程的积分解,主要特点之一是将分子运动和碰撞耦合处理,从而使得该方法的推进步长不受碰撞时间的限制,在包含稠密流动区域的流动模拟时,与将分子运动和碰撞解耦处理的方法相比,在计算效率上存在明显优势.该方法已经成功应用于从低速不可压到高超声速、从连续流到高度稀薄流的许多流动中[3, 4, 5, 6, 7].
数值模拟存在显著稀薄气体效应的流动,无论采用何种数值求解方法,都需要引入离散速度坐标法(DOM)对速度空间进行离散,将对速度空间具有连续依赖性的分布函数转化为离散速度空间的点函数.然而引入DOM之后,将会破坏碰撞过程中的质量、动量和能量守恒特性,导致相容性条件不满足.这是因为在离散的速度空间中,分布函数的各阶矩都是通过数值积分得到的,如通过麦克斯韦分布函数中的有限个点(即速度空间网格点或称之为数值积分节点)来精确还原整个麦克斯韦分布所对应的宏观守恒量不可避免地会引入误差,这就相当于在求解的宏观守恒变量所属方程组的右端有一个数值不确定的源项,因而,可能对计算结果精度产生不利影响,甚至影响到数值求解方法的有效性.李志辉[8, 9, 10, 11]研究了改进的高斯-厄米特无穷积分方法、等间隔的牛顿-科特斯公式为基础的复合积分法以及以勒让德多项 式的根为积分结点的高斯-勒让德数值积分法对计算结果的影响.通过加密速度空间网格点数在一定程度上可以减小该源项,但是会增加显著计算量,在目前的计算机条件下是难以承受的.
基于BGK以及ES-BGK模型,Mieussens等[12]发展了一种守恒型离散速度坐标法(CDOM),该方法通过构造离散形式的麦克斯韦速度分布函数,使得相容性条件得到严格满足. Arslanbekov等[13],Chigullapalli等[14] 的研究中都采用了CDOM.相比DOM,在CDOM中需要引入牛顿迭代,因而会增加单步的工作量,但是Huang[15]的研究结果表明,采用CDOM之后,速度空间的网格量可以适当地减少而不降低计算结果的精度,因而整体计算代价可以得以减小.
在理论分析的基础上,本文考察了DOM下相容性条件不满足引入的数值误差,并与CDOM下的计算结果进行比较,研究了UGKS方法中相容性条件不满足对计算结果及其计算效率的影响.
1 UGKS方法介绍 1.1 控制方程及求解过程本文变量采用如下方式进行无量纲化(顶标"--"代表有量纲量)
| $\begin{gathered} {\text{f}} = \bar f/\left( {{\rho _\infty }/U_\infty ^3} \right),\;{{\text{f}}^ + } = {{\bar f}^ + }/\left( {{\rho _\infty }/U_\infty ^3} \right) \hfill \\ {g_M} = {{\bar g}_M}/\left( {{\rho _\infty }/U_\infty ^3} \right),\;tau = \bar \tau /(L/{U_\infty }) \hfill \\ p = \bar p/({\rho _\infty }U_\infty ^2),\;rho = \bar \rho /{\rho _\infty },\;\mu = \bar \mu /{\mu _\infty } \hfill \\ t = \bar t/(L/{U_\infty }),\lambda = \bar \lambda /\left( {1/U_\infty ^2} \right) \hfill \\ \left( {x,y,z} \right) = \left( {\bar x,\bar y,\bar z} \right)/L,\;(u,v,w) = \left( {\bar u,\bar v,\bar w} \right)/{U_\infty } \hfill \\ \end{gathered} $ |
本文研究基于Shakhov模型方程,二维情形下,无量纲化以后可以写为[16]
| $f_t + uf_x + vf_y = \dfrac{f^ + - f}{\tau }$ | (1) |
该方程修正了标准形式的BGK方程得不到正确普朗特数的缺陷. 其中$f$为粒子热运动分布函数,它是空间坐标$x,y$,时间$t$,粒子速度$u,v$以及内自由度$\xi $的函数,碰撞时间$\tau $与黏性和热传导系数有关. $f^ + $可以表示为 $f^+ = g_M + g^ + $,$g_M$是麦克斯韦平衡态分布函数
| ${g_M} = \rho {\left( {\frac{\lambda }{\pi }} \right)^{\tfrac{{K + 2}}{2}}}\exp \left( { - \lambda \left( {{{\left( {u - U} \right)}^2} + {{\left( {v - V} \right)}^2} + {\xi ^2}} \right)} \right)$ |
| ${g^ + } = {g_{\text{M}}}(1 - Pr)c \cdot q({c^2}/RT - 5)/(5pRT)$ |
守恒变量($\rho $,$\rho U$,$\rho V$,$E$)与分布函数$f$之间的关系为
| ${\left( {\rho ,\rho U,\rho V,E} \right)^{\text{T}}} = {\text{ }}\int {{\psi ^{\text{T}}}f{\text{d}}} {\text{ }}{\rm E}$ | (2) |
对式(1)在速度空间里进行积分可以得到
| $\begin{gathered} \frac{{\partial Q}}{{\partial t}} + \frac{{\partial F}}{{\partial x}} + \frac{{\partial G}}{{\partial y}} = 0 \hfill \\ F = \int {uf{\psi _\alpha }d{\rm E}} ,\;\;G = \int {uf{\psi _\alpha }d{\rm E}} \hfill \\ \end{gathered} $ | (3) |
| $\int {(f - {f^ + }){\psi _\alpha }d{\rm E}} {\text{ }} = 0,\;\;\alpha = 1,2,3,4$ | (4) |
采用有限体积法,可以得到
| $\begin{gathered} \Delta Q = - {V^{ - 1}}\int {_{{t^n}}^{{t^{n + 1}}}} [{(J \cdot S)_{i + 1/2,j}} - {(J \cdot S)_{i - 1/2,j}} + \hfill \\ \qquad {(J \cdot S)_{i,j + 1/2}} - {(J \cdot S)_{i,j - 1/2}}]{\text{d}}t \hfill \\ J = Fi + Gj \hfill \\ \end{gathered}$ | (5) |
单元界面通量 可以表示为
| $\begin{gathered} \iiint {{u_n}}{f_p}{(1\;\;u\;\;v\;\;\frac{1}{2}({u^2} + {v^2}))^{\text{T}}}dudvd\xi + \hfill \\ \qquad \iiint {{u_n}}{f_p}{(0\;\;0\;\;0\;\;\frac{1}{2}{\xi ^2})^{\text{T}}}du{\text{d}}vd\xi = \hfill \\ \qquad \iint {\hat g}{(1\;\;u\;\;v\;\;\frac{1}{2}({u^2} + {v^2}))^{\text{T}}}{u_n}dudv + \hfill \\ \qquad \frac{1}{2}\iint (0\;\;0\;\;0\;\;\hat h{)^{\text{T}}}{u_n}dudv \hfill \\ \end{gathered}$ |
(1) 壁面边界:本文采用动理学壁面边界,详见文献[17].
(2) 超声速来流边界:守恒变量为自由来流值,分布函数按来流变量取平衡态麦克斯韦分布.
(3) 超声速出流边界:守恒变量、分布函数都由内场外推得到.
(4) 对称边界:关于$x$轴对称的情况,$\rho $采用对称条件,$v$采取反对称条件.
2 相容性条件不满足引起的数值误差前文提及的相容性条件式(4)是我们推导守恒变量所遵循的方程(3)的基础.但是当我们引入离散速度坐标法,将对速度空间具有连续依赖性的分布函数转化为离散速度空间的点函数之后,式(4)便不再严格成立.而是变成以下形式
| $\int {(f - {f^ + }){\psi _\alpha }{\text{d}}{\rm E}} = Err(N - C)$ | (6) |
该积分误差导致了在求解宏观变量控制方程(5)式时引入了一个数值源项$\int_{{t^n}}^{{t^{n + 1}}} {\left[{\frac{1}{\tau }Err(N - C)} \right]} {\text{d}}t$.
定义
| $SS = \frac{1}{{\Delta t}}\int {_{{t^n}}^{{t^{n + 1}}}} \left[{\frac{1}{\tau }Err(N - C)} \right]{\text{ d}}t \approx {\left[{\frac{1}{\tau }Err(N - C)} \right]^{n + 1}}$ | (7) |
根据上文提及的无量纲方式,可以推导得到
| $\tau = \frac{\mu }{{pR{e_\infty }}} \propto \frac{{K{n_\infty }}}{{{M_\infty }}}\frac{\mu }{p}$ | (8) |
可以看出,${S S}$与来流条件及数值积分方法有关.
3 守恒型离散速度坐标法为了从根本上消除数值源项,排除数值误差源项对计算结果的不利影响,借鉴Titarev[19]的做法,在原始形式的UGKS算法中我们引入了守恒型的离散速度坐标法.
根据上面相关的表达式,经过推导,可以得到
| $\begin{gathered} \iiint {\frac{{{f^ + } - f}}{\tau }}\psi _1^{\text{T}}dudvd\xi = \hfill \\ \qquad \frac{1}{\tau }{\left( {0,0,0,0,- 2/3{q_x},- 2/3{q_y}} \right)^{\text{T}}} \hfill \\ \end{gathered}$ | (9) |
| $\begin{gathered} \psi _1^{\text{T}} = (1,u,v,\frac{1}{2}\left( {{u^2} + {v^2} + {\xi ^2}} \right),dfrac12\left( {u - U} \right){c^2},\hfill \\ \qquad \frac{1}{2}\left( {v - V} \right){c^2}{)^{\text{T}}} \hfill \\ {c^2} = {\left( {u - U} \right)^2} + {\left( {v - V} \right)^2} + {\xi ^2} \hfill \\ \end{gathered} $ |
考虑到
| $\iiint f\psi _1^{\text{T}}{\text{ d}}u{\text{d}}v{\text{ d}}\xi = {\left( {\rho ,\rho U,\rho V,{\text{E}},{q_x},{q_y}} \right)^{\text{T}}}$ |
| $\begin{gathered} \Sigma {f^ + }\psi _2^{\text{T}} - {\left( {\rho ,\rho U,\rho V,\rho E,{q_x},{q_y}} \right)^{\text{T}}} = \hfill \\ \qquad {\left( {0,0,0,0,- 2/3{q_x},- 2/3{q_y}} \right)^{\text{T}}} \hfill \\ \end{gathered} $ | (10) |
| $\begin{gathered} \psi _2^{\text{T}} = (1,u,v,\frac{1}{2}\left( {{u^2} + {v^2} + {\xi ^2}} \right),\frac{1}{2}\left( {u - U'} \right){{c'}^2},\hfill \\ \qquad \frac{1}{2}\left( {v - V'} \right){{c'}^2}{)^{\text{T}}} \hfill \\ {{c'}^2} = {\left( {u - U'} \right)^2} + {\left( {v - V'} \right)^2} + {\xi ^2} \hfill \\ \end{gathered} $ |
在以这一组变量表达的离散形式的$f^ + $下,宏观量的守恒性得到满足,第2节中提到的数值源项确保为零.在后面的数值计算中,数值误差源项也确实达到了机器零. 此即为守恒型离散速度坐标法.
4 数值模拟结果与分析数值试验采用圆柱,来流条件为
$M_{\infty }=1.8$,$Kn_{\infty }=0.01$,0.40以及$M_{\infty }=10$,$Kn_{\infty }=0.002$,0.050.
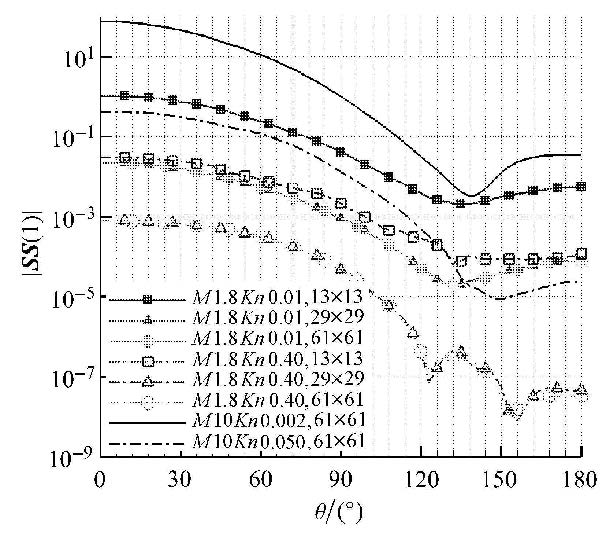
图1给出了采用DOM计算得到的紧挨壁面第一层网格单元$\left| { {SS}(1)} \right|$随速度空间网格的变化.随着速度空间网格的加密,数值源项基本上呈现减小的趋势,但是到一定程度之后,数值源项不再减小,因而,无法仅靠增加速度空间点数来消除该误差. 而采用CDOM之后,数值源项都在10$^{-14}\sim $10$^{-15}$量级(此处未示出).相同的相空间网格下,随着来流马赫数与努森数比值的增加,数值源项增大.
|
图 1 紧挨壁面第一层网格单元|SS(1)| 分布 Fig.1 $\left| {{SS} (1)} \right|$ on the solid surface |
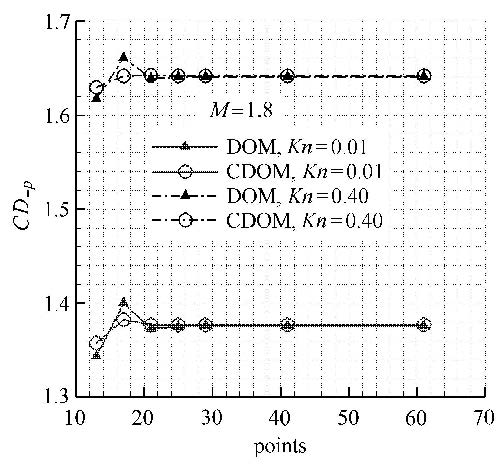
图2给出了$M_{\infty }=1.8$时阻力中压力项贡献随速度空间网格点数的变化,可以看出,速度空间网格点数足够多时,DOM、CDOM会收敛到相同的结果. 采用CDOM之后,阻力对速度空间的网格依赖性要小一些. 对$Kn=0.01$来说,DOM,CDOM分别在29$\times$29和21$\times$21的网格上得到网格收敛解.考虑到采用CDOM之后每一步还需要增加计算量,因而采用CDOM之后计算代价并没有太大的减少(采用DOM计算时间为CDOM的1.5倍).而对$Kn=0.40$来说,采用CDOM之后计算代价降低更不明显.
|
图 2 阻力中压力项贡献随速度空间网格点数的变化 Fig.2 Drag coefficient vs points in u(v) direction |
图3为$M_{\infty }=10$时阻力随速度空间网格点数的变化.可以看出,采用CDOM之后,阻力对速度空间网格的依赖性明显减小.CDOM在61$\times$61的网格上得到的结果就可以认为是速度空间网格收敛解,而采用DOM,只有121$\times$121的网格上才勉强得到与CDOM收敛解相近的结果.

|
图 3 阻力随速度空间网格点数的变化 Fig.3 Drag coefficient vs points in u(v) direction |
表1给出了$M_{\infty}=10$时单步计算相对耗时比较,表中数据以采用CDOM,$Kn=0.002$,速度空间网格61$\times$61的状态进行 无量纲.对于$Kn=0.002$来说,采用CDOM之后,计算量可以从3.14降至1.0.对于$Kn=0.050$来说,采用CDOM之后,计算量可以从3.1降至1.19,都有较大幅度的降低.
| 表 1 单步相对耗时比较 Table 1 Relative cost of one time step |
从超声速和高超声速两个算例可以看出,马赫数比较高、努森数比较低时,采用CDOM能够在较稀的速度空间网格上得到收敛、可信的结果,计算效率最高可提升3.14倍. 这从式(7)和式(8)以及图1中也可以看出,当马赫数比较高、努森数比较低时,数值源项比较大,因而对计算结果的影响较大.
5 结论分析了速度空间离散之后相容性条件不满足而在UGKS中引入的数值误差的表达式,数值验证了该误差与来流条件的相关性. 并与相容性条件严格得到满足的计算结果对比,得到以下结论:
(1)在传统的离散速度坐标法下,相容性条件得不到严格满足,来流马赫数越高,来流努森数越低,数值误差越大,对计算结果影响越大.
(2)采用CDOM之后,相容性条件得到严格满足,尽管单步计算量有所增加,但是能够在较稀的速度空间网格上得到可信的结果. 因而总耗时却能够减少(具体减少多少与来流条件有关),有助于提高计算效率.
| [1] | 费飞, 樊菁. 高雷诺数方腔流动的分子模拟.力学学报, 2013, 45 (5): 653-659 (Fei Fei, Fan Jing. Molecular simulation of driven cavity flows with high Reynolds number. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(5): 653-659 (in Chinese)) |
| [2] | Xu K, Huang JC. A unified gas-kinetic scheme for continuum and rarefied flows. Journal of Computational Physics, 2010, 229(20): 7747-7764 |
| [3] | Huang JC, Xu K, Yu PB. A unified gas-kinetic scheme for continuum and rarefied flows Ⅱ: multi-dimensional cases. Communications in Computational Physics, 2012, 12(3): 662-690 |
| [4] | Chen SZ, Xu K, Lee C, et al.. A unified gas kinetic scheme with moving mesh and velocity space adaptation. Journal of Computational Physics, 2012, 231(20): 6643-6664 |
| [5] | Huang JC, Xu K, Yu PB. A unified gas-kinetic scheme for continuum and rarefied flows Ⅲ: Microflow simulations. Communications in Computational Physics, 2013, 14(5): 1147-1173 |
| [6] | 李启兵, 徐昆. 气体动理学格式研究进展. 力学进展, 2012, 42(5): 522-537(Li Qibing, Xu Kun. Progress in gas kinetic scheme. Advances in Mechanics, 2012, 42(5):522-537 (in Chinese)) |
| [7] | 江定武, 毛枚良, 邓小刚 等. 二维缝隙跨流域流动数值模拟. 见:计算流体力学研究进展, 第十五届全国计算流体力学会议, 山东烟台, 2012 (Jiang Dingwu, Mao Meiliang, Deng Xiaogang, et al. Numerical simulation of the flow through a slit covering various regimes. In: Progress in Computational Fluid Dynamics, The 15th Computational Fluid Dynamics Conference, Yantai, Shangdong, 2012 (in Chinese)) |
| [8] | 李志辉, 张涵信. 稀薄流到连续流的气体运动论统一数值算法初步研究. 空气动力学学报, 2000, 18(3): 255-263 (Li Zhihui, Zhang Hanxin. Study on gas kinetic algorithm for flows from rarefied transition to continuum. Acta Aerodynamica Sinica, 2000, 18(3): 255-263 (in Chinese)) |
| [9] | 李志辉, 张涵信. 稀薄流到连续流的气体运动论统一算法研究. 空气动力学学报, 2003, 21(3): 255-266(Li Zhihui, Zhang Hanxin. Study on gas kinetic unified algorithm for flows from rarefied transition to continuum. Acta Aerodynamica Sinica, 2003, 21(3): 255-266((in Chinese)) |
| [10] | 李志辉, 吴俊林, 蒋新宇 等. 含转动非平衡效应Boltzmann模型方程统一算法与跨流域绕流问题模拟研究. 空气动力学学报, 2014, 32(2): 137-145 (Li Zhihui, Wu Junlin, Jiang Xinyu, et al.. The unified algorithm for various flow regimes solving boltzmann model equation in rotational non-equilibrium. Acta Aerodynamica Sinica, 2014, 32(2): 137-145 (in Chinese)) |
| [11] | 李志辉, 蒋新宇, 吴俊林 等. 转动非平衡玻尔兹曼模型方程统一算法与全流域绕流计算应用. 力学学报, 2014, 46(3): 336-351 (Li Zhihui, Jiang Xinyu, Wu Junlin, et al. Gas-Kinetic unified algorithm for boltzmann model equation in rotational nonequilibrium and its application to the whole range flow regimes. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 336-351 (in Chinese)) |
| [12] | Mieussens L. Discrete velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries. Journal of Computational Physics, 2000, 162(2): 429-466 |
| [13] | Arslanbekov RR, Kolobov VI, Frolova AA, Kinetic solvers with adaptive mesh in phase space. In:Abe T ed. Rarefied Gas Dynamics, Melville: Amer Inst Physics, 2013: 294-301 |
| [14] | Chigullapalli S, Alexeenko A. Unsteady 3D rarefied flow solver based on Boltzmann-ESBGK model kinetic equations. AIAA paper2011-3993, 2011 |
| [15] | Huang JC. A conservative discrete ordinate method for model boltzmann equations. Computers & Fluids, 2011, 45(1): 261-267 |
| [16] | Shakhov EM. Generalization of the krook kinetic equation. Fluid Dynamics, 1968, 3(5): 95-96 |
| [17] | Li QB, Fu S, Xu K. Application of gas kinetic scheme with kinetic boundary conditions in hypersonic flow. AIAA Journal, 2005, 43(10): 2170-2176 |
| [18] | 奚梅成, 刘儒勋. 数值分析方法. 合肥:中国科技大学出版社, 2003 (Xi Meicheng, Liu Ruxun. Numerical Analysis Methods. Hefei:University of Science and Technology of China Press, 2003 (in Chinese)) |
| [19] | Titarev VA. Conservative numerical methods for model kinetic equations. Computers & Fluids, 2007, 36(9): 1446-1459 |
2. National University of Defense Technology, Changsha 410073, China
 2015, Vol. 47
2015, Vol. 47